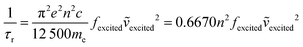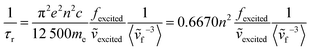Using non-empirically tuned range-separated functionals with simulated emission bands to model fluorescence lifetimes

Abstract

Fluorescence lifetimes were evaluated using TD-DFT under different approximations for the emitting molecule and various exchange–correlation functionals, such as B3LYP, BMK, CAM-B3LYP, LC-BLYP, M06, M06-2X, M11, PBE0, ωB97, ωB97X, LC-BLYP*, and ωB97X* where the range-separation parameters in the last two functionals were tuned in a non-empirical fashion. Changes in the optimised molecular geometries between the ground and electronically excited states were found to affect the quality of the calculated lifetimes significantly, while the inclusion of vibronic features led to further improvements over the assumption of a vertical electronic transition. The LC-BLYP* functional was found to return the most accurate fluorescence lifetimes with unsigned errors that are mostly within 1.5 ns of experimental values.

---

1. Introduction

Fluorescence spectroscopy is widely used in various fields of biological imaging. By using a fluorescence probe to label a sample, it becomes possible to study many important cellular processes of interest, such as apoptosis or cell signalling.^1,2 The non-destructive and relatively non-invasive nature of fluorescence makes it well-suited for imaging in living cells, where the intensity and lifetime of the emission can be monitored. Fluorescence lifetime measurements are generally more robust than intensity-based measurements, since the fluorescence intensity is susceptible to issues such as light scattering and photobleaching.^3,4 One well-known application of fluorescence lifetime imaging microscopy (FLIM) is the use of Förster resonance energy transfer (FRET) to investigate the local conformational changes in a protein.⁵ By measuring how the fluorescence lifetime of the donor molecule in a FRET pair changes in the presence of the acceptor, the distance between the donor and acceptor can be determined. Other applications of fluorescence spectroscopy and microscopy can be found in molecular sensing,^6–8 biomedical imaging,^9,10 and chromatographic detectors.^11–13 Properties that are desirable for a fluorophore include a high molar absorptivity and fluorescence quantum yield, resistance towards photobleaching, good solubility in various solvents, and absorption and emission wavelengths that are suited towards the application of interest. However, fluorophores with an optimal performance in all aspects for a particular application are rarely found. For example, the class of BODIPY dyes satisfies a number of the above criteria: they exhibit high fluorescence quantum yields, are photostable upon irradiation, and have clearly defined absorption and emission peaks.^14–16 However, the BODIPY dyes are generally not very soluble in water, which limits their usage in biological applications. As such, the de novo design of fluorophores with desirable properties or the fine-tuning of existing ones remains an active area of research.

Ab initio calculations are commonly used to study electronic transitions in a molecule and complement experimental efforts in discovering new fluorescent probes. Highly correlated wave function methods, such as CASPT2,^17,18 CC3,¹⁹ ADC(3),²⁰ and EOM-CCSD(T)²¹ have been found to return very accurate excitation energies with respect to experiment,²² but their usage is limited to small or medium-sized molecules. As such, most computational studies of fluorophores have been carried out using time-dependent density functional theory (TD-DFT).

While TD-DFT is a formally exact theory, most applications of TD-DFT are based on the linear response formalism within the adiabatic approximation,²³ which introduces several problems in the modelling of excited states. For example, TD-DFT fails when the excited electronic state has large double excitation character or when the nuclear geometry is far from the Franck–Condon region, e.g., at a conical intersection.^24,25 The use of conventional exchange–correlation (XC) kernels in TD-DFT has also been shown to perform poorly in charge-transfer excitations,^26,27 excitations to triplet states,^28,29 as well as higher excited states such as Rydberg states.^30,31 Nevertheless, TD-DFT has been shown to perform well for low-lying valence excitations,^29–33 which are the excited states of primary interest in our study on the photophysics of fluorophores.

As such, a number of studies have examined various photophysical properties, including the vertical excitation energies,^29–32 absorption and emission maxima,^33–37 0–0 transitions,^37–41 and bandshapes^34,37,42,43 using TD-DFT. Besides these properties, the fluorescence lifetime of a molecule, which is the key quantity in FLIM studies, is also of interest. It is possible to model the fluorescence lifetime of a molecule by using the radiative lifetime calculated using TD-DFT in conjunction with the experimental quantum yield. The oscillator strength of a molecule's electronic transition from an electronically excited state to the ground state, which is related to its radiative lifetime, has been studied using TD-DFT and high level correlated wave function methods. For example, Silva-Junior et al. found mean absolute errors (relative to CASPT2) of 0.128, 0.103, and 0.096 for the oscillator strengths of electronic transitions in 28 molecules calculated using the BP86, B3LYP, and BHLYP functionals in TD-DFT.²⁹ Caricato et al. found that the oscillator strengths of CAM-B3LYP and LC-ωPBE were the best performers with respect to EOM-CCSD values.⁴⁴

In contrast, there has been less work carried out on the calculation of radiative lifetimes using TD-DFT. Previously, Niehaus et al.⁴⁵ used a simplified version of the Strickler–Berg equation that only considers the fluorophore's absorption energies and oscillator strengths. In the Strickler–Berg equation (eqn (1)), the experimental absorption spectrum is used to determine the transition dipole moment (D) (eqn (2)) of the electronic transition in order to calculate the radiative lifetime.⁴⁶

τ_r is the radiative lifetime in s, c is the speed of light in cm s⁻¹, N_A is Avogadro's number, n is the refractive index of the medium, 〈ṽ_f⁻³〉 is the mean value of ṽ_f⁻³ in the emission spectrum of the fluorophore, ṽ_a/f is the wavenumber (in cm⁻¹) of absorption/fluorescence, D is in units of esu² cm², ε(ṽ_a) is the molar extinction coefficient (in M⁻¹ cm⁻¹) of the absorption spectrum, and the integral of is taken over a single electronic absorption band.

The original derivation of the Strickler–Berg equation assumed that the difference between the geometries of the ground and excited electronic states is minimal. The simplified equation that was used also further assumes a “negligible Stokes shift and perfect mirror image relationship of the absorption and fluorescence spectrum”.⁴⁷ The 〈ṽ_f⁻³〉 term that accounts for vibronic and solvent effects is then taken to be an averaged term 〈ṽ〉_Av² corresponding to the 0–0 transition. Finally, by applying the relation between the transition dipole moment and oscillator strength (f) of an electronic transition (eqn (3)), the simplified equation used by Niehaus et al.⁴⁵ can be obtained (eqn (4)).

ṽ is the energy of the electronic transition in cm⁻¹, m_e is the electron mass in kg, e is the electronic charge in C. Savarese et al.⁴⁸ treated the emission process as a vertical transition between the excited and ground electronic state, and uses the excited state optimised geometry in their approach. The 〈ṽ_f⁻³〉 term is assumed to be a constant value corresponding to the energy of the electronic transition, i.e. 〈ṽ_f⁻³〉 ≈ ṽ_f⁻³, which then gives the radiative lifetime as:

However, this approach does not account for transitions between vibronic states. Finally, Banerjee et al.⁴⁹ have extended their work on simulating vibrationally resolved spectra to calculate the radiative rate of azulene, accounting for any differences in geometry between the ground and excited states as well as vibronic effects (eqn (6)). Our recent work studying the photophysics of syn bimane and its derivatives also uses this approach.⁵⁰ In theory, this would be the most rigorous model towards the modelling of fluorescence lifetimes.

Other than the approximations outlined earlier, the quality of the photophysical properties calculated with TD-DFT is also influenced by the choice of XC functionals. It is known that excited states with large charge separation are notoriously problematic for conventional XC functionals.^26,27 To this end, range-separated XC functionals were developed to remedy this shortcoming by partitioning the exchange contribution into a short and long-range component, where the former and latter are dominated by DFT and exact exchange respectively.^51–53 Different schemes for achieving a smooth partitioning exist, such as the use of an error function to split the two-electron operator, where the extent of the short and long-range component can be adjusted in tandem via a single parameter.^54,55 It has been also been demonstrated that this range-separation parameter is system-dependent^{51–53,56–58} and may be adjusted in a non-empirical fashion to satisfy specific properties inherent to the chemical system along with concomitant improvement in calculated quantities such as vertical excitation energies and band gaps.^{39,42,59–66} Since our approach towards the calculation of fluorescence lifetimes depends on the evaluation of fundamental photophysical properties such as the absorption and emission energies, we expect that this approach will be helpful in obtaining accurate lifetimes, as we will show in the Results section of our work.

The present study is centred on two aspects. First, we evaluate the bearing of molecular geometry and vibronic features of the emitting molecule on calculated fluorescence lifetimes. Next, different XC functionals are evaluated with particular emphasis on functionals with non-empirically tuned range-separation parameters. The process used to tune the range-separation parameter will be elaborated upon in the following section. Section 3 provides computational details while the results are given and discussed in Section 4. The final section provides concluding remarks.

2. Methodology

2.1. Calculation of fluorescence lifetimes at three different levels of approximations

We compare three different schemes towards the modelling of fluorescence lifetimes in this work. In Scheme A, the emission process is treated as a vertical transition between the excited and ground electronic states. Nuclear relaxation effects between the two electronic states are assumed to be small and fluorescence is assumed to occur at the ground state optimised geometry. In Scheme B, emission takes place after the nuclei has fully adjusted to the electron density in the excited state; that is, at the optimized geometry in the excited electronic state. Finally, Scheme C models the emission process as vibronic transitions from the minimum of the excited state potential energy surface. After calculating the radiative lifetime, fluorescence lifetimes of various classes of fluorophores are then calculated by incorporating experimental quantum yields viaeqn (7):

τ_f = ϕ_fτ_r (7)

τ_f is the fluorescence lifetime and ϕ_f is the fluorescence quantum yield. All experimental values are taken from the literature, and are tabulated in the ESI† (Table S1). The differences between the three methods studied in this work are summarised in Table 1.

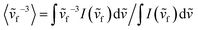Table 1 Summary of the different approaches used to calculate fluorescence lifetimes in this work. τ_r, n, e, m_e, and c have been defined earlier. The subscript ground/excited refers to the electronic state in which the molecular geometry is optimised. 〈ṽ_f⁻³〉 is calculated as , where I(ṽ_f) refers to the intensity of the fluorescence spectra at ṽ_f

Scheme	Final eq.
A
B
C

---

2.2. IP-tuning of γ in range-separated XC functionals

In a range-separated XC functional, one of the ways in which the Coulomb term may be split into short and long-range components is via the error function (eqn (8))⁵⁴where 0 ≤ α + β ≤ 1 and 0 ≤ α, β ≤ 1. The first term on the RHS of eqn (8) gives the short-range component, which is treated with DFT exchange. The second term gives the long-range component, which is handled using Hartree–Fock (HF) exchange. The range-separation parameter γ determines the partitioning of regions between the short and long-range regions. α controls the amount of HF exchange throughout, with the fraction of HF exchange given by α in the short-range region, and increases towards α + β in the long-range region. If a functional obeys α + β = 1, it is fully corrected for long-range HF exchange. For example, α and β are set to 0 and 1, respectively, in the long-range corrected (LC) scheme by Iikura et al.,⁵⁴ while the CAM-B3LYP functional developed by Yanai et al.⁶⁷ uses values of α = 0.19 and β = 0.46. The free parameters used in these range-separated functionals are typically tuned to minimise errors in various molecular properties. As an example, the α, β, and γ parameters of the CAM-B3LYP functional were obtained by fitting calculated atomisation energies and ionisation potentials of molecules in a test set to their experimental values.⁶⁷ Other than the error function, the Yukawa potential, exp(−γr)/r, has also been used as a switching function to achieve range separation.^69,70

However, the value of the range-separation parameter γ has been found to vary among different systems, and has been customised for studying various molecular properties of interest.^{51–53,56–58,65,66} Baer and co-workers have suggested that γ should be tuned for each molecular system to ensure that it satisfies a chosen physical criteria.^61–63 One such criteria is the ionisation potential (IP). In IP-tuning, the value of γ is adjusted such that the negative eigenvalue of the highest occupied molecular orbital (HOMO) for the N and N + 1 electron systems matches the IP of the respective systems simultaneously. It has been shown that such an approach improves the prediction of orbital energies, fundamental and optical gaps, which are expected to be important in computational spectroscopy.^63,66 An error function (J²) that sums up the absolute difference between the HOMO energies and IPs for both systems is then used to determine the value of γ (eqn (9)).⁶³

J²(γ) = [ε_HOMO(N) + IP(N)]² + [ε_HOMO(N + 1) + IP(N + 1)]² (9)

The first term on the RHS accounts for the energy difference between the negative eigenvalue of the HOMO and IP of the neutral N electron system while the second term pertains to the anionic N + 1 electron system. The IP of an N electron system is defined as the difference in the ground state energies between the N electron and the N − 1 electron systems.

IP(N) = E(N − 1) − E(N) (10)

Autschbach and co-workers have shown that this tuning process may not find a minimum value of γ if the functional is not fully corrected for long-range HF exchange, i.e. α + β < 1.^68,69 In addition, they developed a method for obtaining optimal values for α and γ, which then allows the value of β to be calculated, provided that α + β = 1.^68,70 It is thus possible to increase the dimensionality of the tuning process to include both α and β as well, but we eschew this in our work. While range-separation tuning can be performed within a continuum solvation model,^71,72 de Queiroz and Kümmel found “unrealistically small” values of γ that were attributed to inconsistencies in calculation of IPs that were vertical with respective to the solute but non-vertical with respect to the solvent. The tuning of γ in this work was carried out in the gas phase.

J ²(γ) was evaluated at regular intervals of 0.01 Bohr⁻¹ within the domain of 0.1 ≤ γ ≤ 0.35 (Fig. 1). The value of γ that minimizes J²(γ) was then found by fitting a fourth-degree polynomial to data points. The values of α and β were kept unchanged throughout.

Fig. 1 Plot of the error function J² against γ for the tuning of the LC-BLYP and ωB97X functionals for I (see Fig. 2 below). The 6-31+G(d) basis set was used, and the tuning process was carried out in the gas phase.

3. Computational details

We categorised all molecules investigated (Fig. 2) in this work into five different classes of fluorophores: fused aromatic rings (I to V), acridones (VI to VIII), conjugated aromatic rings (IX to XII) bimanes (XIII to XVIII), and coumarins (XIX to XXIV). Single point calculations were carried out for the neutral, anionic, and cationic forms of each molecule in the gas phase with the LC-BLYP⁵⁴ and ωB97X⁷³ functionals to obtain the IP-tuned range-separation parameter for each functional. The resulting functionals are denoted by LC-BLYP* and ωB97X*, respectively. Optimized range-separation parameters for each molecule and functional used are given in the ESI† (Table S4).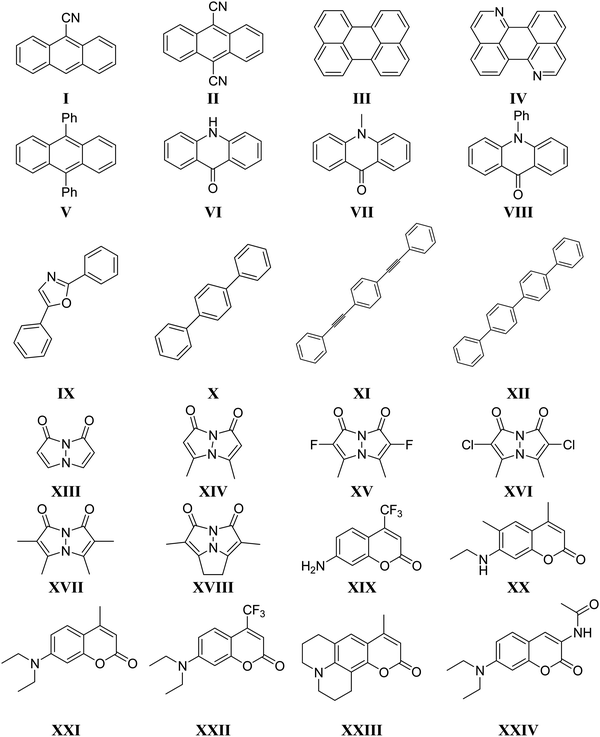

Fig. 2 Chemical structures of all molecules investigated in this work. Ph refers to the phenyl side group.

To characterize the excited electronic states of the fluorophores and assess the performance of TD-DFT relative to wave function methods for computing vertical excitation energies, we construct a subset of the 24 molecules by selecting a molecule from each of the five classes of fluorophores (I, VI, IX, XIII, XIX). The molecules in the subset were studied with various correlated wave function methods such as (i) configuration interaction singles with perturbative doubles [CIS(D)],⁷⁴ (ii) second order approximate coupled cluster method (CC2),⁷⁵ (iii) equation-of-motion coupled-cluster method with singles and doubles substitutions (EOM-CCSD),^76–79 (iv) completely renormalized EOM-CCSD with perturbative triples [CR-EOM-CCSD(T)] method,⁸⁰ and TD-DFT using various XC functionals (v) B3LYP,^81,82 (vi) BMK,⁸³ (vii) CAM-B3LYP,⁶⁷ (viii) LC-BLYP,⁵⁴ (ix) M06,⁸⁴ (x) M06-2X,⁸⁴ (xi) M11,⁸⁵ (xii) PBE0,^86,87 (xiii) ωB97,⁷³ (xiv) ωB97X,⁷³ (xv) LC-BLYP*, (xvi) ωB97X* within the adiabatic approximation framework.²³ The gas phase ground state geometries for all molecules in this part of the study were optimised at the B3LYP/6-31+G(d) level of theory.

For the calculation of fluorescence lifetimes, solvent effects were included using the polarisable continuum model (PCM).⁸⁸ The ground and excited state geometries for all molecules were optimised with the abovementioned XC functionals. Vibrational frequency calculations were carried out to ensure that the optimised molecular geometries correspond to minima on the potential energy surface. The electronic transition energies were calculated using the state-specific method in the non-equilibrium limit.^89,90 For the choice of basis set, we follow the protocol suggested by Jacquemin and co-workers in their work on simulating vibronic bands.^41,42 The smaller 6-31+G(d) basis set^91–94 was used for geometry optimisations and frequency calculations while TD-DFT vertical excitation energies and oscillator strengths were calculated using the larger aug-cc-pVDZ basis set.^95–97 The aug-cc-pVDZ results were found to be very similar to those calculated using the aug-cc-pVTZ basis set,^95–97 hence the choice of the aug-cc-pVDZ basis set for calculating the state-specific vertical transition energies and oscillator strengths (see Tables S5–S9 in the ESI†).

The simulated vibrationally resolved emission spectra were obtained within the harmonic Franck–Condon approximation using the ground and excited state frequencies. The adiabatic Hessian approach implemented in Gaussian09 D.01 was used.⁹⁸ To ensure the convergence of the simulated vibronic spectra, the maximum number of single and two-state overtones were increased up to 100, and the maximum number of integrals of each class was increased up to 10¹², if necessary.^42,43 The state-specific vertical transition energy for emission was set as the transition energy used in obtaining the simulated vibronic spectra for emission. The simulated vibronic spectra were convoluted using Gaussian functions to model solvent broadening. The effect of the half width at half-maximum (HWHM) of the convoluting Gaussian functions on the calculated fluorescence lifetimes was found to be minimal, hence the default value of 135 cm⁻¹ was set as the HWHM throughout (Table S12 in the ESI†).

CC2 calculations were carried out with Dalton 2016.^99,100 EOM-CCSD and CR-EOM-CCSD(T) calculations were carried out with NWChem6.5.¹⁰¹ All TD-DFT calculations, CIS(D) calculations, as well as the simulation of vibrationally resolved spectra within the harmonic approximation, have been carried out with Gaussian09 D.01.⁹⁸

4. Results and discussion

4.1. Vertical excitation energies

Table 2 summarises the vertical excitation energies of the lowest optically bright singlet state for the molecules in the subset calculated with correlated wave function methods and TD-DFT with various functionals. The lowest excited state for all molecules predicted by the correlated wave function methods were found to be characterized by π → π* transitions. Natural transition orbitals from DFT calculations are shown in Fig. 3. We also found that vertical excitation energies calculated using the 6-31+G(d) basis set were within 0.05 eV of those calculated using the larger 6-311+G(d) basis set for all wave function methods (Table S10 of the ESI†). Previous benchmark studies show that EOM-CCSD excitation energies for valence excited states in organic chromophores are generally higher than CC2 and CR-EOM-CCSD(T) values^22,102–105 Our results are in broad agreement with these findings. The CIS(D) results follow a similar trend, with their excitation energies consistently higher (0.1–0.3 eV) than CR-EOM-CCSD(T) values.

Table 2 The lowest dipole-allowed electronic transition for the molecules in our test subset calculated with various correlated wave function methods and TD-DFT using different frequency-independent XC kernels in the gas phase. All vertical excitation energies are in eV. Oscillator strengths for the electronic transitions are given in parentheses where available. The 6-31+G(d) basis set was used for all calculations

	I	VI	IX	XIII	XIX
CIS(D)	3.83	3.79	4.66	3.84	4.18
CC2	3.59 (0.1384)	3.76 (0.1217)	4.46 (0.9718)	3.83 (0.3205)	3.96 (0.4312)
EOM-CCSD	3.90 (0.1682)	3.97 (0.1304)	4.67 (0.9082)	4.02 (0.3237)	4.20 (0.4091)
CR-EOM-CCSD(T)	3.60	3.69	4.37	3.74	3.93
B3LYP	3.03 (0.0963)	3.55 (0.0786)	3.77 (0.8382)	3.81 (0.1986)	3.66 (0.3209)
BMK	3.31 (0.1239)	3.89 (0.1062)	4.11 (0.9043)	4.01 (0.2318)	3.98 (0.3961)
CAM-B3LYP	3.35 (0.1376)	3.95 (0.1152)	4.13 (0.8694)	4.01 (0.2355)	4.00 (0.3963)
LC-BLYP	3.64 (0.1781)	4.30 (0.1483)	4.44 (0.8512)	4.23 (0.2744)	4.28 (0.4417)
M06	3.02 (0.1027)	3.64 (0.0830)	3.76 (0.8047)	3.84 (0.1985)	3.72 (0.3367)
M06-2X	3.38 (0.1314)	3.94 (0.1148)	4.17 (0.8863)	4.00 (0.2371)	4.02 (0.4067)
M11	3.54 (0.1598)	4.10 (0.1333)	4.36 (0.8801)	4.02 (0.2476)	4.15 (0.4245)
PBE0	3.11 (0.1033)	3.66 (0.0856)	3.88 (0.8604)	3.88 (0.2082)	3.76 (0.3440)
ωB97	3.59 (0.1702)	4.23 (0.1396)	4.40 (0.8630)	4.17 (0.2646)	4.24 (0.4260)
ωB97X	3.51 (0.1615)	4.14 (0.1326)	4.32 (0.8745)	4.11 (0.2540)	4.17 (0.4169)
LC-BLYP*	3.27 (0.1281)	3.79 (0.1059)	4.04 (0.8598)	3.93 (0.2327)	3.91 (0.3656)
ωB97X*	3.31 (0.1335)	3.90 (0.1107)	4.10 (0.8805)	4.02 (0.2390)	4.00 (0.3862)

---

Fig. 3 Natural transition orbitals (NTOs) for the lowest optically allowed electronic transition for the molecules in the test subset, as calculated using LC-BLYP*/6-31+G(d) in the gas phase.

Our discussion on the TD-DFT results will be centred on a comparison between functionals with similar characteristics (Table 3). The mean unsigned error (MUE) for each group of XC functionals was calculated by taking the mean of the absolute difference between the TD-DFT and CR-EOM-CCSD(T) values for all five molecules in the test subset and for all the XC functionals in their respective groups. Compared to CR-EOM-CCSD(T) vertical excitation energies, non-range-separated XC functionals with >30% HF exchange (BMK, M06-2X) returned the lowest MUE of 0.211 eV, followed by the range-separated functionals (CAM-B3LYP, LC-BLYP, M11, ωB97, ωB97X) with a MUE of 0.247 eV and lastly XC functionals with <30% HF exchange (B3LYP, PBE0, M06) yielded the highest MUE of 0.299 eV.

Table 3 Mean unsigned error (MUE) for the gas phase TD-DFT vertical excitation energies of the molecules in the test subset with CR-EOM-CCSD(T) values as the reference. The MUE is given in eV. The XC functionals are sorted into three different groups: <30% HF exchange, >30% HF exchange, and range-separated. The MUE for the functionals with IP-tuned γ and the same group of functionals without IP-tuning (Default γ) is also given

XC functionals	MUE
<30% HF exchange (B3LYP, M06, PBE0)	0.299
>30% HF exchange (BMK, M06-2X)	0.211
Range-separated (CAM-B3LYP, LC-BLYP, M11, ωB97, ωB97X)	0.247
IP-tuned γ (LC-BLYP*, ωB97X*)	0.211
Default γ (LC-BLYP, ωB97X)	0.288

---

We then consider the effect of tuning the range-separation parameter, γ. The IP-tuned range-separation parameter was found to be lower than the default value for LC-BLYP (0.4700 Bohr⁻¹) and ωB97X (0.3000 Bohr⁻¹) in Gaussian09 (Table 4). This results in a decrease in the calculated excitation energies and oscillator strengths, which in turn leads to a significant improvement in the MUE for the two selected functionals (LC-BLYP, ωB97X) from 0.288 eV using their default γ value to 0.211 eV after IP-tuning, which is comparable to the result for the XC functionals with >30% HF exchange.

Table 4 Values of the IP-tuned range-separation parameter for the molecules in the test subset. The default values are: LC-BLYP: 0.4700; ωB97X: 0.3000

	LC-BLYP*	ωB97X*
I	0.2216	0.1900
VI	0.2333	0.1974
IX	0.2143	0.1833
XIII	0.2829	0.2398
XIX	0.2468	0.2106

---

To sum up the results for this section, we found that the XC functionals with >30% HF exchange and IP-tuned functionals returned the lowest MUEs for the five molecules in the test subset. IP-tuning of range-separated functionals leads to a significant improvement in the accuracy of calculated vertical excitation energies relative to their non-IP-tuned versions.

4.2. Comparison between different methods of modelling fluorescence lifetimes

The results of using the three different schemes for calculating fluorescence lifetimes are summarised in Table 5 and Fig. 4. Table 5 gives the overall mean percentage errors (MPEs) between experimental and calculated values for each of the different schemes and fluorophore classes, as determined by averaging over the results from all XC functional sans IP-tuned ones, while Fig. 4 provides a breakdown of the MPE for each XC functional across the different schemes and fluorophore classes. On the whole, the accuracy of the calculated fluorescence lifetimes improves when more refined approximations are adopted. Scheme C yields the most accurate fluorescence lifetimes, followed by Scheme B and then A. The only exception to this trend pertains to the acridones. The mean errors for Schemes A and B were found to be similar (Scheme A: 32.3%, Scheme B: 33.4%), while the mean error for Scheme C was slightly higher (Scheme C: 40.4%).

Table 5 Mean percentage errors (MPEs) between experimental and calculated values across the different schemes and the fluorophore classes. The results are obtained in solvent within PCM. The values in the parentheses are the calculated MPEs without B3LYP, M06, and PBE0 (see main text for details)

	A	B	C
Fused aromatic rings	39.8 (50.6)	28.2 (29.8)	26.4 (20.4)
Acridones	32.3 (36.3)	33.4 (25.0)	40.4 (22.7)
Conjugated aromatic rings	50.6 (56.5)	31.9 (36.7)	17.7 (18.5)
Bimanes	58.8 (64.7)	33.3 (40.3)	28.5 (28.5)
Coumarins	50.1 (59.4)	42.1 (47.9)	35.7 (29.6)
All molecules	48.0 (55.5)	34.2 (37.5)	29.6 (24.7)

---

Fig. 4 Mean percentage errors (MPEs) between experimental and calculated fluorescence lifetimes for the various XC functionals using Schemes A, B, and C for each fluorophore class in solvent: (a) fused aromatic rings (b) acridones (c) conjugated aromatic rings (d) bimanes (e) coumarins (f) all molecules. The B3LYP/Scheme C data point for the acridones lies at 102.5%, and is not shown in (b). The dashed lines refer to the overall MPE for each scheme calculated using all XC functionals sans B3LYP, M06, and PBE0 (see main text).

The anomaly can be traced to a number of outlier data points where fluorescence lifetimes calculated with the B3LYP, M06, and PBE0 functionals for Scheme C are extremely poor. A similar occurrence is found for the fused aromatic rings, but the overall effect is much more subdued. Autschbach and co-workers found that the underperformance is related to poor treatment of differential electron correlation between the ground and excited states within TD-DFT.^104,105 When the results for B3LYP, M06 and PBE0 are excluded from the calculation of MPEs, the overall trend for the acridones then matches the other fluorophore classes in showing an improvement in the calculated fluorescence lifetimes going from Schemes A to B and C (Scheme A: 36.3%, Scheme B: 25.0%, Scheme C: 22.7%). For consistency, the MPEs calculated without including B3LYP, M06, and PBE0 results will be used in the discussion henceforth.

The difference in the accuracy of computed fluorescence lifetimes between Schemes A and B comes from the molecular geometry used for the emitting species in the excited electronic state. Scheme A uses molecular equilibrium geometries in the ground electronic state, while the molecular geometries are optimised in the excited electronic state in Scheme B. The calculated MPE for fluorescence lifetimes of all molecules was found to be significantly higher for Scheme A (55.5%) than Scheme B (37.5%), which indicates the sensitivity of the calculated fluorescence lifetimes towards the choice of molecular geometry. We find this to be true even in instances where nuclear relaxation effects are small, which can be correlated to small Stokes shifts. Amongst the five classes of molecules examined, the fused aromatic rings and acridones have an average Stokes shift of about 0.1 eV, while the conjugated aromatic rings, bimanes, and coumarins exhibit a larger average Stokes shift of more than 0.5 eV (Table 6). All five fluorophores classes show an improvement ranging from 10–20% in the calculated lifetimes going from Scheme A to B. Therefore, our results clearly show that using molecular geometries that are fully relaxed in the emitting electronic state generally return calculated fluorescence lifetimes that are superior.

Table 6 Average experimental Stokes shift (in eV) for each class of molecules in solvent (see Table S2 in ESI)

	Average Stokes shift
Fused aromatic rings	0.11
Acridones	0.13
Conjugated aromatic rings	0.65
Bimanes	0.57
Coumarins	0.54

---

We now compare the results obtained using Schemes B and C to study the effect of vibronic features/band shape in the model by the use of a simulated vibrationally resolved emission spectra (see for example, Fig. 5). The quality of the calculated lifetimes was found to improve further going from Scheme B to Scheme C, although the extent of improvement is smaller than that offered by Scheme B over A. It is noteworthy that Scheme C delivers a consistent performance across different fluorophore classes such that the MPE ranges from 18.5% (conjugated aromatic rings) to 29.6% (coumarins), while the lowest and highest MPEs for Scheme B are 25.0% (acridones) and 47.9% (coumarins), respectively. Thus, Scheme B may perform quite poorly for certain classes of fluorophores, while the results for Scheme C shows that it returns better fluorescence lifetimes consistently for all five classes of fluorophores.

Fig. 5 Simulated vibrationally resolved emission spectra for I in cyclohexane using the PBE0, M06-2X, and LC-BLYP* functionals.

In summary, the overall quality of calculated fluorescence lifetimes was found to improve in tandem with the level of sophistication within the model. Scheme C yields the most accurate fluorescence lifetimes, followed by Schemes B and then A. There is a significant improvement in the lifetimes calculated using Scheme B over Scheme A, which suggests the importance of the molecular geometry in the modelling of fluorescence lifetimes. There is also a further improvement in the calculated fluorescence lifetimes going from Scheme B to Scheme C. Scheme C was found to yield accurate fluorescence lifetimes consistently for every class of fluorophore, and is our recommended approach towards modelling fluorescence lifetimes.

Finally, we note as a caveat that the majority of our discussion in this section pertains to the MPEs calculated without including the B3LYP, M06, and PBE0 results. As our results have shown, the use of these functionals together with Scheme C may lead to severe errors in the computed fluorescence lifetimes in some classes of fluorophores. The next section then examines the effect of the choice of XC functional as well as the results of using an IP-tuned functional on the calculated fluorescence lifetimes.

4.3. Calculation of fluorescence lifetimes with different XC functionals

In this section, we evaluate the performance of various XC functionals at modelling fluorescence lifetimes using Scheme C, which has been shown to be the most accurate approach on the whole. The results are summarised in Table 7. It is clear that the best results are obtained with IP-tuned range-separated functionals. LC-BLYP* and ωB97X* functionals were found to be the best performing functionals for all molecules, with MPEs of 16.2% and 16.5% respectively. Among the non-IP-tuned XC functionals, BMK has the best result with a MPE of 18.1%, followed by CAM-B3LYP (MPE: 19.6%), and M06-2X (MPE: 20.2%). The benefits of carrying out IP-tuning for range-separated functionals are especially evident when we consider that the LC-BLYP functional ranks among the poorest performers with a MPE of 36.2%. After IP-tuning, the substantial improvement in LC-BLYP* calculated lifetimes is such that it becomes the top performer among all XC functionals tested.

Table 7 MPEs between experimental and fluorescence lifetimes computed with various XC functionals for the different classes of fluorophores in solvent. All fluorescence lifetimes in this section were calculated using Scheme C

	B3LYP	BMK	CAM-B3LYP	LC-BLYP	M06	M06-2X	M11	PBE0	ωB97	ωB97X	LC-BLYP*	ωB97X*
Fused aromatics rings	48.4	18.3	16.0	34.0	42.3	19.0	12.5	31.0	26.9	22.6	11.3	6.8
Acridones	102.5	24.2	14.5	36.4	74.1	17.0	18.4	68.7	27.5	21.0	24.4	14.4
Conjugated aromatic rings	16.9	16.1	16.3	19.1	15.3	17.2	21.6	15.6	19.9	19.1	16.4	17.8
Bimanes	38.5	15.2	20.9	46.6	25.1	19.7	27.2	21.9	39.4	30.7	17.1	16.4
Coumarins	83.6	19.3	26.1	38.8	23.7	25.3	31.8	42.7	33.7	32.3	14.9	21.8
All molecules	56.2	18.1	19.6	36.2	32.8	20.2	23.3	33.8	29.8	25.7	16.2	16.5

---

Next, we consider the absolute error in the calculated fluorescence lifetimes for the three best performing functionals: LC-BLYP*, ωB97X*, and BMK. The experimental and calculated fluorescence lifetimes for the molecules within the test subset given in Section 4.1 are shown in Table 8. For all molecules in the test set, the lifetimes calculated using the two IP-tuned functionals returned results that are within 1.5 ns of experimental values. A check of the results for all molecules (Table S19 in ESI†) revealed that the fluorescence lifetimes calculated using the LC-BLYP* functional falls within 1.5 ns of experimental values for twenty out of twenty four molecules, which further underlines the superiority of the IP-tuned functionals. It is also worth noting that the computed order of the fluorescence lifetimes matches experiment exactly (IX < XIX < XIII < VI < I). Our findings thus suggest that TD-DFT is a useful tool for in silico modelling of new fluorescent scaffolds.

Table 8 Experimental and computed fluorescence lifetimes (in ns) of the molecules in the test set. The experimental data is taken from the literature (see Table S1 in the ESI). All results are in solvent

	Experiment	BMK	LC-BLYP*	ωB97X*
I	12.7	14.2	13.9	13.0
VI	10.5	11.9	11.6	10.9
IX	1.4	1.3	1.5	1.5
XIII	7.4	6.7	6.5	5.9
XIX	5.2	5.3	5.8	5.7

---

In summary, we have studied the performance of various functionals towards the modelling of fluorescence lifetimes for five different classes of fluorophores. The IP-tuned LC-BLYP* and ωB97X* were found to be the best performing functionals for this purpose. We note that there are other classes of fluorophores that were not included in this study, such as BODIPYs and cyanines. A large number of studies have shown that TD-DFT is unable to treat the excited states of BODIPYs accurately,^106–108 while the conclusion for cyanines appears to be mixed.^109–111 Since our goal lies in the assessment of various approaches towards modelling fluorescence lifetimes, it is essential that the underlying computational tool of choice, TD-DFT, is capable of describing the excited states of the fluorophores reliably. Also, we only consider the radiative rate in this study. Other non-radiative de-excitation processes, such as intersystem crossing, internal conversion, solvent quenching, or energy transfer mechanisms should be included for a more complete modelling of fluorescence lifetimes. Thus, possible future work would be to account for these other de-excitation processes computationally as well, such that the actual fluorescence lifetime of a molecule may be better predicted using ab initio calculations.

5. Conclusion

Three different approaches for modelling the fluorescence lifetimes of five different classes of molecules (fused aromatic rings, acridones, conjugated aromatic rings, bimanes, and coumarins) with TD-DFT were examined in this work. The large improvement in the calculated lifetimes going from Scheme A (MPE 55.5%) to Scheme B (MPE 37.5%) suggests that the molecular geometry of the emitting molecule has a significant influence on the computed fluorescence lifetimes, such that it is worthwhile to obtain the optimized geometry of the molecule in the excited electronic state to obtain more accurate fluorescence lifetimes. The best agreement with experimental values was obtained when vibronic features were incorporated (Scheme C). More importantly, the quality of fluorescence lifetimes calculated using Scheme C (MPE 24.7%) was the most consistent for all five classes of fluorophores studied. Within Scheme C, the IP-tuned range-separated functionals LC-BLYP* and ωB97X* were found to yield the most accurate results (MPEs of 16.2% and 16.5% respectively). The significant improvement in the performance of the IP-tuned functionals further implies that the value of the range-separation parameter should be separately customized for each molecule. The fluorescence lifetimes calculated using the LC-BLYP* functional were found to lie within 1.5 ns of experiment for most of the tested molecules. This suggests that the use of TD-DFT in modelling various optical properties such as the absorption and emission of a fluorophore can be extended to modelling of fluorescence lifetimes.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

ZCW, WYF, TSC, and MBS gratefully acknowledge A*STAR (Agency for Science, Technology and Research) for financial support of this work and A*STAR Computational Resource Centre (A*CRC) and the NUS (National University of Singapore) High Performance Computing services at NUS Computer Centre for generous computer access.

References

1. M. Ben-Johny, D. N. Yue and D. T. Yue, Nat. Commun., 2016, 7, 13709.
2. K. Segawa, S. Kurata, Y. Yanagihashi, T. R. Brummelkamp, F. Matsuda and S. Nagata, Science, 2014, 344, 1164–1168.
3. K. Suhling, L. M. Hirvonen, J. A. Levitt, P.-H. Chung, C. Tregidgo, A. Le Marois, D. A. Rusakov, K. Zheng, S. Ameer-Beg, S. Poland, S. Coelho, R. Henderson and N. Krstajic, Med. Photonics, 2015, 27, 3–40.
4. W. Becker, J. Microsc., 2012, 247, 119–136.
5. V. Raicu and D. R. Singh, Biophys. J., 2013, 105, 1937–1945.
6. M. Strobl, A. Walcher, T. Mayr, I. Klimant and S. M. Borisov, Anal. Chem., 2017, 89, 2859–2865.
7. X. Zhou, S. Lee, Z. Xu and J. Yoon, Chem. Rev., 2015, 115, 7944–8000.
8. W. Xu, J. Bai, J. Peng, A. Samanta, A. Divyanshu and Y. T. Chang, Chem. Commun., 2014, 50, 10398–10401.
9. G. Hong, A. L. Antaris and H. Dai, Nat. Biomed. Eng., 2017, 1, 0010.
10. R. R. Zhang, A. B. Schroeder, J. J. Grudzinski, E. L. Rosenthal, J. M. Warram, A. N. Pinchuk, K. W. Eliceiri, J. S. Kuo and J. P. Weichert, Nat. Rev. Clin. Oncol., 2017, 14, 347–364.
11. M. Russ, S. Hauser, R. Wintersteiger, J. Greilberger, M. Andra and A. Ortner, J. Fluoresc., 2016, 26, 81–86.
12. M. Wada, M. Hirose, M. Kuroki, R. Ikeda, Y. Sekitani, N. Takamura, N. Kuroda and K. Nakashima, Biomed. Chromatogr., 2013, 27, 708–713.
13. M. Swartz, J. Liq. Chromatogr. Relat. Technol., 2010, 33, 1130–1150.
14. T. Kowada, H. Maeda and K. Kikuchi, Chem. Soc. Rev., 2015, 44, 4953–4972.
15. N. Boens, V. Leen and W. Dehaen, Chem. Soc. Rev., 2012, 41, 1130–1172.
16. A. Loudet and K. Burgess, Chem. Rev., 2007, 107, 4891–4932.
17. K. Andersson, P. Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226.
18. K. Andersson, P. A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488.
19. O. Christiansen, H. Koch and P. Jørgensen, J. Chem. Phys., 1995, 103, 7429–7441.
20. P. H. Harbach, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 064113.
21. T. J. Watson, Jr., V. F. Lotrich, P. G. Szalay, A. Perera and R. J. Bartlett, J. Phys. Chem. A, 2013, 117, 2569–2579.
22. M. Schreiber, M. R. Silva-Junior, S. P. Sauer and W. Thiel, J. Chem. Phys., 2008, 128, 134110.
23. M. E. Casida, Time-Dependent Density Functional Response Theory for Molecules, World Scientific, 1995.
24. B. G. Levine, C. Ko, J. Quenneville and T. J. MartÍnez, Mol. Phys., 2006, 104, 1039–1051.
25. N. T. Maitra, F. Zhang, R. J. Cave and K. Burke, J. Chem. Phys., 2004, 120, 5932–5937.
26. A. Dreuw and M. Head-Gordon, J. Am. Chem. Soc., 2004, 126, 4007–4016.
27. A. Dreuw, J. L. Weisman and M. Head-Gordon, J. Chem. Phys., 2003, 119, 2943–2946.
28. D. Jacquemin, E. A. Perpete, I. Ciofini and C. Adamo, J. Chem. Theory Comput., 2010, 6, 1532–1537.
29. M. R. Silva-Junior, M. Schreiber, S. P. Sauer and W. Thiel, J. Chem. Phys., 2008, 129, 104103.
30. M. Isegawa, R. Peverati and D. G. Truhlar, J. Chem. Phys., 2012, 137, 244104.
31. M. J. Peach, P. Benfield, T. Helgaker and D. J. Tozer, J. Chem. Phys., 2008, 128, 044118.
32. D. Jacquemin, V. Wathelet, E. A. Perpete and C. Adamo, J. Chem. Theory Comput., 2009, 5, 2420–2435.
33. D. Jacquemin, E. A. Perpete, G. E. Scuseria, I. Ciofini and C. Adamo, J. Chem. Theory Comput., 2008, 4, 123–135.
34. F. Muniz-Miranda, A. Pedone, G. Battistelli, M. Montalti, J. Bloino and V. Barone, J. Chem. Theory Comput., 2015, 11, 5371–5384.
35. S. Chibani, S. Budzak, M. Medved, B. Mennucci and D. Jacquemin, Phys. Chem. Chem. Phys., 2014, 16, 26024–26029.
36. C. Bernini, L. Zani, M. Calamante, G. Reginato, A. Mordini, M. Taddei, R. Basosi and A. Sinicropi, J. Chem. Theory Comput., 2014, 10, 3925–3933.
37. A. D. Laurent, C. Adamo and D. Jacquemin, Phys. Chem. Chem. Phys., 2014, 16, 14334–14356.
38. D. Jacquemin, I. Duchemin and X. Blase, J. Chem. Theory Comput., 2015, 11, 5340–5359.
39. D. Jacquemin, B. Moore II, A. Planchat, C. Adamo and J. Autschbach, J. Chem. Theory Comput., 2014, 10, 1677–1685.
40. F. J. Avila Ferrer, J. Cerezo, E. Stendardo, R. Improta and F. Santoro, J. Chem. Theory Comput., 2013, 9, 2072–2082.
41. D. Jacquemin, A. Planchat, C. Adamo and B. Mennucci, J. Chem. Theory Comput., 2012, 8, 2359–2372.
42. B. Moore II, A. Charaf-Eddin, A. Planchat, C. Adamo, J. Autschbach and D. Jacquemin, J. Chem. Theory Comput., 2014, 10, 4599–4608.
43. A. Charaf-Eddin, A. Planchat, B. Mennucci, C. Adamo and D. Jacquemin, J. Chem. Theory Comput., 2013, 9, 2749–2760.
44. M. Caricato, G. W. Trucks, M. J. Frisch and K. B. Wiberg, J. Chem. Theory Comput., 2011, 7, 456–466.
45. T. A. Niehaus, T. Hofbeck and H. Yersin, RSC Adv., 2015, 5, 63318–63329.
46. S. J. Strickler and R. A. Berg, J. Chem. Phys., 1962, 37, 814.
47. J. Mohanty and W. M. Nau, Photochem. Photobiol. Sci., 2004, 3, 1026–1031.
48. M. Savarese, A. Aliberti, I. De Santo, E. Battista, F. Causa, P. A. Netti and N. Rega, J. Phys. Chem. A, 2012, 116, 7491–7497.
49. S. Banerjee, A. Baiardi, J. Bloino and V. Barone, J. Chem. Theory Comput., 2016, 12, 774–786.
50. Z. C. Wong, W. Y. Fan, T. S. Chwee and M. B. Sullivan, RSC Adv., 2016, 6, 87237–87245.
51. O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109.
52. O. A. Vydrov, J. Heyd, A. V. Krukau and G. E. Scuseria, J. Chem. Phys., 2006, 125, 074106.
53. Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, J. Chem. Phys., 2004, 120, 8425–8433.
54. H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540–3544.
55. T. Leininger, H. Stoll, H.-J. Werner and A. Savin, Chem. Phys. Lett., 1997, 275, 151–160.
56. M. A. Rohrdanz and J. M. Herbert, J. Chem. Phys., 2008, 129, 034107.
57. J. W. Song, T. Hirosawa, T. Tsuneda and K. Hirao, J. Chem. Phys., 2007, 126, 154105.
58. M. J. Peach, T. Helgaker, P. Salek, T. W. Keal, O. B. Lutnaes, D. J. Tozer and N. C. Handy, Phys. Chem. Chem. Phys., 2006, 8, 558–562.
59. I. T. Lima, S. Prado Ada, J. B. Martins, P. H. de Oliveira Neto, A. M. Ceschin, W. F. da Cunha and D. A. da Silva Filho, J. Phys. Chem. A, 2016, 120, 4944–4950.
60. B. Moore II and J. Autschbach, J. Chem. Theory Comput., 2013, 9, 4991–5003.
61. R. Baer, E. Livshits and U. Salzner, Annu. Rev. Phys. Chem., 2010, 61, 85–109.
62. T. Stein, L. Kronik and R. Baer, J. Chem. Phys., 2009, 131, 244119.
63. L. Kronik, T. Stein, S. Refaely-Abramson and R. Baer, J. Chem. Theory Comput., 2012, 8, 1515–1531.
64. N. Kuritz, T. Stein, R. Baer and L. Kronik, J. Chem. Theory Comput., 2011, 7, 2408–2415.
65. K. Okuno, Y. Shigeta, R. Kishi and M. Nakano, Chem. Phys. Lett., 2013, 585, 201–206.
66. H. Sun and J. Autschbach, J. Chem. Theory Comput., 2014, 10, 1035–1047.
67. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
68. J. Autschbach and M. Srebro, Acc. Chem. Res., 2014, 47, 2592–2602.
69. M. Srebro and J. Autschbach, J. Chem. Theory Comput., 2012, 8, 245–256.
70. M. Srebro and J. Autschbach, J. Phys. Chem. Lett., 2012, 3, 576–581.
71. Z. Zheng, J. L. Bredas and V. Coropceanu, J. Phys. Chem. Lett., 2016, 7, 2616–2621.
72. T. B. de Queiroz and S. Kummel, J. Chem. Phys., 2014, 141, 084303.
73. J. D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106.
74. M. Head-Gordon, R. J. Rico, M. Oumi and T. J. Lee, Chem. Phys. Lett., 1994, 219, 21–29.
75. O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418.
76. M. Kallay and J. Gauss, J. Chem. Phys., 2004, 121, 9257–9269.
77. H. Koch and P. Jørgensen, J. Chem. Phys., 1990, 93, 3333.
78. H. Koch, R. Kobayashi, A. Sanchez de Merás and P. Jørgensen, J. Chem. Phys., 1994, 100, 4393.
79. J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029.
80. K. Kowalski, Chem. Phys. Lett., 2005, 411, 306–310.
81. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
82. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
83. A. D. Boese and J. M. Martin, J. Chem. Phys., 2004, 121, 3405–3416.
84. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2007, 120, 215–241.
85. R. Peverati and D. G. Truhlar, J. Phys. Chem. Lett., 2011, 2, 2810–2817.
86. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158.
87. M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029.
88. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
89. R. Improta, G. Scalmani, M. J. Frisch and V. Barone, J. Chem. Phys., 2007, 127, 074504.
90. R. Improta, V. Barone, G. Scalmani and M. J. Frisch, J. Chem. Phys., 2006, 125, 054103.
91. W. J. Hehre, J. Chem. Phys., 1972, 56, 2257.
92. P. C. Hariharan and J. A. Pople, Theor. Chem. Acc., 1973, 28, 213–222.
93. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665.
94. M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265.
95. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007.
96. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796.
97. D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371.
98. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Rev. D.01, Gaussian Inc., Wallington, CT, 2013.
99. Dalton, a molecular electronic structure program, release Dalton2016.2, 2016, see http://daltonprogram.org.
100. K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekstrom, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernandez, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hattig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenaes, S. Host, I. M. Hoyvik, M. F. Iozzi, B. Jansik, H. J. Jensen, D. Jonsson, P. Jorgensen, J. Kauczor, S. Kirpekar, T. Kjaergaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnaes, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Salek, C. C. Samson, A. S. de Meras, T. Saue, S. P. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thogersen, O. Vahtras, M. A. Watson, D. J. Wilson, M. Ziolkowski and H. Agren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284.
101. M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489.
102. D. Kannar and P. G. Szalay, J. Chem. Theory Comput., 2014, 10, 3757–3765.
103. K. Kowalski, S. Krishnamoorthy, O. Villa, J. R. Hammond and N. Govind, J. Chem. Phys., 2010, 132, 154103.
104. B. Moore II, R. L. Schrader, K. Kowalski and J. Autschbach, ChemistryOpen, 2017, 6, 385–392.
105. B. Moore II, H. Sun, N. Govind, K. Kowalski and J. Autschbach, J. Chem. Theory Comput., 2015, 11, 3305–3320.
106. M. R. Momeni and A. Brown, J. Chem. Theory Comput., 2015, 11, 2619–2632.
107. S. Chibani, A. D. Laurent, B. Le Guennic and D. Jacquemin, J. Chem. Theory Comput., 2014, 10, 4574–4582.
108. S. Chibani, B. Le Guennic, A. Charaf-Eddin, A. D. Laurent and D. Jacquemin, Chem. Sci., 2013, 4, 1950.
109. B. Le Guennic and D. Jacquemin, Acc. Chem. Res., 2015, 48, 530–537.
110. H. Zhekova, M. Krykunov, J. Autschbach and T. Ziegler, J. Chem. Theory Comput., 2014, 10, 3299–3307.
111. D. Jacquemin, Y. Zhao, R. Valero, C. Adamo, I. Ciofini and D. G. Truhlar, J. Chem. Theory Comput., 2012, 8, 1255–1259.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp03418k

---