Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Efficient simulation of ultrafast magnetic resonance experiments
Ludmilla
Guduff
 a,
Ahmed J.
Allami
a,
Ahmed J.
Allami
 b,
Carine
van Heijenoort
b,
Carine
van Heijenoort
 a,
Jean-Nicolas
Dumez
a,
Jean-Nicolas
Dumez
 *a and
Ilya
Kuprov
*a and
Ilya
Kuprov
 *b
*b
aInstitut de Chimie des Substances Naturelles, CNRS UPR2301, Université Paris Sud, Université Paris-Saclay, Avenue de la Terrasse, 91190 Gif-sur-Yvette, France. E-mail: jeannicolas.dumez@cnrs.fr
bSchool of Chemistry, University of Southampton, University Road, Southampton, SO17 1BJ, UK. E-mail: i.kuprov@soton.ac.uk
First published on 6th June 2017
Abstract
Magnetic resonance spectroscopy and imaging experiments in which spatial dynamics (diffusion and flow) closely coexists with chemical and quantum dynamics (spin–spin couplings, exchange, cross-relaxation, etc.) have historically been very hard to simulate – Bloch–Torrey equations do not support complicated spin Hamiltonians, and the Liouville–von Neumann formalism does not support explicit spatial dynamics. In this paper, we formulate and implement a more advanced simulation framework based on the Fokker–Planck equation. The proposed methods can simulate, without significant approximations, any spatio-temporal magnetic resonance experiment, even in situations when spatial motion co-exists intimately with quantum spin dynamics, relaxation and chemical kinetics.
1. Introduction
Spatial coordinates are more convenient in magnetic resonance than temporal ones – unlike the indelible past, any voxel in the![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3 can be accessed repeatedly. The use of spatial coordinates as replacements for temporal ones was the key idea behind the “ultrafast” NMR methods proposed in 2002 by the Frydman group.1 Those methods enabled the study of chemical2 and biological3,4 processes on a time scale that was not previously accessible to multi-dimensional NMR.5 Applied to MRI, the same approach enabled fast localised acquisition of 2D spectra.6 Another useful application of the same idea is the family of “pure-shift” NMR experiments,7 fine-tuned at Manchester University around 20108 – they finally achieved the dream of eliminating homonuclear J-couplings.
3 can be accessed repeatedly. The use of spatial coordinates as replacements for temporal ones was the key idea behind the “ultrafast” NMR methods proposed in 2002 by the Frydman group.1 Those methods enabled the study of chemical2 and biological3,4 processes on a time scale that was not previously accessible to multi-dimensional NMR.5 Applied to MRI, the same approach enabled fast localised acquisition of 2D spectra.6 Another useful application of the same idea is the family of “pure-shift” NMR experiments,7 fine-tuned at Manchester University around 20108 – they finally achieved the dream of eliminating homonuclear J-couplings.
Spatial dimensions do have their problems though – the biggest one is the presence of uncontrolled dynamics (e.g. diffusion and convection) that is coupled to quantum mechanical evolution.9,10 Pulse sequence design must therefore rely on detailed modelling of simultaneous spatial, chemical and quantum dynamics, which would be wonderful if only the required theory and software existed: the usual Liouville–von Neumann equation is not good enough because there is no easy way to combine diffusion and hydrodynamics11 with quantum mechanical spin evolution. The primary nuisance is the J-coupling12,13 – it dephases transverse magnetisation and generates undesirable modulations in echo trains.13,14
Very complicated systems of precisely this kind are emerging in all areas of magnetic resonance: hyperpolarised pyruvate imaging15 requires simultaneous modelling of quantum spin dynamics, diffusion, hydrodynamics, chemical kinetics and spin relaxation theory; the same applies to hyperpolarised singlet state imaging.16 Pure-shift NMR,8 ultrafast NMR,17 metabolite-selective imaging,18 PARASHIFT contrast agents19 and other similar recent developments are all united by their theory and simulation infrastructure requirements that are a level above anything that is currently available.
The methods currently used in MRI (Bloch–Torrey equations,20,21 distributed Bloch equations,22,23k-space Bloch equations,24etc.) are very well developed,25 but insufficient for ultrafast NMR or singlet state MRI because all of those methods are built around Bloch equations for the spin degrees of freedom; this makes accurate treatment of coupled multi-spin systems impossible. Some methods (split propagation,26 random-walk averaging,27etc.) do treat spin dynamics at the density matrix level, but introduce diffusion externally in an approximate way.28
To our knowledge, the only formalism that simultaneously supports diffusion, hydrodynamics, chemical kinetics and Liouville-space spin dynamics in a general and computationally affordable way is the Fokker–Planck equation.29–31 In this paper, we present the corresponding algebraic and numerical framework, and illustrate its performance by simulating (on the MRI side) a singlet state diffusion and flow imaging experiment, and (on the ultrafast NMR side) single-scan diffusion-ordered spectroscopy (DOSY) experiments that rely on spatial encoding of the diffusion dimension.
2. Simulation formalism
The key feature of ultrafast magnetic resonance experiments is the delicate interplay of spin and spatial dynamics. In designing the simulation methods for spatially encoded pulse sequences we will therefore be using the Fokker–Planck formalism29,30 discussed in detail by Kuprov32,33 and recently implemented in Spinach.34 Its fundamental equation of motion is: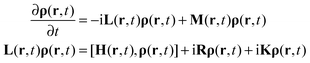 | (1) |
2.1 Fokker–Planck formalism for MRI and spatially encoded NMR
In liquid state spatially encoded NMR spectroscopy and imaging simulations, the laboratory frame spin Hamiltonian in eqn (1) contains the terms describing chemical shifts, pulsed field gradients, radiofrequency pulses and J-couplings:35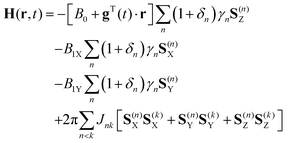 | (2) |
The spatial dynamics generator in eqn (1) has contributions from diffusion and flow:33
| M(r,t) = ∇T·v(r,t) + vT(r,t)·∇ + ∇T·D(r,t)·∇ | (3) |
The use of the flow velocity in eqn (3) eliminates the thorny question of how to combine magnetic resonance simulations (where the equation of motion is linear) with hydrodynamics simulations (where it is not). Because spin degrees of freedom may be very accurately assumed to have no influence on the spatial motion, any hydrodynamics solver may simply be used first to obtain v(r,t) and put into eqn (3). In that way, the equation of motion that we actually need to solve at the spin dynamics simulation stage – eqn (1) – stays linear with respect to the state vector ρ(r,t).
Another advantage of the FP method in the context of spatially encoded NMR and MRI is that RF pulses at any frequency have time-independent generators. The matter is discussed in detail in Kuprov's recent review of the subject;33 here we will only note that the Fokker–Planck RF pulse generator is the derivative with respect to the RF phase, which is simply added to the spatial dynamics operator in eqn (3):
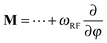 | (4) |
B1X = B1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, B1Y = B1 φ, B1Y = B1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ φ | (5) |
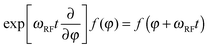 | (6) |
Spin relaxation may be introduced in two different ways. The more general and computationally expensive method is to include the molecular rotation and the internal motion into the spatial dynamics generator M(r,t), and to treat the corresponding spatial coordinates explicitly – this is known as the Stochastic Liouville Equation (SLE) formalism.36,37 A somewhat less general, but also less computationally demanding formulation is to treat the molecular dynamics that drives the relaxation perturbatively, as an external stochastic process that rattles operator coefficients in the spin Hamiltonian – this is called the Bloch–Redfield–Wangsness (BRW) theory.38–40 BRW relaxation superoperator is added algebraically to the spin Hamiltonian commutation superoperator. The use of SLE becomes necessary in EPR systems where the BRW approach breaks down.41 That is not the case here, and we are therefore using BRW relaxation theory in this work – its complete derivation and the technical details of its numerical implementation are published elsewhere.42,43
With all of these in place, eqn (1) has a simple general solution:
| ρ(r,t + dt) = exp{[−iL(r,t) + M(r,t)]dt}ρ(r,t) | (7) |
2.2 Numerical implementation
The choice of the procedure for the generation of spin operators for eqn (2) depends on the size of the spin system. With fewer than ten spins, the standard Pauli matrix product method35 is appropriate| S(k){X,Y,Z} = 1⊗1⊗⋯⊗σ{X,Y,Z}⊗⋯⊗1 | (8) |
The most straightforward practical way of generating matrix representations for spatial derivative operators occurring in eqn (3) and (4) is to discretise the spatial coordinates on finite grids. For periodic boundary conditions, Fourier differentiation matrices on uniform grids50 are convenient:
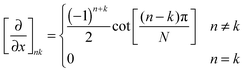 | (9) |
Standard accuracy considerations apply to discrete representations of spatial dynamics operators: the Fourier differentiation method must have a minimum of two points per period of the fastest oscillation (this means gradient spirals in spatial dimensions), and the finite difference method must satisfy the accuracy conditions formulated by Fornberg.51 In practical calculations the number of points is increased from the minimum specified by the Larmor condition until convergence is achieved in the output.
Assuming N, M and K discretisation points in X, Y and Z respectively, the differentiation matrices are multiplied up into the three-dimensional space in the standard way, for example:
![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) X = [∂/∂x]N⊗1M⊗1K X = [∂/∂x]N⊗1M⊗1K | (10) |
The density matrix and the spin Hamiltonian are mapped into the Liouville space in the standard way:35
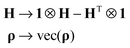 | (11) |
After the spin operators and the space operators are obtained individually, they are projected into the Fokker–Planck space by the final round of direct products, in which it is convenient to place spatial coordinates first. Therefore, the general form of a pure space operator is A⊗1, the general form of a pure spin operator is 1⊗B, and for operators that connect spin and space degrees of freedom (such as pulsed field gradients) we have A⊗B.
The numerical solution process for eqn (7) involves either a sparse matrix exponential (the exponentiation method35) or repeated multiplication of a full vector by a sparse matrix (the Krylov propagation method45). Both operations map well on GPU cards manufactured by Intel and NVidia using standard functionality implemented in Matlab R2017a and later. It bears notice that the complexity of the software implementation process is formidable and falls far beyond the scope of this paper; we would advise the reader to make use of the extensively annotated and documented open-source Matlab code that is available in versions 1.10 and later of Spinach.34
3. Spatially encoded diffusion spectroscopy applications
3.1 Ultrafast DOSY pulse sequence simulation
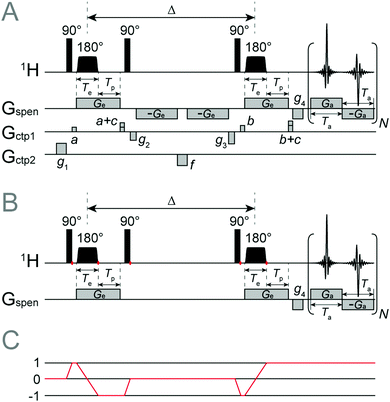
A good example of classical spatial dynamics coexisting with quantum spin dynamics in the same equation of motion is given by the ultrafast DOSY54 pulse sequence (Fig. 1). The sequence is derived from the conventional stimulated-echo DOSY, in which diffusion-encoding gradients (separated by a delay Δ so that spatial motion can have an effect on the spin precession phase) are replaced by frequency-swept chirp pulses applied under a gradient. Such chirp-and-gradient pairs are the defining feature of ultrafast NMR in general.17 The other key ingredient in UF NMR is the use of a spectroscopic imaging acquisition block to acquire, in a single scan, both the direct dimension and the spatially encoded information.The principal advantage of the Fokker–Planck formalism here is that the diffusion operator is a part of the static background Hamiltonian. Another convenient feature is that gradient operators are presented to the user in the same algebraic style as spin operators – in Fokker–Planck space, they are matrices33 that may either be added to the background Hamiltonian, or used with shaped pulse functions in the same way as spin operators. At the pulse sequence level, this makes the simulation code neat and easy to write. Multi-spin systems with internal interactions are also straightforward – Spinach modifies the Hamiltonian and changes all matrix dimensions as appropriate;34 the pulse program code remains the same.
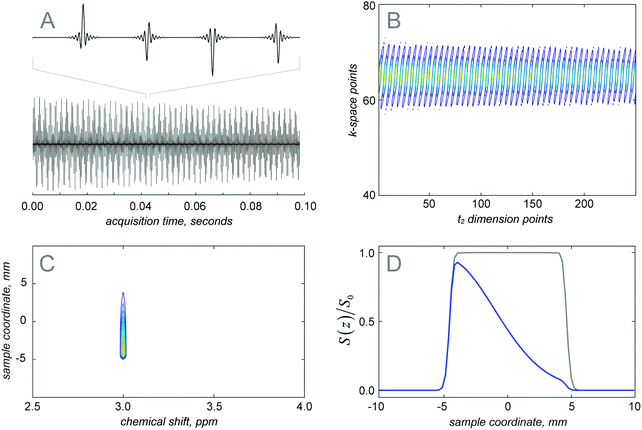
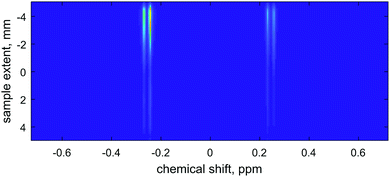
Fig. 2a shows the simulated free induction decay obtained for the SPEN DOSY pulse sequence. It is an echo train created by the train of gradient pulses during acquisition. In order to extract the diffusion information, the data are rearranged in the k–t space (Fig. 2b) and Fourier transformed along both dimensions (Fig. 2c). The diffusion decay curve is then obtained as a slice of the 2D matrix. When the diffusion constant is set to zero, the spatial profile (grey curve in Fig. 2d) reflects the smoothed chirp excitation profile. Otherwise (blue curve in Fig. 2d), the decay induced by the diffusion is observable in the spatial profile. The plateau of the chirp pulse can then be used for diffusion coefficient determination.
3.2 Numerical accuracy and convergence
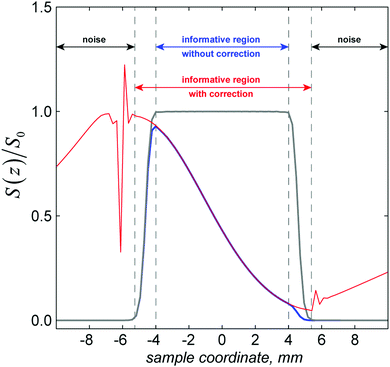
The formalism outlined in Section 2 is exact with respect to spin dynamics: the only accuracy parameter is the time step in eqn (7), which must be sufficiently small. In the spatial dynamics part, the essential factors that influence simulation accuracy are the spatial Nyquist condition (all gradient spirals must be adequately digitised) and the accuracy of the finite difference approximation to the spatial dynamics operators, in this case diffusion. The Nyquist condition55 is that the spatial discretisation grid must have at least two points per period of the fastest gradient spiral.As illustrated in the left panel of Fig. 3 and in Table 1, once the Nyquist condition is satisfied, distortions disappear abruptly and excellent convergence is achieved shortly thereafter. The accuracy of the finite difference approximation is controlled by the grid point spacing and the formal accuracy order of the finite difference stencil.51 The effect of the accuracy order is illustrated, and compared to the formally exact (when the Nyquist condition is satisfied) Fourier differentiation operator in the right panel of Fig. 3. Fourier differentiation operators are very accurate, but computationally expensive because they are not sparse.
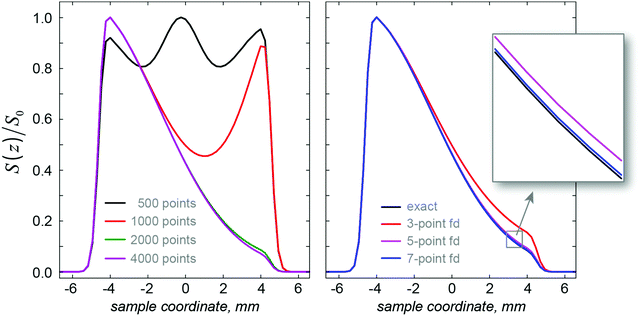 | ||
| Fig. 3 Left panel: the effect of the spatial Nyquist condition on the numerical accuracy of a SPEN DOSY simulation with the same physical parameters as in Fig. 2: the grids with 500 and 1000 points are sub-Nyquist and result in catastrophic loss of accuracy. Grids with 2000 points and more satisfy the Nyquist condition and produce accurate results. Right panel: the effect of the accuracy order of the finite difference approximation51 to the diffusion superoperator. The Fourier differentiation matrix (marked “exact”) is formally exact on a given grid, but has a significantly longer run time (36 minutes) compared to the much sparser finite difference matrix (less than 2 minutes). | ||
| Grid points | Fitted value of the diffusion coefficient, ×10−10 m2 s−1 | Wall clock simulation time, seconds |
|---|---|---|
| 500 | −0.07 | 11.6 |
| 1000 | 1.10 | 17.6 |
| 2000 | 7.83 | 33.2 |
| 3000 | 7.97 | 52.2 |
| 4000 | 7.98 | 70.0 |
| 5000 | 7.98 | 90.3 |
Practical experience indicates that periodic boundary conditions (PBC) on spatial degrees of freedom are easier to implement and simulate than absorptive or reflective boundaries. Technically, the formalism above is not restricted to periodic boundaries (finite difference operators may be built to account for other boundary types), but the implementation process is time-consuming. The use of PBC adds another accuracy consideration: for non-periodic systems, sufficient white space should be allowed on all sides of the simulation box to avoid self-interaction across the periodic boundary.
It is impossible to give a general analytical formula for the minimum number of points in the spatial grid – each pulse sequence would have its own minimal grid size. However, a convenient practical diagnostic criterion may still be formulated: the spatial Fourier transform of the Fokker–Planck state vector should not have any probability density at the high-frequency edge points at any time in the simulation.
3.3 Experimental parameter optimisation
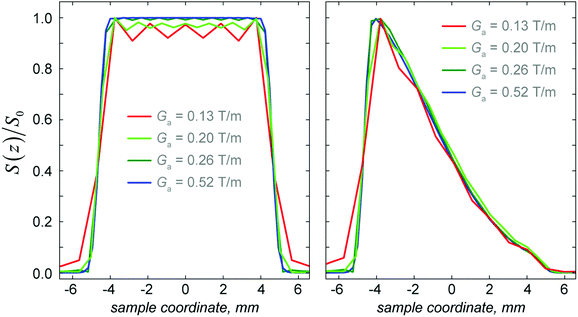
High-fidelity numerical simulations of the SPEN DOSY pulse sequence provide useful insight into the effects of pulse sequence parameters and instrumental imperfections. An example is shown in Fig. 4 – the exact shape of the chirp pulses in Fig. 1 determines the spatial profile of the excitation region. Normalisation by the spatial profile obtained in the absence of diffusion makes it possible to retrieve a larger range of attenuations for the diffusion decay, as illustrated in Fig. 4. This also accounts for deviations from an ideal plateau due to factors like the B1 field inhomogeneity, which is easy to model by assigning different amplitudes and directions of the control operators in eqn (2) to different voxels.Fig. 5 shows the effect of the amplitude of the acquisition gradient Ga. It is clear that a sub-optimal choice of Ga can generate a bias (in this case, an over-estimation is produced) in the calculated diffusion constant because it yields an oscillating lineshape when decreased too much. The cause of the oscillation is signal truncation in k-space. This effect can be corrected when the reference profile is taken into account (Table 2) by dividing the diffusion profile by the reference profile computed with the diffusion coefficient set to zero. In our real experiments, a Ga of 0.20 T m−1 is used; this confirms that it is necessary to correct the diffusion weighted image by a reference image with no diffusion present. Since it is impossible to switch the diffusion off in an actual experiment, the reference profile is obtained by cutting the corresponding pulses and evolution periods out of the pulse sequence in Fig. 1.
| Acquisition gradient (T m−1) | D (raw) × 10−10 m2 s−1 | D (corrected) × 10−10 m2 s−1 |
|---|---|---|
| 0.52 | 7.97 | 7.98 |
| 0.26 | 7.97 | 7.98 |
| 0.20 | 8.06 | 7.98 |
| 0.13 | 8.18 | 7.97 |
In order to extract diffusion coefficients from the experimental SPEN DOSY data, the gradient-induced attenuation in the signal S(z) is usually fitted by the modified Stejskal–Tanner equation:54
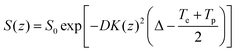 | (12) |
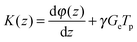 | (13) |
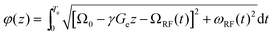 | (14) |
Numerical simulations are also useful in assessing the effect of chemical shift offsets on the errors in the fitting of eqn (12) to the experimental SPEN DOSY data. Chemical shifts cause two types of signal displacements. The displacement upon encoding is accounted for in eqn (14), but the chemical shift displacement during acquisition also has to be taken into account, as it may otherwise result in significant errors. Fig. 6 shows the spatial diffusion profiles obtained for several values of the chemical shift offset, and Table 3 gives the corresponding fitted values of the diffusion coefficients, for corrected and uncorrected z values in eqn (12), with
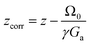 | (15) |
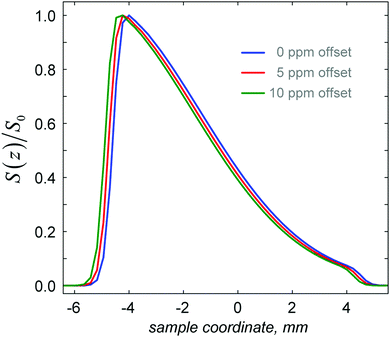 | ||
| Fig. 6 Simulated diffusion profile displacement for three different chemical shift offsets of the working signal from the resonance frequency. All other parameters are as in Fig. 3–5. | ||
| Chemical shift (ppm) | D (raw) × 10−10 m2 s−1 | D (corrected) × 10−10 m2 s−1 |
|---|---|---|
| 0 | 7.97 | 7.97 |
| 5 | 7.73 | 7.97 |
| 10 | 7.52 | 7.97 |
For typical proton chemical shifts and gradient amplitudes of the same order as in Table 2, the chemical shift offset error in the diffusion coefficient is of the order of 5%; the decision on whether this is significant rests with the user, but eqn (15) is in any case straightforward to apply.
5. Quantum mechanical processes
An emerging class of MRI experiments that essentially requires quantum mechanical treatment of spin processes is singlet state imaging.27,56,57 One reason is the delicate interplay of symmetry, chemical shift anisotropy and dipolar coupling in the relaxation superoperator that makes the two-spin singlet state long-lived.58 The other is the M2S and S2M pulse sequences that rely on the J-coupling to get the spin system in and out of the singlet state.59 Accurate Liouville space description of the spin dynamics60 is therefore essential. At the same time, recent proposals for using singlet states as a delivery vehicle for hyperpolarisation in MRI27,56,61 make it necessary to include chemical kinetics, diffusion, and flow.In this situation, the Fokker–Planck equation is clearly superior to the more traditional Liouville–von Neumann equation formalism because all spatial dynamics processes (diffusion, hydrodynamics, magic angle spinning, spatially selective pulses, etc.) are represented by constant matrices that are more convenient from the programming and numerical efficiency point of view than the time-dependent Hamiltonians in the Liouville–von Neumann formalism.33
A simulation of the singlet state diffusion and flow experiment from Fig. 2 of the recent paper by Pileio et al.27 shown in Fig. 7 is a particularly good example, because all of the complexities – shaped pulses, gradients, diffusion, flow, quantum mechanical spin evolution and complicated relaxation theory – are present simultaneously. An average over 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Monte-Carlo instances had to be performed by the authors of the original paper, with only statistical guarantees of convergence;27 here we demonstrate that the Fokker–Planck formalism performs the same simulation deterministically in a single run.
000 Monte-Carlo instances had to be performed by the authors of the original paper, with only statistical guarantees of convergence;27 here we demonstrate that the Fokker–Planck formalism performs the same simulation deterministically in a single run.
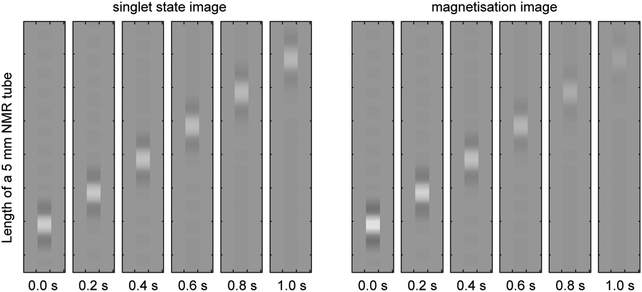 | ||
| Fig. 7 Fokker–Planck theory simulation of a singlet state NMR imaging experiment in the presence of diffusion and flow. The simulation includes soft radiofrequency pulses with simultaneous explicit simulation of flow, diffusion, magnetic field gradients and spin–spin coupling dynamics as prescribed by the Liouville–von Neumann equation, as well as full Redfield relaxation superoperator treatment. The flow rate is set to 5 cm s−1 and the diffusion coefficient to 3.6 × 10−6 m2 s−1. The singlet imaging sequence used is described in a recent paper from the Pileio group.27 It is clear that the very slowly relaxing singlet state flow (left panels) can be tracked at longer distances than magnetisation flow (right panels). | ||
Fig. 8 illustrates the same point – within the Fokker–Planck formalism, diffusion and imaging simulations for systems with multiple coupled spins can be carried out in exactly the same way as for uncoupled spins – eqn (1) supports arbitrary spin Hamiltonian commutation superoperators, arbitrary relaxation theories and a host of other processes, such as chemical kinetics.
6. Conclusions and outlook
It is demonstrated above that NMR and MRI experiments with elaborate spatial encoding and complicated spatial dynamics are no longer hard to simulate, even in the presence of spin–spin couplings and exotic relaxation effects, such as singlet state symmetry lockout. Versions 1.10 and later of Spinach library34 support arbitrary stationary flows and arbitrary distributions of anisotropic diffusion tensors in three dimensions simultaneously with Liouville-space description of spin dynamics, chemical kinetics and relaxation processes. The key simulation design decision that has made this possible is the abandonment of the Bloch–Torrey20,21 and Liouville–von Neumann13,35 formalisms in favour of the Fokker–Planck equation.33 The primary factors that have facilitated this transition are the dramatic recent improvement in the speed and capacity of digital computers, the emergence of transparent and convenient sparse matrix manipulation methods in numerical linear algebra,62 and the recent progress in matrix dimension reduction in magnetic resonance simulations.34,47In the more distant perspective, high-fidelity simulations that are free of significant approximations are expected to play an increasing role in magnetic resonance experiment design and in subsequent data processing. As optimal control theory63,64 illustrates, the understanding of the detailed dynamics taking place in a particular experiment is increasingly hard to achieve; it is slowly being replaced by the understanding of the factors generating the dynamics. Mathematically, this corresponds to the well-known relationship between a Lie group – usually an exceedingly complicated object – and the Lie algebra of its generators, which is fundamentally easier to understand and interpret. For complicated systems and processes, numerical simulation is the only practical way of connecting the two.
Acknowledgements
This research was supported by the Région Ile-de-France, by a CNRS – Royal Society exchange scheme, EPSRC (EP/M003019/1), and by the Agence Nationale de la Recherche (ANR-16-CE29-0012). The authors are indebted to Giuseppe Pileio, Maria Grazia Concilio, Gareth Morris, Lucio Frydman, Davy Sinnaeve and Mohammadali Foroozandeh for stimulating discussions. The authors also acknowledge the use of the IRIDIS High Performance Computing Facility, and associated support services at the University of Southampton, in the completion of this work.References
- L. Frydman, T. Scherf and A. Lupulescu, The acquisition of multidimensional NMR spectra within a single scan, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 15858–15862 CrossRef CAS PubMed.
- Z. D. Pardo, G. L. Olsen, M. E. Fernandez-Valle, L. Frydman, R. Martinez-Alvarez and A. Herrera, Monitoring mechanistic details in the synthesis of pyrimidines via real-time, ultrafast multidimensional NMR spectroscopy, J. Am. Chem. Soc., 2012, 134, 2706–2715 CrossRef CAS PubMed.
- M. Gal, T. Kern, P. Schanda, L. Frydman and B. Brutscher, An improved ultrafast 2D NMR experiment: towards atom-resolved real-time studies of protein kinetics at multi-Hz rates, J. Biomol. NMR, 2009, 43, 1–10 CrossRef CAS PubMed.
- P. Schanda, E. Kupce and B. Brutscher, SOFAST-HMQC experiments for recording two-dimensional heteronuclear correlation spectra of proteins within a few seconds, J. Biomol. NMR, 2005, 33, 199–211 CrossRef CAS PubMed.
- P. Giraudeau and L. Frydman, Ultrafast 2D NMR: an emerging tool in analytical spectroscopy, Annu. Rev. Anal. Chem., 2014, 7, 129–161 CrossRef CAS PubMed.
- R. Schmidt and L. Frydman, New spatiotemporal approaches for fully refocused, multislice ultrafast 2D MRI, Magn. Reson. Med., 2014, 71, 711–722 CrossRef PubMed.
- K. Zangger and H. Sterk, Homonuclear Broadband-Decoupled NMR Spectra, J. Magn. Reson., 1997, 124, 486–489 CrossRef CAS.
- L. Paudel, R. W. Adams, P. Kiraly, J. A. Aguilar, M. Foroozandeh, M. J. Cliff, M. Nilsson, P. Sandor, J. P. Waltho and G. A. Morris, Simultaneously enhancing spectral resolution and sensitivity in heteronuclear correlation NMR spectroscopy, Angew. Chem., 2013, 52, 11616–11619 CrossRef CAS PubMed.
- P. Giraudeau and S. Akoka, Sensitivity losses and line shape modifications due to molecular diffusion in continuous encoding ultrafast 2D NMR experiments, J. Magn. Reson., 2008, 195, 9–16 CrossRef CAS PubMed.
- Y. Shrot and L. Frydman, The effects of molecular diffusion in ultrafast two-dimensional nuclear magnetic resonance, J. Chem. Phys., 2008, 128, 164513 CrossRef PubMed.
- I. Kuprov, Fokker–Planck formalism in magnetic resonance simulations, J. Magn. Reson., 2016, 270, 124–135 CrossRef CAS PubMed.
- P. A. Hardy, R. M. Henkelman, J. E. Bishop, E. C. S. Poon and D. B. Plewes, Why fat is bright in rare and fast spin-echo imaging, J. Magn. Reson. Imaging, 1992, 2, 533–540 CrossRef.
- L. Stables, R. Kennan, A. Anderson and J. Gore, Density matrix simulations of the effects of J coupling in spin echo and fast spin echo imaging, J. Magn. Reson., 1999, 140, 305–314 CrossRef CAS PubMed.
- A. M. Stokes, Y. Feng, T. Mitropoulos and W. S. Warren, Enhanced refocusing of fat signals using optimized multipulse echo sequences, Magn. Reson. Med., 2013, 69, 1044–1055 CrossRef PubMed.
- S. J. Nelson, J. Kurhanewicz, D. B. Vigneron, P. E. Larson, A. L. Harzstark, M. Ferrone, M. van Criekinge, J. W. Chang, R. Bok and I. Park, Metabolic imaging of patients with prostate cancer using hyperpolarized [1-13C] pyruvate, Sci. Transl. Med., 2013, 5, RA108 Search PubMed.
- G. Pileio, S. Bowen, C. Laustsen, M. C. Tayler, J. T. Hill-Cousins, L. J. Brown, R. C. Brown, J. H. Ardenkjaer-Larsen and M. H. Levitt, Recycling and imaging of nuclear singlet hyperpolarization, J. Am. Chem. Soc., 2013, 135, 5084–5088 CrossRef CAS PubMed.
- L. Frydman, A. Lupulescu and T. Scherf, Principles and features of single-scan two-dimensional NMR spectroscopy, J. Am. Chem. Soc., 2003, 125, 9204–9217 CrossRef CAS PubMed.
- S. Yang, J. Lee, E. Joe, H. Lee, Y.-S. Choi, J. M. Park, D. Spielman, H.-T. Song and D.-H. Kim, Metabolite-selective hyperpolarized 13C imaging using extended chemical shift displacement at 9.4 T, Magn. Reson. Imaging, 2016, 34, 535–540 CrossRef PubMed.
- P. K. Senanayake, N. J. Rogers, K. L. N. Finney, P. Harvey, A. M. Funk, J. I. Wilson, D. O'Hogain, R. Maxwell, D. Parker and A. M. Blamire, A new paramagnetically shifted imaging probe for MRI, Magn. Reson. Med., 2016, 77, 1307–1317 CrossRef PubMed.
- T. H. Jochimsen, A. Schäfer, R. Bammer and M. E. Moseley, Efficient simulation of magnetic resonance imaging with Bloch–Torrey equations using intra-voxel magnetization gradients, J. Magn. Reson., 2006, 180, 29–38 CrossRef CAS PubMed.
- D. V. Nguyen, J.-R. Li, D. Grebenkov and D. Le Bihan, A finite elements method to solve the Bloch–Torrey equation applied to diffusion magnetic resonance imaging, J. Comput. Phys., 2014, 263, 283–302 CrossRef.
- H. Benoit-Cattin, G. Collewet, B. Belaroussi, H. Saint-Jalmes and C. Odet, The SIMRI project: a versatile and interactive MRI simulator, J. Magn. Reson., 2005, 173, 97–115 CrossRef CAS PubMed.
- D. A. Yoder, Y. Zhao, C. B. Paschal and J. M. Fitzpatrick, MRI simulator with object-specific field map calculations, Magn. Reson. Imaging, 2004, 22, 315–328 CrossRef PubMed.
- J. S. Petersson, J. O. Christoffersson and K. Golman, MRI simulation using the k-space formalism, Magn. Reson. Imaging, 1993, 11, 557–568 CrossRef CAS PubMed.
- T. Stöcker, K. Vahedipour, D. Pflugfelder and N. J. Shah, High-performance computing MRI simulations, Magn. Reson. Med., 2010, 64, 186–193 CrossRef PubMed.
- P. T. Callaghan, A Simple Matrix Formalism for Spin Echo Analysis of Restricted Diffusion under Generalized Gradient Waveforms, J. Magn. Reson., 1997, 129, 74–84 CrossRef CAS PubMed.
- G. Pileio, J.-N. Dumez, I.-A. Pop, J. T. Hill-Cousins and R. C. D. Brown, Real-space imaging of macroscopic diffusion and slow flow by singlet tagging MRI, J. Magn. Reson., 2015, 252, 130–134 CrossRef CAS PubMed.
- C. Cai, M. Lin, Z. Chen, X. Chen, S. Cai and J. Zhong, SPROM – an efficient program for NMR/MRI simulations of inter- and intra-molecular multiple quantum coherences, C. R. Phys., 2008, 9, 119–126 CrossRef CAS.
- A. D. Fokker, Die mittlere Energie rotierender elektrischer Dipole im Strahlungsfeld, Ann. Phys., 1914, 348, 810–820 CrossRef.
- M. Planck, Über einen Satz der statistischen Dynamik und seine Erweiterung in der Quantentheorie, Sitzungsber. K. Preuss. Akad. Wiss., 1917, 324–341 Search PubMed.
- H. Risken, The Fokker–Planck Equation, Springer, 1984 Search PubMed.
- L. J. Edwards, D. V. Savostyanov, A. A. Nevzorov, M. Concistrè, G. Pileio and I. Kuprov, Grid-free powder averages: On the applications of the Fokker–Planck equation to solid state NMR, J. Magn. Reson., 2013, 235, 121–129 CrossRef CAS PubMed.
- I. Kuprov, Fokker–Planck formalism in magnetic resonance simulations, J. Magn. Reson., 2016, 270, 124–135 CrossRef CAS PubMed.
- H. Hogben, M. Krzystyniak, G. Charnock, P. Hore and I. Kuprov, Spinach – a software library for simulation of spin dynamics in large spin systems, J. Magn. Reson., 2011, 208, 179–194 CrossRef CAS PubMed.
- R. R. Ernst, G. Bodenhausen and A. Wokaun, Principles of nuclear magnetic resonance in one and two dimensions, Clarendon Press Oxford, 1987 Search PubMed.
- G. Moro and J. H. Freed, Efficient computation of magnetic resonance spectra and related correlation functions from stochastic Liouville equations, J. Phys. Chem., 1980, 84, 2837–2840 CrossRef CAS.
- A. Polimeno and J. H. Freed, A many-body stochastic approach to rotational motions in liquids, Adv. Chem. Phys., 1993, 83, 89 CrossRef CAS.
- M. Goldman, Formal theory of spin–lattice relaxation, J. Magn. Reson., 2001, 149, 160–187 CrossRef CAS PubMed.
- A. G. Redfield, On the theory of relaxation processes, IBM J. Res. Dev., 1957, 1, 19–31 CrossRef.
- R. K. Wangsness and F. Bloch, The dynamical theory of nuclear induction, Phys. Rev., 1953, 89, 728 CrossRef CAS.
- J. H. Freed, G. V. Bruno and C. F. Polnaszek, Electron spin resonance line shapes and saturation in the slow motional region, J. Phys. Chem., 1971, 75, 3385–3399 CrossRef CAS.
- D. Goodwin and I. Kuprov, Auxiliary matrix formalism for interaction representation transformations, optimal control, and spin relaxation theories, J. Chem. Phys., 2015, 143, 084113 CrossRef CAS PubMed.
- I. Kuprov, Diagonalization-free implementation of spin relaxation theory for large spin systems, J. Magn. Reson., 2011, 209, 31–38 CrossRef CAS PubMed.
- D. Tannor, Introduction to Quantum Dynamics: A Time-Dependent Perspective, University Science Books, Sausalito, CA, 2007 Search PubMed.
- R. B. Sidje, Expokit: a software package for computing matrix exponentials, ACM Trans. Math. Software, 1998, 24, 130–156 CrossRef.
- C. Moler and C. Van Loan, Nineteen dubious ways to compute the exponential of a matrix, SIAM Rev., 1978, 20, 801–836 CrossRef.
- L. J. Edwards, D. V. Savostyanov, Z. T. Welderufael, D. Lee and I. Kuprov, Quantum mechanical NMR simulation algorithm for protein-size spin systems, J. Magn. Reson., 2014, 243, 107–113 CrossRef CAS PubMed.
- D. M. Brink and G. R. Satchler, Angular momentum, Oxford University Press on Demand, 1993 Search PubMed.
- A. Karabanov, I. Kuprov, G. Charnock, A. van der Drift, L. J. Edwards and W. Köckenberger, On the accuracy of the state space restriction approximation for spin dynamics simulations, J. Chem. Phys., 2011, 135, 084106 CrossRef PubMed.
- L. N. Trefethen, Spectral methods in MATLAB, Siam, 2000 Search PubMed.
- B. Fornberg, Generation of finite difference formulas on arbitrarily spaced grids, Math. Comput., 1988, 51, 699–706 CrossRef.
- T. Liszka and J. Orkisz, The finite difference method at arbitrary irregular grids and its application in applied mechanics, Comput. Struct., 1980, 11, 83–95 CrossRef.
- R. Eymard, T. Gallouët and R. Herbin, Finite volume methods, Handbook of Numerical Analysis, Elsevier, 2000, pp. 713–1018 Search PubMed.
- L. Guduff, I. Kuprov, C. van Heijenoort and J. Dumez, Spatially encoded 2D and 3D diffusion-ordered NMR spectroscopy, Chem. Commun., 2016, 53, 701–704 RSC.
- H. Nyquist, Certain topics in telegraph transmission theory, Trans. Am. Inst. Electr. Eng., 1928, 47, 617–644 CrossRef.
- C. Laustsen, G. Pileio, M. C. D. Tayler, L. J. Brown, R. C. D. Brown, M. H. Levitt and J. H. Ardenkjaer-Larsen, Hyperpolarized singlet NMR on a small animal imaging system, Magn. Reson. Med., 2012, 68, 1262–1265 CrossRef CAS PubMed.
- J.-N. Dumez, J. T. Hill-Cousins, R. C. D. Brown and G. Pileio, Long-lived localization in magnetic resonance imaging, J. Magn. Reson., 2014, 246, 27–30 CrossRef CAS PubMed.
- G. Pileio, Relaxation theory of nuclear singlet states in two spin-1/2 systems, Prog. Nucl. Magn. Reson. Spectrosc., 2010, 56, 217–231 CrossRef CAS PubMed.
- G. Pileio, M. Carravetta and M. H. Levitt, Storage of nuclear magnetization as long-lived singlet order in low magnetic field, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 17135–17139 CrossRef CAS PubMed.
- A. D. Bain and J. S. Martin, FT NMR of nonequilibrium states of complex spin systems. I. A Liouville space description, J. Magn. Reson., 1978, 29, 125–135 CAS.
- G. Pileio, S. Bowen, C. Laustsen, M. C. D. Tayler, J. T. Hill-Cousins, L. J. Brown, R. C. D. Brown, J. H. Ardenkjaer-Larsen and M. H. Levitt, Recycling and Imaging of Nuclear Singlet Hyperpolarization, J. Am. Chem. Soc., 2013, 135, 5084–5088 CrossRef CAS PubMed.
- J. R. Bunch and D. J. Rose, Sparse matrix computations, Academic Press, 2014 Search PubMed.
- P. De Fouquieres, S. Schirmer, S. Glaser and I. Kuprov, Second order gradient ascent pulse engineering, J. Magn. Reson., 2011, 212, 412–417 CrossRef CAS PubMed.
- I. Kuprov, Spin system trajectory analysis under optimal control pulses, J. Magn. Reson., 2013, 233, 107–112 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2017 |