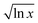Combining random walk and regression models to understand solvation in multi-component solvent systems

Abstract

Polysaccharides, such as cellulose, are often processed by dissolution in solvent mixtures, e.g. an ionic liquid (IL) combined with a dipolar aprotic co-solvent (CS) that the polymer does not dissolve in. A multi-walker, discrete-time, discrete-space 1-dimensional random walk can be applied to model solvation of a polymer in a multi-component solvent mixture. The number of IL pairs in a solvent mixture and the number of solvent shells formable, x, is associated with n, the model time-step, and N, the number of random walkers. The mean number of distinct sites visited is proportional to the amount of polymer soluble in a solution. By also fitting a polynomial regression model to the data, we can associate the random walk terms with chemical interactions between components and probe where the system deviates from a 1-D random walk. The ‘frustration’ between solvents shells is given as ln x in the random walk model and as a negative IL:IL interaction term in the regression model. This frustration appears in regime II of the random walk model (high volume fractions of IL) where walkers interfere with each other, and the system tends to its limiting behaviour. In the low concentration regime, (regime I) the solvent shells do not interact, and the system depends only on IL and CS terms. In both models (and both regimes), the system is almost entirely controlled by the volume available to solvation shells, and thus is a counting/space-filling problem, where the molar volume of the CS is important. Small deviations are observed when there is an IL–CS interaction. The use of two models, built on separate approaches, confirm these findings, demonstrating that this is a real effect and offering a route to identifying such systems. Specifically, the majority of CSs – such as dimethylformide – follow the random walk model, whilst 1-methylimidazole, dimethyl sulfoxide, 1,3-dimethyl-2-imidazolidinone and tetramethylurea offer a CS-mediated improvement and propylene carbonate results in a CS-mediated hindrance. It is shown here that systems, which are very complex at a molecular level, may, nonetheless, be effectively modelled as a simple random walk in phase-space. The 1-D random walk model allows prediction of the ability of solvent mixtures to dissolve cellulose based on only two dissolution measurements (one in neat IL) and molar volume.

---

1 Introduction

Random walks are models of a walker, be it a drunkard, a molecule, or a stock price, exploring space (real space for the drunkard and molecule, phase space for the stock price) randomly. There has been a wealth of research into random walks in many fields.^1,2 Within chemistry and materials science, random walks have been applied to polymer absorption,³ copolymer structure,⁴ electron traps in semiconductors,^5,6 quantum mechanical paths,^2,7 phonons in liquids,⁸ phospholid motion in cell membranes,⁹ diffusion in zeolites,¹⁰ motion of insulin granules in cells,¹¹ intramolecular migration of chemical species along oligomers,¹² rotaxanes diffusing along polymers,¹³ and modelling of polymer motion.¹⁴ The most extensive use has been the that of a self-avoiding random walk to generate polymer conformations.^2,7,15,16

There are several types of random walks. Brownian motion¹⁷ and bacterial motion¹⁸ are examples of continuous-time, continuous-step random walks, where the walker takes a step at random points in time in a random direction. Time and space can also be discretized, giving the discrete-time, discrete-space random walk model, which is useful for modelling lattices^19–21 and is uniquely accessible by cellular automata modelling techniques.²² Most random walks are Markovian (and can be modelled as Markovian chains) because they are memoryless, i.e. the direction (and timing) does not depend on the system's previous history. For Markovian chains, each step depends on the step before. Self-avoiding random walks, contrastingly, must have a complete memory of the system, as the walker must not go where it has been before (it is this rule that allows this type of walk to be used to model polymers: two bonds cannot be in the same place; or quantum mechanics: two electrons cannot occupy the same state).² Random walks can also take place in a number of dimensions: 1-D walks are walks along a line, 2-D over a plane, and 3-D over a volume (and there are higher dimensional random walks).

Most mathematical results are concerned with many walker systems. Studying the motion of a single walker selected from a set can, as the walkers are identical and the walk is selected randomly, be a study of the average properties.²³ Conversely, order statistics, which is the study of the first walkers to arrive at a point, can model single molecule experiments.^24,25 Another useful property is the size of a random walk, which relates to the radius of gyration for a polymer, for example.^26,27 In 1951 Dvoretzky and Erdös suggested that the number of distinct sites visited by any random walker, when there are N interacting random walkers, was an interesting problem.²⁸ The first solution was published in 1992 by Weiss et al.,^29–31 and was solved by describing the system with generating functions for probability distributions, and then approximating the behaviour of a coordinate (Laplace) transform approximation of the generating function at a singular point: this gave solutions that were valid only for the large number of walkers limit and extended time.³⁰

Universality is the concept that the microscopic details of a system do not alter the asymptotic properties of that system,² which is why many systems seem to have similar behaviour. The most well-known result is the central limit theorem, which states that, for many statistically independent random variables, the output distribution will be a Gaussian (normal) distribution regardless of the underlying distribution – and any system that exhibits this behaviour is a member of the Gaussian universality class. (Interestingly, the memoryless random walk belongs to the Gaussian universality class, while the self-avoiding random walk used to model polymer structure belongs to a different universal class.²) Thus, it is possible to model seemingly unrelated systems with a random walk, if that system is a member of the same universality class. In this paper it is posited that the amount of a solute dissolvable in a mixture across phase space can be modelled as a 1-D random walk because once a ‘site’ in a mixture is filled, it does not spontaneously ‘unfill’ (i.e. the polymer come out of solution) and can frustrate the solution of further solute in a manner, similar to queuing effects seen in 1-D random walks. In this paper, a 1-D random walk model is applied to the problem of cellulose solvation in an IL:CS solution.

An alternative model for the system is a multi-polynomial regression model. Polynomial regression models are a particular form of a linear regression model that include higher order terms following the general equation:

y = β₀ + β₁x + β₂x² +⋯+ β_hx^h + ε (1)

where y is the response variable, x is the predictor variable, h is the degree of the polynomial, β₀ − β_h are coefficients, and ε is the error variable. Multiple predictor variables can also be included within a linear regression model, giving rise to interaction terms:

y = β₀ + β₁x + β₂z + β₃xz + β₄x²z + β₅xz² + β₆x²z² +⋯+ β_hxzx^h_xz^h_z + ε (2)

where z is a second predictor variable and xz is the interaction term between x and z. These two models can be combined, resulting in polynomial interaction terms with higher order terms for either predictor variable, e.g. x²z. This skews the interaction term such that the variance of one predictor variable has a greater impact than that of another, i.e. the weighting is not equal. Models including polynomial interaction terms have previously been used to describe the variation of aerosol optical depth,³² flow-induced fibre orientation,³³ and cardiorespiratory interaction.³⁴

In order to process materials, it often necessary to dissolve them. Tuning solvent mixtures to get useful properties and balancing requirements such as chemistry, cost, toxicity, physical properties, environmental-friendliness, and so on, have recently gained traction in industry. The dissolution of polymers is an important problem for the semi-conductor industry (polymeric resists), membrane science, plastics recycling and drug delivery.³⁵ An example is that of cellulose dissolution. Cellulose, the main constituent of plant cell walls, is a naturally occurring biopolymer with an estimated 28.2 billion tonnes produced via biomass each year.³⁶ It is already well established as a raw material for biocompatible and environmentally-friendly products, including synthetic fibres, coatings and additives for foods and cosmetics.³⁶ However, due to strong intra- and intermolecular hydrogen bonding, cellulose does not readily dissolve in typical solvent systems, with the majority of commercial cellulose dissolution processes relying on chemical modification of the cellulose to enable dissolution.^36–38

The recent development of the dissolution of cellulose using ionic liquids (ILs) has enabled the facile dissolution of cellulose without the need for chemical modification.³⁹ Whilst a number of different ILs have been used, the majority are based on an imidazolium cation; hence the focus on 1-ethyl-3-methyl-imidazolium acetate, perhaps the most studied IL for ligno-cellulosic dissolution, in this paper.^38,40 Whilst ILs have negligible vapour pressure and are often miscible with water, the high viscosity and economic cost limit their current use.⁴¹ The observation that mixtures of dipolar aprotic solvents, such as dimethyl sulfoxide (DMSO), with some ILs facilitates instantaneous dissolution of cellulose^42,43 has broadened the range of solvent systems available. Mixtures of ILs and CSs have been termed “organic electrolyte solutions” (OESs).⁴² Recently, we have described a predictive methodology for selection of the CS.⁴⁴

There is now a body of literature reporting investigations into why ILs dissolve cellulose efficiently, from attempts to develop a theoretical understanding to those seeking to optimise the choice of IL.^45–48 Likewise, since their development, there have been a number of publications describing attempts to determine whether the CS components of the OES interact with the cellulose, or are purely viscosity modifiers.^49–52 Whilst computational models have been developed for specific systems at set IL molar fractions (χ_IL),^44,52 there have been, to the best of our knowledge, no studies aimed at developing an operational understanding of the cellulose dissolution curves generated as χ_IL changes.

In this paper, we build a 1-D random walk model for the quantity of cellulose that dissolves in an OES with variable CSs, and compare this to a multi-polynomial regression model of the same system. We demonstrate that the 1-D random walk model can be used to vastly reduce (to two) the number of dissolution experiments required to characterise the cellulose dissolution profile in new OESs, such that the model is of great utility to experimentalists.

2 Model development

2.1 Random walk model

In the 1-dimensional (1-D), discrete-time, discrete-space random walk for many walkers, space is represented as a 1-D lattice. Sites on the lattice can be occupied by a walker, or are empty. Time is discretised into time-steps; walkers can move left or right with equal probability; two walkers cannot occupy the same site; and walkers cannot ‘hop over’ each other (i.e. walkers can get ‘stuck’ behind each other). One of the commonly calculated properties of a random walk is the number of distinct sites visited by N walkers in n steps, often given as an expectation value on a distribution, 〈S_N(n)〉, which is given by:for a large number of N, where σ is the variance.²⁹ For a single walker, , so the effect of extra walkers frustrating each other's random walks is . If N is fixed and n → ∞, then in the case where the walkers have taken enough steps to get out of each other's way and the system is best described as N versions of a single random walker. This is not possible for the 1-D random walk, and walkers always frustrate each other's exploration.

When the number of steps is low, the system is in regime I, where n ≪ N early on in the random walk, then 〈S_N(n)〉 ≈ n. In regime II, n ≈ N, and the walkers start to interact.

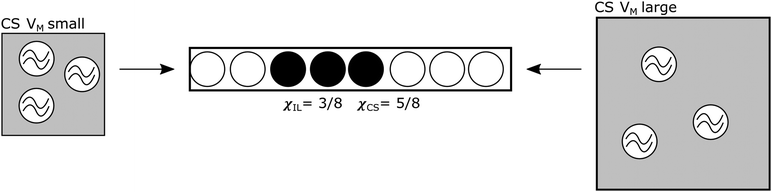
This model is here applied to a system where a solute, Z, dissolves in a mixture of two components, X and Y, where Z is soluble in pure X, insoluble in pure Y, and soluble in some mixtures of X and Y, dependent on the amount of X. The solution comprises solvation shells (SSs), which are the part of the solvent that is interacting with the solute, perturbed by its presence and providing energetic support to keep the solute in solution. These are embedded in a bulk background solvent, which is the part of the solvent that is not perturbed by the solute. This model could apply to colloids, or phase-separated mixtures, as well as true solutions, and the mixture need not be restricted to only two components. For our example system, X is the IL, Y is a CS and Z is cellulose. The solvent shell is expected to be mostly made up of IL embedded in bulk mixture of IL and CS: see Fig. 1. For this particular model, it is assumed there is no interaction between CS and IL.

Fig. 1 Model schematic. The dissolved cellulose is surrounded by an ionic liquid (IL) containing solvent shells (SS) embedded in bulk solvent mixture of IL and CS (bulk OES); the SSs are modelled as filled or empty sites available in the solution. In 1-D model space, only the number of these volumes is included in the model; their spatial arrangement, temporal dynamics or kinetics are ignored. (a) At a low concentration (in this case, χ_IL = ¼) there is plenty of ‘space’ in the solution and little interaction between SSs. (b) At a high concentration (for example, χ_IL = ¾) the SSs compete for space, which is modelled as random walkers frustrating each other's exploration of model space. χ_IL is the molar fraction of IL, and the maximum number of SS that could be fit into the volume, c_max, is 4 in this schematic.

The number of SSs dissolved in the mixture is modelled as the amount that will fit into the physical volume of solvent. The structure of the solvent shells is ignored and modelled only as occupied volumes of space, reflecting the assumption that these do not change size, or shape, for different SS concentrations. Rate of dissolution, or any time-based measure, is not included, so it is assumed that the amount of solute dissolved is the maximum soluble in that solvent mixture, i.e. that it is at equilibrium. As such, this is a counting/space-filling problem: the number of solvent shell volumes that are filled out of the possible maximum number achieved if the volume were maximally occupied by solvent shells is counted. As the number of ‘sites’ filled are being counted, this is a 1-D problem: see Fig. 1. A macroscopic physical model for this would be placing hard spheres into a tube.

There is a measure of spatial frustration here. A volume of mixture can contain only so much of Z and each molecule of Z has a SS of a certain size. The maximum amount of Z that can fit into a volume is c_max,¶ where it is understood that this is the maximum value over all possible combinations of X and Y (i.e. all molar fractions), and is generally expected to be the value measured when χ_X = 1 if Y is a CS that does not dissolve Z. The maximum amount of Z that can dissolve in a mixture at any given χ_X is c(χ_X). This is a measure of how many sites there are in the liquid mixture. Thus, c is a measure of the holding capacity of a solvent mixture (and the fact that we can describe the process in terms of c/c_max explains why the process is 1-dimensional). If a mixture is close to its value of c, then for another molecule of Z to dissolve, the SSs of all molecules of Z must rearrange to admit another molecule of Z. Thus, solvation is modelled as site filling, and the number of sites are proportional to χ_X.

Instead of N random walkers, there are x ‘sites’ in the liquid mixture capable of ‘holding’ a unit of c, i.e. a volume that would be occupied by the solute and its SS. These sites interact with each other because two SSs cannot occupy the same position. Instead of n time-steps, there are n IL ion pairs available, and the process is not considered over time, but over phase-space: it is modeled across chemical phase space on the continuum χ_X from 0 (pure Y) to 1 (pure X).

The theoretical model for the expectation value of the mean number of distinct sites visited by N random walkers is used. Once visited by a walker for the first time, a site cannot be visited again for the first time. In this system, once a site is visited for the first time, a SS is formed around a ‘piece’ of cellulose and the site is occupied.|| The model uses discretized space in the discrete sites available for dissolving Z, bearing in mind that these sites do not exist until Z is added to the mixture and the solvent forms a ‘dissolution site’ around it (this is identified with SSs, as we shall see later). The existence of these sites is predicated on the number of IL ion pairs available (n), thus compositions with greater n can form more SSs. The mean number of distinct sites visited 〈S_N〉 is then proportional to the amount of Z that can dissolve in a mixture.

2.2 Applying the random walk model to cellulose dissolution in ionic liquid mixtures

The system under study is a multi-component liquid consisting of an IL, 1-ethyl-3-methylimidazolium acetate, [EMIM][OAc], (X = [EMIM][OAc]), and a dipolar aprotic CS (Y), one of: dimethyl sulfoxide (DMSO), N,N-dimethylformamide (DMF), N,N-dimethylacetamide (DMAc) or N-methylpyrrolidinone (NMP). These had previously been identified as good OES CSs.⁴⁴ In addition, key solvent parameters were identified from amongst Catalan SP, SdP, SA, SB parameters and Lawrence DI, ES, α₁ and β₁ parameters. Ranges were identified for these parameters that would describe a ‘good’ CS for the formation of OESs for the dissolution of cellulose. Specifically, the Lawrence α₁ and Catalan SA measures were found to be the most important measures of these sets for identifying good CSs.⁴⁴ Random walk model results for the full set of solvents previously tested,⁴⁴ which additionally includes γ-valerolactone (γ-val), γ-butyrolactone (γ-but), 1-methylimidazole (1-MI), 1,3-dimethyl-2-imidazolidinone (DMI), sulfolane, and propylene carbonate (PC), is given in Fig. S1 in the ESI.†

2.3 Multi-polynomial regression model for cellulose dissolution in an OES

In order to investigate the effect of different CSs on the maximum dissolution of cellulose in an OES, a multi-polynomial regression model was independently developed based on the molar ratio of IL (χ_IL) and the molar ratio of CS (χ_CS = 1 − χ_IL):

χ_cell = Aχ_IL + B(1 − χ_IL) + C(χ_IL)^D(1 − χ_IL)^E − F(χ_IL)² (4)

where χ_cell is the molar fraction of cellulose dissolved, normalised to the value obtained in the pure IL (χ_IL = 1), and A–F are constants. The first term describes the linear effect due to the IL; the second is the linear effect due to the CS; the third term describes the CS:IL cross-term interaction; and the final term describes the IL interaction with itself. In all cases, A = 2 and F = 1 to ensure that χ_cell = 1 at χ_IL = 1 (thus the maximum number of fitting parameters used is four).

Given that the pure CS cannot dissolve cellulose, B < 0 and determines the point at which the curve crosses the abscissa, i.e. the point at which dissolution of cellulose is possible. The term C(χ_IL)^D(1 − χ_IL)^E determines whether the dissolution of cellulose is modulated due to interaction between the IL and CS. C can either be positive or negative (for example, CSs that inhibit the dissolution of cellulose in this system have negative C values) and is equal to 0 when there is no interaction between the CS and IL. The coefficients D and E weight the interaction term in favour of the IL or the CS.

Constants B, C, D and E were calculated using the ‘Solver’ function in Microsoft Excel applying the GRG non-linear solving method.⁵⁶ Both the sum of the differences between the modelled and real values, and the sum of the squared differences were minimised.

The minimum IL, χ_IL|_min for each solvent, taken as the abscissa crossing point, was fitted against the molar volume of CS and OES, V^CS_M. This was fitted in Mathematica using the equation:

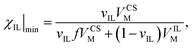where v_IL is the volume of IL in the solution and (1 − v_IL) replaces the volume of CS in the solution v_CS, leaving f as a free fitting parameter. A linear fit with m and g as fitting parameters, was also performed on the transformed data:These fits were executed in Mathematica 11 using the ‘NonlinearModelFit’ and ‘LinearModelFit’ functions, respectively.⁵⁷

3 Results

3.1 The random walk model

The identification of the relation between the site model of a solution and a random walk over space and time leads to the question of how the regimes mentioned above correspond to the solution model. Regime I is identifiable as a low concentration regime, χ_IL ≪ 1, where the number of occupied sites is much less than the maximum available (c_max), and is limited by the amount of IL in the mixture. Thus, there is little interaction between pairs of IL ion pairs and the SSs do not interact or encounter each other. At this point, c ∼ x, where x is the number of solvent shells; all ions of IL are associated with a SS, and c scales linearly with χ_IL.

Regime II occurs when the concentration of IL is high enough that the SSs start to interfere with each other; at this point c is non-linear with χ_IL.

If the amount of cellulose, c, is proportional to the expected number of distinct sites visited by N random walkers, we would expect that:

As the random walk model is valid for the large x case, we calculated the number of dissolved cellobiose units in a mole of OES, n_cell, and plotted it against the number of IL pairs in a mole of OES, n_IL, (which was taken from the molar fraction data), Fig. 2. The data fits the theory with the equation:

which, by comparison with eqn (3), directly relates the number of dissolved cellobiose residues to the expected number of sites visited by N random walkers. In the random walk model the walk starts at ‘1’ because there are many walkers present at the first time step and it is possible to have an expectation value of zero. As we need a certain number of IL molecules present (which is more than 1) in order for the first ‘site’ to be ‘occupied’ (i.e. to form a SS), the random walk is offset from the origin by d, the point where the curve crosses the abscissa.

Fig. 2 Number of cellobiose units of cellulose, n_cell (taken from molar fraction data) in a mole of solution against the number of IL pairs for ‘good’ CSs. The fit is . These good CSs demonstrate curves that resemble 1-D random walk curves. (Data for all solvents tested are given in Fig. S2 of the ESI.†) Points are experimental data measured in pairs of over- and under-estimates of the maximum cellulose dissolvable, the lines are the 1-D random walk fits.

Fitting parameters are given in Table 1. The curvature of the curves in Fig. 2 is m in the fit, which is identified as in our model, and so should be related to the extent of interaction (i.e. frustration) between the solvent shells. This value is different for different CSs. The quantity 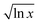is a measure of the volume the CS occupies. Bulky CSs take up a larger volume for a given solvent composition compared with smaller, less bulky CSs – with the proviso that some of the CS ‘bulk’ is a measure of electrostatic interactions, see Fig. 3. The molar volumes of the CS investigated here ranged from 71–107 cm³ mol⁻¹ (see Table S2 in the ESI†), or 43–65% of IL molar volume (which is 166 cm³ mol⁻¹).

Table 1 Coefficients for the n_cellversus n_IL fits in Fig. 2. The equation used was: . The norm of the residuals is given by R². Full data are given in Table S1 of the ESI

Dataset	d	m	R ^2
DMSO	−1.402 × 10^22	1.184 × 10^11	0.998
DMF	−2.011 × 10^22	1.277 × 10^11	0.998
DMAc	−2.651 × 10^22	1.371 × 10^11	0.999
NMP	−1.886 × 10^22	1.274 × 10^11	0.996

---

Fig. 3 Different CSs with different molar volumes (V_M) can correspond to the same χ_IL. The CS with the smaller molar volume (left) has less available volume for SS, and thus a higher frustration interaction than the CS with a larger molar volume (right), which has larger OES volume for the same molar fraction. This effect is the basis for most of the differences between OES formulations.

In Fig. 4 the volume fraction that is available to the IL to form SSs is plotted against the amount of cellulose dissolved: this has removed the effect of the CS in the mixture entirely. There is a linear dependence (R² is over 0.95 for each good CS, see Table 2), and there is no appreciable difference between solvents; in fact, a straight-line fit to the all the good CSs has an R²-value of 0.976. Including all CSs only perturbs this fit slightly (the gradient is unchanged and R² value is 0.930). There is little difference between OESs and certainly any difference is within the spread of the experimental data, thus, the only important quantity is the volume available to the IL. This is precisely what our succinct space-filling model, that has ‘abstracted out’ a large amount of the chemical detail, would predict.

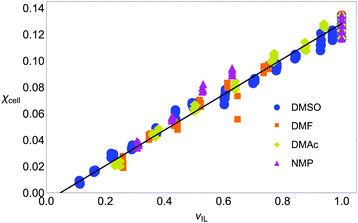Fig. 4 Molar fraction of cellobiose, χ_cell, versus volume fraction of ionic liquid, ν_IL, (as calculated from molar volumes and molar fractions). The amount of cellulose dissolvable in a solution mixture is only related to the volume of IL available, suggesting that a space-filling model of dissolution is appropriate. Blue circles: DMSO; orange squares: DMF; yellow diamonds: DMAc; pink triangles: NMP. The fit parameters are given in Table 2. Note, the excess volume of mixing is ignored as it was found to be very small in experiments.⁴⁴

Table 2 Coefficients for the χ_cellversus ν_IL fits. The equation used was: χ_cell = a + bν_IL. The norm of the residuals is given by R²

Dataset	a	b	R ^2
a All CSs with a positive interaction are: 1-MI, DMSO, DMF, DMI, DMAc, sulfolane, γ-but, γ-val, TMU and NMP (data are plotted in Fig. S3 of the ESI).
DMSO	−0.00117	0.126	0.990
DMF	−0.00768	0.135	0.965
DMAc	−0.00655	0.137	0.986
NMP	0.00717	0.123	0.953
DMSO, DMF, DMAc and NMP	−0.00245	0.130	0.976
All CSs with a positive interaction^a	−0.00109	0.130	0.930

---

Fig. 5 shows the number of IL pairs per cellobiose residue. The system is linear when it is in regime II (between ca. 0.2 < χ_IL ≤ 1), and there is little difference between the different CS-based OESs in this regime. The minimum number of IL pairs required per cellobiose residue is ca. 2.4, and the straight lines are drawn at 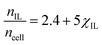and , which gives an estimate (from the ordinate crossing point) of the minimum number of IL pairs that would be required, were the system permanently in regime II, of . This range fits with the values of 2 ≤ IL < 3 found for cellulose in a DMSO-based OES.⁵⁸ Similarly, the number of IL ion pairs per cellobiose in pure IL is between 7.4 and 8.7 (Fig. 5), with NMR experiments suggesting that there are 6–8 IL ion pairs to cellobiose in the primary SS.** ⁵⁸ The gradient is 1/5, so an extra 5 IL pairs are needed to allow each extra cellobiose to be dissolved. This number reflects that determined from NMR studies,^58,60 as there are 5 hydroxyl groups for the IL to interact with, and it has been found that the volume fraction of cellulose in IL is 0.2,⁶⁰ which relates to the gradient (1/5) observed when the system is in regime II. Therefore, the spatial frustration from SSs accounts for a loss of around 2.6 IL pairs from SSs.

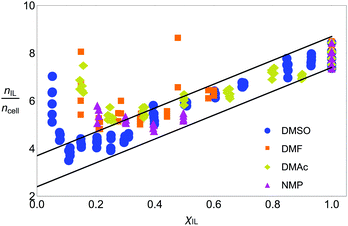Fig. 5 The number of IL pairs per cellobiose residue. Upper and lower boundaries (blue lines) are drawn at and . The full set of data is given in Fig. S4 in the ESI.†

3.2 The multi-polynomial regression model

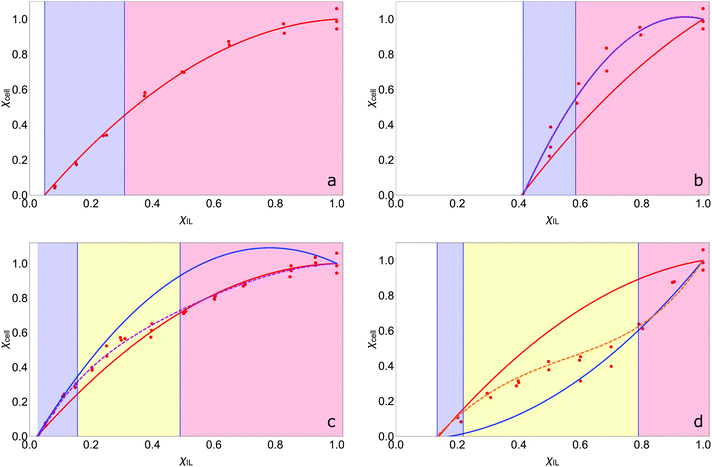
The fitted constants for the multi-polynomial regression model, eqn (4), are given in Table 3. For the majority of the dipolar aprotic CSs tested (NMP, DMF, DMAc, sulfolane, γ-but and γ-val) there is no interaction between the CS and the IL: the constants C, D and E equal 0 (Table 3). An example of the resulting curve is given in Fig. 6a. This gives rise to three regimes (0, I, and II). In regime 0 cellulose dissolution is not possible; the IL is prevented from forming SSs around the cellulose. From a packing perspective, the free-space available to the IL is not large enough to fit a complete SS, thus, cellulose cannot be dissolved. It follows that the larger the CS molar volume, the greater the χ_IL required to initiate dissolution, implying that the χ_IL at which cellulose dissolves should be proportional to CS molar volume, as is shown in Fig. 7. Regime I, where Aχ_IL ≫ Fχ_IL², is equivalent to c ∼ x; the increase in the number of SSs results in a corresponding linear increase in the amount of cellulose that can be dissolved, as described by the random walk model. At a higher proportion of IL, Aχ_IL ≫ Fχ_IL² → Aχ_IL = Fχ_IL², regime II occurs; a greater number of SSs are required to dissolve a cellulose unit due to their interaction with one another, limiting cellulose dissolution. This increase in relative weight of the χ_IL² term is a measure of SS frustration, equivalent to in the random walk model.

Table 3 Upper and lower values for polynomial regression model constants A–F, eqn (4), for tested CSs. PC is propylene carbonate

Co-solvent	Polynomial regression model parameters
	A	B	C	D	E	F
DMSO	2	0.09–0.10	1.55–1.59	1	4.36–3.60	1
1-MI	2	0.27–0.23	4.28–3.85	1	4.05–3.74	1
DMI	2	0.68–0.50	3.21–2.37	1	1.76–1.59	1
TMU	2	2.19–2.18	2.57–2.58	1	0.99	1
NMP	2	0.09–0.08	0	0	0	1
γ-but	2	0.10–0.09	0	0	0	1
DMF	2	0.11–0.10	0	0	0	1
Sulfolane	2	0.14–0.07	0	0	0	1
DMAc	2	0.15–0.14	0	0	0	1
γ-val	2	0.30–0.31	0	0	0	1
PC	2	0.22–0.21	−2.05–2.08	2.2	1	1

---

Fig. 6 Lower-limit (underestimate) experimental (red dots) and theoretical solubility curves for (a) γ-butyrolactone, (b) TMU, (c) DMSO and (d) propylene carbonate. Curves with no (χ_IL)(1 − χ_IL) interaction term denoted in blue; red includes the interaction term (χ_IL)(1 − χ_IL) (equal weighting); orange curves include (χ_IL)^D(1 − χ_IL) and curves with (χ_IL)(1 − χ_IL)^E are in purple. Regime 0 is white, regime I is highlighted in blue, the transition regime IIa in yellow, and regime II in red. ‘Normal’ CSs OES have no CS:IL interaction and follow the random walk model (a), deviations can come from a positive interaction (b and c), or a negative interaction (d), which slightly modify the curve.

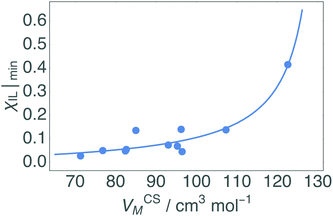Fig. 7 Correlation between co-solvent molar volume, V^CS_M, and minimum χ_IL at which the dissolution of cellulose occurs based on upper and lower limits for each CS. The bulkier the CS, the greater the χ_IL required to initiate dissolution, as less free-space is available for SS formation at low χ_IL. The fit is given in eqn (5).

A positive interaction between the CS and IL is predicted for 1-MI, DMSO, DMI and TMU. For 1-MI, DMSO and DMI, E > 1, resulting in experimental curves that initially follow the modelled curve with an equal weighting between the CS and IL, before falling into line with the curve reflecting no interaction at higher IL fractions (Fig. 6b). However, for TMU, E ≈ 1, giving little deviation from the curve with equal weighting (Fig. 6c). It is theorised that these four CSs (1-MI, DMSO, DMI and TMU) are able to participate in the formation of the SS between the IL and cellulose, resulting in a reduction in the number of IL ion pairs required in the SS and enhancing dissolution over that of the pure IL. This is in agreement with RISM calculations conducted on a glucan chain–[EMIM][OAc]–DMSO system with a low concentration of IL (χ_IL = 0.019), where it was observed that DMSO appeared to solvate the glucan chain in a similar manner to the acetate anion.⁴⁴ The transitional nature of the enhancement is also in agreement with a previous molecular dynamics study in which it was reported that DMSO does not interact with cellulose at χ_IL = 0.5;⁵² at this concentration the CS:IL interaction term is negligible.

In this scenario, regime I is described by Aχ_IL + Cχ_IL(1 − χ_IL)^E ≫ Fχ_IL², and whilst c ∼ x, x is no longer directly proportional to the number of IL molecules in the system, but rather dependent on the number of IL and CS molecules (as x is a measure of SSs, this fits with the supposition that these CSs are participating in the SS). For DMSO, 1-MI and DMI, regime II still tends to the Aχ_IL = Fχ_IL² limit because the Cχ_IL(1 − χ_IL)^E term becomes insignificant. For the TMU-based OES, regime II tends to the Aχ_IL + Cχ_IL(1 − χ_IL)^E = Fχ_IL² limit instead. For DMSO, 1-MI and DMI it is apparent that the number of CS molecules interacting with the SS decreases between regimes I and II, resulting in a transition region, regime IIa, (Fig. 6c), whereas, the number of TMU molecules in the SS remains constant over the entire phase-space resulting in a direct transition from regime I to II (Fig. 6b).

Finally, PC has a negative interaction with the IL, resulting in suppression of the dissolution of cellulose. Its transition from having no interaction, to interacting at higher χ_IL is unexpected. In regime I it conforms to Aχ_IL ≫ Fχ_IL² and then transitions to tending towards Aχ_IL + Cχ^D_IL(1 − χ_IL) = Fχ_IL² in regime II as the CS:IL interaction term becomes more significant. From the perspective of the random walk model, the presence of PC results in an increase in an interaction between the SSs above that of the ‘normal’ system where there is no CS:IL interaction. (Conversely, the presence of DMSO, 1-MI, DMI or TMU results in a decrease in the theoretical interaction at particular molar fractions.) It is theorised that at low χ_IL, where SSs have formed, the PC molecules interact with the shells, but there are enough other PC molecules present in the bulk such that they cannot interact with more than one shell. Therefore, the interactive term is negligible and the curve initially follows the Aχ_IL ≪ Fχ_IL² curve. However, as the χ_IL increases, the ‘shielding’ effect of the free PC molecules decreases, which implies that PC molecules interact with more than one SS and decrease the dissolution of cellulose compared to a non-interactive system, regime IIa. Finally, in regime II the PC molecules interact with the maximum number of SS, minimising dissolution.

3.2.1 Regime 0. The random walk model starts with regime I, as, if there is an empty site, a walker can always move into it. As this model relies on site filling, it is not possible to predict regime 0, i.e. where cellulose is insoluble in the mixture. It is, however, useful to discern the start of regime 1, i.e. the lowest IL concentration at which cellulose begins to be soluble, based on a small number of measured data points, as is discussed in detail below. In our system, an empty site is a SS and the point of transition from the zeroth regime, where there is no cellulose dissolution, is a measure of the amount of cellulose solvated by a SS and the amount of IL in the OES. The transition point between regime 0 and regime I is correlated with the CS molar volume, Fig. 7. This trend is described by the following equation (which comes from the definition of χ_IL):where v_IL is the volume of IL in the mixture, v_CS is the volume of CS in the mixture, and V^IL_M and V^CS_M are the molar volumes of IL and CS, respectively. Eqn (8) fits the data well (R² of 0.957) with the f = −28.89 and v_IL = 0.0414 (this quantity is related to the choice of IL). As a check, the data were also linearised (see eqn (6)), yielding a fit with R² = 0.830 with χ_IL|_min = 0.171x − 0.122, (Fig. S5 in the ESI†).

An intuitive explanation of how SS, with approximately the same volume, could have drastically different χ_IL|_min is given in Fig. 8. In contrast with Fig. 3, where the χ_IL was constant, here we assume that the volume available is constant, and compare the effect of V^CS_M on χ_IL. As shown in Fig. 8, the number of CS molecules that can fill the available volume (v_CS) depends on its V_M. The bulkier the CS, the less fit into the available volume (v_CS), thus the ratio of IL:CS is greater, resulting in a larger χ_IL.

Fig. 8 Cartoon depiction of the relationship between V^CS_M and χ_IL|_min. Assuming a fixed volume available to the solution, and minimal number of SS, fewer bulky CS are required to fill the remaining volume (10 in this example) than the smaller CS (42). As the number of IL ion pairs is fixed (6), this number makes up a larger number proportion for the bulky than for the smaller , as illustrated on the right.

3.3 Comparison of the models

Both models were built separately, from separate assumptions, and both lead to the conclusion that (if the CS is an appropriate OES former, i.e. has suitable solvent properties, as defined previously⁴⁴), the volume available to form solvent shells is the most important aspect of the system. The 1-D random walk, grounded in ideas of universality explains this: once the solvent system is tending towards its limiting behaviour, a deep understanding of the underlying chemistry of the system is not required, the system can be modeled as described (as evidenced by the fact that differences between different high χ_IL OES are within experimental error) and solvent shells act like hard spheres in a finite box. This holds over the range identified as regime II of that model, which is associated with a significant IL:IL term in the linear model (the models are compared in Table 4). That this model is able describe most of the behaviour for most of the OESs is remarkable. The random walk model does not allow direct separation of the effects of a CS and IL interaction, but the multi-polynomial model does: a comparison of the two models shows where this interaction affects the system, and thus where the chemistry of the CS and IL should be considered.

Table 4 Comparison between the models

Quantity	Random walk model	Polynomial regression model
Minimum χIL (crossing point)	∝ d	∝ B
SS frustration		−FχIL^2
Regime I χcell	∝ x	≈AχIL
Regime II χcell		→AχIL − FχIL^2 as χIL → 1
χ cell	∝ νIL
CS:IL interaction	No	Yes = Cχ^DILχ^ECS

---

3.4 Use of the random walk model

The random walk model is useful to the experimentalist, allowing good prediction of experimental data from very few measurements, and should work for other ILs. As a demonstration, the predictions that could be gained from the model and measurements from a single OES composition, for Fig. 2 will be calculated; other figures can be calculated following a similar method. The value of a mixture of χ_IL = 1 is known, the value of χ_IL|_min can be obtained from eqn (8) (or Fig. 7, or eqn (6)), so only a single OES composition need to be measured. For an experimentalist, the most important range is nearest the corner of the curve as this is the most efficient composition.⁴⁴ As this is not known, a value of 0.2 ≤ χ_IL ≤ 0.4 is a good choice for measurement. To demonstrate the method, typical CSs, γ-but and DMAc, were chosen and, to demonstrate the limits, the CS least-well described by the model in Fig. 2, DMSO, was chosen.

A subset of three points was chosen and the fits to these were compared to the fit to the entire data. The molar volumes of γ-but, DMAc, DMSO and IL were input into eqn (8). DMAc has a χ_IL|_min value of 0.09 (the less accurate, linearized eqn (6) gives 0.12 and the value calculated from the fit in Fig. 2 is 0.06), χ_IL|_min DMSO is 0.056 and γ-but is 0.06. The measurements around χ_IL = 0.35, χ_IL = 0.4 and χ_IL|_min = 0.4 were chosen as the single measurement (which is made of 3 repeats for DMSO and DMAc, two repeats for γ-but) for DMAc, DMSO and γ-but respectively. To balance the fit, the points as χ_cell = 0 were repeated the same number of times as the experimentally measured point (i.e. 3 repeats for DMSO and DMAc and 2 repeats for γ-but). The final point was the value for χ_IL = 1 which was known.

As an example, the fit to the chosen subset of points is shown for γ-but in Fig. 9 (the data for DMSO and DMAc are given in Fig. S7 and S8 of the ESI†). For DMAc OES, the single measurement fit had an R² value of 0.995 to the whole data (as the fit to the whole data had an R² of 0.999 (see Table 1) by only measuring one point most of the variance in the data has been explained). The average residual between the single measurement fit and the actual data is only 7.06%. For DMSO, the single measurement fit has an R² to the whole data of 0.991 (again, using just a single measurement point affects only the third decimal place), and an average error of 9.43%. For γ-but, the single measurement fit has an R² to the whole data of 0.995 (the fit using the entire data has an R² of 0.996), and an average error of 7.40%.

Fig. 9 Using the random walk model for prediction of γ-but OES data. Brown: data (dots) and fit (line) to all measured data. Black: fit (line) to measured or estimated points (dots). Only the measurement at around χ_IL = 0.4 needs to be measured, the point at χ_IL = 1 is known and the point at χ_cell = 0 can be estimated from eqn (8). The single measurement fit differs from the actual data by only 7.4% on average.

Thus, to predict the data to within 10% error, an experimentalist need only locate the molar volume of the selected CS and measure one point in the range 0.2 ≤ χ_IL ≤ 0.4 (assuming the solubility in pure IL is known, if not, that measurement is also required). This is valid because, as results presented here have demonstrated, the volume of the SS (which relates to the volume of the CS and IL) is the most important feature for predicting behaviour in these systems. A good predicted solubility curve is provided, even where there are interactions between CS and IL, which cause the OES to deviate slightly from the 1-D random walk model. For example, the predicted curve for the DMSO-based OES fits well with that predicted from the random walk model, even though the regression model suggests CS/IL interactions: the non-random walk terms account for only around 10% of the variance. So, even for these CSs, an experimentalist could save significant time by starting with the predictions from the one measurement fit to the random model and refining any critical regions, if very precise data are required.

If the experimentalist chose to investigate a different IL (provided that it was measured experimentally with a minimum of two data points, including one that was the solubility of cellulose in the neat IL), this method would be appropriate and, moreover, very quick to apply. The key value needed, which is the minimum mole fraction of IL required to initiate cellulose dissolution, could be calculated from eqn (8). An alternative, and simpler approach, especially for finding the OES composition needed to dissolve a known amount of cellulose, is to use the fit to Fig. 4.

4 Conclusions

It has previously been demonstrated that suitable cellulose dissolving OESs may be selected by matching co-solvent parameters.^42,44 Here we show that, once such a co-solvent is identified (either by data-mining of solvent properties,⁴⁴ or by experimental means), minimal experimentation combined with the 1-D random walk model described here allows prediction of the entire experimental dissolution curve of a solute in an OES. In this scenario, the most relevant parameter governing the behavior of ‘good’ OESs is the volume available to form solvent shells, which is related to the molar volumes of both CS and IL. This fits with the previously noted indication of preferential solvation of cellulose chains derived from RISM calculations.⁴⁴

The 1-D random walk model is an example of a type of universal process, which has been applied to complicated multicomponent systems. It is useful to identify and understand the single dimension that a system can be described by, and doing so gives insight into the process and economy of the model. The success of this model helps highlight the important aspects of these systems and the most relevant control parameter (for the OESs in this paper), which is the volume fraction available to the IL. The amount of cellulose soluble in an OES is largely a function of the number of solvent shells that can be formed by the available IL, which relates to the number of IL ion pairs available and the volume of the solvent shell as a proportion of the total volume available. Thus, a space packing/counting model of solvent shells, modelled as hard spheres being added to a box, is sufficient to describe most (and in some cases all) observed behaviour. This model is general and could be applied to other solvent mixtures.

The 1-D random walk model is suitable for rapid and efficient prediction of a dissolution curve with changing composition of a mixed solvent system, such as an OES, requiring only two experimental measurements: maximum solubility of solute in the pure IL and solubility of the solute in the OES in the descending portion of the solubility curve, i.e. where solubility is sensitive to changes in composition. Thus, this provides a useful tool for vastly reducing the number of experiments required to develop the solubility curve for a new co-solvent, as demonstrated here for γ-butyrolactone. The very utility of this model derives from the reductionist approach. However, even the most superficial consideration of the chemistry of the components would suggest that intermolecular/interionic interactions are likely to modulate solvent properties in a manner not modelled by consideration of space-filling alone. Thus, a polynomial regression model was developed independently of the 1-D random walk model, to allow robust comparison. This highlights OESs that demonstrate slight deviations from the behavior predicted by the 1-D random walk model and, thus, points to interactions that are likely to be important. For example interaction, or cross terms, of the form (χ_IL)^D(1 − χ_IL)^E are required to describe some systems. Amongst the CSs tested, consideration of molar volume alone proved adequate to describe OESs formed with [EMIM][OAc] and NMP, γ-but, DMF, sulfolane, DMAc or γ-val, i.e. the CS:IL interaction was negligible. Positive interactions between CS and IL result in enhanced solubility, above that predicted by the 1-D model, for 1-MI, DMSO and DMI at low χ_IL, although it is notable that these require such minor adjustments to the model that most effects would disappear into experimental error, except in very comprehensive testing. In addition a positive CS:IL interaction was indicated for TMU across the entire range and a negative CS:IL interaction suggested for PC (a rather poor solvent for preparing OESs for cellulose dissolution). This shows the value of our approach whereby a simple, analytical and easy to understand model can describe almost all of the measured data, and a fitted regression model can highlight where other aspects, such as CS:IL interactions, are important. In one of these cases, previous results from more detailed theory (RISM) agreed with the findings from the regression model and confirmed the presence of a DMSO:IL interaction at low χ_IL and its absence at mid-range χ_IL.^44,52

Clearly, such intentional simplification of OES systems does not serve to describe the detailed interactions at a molecular, or electronic level, which would require detailed modelling approaches utilising high levels of theory. Nonetheless, the remarkably good fits demonstrated indicate a model that is very useful to reduce experimentation required, allowing rapid selection and implementation of new OESs. Furthermore, the deviations identified in the regression model point to groups of solvents and CS/IL combinations that merit further in-depth modelling to understand the subtle interactions occurring.

Acknowledgements

The authors thank the UK Engineering and Physical Sciences Research Council (EPSRC) for PhD studentship funding for R. H. W. and M. A. J. via the EPSRC Doctoral Training Centre in Sustainable Chemical Technologies, University of Bath (Grant No. EP/G03768X/1), and the British Council for funding via the Global Innovation Initiative program.

References

1. G. H. Weiss, Am. Sci., 1983, 71, 65–71.
2. E. Raposo, S. De Oliveira, A. Nemirovsky and M. Coutinho-Filho, Am. J. Phys., 1991, 59, 633–645.
3. R. J. Rubin, J. Chem. Phys., 1965, 43, 2392–2407.
4. E. Helfand, J. Chem. Phys., 1975, 62, 999–1005.
5. J. Nelson and R. E. Chandler, Coord. Chem. Rev., 2004, 248, 1181–1194.
6. H. J. Mandujano-Ramirez, J. P. Gonzalez-Vazquez, G. Oskam, T. Dittrich, G. Garcia-Belmonte, I. Mora-Sero, J. Bisquert and J. A. Anta, Phys. Chem. Chem. Phys., 2014, 16, 4082–4091.
7. P.-G. De Gennes, Scaling concepts in polymer physics, Cornell university press, 1979.
8. T. Wu and R. F. Loring, J. Chem. Phys., 1992, 97, 8568–8575.
9. H. J. Galla, W. Hartmann, U. Theilen and E. Sackmann, J. Membr. Biol., 1979, 48, 215–236.
10. J. Kaerger, J. Phys. Chem., 1991, 95, 5558–5560.
11. S. M. A. Tabei, S. Burov, H. Y. Kim, A. Kuznetsov, T. Huynh, J. Jureller, L. H. Philipson, A. R. Dinner and N. F. Scherer, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4911–4916.
12. A. G. Campaña, D. A. Leigh and U. Lewandowska, J. Am. Chem. Soc., 2013, 135, 8639–8645.
13. E. Gale, MSc thesis, Imperial College London, 2004.
14. J. Helfferich, F. Ziebert, S. Frey, H. Meyer, J. Farago, A. Blumen and J. Baschnagel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 042604.
15. L. Peliti and L. Pietronero, La Rivista del Nuovo Cimento (1978–1999), 1987, vol. 10, pp. 1–33.
16. P. Flory, Statistical mechanics of chain molecules, Wiley Online Library, 1969.
17. M. Kac, The American Mathematical Monthly, 1947, 54, 369–391.
18. R. Nossal, J. Stat. Phys., 1983, 30, 391–400.
19. J. Machta, J. Stat. Phys., 1983, 30, 305–314.
20. R. Kopelman, J. Hoshen, J. S. Newhouse and P. Argyrakis, J. Stat. Phys., 1983, 30, 335–343.
21. C. A. Helfer, G. Xu, W. L. Mattice and C. Pugh, Macromolecules, 2003, 36, 10071–10078.
22. S. Wolfram, Nature, 1984, 311, 419–424.
23. S. Yuste and L. Acedo, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 2340.
24. S. B. Yuste, L. Acedo and K. Lindenberg, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 052102.
25. S. B. Yuste and L. Acedo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 061107.
26. S. Yuste and L. Acedo, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, R3459.
27. J. Rudnick and G. Gaspari, Science, 1987, 237, 384–389.
28. A. Dvoretzky and P. Erdös, Some Problems on Random Walk in Space, Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability, University of California Press, 1951, pp. 353–367.
29. H. Larralde, P. Trunfio, S. Havlin, H. E. Stanley and G. H. Weiss, Nature, 1992, 355, 423–426.
30. H. Larralde, P. Trunfio, S. Havlin, H. E. Stanley and G. H. Weiss, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 7128.
31. H. Larralde and G. Weiss, J. Phys. A: Math. Gen., 1995, 28, 5217.
32. N. T. O'Neill, T. F. Eck, B. N. Holben, A. Smirnov, O. Dubovik and A. Royer, J. Geophys. Res.: Atmos., 2001, 106, 9787–9806.
33. D. H. Chung and T. H. Kwon, Polym. Compos., 2001, 22, 636–649.
34. V. N. Smelyanskiy, D. G. Luchinsky, A. Stefanovska and P. V. E. McClintock, Phys. Rev. Lett., 2005, 94, 098101.
35. B. A. Miller-Chou and J. L. Koenig, Prog. Polym. Sci., 2003, 28, 1223–1270.
36. D. Klemm, B. Heublein, H.-P. Fink and A. Bohn, Angew. Chem., Int. Ed., 2005, 44, 3358–3393.
37. A. Pinkert, K. N. Marsh, S. Pang and M. P. Staiger, Chem. Rev., 2009, 109, 6712–6728.
38. H. Wang, G. Gurau and R. D. Rogers, Chem. Soc. Rev., 2012, 41, 1519–1537.
39. R. P. Swatloski, S. K. Spear, J. D. Holbrey and R. D. Rogers, J. Am. Chem. Soc., 2002, 124, 4974–4975.
40. A. George, A. Brandt, K. Tran, S. M. S. N. S. Zahari, D. Klein-Marcuschamer, N. Sun, N. Sathitsuksanoh, J. Shi, V. Stavila, R. Parthasarathi, S. Singh, B. M. Holmes, T. Welton, B. A. Simmons and J. P. Hallett, Green Chem., 2015, 17, 1728–1734.
41. D. Klein-Marcuschamer, B. A. Simmons and H. W. Blanch, Biofuels, Bioprod. Biorefin., 2011, 5, 562–569.
42. R. Rinaldi, Chem. Commun., 2011, 47, 511–513.
43. O. Kazutaka, Y. Kohei, H. Shuichi and I. Toshiyuki, Chem. Lett., 2012, 41, 987–989.
44. E. Gale, R. H. Wirawan, R. L. Silveira, C. S. Pereira, M. A. Johns, M. S. Skaf and J. L. Scott, ACS Sustainable Chem. Eng., 2016, 4, 6200–6207.
45. H. Liu, K. L. Sale, B. M. Holmes, B. A. Simmons and S. Singh, J. Phys. Chem. B, 2010, 114, 4293–4301.
46. B. Lu, A. Xu and J. Wang, Green Chem., 2014, 16, 1326–1335.
47. R. S. Payal and S. Balasubramanian, Phys. Chem. Chem. Phys., 2014, 16, 17458–17465.
48. B. D. Rabideau and A. E. Ismail, Phys. Chem. Chem. Phys., 2015, 17, 5767–5775.
49. Y. Zhao, X. Liu, J. Wang and S. Zhang, J. Phys. Chem. B, 2013, 117, 9042–9049.
50. F. Huo, Z. Liu and W. Wang, J. Phys. Chem. B, 2013, 117, 11780–11792.
51. J.-M. Andanson, E. Bordes, J. Devemy, F. Leroux, A. A. H. Padua and M. F. C. Gomes, Green Chem., 2014, 16, 2528–2538.
52. S. Velioglu, X. Yao, J. Devémy, M. G. Ahunbay, S. B. Tantekin-Ersolmaz, A. Dequidt, M. F. Costa Gomes and A. A. Pádua, J. Phys. Chem. B, 2014, 118, 14860–14869.
53. A. Donev, I. Cisse, D. Sachs, E. A. Variano, F. H. Stillinger, R. Connelly, S. Torquato and P. M. Chaikin, Science, 2004, 303, 990–993.
54. J. H. Lindsey, Mathematika, 2010, 33, 137–147.
55. N. J. A. Sloane, Nature, 1998, 395, 435–436.
56. L. S. Lasdon, R. L. Fox and M. W. Ratner, RAIRO – Operations Research – Recherche Opérationnelle, 1974, vol. 8, pp. 73–103.
57. Wolfram Research Incorporated, Wolfram Mathematica 11.
58. J. Zhang, H. Zhang, J. Wu, J. Zhang, J. He and J. Xiang, Phys. Chem. Chem. Phys., 2010, 12, 1941–1947.
59. R. C. Remsing, I. D. Petrik, Z. Liu and G. Moyna, Phys. Chem. Chem. Phys., 2010, 12, 14827–14828.
60. C. S. Lovell, A. Walker, R. A. Damion, A. Radhi, S. F. Tanner, T. Budtova and M. E. Ries, Biomacromolecules, 2010, 11, 2927–2935.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp02873c

‡ Current address: School of Experimental Psychology, University of Bristol, 12a Priory Road, Bristol, BS8 1TU, UK. E-mail: ella.gale@bristol.ac.uk

§ These authors contributed equally to this work.

¶ Note that, the maximum volume is not 100% of the available volume as the solvent shells cannot fill all available space. Instead, they occupy between 68%⁵³ and 77.8%^54,55 of the total volume, dependent on whether the shells are spherical, or elliptical, and maximally packed or randomly packed.

|| There are results for the trapping problem, where a walker can be trapped. This theory is not used here because the usual measure is the survival probability of the walker in the presence of traps – it has been assumed that molecule Z will always dissolve if there is an empty site available.

** Although, the methodology used to calculate these numbers has been questioned.⁵⁹

---