Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Developing force fields when experimental data is sparse: AMBER/GAFF-compatible parameters for inorganic and alkyl oxoanions†
Sadra
Kashefolgheta
 and
Ana
Vila Verde
and
Ana
Vila Verde
 *
*
Department of Theory & Bio-systems, Max Planck Institute for Colloids and Interfaces, Science Park, Potsdam 14476, Germany. E-mail: ana.vilaverde@mpikg.mpg.de; Fax: +49 (0)331 567 9602; Tel: +49 (0)331 567 9608
First published on 17th July 2017
Abstract
We present a set of Lennard-Jones parameters for classical, all-atom models of acetate and various alkylated and non-alkylated forms of sulfate, sulfonate and phosphate ions, optimized to reproduce their interactions with water and with the physiologically relevant sodium, ammonium and methylammonium cations. The parameters are internally consistent and are fully compatible with the Generalized Amber Force Field (GAFF), the AMBER force field for proteins, the accompanying TIP3P water model and the sodium model of Joung and Cheatham. The parameters were developed primarily relying on experimental information – hydration free energies and solution activity derivatives at 0.5 m concentration – with ab initio, gas phase calculations being used for the cases where experimental information is missing. The ab initio parameterization scheme presented here is distinct from other approaches because it explicitly connects gas phase binding energies to intermolecular interactions in solution. We demonstrate that the original GAFF/AMBER parameters often overestimate anion–cation interactions, leading to an excessive number of contact ion pairs in solutions of carboxylate ions, and to aggregation in solutions of divalent ions. GAFF/AMBER parameters lead to excessive numbers of salt bridges in proteins and of contact ion pairs between sodium and acidic protein groups, issues that are resolved by using the optimized parameters presented here.
1 Introduction
Monoatomic and small polyatomic ions are key players in many biological processes, such as DNA folding,1 blood coagulation and anti-coagulation,2,3 protein stability4 and protein crystallization.5 The molecular mechanisms by which ions act are currently incompletely understood, in part because inferring molecular scale details from the signals detected in experiment cannot be unambiguously done. In contrast, molecular scale details are directly accessible from simulations and atomistic models, making the development of such models of critical importance.Because proteins and other biomolecules are typically large (50–3000 kDa), only simulations using classical, non-polarizable force fields give access to the long length and time scales relevant for many processes taking place in bio-systems. To be useful, force fields must strike the correct balance between the various intermolecular interactions: biomolecule–water, biomolecule–biomolecule, water–water, water–ion, ion–counterion and ion–biomolecule interactions; in this last case, the main contribution would come from the interaction between the ions in solution and the charged sites of the biomolecules. Classical, fixed-charge force fields for biomolecules in water have been under evolution for decades and are now quite successful at predicting binding affinities6 and the folded structure of small proteins,7–9 the self-assembly of phospholipid bilayers,10 the importance of electrostatics in DNA, and DNA–protein interactions.11,12 These force fields were parameterized against experimental observables that reflect the balance between ion–water, biomolecule–water and water–water interactions (e.g., free energies of hydration).13,14 More recently, force fields for aqueous solutions of alkali, alkali-earth and halide ions were developed that also show reasonable anion–cation interactions. They are thus able to reproduce experimental osmotic pressures or solution activities at salt concentrations below 1 M,15–19 and in a few cases up to much higher concentrations.20 Simulations based on these force fields have already offered unprecedented insight into the molecular scale origin of ion-specific effects in biological systems.21
In contrast to the advanced state of development of classical molecular models for alkali and halide ions for explicit water simulations, there are currently only a few models of small, polyatomic anions that have been parameterized to reflect the correct balance between their interactions with water, with cationic amino acids or with commonly used counterions.22–24 Such models are of interest because polyatomic anions such as sulfates, phosphates or acetates are present in the physiological context in inorganic and/or alkylated form, and the molecular scale details regarding their interaction with biomolecules are not yet understood.25–27 Simulations of biomolecular systems performed so far with these ions have simply used general parameters based on commonly used biomolecular force fields such as CHARMM or AMBER:13 the partial charges are obtained from low level quantum mechanical calculations and RESP fitting,28 and the Lennard-Jones parameters for each atom type are the same as those used in the chosen biomolecular force field. Parameters obtained this way are typically used for simulations without further tests – either comparison with experimental data or with ab initio calculations – under the assumption that the ion parameters must be reliable because they were obtained with the established protocol used to develop the biomolecular force field. However, these protocols have only been proven reasonable for neutral biomolecules13,14 and they are known to fail for charged species, e.g., they yield hydration free energies substantially more negative than those experimentally measured.13
In this work, we aim to overcome the above limitations of existing classical, fixed-charge models of polyatomic ions for simulations of biomolecular systems in explicit water. We focus specifically on the polyatomic anions methyl-sulfonate (CH3SO3−), methyl-sulfate (CH3SO4−), acetate (CH3COO−), dimethyl-phosphate ((CH3)2PO4−), methyl-hydrogenphosphate (CH3HPO4−) and methyl-phosphate (CH3PO42−); these anions were selected because they are good analogues of anionic polymers with longer alkyl chains. We also develop parameters for the non-methylated versions of the sulfate and phosphate ions (SO42−, HSO4−, HPO42−, H2PO4−). The parameterization approach we present ensures that the ion parameters reflect the correct balance of the ion interactions with water, with the commonly used counterion Na+ and with analogues (methylammonium, CH3NH3+, and ammonium, NH4+) of the amino acid lysine, while ensuring that the parameters for all the ions remain internally consistent. The parameters developed here are compatible with widely used force fields for molecular simulations: the AMBER13 force field for proteins, the accompanying TIP3P29 water model, and the sodium model of Joung and Cheatham which is often used as counterion.15
Intramolecular parameters for the anions already exist;13,30–32 the main issue is to parameterize their intermolecular interactions. In the context of the AMBER13 force field for proteins, intermolecular interactions depend on the Lennard-Jones parameters and on the partial charges of the atoms composing the interacting species. We obtain the partial charges of the ions following the standard procedure used in AMBER13 – low level ab initio calculations followed by RESP fitting – so only the Lennard-Jones parameters of the ions are optimized.‡
Difficulties optimizing Lennard-Jones parameters for polyatomic anions
To parameterize intermolecular potentials, it would be desirable to reproduce high quality thermodynamic data that strongly depends on intermolecular interactions: e.g., free energies of hydration, which reflect ion–water interactions, or solution activities, which reflect anion–cation interactions. This approach was followed by several groups to develop better models of alkali halides.15,16,19 However, experimental data exists only for a few of the cases of interest here. For example, hydration free energies exist for CH3COO−, but not for CH3SO3−, CH3SO4−, CH3PO42−, CH3HPO4− or (CH3)2PO4−.33 Osmotic pressure or solution activity data for solutions containing the cationic amino acids arginine and lysine, or suitable small-molecule analogues, and polyatomic anions are also not available. For solutions involving polyatomic anions and Na+, data exists only for CH3SO3− and CH3COO−.Given that there is no complete set of experimental information that we can use to obtain an internally consistent set of parameters for all the anions mentioned above, an alternative would be to develop classical models solely based on ab initio calculations. One possibility would be to develop parameters to match observables (e.g., the potential of mean force between two ions) calculated from ab initio molecular dynamics (MD) in explicit solvent. The main shortcoming of this approach is that, currently, ab initio MD can only access timescales of tens of picoseconds, so the calculated free energy profiles have high statistical uncertainty.34,35 A second possible shortcoming could be that a low level of theory must necessarily be used in these calculations, which could introduce systematic errors. Recent results, however, indicate that DFT with appropriate dispersion corrections yields reasonable results: structural properties of iodate in water calculated with MD-DFT simulations agree well with results from X-ray absorption fine structure spectroscopy (XAFS).36 Another possibility would be to develop parameters based solely on single-point ab initio calculations, for example water–ion dimers, dry ion pairs or even small hydrated systems (e.g., an ion-pair or a single ion surrounded by a first hydration layer); dry ion pairs or water–ion dimers are here referred to as systems in the gas-phase. Multiple studies, however,14,37 show that these approaches fail to produce parameters that are adequate for simulations of aqueous systems: the gas-phase intermolecular interaction energies calculated using ab initio methods differ significantly from those calculated using classical models optimized to reproduce properties of aqueous systems. How, then, can we obtain an internally consistent set of parameters for the ions in question, given the existing limitations in experimental data and in ab initio methods?
Proposed approach
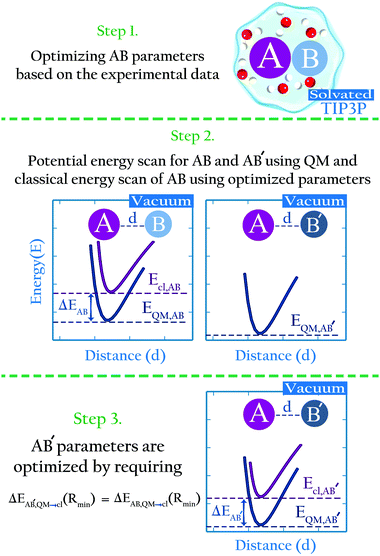
We propose an approach to develop non-bonded parameters for ionic species in aqueous systems, that combines experimental data and ab initio simulations. This combination is done in a manner that yields an internally consistent set of parameters for the anion–cation and ion–water interactions.Here we briefly described the main points behind the approach; in the Methods section we present a detailed algorithm that may be followed by interested users. Let us consider species A, B and B′. B and B′ are similar, i.e., they have identical charge and similar composition (e.g., CH3SO4− and CH3COO−), yet different enough that they may not necessarily share identical parameters (e.g., the oxygen Lennard-Jones parameters in CH3SO4− and CH3COO− are not necessarily identical). AB and AB′ denote dimers of these species interacting non-covalently. Lennard-Jones parameters for the intermolecular interactions in AB in water have been developed based on experimental data (Fig. 1, step 1), but analogous experimental data for the AB′ system does not exist. Using high level ab initio calculations, we calculate the intermolecular energies in the AB and AB′ systems in the gas phase, as a function of the intermolecular distance (Fig. 1, step 2). We also perform the analogous potential energy scan for the AB system using the classical, optimized parameters. As illustrated in cartoon form in Fig. 1 (step 2), the interaction energy for system AB from ab initio calculations differs from that calculated using the classical model. This difference reflects the fact that the classical parameters were optimized for the intermolecular interactions of AB in water, and that the polarization state of molecules or ions in a dimer in the gas phase is very different from their polarization state in water.14,38 Therefore, the AB parameters offer a poor description of the intermolecular interactions of this dimer in the gas phase. We then assume that the polarization state of similar species should be perturbed to a similar extent when they are immersed in water. If this assumption is true, then the difference in the minimum interaction energy between the classical and ab initio methods for AB, Ecl,AB(Rmin) − EQM,AB(Rmin), should be very similar to the same difference for the AB′ system, Ecl,AB′(Rmin) − EQM,AB′(Rmin). In this article we show that this assumption indeed holds. This finding implies that classical parameters for the intermolecular interactions of the AB′ system can be determined by requiring that
| ΔEAB′,QM→cl(Rmin) = ΔEAB,QM→cl(Rmin) | (1) |
| ΔEAB,QM→cl(Rmin) = Ecl,AB(Rmin) − EQM,AB(Rmin) | (2) |
We use this approach to develop a set of classical parameters for polyatomic anions which is internally consistent and which is fully compatible with the AMBER13 force field for proteins, the TIP3P29 water model and the sodium ion model of Joung and Cheatham.15 The experimental properties we use for parameterization are the solution activity derivatives and the hydration free energies. Solution activities exist only for NaCH3SO3, NH4CH3SO3, NaCH3COO, Na2SO4 and (NH4)2SO4; reliable hydration free energies exist only for HSO4−, CH3COO− and SO42−. We optimize the parameters for the ions based on this experimental information, and then use ab initio calculations and the approach described above to obtain parameters for the remaining cases.
2 Methods
2.1 Molecular dynamics simulations
For sodium (Na+) and chloride (Cl−) we use Joung and Cheatham parameters,15 which are shown to reproduce reasonably well solvation free energies and ion–water binding energies when used in combination with TIP3P water.29
We introduce a general notation for the anions, An−, here investigated: (RO)kXOmn−, where X = {S,P,C} and R = {H,CH3}. The anions have up to three different oxygen types, represented as follows: atom type O2 represents terminal oxygens, atom type OH represents acidic oxygens and atom type OS represents X–O–X oxygens (e.g., C–O–P in (CH3)2PO4−). We use  to represent any of the three oxygen types,
to represent any of the three oxygen types, 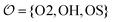 . The hydrogen atoms connected to the nitrogen in NH4+ and CH3NH3+ are indicated as HN.
. The hydrogen atoms connected to the nitrogen in NH4+ and CH3NH3+ are indicated as HN.
Intramolecular bond, angle and dihedral parameters for the anions, NH4+ and CH3NH3+ are taken from GAFF;13,30–32 for a few angles and dihedrals of the anions, it was necessary to change the strength of the potential, as indicated in the parameter files given as ESI,† to avoid unphysical intramolecular clashes. The partial charges for the atoms composing the anions, NH4+ and CH3NH3+ are obtained using the standard RESP fitting protocol used in the AMBER13 force field, as described in Section 2.2.1.
The ε and σ parameters determine the Lennard-Jones interaction energy of two species i and j as
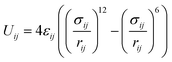 | (3) |
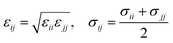 | (4) |
 ), and between the anion-oxygens and nitrogen and HN atoms in NH4+ or CH3NH3+ (
), and between the anion-oxygens and nitrogen and HN atoms in NH4+ or CH3NH3+ (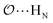 and
and 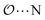 ), that should be used instead of eqn (4).
), that should be used instead of eqn (4).
The optimization of the anion-oxygen Lennard-Jones parameters proceeded in multiple stages. These are now described in the form of a road map that may be followed when applying our approach to parameterize intermolecular interactions for any species in water:
(1) Select a starting parameter set for the species to be parameterized. Intramolecular parameters are indispensable because the approach we propose applies only to non-bonded interactions. GAFF provided good initial parameters for the oxoanions.
(2) Select which interactions should be optimized; select which experimental target properties exist for parameterization. In our case, the difference in the hydration free energies between the anions and a reference ion (Cl−) is selected to optimize ion–water interactions:
| ΔΔGsolv = ΔGsolv(An−) − n × ΔGsolv(Cl−) | (5) |
The solution activity derivative at 0.5 m is selected to optimize anion–cation cation interactions. Details of these simulations are given in Sections 2.1.2 and in the ESI† (SI 2.2).
Ion–water interactions should be optimized before anion–cation interactions; the remainder of this road map reflects this order.
(3) Evaluate the quality of the initial parameter set with respect to the primary experimental target property, and select which ion parameters will be optimized. We calculated the hydration free energies of the anions for which that information was available. We found that GAFF parameters failed in some cases, leading to ΔΔGsolv that differed from the target more than 2 kcal mol−1, i.e., more than the uncertainty associated with the experimental target values.33,39 For the ions for which GAFF parameters proved insufficient, we optimize ion–water interactions.
Because we only have one target experimental property – the hydration free energy – for parameterization of ion–water interactions, we opt to optimize only the self-interaction Lennard-Jones parameters associated with the anion oxygens. The oxygens form the outer part of the anions, and for that reason dominate the Lennard-Jones interactions of the anions with any nearby species. If multiple target properties exist, then parameters for multiple atoms may be optimized.
(4) Optimize self-interaction parameters based on hydration free energies, for the species for which these energies exist. The self-interaction 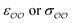 parameters of the oxygens in CH3COO− and SO42− are optimized to reproduce the experimentally determined difference in solvation free energy between those anions and Cl−, ΔΔGsolv.
parameters of the oxygens in CH3COO− and SO42− are optimized to reproduce the experimentally determined difference in solvation free energy between those anions and Cl−, ΔΔGsolv.
Given that only one target property was selected for optimization, an infinite number of combinations of 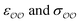 values could yield equally good agreement with the target, possibly at the expense of the performance of the model regarding other observables. Because the original GAFF parameters are physically-based – they are derived to reproduce the density and heats of vaporization of organic liquids13,30–32 – we retain them for either
values could yield equally good agreement with the target, possibly at the expense of the performance of the model regarding other observables. Because the original GAFF parameters are physically-based – they are derived to reproduce the density and heats of vaporization of organic liquids13,30–32 – we retain them for either 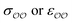 , and optimize the remaining parameter only. We optimize
, and optimize the remaining parameter only. We optimize 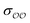 for the cases where the original GAFF13,30–32 parameters led to deviations greater than 10 kcal mol−1 from the target ΔΔGsolv, but we optimize
for the cases where the original GAFF13,30–32 parameters led to deviations greater than 10 kcal mol−1 from the target ΔΔGsolv, but we optimize 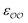 for the cases where the deviation was lower than 10 kcal mol−1. This threshold energy was chosen because a change of ΔΔGsolv > 10 kcal mol−1 is approximately equal to half the ΔΔGsolv between Na+ and K+, two ions which differ substantially in radius.§
for the cases where the deviation was lower than 10 kcal mol−1. This threshold energy was chosen because a change of ΔΔGsolv > 10 kcal mol−1 is approximately equal to half the ΔΔGsolv between Na+ and K+, two ions which differ substantially in radius.§![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33
33
To find the optimal parameters, we calculate the hydration free energies for a range of the scaling factor, f, applied to 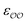 or to
or to 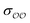 parameters; 4–6 different values of f ranging from 0.7 to 1.3 are used. We fit a linear function to the results. The optimal parameters are found by solving the linear function for the experimental SolvFE difference, ΔΔGExpsolv.
parameters; 4–6 different values of f ranging from 0.7 to 1.3 are used. We fit a linear function to the results. The optimal parameters are found by solving the linear function for the experimental SolvFE difference, ΔΔGExpsolv.
(5) Optimize the self-interaction parameters of the oxygen atoms of the remaining anions (for which reliable hydration free energies are not available) following the ab initio approach described in the introduction.
(a) For each species still to be parameterized (B′), identify a similar species that was already parameterized (B). Similar species must have the same charge and must have similar general composition, primarily evaluated in terms of the characteristics (e.g., identity, hybridization, polarization) of the atoms being parameterized. Here we considered oxoanions of the same charge as similar species.
(b) For the water-B and water-B′ dimers, select an initial relative orientation that is expected to yield similar and strong intermolecular interactions. For example, relative orientations where one of the water hydroxyl groups is pointing to the O2 oxygens in both B and B′ are similar; relative orientations where the water hydroxyl groups point to an O2 oxygen in one of the species, but to an OH or OS oxygen in the other species are not similar. Strong intermolecular interactions refer to orientations that are expected to have particularly favourable interaction energies.
For the chosen initial structures, perform gas phase ab initio potential energy scans as described in Section 2.2.2. If water-B and water-B′ differ in hyperconjugation effects (this situation did not happen in our systems), repeat the ab initio calculations with different relative orientations (identical for the two dimers) until one is found that yields similar hyperconjugation effects for both dimers. The importance of hyperconjugation effects in our parameterization approach is described in the context of anion–cation gas phase scans in Section 3.2.2.1.
(c) For the water-B dimer, perform a gas phase potential energy scan with the classical model and the optimized parameters, and using the same structures used in the ab initio scan. Calculate the difference, ΔEwater-B,QM→cl(Rmin), between the position of the energy minimum in the ab initio and the classical curves. This calculation is done by first fitting each set of data to a function of the form A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(B × R) + C(R−6) + (D/R), where A, B, C and D are fitting parameters, corresponding to the Buckingham potential form with an added electrostatic (1/R) term, and then identifying the minimum of the fitted functions.
exp(B × R) + C(R−6) + (D/R), where A, B, C and D are fitting parameters, corresponding to the Buckingham potential form with an added electrostatic (1/R) term, and then identifying the minimum of the fitted functions.
(d) For the water-B′ dimer, perform multiple gas phase potential energy scan with the classical model and multiple values of 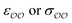 parameters, until a parameter value is found for which ΔEwater-B,QM→cl(Rmin) = ΔEwater-B′,QM→cl(Rmin) (eqn (1)) to within 0.5 kcal mol−1. We tested values of
parameters, until a parameter value is found for which ΔEwater-B,QM→cl(Rmin) = ΔEwater-B′,QM→cl(Rmin) (eqn (1)) to within 0.5 kcal mol−1. We tested values of 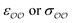 ranging from 0.6 to 1.3 times the original values, in intervals of 0.01 for
ranging from 0.6 to 1.3 times the original values, in intervals of 0.01 for 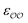 and 0.001 for
and 0.001 for 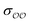 . For similar reasons as those indicated in point 4, we optimize
. For similar reasons as those indicated in point 4, we optimize 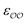 when the original ΔEwater-B′,QM→cl(Rmin) differs less than 1 kcal mol−1 from the target, and optimize
when the original ΔEwater-B′,QM→cl(Rmin) differs less than 1 kcal mol−1 from the target, and optimize 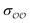 otherwise.
otherwise.
(6) Evaluate whether the Lorentz–Berthelot combination rules (eqn (4)) together with the current parameter set – already including the optimized self-interaction parameters – allows the reproduction of experimental properties that strongly depend on anion–cation interactions; select which ion parameters will be optimized. We tested whether the current parameter set yields reasonable solution activity derivative at 0.5 m, for the salts for which experimental solution activities are available. The combination rules proved insufficient for all test cases, as described in the Results section, leading to deviations larger than 0.03 – the statistical uncertainty associated with our calculations – from the target values.
As for the case of the self-interaction parameters, we only have one target property against which to optimize anion–cation interactions – the solution activity derivative. For this reason, we opt to tune the Lennard-Jones ε or σ parameters corresponding to the interaction between the anion-oxygens and Na+, and between the anion-oxygens and N and HN in NH4+. Both parameters for N and for HN are optimized because in this case the buried atom, N, is expected to contribute significantly to the intermolecular interactions; hydrogen atoms always have weak or zero Lennard-Jones potentials.
(7) Optimize anion–cation interaction parameters based on experimental properties, for the salts for which they exist. The Lennard-Jones ε or σ parameters corresponding to the interaction between the anion-oxygens and Na+ (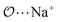 ), and between the anion-oxygens and N and HN in NH4+ (
), and between the anion-oxygens and N and HN in NH4+ (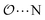 and
and 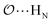 ) are parameterized to reproduce the activity derivative of 0.5 m solutions of salts for which that information was available.
) are parameterized to reproduce the activity derivative of 0.5 m solutions of salts for which that information was available.
For similar reasons as those indicated in point 4, we optimize either ε or σ, and retain the parameters obtained via the combination rules (eqn (4)) for the remaining parameter. We optimize σ when the initial solution activity derivative deviates from the target more than 0.1. and optimize ε otherwise. The determination of the optimal parameters followed an analogous procedure as that described in point 4.
(8) Optimize the intermolecular interaction parameters for the remaining salts (for which experimental target properties are not available) following the ab initio approach described in the introduction. We optimized the Lennard-Jones parameters determining the 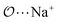 ,
, 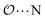 and
and 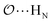 interactions.
interactions.
(a) For each anion–cation pair to be parameterized (AB′), identify a similar pair for which intermolecular interactions are already parameterized (AB). The pairs must share a common ion (A), and B and B′ must be similar species; see point 5a for the conditions defining similarity between B and B′.
(b) For the AB and AB′ dimers, select an initial relative orientation that is expected to yield similar and strong intermediate interactions. Here we consider only orientations where the O2 oxygens face the cations. Perform gas phase, ab initio potential energy scans as described in point 5b, evaluate hyperconjugation effects, and find new orientations if necessary. A detailed discussion of the impact of hyperconjugation effects on anion–cation interactions is given in Section 3.2.2.1.
(c) For the AB dimer, perform a gas phase potential energy scan with the classical model and the optimized parameters, and with the same configurations used in the ab initio scan. Calculate ΔEAB,QM→cl(Rmin) (see eqn (1)).
(d) For the AB′ dimer, perform multiple gas phase potential energy scans with the classical model and multiple values of ε or σ for the 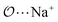 ,
, 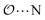 and
and 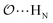 interactions until a parameter value is found for which ΔEAB,QM→cl(Rmin) = ΔEAB′,QM→cl(Rmin) to within 0.5 kcal mol−1. Further details analogous to those in point 5d.
interactions until a parameter value is found for which ΔEAB,QM→cl(Rmin) = ΔEAB′,QM→cl(Rmin) to within 0.5 kcal mol−1. Further details analogous to those in point 5d.
In the Results section we discuss further aspects concerning the application of this approach to our systems. The final parameters, expressed as a scaling factor relative to the original GAFF13,30–32 parameters to facilitate comparisons, are shown in the Tables presented in the Results section, as well as in the ESI† in Gromacs-readable files.
The solution activity derivatives are calculated according to the Kirkwood–Buff theory,46 with expressions for the integrals formulated specifically for closed systems.47 A summary of the most relevant aspects of this theory and how it was applied here is given in the ESI.† The simulation box for the calculation of the activity derivative was prepared by putting 72 anions and 72 cations (144 when using divalent anions) in a cubic box with dimensions 4.0 × 4.0 × 4.0 nm3 and solvating the system by adding ≈8000 TIP3P29 water molecules using editconf and solvate tools from Gromacs 5.0.40,41 The salt concentration simulated is thus 0.5 m. The system is equilibrated for 10 ns in the NPT ensemble. We select three distinct configurations from the equilibration run, with a box volume similar to the average box volume obtained during the equilibration. Each of these configurations is then used as the initial state for a 50 ns simulation in the NVT ensemble. The total simulation time for each production run is thus 150 ns; this large simulation time is necessary to provide enough sampling to calculate activity derivatives. The statistical uncertainty associated with the calculated activity derivatives is 0.03, as shown in Table S4 of the ESI.†
The starting configuration for the solvation free energy calculations is prepared by placing a single ion in a simulation box of dimensions ∼4.0 × 4.0 × 4.0 nm3 and solvating it in TIP3P water.29 The free energy is obtained along the path coordinates of λLJ and λC, which are the scaling factor to the Lennard-Jones and the electrostatic potentials, respectively. These scaling factors range from 0 to 1 (1 for the decoupled state and 0 for the fully coupled state). To ensure adequate ensemble overlap, we use 21 steps for each of λLJ and λC; the steps are evenly spaced for λC; for the λLJ spacing we use 21 unevenly spaced points, where λLJ ∈ {0.00 0.06 0.12 0.18 0.24 0.30 0.36 0.42 0.46 0.50 0.52 0.54 0.56 0.58 0.60 0.64 0.68 0.72 0.76 0.80 1.00}. Soft core potentials are used during the LJ coupling. For each λ we perform an equilibration of 100 ps followed by a production run of 1 ns in the NPT ensemble. The total solvation free energies are calculated from the partial results along the path coordinates using Bennett's acceptance ratio (BAR),48 as implemented in Gromacs 5.0.40,41 The estimated uncertainty associated with the calculated solvation free energies is 0.1 kcal mol−1, as shown in Table S3 of the ESI.† This value is estimated by performing different simulations for the same systems, using 0.5 ns simulations for each 21 lambda values. For divalent anions 41 lambda spacing was used as well for comparision, and the result did not change from the one obtained from 21 lambdas. The solvation free energies calculated directly from simulation must be corrected before they can be compared with experiment.39 In the ESI† (SI 2.1) we describe in detail which correction terms are included in the values here reported.
2.2 Ab initio calculations
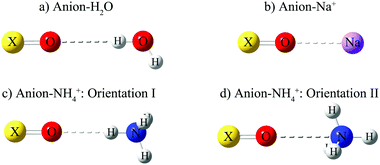 | ||
| Fig. 2 Example configurations for the 1-D potential energy scans of anions: (a) with H2O, (b) with Na+, (c) with NH4+ in orientation I, (d) with NH4+ in orientation II. Orientation I results in a stronger hydrogen bond than orientation II.53 | ||
3 Results and discussion
The optimized parameters are presented in the ESI,† in.top/.itp format for gromacs users; the original values are shown as comments, to facilitate comparisons. Amber-format parameters are given in the same files in the form of comments.3.1 Determining self-interaction parameters for the oxygens of the anions
The optimized parameters for HSO4−, SO42− and CH3COO−, as well as their experimental and computational SolvFEs, are given in Table 1. The GAFF13,30–32 parameters lead to a −0.6 kcal mol−1 deviation from the target value for HSO4−. Because the uncertainty associated with experimentally determined solvation free energies of single ions39 is at least of the order of this deviation, we do not further parameterize HSO4− against the SolvFE and we use the GAFF13,30–32 Lennard-Jones parameters for this anion.
| Anion | Parameters | n × ΔGCompsolv(Cl−) (kcal mol−1) | ΔGComp,GAFFsolv(An−) (kcal mol−1) | ΔGComp,OPTsolv(An−) (kcal mol−1) | ΔΔGComp,GAFFsolv (kcal mol−1) | ΔΔGComp,OPTsolv (kcal mol−1) | ΔΔGExpsolv (kcal mol−1) | Deviationsc (kcal mol−1) | |
|---|---|---|---|---|---|---|---|---|---|
| GAFF | OPT | ||||||||
| a No scaling. b Ref. 33. c ΔΔGCompsolv − ΔΔGExpsolv; ΔΔGsolv is defined in eqn (5). | |||||||||
| HSO4− | —a | 1 × (−87.3) | −85.1 | —a | 2.2 | —a | 2.8b | −0.6 | —a |
| CH3COO− | 0.77 × εO2–O2 | 1 × (−87.3) | −92.0 | −93.0 | −4.7 | −5.7 | −6.2b | +1.5 | +0.5 |
| SO42− | 1.17 ×σO2–O2 | 2 × (−87.3) | −297.1 | −270.0 | −122.5 | −95.4 | −94.6b | −27.9 | −0.8 |
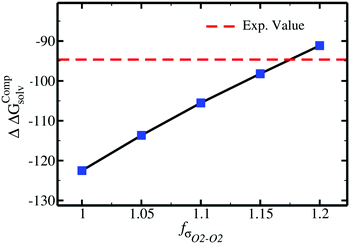
For acetate (CH3COO−), the original εO2–O2 needs to be scaled by a factor of 0.77 to retrieve the experimental SolvFE for this ion. The optimized parameter thus reproduces the difference in hydration free energies between Cl− and CH3COO− better than the GAFF13,30–32 parameters. We note, however, that the deviation from experiment using the GAFF13,30–32 parameters is only +2.3 kcal mol−1, so using GAFF parameters to investigate the interactions of this anion with water is acceptable. In contrast, GAFF13,30–32 parameters yield a far too low hydration free energy for SO42−: the deviation from experiment is −27.9 kcal mol−1. A scaling factor of 1.17 to the original σO2–O2 parameter is required to reproduce the target ΔΔGExpsolv of the sulfate. GAFF13,30–32 parameters dramatically fail to reproduce the SolvFE of multivalent ions, emphasizing the importance of parameter optimization with respect to SolvFE for those anions.
For each of the CH3SO4−, CH3SO3−, HPO42− and CH3PO42− anions, we perform an ab initio gas phase potential energy scan of the anion–water dimer, as described in Section 2.2.2. For parameter optimization, we require the same type of potential energy scan to be performed for a reference species for which classical parameters already exist: we use SO42− as the reference compound for CH3PO42− and HPO42−, and HSO4− as the reference compound for CH3SO4−, CH3SO3−, H2PO4− and (CH3)2PO4− because of their similarities in total charge and structure. Example scans, for CH3SO3−–water and CH3COO−–water, are shown in Fig. S3 of the ESI;† the energy and interparticle separation at the energy minimum are shown in Table S2 of the ESI† for all cases. We then proceed to optimize the self-interaction parameters as described in point 5 of the road map given in the Methods section.
The optimized self-interaction parameters for the oxygens in all the anions are shown in Table 2. The same table also shows ΔRQM→cl(Rmin), the difference in the position of the potential energy minimum calculated using ab initio and using classical parameters. For the divalent anions, the optimized parameters result in larger anion–water separation at the energy minimum of the dimer than the original GAFF13,30–32 parameters. This increase has been observed in other parameterizations of multivalent oxoanions based on experimental data,54 and illustrates the inadequacy of applying GAFF13,30–32 parameters, derived for neutral molecules, to heavily charged species.
| Anion | Opt.b | Parametersc | ΔEGAFFQM→cl(Rm)d (kcal mol−1) | ΔEOPTQM→cl(Rm)d (kcal mol−1) | ΔRGAFFm,QM→cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e (Å) e (Å) |
ΔROPTm,QM→cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e (Å) e (Å) |
|---|---|---|---|---|---|---|
| a No scaling. b Parameters optimized based on hydration free energies (Exp), repeated here to facilitate comparisons, or based on the ab initio approach (Comp). c Expressed as a scaling factor relative to the original GAFF parameters (given in the ESI). d ΔEQM→cl(Rm) is defined in eqn (2). e ΔRm,QM→cl: the difference between the position of the dimer energy minimum obtained using ab initio calculations and using classical parameters. f See text for explanation; NC: not calculated. | ||||||
| HSO4− | Exp | —a | −1.3 | —a | −0.14 | —a |
| CH3SO4− | Comp | —a | −1.4 | —a | −0.15 | —a |
| CH3SO3− | Comp | —a | −1.7 | —a | −0.15 | —a |
| H2PO4− | Comp | —a | −1.4 | —a | −0.12 | —a |
| CH3HPO4− | —a | NC | —a | NC | —a | |
| (CH3)2PO4− | Comp | —a | −1.1 | —a | −0.11 | —a |
| CH3COO− | Exp |
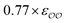
|
−0.8 | −1.2 | −0.10 | −0.14 |
| SO42− | Exp |
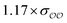
|
1.0 | 4.8 | −0.06 | 0.22 |
| HPO42− | Comp |
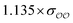
|
1.1 | 4.8 | −0.05 | 0.16 |
| CH3PO42− | Comp |
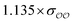
|
1.3 | 4.8 | −0.05 | 0.16 |
The original GAFF parameters for CH3SO4− yield ΔEQM→cl(Rmin) = −1.4 kcal mol−1; for CH3SO3−, H2PO4− and (CH3)2PO4− they yield ΔEQM→cl(Rmin) = (−1.7, −1.4, −1.1) kcal mol−1 (see Table 2), respectively. Tuning the oxygen parameters of these anions to reproduce the target ΔEQM→cl(Rmin) = −1.3 kcal mol−1 obtained for HSO4− leads to changes in hydration free energy lower than 2 kcal mol−1. Because this difference is slight, we opt to retain the original GAFF13,30–32 parameters for CH3SO4−, H2PO4−, (CH3)2PO4− and CH3SO3−. Given that our results show that the same Lennard-Jones parameters can be used for H2PO4− and for (CH3)2PO4−, we propose that the same parameters are also used for CH3HPO4−.
The original GAFF13,30–32 parameters lead to a ΔEQM→cl(Rmin) = +1.1 kcal mol−1 for HPO42−, and to ΔEQM→cl(Rmin) = +1.3 kcal mol−1 for CH3PO42−. Because these values differ markedly from the target ΔEQM→cl(Rmin) = +4.8 kcal mol−1 obtained for SO42−, the oxygens of the two divalent ions are optimized to reproduce the target ΔEQM→cl(Rmin). The value of ΔEQM→cl(Rmin) depends on the parameters of the O2 oxygens and is essentially independent of the parameters of the other oxygens; however, for consistency, the σ parameter of the OH oxygens in HPO42− is scaled by the same prefactor used to scale σO2; following the same logic, the σ parameter of the OS oxygens in CH3PO42− is also scaled by the same scaling factor applied to σO2 of that species. Applying these scaling factors to OH or OS is recommended, despite the fact that they should lead to relatively small changes in the overall interaction between these species and water; e.g., scaling or not the OH oxygen in HPO42− leads to changes of ∼2 kcal mol−1 in SolvFE.
The calculated uncorrected (ΔGcav + ΔGchg) SolvFE of HPO42− are −311.8 kcal mol−1 and −285.8 kcal mol−1, for GAFF13,30–32 and our parameters, respectively. This large change in solvation free energy illustrates the critical importance of optimizing ion–water interactions for divalent anions.¶
3.2 Developing specific anion–cation parameters
| Anion | Cation | Parameters |
a
Calccc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
a
Calccc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
a
Calccc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
a
Expcc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e e |
|---|---|---|---|---|---|---|
a Could not be calculated because of aggregation.
b Optimized 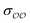 , , 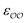 and anion–cation parameters.
c Optimized and anion–cation parameters.
c Optimized 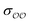 and and 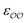 , with anion–cation parameters derived from combination rules (for some salts, this set of parameters coincides with the original GAFF parameters).
d Original GAFF parameters.
e
Ref. 56. , with anion–cation parameters derived from combination rules (for some salts, this set of parameters coincides with the original GAFF parameters).
d Original GAFF parameters.
e
Ref. 56.
|
||||||
| CH3SO3− | Na+ |
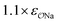
|
0.95 | 0.89 | 0.89 | 0.93 |
| NH4+ |
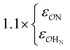
|
0.89 | 0.85 | 0.85 | 0.90 | |
| CH3COO− | Na+ |
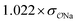
|
0.99 | 0.35 | 0.22 | 1.00 |
| SO42− | Na+ |
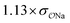
|
0.64 | 0.62 ± 0.02 | ||
| NH4+ |
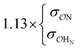
|
0.60 | 0.62 ± 0.02 | |||
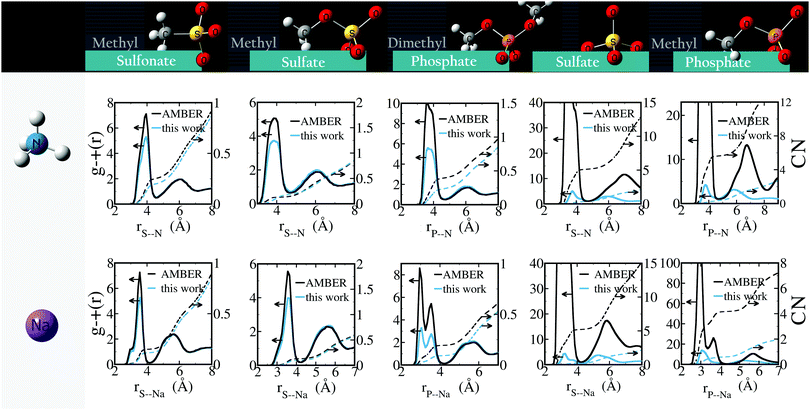
The unoptimized anion–cation parameters fail, often dramatically, to adequately describe anion–cation interactions in all cases; the original set of GAFF13,30–32 parameters also fails. These failures point to the need of specifically optimizing the anion–cation interactions. Modifications to the anion–cation parameters (see Table 3) are indispensable to attain agreement with experiment for solutions of Na2SO4 or (NH4)2SO4: for both salts, using either unoptimized anion–cation parameters or using the original GAFF13,30–32 parameters led to dramatic aggregation, as illustrated in Fig. 4a for Na2SO4. Such large aggregation is clearly unphysical, because our simulations are done at 0.5 m, far below the solubility limit of Na2SO4 (2.0 m at 25 °C),57 and of (NH4)2SO4 (5.8 m at 25 °C).58,59 As shown in Fig. 6, the optimized anion–cation parameters lead to very few contact ion-pairs formed per ion, with both ions forming primarily solvent shared ion-pairs, i.e., configurations where the ions share their first hydration layer.
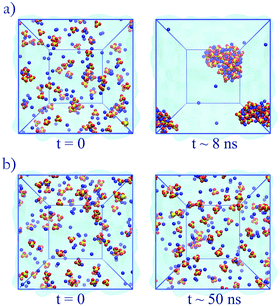 | ||
| Fig. 4 Simulations of Na2SO4. (a) Original GAFF13,30–32 parameters: aggregation becomes visible at 500 ps and large aggregates are seen at 8 ns. (b) Optimized anion–cation parameters: aggregation is not observed within the time scope of the simulation. | ||
For NaCH3COO, using unoptimized anion–cation parameters leads to a solution activity derivative, aCalccc = 0.35, which is far lower than the target value of aExpcc = 1.00; the original GAFF13,30–32 parameters perform even worse, yielding aCalccc = 0.22. To achieve good agreement with experiment, it is necessary to modify 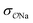 . The optimized parameters lead to only 1/5 of the contact ion pairs obtained using the original GAFF13,30–32 parameters, as shown in Fig. 5a. Our results thus indicate that the interactions between Na+ and acidic amino acids are markedly overestimated when using the sodium model of Joung and Cheatham15 in the AMBER13 force field with TIP3P water.
. The optimized parameters lead to only 1/5 of the contact ion pairs obtained using the original GAFF13,30–32 parameters, as shown in Fig. 5a. Our results thus indicate that the interactions between Na+ and acidic amino acids are markedly overestimated when using the sodium model of Joung and Cheatham15 in the AMBER13 force field with TIP3P water.
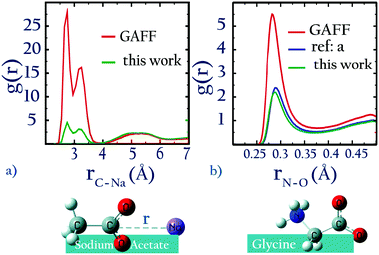 | ||
| Fig. 5 (a) 0.5 m solution of sodium acetate, (b) 3 m solution of glycine (a = ref. 22). | ||
Our optimized potentials for Na+⋯CH3COO− agree much better with recent ab initio molecular dynamics results based on DFT methods with dispersion corrections35 than the original GAFF potentials for TIP3P water: our potential of mean force calculations (ESI,† Fig. S5) for Na+⋯CH3COO− show that the difference in free energy between the minimum near 0.33 nm and that near 0.5 nm using our optimized parameters (≈0.7 kcal mol−1) is comparable to the same free energy difference (≈1 kcal mol−1) obtained using ab initio MD.35 In contrast, for the original GAFF parameters in TIP3P water this difference is 1.5 kcal mol−1. We note, however, that our classical simulation results still show marked differences from those obtained using ab initio MD: our parameters yield a free energy minimum at 0.27 nm which is not seen in ab initio MD. In the absence of reliable experimental information reporting on the (non)existence of the ion pair at 0.27 nm separation, it remains unclear which of these descriptions is better.
For NaCH3SO3 and NH4CH3SO3, the activity derivative calculated without optimizing anion–cation interactions differs less than 5% from experiment. Despite this seemingly small difference, we provide optimized anion–cation parameters for these salts (see Table 3) because they lead to quantitative differences in the number of ion-pairs: Fig. 6 show that the optimized anion–cation parameters lead to 25% fewer contact ion-pairs – defined as ions in direct contact with each other – than the non-optimized ones.
3.2.2.1 Determining optimal anion–cation orientations to be used in gas-phase potential energy scans. In ab initio calculations, contact ion-pairs in the gas phase benefit from extra delocalization stability due to the overlap of cation and anion orbitals; this extra stabilization is sometimes referred to as intermolecular hyperconjugation energy.60–63 However, quantum effects such as electron delocalization and charge transfer between two ions are not expected to be dominant in aqueous solution; in this case the charge transfer preferentially occurs between the ions and the water molecules in the first hydration shell.64–66
The fact that quantum effects stabilize ion–ion interactions in the gas phase but not in solution represents a problem when using our approach to develop classical parameters for ions in aqueous solution. Given that the magnitude of the hyper-conjugation energy varies amongst contact ion-pairs – depending on the electronic structure and the relative orientation of the two ions – our ab initio approach might introduce artifacts if the two ion-pairs being compared benefit from different hyper-conjugation stabilities. To resolve this issue, we must ensure that the anions for which we want to make the ab initio comparison have similar interactions with the same cation. We assess the similarity of interactions by performing natural bond orbital (NBO)60 analysis. This analysis proved to well-capture the electron density transfers,61–63 on the geometries shown in Fig. 2a–c and at distances corresponding to the minimum energy on the 1-D potential curves for each ion-pair. To perform this analysis we use the geometries from MP2 calculations and perform B3LYP67–69/aug-cc-pVTZ calculations to obtain the electron densities. Using the B3LYP method is necessary to obtain the well-defined one-electron densities required by NBO calculations.61
The results of the NBO analysis are shown in Table 4. In ion-pairs with Na+, the electron density transfers from the lone pair (LP) of the oxygen in the anion to the unfilled valence-shell (LP*) in Na+. The hyperconjugation energies vary in a very small range, between 6.5–10.0 kcal mol−1 for monovalent and between 11.0–11.5 kcal mol−1 for divalent anions, suggesting that the donor–acceptor interactions are similar for all ion-pairs involving Na+. Therefore, the configuration shown in Fig. 2b can be used for the ab initio calculations needed to derive optimized anion–cation parameters. In contrast to the ion-pairs involving Na+, those involving NH4+ in configuration I (see Fig. 2c) exhibit two different electron density transfers, one from the LP of the oxygen to the valence antibonding (BD*) orbital of (H–N) and the other from BD* of (S–O) to BD* of (H–N). The total hyperconjugation energies lie between 51.0–94.0 kcal mol−1 for monovalent and 130.0–283.5 kcal mol−1 for divalent ions. This wider range of hyperconjugation energies arises from different donor–acceptor interactions in these ion-pairs, making impossible the type of comparison necessary for our parameterization approach. To resolve this problem we searched for different relative orientations of the ions involved in NH4+ ion pairs, to find an orientation in which hyperconjugation energies are both minimized and are similar for the various ion pairs. For orientation II (see Fig. 2d), the hyper-conjugation energies are in the narrow range of 4.5–6.0 kcal mol−1 for monovalent anions and 8.0–8.5 kcal mol−1 for divalent anions. We use this configuration to find the parameters for the ion-pairs containing ammonium and methyl ammonium.
| Ion-pair | Donor (i) | Acceptor (j) | E(2)(Rm)a (kcal mol−1) | Sum |
|---|---|---|---|---|
a Stabilization energy E(2) estimated as 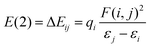 , where qi is the donor orbital occupancy, εi, εj are diagonal elements (orbital energies) and F(i,j) is the off-diagonal elements of NBO Fock matrix.70LP = lone pair. LP* = unfilled valence-shell. BD* = valence anti-bonding. , where qi is the donor orbital occupancy, εi, εj are diagonal elements (orbital energies) and F(i,j) is the off-diagonal elements of NBO Fock matrix.70LP = lone pair. LP* = unfilled valence-shell. BD* = valence anti-bonding. |
||||
| Anion–Na+ | ||||
| CH3SO3−⋯Na+ | LP(1–3)O | LP*(1–3)Na | 7.5 | |
| CH3SO4−⋯Na+ | LP(1–3)O | LP*(1–3)Na | 6.5 | |
| CH3COO−⋯Na+ | LP(1–3)O | LP*(1–3)Na | 10.0 | |
| H2PO4−⋯Na+ | LP(1–3)O | LP*(1–3)Na | 7.0 | |
| (CH3)2PO4−⋯Na+ | LP(1–3)O | LP*(1–3)Na | 7.0 | |
| SO42−⋯Na+ | LP(1–3)O | LP*(1–3)Na | 11.5 | |
| CH3PO42−⋯Na+ | LP(1–3)O | LP*(1–3)Na | 11.0 | |
| Anion–NH4+: orientation I | ||||
| CH3SO3−⋯NH4+ | LP(2)O | BD*(1)H–N | 48.0 | 88.0 |
| BD*(2)S–O | BD*(1)H–N | 40.0 | ||
| CH3SO4−⋯NH4+ | LP(2)O | BD*(1)H–N | 45.0 | 94.0 |
| BD*(2)S–O | BD*(1)H–N | 49.0 | ||
| CH3COO−⋯NH4+ | LP(2)O | BD*(1)H–N | 51.0 | |
| SO42−⋯NH4+ | LP(2)O | BD*(1)H–N | 77.0 | 130.0 |
| BD*(2)S–O | BD*(1)H–N | 53.0 | ||
| CH3PO42−⋯NH4+ | LP(2)O | BD*(1)H–N | 85.5 | 233.5 |
| BD*(2)S–O | BD*(1)H–N | 148.0 | ||
| Anion–NH4+: orientation II | ||||
| CH3SO3−⋯NH4+ | LP(1)O | BD*(1)N–H(1–3) | 4.5 | |
| CH3SO4−⋯NH4+ | LP(2)O | BD*(1)N–H(1–3) | 4.5 | |
| CH3COO−⋯NH4+ | LP(2)O | BD*(1)N–H(1–3) | 6.0 | |
| H2PO4−⋯NH4+ | LP(1)O | BD*(1)N–H(1–3) | 5.0 | |
| (CH3)2PO4−⋯NH4+ | LP(1)O | BD*(1)N–H(1–3) | 5.0 | |
| SO42−⋯NH4+ | LP(2)O | BD*(1)N–H(1–3) | 8.0 | |
| CH3PO42−⋯NH4+ | LP(2)O | BD*(1)N–H(1–3) | 8.5 | |
3.2.2.2 Parameter optimization. For parameter optimization, we require potential energy scans for reference species for which classical parameters already exist: we use NaCH3SO3 as the reference for NaCH3SO4, NaH2PO4 and Na(CH3)2PO4; Na2SO4 as the reference for Na2CH3PO4; NH4CH3SO3 as the reference for NH4+ or CH3NH3+ salts of all monovalent anions; (NH4)2SO4 as the reference for NH4+ or CH3NH3+ salts of all divalent anions. Parameter optimization then follows point 8 of the road map given in the Methods section. Example scans, for CH3COO− and CH3SO3−, are shown in Fig. S3 of the ESI.† In Table S2 of the ESI† we show the energy and interparticle separation at the energy minimum for all cases.
The optimized anion–cation interaction parameters are shown in Tables 5 and 6. The anion–cation distances for monovalent anions are slightly larger using the optimized parameters than using GAFF.13,30–32 The same trend is observed for the divalent anions, although for those systems the increase in anion–cation distance is substantially larger than for the monovalent anions. Such an increase is not surprising: as mentioned above and as observed also by others,54 it reflects the fact that Lennard-Jones parameters optimized for neutral species are not appropriate for charged species.
| Anion | Opt.a | Parametersb | ΔEGAFFQM→cl(Rm)c (kcal mol−1) | ΔEOPTQM→cl(Rm)c (kcal mol−1) | ΔRGAFFm,QM→cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d (Å) d (Å) |
ΔROPTm,QM→cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d (Å) d (Å) |
|---|---|---|---|---|---|---|
| a Parameters optimized based on activity derivatives (Exp), repeated here to facilitate comparisons, or based on the ab initio approach (Comp). b Expressed as a scaling factor relative to the original GAFF parameters, calculated using eqn (4) from the GAFF self-interaction parameters given in the ESI. c ΔEQM→cl(Rm) is defined in eqn (2). d ΔRm,QM→cl: the difference between the position of the dimer energy minimum obtained using ab initio calculations and using classical parameters. e The parameters for (CH3)2PO4− and H2PO4− are very similar; either set can be used for CH3HPO4−. | ||||||
| CH3COO− | Exp |
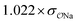
|
3.9 | 5.3 | 0.06 | 0.08 |
| CH3SO3− | Exp |
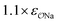
|
4.6 | 5.1 | 0.05 | 0.06 |
| CH3SO4− | Comp |
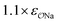
|
4.7 | 5.1 | 0.05 | 0.06 |
H2PO4−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e e |
Comp |
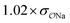
|
3.0 | 5.2 | 0.05 | 0.09 |
(CH3)2PO4−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e e |
Comp |
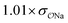
|
3.8 | 4.9 | 0.05 | 0.07 |
| SO42− | Exp |
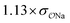
|
5.1 | 22.4 | 0.07 | 0.35 |
| CH3PO42− | Comp |
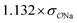
|
3.1 | 22.0 | 0.06 | 0.35 |
| Anion | Cation | Opt.a | Parametersb | ΔEGAFFQM→cl(Rm)c (kcal mol−1) | ΔEOPTQM→cl(Rm)c (kcal mol−1) | ΔRGAFFm,QM→cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d (Å) d (Å) |
ΔROPTm,QM→cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d (Å) d (Å) |
|---|---|---|---|---|---|---|---|
| a Parameters optimized based on activity derivatives (Exp) or based on the ab initio approach (Comp). b Expressed as a scaling factor relative to the original GAFF parameters, calculated using eqn (4) from the GAFF self-interaction parameters given in the ESI. c ΔEQM→cl(Rm) is defined in eqn (2). d ΔRm,QM→cl: the difference between the position of the dimer energy minimum obtained using ab initio calculations and using classical parameters. e No scaling of anion–cation interactions. f The parameters for (CH3)2PO4− and H2PO4− are very similar; either set can be used for CH3HPO4−. | |||||||
| CH3SO3− | NH4+ | Exp |
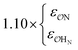
|
9.7 | 10.1 | 0.23 | 0.25 |
| CH3NH3+ | Comp |
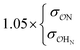
|
6.8 | 10.2 | 0.21 | 0.34 | |
| CH3SO4− | NH4+ | Comp |
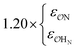
|
9.1 | 9.9 | 0.24 | 0.27 |
| CH3NH3+ | Comp |
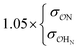
|
7.4 | 10.6 | 0.21 | 0.35 | |
H2PO4−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f f |
NH4+ | Comp |
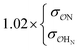
|
8.9 | 10.4 | 0.20 | 0.26 |
| CH3NH3+ | Comp |
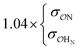
|
7.0 | 10.0 | 0.19 | 0.30 | |
(CH3)2PO4−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f f |
NH4+ | Comp |
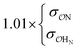
|
9.5 | 10.1 | 0.21 | 0.22 |
| CH3NH3+ | Comp |
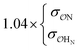
|
7.5 | 10.4 | 0.19 | 0.30 | |
| CH3COO− | NH4+ | Comp | —e | 10.9 | 10.2 | 0.23 | 0.20 |
| CH3NH3+ | Comp |
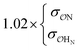
|
8.9 | 9.9 | 0.21 | 0.24 | |
| SO42− | NH4+ | Exp |
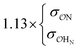
|
16.9 | 30.3 | 0.26 | 0.59 |
| CH3NH3+ | Comp |
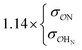
|
15.8 | 30.0 | 0.25 | 0.61 | |
| CH3PO42− | NH4+ | Comp |
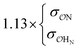
|
16.0 | 30.0 | 0.25 | 0.58 |
| CH3NH3+ | Comp |
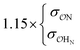
|
14.7 | 30.7 | 0.23 | 0.62 | |
Our results show that optimum parameters for the NH4+–anion interactions differ markedly from those for CH3NH3+–anion interactions. This result indicates that transferring parameters determined for NH4+ to other amines, which yields reasonable results for the interactions of these cations with water,71 should be avoided for anion–cation interactions. The need for different NH4+–anion and CH3NH3+–anion classical parameters that was detected with our approach illustrates the power of that approach to optimize intermolecular interactions: these two cations can be considered qualitatively similar (as defined in points 5a and 8a in the road map given in the Methods) for the purpose of our ab initio approach but, simultaneously, this approach is sensitive enough to detect how the interactions of the nitrogen and HN with other species quantitatively differ between NH4+ and CH3NH3+, because of the impact of the methyl group on the electronic distribution around those atoms. Similarly, the parameters governing the interactions between the  in H2PO4− and the various cations are not identical to those for CH3SO4−, again because the different substituents alter how the
in H2PO4− and the various cations are not identical to those for CH3SO4−, again because the different substituents alter how the  s interact with nearby species.
s interact with nearby species.
Our results also show that (CH3)2PO4−–cation interaction parameters are almost identical to those of H2PO4−–cation. We thus propose that either parameter set is suitable for CH3HPO4−–cation systems.
Similarly to the systems for which parameters are optimized based on experimental data, we find that the optimized parameters reduce the net anion–cation attraction relative to GAFF13,30–32 parameters (Fig. 6). These results suggest that GAFF13,30–32 parameters in general overestimate cation–anion interactions and may lead to aggregation, particularly in solutions with higher salt concentration. The most dramatic changes are seen in solutions of divalent ions: GAFF13,30–32 parameters lead to very rapid (<1 ns) aggregation of the ions and crystal formation, whereas our parameters yield solubilized systems. For all solutions containing monovalent anions, the optimized parameters decrease the number of contact ion pairs while leaving the number of solvent-shared ion-pairs unchanged. The overestimation of monovalent anion–cation interactions by GAFF is particularly marked for Na+⋯CH3COO−, NH4+⋯(CH3)2PO4− and Na+⋯(CH3)2PO4−.
GAFF13,30–32 also particularly overestimates the interactions between CH3NH3+ and CH3COO−. This effect is illustrated in Fig. 5b, by comparing the radial distribution of a 3 m solution of glycine zwitterion using GAFF72 and using optimized parameters. Overestimation of interactions between anionic and cationic side-chains, i.e., salt-bridge formation, has also been observed by others.73 This artifact can be prevented by using our optimized anion–cation interaction parameters.
3.3 Parameters obtained using the ab initio approach yield correct solution properties
As described in the introduction, our approach to optimize parameters based on ab initio calculations relies on an assumption: that, for similar anions, the difference, ΔEQM→cl(Rmin), between the minimum binding energy of dimers from ab initio calculations and that calculated using optimized classical parameters should be similar for similar dimers (see Fig. 1). To evaluate whether this assumption holds, we compare the classical and ab initio gas phase potential energy scans for the CH3COO−⋯H2O and the HSO4−⋯H2O systems, and also for CH3SO3−⋯Na+ and the CH3COO−⋯Na+ systems. These are the only systems for which Lennard-Jones parameters were optimized based on experimental data and which contain.For the anion–water case the scans are performed in the system configuration shown in Fig. 2a; these results are shown in Fig. 7. We find (see Table 2) that ΔEQM→cl(Rmin) = −1.3 kcal mol−1 for HSO4−, and ΔEQM→cl(Rmin) = −1.2 kcal mol−1 for CH3COO−; the similarity in the ΔEAB,QM→cl(Rmin) values for these two anions confirms that the ab initio approach proposed here holds for anion–water dimers. The scans also confirm that developing parameters by requiring that the classical potential energy curve overlaps with the ab initio is unsuitable. Parameters developed that way would greatly overestimate anion–water interactions.
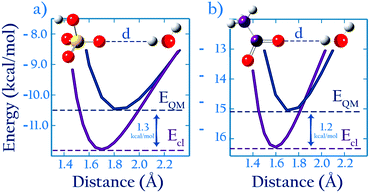 | ||
| Fig. 7 (a) HSO4−–H2O (b) CH3COO−–H2O, 1D energy scan with both QM and classical methods. The curves in (a) are averaged over scans of different symmetries, as described in the ESI.† | ||
For the anion–Na+ systems the potential energy scans are performed in the configuration shown in Fig. 2b. We find, as shown in Table 5, that ΔEQM→cl(Rmin) = +5.1 kcal mol−1 for CH3SO3− and ΔEQM→cl(Rmin) = +5.3 kcal mol−1 for CH3COO−. The two values are very similar, confirming that the approach holds also for anion–cation systems.
Our parameters for the (CH3)2PO4−⋯CH3NH3+ interaction are very close to recently proposed parameters based that reproduce osmotic pressure measurements made on DNA arrays: we propose that 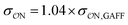 , which corresponds to a +0.124 Å increase in the
, which corresponds to a +0.124 Å increase in the 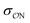 value. This value is very close to the 0.14 Å increase proposed by Aksimentiev and Yoo.22
value. This value is very close to the 0.14 Å increase proposed by Aksimentiev and Yoo.22
As a further check of our ab initio approach, in Fig. 5b we also compare the anion–cation rdf for glycine obtained using our optimized parameters for CH3COO−⋯CH3NH3+ interactions, with that obtained using parameters optimized from recent osmotic pressure measurements.22 The similarity between our parameter values and those of Aksimentiev (see ref. 22, Table 2), and also of the radial distribution function further confirms the success of our approach.
Finally, for a few of the salts for which the experimental solution activities are available, we calculate the densities of 0.5 m solutions and compare it against experimental data. The results, shown in Fig. 8, indicate that our parameters improve agreement with experiment, especially in the case of the divalent salts for which the densities obtained using the original GAFF parameters deviated substantially from the reference values.
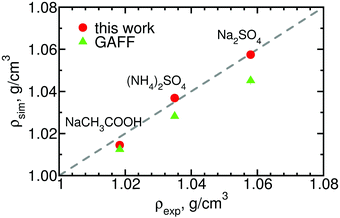 | ||
| Fig. 8 Densities of three salts calculated using the optimized and the original GAFF parameters experimental densities.59 The standard deviation of the simulation values is of order the height of the symbols. See ESI,† Table S6, for the numerical values. | ||
4 Concluding remarks
We present an approach to develop classical Lennard-Jones parameters for ions, that can be used when experimental data for parameterization is sparse. The approach is based on MP2 level ab initio calculations but simultaneously integrates experimental data, to create a parameter set for multiple ions that is internally consistent and grounded on experiment. We chose the MP2 level of theory for the gas phase ab initio scans because MP2 reproduces relative binding energies in systems with hydrogen bonding or dispersive interactions well.74 DFT methods that correct for the dispersion terms, such as DFT-D75,76 and M06-2X,77–79 however, might also yield reasonable results at a lower computational cost; this possibility remains to be tested.Our tests show that our simple approach is very powerful, and is suitable to obtain both ion–water and anion–cation interaction parameters. The approach may be used to rapidly optimize parameters for one or multiple atom types in any species – mono- and polyatomic; mono- and polyvalent. When optimizing multiple atom types, however, it is desirable that multiple target experimental properties exist.
We use this parameterization approach to obtain a set of Lennard-Jones ion–water and anion–cation parameters for salts of various sulfate, sulfonate, phosphate and carboxylate ions and the cations Na+, NH4+ and CH3NH3+, in TIP3P water.29 The entire parameter set is compatible with the GAFF13,30–32 force field and the sodium model of Joung and Cheatham.15 GAFF30 uses the same atom types as the AMBER13 force field for proteins, so the parameters presented are also compatible with AMBER. The large range of anions tested and parameterized here and the compatibility with GAFF/AMBER should prove useful to investigate ion-specific effects in biology that arise from the presence of multivalent ions.
Our results show that the GAFF13,30–32 Lennard-Jones parameters, which were developed based on data for neutral species, often yield incorrect ion–TIP3P water and anion–cation interactions; the results suggest that the same may occur for other similar, general, force fields. GAFF13,30–32 divalent anions consistently interact far too favorably with TIP3P water; in contrast, ion–TIP3P water interactions for monovalent anions are typically well-represented in GAFF.13,30–32 GAFF13,30–32 parameters typically overestimate anion–cation attraction. Excessive anion–cation attraction is particularly marked for divalent anions, for which GAFF13,30–32 parameters lead to complete aggregation of 0.5 m solutions within timescales of nanoseconds. GAFF13,30–32 also markedly overestimates the attraction between acetate and the Na+ ion of Joung and Cheatham,15 as well as attraction between acetate and CH3NH3+; these findings demonstrate that strong Na+–protein or salt bridges between cationic and anionic amino acids in proteins in simulations using AMBER13 and the Na+ ion from Joung and Cheatham15 are unphysical.
Lennard-Jones parameters developed for NH4+–anion interactions are often used for primary amines – and thus of the amino acid lysine.22 Our results indicate, however, that that usage is flawed because the parameters governing the interaction of NH4+ with the anions tested here are substantially different from those of CH3NH3+. Applying parameters derived for NH4+–anion interactions to simulate CH3NH3+–anion systems will typically overestimate the attraction between the amine group and the anion.
Parameters developed for oxygen atoms in sulfate and phosphate are often considered interchangeable.22 We find this approximation holds for the divalent sulfate or phosphate ions we investigated here (SO42−, CH3PO42−), but not for monovalent variants of those anions (CH3SO4−, CH3SO3−, H2PO4−, (CH3)2PO4−). These differences between mono and divalent ions likely result from the fact that the net anion–cation attraction has a larger contribution from the electrostatic component for the divalent cations.
Acknowledgements
This research is supported by the International Max Planck Research School (IMPRS) on Multiscale Bio-Systems. We gratefully acknowledge Marco Ehlert and René Genz from the IT team of Max Planck Institute of colloids and interfaces (MPIKG) for their help with computational facilities. AVV thanks CECAM for financial support to disseminate this work in CECAM workshops. Open Access funding provided by the Max Planck Society.References
- H. G. Garg, L. Yu, C. A. Hales, T. Toida, T. Islam and R. J. Linhardt, Biochim. Biophys. Acta, Mol. Basis Dis., 2003, 1639, 225–231 CrossRef CAS.
- S. A. Smith, N. J. Mutch, D. Baskar, P. Rohloff, R. Docampo and J. H. Morrissey, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 903–908 CrossRef CAS PubMed.
- J. T. Gallagher, Handb. Exp. Pharmacol., 2012, 207, 347–360 CAS.
- R. Baldwin, Biophys. J., 1996, 71, 2056–2063 CrossRef CAS PubMed.
- K. D. Collins, Methods, 2004, 34, 300–311 CrossRef CAS PubMed.
- W. L. Ash, M. R. Zlomislic, E. O. Oloo and D. P. Tieleman, Biochim. Biophys. Acta, Biomembr., 2004, 1666, 158–189 CrossRef CAS PubMed.
- D. E. Shaw, P. Maragakis, K. Lindorff-Larsen, S. Piana, R. O. Dror, M. P. Eastwood, J. A. Bank, J. M. Jumper, J. K. Salmon, Y. Shan and W. Wriggers, Science, 2010, 330, 341–346 CrossRef CAS PubMed.
- K. Lindorff-Larsen, N. Trbovic, P. Maragakis, S. Piana and D. E. Shaw, J. Am. Chem. Soc., 2012, 134, 3787–3791 CrossRef CAS PubMed.
- C. Zhang and J. Ma, J. Chem. Phys., 2010, 132, 244101 CrossRef PubMed.
- A. A. Skjevik, B. D. Madej, C. J. Dickson, C. Lin, K. Teigen, R. C. Walker and I. R. Gould, Phys. Chem. Chem. Phys., 2016, 18, 10573–10584 RSC.
- A. Savelyev and G. A. Papoian, J. Am. Chem. Soc., 2007, 129, 6060–6061 CrossRef CAS PubMed.
- A. van der Vaart, Biochim. Biophys. Acta, Gen. Subj., 2015, 1850, 1091–1098 CrossRef CAS PubMed.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197 CrossRef CAS.
- A. D. Mackerell and M. Karplus, J. Phys. Chem., 1991, 2, 10559–10560 CrossRef.
- I. S. Joung and T. E. Cheatham, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS PubMed.
- B. Klasczyk and V. Knecht, J. Chem. Phys., 2010, 132, 024109 CrossRef PubMed.
- D. Horinek, S. I. Mamatkulov and R. R. Netz, J. Chem. Phys., 2009, 130, 124507 CrossRef PubMed.
- M. Fyta, I. Kalcher, J. Dzubiella, L. Vrbka and R. R. Netz, J. Chem. Phys., 2010, 132, 024911 CrossRef PubMed.
- M. Fyta and R. R. Netz, J. Chem. Phys., 2012, 136, 124103 CrossRef PubMed.
- V. Satarifard, S. Kashefolgheta, A. Vila Verde and A. Grafmueller, J. Chem. Theory Comput., 2017, 13, 2112–2122 CrossRef CAS PubMed.
- M. Kanduc, A. Schlaich, E. Schneck and R. R. Netz, Langmuir, 2016, 32, 8767–8782 CrossRef CAS PubMed.
- J. Yoo and A. Aksimentiev, J. Chem. Theory Comput., 2016, 12, 430–443 CrossRef CAS PubMed.
- A. Vila Verde, M. Santer and R. Lipowsky, Phys. Chem. Chem. Phys., 2016, 18, 1918–1930 RSC.
- A. Vila Verde and R. Lipowsky, J. Phys. Chem. B, 2013, 117, 10556–10566 CrossRef CAS PubMed.
- M. Weinhart, D. Gröger, S. Enders, J. Dernedde and R. Haag, Biomacromolecules, 2011, 12, 2502–2511 CrossRef CAS PubMed.
- K. D. Collins, Biophys. Chem., 2012, 167, 33–49 CrossRef CAS PubMed.
- Y. J. Zhang and P. S. Cremer, Curr. Opin. Chem. Biol., 2006, 10, 658–663 CrossRef CAS PubMed.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- J. Wang, P. Cieplak and P. A. Kollman, J. Comput. Chem., 2000, 21, 1049–1074 CrossRef CAS.
- W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657–1666 CrossRef CAS PubMed.
- Y. Marcus, Ion properties, Marcel Dekker, Inc., New York, USA, 1997 Search PubMed.
- E. Pluharova, O. Marsalek, B. Schmidt and P. Jungwirth, J. Phys. Chem. Lett., 2013, 4, 4177–4181 CrossRef CAS.
- M. D. Daily, M. D. Baer and C. J. Mundy, J. Phys. Chem. B, 2016, 120, 2198–2208 CrossRef CAS PubMed.
- M. D. Baer, V.-T. Pham, J. L. Fulton, G. K. Schenter, M. Balasubramanian and C. J. Mundy, J. Phys. Chem. Lett., 2011, 2, 2650–2654 CrossRef CAS.
- W. L. Jorgensen, J. Phys. Chem., 1986, 90, 1276–1284 CrossRef CAS.
- I. Leontyev and A. Stuchebrukhov, Phys. Chem. Chem. Phys., 2011, 13, 2613–2626 RSC.
- P. Hunenberger and M. Reif, Single-ion solvation – experimental and theoretical approaches to elusive thermodynamic quantities, RSC, 2011 Search PubMed.
- H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- W. F. van Gunsteren and J. C. Berendsen, Mol. Simul., 1988, 1, 173–185 CrossRef.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- J. G. Kirkwood and F. P. Buff, J. Chem. Phys., 1951, 19, 774–777 CrossRef CAS.
- P. Krüger, S. K. Schnell, D. Bedeaux, S. Kjelstrup, T. J. H. Vlugt and J. M. Simon, J. Phys. Chem. Lett., 2013, 4, 235–238 CrossRef PubMed.
- C. H. Bennett, J. Comput. Phys., 1976, 22, 245–268 CrossRef.
- U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision E.01, Gaussian, Inc., Wallingford, CT, 2004 Search PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007 CrossRef.
- T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76 CrossRef CAS.
- T. Steinbrecher, J. Latzer and D. A. Case, J. Chem. Theory Comput., 2012, 8, 4405–4412 CrossRef CAS PubMed.
- P. George, R. J. Witonsky, M. Trachtman, C. Wu, W. Dorwart, L. Richman, W. Richman, F. Shurayh and B. Lentz, Biochim. Biophys. Acta, Bioenerg., 1970, 223, 1–15 CrossRef CAS.
- Activity coefficients in electrolyte solutions, ed. K. S. Pitzer, CRC Press, Boca Raton, Fl., USA, 2nd edn, 1991, pp. 75–153 Search PubMed.
- R. W. Potter II and M. A. Clynne, J. Res. U.S. Geol. Surv., 1978, 6, 701–705 Search PubMed.
- J. Barthel, Ber. Bunsen-Ges., 1985, 89, 722–723 CrossRef.
- CRC handbook of Chemistry and Physics, ed. W. M. Haynes and D. R. Lide, CRC Press, Boca Raton, Fl, USA, 2011 Search PubMed.
- A. E. Reed, L. a. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- E. Mrázková and P. Hobza, J. Phys. Chem. A, 2003, 107, 1032–1039 CrossRef.
- P. Hobza and Z. Havlas, Theor. Chem. Acc., 2002, 108, 325–334 CrossRef CAS.
- B. J. Van der Veken, W. A. Herrebout, R. Szostak, D. N. Shchepkin, Z. Havlas and P. Hobza, J. Am. Chem. Soc., 2001, 123, 12290–12293 CrossRef CAS PubMed.
- C. P. Petersen and M. S. Gordon, J. Phys. Chem. A, 1999, 103, 4162–4166 CrossRef CAS.
- M. Soniat, PhD thesis, University of New Orleans, 2014.
- M. Soniat and S. W. Rick, J. Chem. Phys., 2012, 137, 44511 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter and A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, J. NBO 6. 0., Theoretical and Chemistry Institute, University of Wisconsin, Madison, 2013 Search PubMed.
- W. L. Jorgensen and J. Gao, J. Phys. Chem., 1986, 90, 2174–2182 CrossRef CAS.
- A. H. C. Horn, J. Mol. Model., 2014, 20, 2478 CrossRef PubMed.
- S. Sukenik, Y. Boyarski and D. Harries, Chem. Commun., 2014, 50, 8193–8196 RSC.
- K. E. Riley, M. Pitoňak, J. Černý and P. Hobza, J. Chem. Theory Comput., 2010, 6, 66–80 CrossRef CAS PubMed.
- J.-i. Fujisawa, N. Tajima, K. Tamaki, M. Shimomura and T. Ishihara, J. Phys. Chem. C, 2007, 111, 1146–1149 CAS.
- P. Jurečka, J. Černý, P. Hobza and D. R. Salahub, J. Comput. Chem., 2007, 28, 555–569 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2007, 3, 289–300 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Parameter files in Gromacs (*top and *itp) format, correction terms to the solvation free energies, details of the activity derivative calculations, details of the counterpoise correction applied to the potential energy scan, study of the sensitivity of the optimized parameters to the orientation used for the potential energy scans, classical and ab initio potential energy scans for two example anions, list of ab initio and classical minimum energies and distances of all dimers, error estimates of the solvation free energies and activity derivatives, potential of mean force of Na+⋯CH3COO−, densities of chosen salt solutions. See DOI: 10.1039/c7cp02557b |
| ‡ In principle, the opposite approach – keeping GAFF Lennard-Jones parameters and tuning the charge distribution of the ions to reproduce the desired target properties – would also be possible. Doing so, however, would require establishing a new and well-defined procedure to obtain partial charges for polyatomic ions, which would be more time-consuming than the present approach and does not present obvious advantages. |
§ We note that the Lennard-Jones potential depends linearly on ε but depends on σ to the power of 12, so similar fractional changes in σ and ε result in much larger changes in the potential for the case of σ; optimizing 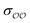 for the cases where the initial parameters deviate more than our threshold from the target ΔΔGsolv and optimizing for the cases where the initial parameters deviate more than our threshold from the target ΔΔGsolv and optimizing 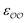 otherwise thus results in optimized parameters that remain in the same magnitude as the original GAFF parameters. If multiple reliable experimental observables are available, then both parameters can be optimized thus avoiding this somewhat arbitrary decision. Because of this arbitrariness, our optimized parameter set is not unique; however, because it is grounded on experimental data, it is nevertheless a marked improvement over the original GAFF parameters. otherwise thus results in optimized parameters that remain in the same magnitude as the original GAFF parameters. If multiple reliable experimental observables are available, then both parameters can be optimized thus avoiding this somewhat arbitrary decision. Because of this arbitrariness, our optimized parameter set is not unique; however, because it is grounded on experimental data, it is nevertheless a marked improvement over the original GAFF parameters. |
| ¶ We do not compare these results to the only available experimental value55 for SolvFE of HPO42− because that value (not shown) is highly unreliable. That value was not directly measured, but instead was estimated based on lattice energies. |
| This journal is © the Owner Societies 2017 |