 Open Access Article
Open Access ArticleAssessing the predictability of anharmonic vibrational modes at the example of hydroxyl groups – ad hoc construction of localised modes and the influence of structural solute–solvent motifs†
Manuel J.
Schuler
 a,
Thomas S.
Hofer
*a and
Christian W.
Huck
b
a,
Thomas S.
Hofer
*a and
Christian W.
Huck
b
aTheoretical Chemistry Division, Institute of General, Inorganic and Theoretical Chemistry, Center for Chemistry and Biomedicine, University of Innsbruck, Innrain 80-82, A-6020 Innsbruck, Austria. E-mail: T.Hofer@uibk.ac.at; Fax: +43-512-507-57199; Tel: +43-512-507-57111
bInstitute of Analytical Chemistry and Radiochemistry, Center for Chemistry and Biomedicine, University of Innsbruck, Innrain 80-82, A-6020 Innsbruck, Austria. Fax: +43-512-507-53399; Tel: +43-512-507-57304
First published on 18th April 2017
Abstract
The performance of the grid-based Numerov procedure for the prediction of fundamental as well as the first vibrational overtone has been systematically probed for harmonic and anharmonic model systems. In addition to monitor the prediction with respect to the spacing of the potential grid the influence of higher order approximations to the second derivative (i.e. stencils) in Schrödingers equation is evaluated. The latter enable a significant increase of the grid-spacing to achieve results of similar accuracy obtained with smaller stencil sizes. Application to the hydroxyl vibrational mode of methanol, phenol and the natural product thymol in vacuum and carbon tetrachloride predicted wavenumbers within less than 1% of experiment. Due to the highly localised character of the OH-vibration the ad hoc construction of the associated normal mode yields results of similar accuracy than those obtained using the analytical normal modes, effectively eliminating the requirement of an analytical normal mode evaluation of the entire system. This property was shown to be of particular advantage when considering explicit solute–solvent contacts, which have been demonstrated to be superior compared to an implicit representation of solvent effects. The combination of the observed findings (i.e. enlarged grid-spacing due to the application of higher order stencils, construction of localised normal modes) is envisaged to be of particular benefit when investigating localised modes in large systems, such as OH or NH groups in large (bio)macromolecules or solid-state surfaces.
1 Introduction
Due to its straightforward applicability and high throughput capacity vibrational spectroscopy is among the most widely used methods for the classification of small molecules in science and technology. Since the mode assignment in complex spectra can be cumbersome computational approaches to aid in the classification are of particular interest. Especially in view of the continuously increasing computational capacities a broad variety of approaches are currently available.The simplest and most widely used method for the prediction of vibrational modes is the harmonic approximation, in the majority of cases employed in the context of density functional theory. Here the potential close to the energy minimum conformation is approximated by a parabola, i.e. the potential of the harmonic oscillator model. This simple approach works surprisingly well for the calculation of fundamental vibrations of selected functional groups, but may lead to a significant deviation from experimental data for other chemical systems. Also, because of the neglect of anharmonicity and mode–mode coupling, it fails dramatically in the prediction of higher order excitations (overtones) and combination bands, observed in the NIR region. In cases these two effects compensate acceptable results are obtained albeit for the wrong reasons.
Various methods have been developed to take mode anharmonicity and coupling into account. The most prominent ones being the vibrational self consistent field (VSCF) method and the vibrational second order perturbative (VPT2) ansatz.1 The VPT2 ansatz is based on the calculation of higher order derivatives (third and upwards) of the system's energy, as shown by Barone.2 While it is only applicable for potentials with high harmonicity, the method gives a quite accurate, albeit computational costly prediction of higher excitation states for these systems.1,2 The VSCF method3–7 on the other hand tries to optimize a linear combination of vibrational wave functions (e.g. analytical solutions of harmonic oscillator wave functions) by variation of the linear combination's coefficients. Since in this approach the vibrational wave function is based on a product approach similar as the electronic wave function used in the Hartree Fock (HF) electronic structure theory, correlated vibrational methods such as perturbation theory-VSCF (VSCF-PT)8,9 and configuration interaction VSCF (VSCF-CI)10–12 have been developed.
Another approach currently gaining popularity is numerically solving the time-independent Schrödinger equation by grid-based approaches, such as Numerov's method13–16 or discrete variable representation (DVR).17–19 The DVR method is often the method of choice, since it employs an infinite order in the formulation of the finite difference approximation employing a sinc() basis. However, the associated matrix formulation requires a fully occupied dense matrix,20 whereas in the Numerov case only banded-matrices occur, the respective band width being equal to the finite size of the stencil. This feature enables the application of sparse matrix routines greatly reducing computing time and memory requirements.21 While for modern computational architectures the exploitation of matrix sparsity is of no noticeable benefit in one-dimensional applications, it becomes of particular advantage in applications with more degrees of freedom (see ref. 21 and 20 for 2D- and 3D-examples). Since these grid-based methods can be applied to any arbitrary potential curve, the influence of various forms of anharmonicity can be easily taken into account by application of a suitable coordinate scan of a given molecule. The reduced masses in the kinetic energy operator of Schrödinger's eqn (1) also enable an explicit consideration of quantum chemical effects, such as the magnitude of tunnelling outside of the classically accessible region. Especially if only a localised signature mode such as the vibration of a hydroxyl group investigated in this work is of interest, grid-based methods provide a highly efficient ansatz yielding also excellent predictions of the respective first overtone. This vibrational mode has been chosen, because of its high infrared and near infrared activity as well as its local character resulting from the weak coupling with other vibrations.
For this reason this work aims at the determination of the applicability of a matrix implementation of Numerov's method for the prediction of OH vibrational modes. First, results obtained for model potentials differing in their degree of anharmonicity and grid density are compared to the respective analytical solution. Furthermore, IR measurements of the OH-stretch vibration of phenol and the natural product thymol in carbon tetrachloride have been performed and compared to the theoretically predicted frequencies and oscillator strengths. Special focus was given to reduce the number of computations thus providing a general and efficient work flow, e.g. without the requirement of a harmonic frequency analysis. Finally, the sensitivity of the method to the influence of solvent effects is investigated at the example of carbon tetrachloride, comparing an implicit description of the solvation with the costly explicit inclusion of solvent molecules.
2 Methods
2.1 The Numerov method
To predict the vibrational energy eigenstates an ansatz for solving the time independent Schrödinger eqn (1) for a given finite-spaced potential, namely the Numerov method,13,14,22 has been employed | (1) |
Numerov's method is based on the representation of the given function Ψ(q) as Taylor polynomial at the points q (index 0), q + Δq (index +1) and q − Δq (index −1).
 | (2) |
Summation of Ψ+1 and Ψ−1 leads to the cancellation of all odd and the doubling of all even entries. Rearrangement yields an approximate expression for the second derivative of Ψ.
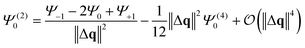 | (3) |
Due to the nature of second order ordinary differential equations without linear terms, the second derivative of a function Ψ(q) is equal to a function value f(q) times the function Ψ(q) itself, which is used to define the fourth (and higher order) derivatives.
 | (4) |
In case of the time independent Schrödinger equation the function f(q) is described in eqn (1). With this expression the approximation of its second derivative can be written as
 | (5) |
By applying Dirichlet boundary conditions, the terms  and
and  can be simplified to the matrix terms
can be simplified to the matrix terms ![[Doublestruck A]](https://www.rsc.org/images/entities/char_e164.gif) Ψ(q) and
Ψ(q) and ![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) Ψ(q) (see eqn (S1), ESI†).13,14,21
Ψ(q) (see eqn (S1), ESI†).13,14,21
Using the matrices ![[Doublestruck A]](https://www.rsc.org/images/entities/char_e164.gif) and
and ![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) as well as the diagonal matrix
as well as the diagonal matrix ![[Doublestruck V]](https://www.rsc.org/images/entities/char_e179.gif) , containing V(q) as elements, eqn (5) can be written as
, containing V(q) as elements, eqn (5) can be written as
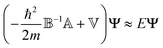 | (6) |
![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) Ψ = EΨ, with
Ψ = EΨ, with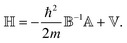 | (7) |
Eigendecomposition of ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) yields the diagonal eigenvalue-matrix
yields the diagonal eigenvalue-matrix ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) , the associated eigenvectors are collected in Ψ. Similar methods have also been employed in the description of the electronic structure of atoms and small molecular systems.23–30
, the associated eigenvectors are collected in Ψ. Similar methods have also been employed in the description of the electronic structure of atoms and small molecular systems.23–30
The method can be extended to higher order numerical derivatives by defining the Taylor series for higher degrees (e.g. ![[Doublestruck A]](https://www.rsc.org/images/entities/char_e164.gif) and
and ![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) matrices with seven diagonal entries would require a Taylor series of the eighth degree). A generalisation to higher orders of Numerov's method is presented elsewhere.15,21
matrices with seven diagonal entries would require a Taylor series of the eighth degree). A generalisation to higher orders of Numerov's method is presented elsewhere.15,21
To predict the IR intensities the transition moment integral μmn(8), consisting of the respective wave functions Ψ of the two involved states m and n, as well as the transition moment operator ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) (q), has to be calculated.
(q), has to be calculated.
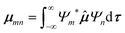 | (8) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) (q) equals the dipole moment μ as a function of the molecule's normal coordinates q, making infrared measurements especially sensitive on polar functional groups like OH or CO. A slightly more common representation of the intensities in vibrational spectroscopy is the use of the oscillator strength fmn
(q) equals the dipole moment μ as a function of the molecule's normal coordinates q, making infrared measurements especially sensitive on polar functional groups like OH or CO. A slightly more common representation of the intensities in vibrational spectroscopy is the use of the oscillator strength fmn | (9) |
2.2 Experimental setup
For the measurements 10% (m/v) solutions of the analytes phenol (university supply) and thymol (Sigma, 99.5% purity) have been prepared in carbon tetrachloride. For the investigation of structural motifs an additional measurement was taken with the same analytes in a 10% (m/v) n-hexane solution. The solutions have been transferred into quartz cuvettes with a pass length of 2 mm and sealed to avoid evaporation of the solvents. The dilutions have been measured using the Fourier-transform infrared spectrophotometer Spectrum 400 FT-IR/FT-NIR (PerkinElmer, Massachusetts, USA) in transmission mode. The spectral range was set from 2000 cm−1 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 with a spectral resolution of ±2 cm−1. All measurements have been carried out at room temperature with 16 scans per sample to amplify the signal to noise ratio. Additionally experimental data of methanol have been taken from the work of Futami et al.31 Since only position and intensity of specific known peaks of high intensity were needed for this work, the interpretation of the resulting, baseline corrected spectra could be carried out without the need of advanced statistical methods. Spectrum IMAGE R1.8.0.0410 was used for recording spectra.
000 cm−1 with a spectral resolution of ±2 cm−1. All measurements have been carried out at room temperature with 16 scans per sample to amplify the signal to noise ratio. Additionally experimental data of methanol have been taken from the work of Futami et al.31 Since only position and intensity of specific known peaks of high intensity were needed for this work, the interpretation of the resulting, baseline corrected spectra could be carried out without the need of advanced statistical methods. Spectrum IMAGE R1.8.0.0410 was used for recording spectra.
As a measure for the anharmonic contribution of the obtained potentials the anharmonicity factor χ is commonly used
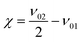 | (10) |
2.3 Model systems
In addition to the assessment of its applicability to real chemical systems the accuracy of Numerov's method was tested against three analytically solvable systems with different degrees of anharmonicity, namely a harmonic and two Morse models M1 and M2. | (11) |
| VMorse = D(1 − e−α(r−r0))2 | (12) |
The three potentials share the same curvature at the equilibrium position, with M1 showing the highest degree of anharmonicity. The harmonic force constant kharm of 4621.4 kJ (mol Å2)−1 was chosen, since it corresponds to that of a typical O–H bond.33,34 The α parameter of M1 has been chosen from the work of Arai et al.34 and was set to 2.511 Å−1. This results in a well depth of D = 366.48 kJ mol−1. The second, less anharmonic, Morse potential M2 was constructed by doubling the well depth D to 724.96 kJ mol−1 while maintaining the curvature in the equilibrium position. This results in an α value of 1.776 Å−1. The equilibrium distance r0 of all potentials has been set to zero, thus r formally represents the elongation and contraction of the bond from its minimum position. The reduced mass μOH has been determined from the values of 16O and 1H taken from the National Institute of Standards and Technology database.35 The potentials of the three different model systems along with the respective wavefunctions of the five lowest eigenvalues are depicted in Fig. 1.
2.4 Quantum chemical calculations
To obtain the potentials needed to apply Numerov's method, DFT calculations on generalized gradient approach (GGA) level, using the BP8636,37 functional, and hybrid level, using the B3LYP38 functional with the 6-311++G(3df,3pd) basis set,39–42 have been carried out in vacuum and in carbon tetrachloride using the density based polarized continuum model for implicit solvents SMD.43Following an initial energy minimisation with tight convergence settings for energy and gradient, harmonic frequencies have been determined at the minimum geometry. For the energy scan a variation along the respective degree of freedom (dof) in discrete steps of 0.01 Å has been performed and the molecule's energy and dipole moment were evaluated at every point.
For the OH-stretch vibration three different definitions of the dof have been chosen. First, only the OH-distance rOH was varied by only changing the coordinate of the hydrogen atom serving as a simple approximation to the vibration. Secondly, the appropriate normal coordinate scan of the hydroxyl vibrational mode has been employed. The atom displacement was carried out alongside the OH-stretch normal coordinate q, allowing for a similar atom displacement to experimental observations. A disadvantage of this approach is the requirement of a harmonic frequency analysis of the entire system, which may become a demanding and time-consuming prerequisite in case of larger molecules.
For this reason a constructed normal coordinate ![[q with combining macron]](https://www.rsc.org/images/entities/b_char_0071_0304.gif) has been considered as third option. The associated normal mode components of the oxygen and hydrogen atoms
has been considered as third option. The associated normal mode components of the oxygen and hydrogen atoms ![[q with combining macron]](https://www.rsc.org/images/entities/b_char_0071_0304.gif) O and
O and ![[q with combining macron]](https://www.rsc.org/images/entities/b_char_0071_0304.gif) H have been determined according to their respective masses mO and mHvia
H have been determined according to their respective masses mO and mHvia
 | (13) |
 | (14) |
This approach can be justified by the strongly local character of the OH vibration. The absolute values of the associated normal coordinates considering only the oxygen and hydrogen atoms (B3LYP level, vacuum) amount to 0.9999 in case of methanol, phenol and thymol, respectively, implying the contribution of all other atoms to the normal coordinate is less than 0.01%. The associated reduced masses of the three systems of 1.067 g mol−1, 1.066 g mol−1 and 1.066 g mol−1 also demonstrate excellent agreement with the estimated mass of the constructed mode, the respective deviations being on the order of mg mol−1. This approach has the advantage that no frequency analysis is required to formulate the direction of the potential energy scan, while at the same time the representation of the normal mode is more accurate compared to the simple variation of the H position along the hydroxyl bond vector.
Afterwards, a Numerov calculation of the resulting potential curves is carried out to obtain the energy eigenstates and the transition moment integrals44,45 are calculated for the prediction of relative intensities.
All quantum chemical molecule calculations were performed using the Gaussian09 package,46 while the Numerov calculations were performed on in house code, implemented in GNU octave47 and the C programming language, using the GNU Scientific library.48 For better utilisation of multi-core systems the GNU Parallel49 load balancer was used.
3 Results and discussion
3.1 Analytically solvable model potentials
In case of the analytically solvable systems the accuracy of eigenvalues predicted by Numerov's method depending on the density of data points is evaluated. Each potential has been prepared in the range of ±2.5 Å around the energy minimum, the distance of h between the individual data points is given as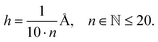 | (15) |
Besides the influence of the grid density also the impact of higher order derivatives of the matrix Numerov method are investigated.15,21 To accomplish this all calculations were performed with matrix stencils inheriting three, five, seven and nine points per row, corresponding to an error order of ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (h4) to
(h4) to ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (h8) in the
(h8) in the ![[Doublestruck A]](https://www.rsc.org/images/entities/char_e164.gif) -matrix, as well as a second, fourth, sixth and eight order derivative in the
-matrix, as well as a second, fourth, sixth and eight order derivative in the ![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) -matrix.
-matrix.
The absolute difference between the Numerov results and the analytical solutions for selected eigenstates as a function of the grid density for the used harmonic oscillator is depicted in Fig. 2 for different Numerov matrix stencil sizes.
For a reliable prediction of infrared spectra (MIR/NIR) at least an accuracy of 10−2 kJ mol−1 (0.8 cm−1) for the first eigenstates is required. Fig. 2 shows that even the simplest implementations of the method are sufficiently accurate for this task. Using larger stencils (seven point onwards) reach this limit even for the 10th eigenstates with less than 80 points per Ångström. For the ground state, the calculation with a nine point stencil even reaches the precision limit of the implementation at around 10−11 kJ mol−1. This level of accuracy even meets the required precision to compare to experimental data obtained via laser spectroscopy reporting uncertainties on the order of 10−4 cm−1.50
Since the computational overhead of larger stencils is effectively negligible, the largest available stencil should be employed. This has the advantage that coarser grids can be employed, reducing the number of computations along the vibrational mode. To achieve a precision of 10−2 kJ mol−1 for the first excited state E1 the three-point stencil requires a minimum grid spacing of approximately 0.030 Å, while in case of the nine-point stencil a spacing of 0.056 Å is sufficient, effectively reducing the number of grid points by a factor of two.
In case of the Morse systems M1 and M2 very similar characteristics have been observed, the respective plots are provided in the ESI† (Fig. S1 and S2). It can be concluded that the performance of the higher order stencils is not reduced due to the anharmonicity in the potentials.
3.2 Prediction of hydroxyl vibrational states
Based on the findings of the analytically solvable potentials the methodology is applied to the OH vibrational mode of the molecules methanol, phenol and thymol. Since it shows a strong local character and high infrared activity in the mid- and near-infrared region, it is possible to study this mode independently from the other vibrations in the molecule. Due to the comparably large wavenumbers of the OH vibration it can be easily identified even in the presence of C–H and N–H vibrations of the solute or the solvent.Tables 1 and 2 list the experimental and calculated wavenumbers as well as the respective infrared intensities for the normal mode and OH-distance scans, respectively. Both the B3LYP and BP86 functionals as well as the treatment in vacuum and implicit solvent are considered.
| BP86 vacuum | B3LYP vacuum | Exp. gas | BP86 SMD | B3LYP SMD | Exp. CCl4 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ν | I | ν | I | ν | ν | I | ν | I | ν | I | ||
| a This work. | ||||||||||||
| Methanol | ν 01 | 3550.5 | 1.000 | 3676.7 | 1.000 | 368131 | 3532.2 | 1.000 | 3657.3 | 1.000 | 364531 | 1.0031 |
| ν 02 | 6934.0 | 0.220 | 7189.8 | 0.154 | 719631 | 6898.3 | 0.130 | 7151.1 | 0.097 | 712131 | 0.0631 | |
| χ | −83.5 | — | −81.8 | — | −83 | −83.1 | — | −81.8 | — | −85 | — | |
| Phenol | ν 01 | 3527.8 | 1.000 | 3664.7 | 1.000 | 3654, 365754,55 | 3502.2 | 1.000 | 3637.5 | 1.000 | 3612,a 361154,56 | 1.00 |
| ν 02 | 6889.3 | 0.132 | 7167.5 | 0.090 | 714154 | 6838.6 | 0.080 | 7112.4 | 0.058 | 7056,a 7053, 705254,56 | 0.05 | |
| χ | −83.2 | — | −81.0 | — | 84 | −82.9 | — | −81.3 | — | −84 | — | |
| Thymol | ν 01 | 3528.0 | 1.000 | 3667.0 | 1.000 | — | 3503.4 | 1.000 | 3640.6 | 1.000 | 3616a | 1.00 |
| ν 02 | 6889.1 | 0.148 | 7171.5 | 0.097 | — | 6840.4 | 0.086 | 7118.0 | 0.061 | 7060a | 0.04 | |
| χ | −83.4 | — | −81.2 | — | — | −83.2 | — | −81.6 | — | −86 | — | |
| BP86 vacuum | B3LYP vacuum | Exp. gas | BP86 SMD | B3LYP SMD | Exp. CCl4 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ν | I | ν | I | ν | ν | I | ν | I | ν | I | ||
| a This work. | ||||||||||||
| Methanol | ν 01 | 3552.4 | 1.000 | 3678.7 | 1.000 | 368131 | 3533.7 | 1.000 | 3658.6 | 1.000 | 364531 | 1.0031 |
| ν 02 | 6938.7 | 0.247 | 7194.4 | 0.166 | 719631 | 6902.1 | 0.133 | 7154.3 | 0.097 | 712131 | 0.0631 | |
| χ | −83.1 | — | −81.5 | — | −83 | −82.7 | — | −81.5 | — | −85 | — | |
| Phenol | ν 01 | 3531.7 | 1.000 | 3668.5 | 1.000 | 3654, 365754,55 | 3505.2 | 1.000 | 3640.3 | 1.000 | 3612a, 361154,56 | 1.00 |
| ν 02 | 6898.4 | 0.140 | 7176.1 | 0.092 | 714154 | 6846.4 | 0.078 | 7119.4 | 0.056 | 7056a, 7053, 705254,56 | 0.05 | |
| χ | −82.5 | — | −83.0 | — | 84 | −82.0 | — | −80.6 | — | −84 | — | |
| Thymol | ν 01 | 3532.3 | 1.000 | 3671.0 | 1.000 | — | 3507.5 | 1.000 | 3644.5 | 1.000 | 3616a | 1.00 |
| ν 02 | 6898.8 | 0.161 | 7180.7 | 0.100 | — | 6850.1 | 0.087 | 7127.2 | 0.060 | 7060a | 0.04 | |
| χ | −82.9 | — | −80.7 | — | — | −82.5 | — | −80.9 | — | −86 | — | |
Comparison of the two used DFT functionals shows, that for all three investigated systems, the B3LYP functional's results are more consistent with the measured data compared to the BP86 case. The deviation from the experimentally observed wavenumber varies between 0.02% for the first overtone of methanol in the gas phase and 0.95% for the first overtone of the thymol OH vibration in CCl4. On the other hand the accuracy of the BP86 functional varies between 3.0% for the first phenol overtone in CCl4 and 3.6% for the first methanol overtone in vacuum. The same applies to the prediction of the intensity ratios between the fundamental vibration and its first overtone. In all three investigated systems the B3LYP functional predicts the correct order of magnitude, but slightly overestimates the intensity of the first overtone. The BP86 functional on the other hand overestimates the overtone intensity by a factor of two in the methanol and thymol case. Interestingly the anharmonicity factors χ resulting from BP86 show a slightly better agreement with experiment than observed in the B3LYP case, which is a result of a compensation of errors between the fundamental and overtone. However, the deviation in χ is typically on the order of a few wave numbers only.
Another important finding is the fact that the BP86 functional required a notably higher number of SCF cycles to converge for configurations notably displaced from the minimum structure. Thus, despite its simpler formulation no advantage in computation time could be observed when using this functional and the application of the hybrid B3LYP approach proved to be preferred. For this reason only the B3LYP level of theory was applied in all investigations using the constructed normal modes ![[q with combining macron]](https://www.rsc.org/images/entities/b_char_0071_0304.gif) . Since the OH-stretch modes in the investigated systems show only contributions of the associated bond partners with virtually no motion of the other atoms, the constructed modes provide results of similar accuracy (see Table 3). To highlight the deviation between the q and
. Since the OH-stretch modes in the investigated systems show only contributions of the associated bond partners with virtually no motion of the other atoms, the constructed modes provide results of similar accuracy (see Table 3). To highlight the deviation between the q and ![[q with combining macron]](https://www.rsc.org/images/entities/b_char_0071_0304.gif) , the associated angles and the difference in reduced mass has been listed in the ESI,† (cf. Table S1). It can be seen that the constructed mode differs by approximately 1° from the analytical modes, with a decrease in angle upon increase of the system size. The deviation between the reduced masses are on the order of mg mol−1. In this case the lowest deviation is observed in the methanol case, which can be explained by the smaller mass of the methyl group when compared to the aromatic systems. The deviation of the predicted wave numbers to those using the analytical wavenumbers is on the order of 1 cm−1 for the fundamental modes and 2 cm−1 in case of the respective overtones.
, the associated angles and the difference in reduced mass has been listed in the ESI,† (cf. Table S1). It can be seen that the constructed mode differs by approximately 1° from the analytical modes, with a decrease in angle upon increase of the system size. The deviation between the reduced masses are on the order of mg mol−1. In this case the lowest deviation is observed in the methanol case, which can be explained by the smaller mass of the methyl group when compared to the aromatic systems. The deviation of the predicted wave numbers to those using the analytical wavenumbers is on the order of 1 cm−1 for the fundamental modes and 2 cm−1 in case of the respective overtones.
| B3LYP vacuum | Exp. gas | B3LYP SMD | Exp. CCl4 | |||||
|---|---|---|---|---|---|---|---|---|
| ν | I | ν | ν | I | ν | I | ||
| a This work. | ||||||||
| Methanol | ν 01 | 3675.8 | 1.000 | 368131 | 3656.4 | 1.000 | 364531 | 1.0031 |
| ν 02 | 7187.7 | 0.155 | 719631 | 7148.9 | 0.097 | 712131 | 0.0631 | |
| χ | −82.0 | — | −83 | −81.9 | — | −85 | — | |
| Phenol | ν 01 | 3663.8 | 1.000 | 3654, 365754,55 | 3636.6 | 1.000 | 3612,a 361154,56 | 1.00 |
| ν 02 | 7165.3 | 0.093 | 714154 | 7110.3 | 0.059 | 7056,a 7053, 705254,56 | 0.05 | |
| χ | −81.1 | — | −84 | −81.4 | — | −84 | — | |
| Thymol | ν 01 | 3666.0 | 1.000 | — | 3639.7 | 1.000 | 3616a | 1.00 |
| ν 02 | 7169.4 | 0.100 | — | 7116.0 | 0.062 | 7060a | 0.04 | |
| χ | −81.3 | — | — | −81.7 | — | −86 | — | |
Overall the B3LYP level potential energy scans based on normal coordinates q and ![[q with combining macron]](https://www.rsc.org/images/entities/b_char_0071_0304.gif) yield slightly more accurate results except in the case of methanol in vacuum. The deviation with respect to the experiment values being approximately 0.2% in the gas phase and 0.8% in CCl4. The larger deviation in the latter case can be attributed to the implicit treatment of solvation effects in the SMD approach, which does not take a possible formation of structural motifs between the solute and the solvent into account. A comparison of the potential energy scans for the three systems, two functionals and the three different definition of the scanning coordinate in vacuum is depicted in Fig. S3 (ESI†).
yield slightly more accurate results except in the case of methanol in vacuum. The deviation with respect to the experiment values being approximately 0.2% in the gas phase and 0.8% in CCl4. The larger deviation in the latter case can be attributed to the implicit treatment of solvation effects in the SMD approach, which does not take a possible formation of structural motifs between the solute and the solvent into account. A comparison of the potential energy scans for the three systems, two functionals and the three different definition of the scanning coordinate in vacuum is depicted in Fig. S3 (ESI†).
3.3 Investigation of solvent effects – implicit solvation versus explicit structural motifs
Despite its low permittivity of 2.228 carbon tetrachloride may act as both hydrogen bond acceptor as well as halogen bond donor. In order to estimate the magnitude of the C–Cl⋯O and O–H⋯Cl interactions an energy minimisation of the phenol⋯CCl4 complex has been carried out. The resulting interaction energies at B3LYP/vacuum level amount to −3.4 kJ mol−1 and −4.8 kJ mol−1 in case of hydrogen and halogen bonding. If both structural motifs are present (i.e. phenol⋯(CCl4)2) a total energy of binding of −10 kJ mol−1 has been obtained after energy minimisation. These values confirm the possibility of explicit interaction between solute and solvent, which in turn can be expected to have a direct influence on the hydroxyl bond strength.In order to assess the impact of these structural motifs the model system used for the Numerov approach has been extended to include two explicitly treated solvent molecules. In addition to the treatment in vacuum the entire complex has also been treated subject to implicit solvation in CCl4, the respective model systems are labeled explicit CCl4in vacuum and explicit CCl4 in implicit solvent. Fig. 4 depicts the respective minimum structure for thymol obtained at B3LYP/6-311++G(3df,3pd)/vacuum level. The formation of a hydrogen bond-like motif and the halogen bond are clearly visible. Despite the substantially increased computational effort of the complex systems (each CCl4 molecule contributes 74 electrons to the DFT calculation) a normal mode analysis at the minimum geometry has been carried out followed by a potential energy scan along the OH mode using a tight resolution of 0.01 Å for methanol, phenol and thymol, respectively.
In order to support the results obtained from the Numerov analysis an anharmonic frequency calculation at VPT2 level has been performed as well using two different strategies. First, only the OH-mode is included in the anharmonic treatment while in the second calculation all modes have been considered. Due to the dramatic increase in computational demand the latter was only possible in the methanol case. The comparison of wave numbers resulting from the two VPT2 settings yield differences in wavenumbers of just a few cm−1, thus confirming the highly local character of the hydroxyl vibration in the three molecules.
The comparison of all predicted wave numbers for the fundamental and first overtone are listed in Table 4 including experimental data where available. In each case a decrease of the wave numbers from vacuum to implicit solvation to the explicit CCl4 model in vacuum can be observed, demonstrating that despite the increased computational effort the explicit consideration of solute–solvent contacts results in an improvement over an implicit treatment of solvation effects. In case of the harmonic and Numerov approaches a further extension of the model to explicit solvent molecules plus implicit solvation yields similar results as to treating just the solute in implicit solvation. Thus, the best predictions of the Numerov approach are obtained when using the explicit CCl4 model, the resulting deviations from experiment amounting to 5, 20 and 18 cm−1 in case of the fundamental bands and 10, 39 and 40 cm−1 for the first overtone of methanol, phenol and thymol, respectively. Thus, the deviation from experimental data is on the order of 0.5% or less which can be attributed to the approximations inherent to density functional theory.
| Vacuum | Carbon tetrachloride | ||||||
|---|---|---|---|---|---|---|---|
| Theoretical | Experimental | Implicit solvent | Explicit CCl4 | Explicit CCl4 + implicit | Experimental | ||
| a This work. | |||||||
| Methanol | h01 | 3846 | 368131 | 3825 | 3823 | 3830 | 364531 |
| a01* | 3651 | 3641 | 3601 | 3592 | |||
| a01 | 3650 | 3639 | — | — | |||
| n01 | 3677 | 3657 | 3650 | 3657 | |||
| a02* | 7122 | 719631 | 7109 | 7025 | 7002 | 712131 | |
| a02 | 7120 | 7105 | — | — | |||
| n02 | 7190 | 7151 | 7131 | 7147 | |||
| Phenol | h01 | 3832 | 3654, 365754,55 | 3803 | 3803 | 3809 | 3612,a 361154,56 |
| a01* | 3629 | 3636 | — | — | |||
| a01 | 3633 | 3643 | — | — | |||
| n01 | 3665 | 3638 | 3632 | 3638 | |||
| a02* | 7079 | 714154 | 7107 | — | — | 7056,a 7053, 705254,56 | |
| a02 | 7088 | 7120 | — | — | |||
| n02 | 7168 | 7112 | 7095 | 7111 | |||
| Thymol | h01 | 3834 | — | 3808 | 3808 | 3810 | 3616a |
| a01* | 3642 | 3631 | — | — | |||
| a01 | — | — | — | — | |||
| n01 | 3667 | 3641 | 3634 | 3640 | |||
| a02* | 7110 | — | 7099 | — | — | 7060a | |
| a02 | — | — | — | — | |||
| n02 | 7172 | 7118 | 7100 | 7116 | |||
Using the VPT2 approach wave numbers of similar accuracy are predicted, however, the best agreement with experiment is obtained in case of implicit solvation without consideration of explicit solute–solvent contacts. The influence of the latter could only be tested for the smallest system due to the dramatic increase in computational demand of the VPT2 approach upon inclusion of two CCl4 molecules. A significant decrease in the wavenumbers yielding a deviation of more than 1.0% is obtained, that is further increased by combining explicit solvent molecule with implicit solvation. The reason for this deviation in the methods can be explained by the mechanics of the different approaches. While the potential energy scan required for the Numerov approach has to include regions of high potential, the VPT2 method employs curvature information close to the minimum structure to construct the potential energy curve. This is also the reason why the VPT2 method requires a significantly higher computational effort even when restricted to just a single active normal mode.
To provide an experimental confirmation of the hypothesis of structural motifs in CCl4 measurements in a solvent unable to form explicit interactions with the solute, should yield a notable shift in frequency. Thus, additional measurements of phenol and thymol in n-hexane have been performed, since its permittivity of ε(C6H14 = 1.882) is close to that of carbon tetrachloride (ε(CCl4) = 2.228). Although an overlap of n-hexane bend- and stretch vibrations with those of the analyte, especially thymol, can be observed, the OH excitation energies are well isolated in both, the MIR and NIR regions, thus enabling an investigation of this mode despite the presence of the CH signals of the solute.
The OH-stretch peaks of the corresponding spectra are shown in Fig. 3. A decrease of the experimentally determined frequency of 8 and 12 cm−1 for the fundamental and 16 to 20 cm−1 for the overtone have been obtained for phenol and thymol. These changes in wave number agree well with the predicted decrease of 6 to 7 cm−1 for the fundamental and 17 to 18 cm−1 in case of the first overtone when changing from implicit solvation to the explicit solvation model shown in Table 4.
 | ||
| Fig. 3 Measured MIR (left) and NIR (right) spectra of the OH vibration of phenol (top) and thymol (bottom). | ||
 | ||
| Fig. 4 Thymol in vacuum interacting with two molecules of carbon tetrachloride to estimate the influence of structural motifs between solute and solvent. | ||
3.4 Simplified Morse model
Since analytic solutions of Schrödinger's equation for the Morse potential are available, a simple yet effective strategy to account for anharmonicity is to fit a Morse model to the point wise potential energy scan (PES). However, this approach suffers from an inherent uncertainty, resulting from the actual number of data points used in the fitting procedure. In order to obtain the three parameters of the Morse potential a minimum of three data points is required. Even if the minimum position is constrained to the equilibrium distance of the PES (thus formally only requiring two data-points for the fit), the inclusion of the minimum and two neighbouring points is essential to account for the observed anharmonicity. Such a 3-point fit results in the most accurate representation of the potential close to the minimum, but typically suffers for larger displacements and thus in the prediction of higher order excitations. Any choice to include more than three points can be expressed via an arbitrarily chosen threshold, for instance including all data points below a pre-selected maximum energy Emax in the fitting procedure. Thus, in addition to the 3-point fitting a systematic increase of Emax in the range of 5, 10, 15, 25 and 50 kJ mol−1 have been carried out. This strategy highlights the arbitrary character of the “best-fit” Morse approach, which is even further complicated if a weighting scheme is chosen to adjust the impact of data points in the fitting procedure.All fits have been carried out using gnuplot51 without any additional weighting of data points, the employed initial values of D and α have been chosen as 500 kJ mol−1 and 2.2 Å−1. The predicted wave-numbers for the fundamental and first overtone of the OH vibrational mode for methanol, phenol and thymol in implicit solvent are summarised in Table 5. It can be seen that the Morse approach yields data of similar accuracy as the Numerov procedure, but the actual values are highly sensitive to the chosen energy threshold. Furthermore, it is not possible to improve the predicted wave numbers of the fundamental and first overtone simultaneously – while the overtone frequency is increasing upon increase of Emax, the same applies to the wavenumber of the fundamental excitation.
| Harmonic | Morse fit implicit solvent | Numerov | Experimental | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 point | T5 | T10 | T15 | T25 | T50 | Best | Implicit solvent | ||||
| a This work. | |||||||||||
| Methanol | 01 | 3825 | 3665 | 3658 | 3667 | 3676 | 3677 | 3693 | 3657 | 3657 | 364531 |
| 02 | 7650 | 7131 | 7117 | 7134 | 7153 | 7154 | 7186 | 7115 | 7151 | 712131 | |
| Phenol | 01 | 3803 | 3876 | 3665 | 3667 | 3674 | 3673 | 3682 | 3625 | 3638 | 3612,a 361154,56 |
| 02 | 7606 | 7552 | 7131 | 7134 | 7149 | 7146 | 7164 | 7051 | 7112 | 7056,a 7053, 705254,56 | |
| Thymol | 01 | 3808 | 3706 | 3661 | 3668 | 3676 | 3674 | 3681 | 3626 | 3641 | 3616a |
| 02 | 7616 | 7212 | 7123 | 7137 | 7152 | 7149 | 7162 | 7053 | 7118 | 7060a | |
A further aspect that has been noted during the fitting procedure is the fact that due to its steep increase the repulsive branch is underrepresented when compared to the attractive part of the potential. Thus, instead of employing the intuitive Emax threshold a selection of data points based on the distance was employed, thereby ensuring that the number of included data points in the attractive and repulsive branch is equal. In this case the accuracy in the predicted wave numbers was noticeably improved, leading to the most accurate prediction termed “best” in Table 5. However, similar as in the case of Emax the ideal number of data points to achieve this best prediction is unknown and was found to be different for the three different systems, namely ±17, 49 and 47 data points in case of methanol, phenol and thymol, respectively.
Despite the overall good predictive properties of a Morse model great care has to be taken in actual applications. The comparison of the potential energy scan with three different Morse fits (3-point, T10 and best) in the thymol case shown in Fig. S4 (ESI†) demonstrates that the differences in the predicted wave numbers results from considerably small deviations in the fitted Morse potentials. These minor differences result in deviations of up to 80 and 160 cm−1 in the fundamental and first overtone wave numbers, due to the high sensitivity of the eigenvalues to the smallest change in the repulsive branch of the potential. The comparison in Fig. S4 (ESI†) also reveals a wrong asymptotic behaviour at large distances and predictions of overtone frequencies beyond the first can be expected to show large deviations. The reason for this is that although the Morse model employs three parameters to represent the anharmonic character of the potential, the attractive as well as the repulsive branch depend on the same α coefficient and it is not possible to take steepness and curvature of the two branches independently into account. In this case a potential using four or more parameters is required, however, analytical solutions of Schrödinger's equation are typically not available for this more general case.
Another situation requiring a careful assessment of a best-fit Morse model arises in potentials subject to different kinds of anharmonicity such as quartic and higher order oscillators.52,53 In these cases a Morse approach will prove as a bad choice, since the properties of the energy eigenvalues will display a characteristic comparable to the “particle-in-the-box” model systems, i.e. subsequent energy levels will show an increase in separation. Vibrational modes in more complex systems may also display a Morse-like potential while at the same time a dominant higher order contribution (quartic, sextic,…) is present close to the minimum. In such a case the influence of Morse and higher order anharmonicity may even compensate. While such effects cannot be properly described by a Morse fit approach, Numerov's procedure will properly consider such effects if the grid-spacing is properly chosen as discussed above.
4 Conclusion
The data presented clearly demonstrates that the Numerov procedure is a reliable approach for the determination of vibrational frequencies of localised normal modes. The generalisation to higher order stencils enable a significant reduction in the number of data points of the associated vibrational potential, thus greatly improving the overall computational demand. Using a 9-point stencil to approximate the second derivative of the wave function in Schrödinger's equation, a spacing of approximately 0.05 Å to 0.06 Å was found to be sufficient, which can be further increased by extending to even higher order formulations. The comprehensive tests carried out with various analytically solvable model potentials also indicated that the approach shows equal scaling and performance in the harmonic and anharmonic case.In conjunction with well-established density functionals and a suitable basis set the predicted OH wave numbers proved to be in excellent agreement with experiment for both fundamental and first overtone. This is especially true in case of the gas-phase. The influence of solvent can be represented in fair agreement with experiment by application of an implicit solvation model and the explicit consideration of solute–solvent contacts resulted in a further improvement of the prediction. The respective shift in wave numbers agrees well to the observed changes when moving from CCl4 to n-hexane despite the very similar permittivity of the two solvents. The combination of explicit solvent molecules together with implicit solvation did not provide any improvement, however. This is most likely due to the approximation inherent to implicit solvation models which can be expected to be the limiting factor in such a computational setup.
Fitting of a Morse potential to predict the resulting wave numbers via the corresponding analytical solution of Schrödinger's equation proved to be a successful strategy for the investigated systems. However, a number of potentially limiting factors have been highlighted, namely the arbitrary choice of data points included in the fitting procedure and the wrong asymptotic properties for large distances. A further potential limitations the requires a careful consideration will occur in case of potentials showing different kind of anharmonicity as observed in quartic and higher order oscillators.
As a further strategy to reduce the associated computational effort the performance of constructed normal modes for the OH vibration was investigated based on the consideration that this modes are in general highly localised. This conjecture was also confirmed by vibrational perturbation theory including all normal modes and alternatively just the OH mode into the VPT2 treatment. The resulting wave numbers showed only a deviation of 1 to 2 wave numbers when compared to those predicted using the analytical normal mode.
These results confirm that it is possible to avoid the normal mode analysis to formulate the direction of the potential energy scan. For this localised vibrational state the demanding frequency computation is not required. This is of particular benefit for large systems, in which the computational effort of the normal mode analysis is increasing dramatically with the number of atoms. As can be expected the approximation proved more reliable in case of phenol and thymol, which can be attributed to the higher mass of the organic residue. Thus it can be concluded that the higher the mass of the moiety bound to the oxygen atom the better the performance of the constructed normal mode. A typical application of this advantage are investigations of hydroxyl groups on metal and metal oxide surfaces, since the respective difference in mass is typically even higher compared to the case of organic molecules. Since the application of the Numerov procedure is independent of the quantum chemical computation of the potential, an extension to periodic DFT approaches is straightforward and will be pursued in future work.
References
- O. M. D. Lutz, B. M. Rode, G. K. Bonn and C. W. Huck, Molecules, 2014, 19(12), 21253 CrossRef PubMed.
- V. Barone, J. Chem. Phys., 2005, 122(1), 014108 CrossRef PubMed.
- T. K. Roy and R. B. Gerber, Phys. Chem. Chem. Phys., 2013, 15, 9468–9492 RSC.
- J. M. Bowman, J. Chem. Phys., 1978, 68(2), 608–610 CrossRef CAS.
- G. D. Carney, L. L. Sprandel and C. W. Kern, Advances in Chemical Physics, 2007, vol. 37, pp. 305–379 Search PubMed.
- M. Cohen, S. Greita and R. McEarchran, Chem. Phys. Lett., 1979, 60(3), 445–450 CrossRef CAS.
- R. Gerber and M. Ratner, Chem. Phys. Lett., 1979, 68(1), 195–198 CrossRef CAS.
- L. S. Norris, M. A. Ratner, A. E. Roitberg and R. Gerber, J. Chem. Phys., 1996, 105(24), 11261–11267 CrossRef CAS.
- J. O. Jung and R. B. Gerber, J. Chem. Phys., 1996, 105(24), 10682–10690 CrossRef CAS.
- J. M. Bowman, K. Christoffel and F. Tobin, J. Phys. Chem., 1979, 83(8), 905–912 CrossRef CAS.
- M. A. Ratner, V. Buch and R. Gerber, Chem. Phys., 1980, 53(3), 345–356 CrossRef CAS.
- T. C. Thompson and D. G. Truhlar, Chem. Phys. Lett., 1980, 75(1), 87–90 CrossRef CAS.
- B. V. Noumerov, Mon. Not. R. Astron. Soc., 1924, 84(8), 592–602 CrossRef.
- D. G. Kenhere, Phys. Educ., 2007, 55–60 Search PubMed.
- T. Dongjiao, Generalized Matrix Numerov Solutions to the Schrödinger Equation, Master's thesis, National University of Singapore, 2014 Search PubMed.
- B. Lindberg, J. Chem. Phys., 1988, 88(6), 3805–3810 CrossRef CAS.
- A. Bulgac and M. M. Forbes, Phys. Rev. C: Nucl. Phys., 2013, 87(5), 051301 CrossRef.
- J. C. Light and T. Carrington Jr, Adv. Chem. Phys., 2000, 114, 263–310 CrossRef.
- D. T. Colbert and W. H. Miller, J. Chem. Phys., 1992, 96(3), 1982–1991 CrossRef CAS.
- T. Graen and H. Grubmüller, Comput. Phys. Commun., 2016, 198, 169–178 CrossRef CAS.
- U. Kuenzer, J.-A. Soraru and T. S. Hofer, Phys. Chem. Chem. Phys., 2016, 18, 31521–31533 RSC.
- I. N. Levine, Quantum Chemistry, Prentice-Hall, New Jersey, 7th edn, 2013 Search PubMed.
- L. Laaksonen, P. Pyykkö and D. Sundholm, Comput. Phys. Rep., 1986, 4, 313–344 CrossRef CAS.
- P. Pyykkö, in Recent Progress in Many-Body Theories, ed. A. Kallio, E. Pajanne and R. Bishop, Plenum Press, New York, 1988, vol. 1, pp. 349–355 Search PubMed.
- P. Pyykkö, in Numerical Determination of the Electronic Structure of Atom Diatomic and Polyatomic Molecules, ed. M. Defranceschi and J. Delhalle, Kluwer, Dordrecht, 1989, pp. 161–175 Search PubMed.
- P. Pyykkö, in Scientific Computing in Finland, ed. K. Kankaala and R. Nieminen, CSC Res. Report R1/89, Espoo, 1989, pp. 183–213 Search PubMed.
- P. Pyykkö, D. Sundholm, L. Laaksonen and J. Olson, in The CP 90 Europhysics Conference on Computational Physics, ed. A. Tenner, World Scientific, Singapore, 1991, pp. 455–457 Search PubMed.
- E. A. McCullough, Jr., in Encyclopedia of Computational Chemistry, ed. P. von Rague Schleyer, Wiley, Chichester, 1998, pp. 1941–1947 Search PubMed.
- L. Frediani and D. Sundholm, Phys. Chem. Chem. Phys., 2015, 17(47), 31357–31359 RSC.
- J. R. Jones, F.-H. Rouet, K. V. Lawler, E. Vecharynski, K. Z. Ibrahim, S. Williams, B. Abeln, C. Yang, W. McCurdy, D. J. Haxton, X. S. Li and T. N. Rescigno, Mol. Phys., 2016, 114(13), 2014–2028 CrossRef CAS.
- Y. Futami, Y. Ozaki and Y. Ozaki, Phys. Chem. Chem. Phys., 2016, 18, 5580–5586 RSC.
- Y. Chen, Y. Morisawa, Y. Futami, M. A. Czarnecki, H.-S. Wang and Y. Ozaki, J. Phys. Chem. A, 2014, 118(14), 2576–2583 CrossRef CAS PubMed.
- J. Tennyson, P. F. Bernath, L. R. Brown, A. Campargue, A. G. Császár, L. Daumont, R. R. Gamache, J. T. Hodges, O. V. Naumenko, O. L. Polyansky, L. S. Rothman, A. C. Vandaele, N. F. Zobov, A. R. A. Derzi, C. Fábri, A. Z. Fazliev, T. Furtenbacher, I. E. Gordon, L. Lodi and I. I. Mizus, J. Quant. Spectrosc. Radiat. Transfer, 2013, 117, 29–58 CrossRef CAS.
- C. C. Liew, H. Inomata and K. Arai, Fluid Phase Equilib., 1998, 144(1–2), 287–298 CrossRef CAS.
- National Institute of Standards and Technology, Atomic Weights and Isotopic Compositions for All Elements, 2016 Search PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33(12), 8822 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98(7), 5648–5652 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72(1), 650–654 CrossRef CAS.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72(10), 5639–5648 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4(3), 294–301 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80(7), 3265–3269 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113(18), 6378–6396 CrossRef CAS PubMed.
- T. Helgaker, P. Jørgensen and J. Olsen, Molecular Electronic Structure Theory, Wiley, Chichester, 2000 Search PubMed.
- G. Wedler, Lehrbuch der Physikalischen Chemie, Wiley-VCH, 5th edn, 2004 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, 2009, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- J. W. Eaton, D. Bateman, S. Hauberg and R. Wehbring, GNU Octave version 4.0.0 manual: a high-level interactive language for numerical computations, 2015 Search PubMed.
- M. Galassi, J. Davies, J. Theiler, B. Gough, G. Jungman, P. Alken, M. Booth and F. Rossi, GNU Scientific Library Reference Manual, Network Theory Ltd, 3rd edn, 2009 Search PubMed.
- O. Tange, et al. , The USENIX Magazine, 2011, 36(1), 42–47 Search PubMed.
- G. D. Dickenson, M. L. Niu, E. J. Salumbides, J. Komasa, K. S. Eikema, K. Pachucki and W. Ubachs, Phys. Rev. Lett., 2013, 110(19), 193601 CrossRef CAS PubMed.
- T. Williams, C. Kelley and many others, Gnuplot 5.0: An interactive plotting program, 2016, http://gnuplot.sourceforge.net/ Search PubMed.
- D. Brizuela, Phys. Rev. D: Part. Fields, 2002, 90, 125018 CrossRef.
- A. Pathak and S. Mandal, Phys. Lett. A, 2002, 298(4), 259–270 CrossRef CAS.
- M. Couzi and P. Huong, Spectrochim. Acta, Part A, 1970, 26(1), 49–58 CrossRef CAS.
- G. N. Patwari, A. Fujii and N. Mikami, J. Chem. Phys., 2006, 124(24), 241103 CrossRef PubMed.
- M. Rospenk, B. Czarnik-Matusewicz and T. Zeegers-Huyskens, Spectrochim. Acta, Part A, 2001, 57(1), 185–195 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp01662j |
| This journal is © the Owner Societies 2017 |


