Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The elusive silica/water interface: isolated silanols under water as revealed by vibrational sum frequency spectroscopy†
Laetitia
Dalstein
,
Elizaveta
Potapova
and
Eric
Tyrode
*
Department of Chemistry, School of Chemical Science and Engineering, KTH Royal Institute of Technology, SE-10044 Stockholm, Sweden. E-mail: tyrode@kth.se
First published on 24th March 2017
Abstract
It has been long recognized that the surface chemistry of silica, and in particular the type and relative amount of surface bound silanol groups, plays a critical role in many of the properties associated with the material, where a typical example is the discrepant adsorption behavior observed depending on the pretreatment history of the surface. However, in spite of its importance, the direct probing of specific surface silanol groups under water has been hampered by instrumental limitations. Here we make use of vibrational sum frequency spectroscopy (VSFS) to first, identify under water the OH stretch of isolated surface silanols, and second, explore its acid/base behavior and dependence on the surface pretreatment method. The properties of other types of silanol groups (i.e. hydrogen bonded/geminal) are also inferred from the data. The ability to directly probe these functional groups under water represents a crucial step to further improving our understanding of this widely used mineral oxide.
Introduction
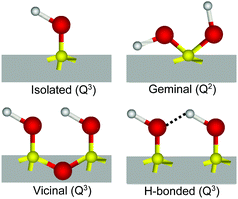
The interaction of water with silicon dioxide (SiO2), the most abundant mineral in the continental Earth crust,1 is of obvious fundamental and practical importance in a large range of geochemical, environmental, pharmaceutical, biological and catalytical processes.2–5 In contact with water, silica surfaces typically expose siloxane (Si–O–Si), silanol (Si–OH), and silanolate (Si–O−) groups, the latter resulting from the partial deprotonation of silanols at pHs above the isoelectric point (pH ∼ 2–3),2 which renders the surface negatively charged under most common conditions. The relative population, speciation and distribution of these surface groups largely control and modulate the surface chemistry and associated properties of silica.6Compared to the bulk, where silicon atoms are typically coordinated through oxygen bridges to four additional Si atoms (Q4), on the surface, this number can be lower as silicon may instead bind to one (Q3) or two (Q2) hydroxyl groups.3,7,8 Depending on this coordination, but also on the relative lateral proximity, different kinds of silanols have been identified2,3,6,7 (see Scheme 1): (i) isolated, single or terminal Si–OH (Q3) separated by at least 3.3 Å from its closest silanol neighbor and consequently not capable of forming mutual hydrogen bonds; (ii) vicinal, pair of Si–OHs (both Q3) sharing a common oxygen vertex and thus separated by less than 3 Å; (iii) interacting or hydrogen bonded, Q3 silanols that are not vicinal, but nonetheless close enough to form hydrogen bonds, and finally, (iv) geminal, having two OHs connected to the same silicon atom (Q2). Conclusive experimental evidence for the presence of isolated and geminal silanols has been found by IR (narrow band at ∼3750 cm−1)3,9,10 and NMR spectroscopy (29Si signals from Q2 silicon species),7,8 respectively. Together with the total amount of hydroxyl groups determined from deuterium exchange measurements,6,11 the relative amounts of the different types of silanols have been estimated as the surface dehydroxylates with increasing temperature.3,6 These techniques require however, large surface to volume ratios and experiments must be typically performed under vacuum or at relatively high temperatures to avoid overlapping contributions from bulk or adsorbed water molecules.
When silica is in contact with water, the silanol OH signatures become largely indistinguishable from the overwhelming majority of those found in bulk H2O, which limits the applicability of the above mentioned experimental approaches. Nonetheless, intrinsic surface specific techniques, such as vibrational sum frequency spectroscopy (VSFS)12,13 and second harmonic generation (SHG),14 have been able to provide information on the interfacial water in close or direct proximity to the silica surface, and in particular, upon variation of the solution pH.15–26 The VSFS spectra of the silica/water interface are characterized by two broad bands centred at ∼3200 cm−1 and ∼3400 cm−1. Although the precise assignments of the two bands remain a source of debate,21,22,25,26 they are consistently linked to water vibrations in the interfacial region. Indirect information of the fate of silanols under water has been inferred by SHG, where depending on the pH history of the silica substrate, two or three successive jumps in the second harmonic response have been observed with increasing pH. This behavior was attributed to the deprotonation of specific populations of Si–OH having different pKas,17,23 an interpretation that has been supported by molecular dynamic simulations.27–29 It is worth noting, however, that a large majority (>75%) of surface silanols remains protonated (i.e. Si–OH) even at a pH as high as 10.23,30 Although recent ATR-FTIR measurements on silica nanoparticles have been able to correlate a frequency shift in the Si–O stretch of surface silanols to the density of silanolate groups,31 the direct probing of specific types of SiOHs in solution remains elusive.
In the present study we have used VSFS to provide direct evidence of isolated surface silanols at the buried silica/water interface and examine some of their properties. Measurements were performed using an experimental geometry that not only significantly improves the signal to noise ratio, but also enhances the sum frequency (SF) response in the spectral region of interest.32 To facilitate the discussion of the observed features, otherwise identical fused silica hemispherical substrates were pretreated following two different procedures: plasma cleaning and heat treatment at 1000 °C in air. As will be elaborated below, we find these methods to give the largest relative variation of silanol populations at the buried interface.
Experimental
Materials
Sodium hydroxide (99.99% trace metal basis) and hydrochloric acid (37 wt% in water, 99.999% trace metal basis) were obtained from Sigma Aldrich. Chromosulphuric acid, used during the cleaning procedure of the hemispheres, was from Merck. Sodium chloride (Puratronic, 99.999% metal basis) was purchased from Alfa Aeser and then baked for at least 60 minutes at 500 °C to remove organic contaminants. Hexadecyltrimethylammonium bromide (CTAB) was obtained from Aldrich, and recrystallized three times from a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of acetone/methanol before use. The water used in the experiments was obtained from an Integral 15 Millipore filtration unit (18.2 MΩ cm in resistivity, total organic carbon <3 ppb). All glassware was cleaned with a commercial alkaline agent (Deconex from Borer) and rinsed thoroughly with water. The IR grade fused silica substrates (Infrasil 302) were custom-made (CVI, Melles-Griot) hemispherically shaped optics of 10 mm in diameter. The flat side of the hemispheres displayed a surface arithmetic average roughness (Ra) of less than 0.5 nm. This roughness was not seen to be much affected by the pretreatment methods (i.e. plasma and heat treatments), as concluded from profilometry measurements (Newview 5010, Zygo Corporation, USA).
1 mixture of acetone/methanol before use. The water used in the experiments was obtained from an Integral 15 Millipore filtration unit (18.2 MΩ cm in resistivity, total organic carbon <3 ppb). All glassware was cleaned with a commercial alkaline agent (Deconex from Borer) and rinsed thoroughly with water. The IR grade fused silica substrates (Infrasil 302) were custom-made (CVI, Melles-Griot) hemispherically shaped optics of 10 mm in diameter. The flat side of the hemispheres displayed a surface arithmetic average roughness (Ra) of less than 0.5 nm. This roughness was not seen to be much affected by the pretreatment methods (i.e. plasma and heat treatments), as concluded from profilometry measurements (Newview 5010, Zygo Corporation, USA).
Sample preparation
Prior to a given pretreatment, the fused silica hemispheres were first sonicated in ethanol, rinsed in water, immersed in chromosulfuric acid for 30 minutes, and then finally rinsed once again in water. Thereafter, depending on the pretreatment method, samples were either placed in an oven (Thermolyne-47900-Furnace) for 4 hours at 1000 °C and then left to cool-down overnight, or plasma cleaned for 10 minutes using air as carrier gas (Harrick, PDC-32G). Finally, to remove traces of organic contamination, just before experiments, all hemispheres were once again immersed in chromosulfuric acid for 5 minutes and thoroughly rinsed in ultrapure water. Additional details can be found in the ESI.†For the pH dependent measurements, the pH was adjusted with either HCl or NaOH, and solutions were then promptly drawn into gas-tight syringes. Solutions were then transferred into a gas-tight measuring cell, the design of which is described in detail elsewhere.32 For performing the measurements of the free silanol in air (see Fig. 3 below), the hemispheres were placed wet in an open cell exposed to a laminar flow of carbon-filtered dry air. SF spectra were then collected during the drying procedure, until the thin wetting film of liquid water evaporated from the surface. The free silanol vibration was then measured without delay at the different polarization combinations. We note that after 20–50 minutes, hydrocarbon contaminants could be detected on the silica surface, together with a measurable decrease in the free silanol vibration intensity at 3750 cm−1. This was not surprising considering the high surface energy of a clean silica surface. Further, we found that drying the hemisphere by forced convection using either filtered dry air or nitrogen, only quickened the rate at which organic contaminants were adsorbed.
Sum frequency spectrometer
Spectra were collected using a femtosecond SF spectrometer and following a normalization procedure described in detail elsewhere.32 Briefly, the spectrometer consists of a Ti:Sapphire ∼90 fs, 1 kHz, 6 W amplifier (Integra-C, Amplitude Technologies, France), which is partly used to pump a HE-TOPAS (Light Conversion, Lithuania) to generate a broadband (∼250 cm−1) tunable IR pulse. Measurements were carried out with a spectral resolution of <2 cm−1. Angles of incidence for the IR and visible pulses were set to 55.0° and 70.0°, respectively. Laser energies for the IR and visible beams were set at ∼3 μJ per pulse and ∼7 μJ per pulse, respectively. The non-resonant background from a gold-coated hemisphere was used for normalization. All experiments were repeated on at least three different occasions and using different silica substrates. In all cases, the general spectral features presented here were reproduced, and the effect of the pretreatment methods was found to be reversible. To highlight the differences in the spectral region of interest and following SF community standards, the spectra shown here have not been Fresnel-factor corrected (see ESI† for details of the Fresnel-factor correction procedure and corresponding spectra).The spectra were fitted by convoluted Lorentzian and Gaussian line shapes of the form presented in eqn (1), which accounts for homogeneous (Lorentzian line shapes) and inhomogeneous broadening (Gaussian line shape), as well as the complex interference between neighbouring bands.34
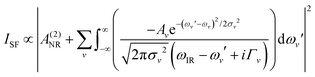 | (1) |
A NR refers to the non-resonant contribution to the SF signal, Av to the amplitude or oscillator strength of the vth resonant mode, ωIR, to the infrared frequency, and ωv, Γv, and σv to the peak position, Lorentzian line width, and Gaussian line width of the vth resonant mode, respectively. As bands in the OH stretching region are typically dominated by inhomogeneous broadening (σv > Γv), the Γv was set to 15 cm−1.
Results and discussion
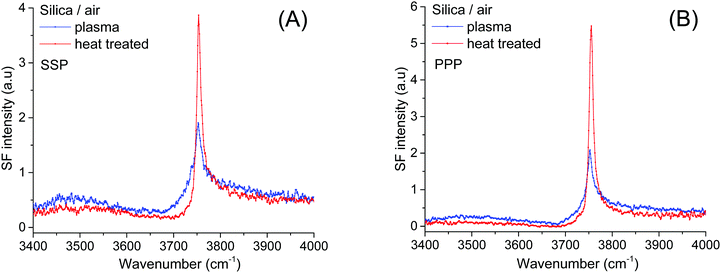
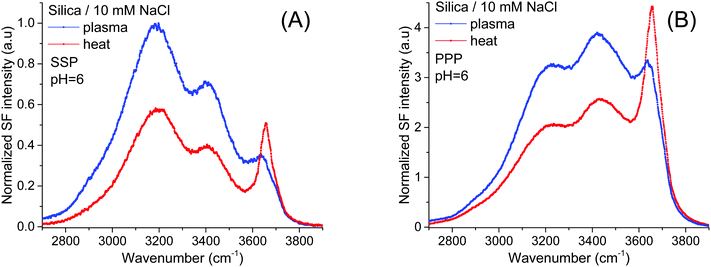
The starting point of the discussion is the SF spectra of plasma and heat treated fused silica surfaces collected in pure H2O under three different polarization combinations (SSP, PPP and SPS; Fig. 1A and B). In addition to the previously identified broad OH stretching bands, centered at ∼3200 cm−1, ∼3400 cm−1,15,16,19,21,35 and ∼3500 cm−1 (the latter more clearly resolved in the SPS spectra),21 which have all been linked to interfacial water molecules, at higher frequencies, a sharper feature can be observed. This peak centered at ∼3680 cm−1 appears more prominently in the heat treated sample, and in contrast to a similar feature observed in the TIR Raman spectra of identical hemispheres,36 it originates from accessible surface OH groups as they can be easily exchanged upon isotopic dilution (Fig. 1C). Thermal treatment, particularly at temperatures above 1000 °C, results in an almost total dehydroxylation of silica surfaces with the interconversion of most silanol groups into siloxane bridges (Si–O–Si).4,6,7,10,37 During the heating process, the hydrogen-bonded and vicinal silanols are the first to disappear, followed later by the geminals.3,6 On the other hand, isolated silanols first increase in numbers, peaking at ∼400 °C, before totally dehydroxylating at temperatures above 1100 °C.2,6,10 Once the silica substrate is immersed in water the surface rapidly rehydroxylizes, yet only partially.6 This effect can be visualized when comparing the SF spectra in Fig. 1A and B. The intensities of the broad water bands at 3200 cm−1 and ∼3400 cm−1 in the heat treated sample are approximately 40% lower than for plasma cleaned silica. Most of the intensity observed in the SF spectra at lower wavenumbers is coupled to water molecules aligned or perturbed by the surface electric field that emanates from deprotonated surface silanols (i.e. silanolate groups).15,21,25 The lower intensity in the heat treated sample is then explained by a reduction in the number of silanols that are more easily deprotonated.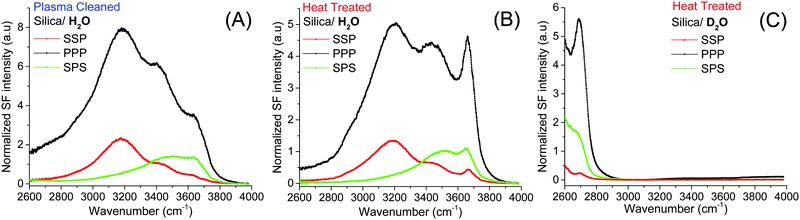 | ||
| Fig. 1 VSF spectra recorded in the SSP, PPP, and SPS polarization combinations of the (A) plasma, and (B) heat treated fused silica in pure H2O. (C) VSF spectra of heat treated silica in D2O. Equivalent Fresnel factor corrected spectra can be found in the ESI.† The absolute intensities between the different spectra can be directly compared. | ||
The band of interest at higher frequencies follows a different behavior, as in absolute terms it appears not to significantly change between the two pretreatment methods (see Fig. 1A and B). Interferences with neighboring bands, however, as well as a lack of unique fits to the spectra (see below), make difficult a more detailed and reliable analysis. This limitation can be largely overcome screening the surface electric field by increasing the ionic strength, as the dominant contribution from the water bands on the red side of the spectra will be significantly diminished.21,35Fig. 2A and B show SF spectra for the two pretreated silica samples in a 10 mM NaCl solution. When compared to pure H2O, the intensity of the ∼3200 cm−1 peak, but also of that at ∼3400 cm−1 are, as expected, much reduced by the screening effect of ions in solution. Still, as for the case of pure water, these latter bands remain less intense in both polarizations (Fig. 2A and B) for the heat treated sample, a fact that is consistent with the above mentioned interpretation of having a smaller population of the more acidic silanols.
 | ||
| Fig. 2 VSF spectra recorded in the (A) SSP, and (B) PPP polarization combinations of plasma and heat treated fused silica in contact with a 10 mM NaCl solution. Equivalent Fresnel factor corrected spectra can be found in the ESI.† The absolute intensities between the different spectra can be directly compared with those of Fig. 1 and 4. | ||
On the other hand, the ∼3680 cm−1 band that is now more evident, not only shows an opposite trend, being clearly stronger in the heat treated sample in both the SSP and PPP spectra; but also, it transpires to be largely insensitive to the surface electric field as it is not much affected by the increase in the ionic strength. The fact that in all polarization combinations the intensity of the ∼3680 cm−1 band is higher for the heat treated sample (see Fig. 2A and B and ESI†), is rationalized by a relative increase of the total number of contributing oscillators, and not by a simple change in their average orientation. Due to its high frequency, the band could, in principle, be assigned to either the OH stretch of water molecules vibrating free from hydrogen bonds38 (i.e. next to surface siloxane groups) or to the OH stretch of specific surface silanol groups (i.e. isolated). As developed below, here we argue in favor of the latter.
Isolated silanols in air
To determine the relative amounts of silanol groups in both pretreated fused silica substrates, SF spectra were collected on the same surfaces after exposure to a gentle stream of filtered dry air (Fig. 3A and B). As shown in Fig. 3, the spectra are dominated by a narrow peak centered at ∼3750 cm−1, which has been unambiguously assigned to the OH stretch of isolated silanols vibrating in air.3,7,9,39 From previous IR studies,4,7,39,40 the vibrational signature for hydrogen bonded silanols in air (see Scheme 1) is expected to be broader and red shifted to ∼3450–3550 cm−1, while those for vicinal and geminal remain a source of debate, with tentative assignments ranging anywhere between 3500 and 3740 cm−1. Interestingly, in the SF spectra shown in Fig. 3 the population of isolated silanols is clearly higher for the heat-treated sample. Since as discussed above, a larger number of the more acidic silanols (i.e. hydrogen bonded silanols) is formed when plasma cleaning, the direct implication is that isolated silanols are less readily deprotonated. Further, the slightly higher intensities observed at ∼3500 cm−1 and ∼3700 cm−1 in plasma treated sample (see Fig. 3), are then consistent with the expected relatively larger number of hydrogen bonded silanols, but also probably vicinal and/or geminal. It is worth mentioning, however, that the relatively low contribution of these latter silanol groups to the SF intensity, likely results from the orientation of their OH groups being aligned, on average, close to the plane of the surface (VSFS is insensitive to such molecular orientations41).Accordingly, we assign the ∼3680 cm−1 feature to the OH stretch of isolated silanols vibrating under water (νiSiOH). The red shift of ∼70 cm−1 is compatible with the gradual shift observed in silica powders when exposed to a series of gases, including water vapor at low surface coverages.9 The advantage here is that VSFS allows detecting such vibrations when silica is in contact with a bulk liquid (Fig. 2). The high frequency of this band indicates that the OH of these isolated silanols is a relatively strong covalent bond that is not significantly perturbed (i.e. ∼70 cm−1 red shift) by hydrogen bonding with adsorbed water molecules. Here, we note that an OH band with similar characteristics to the νiSiOH has been identified on the surfaces of α-Alumina and assigned to a “dangling (Al)nOH”.42 However, in contrast to silica, the frequency of the (Al)nOH band centred at ∼3700 cm−1, remains unchanged whether it is exposed to water or air.42
Acid/base behavior of isolated silanols
Given the assignment of isolated silanols under water, one of the first properties to explore is its pH behavior and the determination of its eventual pKa. Fig. 4 shows the SF spectra of a heat treated silica sample at three different pHs using 10 mM sodium chloride as background electrolyte (equivalent PPP spectra can be found in the ESI†). As expected, the contribution from the broad water bands at 3200 cm−1 and ∼3400 cm−1 increases with solution pH, as the surface charge increases with the partial deprotonation of surface silanol groups.15,16 Interestingly, the νiSiOH remains visible even at pH = 10.5, which implies that the isolated silanols do not easily deprotonate. A more quantitative description can be obtained by fitting the spectra to the convoluted Lorentzian and Gaussian lineshapes described in more detail in the Experimental section. The fitted amplitudes for three resonant contributions as a function of pH are summarized in the inset of Fig. 4 (see ESI† for additional details). The results show that while the amplitudes for the 3200 cm−1 and ∼3400 cm−1 bands increase with pH, the one linked to the isolated silanols not only remains approximately constant, but also displays an opposite sign. Due to the coherent nature of the SF process, information is carried both in the magnitude and phase of the SF signal.35 Consistent with the proposed assignment, the reversed sign indicates that the OH groups of isolated silanols have an opposite net polar orientation from those in water molecules aligned by the negative surface electric field (i.e. water hydrogens are oriented on average towards the surface,22 while those in silanols point away from the surface). Had the surface been positively charged, all three modes would have had the same phase (i.e. sign), as the OH groups from both the interfacial water molecules and isolated silanols would be, on average, oriented away from the surface. As shown in Fig. 5, this is indeed the case when the positively charged surfactant CTAB adsorbs to silica at a concentration above its critical micellar concentration (see ESI† for fitting parameters).43 Interestingly, due to interference with the water neighboring band, the νiSiOH is now observed as a dip, instead of a peak in the spectrum (see Fig. 5). Clearly, this situation illustrates how the νiSiOH can be used as an internal reference for determining the absolute polar orientation of water molecules in the interfacial region. Moreover, the fact that the νiSiOH band remains visible for the CTAB case, also helps discarding the possibility of associating the ∼3680 cm−1 band to water molecules weakly interacting with the silica substrate (see above), as these water molecules would have necessarily been displaced by the adsorbing surfactant.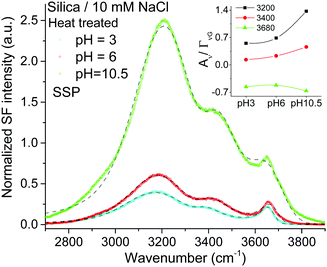 | ||
| Fig. 4 VSF spectra recorded in the SSP polarization combination of a heat treated fused silica hemisphere in contact with 10 mM NaCl solution at three different pHs (PPP spectra can be found in the ESI†). The short-segmented lines are the fitted curves to the experimental data. Data were collected in the following sequence: pH 6, pH 3, and finally pH 10.5. The absolute intensities between the different spectra can be directly compared with those of Fig. 1 and 2. Equivalent Fresnel factor corrected spectra can be found in the ESI.† Inset: Fitted amplitude of the bands at ∼3200 cm−1, ∼3400 cm−1 and ∼3680 cm−1 (see ESI† for details). | ||
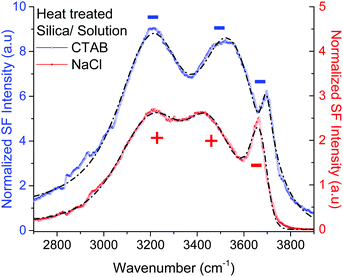 | ||
| Fig. 5 VSF spectra recorded in the PPP polarization combination of a heat treated fused silica hemisphere in contact with a 2 mM CTAB solution (positively charged surface), and a 10 mM NaCl solution (negatively charged surface). The short-segmented lines are the fitted curves to the experimental data where the CH modes have been neglected (see ESI† for details of the fitting parameters). For the positively charged surface (CTAB) the amplitudes of the water bands at ∼3200 cm−1, ∼3400 cm−1 have the same sign (i.e. minus) as for νiSiOH at ∼3680 cm−1, while for the negatively charged surface (10 mM NaCl), the water bands have opposite sign since the water OHs are now oriented, on average, towards the silica substrate. Note that because of interference, the νiSiOH appears as a dip instead of peak in the CTAB spectrum. | ||
Returning to Fig. 4, the lack of significant changes in the fitted amplitudes for νiSiOH with increasing pH, indicates that the pKa of isolated silanols is higher than 10.5. Studies using higher ionic strength solutions to be presented elsewhere situate the pKa above 11.5. It is worth noting, however, that the experimentally accessible range is limited due to the dissolution of silica at high pH, which is already expected at pH above 11 for amorphous precipitated silica,2 and is indeed observed in our substrates when exceeding pH 12 at room temperature. In line with these experimental findings, recent molecular dynamic simulations27,29 have estimated the pKa of isolated silanols to be higher than those for hydrogen bonded and geminal silanols, with calculated values ranging between 8.9 and 11.2, although in the presence of specific monovalent ions the pKa have been estimated to shift several units upwards.44
In context of the results presented here, and recalling that a large majority (>75%) of surface silanols do not dissociate even at pH as high as 10,23,30 the silanols sites inferred from second harmonic data having a pKa ∼ 4.5 and ∼8.5,17 are clearly not associated with isolated Si–OHs, but instead with those having closely neighboring silanols: vicinal, geminal, and/or hydrogen-bonded. Further, the relative populations of the different silanol sites, will evidently depend on the pretreatment history of the silica substrate, a fact that may partly explain the differences observed in more recent SH studies.23
Conclusions
In summary, we have used VSFS to identify the SiO–H stretch of isolated Q3 surface silanols in contact with bulk water. Although relatively narrow, the feature (νiSiOH) is broader and red-shifted by ∼70 cm−1 when compared to its free vibration in air. In addition, we show that depending on the silica pretreatment, the relative population of the different types of silanols under water can be modified. Preheating the fused silica sample to 1000 °C results in a larger number of isolated silanols when compared to plasma cleaning using air as carrier gas, while the opposite trend is observed for the more acidic Si–OHs (i.e. hydrogen bonded and/or geminal). This behavior was found to be reversible. Moreover, pH dependent studies show that the pKa of the isolated silanols is higher than 10.5. Finally, the identification of the isolated silanol band opens new opportunities to further understand the mechanism of adsorption of various molecules, including specific ion interactions,44–47 on the surface of this commonly used material.Acknowledgements
This work was financially supported by the Swedish Foundation for Strategic Research (SSF-FFL-5 program) and the Swedish Research Council (VR). The authors thank Marie-Pierre Gaigeot and Julianne Gibbs-Davis for insightful discussions. Jonathan Liljeblad is acknowledged for developing the routine used for fitting the SF spectra.References
- G. Schubert, Treatise on Geophysics, Elsevier Science, 2015 Search PubMed.
- R. K. Iler, The chemistry of silica: solubility, polymerization, colloid and surface properties, and biochemistry, Wiley, 1979 Search PubMed.
- A. Rimola, D. Costa, M. Sodupe, J. F. Lambert and P. Ugliengo, Chem. Rev., 2013, 113, 4216–4313 CrossRef CAS PubMed.
- H. E. Bergna and W. O. Roberts, Colloidal Silica: Fundamentals and Applications, CRC Press, 2005 Search PubMed.
- W. Tan, K. Wang, X. He, X. J. Zhao, T. Drake, L. Wang and R. P. Bagwe, Med. Res. Rev., 2004, 24, 621–638 CrossRef CAS PubMed.
- L. T. Zhuravlev, Colloids Surf., A, 2000, 173, 1–38 CrossRef CAS.
- E. Papirer, Adsorption on Silica Surfaces, Taylor & Francis, 2000 Search PubMed.
- G. E. Maciel and D. W. Sindorf, J. Am. Chem. Soc., 1980, 102, 7606–7607 CrossRef CAS.
- R. S. McDonald, J. Am. Chem. Soc., 1957, 79, 850–854 CrossRef CAS.
- V. I. Lygin, Russ. J. Gen. Chem., 2001, 71, 1368–1372 CrossRef CAS.
- L. T. Zhuravlev, Langmuir, 1987, 3, 316–318 CrossRef CAS.
- A. G. Lambert, P. B. Davies and D. J. Neivandt, Appl. Spectrosc. Rev., 2005, 40, 103–145 CrossRef CAS.
- C. D. Bain, J. Chem. Soc., Faraday Trans., 1995, 91, 1281–1296 RSC.
- K. B. Eisenthal, Chem. Rev., 2006, 106, 1462–1477 CrossRef CAS PubMed.
- Q. Du, E. Freysz and Y. R. Shen, Phys. Rev. Lett., 1994, 72, 238–241 CrossRef CAS PubMed.
- V. Ostroverkhov, G. A. Waychunas and Y. R. Shen, Chem. Phys. Lett., 2004, 386, 144–148 CrossRef CAS.
- S. Ong, X. Zhao and K. B. Eisenthal, Chem. Phys. Lett., 1992, 191, 327–335 CrossRef CAS.
- S. Dewan, M. S. Yeganeh and E. Borguet, J. Phys. Chem. Lett., 2013, 4, 1977–1982 CrossRef CAS PubMed.
- O. Isaienko, S. Nihonyanagi, D. Sil and E. Borguet, J. Phys. Chem. Lett., 2013, 4, 531–535 CrossRef CAS PubMed.
- P. A. Covert, K. C. Jena and D. K. Hore, J. Phys. Chem. Lett., 2014, 5, 143–148 CrossRef CAS PubMed.
- K. C. Jena and D. K. Hore, J. Phys. Chem. C, 2009, 113, 15364–15372 CAS.
- A. Myalitsin, S.-H. Urashima, S. Nihonyanagi, S. Yamaguchi and T. Tahara, J. Phys. Chem. C, 2016, 120, 9357–9363 CAS.
- A. M. Darlington and J. M. Gibbs-Davis, J. Phys. Chem. C, 2015, 119, 16560–16567 CAS.
- D. Lis, E. H. G. Backus, J. Hunger, S. H. Parekh and M. Bonn, Science, 2014, 344, 1138–1142 CrossRef CAS PubMed.
- V. Ostroverkhov, G. A. Waychunas and Y. R. Shen, Phys. Rev. Lett., 2005, 94, 046102 CrossRef PubMed.
- M. Sovago, R. Kramer Campen, H. J. Bakker and M. Bonn, Chem. Phys. Lett., 2009, 470, 7–12 CrossRef CAS.
- K. Leung, I. M. B. Nielsen and L. Criscenti, Geochim. Cosmochim. Acta, 2010, 74, A584–A584 CrossRef.
- M. Sulpizi, M. P. Gaigeot and M. Sprik, J. Chem. Theory Comput., 2012, 8, 1037–1047 CrossRef CAS PubMed.
- M. Pfeiffer-Laplaud, D. Costa, F. Tielens, M.-P. Gaigeot and M. Sulpizi, J. Phys. Chem. C, 2015, 119, 27354–27362 CAS.
- M. A. Brown, A. Goel and Z. Abbas, Angew. Chem., Int. Ed., 2016, 55, 3790–3794 CrossRef CAS PubMed.
- T. Lagstrom, T. A. Gmur, L. Quaroni, A. Goel and M. A. Brown, Langmuir, 2015, 31, 3621–3626 CrossRef CAS PubMed.
- J. F. D. Liljeblad and E. Tyrode, J. Phys. Chem. C, 2012, 116, 22893–22903 CAS.
- O. Isaienko and E. Borguet, Langmuir, 2013, 29, 7885–7895 CrossRef CAS PubMed.
- C. D. Bain, P. B. Davies, T. H. Ong, R. N. Ward and M. A. Brown, Langmuir, 1991, 7, 1563–1566 CrossRef CAS.
- Y. R. Shen and V. Ostroverkhov, Chem. Rev., 2006, 106, 1140–1154 CrossRef CAS PubMed.
- J. F. D. Liljeblad, I. Furo and E. C. Tyrode, Phys. Chem. Chem. Phys., 2017, 19, 305–317 RSC.
- J. P. Gallas, J. C. Lavalley, A. Burneau and O. Barres, Langmuir, 1991, 7, 1235–1240 CrossRef CAS.
- Q. Du, E. Freysz and Y. R. Shen, Science, 1994, 264, 826–828 CAS.
- B. A. Morrow and A. J. McFarlan, J. Phys. Chem., 1992, 96, 1395–1400 CrossRef CAS.
- S. P. Zhdanov, L. S. Kosheleva and T. I. Titova, Langmuir, 1987, 3, 960–967 CrossRef CAS.
- R. Lu, W. Gan, B.-H. Wu, Z. Zhang, Y. Guo and H.-F. Wang, J. Phys. Chem. B, 2005, 109, 14118–14129 CrossRef CAS PubMed.
- L. Zhang, C. Tian, G. A. Waychunas and Y. R. Shen, J. Am. Chem. Soc., 2008, 130, 7686–7694 CrossRef CAS PubMed.
- E. Tyrode, M. W. Rutland and C. D. Bain, J. Am. Chem. Soc., 2008, 130, 17434–17445 CrossRef CAS PubMed.
- M. Pfeiffer-Laplaud, M.-P. Gaigeot and M. Sulpizi, J. Phys. Lett., 2016, 7, 3229–3234 CAS.
- S. Dewan, V. Carnevale, A. Bankura, A. Eftekhari-Bafrooei, G. Fiorin, M. L. Klein and E. Borguet, Langmuir, 2014, 30, 8056–8065 CrossRef CAS PubMed.
- M. S. Azam, C. N. Weeraman and J. M. Gibbs-Davis, J. Phys. Lett., 2012, 3, 1269–1274 CAS.
- T. A. Gmür, A. Goel and M. A. Brown, J. Phys. Chem. C, 2016, 120, 16617–16625 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional experimental details, Fresnel factor corrected spectra and fitting details. See DOI: 10.1039/c7cp01507k |
| This journal is © the Owner Societies 2017 |