 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Time-resolved terahertz spectroscopy reveals the influence of charged sensitizing quantum dots on the electron dynamics in ZnO
Sesha Bamini
N.†
 ab,
Hynek
Němec†
c,
Karel
Žídek‡
a,
Mohamed
Abdellah
ad,
Mohammed J.
Al-Marri
e,
Pavel
Chábera
a,
Carlito
Ponseca§
a,
Kaibo
Zheng
*ae and
Tönu
Pullerits
*a
ab,
Hynek
Němec†
c,
Karel
Žídek‡
a,
Mohamed
Abdellah
ad,
Mohammed J.
Al-Marri
e,
Pavel
Chábera
a,
Carlito
Ponseca§
a,
Kaibo
Zheng
*ae and
Tönu
Pullerits
*a
aDepartment of Chemical Physics and NanoLund, Lund University, Box 124, 22100 Lund, Sweden. E-mail: kaibo.zheng@chemphys.lu.se; tonu.pullerits@chemphys.lu.se
bNational Center for Ultrafast Processes, University of Madras, Chennai 600113, India
cInstitute of Physics, Czech Academy of Sciences, Na Slovance 2, 18221 Prague, Czech Republic
dDepartment of Chemistry, Faculty of Science, South Valley University, Qena 83523, Egypt
eGas Processing Center, College of Engineering, Qatar University, P.O. Box 2713, Doha, Qatar
First published on 9th February 2017
Abstract
Photoinitiated charge carrier dynamics in ZnO nanoparticles sensitized by CdSe quantum dots is studied using transient absorption spectroscopy and time-resolved terahertz spectroscopy. The evolution of the transient spectra shows that electron injection occurs in a two-step process, where the formation of a charge transfer state (occurring in several picoseconds) is followed by its dissociation within tens of picoseconds. The photoconductivity of electrons injected into the ZnO nanoparticles is lower than that of charges photogenerated directly in ZnO. We conclude that the motion of injected electrons in ZnO nanoparticles is strongly influenced by their interaction with positive charges left in the sensitizing quantum dots.
A Introduction
Semiconductor quantum dots (QDs) are promising building blocks in photovoltaic devices due to their size-tunable band gap, strong absorption, long-term photostability and possible carrier multiplication.1–7 In a typical QD-based solar cell, incident light is absorbed in QDs producing electron–hole pairs. The QDs can be attached to wide-band-gap semiconductor nanoparticles. In such semiconductors, the bottom of the conduction band can have lower energy than the excited electron in the QDs. Consequently, energetically downhill electron injection from the QD into the semiconductor occurs. The electron injection competes with various recombination processes, therefore high speed of reaching stabilized separated charges is required to achieve a high charge collection efficiency of the solar cells.8,9The time-scale of the injection and its dependence on the electronic band alignment, sensitization geometry and linker molecules have been widely investigated via time-resolved photoluminescence and visible transient absorption spectroscopy.10–13 These conventional approaches can only probe the depopulation of the excited states in the QDs. However, probing the electron dynamics in the semiconductor is also important, particularly in systems where electron dynamics includes a charge transfer state (CTS) due to an electrostatic interaction between the injected electron and the hole remaining in the donor.8,14,15
In this work, we combine transient absorption (TA) spectroscopy and time-resolved terahertz (THz) spectroscopy to investigate photoinitiated processes in ZnO nanoparticles (NPs) sensitized by CdSe QDs (referred to as CdSe/ZnO in the following text). While TA probes mainly the oxidation state of the sensitizer, THz spectroscopy probes predominantly the population of free charges in the NPs and their transport properties on a nanometer distance scale.16 A combination of these results with Monte-Carlo simulations provides a detailed picture of the electron dynamics, including the interaction of the injected electrons with positively charged QDs. We show that the Coulombic interaction not only affects the injection rate, but it also considerably reduces electron mobility in the ZnO NPs. We also show that all the processes are controlled by the effective permittivity of the system, which implies that significant differences appear between various forms of ZnO nanostructures.
B Experimental details
ZnO films were deposited by the doctor-blade technique using colloidal ZnO NPs (Sigma Aldrich) with various sizes; subsequently, they were sintered in air at 450 °C for 30 minutes, resulting in about 1 micron thick films. Although the films became mesoporous after annealing, we can still distinguish the boundaries of individual nanoparticles (Fig. 1). The mean NP diameters identified from the SEM image (25, 48, and 61 nm) are close to the nominal sizes specified by the manufacturer (35, 50 and 70 nm, respectively).Sensitization by mercaptopropionic-acid-capped CdSe QDs8 was accomplished by immersing the preheated nanoparticulate ZnO films into QD solution for 2 h. Based on the investigations in ref. 10, this leads to approximately monolayer adsorption of QDs on the NP surface. The steady-state absorption spectrum of neat QDs exhibits a pronounced 1S3/2–1Se exciton band at 542 nm (Fig. 1), which corresponds to the mean QD diameter of ∼2.9 nm.8,17 The blue shift of the exciton peak for CdSe/ZnO is due to structural and environmental changes upon adsorption to ZnO.18 All pump–probe studies were performed under a N2 atmosphere in order to eliminate possible effects of cumulative photodegradation.8,15,19–21
The transient absorption spectra were recorded in a standard pump–probe setup8 based on a regenerative Ti:sapphire laser amplifier (Spitfire, Spectra Physics; 1 kHz repetition rate). The excitation beam was tuned to 470 nm; the photon fluence of 1.4 × 1015 photons per cm2 per pulse ensures a sufficient signal to noise ratio. Although this intensity generates ∼2.6 electron–hole pairs per QD,17 we verified that it is still low enough to prevent non-linear phenomena.22
C Results and discussion
The probing wavelength (530 nm) was tuned to the band-edge transition of the QDs, therefore the instantaneous decay observed in the kinetics of bare CdSe QDs (Fig. 2a) corresponds to the state filling of the QD 1S electron levels8,12,23–26 (the hole contribution to the TA signal is negligible due to their higher effective mass). The nanosecond decay of the TA kinetics for the neat CdSe QDs represents a slow recombination of the photoexcited electron–hole pairs.The decay of the TA dynamics of CdSe/ZnO is significantly faster due to electron injection into the ZnO NPs.22 The observed decay kinetics is rather complex, since the electron transfer from the QDs to the ZnO NPs can occur via multiple channels; the dynamics at longer time scales is further complicated by electron–hole recombination. We can identify three distinct characteristic decay times: a fast one (about 4 ps), a slow one (30–40 ps), and a long-lived one (∼600 ps). This kind of dynamics has been observed in many similar QD-sensitized metal-oxide nanostructures.18,27–31
The components faster than a few hundreds of picoseconds are due to electron injection from QDs directly attached to the metal-oxide;8,18,27 the bi-exponential nature can be explained by injection via a CTS.8,22,32 The long-lived component is typically associated with QDs without a direct connection to the ZnO NPs: the injection is then either very slow or even inhibited.10,23 A certain fraction of the sensitizing QDs can be attached to the metal-oxide indirectly via other QDs in which case energy transfer may take place.10Via energy transfer the excitation will ultimately reach the QDs which are directly attached to a ZnO NP.
Transient THz conductivity spectra were recorded in a usual setup for time-resolved THz spectroscopy21 driven by the same laser amplifier as in the TA measurements. In order to reveal the influence of a QD sensitizer on the electron dynamics in ZnO NPs, we investigated both CdSe and ZnO upon photoexcitation of the QDs (542 nm), and directly excited neat ZnO NPs (266 nm). The wavelength of 542 nm is well below the band gap of ZnO; therefore, it is absorbed only by the QDs. Conversely, the excitation at 266 nm is well above the band gap of ZnO, leading to the generation of electron–hole pairs directly inside the NPs.
Measurement of transient THz transmittance spectra ΔT/T (=ΔE/E where E is the spectrum of the electric field transmitted through the sample without photoexcitation, and ΔE is the photo-induced change in the transmitted electric field spectrum) allows retrieval of charge mobility μ and quantum yield of mobile charge carriers. For a thin photoconducting layer deposited on a substrate with refractive index ns and completely absorbing the excitation power,
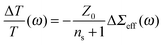 | (1) |
 | (2) |
For carriers directly photogenerated in neat ZnO NPs, the real part of the measured THz conductivity increases with frequency, whereas the imaginary part is mostly negative (Fig. 3a), indicating a certain degree of charge localization. In order to better assess the properties of these bare nanoparticles, we carried out Monte–Carlo calculations of conductivity of charges confined in nanospheres.35 In brief, Newton's equations of motion are solved to obtain thermal trajectories of an ensemble of charges. When a charge hits the boundary of a NP, it is either scattered into a neighboring NP with probability pF, or it is scattered back into the original NP with probability pB = 1 − pF. The Kubo formula is subsequently employed to retrieve the mobility spectrum from the calculated velocity autocorrelation function. Unlike the parameters V and B (which describe the distribution of the THz electric field in the inhomogeneous system), the probabilities pB and pF are related solely to the charge transport among nanocrystals. With electron effective mass meff = 0.24me and scattering time τs = 27 fs (which stems from the Drude dc mobility μ = e0τs/meff),36 the fits of the measured spectra (Fig. 3a) yield pB = 99%, 89% and 86% and V + B = 0.07, 0.18 and 0.11 for samples with mean NP diameters of 25, 48 and 61 nm, respectively (the initial quantum yield φ is 1). The sum V + B is higher for the 48 nm NPs, which indicates that they are better percolated (the NPs are better electrically connected with their neighbors) than the others; this is also the reason why the transient conductivity of these particles is higher than that of larger NPs. The large values of pB provide evidence that NP boundaries constitute a significant barrier for charge transport in all studied films. The deviations between the calculated and measured imaginary parts in Fig. 3a are attributed to the possible minor drift of the experimental setup, which can mix a small part of the dominating real component of the signal with the imaginary component.37
The shape of the normalized transient conductivity spectra of carriers injected into the ZnO NPs (Fig. 3b) is very similar to that of the photogenerated carriers, but the amplitude is a factor of 4 to 5 lower. We attribute the difference in amplitude to the Coulombic interaction between the electron injected into the ZnO NP and the hole left in the CdSe QD, similarly to that observed for zinc-porphyrin-sensitized ZnO NPs.15 We can rule out other effects, possibly responsible for the decrease in the conductivity amplitude.
• Low injection efficiency is incompatible with TA kinetics. The TA kinetics decays to <20% of its peak value within 100 ps; the injection efficiency thus exceeds 80%.
• Structural differences between bare and sensitized samples are improbable. This is supported by ref. 15, where sensitization by zinc-porphyrin dye did not change the THz photoconductivity of photogenerated electrons.
• Ultrafast recombination or trapping of electrons in ZnO NPs would appear as a rapid initial decay component of THz photoconductivity, while the measured kinetics varies only slowly (Fig. 2b).
The THz kinetics (which is a measure of the population change of mobile charges) exhibits similar features to the TA kinetics. The 4 ps increase is due to the injection of electrons from directly attached CdSe QDs. Less pronounced is the increase with 37 ps time constant (which is not present when electrons in ZnO are generated directly by above-band-gap photoexcitation). In principle, it could represent a slower injection from QDs not directly attached to the ZnO NPs; however, our previous research revealed that such a process is mediated by inter-QD energy transfer which appears on a nanosecond timescale.10 For this reason, we attribute the observed process to CTS-mediated electron injection.8,15,38,39 The CTS then undergoes continuous dissociation which increases the THz photoconductivity up to 40 ps. At this time—when the amplitude is maximum—, most of the electrons are already injected into the ZnO NPs.8 Finally, the THz kinetic decays on the hundreds-picoseconds timescale due to trapping or recombination of the electrons in ZnO NPs.
The behavior of injected electrons is strongly affected by Coulombic interaction with positively charged QDs. Here we focus on two such effects. Firstly, we discuss the dynamics of the CTS and estimate the injection rate of electrons into the NPs. Secondly, we develop Monte-Carlo calculations to assess the influence on electron transport after CTS dissociation.
The dissociation rate Kdiss of a CTS can be estimated using the Braun–Onsager model:25
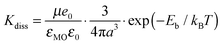 | (3) |
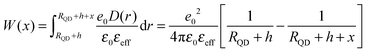 | (4) |
According to eqn (3), the dissociation rate depends very sensitively on the binding energy. Coulombic interaction attracts the hole towards the electron: the decreased distance between the electron and the hole would lead to a higher binding energy, and in turn, to a slower dissociation rate. A particular environment of each individual QD is another issue influencing the binding energy through the effective permittivity εeff. For example, the packing of NPs leads to much larger filling factors than for nanowires; in turn, the effective permittivity of the nanowire system is lower.11 In this situation, the binding energy would increase [eqn (4)], leading to slower dissociation [eqn (3)]. This is in agreement with the longer CTS dissociation time (200 ps) observed in CdSe-QD-sensitized ZnO nanowires.8 The faster injection rates in NPs would be favorable for the overall charge injection efficiency in solar cells.41
The effective permittivity depends on the permittivity, filling factor, shape and percolation degree of the electron acceptor. Our results thus clearly show that the electron injection efficiency depends on the shape of the electron acceptor (nanoparticles or nanowires) as well as on the detailed morphology of the acceptor network. In other words, shape and morphology are fundamental parameters which need to be considered in the studies of electron injection.
In order to simulate the electron mobility in QD sensitized ZnO nanoparticles the Coulombic interaction in Monte–Carlo calculations was represented using an electric potential Φ(r) in which electrons move. We approximated it by a potential of a positive charge q placed in the distance δ from a planar interface (Fig. 4a and b):
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) is the reduced permittivity defined as42
is the reduced permittivity defined as42![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) = (εMO + εQD)/2. In order to illustrate the effects of this interaction, we considered mutually isolated NPs (i.e., pF = 0). When the Coulombic binding energy is smaller than the thermal energy of charges, the electron response is only weakly influenced by the Coulombic interaction. With increasing interaction strength, electrons are more attracted to the positive charges and their motion becomes more confined. This is accompanied by a decrease in the mobility amplitude (Fig. 4c), and for even stronger interaction, by a change in the shape of the mobility spectrum. This behavior is in agreement with experimental observations, showing a substantial difference in amplitudes of normalized conductivities of injected and directly photogenerated charges, and only insignificant differences in the spectra shapes.
= (εMO + εQD)/2. In order to illustrate the effects of this interaction, we considered mutually isolated NPs (i.e., pF = 0). When the Coulombic binding energy is smaller than the thermal energy of charges, the electron response is only weakly influenced by the Coulombic interaction. With increasing interaction strength, electrons are more attracted to the positive charges and their motion becomes more confined. This is accompanied by a decrease in the mobility amplitude (Fig. 4c), and for even stronger interaction, by a change in the shape of the mobility spectrum. This behavior is in agreement with experimental observations, showing a substantial difference in amplitudes of normalized conductivities of injected and directly photogenerated charges, and only insignificant differences in the spectra shapes.
D Conclusions
In summary, we have investigated photoinduced charge carrier dynamics in CdSe QD sensitized ZnO NPs. The Coulombic interaction between injected electrons in ZnO and the holes in the QDs significantly influences the electron dynamics after photoexcitation in various aspects: first, the electron injection from CdSe to ZnO is meditated by a CTS formed within a few picoseconds and dissociated within tens of picoseconds. We extended the Braun–Onsager model to reflect the environment of the constituents and applied it for the estimation of the dissociation rate in CdSe-QD-sensitized ZnO NPs. This model also explains the different dissociation rate in the nanowires system as a result of different effective permittivities of NPs and nanowires systems. More generally, dependence of the injection rate on the effective permittivity of the system implies a fundamental influence of the shape and morphology of the nanostructures forming the electron acceptor network on the charge injection efficiency. In addition, the Coulombic interaction between the electron and the hole reduces mobility of injected electrons by a factor of 4–5. Such a behavior was explained by Monte-Carlo calculations of THz conductivity of electrons moving in an electrostatic potential.Acknowledgements
This work was supported by the Knut and Alice Wallenberg Foundation, Swedish Research Council, Czech Science Foundation (Grant 17-03662S) and Carl Tryggers Foundation in Stockholm (Project CTS 14:390). KZ acknowledges support from NPRP grant #NPRP7-227-1-034 from the Qatar National Research Fund (a member of Qatar Foundation).References
- P. V. Kamat, Quantum Dot Solar Cells Semiconductor Nanocrystals as Light Harvesters, J. Phys. Chem. C, 2008, 112, 18737 CAS.
- O. E. Semonin, J. M. Luther, S. Choi, H. Y. Chen, J. Gao, A. J. Nozik and M. C. Beard, Peak External Photocurrent Quantum Efficiency Exceeding 100% via MEG in a Quantum Dot Solar Cell, Science, 2011, 334, 1530 CrossRef CAS PubMed.
- J. J. H. Pijpers, E. Hendry, M. T. W. Milder, R. Fanciull, J. Savolainen, J. L. Herek, D. Vanmaekelbergh, S. Ruhman, D. Mocatta, D. Oron, A. Aharoni, U. Banin and M. Bonn, Carrier multiplication and its reduction by photodoping in colloidal InAs quantum dots, J. Phys. Chem. C, 2007, 111, 4146 CAS.
- K. Zheng, K. Karki, K. Žídek and T. Pullerits, Ultrafast Photoinduced Dynamics in Quantum Dot-Based Systems for Light Harvesting, Nano Res., 2015, 8, 2125 CrossRef CAS.
- K. J. Karki, F. Ma, K. Zheng, K. Žídek, A. Mousa, M. Abdellah, M. E. Messing, L. R. Wallenberg, A. Yartsev and T. Pullerits, Multiple Exciton Generation in Nano-Crystals Revisited: Consistent Calculation of the Yield Based on Pump-Probe Spectroscopy, Sci. Rep., 2013, 3, 2287 Search PubMed.
- K. J. Karki, J. R. Widom, J. Seibt, I. Moody, M. C. Lonergan, T. Pullerits and A. H. Marcus, Coherent Two-Dimensional Photocurrent Spectroscopy in a PbS Quantum Dot Photocell, Nat. Commun., 2014, 5, 5869 CrossRef CAS PubMed.
- H. J. Lee, J. H. Yum, H. C. Leventis, S. M. Zakeeruddin, S. A. Haque, P. Chen, S. I. Seok, M. Grätzel and M. K. Nazeeruddin, CdSe Quantum Dot-Sensitized Solar Cells Exceeding Efficiency 1% at Full-Sun Intensity, J. Phys. Chem. C, 2008, 112, 11600 CAS.
- K. Žídek, K. Zheng, C. S. Ponseca Jr, M. E. Messing, L. R. Wallenberg, P. Chábera, M. Abdellah, V. Sundström and T. Pullerits, Electron Transfer in Quantum-Dot-Sensitized ZnO Nanowires: Ultrafast Time-Resolved Absorption and Terahertz Study, J. Am. Chem. Soc., 2012, 134, 12110 CrossRef PubMed.
- M. Abdellah, R. Marschan, K. Žídek, M. E. Messing, A. Abdelwahab, P. Chábera, K. Zheng and T. Pullerits, Hole Trapping: The Critical Factor for Quantum Dot Sensitized Solar Cell Performance, J. Phys. Chem. C, 2014, 118, 25802 CAS.
- K. Zheng, K. Žídek, M. Abdellah, M. Torbjörnsson, P. Chábera, S. Shao, F. Zhang and T. Pullerits, Fast Monolayer Adsorption and Slow Energy Transfer in CdSe Quantum Dot Sensitized ZnO Nanowires, J. Phys. Chem. A, 2012, 117, 5919 CrossRef PubMed.
- K. Zheng, K. Žídek, M. Abdellah, P. Chábera, M. S. Abd El-sadek and T. Pullerits, Effect of Metal Oxide Morphology on Electron Injection from CdSe Quantum Dots to ZnO, Appl. Phys. Lett., 2013, 102, 163119 CrossRef.
- G. Schlegel, J. Bohnenberger, I. Potapova and A. Mews, Fluorescence Decay Time of Single Semiconductor Nanocrystals, Phys. Rev. Lett., 2002, 88, 137401 CrossRef PubMed.
- T. Hansen, K. Žídek, K. Zheng, M. Abdellah, P. Chábera, P. Persson and T. Pullerits, Orbital Topology Controlling Charge Injection in Quantum-Dot-Sensitized Solar Cells, J. Phys. Chem. Lett., 2014, 5, 1157 CrossRef CAS PubMed.
- C. Deibel, T. Strobel and V. Dyakonov, Role of the Charge Transfer State in Organic Donor–Acceptor Solar Cells, Adv. Mater., 2010, 22, 4097 CrossRef CAS PubMed.
- H. Němec, J. Rochford, O. Taratula, E. Galoppini, P. Kužel, T. Polívka, A. Yartsev and V. Sundström, Influence of the Electron-Cation Interaction on Electron Mobility in Dye-Sensitized ZnO and TiO2 Nanocrystals: a Study Using Ultrafast Terahertz Spectroscopy, Phys. Rev. Lett., 2010, 104, 197401 CrossRef PubMed.
- H. Němec, P. Kužel and V. Sundström, Charge Transport in Nanostructured Materials for Solar Energy Conversion Studied by Time-Resolved Terahertz Spectroscopy, J. Photochem. Photobiol., A, 2010, 215, 123 CrossRef.
- W. Yu, L. Qu, W. Guo and X. Peng, Experimental Determination of the Extinction Coefficient of CdTe, CdSe, and CdS Nanocrystals, Chem. Mater., 2003, 15, 2854 CrossRef CAS.
- D. R. Pernik, K. Tvrdy, J. Radich and P. V. Kamat, Tracking the Adsorption and Electron Injection Rates of CdSe Quantum Dots on TiO2: Linked versus Direct Attachment, J. Phys. Chem. C, 2011, 115, 13511 CAS.
- K. Tvrdy and P. V. Kamat, Substrate Driven Photochemistry of CdSe Quantum Dot Films: Charge Injection and Irreversible Transformations on Oxide Surfaces, J. Phys. Chem. A, 2009, 113, 3765 CrossRef CAS PubMed.
- K. Žídek, K. Zheng, P. Chábera, M. Abdellah and T. Pullerits, Quantum Dot Photodegradation due to CdSe-ZnO Charge Transfer: Transient Absorption Study, Appl. Phys. Lett., 2012, 100, 243111 CrossRef.
- R. Ulbricht, E. Hendry, J. Shan, T. F. Heinz and M. Bonn, Carrier dynamics in semiconductors studied with time-resolved terahertz spectroscopy, Rev. Mod. Phys., 2011, 83, 543 CrossRef CAS.
- K. Žídek, K. Zheng, M. Abdellah, N. Lenngren, P. Chábera and T. Pullerits, Ultrafast Dynamics of Multiple Exciton Harvesting in the CdSe–ZnO System: Electron Injection versus Auger Recombination, Nano Lett., 2012, 12, 6393 CrossRef PubMed.
- K. Žídek, K. Zheng, M. Abdellah, P. Chábera and T. Pullerits, Simultaneous Creation and Recovery of Trap States on Quantum Dots in a Photoirradiated CdSe–ZnO System, J. Phys. Chem. C, 2014, 118, 27567 Search PubMed.
- K. Zheng, K. Žídek, M. Abdellah, W. Zhang, P. Chábera, N. Lenngren, A. Yartsev and T. Pullerits, Charge-Transfer Processes in Dye-Sensitized NiO Solar Cells, J. Phys. Chem. C, 2014, 118, 18462 CAS.
- V. I. Klimov, Spectral and Dynamical Properties of Multiexcitons in Semiconductor Nanocrystals, Annu. Rev. Phys. Chem., 2007, 58, 635 CrossRef CAS PubMed.
- S. N. Sharma, Z. S. Pillai and P. V. Kamat, Photoinduced Charge Transfer between CdSe Quantum Dots and p-Phenylenediamine, J. Phys. Chem. B, 2003, 107, 10088 CrossRef CAS.
- K. Tvrdy, P. A. Frantsuzov and P. V. Kamat, Photoinduced Electron Transfer From Semiconductor Quantum Dots to Metal Oxide Nanoparticles, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 29 CrossRef CAS PubMed.
- J. L. Blackburn, D. C. Selmarten and A. J. Nozik, Electron Transfer Dynamics in Quantum Dot/Titanium Dioxide Composites Formed by in Situ Chemical Bath Deposition, J. Phys. Chem. B, 2003, 107, 14154 CrossRef CAS.
- I. Robel, V. Subramanian, M. Kuno and P. V. Kamat, Quantum Dot Solar Cells. Harvesting Light Energy with CdSe Nanocrystals Molecularly Linked to Mesoscopic TiO2 Films, J. Am. Chem. Soc., 2006, 128, 2385 CrossRef CAS PubMed.
- I. Robel, M. Kuno and P. V. Kamat, Size-Dependent Electron Injection from Excited CdSe Quantum Dots into TiO2 Nanoparticles, J. Am. Chem. Soc., 2007, 129, 4136 CrossRef CAS PubMed.
- N. Guijarro, Q. Shen, S. Gimenez, I. Mora-Sero, J. Bisquert, T. Lana-Villarreal, T. Toyoda and R. Gomez, Direct Correlation between Ultrafast Injection and Photoanode Performance in Quantum Dot Sensitized Solar Cells, J. Phys. Chem. C, 2010, 114, 22352 CAS.
- P. Kužel and H. Němec, Terahertz Conductivity in Nanoscaled Systems: Effective Medium Theory Aspects, J. Phys. D: Appl. Phys., 2014, 47, 374005 CrossRef.
- H. Němec, V. Zajac, I. Rychetský, D. Fattakhova-Rohlfing, B. Mandlmeier, T. Bein, Z. Mics and P. Kužel, Charge Transport in TiO2 Films with Complex Percolation Pathways Investigated by Time-Resolved Terahertz Spectroscopy, IEEE THz Sci. Technol., 2013, 3, 302 CrossRef.
- The constants V and B, respectively, describe the contributions of percolated and non-percolated parts of the sample, respectively. They can be calculated for known geometry as discussed in ref. 33. In a crude approximation, V + B can be regarded as the filling factor of the NPs.
- H. Němec, P. Kužel and V. Sundström, Far-Infrared Response of Free Charge Carriers Localized in Semiconductor Nanoparticles, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115309 CrossRef.
- S. J. Pearton, D. P. Norton, K. Ip, Y. W. Heo and T. Steiner, Recent Progress in Processing and Properties of ZnO, Prog. Mater. Sci., 2005, 50, 293 CrossRef CAS.
- A long-term drift may shift the probing pulse by a small time-delay Δt. Such a delay causes a phase shift in the spectra, i.e., the transient transmittance spectrum as well ΔTnorm are multiplied by a factor exp(2πifΔt). For spectra with dominating real part, such a phase shift appears as an artificial slope in the imaginary part [exp(2πifΔt) ∼ 1 + 2πifΔt]. For a typical drift Δt ∼ 10 fs, we get the slope ∼6%/THz.
- A. Furube, R. Katoh, T. Yoshihara, K. Hara, S. Murata, H. Arakawa and M. Tachiya, Ultrafast Direct and Indirect Electron-Injection Processes in a Photoexcited Dye-Sensitized Nanocrystalline Zinc Oxide Film: The Importance of Exciplex Intermediates at the Surface, J. Phys. Chem. B, 2004, 108, 12583 CrossRef CAS.
- D. Stockwell, Y. Yang, J. Huang, C. Anfuso, Z. Huang and T. Lian, Comparison of Electron-Transfer Dynamics from Coumarin 343 to TiO2, SnO2, and ZnO Nanocrystalline Thin Films: Role of Interface-Bound Charge-Separated Pairs, J. Phys. Chem. C, 2010, 114, 6560 CAS.
- N. Ashkenov, B. N. Mbenkum, C. Bundesmann, V. Riede, M. Lorenz, D. Spemann, E. M. Kaidashev, A. Kasic, M. Schubert, M. Grundmann, G. Wagner, H. Neumann, V. Darakchieva, H. Arwin and B. Monemar, Infrared Dielectric Functions and Phonon Modes of High-Quality ZnO Films, J. Appl. Phys., 2003, 93, 126 CrossRef CAS.
- P. Tiwana, P. Docampo, M. B. Johnston, H. J. Snaith and L. M. Herz, Electron Mobility and Injection Dynamics in Mesoporous ZnO, SnO2, and TiO2 Films Used in Dye-Sensitized Solar Cells, ACS Nano, 2011, 5, 5158 CrossRef CAS PubMed.
- T. S. Sherkar and L. J. A. Koster, Dielectric Effects at Organic/Inorganic Interfaces in Nanostructured Devices, ACS Appl. Mater. Interfaces, 2015, 7, 11881 CAS.
Footnotes |
| † These authors contributed equally. |
| ‡ Present address: Regional Centre for Special Optics and Optoelectronic Systems, Institute of Plasma Physics, Czech Academy of Sciences, Za Slovankou 3, 18200 Prague, Czech Republic. |
| § Present address: MAX IV Laboratory, Fotongatan 2, 22594 Lund, Sweden. |
| This journal is © the Owner Societies 2017 |





