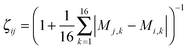Exploration of hydrogen bond networks and potential energy surfaces of methanol clusters using a two-stage clustering algorithm

Abstract

The potential energy surface (PES), structures and thermal properties of methanol clusters (MeOH)_n with n = 8–15 were explored by replica-exchange molecular dynamics (REMD) simulations with an empirical model and refined using density functional theory (DFT) methods. For a given size, local minima structures were sampled from REMD trajectories and archived by a newly developed molecular database via a two-stage clustering algorithm (TSCA). Our TSCA utilizes both the topology of O–H⋯O hydrogen bonding networks and the similarity of the shapes to filter out duplicates. The screened molecular database contains only distinct conformers sampled from REMD and their structures are further optimized by the two DFT methods with and without dispersion correction to examine the influence of dispersion on their structures and binding energies. Inspecting different O–H⋯O networks, the binding energies of methanol clusters are highly degenerated. The degeneracy is more significant with the dispersion effect that introduces weaker but more complex C–H⋯O bonds. Based on the structures we have searched, we were able to extract general trends and these datasets can serve as a starting point for further high-level ab initio calculations to reveal the true energy landscape of methanol clusters.

---

Introduction

Clusters of methanol in condensed and gas phases have drawn intensive attention in the past decade. It is believed that methanol in the bulk liquid phase consists of hydrogen bond clusters, in which the intermolecular interactions are dominated by the number of hydrogen bonds. Unlike the hydrogen-bonded network in water that each oxygen atom in water can donate and accept up to two hydrogen bonds simultaneously, the oxygen atom of methanol can serve only as a single hydrogen bond donor and accept up to two hydrogen bonds.^1,2 Therefore, the topology of the hydrogen bond network can either be linear, simple ring or a combination of the two. Since more complicated topologies are not possible, methanol is generally considered as a simpler model of a hydrogen bond than water.

The interests in methanol clusters can be traced back to the 1960s when Pauling proposed a hypothesis that methanol molecules form simple cyclic hexamers in the liquid phase due to energy stabilization.³ However, since the 1980s various computer simulations including molecular dynamics, Monte Carlo, and ab initio molecular dynamics pointed out the dominance of linear structures in liquid methanol.^4–9 Moreover, X-ray diffraction experiments revealed that on average the length of the chain is about three or four methanol molecules.¹⁰ Neutron diffraction experiments, on the other hand, conclude that the hydrogen bond chains can be up to 10 molecules long and the average chain length is only about 2.7 molecules.¹¹ More recently, X-ray emission spectroscopy and X-ray diffraction showed that liquid methanol consists of rings and chains of methanol with the size of six to eight molecules.^12,13 In contrast to liquid methanol, crystal phases of methanol were known to consist simply of infinite chains, but this notion has been recently challenged by ab initio simulations that under high pressure, stable crystal phases with small-size rings (4 and 6 molecules) can have competitive free energies.¹⁴

One of the possible reasons behind the difficulty in reaching a conclusion on the analysis of the O–H⋯O hydrogen bond in methanol is that weaker interactions between the oxygen of a hydroxyl group and the hydrogen of a nearby methyl group can influence the relative stabilities of different conformations of the methanol clusters. It has been suggested that under high pressure (>4.5 GPa), the considerable increase in C–H⋯O bonds stabilizes the methanol crystal by balancing the repulsive interactions under compression.¹⁴ In gas-phase experiments, methanol clusters have been studied, but the C–H⋯O interactions can be significant only if the cluster size is large enough to allow the formation of folded and compact conformations,¹⁵ but how the C–H⋯O bonds influence the PES has not been carefully examined yet.

The main advantage in studying clusters in the gas-phase is that experimental data of clusters can be characterized by their sizes that can be controlled with a better precision. For example, size-selected infrared spectroscopy has been carried out for both neutral^16–20 and protonated methanol clusters.^20–23 In neutral clusters, size selectivity is more difficult to achieve. Nevertheless, the OH- and CH-stretching modes of methanol trimers and tetramers were explored by Larsen et al. and Han et al.^18,19 For medium sized clusters, IR + VUV ionization coupled with time-of-flight mass spectrometry enables size-selected infrared (IR) spectra of 4 to 8 molecules as reported by Fu et al.,¹⁷ and those of up to 9 molecules have been recorded by Buck et al. using momentum transfer scattering experiments.¹⁶ Other types of clusters such as benzene–(MeOH)_n²⁴ and phenol–(MeOH)_n clusters²⁰ can be observed in up to 6 and 50 methanol molecules, respectively. In spite of the rich study in the IR experiments, mode assignment using quantum chemistry theory was limited to only small-sized clusters. It has been shown that anharmonic frequency analysis using ab initio methods is important to understand trimers and tetramers.^18,19 Theoretical interpretation of larger clusters using quantum chemistry methods, however, has not been fully accomplished due to the complexity of the PES of methanol clusters and the fact that the number of sensible isomers increases exponentially with the cluster size.

To successfully interpret the experimental observables such as free energies or vibrational spectra, it is crucial to use both a reliable theoretical model and sufficiently “good” representative isomers through the PES sampling techniques. In fact, most theoretical studies so far were achieved either with a comprehensive random/biased search using empirical models or high-level ab initio calculations on a limited number of isomers. Boyd and Pires et al. worked on (MeOH)_n with n = 2–12 using different levels of ab initio methods and a hybrid density functional theory (DFT) calculation.^25,26 Kazachenko et al. carried out the modified minima-hopping method associated with empirical models to study the global structures of (MeOH)_n for n ≤ 15 with limited calculations.¹⁵ Nowadays, exploration of the PES using the quantum chemistry method is possible. For instance, David et al. studied the PES of the methanol tetramer with the aid of DFT and random walk algorithm.²⁷ Do et al. also combined the DFT method with a basin hopping search algorithm to probe the dispersion nature of (MeOH)_n for n = 4–7.²⁸ While these ab initio method based searching algorithms can be applied to only small-sized clusters, they have motivated us to rethink the importance of the sampling procedure and how to obtain a sufficient number of isomers using efficient screening techniques.

There is always a computational trade-off between modeling accuracy and sampling statistics. In this work, we proposed a molecular database as a universal framework to overcome this problem. Instead of directly carrying out molecular sampling using quantum chemistry models, we first performed replica-exchange molecular dynamics (REMD) simulation using an OPLS-AA empirical force field to speed up MD and local optimized isomers at different temperatures can be collected in parallel. The resulting set of isomers will be highly duplicated so we develop a sophisticated screening technique to screen out duplicates before archiving them into our database. The screening process involves pattern recognition on O–H⋯O hydrogen bond networks and determination of molecular shape similarity. After these steps, the molecular database is small enough for further verification of quantum chemistry calculations. The computationally expensive part, quantum chemistry calculations, can thus also be performed in parallel to speed up the calculations. Moreover, the hydrogen bond networks in the optimized isomers can be ranked according to their statistics, which can guide us to choose the important isomers. To demonstrate the advantage of our framework, we used the popular B3LYP/6-31+G(d,p) with and without D3 dispersion correction as suggested by Kruse et al.²⁹ to study the cluster sizes of n = 8–15. We found many energetically almost degenerated isomers with different hydrogen bond topologies and zero-point energy (ZPE) also plays a non-negligible role. Thus the existence of many conformations and the possibilities of the anharmonic effect on ZPE are challenging the accuracy of DFT methods to conclude the precise global minima. Nevertheless, we are able to extract general trends based on the structures we have searched and these structures can serve as a starting point for further high-level ab initio calculations to reveal the true energy landscape of methanol clusters.

Methodology

Replica-exchange MD simulation

REMD simulations were performed using the LAMMPS software³⁰ with the empirical OPLS-AA (Optimized Potentials for Liquid Simulation-All Atoms) force field to explore the energy landscape of methanol clusters and to collect the isomer candidates for further studies. The temperature range of all 32 replicas is from 10 K to 300 K and their temperature intervals were carefully chosen to have a sufficient acceptance rate (30–50%) during the exchange of replicas.³¹

The initial configurations for starting MD simulation were generated randomly. For a given run of REMD, each replica goes through a total of 10⁸ steps with a time step of 1 fs to ensure the accuracy of integration of equations of motion in the MD. The attempt to swap adjacent replicas is fixed at 2 ps. In each 100 ns run of REMD, we only use the last 4 ns of trajectory for sampling. The sampling rate is fixed at 2 ps, so we collect 2000 snapshots for each replica. In total, we collect 64 000 snapshots from 32 replicas of REMD. Local geometry optimizations using the conjugate gradient method were then performed to look for the tentative global minimum (the isomer with lowest energy). The equilibrium at lower temperatures can be difficult to achieve because the statistics at lower temperature is more sensitive to the initial configuration of MD than that at higher temperature. To overcome this problem, we initiated another run of REMD simulation with the same 32 temperature points from the newly found global structure to accelerate the equilibrium.

To achieve reliable thermal properties, we repeated REMD simulations until no lower global energy was found. In general, the “real” global structures were successfully located after the third or the fourth REMD run. The local minima collected from different replicas have different characteristics. It is reasonable to expect that minima derived from high-temperature ensembles have a greater variety in their structures and low-temperature ensembles will be limited to low-energy isomers. With the frequent sampling rate at 2 ps, it is likely we will encounter the same local minima, and thus our database of 64 000 isomers shall be trimmed down leaving only the distinct ones to be archived in our database by the screening technique and re-optimized again by the DFT method.

Distributed molecular structure database

It is not practical to perform DFT calculations on all 64 000 methanol clusters extracted from the REMD trajectories. To handle such large sets of cluster confirmations, we developed a flexible and efficient framework – a distributed molecular structure database using the SQL (Structural Query Language) technique to classify and sort these molecular clusters. Among many SQL databases, we chose SQLite for the following reasons. First, the SQLite database is portable and easily distributed. All the collected structural and energetic information is stored in a single database. Second, it can be easily integrated in a program and is directly supported by many programming languages. Finally, the SQLite library has been pre-installed in most of the Unix/Linux systems, and thus no additional installation is required in most cases. Our molecular structure database has two basic tables (right-bottom block of Fig. 1). One stores the xyz coordinates in the text format. The other stores the corresponding energies for sorting and retrieving the coordinates. These tables can be extended to include more molecular indices to aid the molecular screening such as hydrogen-bonding networks (top_table) and the spatial atomic distribution signatures (mom_table). In the following section, we will elaborate on the details of these two indices.

Fig. 1 Flow chart for the TSCA method. This method encodes the xyz samples to several SQLite databases and computes the moment descriptors of shape similarity and the O–H⋯O hydrogen bond topology as clustering indices for each sample. The energy sorting and two clustering process (USR and topology) are then applied using the aforementioned indices. Multiprocessing techniques utilizing multiple CPUs are used to speed up all the computations. The resulting databases (*_sort.db) will be included in a temporary database (tmp.db) for final TSCA processing. The representative isomers will be generated in final.db and new xyz files named by the topology. The structure of the molecular database is depicted in the bottom-right block.

A distributed database provides a unified framework and opens many possibilities to the molecular structural analysis. Our experiments revealed that a database with ∼5000 clusters offers the best performance in our parallel computing environment. That is, we distributed the cluster sets to several databases (xyz01.db, xyz02.db, and so on) for screening and analyzing in parallel. The remaining clusters after screening in each database will be included in a temporary database (tmp.db) for final processing. Our multiprocessing mechanism on separated databases with 5000 cluster restriction ensures an efficient memory usage and prevents the time complexity of O(n²) in our screening algorithm for large n (number of clusters). Before any screening or clustering procedure, the coordinates are always sorted from the lowest energy to the highest one.

Two-stage clustering algorithm

The molecular screening method we reported here, the two-stage clustering algorithm (TSCA, Fig. 1), can be viewed as a destructive compression technique for the molecular structure database. It filters out clusters with similar structures and preserves the diversity of the hydrogen bonding networks. The observed bonding topologies can be chain-like, cyclic, and a mixture of the two. The first clustering stage treats the hydrogen bonding topology as the clustering index and partitions these clusters into different groups based on their hydrogen bond topologies. In the second stage, we further divided the clusters with the same clustering index into two groups, one refers to highly similar spatial atomic distribution, and the other denotes lower similarity. The former is treated as a “duplicated” cluster group that will be discarded since they have identical bonding networks and similar shapes. In our experience, we found that without the first clustering stage, one may accidentally delete the clusters that are geometrically similar but pose distinct bonding topologies.

Topological clustering

The oxygen of a hydroxyl group in methanol can serve as a single hydrogen bond donor and accept up to two hydrogen bonds, and thus the number of hydrogen bonds on each methanol molecule can be 1, 2, and 3. Most methanol molecules are ADs with a coordination number of 2. If the coordination number is 3, the methanol must be an AAD at a branch site. The basic O–H⋯O topologies are linear (chain) and ring (cyclic) structures (Fig. 2(a) and (b)). The latter is made of ADs only and the former has a D on one end and an A at the terminal site. Moreover, both topologies can be linked by an AAD site as shown in Fig. 2(c) and (d). For simplicity, we refer to those exclusively with a coordination number of 2 as r (single ring) or r_r (double ring). For those having other coordination numbers such as 1 or 3, we roughly referred to them as “other” topologies, which can be further divided into l (linear chain), t (tree structure), r_t (separated ring and tail), rt (linked ring and tail), mt (multi-tails), and so on.

Fig. 2 Symbolic representation of the hydrogen bond topology of methanol clusters (MeOH)_n. All the methyl groups and hydrogen atoms are omitted in this representation. The oxygen atom on MeOH is represented by an open circle and an arrow indicates a hydrogen bond that binds two oxygen atoms. The direction of the arrow shows the donor (D) to acceptor (A) relationship in a hydrogen bond. Linear (consisting of single donor (D) and acceptor (A) on both sides) and ring structures (consisting of only acceptor–donor (AD)) are the basic building blocks shown in (a) and (b), respectively. One can begin to construct more complex networks such as ring + tail (shown in (c)) and tree (shown in (d)) by attaching a hydrogen-bond on the single-donor–double-acceptor (AAD) site.

Finally, we adapt a nomenclature to describe the detailed configuration of the hydrogen bond topology as follows: the ring, linear, and tree topologies are referred to as r(m), l(m), and t(m), respectively, where m is the number of methanol molecules. The symbol “–” refers to branching on the AAD site and “_” represents separation. For instance, a single ring consisting of 14 methanol molecules is named r14. For two separated rings each with 6 and 8 methanol molecules, respectively, we refer its topology as r6_r8. For a branch of 1 methanol molecule on a ring of size of 13 molecules, we denote it as r13–t1. In TSCA, this detailed topology labeling scheme serves as a clustering index to group the clusters with the same topology. It is worth mentioning that the screening process by shape similarity will not be carried out across different topology groups.

Shape clustering

The efficient ultrafast shape recognition (USR) technique³² was applied in the second clustering stage of TSCA. In this stage, we compare the spatial atomic distributions between two clusters and compute the normalized similarity index in a range from the least similar (0) to identical shape (1). The spatial atomic distribution can be characterized by the moment analysis of the atomic distances. First, we obtain 4 referenced coordinates using the center of mass, the closest atom to the center of mass, the farthest atom from the center of mass, and the farthest atom from the third coordinate. Then, we accumulate atomic distances with respect to the four referenced coordinates. Finally, we calculate 4 moments of 4 sets of atomic distances and obtain 16 moment descriptors M_k for k = 1,…,16. The similarity index of configurations i and j is defined by the inverse Manhattan distance:

The USR technique has been widely adopted in many materials including proteins,^32–36 polymers,³⁷ metal clusters,³⁸ and water clusters.^39–42 In the preliminary analysis of the methanol structure, we realized that there is no clear gap between similar and dissimilar configurations. Without the aforementioned topological clustering, we found that a large amount of clusters is eliminated because USR cannot distinguish different bonding patterns. After successfully preserving the distinct bonding networks by the first clustering stage, the clustered isomers will be further divided into two groups by a similarity threshold. We preserve those clusters with an index lower than the threshold since they are more distinguishable in shape. We chose 0.85 as the similarity threshold since it gives a reasonable amount of cluster sets. A more aggressive USR filtering is possible by using a lower threshold. As shown in Fig. 1, the output of TSCA guarantees representing all the possible bonding networks, and excludes the duplicated or highly similar configurations.

Density functional theory optimization

The size of the molecular database has been significantly reduced through the TSCA screening. Our next attempt is to apply DFT methods that explicitly take electrons into account for the methanol isomers. All DFT calculations reported here were carried out using Gaussian 09 computational chemistry program.⁴³ The B3LYP/6-31+G(d,p) method^44,45 was used to re-optimize the configuration of isomers and obtain the vibration spectra. The possible role of C–H⋯O motivates us to also examine the dispersion effect using the D3 damping function proposed by Grimme et al.⁴⁶ For simplicity, we name the former as B3LYP and the latter as B3LYP-D3 in the following discussions. We chose these two levels of theories with small basis sets as referenced calculations since they are known over- and under-estimated methods compared with larger basis sets.²⁹

Results and discussion

Thermal properties and intrinsic isomers collected from REMD using OPLS-AA

The temperature dependence of the percentage of different O–H⋯O bonding topologies obtained from REMD simulations using the OPLS-AA force field is summarized in Fig. 3. Previous works¹⁵ have been focusing on searching for global minima and they found that the structure of global minima is either in the single ring (r) topology for n ≤ 12 or the double ring (r_r) topology for n ≥ 13. If we focus on the low-temperature region, the dominating species are in agreement with the global minima structure found by Kazachenko et al. which is a reassurance that our REMD has been well equilibrated. From Fig. 3, it is clear that even for a given size the structure and the topology of methanol clusters are sensitive to temperature.

Fig. 3 Temperature dependence of the probability of different O–H⋯O bonding topologies of (MeOH)_n (n = 8–15) obtained from REMD simulations with the OPLS-AA force field. Dominating species at low-temperature agree with the global minima found by Kazachenko et al.¹⁵ When temperature increases to 70–80 K, other topologies containing single-donor (D) or single-acceptor (A) begin to gain dominance.

In the high-temperature region, the other types (linear and tree) of bonding topologies containing single-donor (D) or single-acceptor (A) start to gain dominance. As temperature increases, the entropic effect becomes more significant and favors this group of topologies, the structures of which are more open and flexible. It is interesting to note that the onset temperature of linear and tree topologies in the OPLS-AA model (see the red dashed black solid curves in Fig. 3) is nearly the same within the size range we have examined.

Unlike other methods' search for global minima, the REMD simulation generates isomers by thermally perturbing the system. This approach allows us to sample structures that have competitive free energies at different temperatures. The subsequent geometry optimizations generate intrinsic structures sampled at different temperatures described using the OPLS-AA model. In principle, we can analyze the intrinsic structures obtained at different temperatures, however, our main goal here is to collect sensible structures for further analysis using DFT and/or high-level ab initio calculations. Thus, we have stored all intrinsic structures that cover a wide range of phase space in our database.

The overall occurrence (counts) of the hydrogen bond topology of the intrinsic structures sampled in the REMD trajectories is shown in Fig. 4. In our database, we further divide the topology groups based on the length of the hydrogen bond, for example, within the ring–tail group of n = 8, one can have r7–t1, r6–t2, r5–t3 and so on. There are many distinct topological groups ranging from 59 (n = 8) to 579 (n = 15) (see the row of # of topologies in Table 1). So, the x-axis of the occurrence diagrams is simply an index referring to the order of the abundance of topologies. We should also emphasize that the y-axes are shown on the logarithmic scale. If drawn on the linear scale, every occurrence curve will clearly show a long-tail tendency. This general tendency allows us to discard most of the complex topologies since their occurrences are very low, namely, less than 10 times (Fig. 4). While the total numbers of distinct hydrogen bond topologies are large, there are not too many dominating topologies. The possibility to discard those “rarely sampled” topologies which are mostly ring–tail topologies helps us to target relevant topologies and to further reduce the size of the molecular database.

Fig. 4 The occurrence (counts) of O–H⋯O topologies for a given size of (MeOH)_n (n = 8–15) on the logarithmic scale. The topology index includes all the possible hydrogen bond topologies (not shown) extracted from the 64 000 intrinsic structures (local minima) of REMD simulation. Names of top five occurring topologies are shown explicitly. More than half of the topologies with less than 10 occurrences can be excluded to further reduce the size of the molecular database after the TSCA method (see Table 1).

Table 1 Statistics of topologies and isomers for (MeOH)_n (n = 8–15). From the top to bottom row are: (1) number of isomers in the database after applying the TSCA screening method to the 64 000 intrinsic structures (local minima) obtained from REMD simulations, (2) number of topologies screened using the TSCA method, (3) number of topologies occurring more than 10 times, (4) number of final isomers in the OPLS-AA molecular database, (5) number of isomers successfully optimized using the B3LYP method, and (6) number of isomers successfully optimized using the B3LYP-D3 method. Both DFT optimizations adopted the isomer sets of the OPLS-AA database which are grouped by the O–H⋯O bonding topology

n	8	9	10	11	12	13	14	15
# of isomers after TSCA	732	1288	1813	2383	2848	3411	3897	4283
# of topologies	59	87	124	179	238	339	452	579
# of topologies (>10 times)	24	37	46	61	66	79	92	117
# of final isomers (OPLS-AA)	469	839	1144	1494	1747	1978	2051	1924
# of finished (B3LYP)	452	818	1116	1452	1057	1026	1213	1081
# of finished (B3LYP-D3)	438	810	934	1038	1184	978	1187	1356

---

For a better visualization, the five most abundant topologies are shown explicitly in Fig. 4. For n ≤ 13, single ring topologies are most frequently found. The ring–tail topologies come next with the second and the third abundant being r(n − 1)–t1 and r(n − 2)–t2. The r_r topologies appear in the leading group as small as n = 11. In n = 13, while the global minimum is r6_r7, there also exist other r_r topologies (such as r5_r8 and r4_r9) with lower occurrence. As for n = 14 and 15, populations of double-ring topologies (r6_r8 and r7_r8) are almost as rich as those of single-ring topologies (r14 and r15). Since we have integrated structures sampled at different temperatures together, the abundance of a topology is not necessarily its energetic order. For example, in n = 13, the global minimum belongs to r6_r7, but the most abundant topology is r13. Furthermore, the analysis on the occurrence (shown in Fig. 4) is based on the structure of locally optimized conformation (that is an intrinsic structure) which is different from the instantaneous snapshots sampled at different temperatures by REMD trajectories (shown in Fig. 3).

The efficiency of our screening methods is highlighted in Table 1. It is clear that the TSCA method significantly reduces the amount of intrinsic structures from 64 000 to several hundreds/thousands of isomers. These isomers are distributed in dozens/hundreds of hydrogen bond topologies, and more than half of the topologies contain less than 10 isomers. Discarding those isomers with low occurrence can further reduce the amount of isomers to 65% for n = 8 and 45% for n = 15. The quantum chemistry calculations were carried out using these isomers from higher ranked topologies to lower ones, which makes the exploration of the PES on larger clusters feasible.

To summarize, there are a few advantages in our approach: (1) Because our REMD is well equilibrated, the global minimum and its related structures will not be missed in the low-temperature ensembles. (2) Since one cannot guarantee the accuracy of the empirical models, the thermal energy in REMD assists the automatic sampling of the PES of OPLS-AA. Therefore, most (if not all) statistically sensible structures will be included in our database. (3) It is understandable that canonical ensembles with adjacent temperatures typically sample a similar region in the phase space, and integrating all intrinsic structures in one big database allows our TSCA to efficiently screen out the duplicates based on the similarity in their geometries and leave a small but well represented set for further refinements.

Structure and binding energy of different types of hydrogen bond networks

The size dependence of the binding energy of clusters is an important property. In Fig. 5, binding energy per molecule of methanol clusters under OPLS-AA, B3LYP, and B3LYP-D3 is summarized in Fig. 5(a), (b), and (c), respectively. For simplicity, we will use normalized binding (that is binding energy per molecule) throughout this manuscript. Also, due to the large number of isomers we have collected, it is not practical to shown all of them, and thus only the most stable conformation in r, r_r, and t families is shown. While the value of the binding energies of OPLS-AA is closer to the B3LYP method, the overall trend in the size dependence in B3LYP is not very smooth. In particular, within the r family the binding energy does not change much from n = 8 to n = 15 which is likely due to the lack of van der Waals dispersion. Furthermore, the overall trend in B3LYP-D3 is much closer to OPLS-AA which suggests that van der Waals dispersion likely plays an important role in determining the size dependence of the binding energy of mid to large size methanol clusters.

Fig. 5 Size dependence of the binding energy (kcal per mol per MeOH) of (MeOH)_n, n = 8–15 by (a) OPLS-AA, (b) B3LYP, and (c) B3LYP-D3. As there are too many topological groups, for simplicity, only the energies of the most stable form in single ring (r), double ring (r_r) and other topologies are shown in this figure. Binding energies under OPLS-AA and B3LYP-D3 have a monotonic decreasing trend with respect to the cluster size. In B3LYP, the binding energy of the single ring does not change in this size range. More detailed data on the binding energies of other topologies/isomers can be found in the ESI† (Fig. S1–S8).

Structures of the low-energy minima also indicate the importance of van der Waals interaction. In Fig. 6, we can find the most stable minima of different topologies of (MeOH)₁₄ described by the three methods. In B3LYP models, the optimized structures tend to be relatively open to keep the directionality of the O–H⋯O hydrogen-bonding. In B3LYP-D3, dispersion can bend the hydrogen bond to make the structure more compact, for example, in r14 and r6_r8, the hydrogen bond rings are both more folded than their counterparts optimized with B3LYP. The similarity between the structures of OPLS-AA and that of B3LYP-D again suggests that van der Waals dispersion likely is the dominating factor. Structures of low-energy minima for n = 8 and n = 11 are compiled in the ESI† for those who are interested in a more detailed comparison.

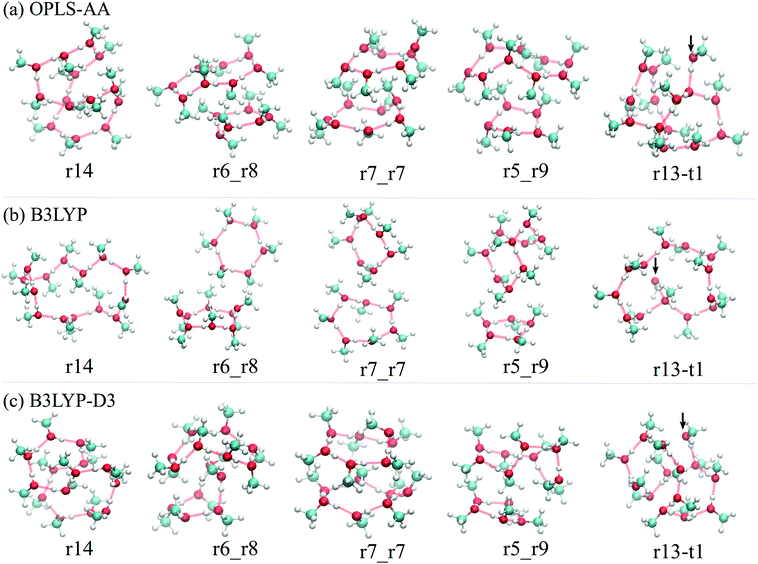Fig. 6 Structure of the most stable isomers of (MeOH)₁₄ in the leading five topologies of (a) OPLS-AA, (b) B3LYP, and (c) B3LYP-D3 models. Intrinsic structures under OPLS-AA and B3LYP-D3 are generally more compact than those by B3LYP. The same observations can be found from the structures of low-energy isomers of (MeOH)₈ and (MeOH)₁₁ shown in the ESI† (Fig. S17 and S18).

One of the important points that cannot be seen from Fig. 5 and 6 is that there are many possible conformations with very close binding energies. In Fig. 7, we show the binding energies of isomers we have collected for n = 8, n = 11 and n = 14. Due to the limit of space, we only show the energies of the conformations in the first five topological groups. A more extended list covering different topologies in n = 8 to n = 15 is compiled in the ESI† (Fig. S1–S8, ESI†). One can clearly see from Fig. 7 and the ESI† that the relative energy between the most stable isomers among the leading group is not large. For example, in B3LYP-D3, the energetic difference between the most stable and the 5th stable is less than 0.2 kcal mol⁻¹. Furthermore, within each topological group there are many isomers having a more significant variation in their binding energies. Thus, one shall always keep in mind that the difference in the binding energy of isomers within the same topological family is not less than the difference between two topological families. Therefore, if one looks at one or two conformations within each topological group, it is possible to come to different conclusions based on the conformations one selects. Our methodology is a design to overcome such problems, because our sampling scheme utilizes thermal perturbation in REMD, and thus different statistically important conformations can be properly sampled.

Fig. 7 Binding energy (kcal per mol per MeOH) of (MeOH)_n, n = 8, 11, and 14 by OPLS-AA, B3LYP, and B3LYP-D3. There are too many topological groups, for simplicity, the energies of all stable isomers in the leading five topologies (ranked by the energies of the most stable isomer in each topology) are shown here. Relative energy between the most stable isomers among the leading group is not large. For example, in B3LYP-D3, the energetic difference between the most stable and the 5th stable is less than 0.2 kcal mol⁻¹. On the other hand, within each topological group there are many isomers having a more significant variation in their binding energies. This general trend, verified in three methods, reminds us the importance of molecular sampling and screening using the hydrogen bond topology in the exploration of the PES.

Role of zero-point energy

In some protonated hydrogen-bonded clusters, it was found that zero-point energy corrections can alter the relative stabilities of conformations and thus the structure of the most stable forms and relative stability between different topological groups with or without ZPE corrections can be different.^22,47–49 In our DFT calculations, analytical second derivatives have always been calculated to ensure that the structures we found are true local minima. Therefore, we can estimate ZPE with harmonic approximations using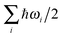 . Using structures optimized with B3LYP-D3 as an example, in Fig. 8 we show the binding energy of a more extended list for n = 8, 11 and 14 with and without ZPE. Due to the small energetic difference between the isomers, it is possible that ZPE can alter the energetic order and the most stable isomer within a topological family and the global minima structure can be different. For example, when n = 14, we would conclude that r14 is the most stable topology based only on the PES. If ZPE is included, r7_r7 becomes the most stable topological group. In the same size, the energetic order between r13–t1 and r11–t3 is also switched. Except these occasional switches in the energetic order, we should emphasize that the overall trend in the energetic order is not significantly altered in the neutral methanol clusters.

Fig. 8 Influence of zero-point energy on the binding energy (kcal per mol per MeOH) of (MeOH)_n, n = 8, 11, and 14 by B3LYP-D3 is shown. ZPE reduces the binding energy by 1.5 kcal per mol per MeOH which is mainly due to the redshift in the O–H as a result of the formation of the hydrogen bond. More topological groups are shown in Fig. 9 than Fig. 7. The more extended lists that we have searched, covering all sizes, can be found in Fig. S1–S8 (ESI†).

There are a few general properties that we can draw by analyzing the whole dataset. First, the binding energy is reduced by 1.5–1.6 kcal per mol per MeOH by adding ZPE. This reduction is mainly due to the formation of a hydrogen bond. In methanol clusters, the number of hydrogen bonds per molecule is almost one. With the formation of O–H⋯O hydrogen bonds, the free O–H stretch mode shifts from about 3700 cm⁻¹ (in monomer) to 3200 cm⁻¹ in O–H⋯O. Thus in methanol clusters, the ZPE is reduced by ∼500 cm⁻¹–1.4 kcal mol⁻¹. Since the coordination number of methanol does not change much, this reduction in binding energy by ZPE is not sensitive to the change in the cluster size. From previous works on protonated water and methanol clusters,^22,48,49 it is often found that the PES and the ZPE have opposite contributions to the binding energy, the former tends to favor more compact structures with a great number of hydrogen bonds. In neutral methanol clusters, since the coordination number does not change much one may anticipate a less significant effect on ZPE. In Fig. 9, we show the correlation between the binding energies with and without ZPE correction. The nice correlation confirms that ZPE plays a secondary role. But due to the small energetic difference in the PES, a difference in ZPE is still sufficient to switch the energetic order. We should point out that within such a small energetic difference, vibrational anharmonicity⁴⁷ may be another factor that should be taken into consideration.

Fig. 9 Correlation between binding energy (kcal per mol per MeOH) of (MeOH)_n with (x-axis) and without (y-axis) zero-point energy correction. In this figure, we use a simple grouping of the topology as the one used in Fig. 5 for n = 8 (a), 11 (b), and 14 (c). Single ring (r, red dots), double ring (r_r, blue dots) and other topologies (green dots) are shown in different colors. Linear regression analysis is presented by red lines and the corresponding linear fitted functions are referred to in the bottom-right corners.

While only a limited selection of empirical models and DFT methods have been used in this work, because a large set of isomers have been analyzed, we are optimistic that these conclusions will still be valid if higher level ab initio calculations can be applied to examine methanol clusters in this size range.

Conclusions

In this work, we explored the PES of methanol clusters using a combination of an empirical model and two DFT methods. REMD simulations with an empirical OPLS-AA force field were first engaged to properly sample the energy landscape and to archive a sufficient number of local minima for further refinement using DFT methods. At both levels of simulations, calculations can be carried out in parallel to increase the overall efficiency of our approach.

To bridge the difference in the computational resources required by empirical models and DFT methods, we implemented a standard procedure to select energetically important and structural distinct isomers for building up our universal molecular database. We first utilize the traditional concept based on the O–H⋯O hydrogen bond topology to sort the structures of isomers. Since the relative weaker C–H⋯O bonds can also play a role in determining the structure and the stability of methanol clusters, we go beyond the idea of relying entirely on the O–H⋯O hydrogen bond topology and include both topological and spatial (similarity in shape) indices in the newly proposed TSCA algorithm. It is our hope that our clustering algorithm can become a useful tool in other molecular sampling methods. The newly developed TSCA is published along with this work as open source software⁵⁰ under GNU Public License.

We use B3LYP and B3LYP-D3 with 6-31+G* to carry out extensive DFT calculations on the large set of isomers created by our TSCA algorithm both because of their computational efficiency and also the fact they are known to be over- and under-estimating methods. Furthermore, these two DFT methods are different only in the dispersion interaction which allows us to directly look into the effect of dispersion in determining the properties of methanol clusters. Within the size (n = 8 to n = 15) we have searched, there are many low-energy minima with a very small energetic difference and the exact global minimum structure is thus sensitive to the choice of method. The role of zero-point energy correction has been analyzed and we hope that the low-energy isomers we found can stimulate further investigations using more sophisticated DFT and/or high-level ab initio calculations.

Acknowledgements

The author would like to acknowledge Prof. Asuka Fujii for helpful discussions that initiated this project, Dr Tzu-Jen Lin for useful discussions on the role of C–H⋯O bonds, and referees for the constructive suggestions to this work. This study was supported by grants from Academia Sinica and the Ministry of Science and Technology (MOST 105-2811-M-001-165 and MOST 104-2811-M-009-063). The authors also gratefully acknowledge the computing resources provided by the Computation Center of Institute of Atomic and Molecular Sciences, Academia Sinica and National Center for High-Performance Computing.

References

1. K. J. Tauer and W. N. Lipscomb, Acta Crystallogr., 1952, 5, 606–612.
2. B. Torrie, S.-X. Weng and B. Powell, Mol. Phys., 1989, 67, 575–581.
3. L. Pauling, The Nature of Chemical Bond, Oxford University, Oxford, 3rd edn, 1967.
4. W. L. Jorgensen, J. Am. Chem. Soc., 1981, 103, 335–340.
5. M. Haughney, M. Ferrario and I. R. McDonald, J. Phys. Chem., 1987, 91, 4934–4940.
6. E. Tsuchida, Y. Kanada and M. Tsukada, Chem. Phys. Lett., 1999, 311, 236–240.
7. J. A. Morrone and M. E. Tuckerman, J. Chem. Phys., 2002, 117, 4403.
8. J.-W. Handgraaf, T. S. van Erp and E. J. Meijer, Chem. Phys. Lett., 2003, 367, 617–624.
9. M. Pagliai, G. Cardini, R. Righini and V. Schettino, J. Chem. Phys., 2003, 119, 6655–6662.
10. Y. Tanaka, N. Ohtomo and K. Arakawa, Bull. Chem. Soc. Jpn., 1985, 58, 270–276.
11. T. Yamaguchi, K. Hidaka and A. K. Soper, Mol. Phys., 1999, 97, 603–605.
12. S. Sarkar and R. N. Joarder, J. Chem. Phys., 1993, 99, 2032.
13. S. Kashtanov, A. Augustson, J.-E. Rubensson, J. Nordgren, H. Ågren, J.-H. Guo and Y. Luo, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 104205.
14. T.-J. Lin, C.-R. Hsing, C.-M. Wei and J.-L. Kuo, Phys. Chem. Chem. Phys., 2015, 18, 2736–2746.
15. S. Kazachenko, S. Bulusu and A. J. Thakkar, J. Chem. Phys., 2013, 138, 224303.
16. U. Buck and F. Huisken, Chem. Rev., 2001, 100, 3863–3890.
17. H. B. Fu, Y. J. Hu and E. R. Bernstein, J. Chem. Phys., 2006, 124, 024302.
18. R. W. Larsen, P. Zielke and M. A. Suhm, J. Chem. Phys., 2007, 126, 194307.
19. H.-L. Han, C. Camacho, H. A. Witek and Y.-P. Lee, J. Chem. Phys., 2011, 134, 144309.
20. T. Kobayashi, R. Shishido, K. Mizuse, A. Fujii and J.-L. Kuo, Phys. Chem. Chem. Phys., 2013, 15, 9523–9530.
21. J.-L. Kuo, A. Fujii and N. Mikami, J. Phys. Chem. A, 2007, 111, 9438–9445.
22. T. Hamashima, Y.-C. Li, M. C. H. Wu, K. Mizuse, T. Kobayashi, A. Fujii and J.-L. Kuo, J. Phys. Chem. A, 2013, 117, 101–107.
23. Y.-C. Li, T. Hamashima, R. Yamazaki, T. Kobayashi, Y. Suzuki, K. Mizuse, A. Fujii and J.-L. Kuo, Phys. Chem. Chem. Phys., 2015, 17, 22042–22053.
24. R. N. Pribble, F. C. Hagemeister and T. S. Zwier, J. Chem. Phys., 1997, 106, 2145–2157.
25. S. L. Boyd and R. J. Boyd, J. Chem. Theory Comput., 2007, 3, 54–61.
26. M. M. Pires and V. F. Deturi, J. Chem. Theory Comput., 2007, 3, 1073–1082.
27. J. David, D. Guerra and A. Restrepo, J. Phys. Chem. A, 2009, 113, 10167–10173.
28. H. Do and N. A. Besley, J. Chem. Phys., 2012, 137, 134106.
29. H. Kruse, L. Goerigk and S. Grimme, J. Org. Chem., 2012, 77, 10824–10834.
30. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
31. C. Predescu, M. Predescu and C. V. Ciobanu, J. Phys. Chem. B, 2005, 109, 4189–4196.
32. P. J. Ballester and W. G. Richards, J. Comput. Chem., 2007, 28, 1711–1723.
33. E. O. Cannon, F. Nigsch and J. B. O. Mitchell, Chem. Cent. J., 2008, 2, 3.
34. P. J. Ballester, P. W. Finn and W. G. Richards, J. Mol. Graphics Modell., 2009, 27, 836–845.
35. T. Zhou, K. Lafleur and A. Caflisch, J. Mol. Graphics Modell., 2010, 29, 443–449.
36. J. O. Ebalunode and W. Zheng, Curr. Top. Med. Chem., 2010, 10, 669–679.
37. P. J. Hsu, S. A. Cheong and S. K. Lai, J. Chem. Phys., 2014, 140, 204905.
38. P. J. Hsu, J. Comput. Chem., 2014, 35, 1082–1092.
39. Q. C. Nguyen, Y. S. Ong, H. Soh and J.-L. Kuo, J. Phys. Chem. A, 2008, 112, 6257–6261.
40. Q. C. Nguyen, Y.-S. Ong and J.-L. Kuo, J. Chem. Theory Comput., 2009, 5, 2629–2639.
41. H. Soh, Y. S. Ong, Q. C. Nguyen, Q. H. Nguyen, M. S. Habibullah, T. Hung and J.-L. Kuo, IEEE Trans. Evol. Comput., 2010, 14, 419–437.
42. E.-P. Lu, P.-R. Pan, Y.-C. Li, M.-K. Tsai and J.-L. Kuo, Phys. Chem. Chem. Phys., 2014, 16, 18888–18895.
43. M. J. Frisch, et al., Gaussian09 Revision E.01., Gaussian Inc., Wallingford, CT, 2009.
44. G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193.
45. G. A. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081.
46. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
47. J.-L. Kuo, J. Phys.: Conf. Ser., 2006, 28, 87–90.
48. J.-L. Kuo, Z.-Z. Xie, D. Bing, A. Fujii, T. Hamashima, K. I. Suhara and N. Mikami, J. Phys. Chem. A, 2008, 112, 10125–10133.
49. D. Bing, J.-L. Kuo, K. I. Suhara, A. Fujii and N. Mikami, J. Phys. Chem. A, 2009, 113, 2323–2332.
50. P. J. Hsu, 2016, http://https://github.com/sophAi/TSCA.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp07120a

---