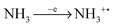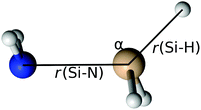Reactions in silicon–nitrogen plasma†
Received
3rd August 2016
, Accepted 15th December 2016
First published on 21st December 2016
Abstract
Reaction mechanisms that lead to creation of silicon–nitrogen bonds are studied in detail. These reactions are of fundamental importance for silicon nitride synthesis by plasma enhanced chemical vapour deposition from the gas mixture of silane (SiH4) and ammonia (NH3). All reactions in SiH4–NH3 plasma can be categorised as some of the basic types of reactions: bond dissociation, neutral nucleophilic substitution, radical neutralisation, neutral–radical addition, silylene addition, silylene rearrangement, radical nucleophilic addition or hydrogen abstraction reaction. Energetics of these reactions is analysed in detail for a great number of reactions belonging to these categories, by using theoretical modelling. Geometry optimisations are carried out with the MP2/aug-cc-pVTZ level of theory and energetics is further determined with high level ab initio calculations at the CASPT2/aug-cc-pVTZ level, which enabled confirmation of relevance of several mechanisms as reactions that lead to silicon nitride growth from plasma enhanced chemical vapour deposition, as well as introduction of new, energetically favourable mechanisms. Besides amine radical assisted eliminative addition and proton transfer reactions, silylene addition reactions are thermodynamically and kinetically favourable since they lack energy barriers. A new reaction pathway for synthesis of silicon nitride from plasma is proposed. This pathway is enabled by the ability of silylene to create two weak dative bonds, which enables silylene–amine complexes to stick to the silicon nitride surface. Upon dissociation of amine from the surface-bound complex, silylene remains on the surface, available for reaction with other reactive species from plasma.
1 Introduction
Silicon nitride is a material with growing usage as an insulator in the manufacturing of solar cells and electronic devices or as an anti-reflection coating in optical elements. The most common method for its synthesis and deposition is plasma enhanced chemical vapour deposition (PECVD).1 Ion implantation, reactive sputtering, and thermal nitridation of silicon are also used, but in a less extent.1 The usual gas mixtures used in PECVD for deposition of silicon nitride consist of elementary nitrogen (N2) or ammonia (NH3) as a source of nitrogen and silane SiH4 as a source of silicon.1–7 The silicon nitride, grown by PECVD, is not necessarily stoichiometric and it can contain a large concentration of hydrogen (up to 39%, atomic ratio).1,5,8 The composition of deposited silicon nitride (SiNx:H) can be adjusted by selecting the deposition temperature or by adjusting the ratio of silicon and nitrogen in the gas mixture.
Although the temperature of the plasma used in SiNx:H PECVD is low (<400 °C), electrons in the plasma have significantly more energy (typically about 2 eV) than the thermal energy of the plasma.9 These electrons cause dissociation of source gases into a reactive species that either react in the gas phase and produce precursor molecules, whose deposition makes SiNx:H, or directly react on the surface in order to make SiNx:H.
In the SiH4–NH3 plasma, it is believed that all SiH4 is converted into either a Si(NH2)4 or a Si(NH2)3˙ radical.4,6 At the surface, Si(NH2)3˙ undergoes a series of NH3 elimination reactions (depending on a temperature) before converting into SiNx:H.2,6 However, unlike the Si(NH2)3˙ radical, the SiH3˙ radical was found to have high sticking probability to a SiNx:H surface.4,10
Silane dissociation channels in plasma,11,12 with significant yield, are shown in eqn (1) and (2).
More SiH
3˙ is produced by secondary
reaction (3).
13| | | SiH4 + H˙ → SiH3˙ + H2 | (3) |
It is believed
13,14 that
reaction (2) is responsible for the majority of SiH
4 removal events at lower electron energies.
At low pressures (<100 Pa), association of SiH3˙ and SiH2 is rare, and therefore higher silanes are not observed.15 The most probable outcome in inelastic collision of electrons with silane is SiH4 in the vibrationally exited state,16 while the collisions that produce ionic species have an order of magnitude lower cross sections.15–17 Moreover, it was shown18,19 that the product of a reaction of ionic silicon species with NH3 does not propagate beyond SiNH4+. Therefore, since Si(NH2)4 and Si(NH2)3˙ were detected in SiH4–NH3 plasma, ionic reactions are probably not important in SiNx:H synthesis.
In ammonia plasma, the most important primary process for removal of NH3 molecules is by electron impact ionisation (eqn (4)).20 The most abundant ion in plasma is a secondary product (NH4+), created by proton transfer, during the collision of NH3+ and NH3 molecules (eqn (5)). NH4+ is completely nonreactive towards SiH4 due to its thermodynamic stability.18
| | 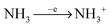 | (4) |
| | | NH3+ + NH3 → NH2˙ + NH4+ | (5) |
The alternative reaction is the direct dissociation of NH
3 molecules:
Dissociation of silane is believed to be more abundant than the dissociation of ammonia in silane–ammonia gas mixtures since the dissociation energy of silane is lower.
21
1.1 Reaction mechanisms
One of the most accurate experimental determination of the reaction mechanism is done by Beach and Jasinski22 by exposing the ammonia rich SiH4–NH3 mixture to the 193 nm excimer laser. The laser radiation selectively dissociates ammonia molecules making a simple initial reaction mixture. A whole series of aminosilanes (SiH3NH2, SiH2(NH2)2, SiH(NH2)3, Si(NH2)4) were detected in the irradiated mixture. Aminosilanes were also confirmed in the SiH4–NH3 mixture, heated with a hot wire.23 The proposed mechanism22 for formation of aminosilanes (SiHx(NH2)4−x, where 0 ≤ x ≤ 4) is explained by eqn (7)–(9):| | | SiH3−x(NH2)x˙ + NH2˙ → SiH2−x(NH2)x+1˙ + H˙; 0 ≤ x < 3 | (7) |
| | | SiH3−x(NH2)x˙ + H˙ → SiH4−x(NH2)x; 0 < x ≤ 3 | (8) |
| | | SiH3−x(NH2)x˙ + NH2˙ → SiH3−x(NH2)x+1; 0 ≤ x ≤ 3. | (9) |
The main reaction in this mechanism, responsible for the synthesis of aminosilanes, and in the formation of a Si–N bond is radical eliminative addition (eqn (7)). Eqn (8) and (9) represent radical neutralisation reactions that stop the radical chain reaction and produce aminosilanes from the corresponding radicals. The reaction mixture, created by Beach and Jasinski,22 is more simple than the plasma in the conventional PECVD since the reactions are initialised exclusively by the NH2˙ radicals, the proposed reaction mechanism (eqn (7)–(9)) is not the only explanation.
The alternative mechanism, proposed by the same authors,22 is a combination of the hydrogen abstraction (eqn (10)) and the radical neutralisation (reactions (8) and (9)):
| | | SiH4−x(NH2)x + R˙ → SiH3−x(NH2)x˙ + R–H; 0 < x ≤ 3; R˙ = H˙ or NH2˙ | (10) |
Another mechanism, also proposed by Beach and Jasinski,
22 although sceptically, is eliminative addition on neutral aminosilane (
eqn (11)), coupled with radical neutralisation reactions (
reactions (8) and (9)).
| | | SiH4−x(NH2)x + NH2˙ → SiH3−x(NH2)x+1 + H˙; 0 ≤ x ≤ 3 | (11) |
Beach and Jasinski
22 also proposed the mechanism that involves the formation of silylene (SiH
2) and aminosilylene (SiHNH
2):
| | | SiH3˙ + NH2˙ ⇌ SiH3NH2* → SiH2NH2˙ + H˙ | (12) |
| | | SiH3NH2* → SiH2 + NH3 | (13) |
| | | SiH3NH2* → SiHNH2 + H2 | (14) |
Aminosilylene reacts with NH
2˙ in order to produce a radical that is (
eqn (15)) neutralised by NH
2˙ (or H˙) into a higher aminosilane (
eqn (16)):
| | | SiH2−x(NH2)x + NH2˙ → SiH2−x(NH2)x+1˙; 0 ≤ x < 2 | (15) |
| | | SiH2−x(NH2)x+1˙ + NH2˙ → SiH2−x(NH2)x+2; 0 ≤ x < 2 | (16) |
This mechanism alone cannot explain the formation of all aminosilanes. If
reactions (15) and (16) are proceeding, there must be another mechanism in action, parallel to this one. Observation of silicon diimide (Si(NH)
2) at low deposition temperatures (about 100 °C) can be explained only by this mechanism.
2 Unlike in PECVD, the SiH
4–NH
3 mixture exposed to 193 nm UV light produces silanes even at high NH
3/SiH
4 ratios (50
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
1) indicating that reactions in plasma are either a different mechanism, or an interplay of several mechanisms.
22
In addition, there is a neutral addition mechanism (eqn (17)) that is found to be exothermic (for x = 0), but with a reaction barrier large enough for external energy excitation necessary.24
| | | SiH4−x(NH2)x + NH3 → SiH3−x(NH2)x+1 + H2; 0 ≤ x < 4 | (17) |
From quantum chemical modelling of reactions taking place in the mixture of SiH
4 and NH
3 gases, there is a conclusion that reactions proceed exclusively as radical chain reactions.
21 The SiH
3˙ radical is believed to play a central role in the chain mechanism, since its formation is kinetically and thermodynamically favourable over NH
2˙.
21 This mechanism is a combination of mechanisms of Beach and Jasinski (
vide supra) composed of the hydrogen abstraction (
eqn (10)) and the modification of the radical eliminative addition (
eqn (11)), in which the reactive species are the aminosilane SiH
3−x(NH
2)
x˙ radicals instead of the NH
2˙ (
eqn (18)).
| | | SiH3−x(NH2)x˙ + NH3 → SiH3−x(NH2)x+1 + H˙; 0 < x ≤ 3 | (18) |
In the SiH
4–NH
3 gas mixture, exposed to a resistively heated wire, both SiH
3˙ and NH
2˙ (with some amount of NH) radicals were observed, however no aminosilane was detected.
25 The difference between plasma composition, reported by different groups, strongly suggests that no single mechanism can explain the deposition of silicon nitride.
22,25 Longer residence times of SiH
4 in a reaction chamber increase the possibility of reactions and the production of higher aminosilanes.
26
The uncertainties in reactions in ammonia–silane gas mixtures demonstrate the need for more detailed analysis of these reactions. These reactions not only explain gas phase reactions in ammonia–silane plasma, but also represent the elementary reactions for forming the silicon–nitrogen bond. Our motive for investigating these reactions, besides the explanation of reactions between silicon and nitrogen, comes from the need to explore the energy landscape for silicon and nitrogen atoms in order to make possible analysis of phenomena in the bulk, the interface and on the surface of silicon nitride. The potential energy surfaces from this research, obtained from high level ab initio calculations, will be used for parametrisation and testing other computational methods, capable of handling solid state and interface phenomena.
2 Theoretical methods
Reactions in silicon/nitrogen plasma are modelled with multiconfigurational quantum chemical methods and large basis sets; a combination that can determine high precision energetics for chemical species undergoing through bonding rearrangements. Geometry optimisation was carried out on the basis of energy and the gradient, calculated with Møller–Plesset second order perturbation theory (MP2)27 with the Dunning triple zeta basis set augmented with diffuse functions (aug-cc-pVTZ).28–30 The version of aug-cc-pVTZ with extra d function (aug-cc-pV(T+d)Z)31 was used for the silicon atoms. Coordinates of all optimised geometries are available in the ESI† (see supplement_01.pdf). Second order derivatives of energy were calculated on all optimised geometries in order to obtain vibrational frequencies, and thus vibrational zero point energy and vibrational contribution to enthalpy and entropy of each species. The rotational contribution to the entropy of the hydrogen molecule was calculated from partition functions published in NIST-JANAF thermochemical tables,32 since the classical approximation of molecular rotations is not precise in this case. Reactions with energy barriers were characterised by optimisation of their transition state geometries. Frequencies, calculated on these geometries, were inspected for the presence of the single imaginary value and the corresponding normal mode was visualised in order to confirm that the optimised geometry corresponds to the desired transition state. In cases of pre-reaction and post-reaction complexes, some imaginary frequencies with a low magnitude would appear. Their corresponding normal modes were also visualised in order to confirm that they correspond to large amplitude intermolecular motion. The intrinsic reaction coordinate (IRC) was also calculated in order to undoubtedly prove that the calculated transition geometry lies on the reaction path that connects desired energy-minimum geometries. The IRC is defined as the coordinate along the minimum energy path (expressed in mass weighted nuclear coordinates) that connects the reactant, the transition state and the product.33 The coordinates along the energy path were determined by sequentially moving atoms along the vector parallel to the normal mode that corresponds to the imaginary frequency in the transition state and optimising resulting geometries along all coordinates that are perpendicular to the vector. As a result, two series of geometries that lie on the minimum energy path are produced: one progressively moving from the transition state to the reactant and one that moves toward the product. Potentials along IRC coordinates are available in the ESI† (see supplement_02.pdf). The GAMESS program package34–36 was used for all geometry optimisations, frequency and IRC calculations. Single point calculations were performed on each optimised stationary point. The complete active space with the second-order perturbation theory (CASPT2)37,38 was used for single point energy calculations. The active space was selected by visual inspection of orbitals calculated with simple Hartree–Fock (HF) self-consistent field (SCF) calculations. The Luscus39 program was used in the process of inspecting and selecting of the active orbitals. Since in the studied reactions Si–N, Si–H and N–H are being formed or split, we composed active spaces from molecular orbitals, created by the linear combination of 2s, 2px, 2py, 2pz atomic orbitals on a N atom, the 1s atomic orbital on a H atom and the 3s atomic orbital on a Si atom and the corresponding antibonding orbitals. That leads to the active space that consists of 10 electrons in 10 orbitals. In some cases other active spaces are also used if the reaction centre lacks some of the mentioned atoms. All CAS orbitals from all active spaces of all reactions are shown in the ESI† (see supplement_03.pdf). The MOLCAS40,41 program package was used for all CASPT2 calculations. All CASPT2 calculations were done with the aug-cc-pVTZ basis set. If a reaction lacks the transition state, the potential energy surface (PES), spanned by selected bond lengths and angle bends, was scanned. PES scan was done by translating and rotating molecular fragments in order to bring selected bonds and angles to desired values and by subjecting created geometries to optimisation with constraints. Constraints were in the form of fixed bonds and angles that were adjusted during the geometry preparation step. Constrained optimisations were done at the MP2/aug-cc-pVTZ level of theory. Single point calculations were done at the MP2 optimised geometries at the CASPT2/aug-cc-pVTZ level.
3 Results and discussion
The driving force for chemical reactions in PECVD comes from energetic electrons in plasma. Impact of these electrons causes ionisation, cleavage of chemical bonds, or leaves molecules in the excited electronic and/or vibrational state. Under these conditions, it is hard to rationalise thermodynamics and consequentially, kinetics of modelled reactions, since electron impacts leave molecules in non-Boltzmann energy distribution. Moreover, different operating conditions of PECVD can result in different distributions of electron kinetic energies, and thus different distributions in resulting molecules. Even in a single plasma reactor, operated under steady conditions, the gas in different parts of the reactor chamber can experience different rates of dissociation and different decomposition pathways.11 Therefore, we will analyse energies and reaction pathways of reactions in SiH4–NH3 plasma without referring to reaction rates. Since reactions in plasma are at certain temperature, their enthalpies will also be reported, however one must have in mind that enthalpies are calculated by assuming the Boltzmann distribution of energies, a condition that is not necessarily met in plasma, but applicable for active species that react after leaving the area affected by the plasma. In SiH4–NH3 plasma there are reactions that lead to creation of Si–Si bonds and creation of disilane and trisilane.4,6,10,22,23,42 These reactions will not be discussed here.
In addition to the proposed mechanisms for reactions in silane–ammonia plasma, several new reactions belonging to the new mechanism are proposed. These reactions have low energy barriers, making them competitive with the already proposed reactions. The new, alternative mechanism consists of silylene addition reactions:
| | | NH3−x(SiH3)x + SiH2 → SiH2–NH3−x(SiH3)x; 0 ≤ x < 3. | (19) |
The product from
reaction (19) is a molecule with dative bond (N→Si) with silylene as the electron acceptor. That product can rearrange into an aminosilane:
| | | NH3−x(SiH3)x(SiH2) → NH2−x(SiH3)x+1; 0 ≤ x < 3. | (20) |
The end product of
reaction (20) (
x = 2) is trisilylamine ((SiH
3)
3N). Since in silane–ammonia gas mixtures with a high ammonia to silane ratio,
22 the end-products of reactions are triaminosilane (SiH(NH
2)
3) and tetraaminosilane (Si(NH
2)
4), these reactions should stop by depletion of SiH
2 in the first stage (
x = 0) making SiH
3NH
2, which can further react according to
reactions (7)–(18). We propose the alternative to
reaction (20) as the formation of a complex with two dative (N→Si←N) bonds:
| | | SiH2–NH3−x(SiH3)x + NH3−y(SiH3)y → (SiH3)yNH3−y–SiH2–NH3−x(SiH3)x; 0 ≤ x < 3 0 ≤ y < 3. | (21) |
If conditions in plasma permit survival of silane complexes from
reactions (20) and (21), these can serve as reactive species in the surface deposition process. The another new class of reactions, considered in this paper, is the addition of a silyl radical to an ammonia molecule (
eqn (22)):
| | | (NH2)3−xSiHx˙ + NH3 → (NH2)3−xSiHxNH3˙; 0 ≤ x < 3 | (22) |
Also, nucleophilic additions of silane–amines to silane are also considered in order to check if they could play a role as surface reactions during PECVD of SiN
x:H.
| | | (SiH3)3−xNHx + SiH4 → (SiH3)2−xNHx−1 + H2; 0 < x < 3. | (23) |
We modelled a series of reactions, staring from source gases: SiH
4 and NH
3, up to the point where the initial silicon atom is completely surrounded with nitrogen atoms or
vice versa.
Fig. 1 shows schematically these reaction pathways. The surface of the silicon nitride is represented by Si
xN
yH
z in
Fig. 1. All of these reactions are not necessarily energetically favourable. The possibility of a reaction taking place during PECVD will be judged by the reaction energetics (activation energy,
Ea, and reaction enthalpy Δ
H). In addition, Gibbs-free energies are calculated at different pressures and temperatures (see the ESI,
† supplement_04.pdf). Hydrogen abstraction reactions in
Fig. 1 are marked with –H˙ for simplicity, however it must be kept in mind that their mechanism is more complex than simple cleavage of the Si–H or the N–H bond. Mechanisms of these reactions are scrutinised in Section 3.8. In some reactions H˙ is being eliminated concertedly with addition of a radical. These reactions (nucleophilic substitution) are studied in Section 3.7. Silylene addition reactions with a newly proposed mechanism for SiN
x:H are reported in Section 3.5. In
Fig. 1 these reactions are shown with both: +˙NH
2 and −H˙. Reactions that initialise the chain of reactions in PECVD (
reactions (1)–(6)) are in separate Section 3.1. Radical neutralisation and neutral addition reactions are discussed in separate Sections 3.4.1 and 3.4.
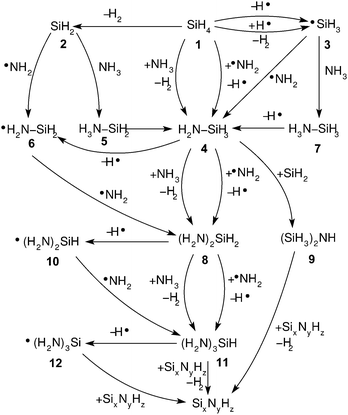 |
| | Fig. 1 Possible reactions in plasma created from a gas mixture of ammonia and silane. SixNyHz represents a surface of the silicon nitride. | |
3.1 Reactions in plasma caused by electron impact
Electron impact reactions are responsible for creating initial reactive species in plasma, enabling further reactions and the creation of more complex molecules or materials. In these reactions, no Si–N bond is being created, however their importance is in creating of reactive species that enable creation of molecules with the Si–N bond. These reactions are represented by eqn (1)–(6) and their threshold dissociation energies are shown in Table 1. Energetically the most efficient process is the dissociation of SiH4 into a silylene (eqn (2)). The ionisation of ammonia molecules (eqn (4)) requires significantly larger energy than the dissociation into radicals (eqn (6)). This is in agreement with the observation that at low electron energies, the main product of silane dissociation is SiH2.13,14 Calculated values for the dissociation are in very good agreement with the experimental results14,43 (see Table 1).
Table 1 Dissociation threshold energies (Ed0) of silane and ammonia. Values are calculated with the CASPT2/aug-cc-pVTZ method and corrected for zero point energy calculated at MP2/aug-cc-pVTZ. Experimental values are given in parentheses
| Reaction |
Active space |
E
d0/eV |
|
Measured in the molecular beam with vacuum ultraviolet synchrotron radiation.43
Transition state energy is lower than reactants by 1.06 eV.
|
| SiH4 → SiH3˙ + H˙ |
(8,8) |
4.05 (4.1)14 |
| SiH4 → SiH2 + H2 |
(8,8) |
2.25 (2.2)14 |
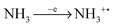
|
(8,8), (7,8) |
10.77 (10.16a) |
| NH3+˙ + NH3 → NH2˙ + NH4+ |
(11,12) |
0.0b |
| NH3 → NH2˙ + H˙ |
(8,8) |
4.93 (4.97a) |
3.2 Nucleophilic substitution
These reactions create chemical bonds between silicon and nitrogen atoms without involvement of radicals or silylenes, either as reactants, products or intermediates. In all these reactions there is a nucleophilic attack of a nitrogen atom on a silicon atom accompanied by the elimination of hydrogen molecules (eqn (17)). We analysed substitution reactions of the ammonia molecules with the silicon atoms with different number of nitrogen atoms attached. The mechanism for addition of NH3 to SiH4 is different from the accepted mechanism for nucleophilic substitution on silicon atoms, described by Deiters and Holmes,44 where nucleophile approaches silicon through a tetrahedral face direction in order to create the pentacoordinated reaction intermediate. In this case the geometry of the approach is the edge of the tetrahedron on the silicon atom, which is determined by the emerging H–H bond. This is evident in the geometry of the transition state, shown in Fig. 2. Another difference is the lack of a pentacoordinated reaction intermediate.
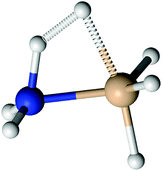 |
| | Fig. 2 Transition state for nucleophilic substitution. Transition state for the reaction of NH3 and SiH4 is shown. Transition states for the reaction with substituted NH3 or SiH4 have the same stereochemistry. | |
For all these reactions, potential energy along the reaction coordinate (see supplement_02.pdf, ESI†) shows only one maximum that corresponds to the pentacoordinated transition state. No minima, that have the pentacoordinated silicon atoms, were found on reaction coordinates. All reactions have transition states, very high in energy (Table 2) (and consequentially in enthalpy (Table 3 and supplement_04.pdf, ESI†)), much higher than the thermal energy (about 25 meV at 300 K) and also much higher than transition states of other studied reactions. This makes nucleophilic substitution reactions noncompetitive to other reactions. If only energies of hydrogen stretching vibrations in silane (2187 cm−1)45 are taken into account, at least six vibrational quanta are needed to overcome the energy barrier for the nucleophilic substitution.24 The reaction barrier for NH3 addition to SiH3NH2 drops by about 0.4 eV with respect to the addition to SiH4 due to increased electrophilicity of the silicon atom inside SiH3NH2. Reaction barriers with higher aminosilanes (SiH2(NH2)2 and SiH(NH2)3) have increased steric requirements making energy barriers for these reactions larger. In these reactions, pre-reaction complexes have a stabilisation energy significantly lower than the thermal energy. In addition, there are reactions that lead to polysubstituted amines (eqn (23)). These reactions also have a lower reaction energy barrier with respect to the reaction with silane due to increased nucleophilicity of the attacking nitrogen atom. The nucleophilic substitution of (NH2)3SiH with the NH2 group at the surface of SiNx:H was also modelled as the reaction of (NH2)3SiH with NH2SiH3 in order to check if combined effects of the increased nucleophilicity of the nitrogen atoms and the increased electrophilicity of the silicon atoms would make the reaction barrier small enough in order to be a candidate for a surface reaction responsible for the growth of SiNx:H. Unfortunately, no significant change in the reaction barrier is observed.
Table 2 Relative energies of reactants (Er), pre-reaction complexes (Epk1), transition states (reaction barrier, E‡), post-reaction complexes (Epk2) and products (Ep) for reactions in silane–ammonia plasma. All energies are calculated with the MP2/aug-cc-pVTZ//CASPT2/aug-cc-pVTZ method and corrected for the single point vibration energy, calculated with MP2/aug-cc-pVTZ. Energies are shown relative to reactants
| Reaction |
Active space |
E
r/eV |
E
pk1/eV |
E
‡/eV |
E
pk2/eV |
E
p/eV |
| NH3 + SiH4 → SiH3NH2 + H2 |
(10,10) |
0.0 |
−0.02 |
1.82 |
−0.47 |
−0.47 |
| NH3 + SiH3NH2 → SiH2(NH2)2 + H2 |
(10,10) |
0.0 |
−0.12 |
1.43 |
−0.72 |
−0.71 |
| NH3 + SiH2(NH2)2 → SiH(NH2)3 + H2 |
(10,10) |
0.0 |
−0.17 |
1.72 |
−0.79 |
−0.77 |
| NH3 + SiH(NH2)3 → Si(NH2)4 + H2 |
(10,10) |
0.0 |
−0.13 |
1.71 |
−0.83 |
−0.82 |
| SiH4 + NH2SiH3 → (SiH3)2NH + H2 |
(10,10) |
0.0 |
−0.12 |
1.74 |
−0.65 |
−0.63 |
| SiH4 + (SiH3)2NH → (SiH3)3N + H2 |
(10,10) |
0.0 |
−0.16 |
1.72 |
−0.75 |
−0.72 |
| SiH3NH2 + (NH2)3SiH → SiH3–NH–Si(NH2)3 + H2 |
(10,10) |
0.0 |
−0.21 |
1.71 |
−0.93 |
−0.91 |
| SiH3NH2 → SiHNH2 + H2 |
(10,10) |
0.0 |
— |
2.60 |
1.56 |
1.56 |
| SiH2(NH2)2 → Si(NH2)2 + H2 |
(10,10) |
0.0 |
— |
3.01 |
1.18 |
1.18 |
| NH2˙ + SiH3˙ → SiH3NH2 |
(10,10) |
0.0 |
— |
— |
— |
−4.51 |
| NH2˙ + SiH2NH2˙ → SiH2(NH2)2 |
(10,10) |
0.0 |
— |
— |
— |
−4.83 |
| NH2˙ + SiH(NH2)2˙ → SiH(NH2)3 |
(10,10) |
0.0 |
— |
— |
— |
−4.99 |
| NH2˙ + Si(NH2)3˙ → Si(NH2)4 |
(10,10) |
0.0 |
— |
— |
— |
−5.08 |
| SiH3˙ + SiH3NH˙ → (SiH3)2NH |
(10,10) |
0.0 |
— |
— |
— |
−4.91 |
| SiH3˙ + (SiH3)2N˙ → (SiH3)3N |
(10,10) |
0.0 |
— |
— |
— |
−5.63 |
| SiH3˙ + NH3 → SiH3NH3˙ |
(7,7) |
0.0 |
−0.06 |
0.54 |
— |
0.50 |
| NH2SiH2˙ + NH3 → NH2SiH2NH3˙ |
(7,7) |
0.0 |
−0.09 |
0.49 |
— |
0.35 |
| (NH2)2SiH˙ + NH3 → (NH2)2SiHNH3˙ |
(9,10) |
0.0 |
−0.15 |
0.47 |
— |
0.19 |
| NH3SiH3˙ → NH2SiH3 + H˙ |
(9,10) |
0.0 |
— |
0.28 |
−0.36 |
−0.36 |
| NH2SiH2NH3˙ → (NH2)2SiH2 + H˙ |
(9,10) |
0.0 |
— |
0.20 |
−0.53 |
−0.52 |
| (NH2)2SiHNH3˙ → (NH2)3SiH + H˙ |
(9,10) |
0.0 |
— |
0.11 |
−0.57 |
−0.56 |
| (NH2)3SiNH3˙ → (NH2)4Si + H˙ |
(9,10) |
0.0 |
— |
0.13 |
−0.46 |
−0.45 |
| SiH2 + NH3 → SiH2–NH3 |
(10,10) |
0.0 |
— |
— |
— |
−1.12 |
| SiH2 + NH2SiH3 → SiH2–NH2SiH3 |
(10,10) |
0.0 |
— |
— |
— |
−1.09 |
| SiH2 + NH(SiH3)2 → SiH2–NH(SiH3)2 |
(10,10) |
0.0 |
— |
— |
— |
−0.98 |
| SiH2–NH3 + NH3 → NH3–SiH2–NH3 |
(14,14) |
0.0 |
— |
— |
— |
−0.14 |
| SiH2–NH3 → SiH3NH2 |
(10,10) |
0.0 |
— |
1.46 |
— |
−1.75 |
| SiH2–NH2SiH3 → NH(SiH3)2 |
(10,10) |
0.0 |
— |
1.23 |
— |
−1.93 |
| SiH2–NH(SiH3)2 → N(SiH3)3 |
(10,10) |
0.0 |
— |
1.02 |
— |
−2.06 |
| NH2˙ + SiH4 → NH2SiH3 + H˙ |
(9,10) |
0.0 |
−0.07 |
0.27 |
−0.56 |
−0.56 |
| NH2˙ + NH2SiH3 → (NH2)2SiH2 + H˙ |
(9,10) |
0.0 |
−0.15 |
0.02 |
−0.80 |
−0.80 |
| NH2˙ + (NH2)2SiH2 → (NH2)3SiH + H˙ |
(9,10) |
0.0 |
−0.16 |
−0.05 |
−0.97 |
−0.96 |
| NH2˙ + (NH2)3SiH → (NH2)4Si + H˙ |
(9,10) |
0.0 |
−0.11 |
0.07 |
−0.96 |
−0.95 |
| SiH3˙ + SiH4 → SiH4 + SiH3˙ |
(7,7) |
0.0 |
−0.04 |
0.30 |
−0.04 |
0.0 |
| SiH3˙ + NH2SiH3 → NH2SiH2˙ + SiH4 |
(7,7) |
0.0 |
−0.08 |
0.32 |
−0.10 |
0.0 |
| SiH3˙ + (NH2)2SiH2 → (NH2)2SiH˙ + SiH4 |
(7,7) |
0.0 |
−0.13 |
0.32 |
−0.04 |
0.06 |
| SiH3˙ + (NH2)3SiH → (NH2)3Si˙ + SiH4 |
(7,7) |
0.0 |
−0.09 |
0.46 |
0.13 |
0.18 |
| NH2˙ + SiH4 → SiH3˙ + NH3 |
(9,10) |
0.0 |
−0.07 |
0.25 |
−0.64 |
−0.63 |
| NH2˙ + NH2SiH3 → NH2SiH2˙ + NH3 |
(9,10) |
0.0 |
−0.10 |
0.25 |
−0.68 |
−0.65 |
| NH2˙ + (NH2)2SiH2 → (NH2)2SiH˙ + NH3 |
(9,10) |
0.0 |
−0.13 |
0.23 |
−0.69 |
−0.54 |
| NH2˙ + (NH2)3SiH → (NH2)3Si˙ + NH3 |
(9,10) |
0.0 |
−0.11 |
0.20 |
−0.55 |
−0.43 |
| SiH4 + H˙ → SiH3˙ + H2 |
(5,6) |
0.0 |
0.00 |
0.22 |
−0.48 |
−0.47 |
| NH2SiH3 + H˙ → NH2SiH2˙ + H2 |
(5,6) |
0.0 |
0.00 |
0.13 |
−0.49 |
−0.46 |
| (NH2)2SiH2 + H˙ → (NH2)2SiH˙ + H2 |
(5,6) |
0.0 |
0.00 |
0.23 |
−0.40 |
−0.39 |
| (NH2)3SiH + H˙ → (NH2)3Si˙ + H2 |
(5,6) |
0.0 |
0.00 |
0.21 |
−0.30 |
−0.27 |
Table 3 Relative enthalpies of reactants (ΔHr) pre-reaction complexes (ΔHpk1), transition states (reaction barrier, ΔH‡), post-reaction complexes (ΔHpk2) and products (ΔHp) for reactions in silane–ammonia plasma at 300 K. All enthalpies are calculated with the MP2/aug-cc-pVTZ//CASPT2/aug-cc-pVTZ method and vibrational contribution to enthalpy is calculated with MP2/aug-cc-pVTZ. Enthalpies are shown relative to reactants
| Reaction |
Active space |
ΔHr/eV |
ΔHpk1/eV |
ΔH‡/eV |
ΔHpk2/eV |
ΔHp/eV |
| NH3 + SiH4 → SiH3NH2 + H2 |
(10,10) |
0.0 |
−0.01 |
1.76 |
−0.46 |
−0.45 |
| NH3 + SiH3NH2 → SiH2(NH2)2 + H2 |
(10,10) |
0.0 |
−0.10 |
1.36 |
−0.71 |
−0.69 |
| NH3 + SiH2(NH2)2 → SiH(NH2)3 + H2 |
(10,10) |
0.0 |
−0.16 |
1.66 |
−0.75 |
−0.75 |
| NH3 + SiH(NH2)3 → Si(NH2)4 + H2 |
(10,10) |
0.0 |
−0.14 |
1.65 |
−0.83 |
−0.80 |
| SiH4 + NH2SiH3 → (SiH3)2NH + H2 |
(10,10) |
0.0 |
−0.11 |
1.70 |
−0.61 |
−0.60 |
| SiH4 + (SiH3)2NH → (SiH3)3N + H2 |
(10,10) |
0.0 |
−0.15 |
1.67 |
−0.71 |
−0.69 |
| SiH3NH2 + (NH2)3SiH → SiH3–NH–Si(NH2)3 + H2 |
(10,10) |
0.0 |
−0.20 |
1.66 |
−0.89 |
−0.87 |
| SiH3NH2 → SiHNH2 + H2 |
(10,10) |
0.0 |
— |
2.59 |
1.63 |
1.62 |
| SiH2(NH2)2 → Si(NH2)2 + H2 |
(10,10) |
0.0 |
— |
3.00 |
1.24 |
1.25 |
| NH2˙ + SiH3˙ → SiH3NH2 |
(10,10) |
0.0 |
— |
— |
— |
−4.58 |
| NH2˙ + SiH2NH2˙ → SiH2(NH2)2 |
(10,10) |
0.0 |
— |
— |
— |
−4.89 |
| NH2˙ + SiH(NH2)2˙ → SiH(NH2)3 |
(10,10) |
0.0 |
— |
— |
— |
−5.05 |
| NH2˙ + Si(NH2)3˙ → Si(NH2)4 |
(10,10) |
0.0 |
— |
— |
— |
−5.16 |
| SiH3˙ + SiH3NH˙ → (SiH3)2NH |
(10,10) |
0.0 |
— |
— |
— |
−4.98 |
| SiH3˙ + (SiH3)2N˙ → (SiH3)3N |
(10,10) |
0.0 |
— |
— |
— |
−5.68 |
| SiH3˙ + NH3 → SiH3NH3˙ |
(7,7) |
0.0 |
−0.06 |
0.00 |
— |
0.44 |
| NH2SiH2˙ + NH3 → NH2SiH2NH3˙ |
(7,7) |
0.0 |
−0.08 |
0.43 |
— |
0.29 |
| (NH2)2SiH˙ + NH3 → (NH2)2SiHNH3˙ |
(9,10) |
0.0 |
−0.14 |
0.41 |
— |
0.13 |
| NH3SiH3˙ → NH2SiH3 + H˙ |
(9,10) |
0.0 |
— |
0.27 |
−0.36 |
−0.31 |
| NH2SiH2NH3˙ → (NH2)2SiH2 + H˙ |
(9,10) |
0.0 |
— |
0.18 |
−0.51 |
−0.46 |
| (NH2)2SiHNH3˙ → (NH2)3SiH + H˙ |
(9,10) |
0.0 |
— |
0.11 |
−0.56 |
−0.51 |
| (NH2)3SiNH3˙ → (NH2)4Si + H˙ |
(9,10) |
0.0 |
— |
0.12 |
−0.43 |
−0.40 |
| SiH2 + NH3 → SiH2–NH3 |
(10,10) |
0.0 |
— |
— |
— |
−1.18 |
| SiH2 + NH2SiH3 → SiH2–NH2SiH3 |
(10,10) |
0.0 |
— |
— |
— |
−1.14 |
| SiH2 + NH(SiH3)2 → SiH2–NH(SiH3)2 |
(10,10) |
0.0 |
— |
— |
— |
−1.01 |
| SiH2–NH3 + NH3 → NH3–SiH2–NH3 |
(14,14) |
0.0 |
−0.03 |
— |
— |
−0.15 |
| SiH2–NH3 → SiH3NH2 |
(10,10) |
0.0 |
— |
1.44 |
— |
−1.73 |
| SiH2–NH2SiH3 → NH(SiH3)2 |
(10,10) |
0.0 |
— |
1.24 |
— |
−1.95 |
| SiH2–NH(SiH3)2 → N(SiH3)3 |
(10,10) |
0.0 |
— |
1.03 |
— |
−2.07 |
| NH2˙ + SiH4 → NH2SiH3 + H˙ |
(9,10) |
0.0 |
−0.08 |
0.20 |
−0.59 |
−0.57 |
| NH2˙ + NH2SiH3 → (NH2)2SiH2 + H˙ |
(9,10) |
0.0 |
−0.14 |
−0.05 |
−0.82 |
−0.80 |
| NH2˙ + (NH2)2SiH2 → (NH2)3SiH + H˙ |
(9,10) |
0.0 |
−0.25 |
−0.11 |
−0.92 |
−0.97 |
| NH2˙ + (NH2)3SiH → (NH2)4Si + H˙ |
(9,10) |
0.0 |
−0.12 |
0.01 |
−0.98 |
−0.96 |
| SiH3˙ + SiH4 → SiH4 + SiH3˙ |
(7,7) |
0.0 |
−0.12 |
0.30 |
−0.12 |
0.00 |
| SiH3˙ + NH2SiH3 → NH2SiH2˙ + SiH4 |
(7,7) |
0.0 |
−0.06 |
0.33 |
−0.08 |
−0.00 |
| SiH3˙ + (NH2)2SiH2 → (NH2)2SiH˙ + SiH4 |
(7,7) |
0.0 |
−0.12 |
0.32 |
−0.03 |
0.06 |
| SiH3˙ + (NH2)3SiH → (NH2)3Si˙ + SiH4 |
(7,7) |
0.0 |
−0.08 |
0.45 |
0.12 |
0.18 |
| NH2˙ + SiH4 → SiH3˙ + NH3 |
(9,10) |
0.0 |
−0.08 |
0.21 |
−0.62 |
−0.63 |
| NH2˙ + NH2SiH3 → NH2SiH2˙ + NH3 |
(9,10) |
0.0 |
0.01 |
0.22 |
−0.79 |
−0.66 |
| NH2˙ + (NH2)2SiH2 → (NH2)2SiH˙ + NH3 |
(9,10) |
0.0 |
−0.12 |
0.21 |
−0.68 |
−0.54 |
| NH2˙ + (NH2)3SiH → (NH2)3Si˙ + NH3 |
(9,10) |
0.0 |
−0.12 |
0.18 |
−0.56 |
−0.43 |
| SiH4 + H˙ → SiH3˙ + H2 |
(5,6) |
0.0 |
−0.05 |
0.18 |
−0.49 |
−0.44 |
| NH2SiH3 + H˙ → NH2SiH2˙ + H2 |
(5,6) |
0.0 |
−0.05 |
0.09 |
−0.50 |
−0.44 |
| (NH2)2SiH2 + H˙ → (NH2)2SiH˙ + H2 |
(5,6) |
0.0 |
−0.04 |
0.20 |
−0.42 |
−0.37 |
| (NH2)3SiH + H˙ → (NH2)3Si˙ + H2 |
(5,6) |
0.0 |
−0.05 |
0.18 |
−0.31 |
−0.25 |
3.3 Hydrogen molecule elimination
This reaction was proposed by Beach and Jasinski22 as an alternative path for formation of silylenes (reaction (14)). These reactions are generalisation of the reaction that is the most important for initial production of SiH2 (reaction (2)), described in Section 3.1. Although reaction barriers for these reactions are large (>2.5 eV), it is the most favourable dissociation pathway of an excited aminosilylene (reactions (12)–(14)).
3.4 Radical addition reactions
3.4.1 Radical neutralisation.
This class of reactions (eqn (8) and (9)) represent a part of reaction mechanisms22 that explain observation of aminosilanes in silane–ammonia plasma. It is believed that these reactions are responsible for the growth of SiNx:H.6,10,22,23 Radical neutralisation reactions have no reaction barrier, making them kinetically most competitive reactions, since the reaction rate depends only on the rate at which radicals collide with each other. In Tables 2 and 3, reaction energies and enthalpies are reported as a difference between reactants (radicals) and products. The amount of energy, obtained from these reactions, is the highest among all reactions considered. This amount of energy is also significantly higher than any reaction barrier of any studied reaction. This makes possible other addition reactions on the vibrationally hot radical neutralisation product, even if their reaction barrier is prohibitively large for reactants in thermal equilibrium.
3.4.2 Addition of NH3 to silyl radicals.
According to MP2/aug-cc-pVTZ and CASPT2/aug-cc-pVTZ calculations, NH3 molecules can react with silyl radicals in order to create a weak bond. MP2/aug-cc-pVTZ//CASPT2/aug-cc-pVTZ calculations have shown that the reaction has a transition state of 0.44 eV above reactants and the resulting product is stabilised by only 93 meV with respect to the transition state. If vibrational zero-point energies are counted in, product energies become higher than the transition state energy, making the adduct NH3–SiH3˙ unstable. This species would be important only if it could stabilise by elimination of hydrogen radicals (H˙) immediately after association. Unfortunately, hydrogen elimination requires additional energy (0.2 eV), so this molecule is interesting only in a theory of weak chemical bonds. This class of reactions is not further investigated.
3.5 Silylene addition reactions
Silylene is a very reactive molecule, containing a two-valent silicon atom.46,47 The electronic structure of silylene is characterised by sp2 hybridisation on the silicon atom, which causes a bent geometry of SiH2.47,48 The third position in “triangular” SiH2 is occupied with the free electron pair. The remaining p orbital is empty and non-bonding, situated perpendicularly to the molecular plain.47,48 Silylene in its ground state is in the singlet state (has no unpaired electrons) and without charge.
Although silylene is not a radical, addition of silylene to amines (reaction 19) has no transition state. Instead of the IRC energy profile, scan of the energy, calculated at CASPT2/aug-cc-pVTZ, as a function of Si–N bond length is shown in the ESI,† supplement_2.pdf. Scan is made for Si–N distances in the range 2–8 Å. In that range, no maximum in energy is found, undoubtedly proving that the addition of silylene to amines has no transition state. The stabilisation energy of created adducts is little over 1 eV (see Table 2), which is significantly lower than the stabilisation energies in radical neutralisation reactions. The reason for that is creation of aminosilylene (SiH2←NH3, or SiH2←NH3−x(SiH3)x in general) molecules with a dative, rather than a normal covalent bond. Unlike SiH3NH2, where negative charge is concentrated on the lone electron pair on the N atom (Fig. 3a), the SiH2←NH3 molecule (Fig. 3b) has a lone electron pair on the Si atom, which makes it a polar molecule (SiH2−NH3+) with the polarity opposite from SiH3NH2. As a reactive species, SiH2 is consumed fast and if the gas mixture contains excess of NH3, the most probable removal pathway for SiH2 is the formation of SiH2←NH3. The lack of products of SiH2←NH3 in the mass spectra of the SiH4–NH3 plasma indicates that it does not rearrange into a more stable isomer (SiH3–NH2), nor reacts with other molecules via N–H insertion.22
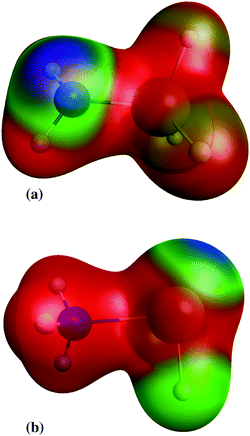 |
| | Fig. 3 Electrostatic potential of: (a) aminosilane and (b) aminosilylene; red colour denotes positive charge, blue negative charge and green denote charge neutral. | |
Silylene is a planar molecule with a silicon atom in sp2 hybridisation, where three sp2 positions are filled with two σ bonds and one free electron pair. The remaining p orbital is empty and non-bonding, situated perpendicularly to the molecular plain.47,48 That orbital receives the electron pair from ammonia molecules in SiH2←NH3. Since the empty p orbital in the silylene extends to both sides of the molecule, it provides two bonding sites for the dative bond, however the empty p orbital can accommodate only one electron pair. Nevertheless, SiH2 can accommodate two dative bonds with two different ammonia molecules by weak, partial bonds. From the dissociation energies (0.14 eV for the dissociation of NH3→SiH2←NH3 and 1.12 eV for the dissociation of NH3→SiH2), it is evident that the addition of the second NH3 ligand to SiH2 leads to relatively small energy stabilisation. Nevertheless, NH3→SiH2←NH3 is the minimum on the PES with very weak Si–N bonds, in the range of the hydrogen bond. NH3→SiH2←NH3 is a symmetric species with C2v symmetry (see Fig. 4), implying two equal Si–N bonds, 2.26 Å long. That bonds are substantially longer than the dative Si–N bond in SiH2←NH3 (2.03 Å, MP2/aug-cc-pVTZ) and the standard, covalent Si–N bond (1.73 Å, SiH3–NH2, optimised on MP2/aug-cc-pVTZ). Nitrogen and silicon atoms are not colinear, but make a N–Si–N angle of 160.7°. The symmetry of NH3→SiH2←NH3 and the difference in dissociation energies show that the association of the second NH3 with NH3→SiH2 weakens the first Si–N bond. This is clearly visible in Fig. 5a where one of the Si–N bond length (r) is shown as the function of the other (rfixed) Si–N bond length in NH3→SiH2←NH3. The bond length dependence in Fig. 5a is determined by the optimisation of NH3 while other two moieties are frozen with the selected Si–N separation (rfixed). When one of the NH3 ligands moves away from the rest of SiH2←NH3, the remaining Si–N bond converges to the bond length in SiH2←NH3 (2.03 Å). In Fig. 5b, energy of NH3→SiH2←NH3 is shown as a function of the Si–N bond length (rfixed). Energies are calculated on the CASPT2/aug-cc-pVTZ level on the same geometries that were used for determining the dependence of the Si–N bond length upon approaching another NH3 ligand. The energy dependence of NH3 approaching to SiH2←NH3 shows a single minimum at 2.26 Å without a transition state.
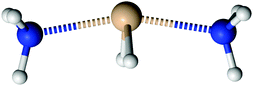 |
| | Fig. 4 The structure of NH3→SiH2←NH3. | |
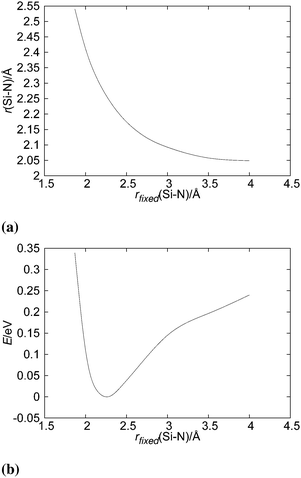 |
| | Fig. 5 Change in (a) Si–N bond length and in (b) energy of the SiH2←NH3 complex as a function the Si–N distance (rfixed) of the approaching second NH3 ligand. | |
Although the low dissociation energy makes bonding in NH3→SiH2←NH3 weak, this species could be present in low temperature SiH4–NH3 plasma or as a transient species in certain reactions. Any SiH2←NH3 that does not react in the plasma can stick to the amine group on the surface via the doubly complexed SiH2 (eqn (24)).
| | | SixNy–NH2 + SiH2←NH3 → SixNy–NH2→SiH2←NH3 → SixNy–NH2→SiH2 + NH3 | (24) |
The low energy for dissociation of one of the Si←N bonds makes highly possible the dissociation of NH
3. This leaves SiH
2 bound to the surface of the silicon nitride. SiH
2, chemisorbed on the surface, then provides a site that is ready for reactions with other reactive species from the plasma. This mechanism is energetically very favourable since all complexes are formed without energy barrier and the barrier for surface dissociation of NH
3 is very low (about 0.14 eV). Moreover, the rate of formation of SiH
2←NH
3 depends on the rate of formation of SiH
2, which has the lowest activation energy among all reactive species in SiH
4–NH
3 plasma. Energy stabilisation of SiH
2←NH
3 is large enough to withstand collisions with thermalized non-reactive molecules in low-temperature plasma.
3.6 Silylene rearrangement reactions
This reaction converts amino-silylenes into aminosilanes (eqn (20)), by migrating one hydrogen atom from the nitrogen atom to the silicon atom. Since the migration of hydrogen atoms is between neighbouring atoms (1,2-shift), the transition state has a triangular geometry with hydrogen atoms in one of the corners. Energy barriers are over 1.2 eV (see Table 2), but the reactants are created by the barrierless SiH2 addition (see Section 3.5) with excess energy of over 1 eV. That energy is available to NH3−x(SiH3)x in the form of vibrational energy immediately after formation. Thus, the “collective” energy barriers for consecutive reactions (19) and (20) are therefore only 0.35 eV for x = 0 and 0.14 eV for x = 1 (x denotes the number of silyl groups in eqn (19) and (20)). Since higher polysubstituted amines are not observed in SiH4–NH3 plasma, either SiH2←NH3 thermally equilibrates before the reaction takes place, or this reaction can have importance only in the formation of SiH3NH2 (eqn (20), x = 0). The reaction mechanism that includes activated aminosilane (eqn (13)) is represented by the reverse silylene rearrangement (conversion of SiH3NH2 into SiH2←NH3) and the subsequent dissociation of the SiH2←NH3 complex. The rate-determining step of this two-stage reaction is the rearrangement since its large energy barrier (3.21 eV) surpasses the dissociation energy of SiH2←NH3.
3.7 Radical nucleophilic addition
Two versions of radical eliminative addition reactions were proposed: radical–neutral eliminative addition reactions are proposed by Beach and Jasinski21,22 (eqn (10)) with a variant, proposed by Tachibana et al.21 (eqn (18)) and the radical–radical eliminative addition reactions, proposed also by Beach and Jasinski22 (eqn (7)). This reaction is reported22 to be the most plausible explanation for laser induced reactions in SiH4–NH3 gas mixtures.
3.7.1 Neutral–radical eliminative addition.
The geometry of the reported21 transition state for eqn (11), x = 0, optimised at the HF/6-31G(d) level is quantitatively the same as the geometry, obtained in this work by optimisation at a higher level of theory (MP2/aug-cc-pVTZ). Reaction barriers for these reactions are very low, confirming the importance of these reactions as one of the important mechanisms in the growth of SiNx:H. Reaction barriers for reaction (11) with aminosilanes (x > 0) decrease with increasing number of amine groups on the silicon atom. For x = 2, reaction energy of the transition state, relative to reactants, reduces to effectively a negative value. Although the reaction energy barrier relative to a pre-reaction complex still exists, the relatively large stabilisation of pre-reaction complexes makes the overall reaction energy barrier negative.
3.7.2 Radical–radical eliminative addition.
The transition state for the radical–radical eliminative addition reactions (eqn (7)) could not be located. In order to clarify the mechanism of reaction (7), we scanned the potential energy surface, by extending Si–N and S–H bond lengths and by changing the H–Si–N angle values (Fig. 6). Energies at each point at the potential energy surface are evaluated by constrained geometry optimisation, with constraints in the form of frozen Si–N and S–H bonds and the H–Si–N angle. The resulting potential energy surface is shown in Fig. 7 as a series of two-dimensional surfaces, each for a specific H–Si–N angle. The potential energy surface shows no saddle points that would correspond to a transition state. The global minimum is aminosilane (SiH3NH2). Expanding bond lengths of Si–N and N–H (or both) monotonically increase the energy, which is in accordance with bond breaking reactions. That makes the radical–radical eliminative addition (eqn (7)) two separate elementary processes, which could be represented with eqn (12). This reaction can proceed if reactants collide with enough energy in order to break the bond at the opposite side of the molecule and to compensate the energy dissipated in IR emission or intermolecular collisions. Since the energy for dissociation of a Si–N bond is larger than the dissociation energy of a Si–H bond, there is a greater chance that this reaction will proceed in the direction where NH2˙ replaces the H˙ radical, than the reaction in the reverse direction.
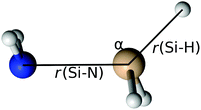 |
| | Fig. 6 Bond lengths (r(Si–N) and r(Si–H)) and the angle (α) used in the potential energy surface scan of the radical–radical eliminative addition reaction. | |
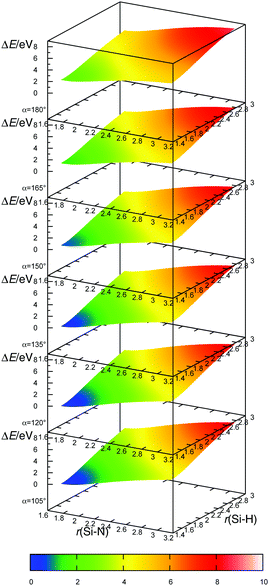 |
| | Fig. 7 The potential energy surface for radical–radical eliminative addition for reaction between NH2˙ and SiH4. Angle α is the angle between the approach vector of NH2˙ and the recede vector of H˙. Potential energy surfaces are calculated on the MP2/aug-cc-pVTZ level. Energies are shown relative to the energy minimum (SiH3NH2). | |
3.8 Hydrogen abstraction reactions
The deposition of silicon from a low temperature (T = 400 K) silane plasma49 without the presence of ammonia proceeds through these reactions. Hydrogen abstraction reactions require rather high activation energies (above 0.2 eV; see Table 2) than radical eliminative additions or silylene additions. The energy barrier for the trivial reaction of proton exchange between SiH3˙ and SiH4 is 0.3 eV, which further increases as the number of NH2 groups on the silicon atom is increased. Hydrogen abstraction from aminosilanes by SiH3˙ has positive reaction enthalpy, which also increases with a larger number of NH2 groups. Therefore, silane radicals do not have an important role in propagating radical chain reactions by hydrogen abstraction of aminosilanes. NH2˙ radicals abstract hydrogen atoms from silanes more readily since the N–H bond is stronger than the Si–H bond. That makes energy gain from the formation of the N–H bond larger than the consumption needed by breaking the Si–H bond, which is reflected in much more favourable reaction enthalpies. These reactions also have lower energy barriers (about E‡ = 0.25 eV for SiH4), which reduce in the case of higher aminosilanes (up to E‡ = 0.20 eV for (NH2)3SiH). The stability of pre-reaction complexes in hydrogen abstraction reactions by NH2˙ or SiH3˙ indicates that these radicals can form complexes with molecules, whose stability is significantly larger than the thermal energy in low-temperature plasma. In that case, even if the reaction does not occur, these molecules can still serve as a shuttle for radicals to the surface of SiNx:H.
There are H˙ atoms in SiH4–NH3 plasma that are also available for hydrogen abstraction reactions. These reactions have energy barriers as high as in hydrogen abstraction reactions by NH2˙ radicals, although the overall reaction enthalpy is not so large. H˙ radicals do not form such stable complexes as do NH2˙ and SiH3˙ radicals.
4 Conclusions
Nucleophilic substitution reactions, where neutral amines react with neutral silane molecules, have energy barriers that are too large to allow such reactions in a thermally equilibrated system. Pentacoordinate reaction intermediates, which were considered to be characteristic of nucleophilic substitution reactions on silicon atoms, were not observed. These reactions proceed through an edge attack of the amine on the tetrahedral silicon, rather than through approach from the tetrahedral face direction. Neutralisation of amine and silane radicals proceeds without energy barrier and creates a product with energy stabilisation large enough to enable even otherwise prohibitive reactions on the hot reaction product. Addition of silyl radicals to ammonia produces a product that is less stable than the transition state for this reaction. Although the resulting adduct could stabilise by elimination of hydrogen atoms, the existence of an additional reaction barrier prevents these reactions to happen. Addition of silylene to amines creates a relatively stable complex with a dative bond without an energy barrier. The ability of the silylene to create a second dative bond with an amine molecule can cause sticking of the complex to the surface of silicon nitride. Subsequent dissociation of the complex leaves silylene, bound at the surface, making it available for further growth reactions at the surface. A radical substitution reaction, where an amine radical substitutes a hydrogen atom on neutral silane, proceeds with a low or an even negative transition state. Equivalent substitution on a silyl radical (radical–radical eliminative addition) does not pose as an elementary reaction, but rather a combination of radical neutralisation and bond breaking. Unlike hydrogen abstraction by silane radicals, abstraction by amine radicals and hydrogen atoms is thermodynamically favourable and also proceeds with a lower energy barrier. The existence of complexes where silane and amine radicals are bonded with other molecules indicates the possibility of the transfer of these radicals to the silicon nitride surface by these complexes.
Contributions
GK did all calculations and prepared the manuscript; BP: project leader, approved the manuscript.
Acknowledgements
Computational resources provided by the Isabella cluster (isabella.srce.hr) at the Zagreb University Computing Centre (Srce) were used for some calculations in this paper. Some calculations were performed on equipment donated by the Zagreb University Computing Centre (Srce). This work has been supported by the Croatian Science Foundation under the project 6135.
References
- F. Habraken and A. Kuiper, Mater. Sci. Eng., R, 1994, 12, 123–175 CrossRef.
- G. Lucovsky, P. D. Richard, D. V. Tsu, S. Y. Lin and R. J. Markunas, J. Vac. Sci. Technol., A, 1986, 4, 681–688 CAS.
- G. Lucovsky and D. V. Tsu, J. Non-Cryst. Solids, 1987, 90, 259–266 CrossRef CAS.
- D. L. Smith, A. S. Alimonda and F. J. von Preissig, J. Vac. Sci. Technol., B: Microelectron. Process. Phenom., 1990, 8, 551–557 CAS.
- J. A. Theil, S. V. Hattangady and G. Lucovsky, J. Vac. Sci. Technol., A, 1992, 10, 719–727 CAS.
- D. L. Smith, J. Vac. Sci. Technol., A, 1993, 11, 1843–1850 CAS.
- B. F. Hanyaloglu and E. S. Aydil, J. Vac. Sci. Technol., A, 1998, 16, 2794–2803 CAS.
- G. N. Parsons and G. Lucovsky, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1664–1667 CrossRef CAS.
- W. A. P. Claassen, W. G. J. N. Valkenburg, M. F. C. Willemsen and W. M. v. d. Wijgert, J. Electrochem. Soc., 1985, 132, 893–898 CrossRef CAS.
- D. L. Smith, A. S. Alimonda, C. Chen, S. E. Ready and B. Wacker, J. Electrochem. Soc., 1992, 137, 614–623 CrossRef.
- O. Leroy, G. Gousset, L. L. Alves, J. Perrin and J. Jolly, Plasma Sources Sci. Technol., 1998, 7, 348 CrossRef CAS.
- G. Turban, Pure Appl. Chem., 1984, 56, 215–230 CrossRef CAS.
- M. J. Kushner, J. Appl. Phys., 1987, 62, 2803–2811 CrossRef CAS.
- G. Turban, Y. Catherine and B. Grolleau, Thin Solid Films, 1981, 77, 287–300 CrossRef CAS.
- G. Turban, Y. Catherine and B. Grolleau, Thin Solid Films, 1980, 67, 309–320 CrossRef CAS.
- M. J. Kushner, J. Appl. Phys., 1988, 63, 2532–2551 CrossRef CAS.
- G. Turban, Y. Catherine and B. Grolleau, Thin Solid Films, 1979, 60, 147–155 CrossRef CAS.
- I. Haller, J. Phys. Chem., 1990, 94, 4135–4137 CrossRef CAS.
- A. Tachibana, S. Kawauchi, N. Yoshida, T. Yamabe and K. Fukui, J. Mol. Struct., 1993, 300, 501–508 CrossRef CAS.
- S. D. Pringle, V. S. Joss and C. Jones, Surf. Interface Anal., 1996, 24, 821–829 CrossRef CAS.
- A. Tachibana, K. Yamaguchi, S. Kawauchi, Y. Kurosaki and T. Yamabe, J. Am. Chem. Soc., 1992, 114, 7504–7507 CrossRef CAS.
- D. B. Beach and J. M. Jasinski, J. Phys. Chem., 1990, 94, 3019–3026 CrossRef CAS.
- Y. Shi, B. Eustergerling and X. Li, Thin Solid Films, 2008, 516, 506–510 CrossRef CAS.
- A. Tachibana, Y. Kurosaki, T. Sera, E. Tanaka, H. Fueno and T. Yamabe, J. Phys. Chem., 1990, 94, 5234–5240 CrossRef CAS.
- H. Umemoto, T. Morimoto, M. Yamawaki, Y. Masuda, A. Masuda and H. Matsumura, Thin Solid Films, 2003, 430, 24–27 CrossRef CAS.
- D. Murley, R. Gibson, B. Dunnett, A. Goodyear and I. French, J. Non-Cryst. Solids, 1995, 187, 324–328 CrossRef CAS.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- T. H. Dunning, K. A. Peterson and A. K. Wilson, J. Chem. Phys., 2001, 114, 9244–9253 CrossRef CAS.
- M. W. Chase, J. Phys. Chem. Ref. Data, Monogr., 1998, 9, 1–1951 Search PubMed.
- K. Baldridge and L. A. Pederson, Pi Mu Epsilon Journal, 1993, 9, 513–521 Search PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
-
M. S. Gordon and M. W. Schmidt, in Theory and Applications of Computational Chemistry, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. E. Scuseria, Elsevier, Amsterdam, 2005, pp. 1167–1189 Search PubMed.
- P. Piecuch, S. A. Kucharski, K. Kowalski and M. Musiał, Comput. Phys. Commun., 2002, 149, 71–96 CrossRef CAS.
-
B. O. Roos, The Complete Active Space Self-Consistent Field Method and its Applications in Electronic Structure Calculations, John Wiley & Sons, Inc., 2007, pp. 399–445 Search PubMed.
- K. Andersson, P. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS.
- G. Kovačević and V. Veryazov, J. Cheminf., 2015, 7, 1–10 Search PubMed.
- G. Karlström, R. Lindh, P.-Å. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P.-O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrady and L. Seijo, Comput. Mater. Sci., 2003, 28, 222–239 CrossRef.
- F. Aquilante, L. De Vico, N. Ferré, G. Ghigo, P.-Å. Malmqvist, P. Neogrády, T. B. Pedersen, M. Pitoňák, M. Reiher, B. O. Roos, L. Serrano-Andrés, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224–247 CrossRef CAS PubMed.
- F. R. Ornellas and S. Iwata, J. Phys. Chem., 1996, 100, 16155–16161 CrossRef CAS.
- F. Qi, L. Sheng, Y. Zhang, S. Yu and W.-K. Li, Chem. Phys. Lett., 1995, 234, 450–454 CrossRef CAS.
- J. A. Deiters and R. R. Holmes, J. Am. Chem. Soc., 1987, 109, 1686–1692 CrossRef CAS.
- F. B. Stitt and D. M. Yost, J. Chem. Phys., 1936, 4, 82 CrossRef CAS.
- S. Nagendran and H. W. Roesky, Organometallics, 2008, 27, 457–492 CrossRef CAS.
- J. Olah, T. Veszpremi, J. D. Woollins and F. Blockhuys, Dalton Trans., 2010, 39, 3256–3263 RSC.
- J. M. Jasinski, R. Becerra and R. Walsh, Chem. Rev., 1995, 95, 1203–1228 CrossRef CAS.
- M. Brandt, J. Chrysostomides, S. Koynov and V. Petrova-Koch, J. Non-Cryst. Solids, 1989, 115, 105–107 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: (1) Selection of active spaces in CASPT2 calculations, (2) Cartesian coordinates of all stationary points along reaction pathways, (3) reaction energy profiles for studied reactions and (4) enthalpies and Gibbs free energies. See DOI: 10.1039/c6cp05395e |
|
| This journal is © the Owner Societies 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article * and
Branko
Pivac
* and
Branko
Pivac

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) indicating that reactions in plasma are either a different mechanism, or an interplay of several mechanisms.22
1) indicating that reactions in plasma are either a different mechanism, or an interplay of several mechanisms.22