Diiodomethane as a halogen bond donor toward metal-bound halides

Abstract

A 1,3,5,7,9-pentaazanona-1,3,6,8-tetraenate (PANT) chloride platinum(II) complex (1) was obtained via the metal-mediated double coupling of 2,3-diphenylmaleimidine with both nitrile ligands in trans-[PtCl₂(NC^tBu)₂]. Compound 1 was then co-crystallized with diiodomethane forming solvate 1·½CH₂I₂. The XRD experiment reveals that this solvate displays the halogen bonds H₂C(I)–I⋯Cl–Pt and hydrogen bonds I₂C(H)–H⋯Cl–Pt, which join two complex and one CH₂I₂ molecules in a heterotrimeric supramolecular cluster. Inspection of the CCDC database reveals only one example of the halogen bond H₂C(I)–I⋯I–Pt between the CH₂I₂ molecule and metal-coordinated halide in the structure of VEMWOA. In VEMWOA, CH₂I₂ serves solely as a halogen bond donor with no hydrogen bond contribution. Results of the Hirshfeld surface analysis and DFT calculations (M06/DZP-DKH level of theory) followed by topological analysis of the electron density distribution within the formalism of Bader's theory (QTAIM method) for both 1·½CH₂I₂ and VEMWOA confirmed the formation of these weak interactions. The evaluated energies of halogen bonds involving CH₂I₂ are in the 2.2–2.8 kcal mol⁻¹ range.

---

Introduction

Halogen bonding¹ (XB) is one of the most actively studied types of weak interactions^2–4 insofar as along with hydrogen bonding, metallophilic interactions, and π-stacking, XB is efficiently used as a tool in crystal engineering and in supramolecular organization.^2,3,5 Recent applications of XB include stabilization of explosives⁶ and synthesis of systems with tunable photophysical properties.⁷ XBs also play important roles in organocatalysis⁸ and in the metabolism of biologically active halogen-containing compounds.⁹

In many reports devoted to XB, iodine-based bifunctional XB donors such as 1,2- and 1,4-diiodoperfluorobenzenes were employed because of their availability, large σ-holes, and high solubility in most common organic solvents.^2,10 However, more and more attention is now paid to halomethanes, which can also behave as polyfunctional XB donors.^11–20 Concurrently, halide complexes of d-metals can be employed as XB acceptors and their combination with halomethanes leads to supramolecular clusters, chains, and 3D networks.^{17,18,20–22}

The halomethanes CBr₄,^{11–13,18–20} CHI₃,^14,15,17,23 CHBr₃,^11,12,20 and CFBr₃ ^12,19 are the most commonly used among other halomethanes in the formation of XBs with uncomplexed halides and polyhalometalate anions. Our recent works indicated that even weak XB donors such as CHCl₃, CH₂Cl₂, and CH₂Br₂ (Fig. 1) are still able to form supramolecular clusters with chloride anions and chloride ligands in metal complexes held by XBs and HBs^16,21,22 or by simultaneous XB and HB.^16,21,22

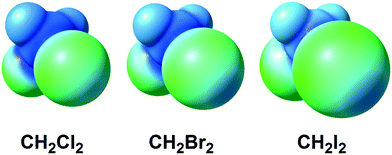Fig. 1 ESP distribution in the CH₂X₂ (X = Cl, Br, I) dihalomethane molecules (M06-2X/CEP-121G level of theory).²⁴ Green color – negative ESP, blue color – positive ESP.

In contrast to a rather broad application of halomethanes in crystal engineering, diiodomethane (CH₂I₂) – despite its relatively large σ-holes (Fig. 1; positive potential is up to 23.1 kcal mol⁻¹ on the 0.001 a.u. molecular surface) – was poorly studied^25–28 as an XB donor. Nassimbeni et al. reported a series of halomethane solvates of tetrakis(4-bromophenyl)- and tetrakis(4-iodophenyl)ethylenes, where diiodomethane forms H₂C(I)–I⋯Br–C and H₂C(I)–I⋯I–C contacts assigned²⁵ to XB after comparison of their geometrical parameters with the IUPAC geometrical criteria¹ for XB. The other three reports^25–28 were focused on crystalline CH₂I₂ exhibiting numerous C–I⋯I–C XBs, where one diiodomethane molecule is an XB donor and another molecule behaves as an XB acceptor, again in full agreement with the IUPAC criteria.¹ In addition, Geiser et al.²⁹ observed weak H₂C(I)–I⋯C₆₀ interactions by XRD in the crystals of C₆₀·C₆H₆·CH₂I₂, but these contacts were not treated as XBs.

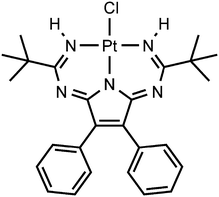
Upon our studies of XB between platinum chloride complexes and halomethanes,^17,22 we found that 1,3,5,7,9-pentaazanona-1,3,6,8-tetraenate (PANT) chloride platinum(II) complex³⁰1 (Fig. 2) co-crystallizes with diiodomethane forming solvate 1·½CH₂I₂. The XRD experiment reveals that this solvate displays H₂C(I)–I⋯Cl–Pt XBs and I₂C(H)–H⋯Cl–Pt HBs, which join two complexes and one CH₂I₂ molecule in one heterotrimeric supramolecular cluster. The nature of these weak interactions was also studied theoretically and their energies were evaluated in the range from 2.2 to 2.5 kcal mol⁻¹ showing the ability of CH₂I₂ to behave as an XB donor. We also verified by theoretical calculations overlooked XBs associated with CH₂I₂ in the structure of VEMWOA (2.4–2.8 kcal mol⁻¹). All these results are consistently disclosed in the sections that follow.

Fig. 2 Schematic representation of 1.

Experimental

X-ray structure determination

A suitable crystal of 1·½CH₂I₂ was studied using an Agilent Technologies Supernova Atlas diffractometer (monochromated MoKα radiation, λ = 0.71073 Å). The temperature was kept at 100 K. The structure has been solved by direct methods and refined by means of the SHELXL-97³¹ program incorporated in the OLEX2 program package³² using Least Squares minimization. The carbon-bound H atoms were placed in calculated positions and were included in the refinement in the ‘riding’ model approximation with U_iso(H) set to 1.5U_eq(C) and C–H = 0.96 Å for the CH₃ groups, U_iso(H) set to 1.2U_eq(C) and C–H = 0.93 Å for the CH groups, and U_iso(H) set to 1.2U_eq(N) and N–H = 0.86 Å for the NH groups. Empirical absorption correction was applied in the CrysAlisPro³³ program complex using spherical harmonics, implemented in the SCALE3 ABSPACK scaling algorithm.

The crystallographic details are summarized in ESI† Table S2.

Computational details

Single point calculations based on the experimental X-ray geometry (quasi-solid-state approach) have been carried out at the DFT level of theory using the M06 functional³⁴ (this functional was specifically developed to describe weak dispersion forces and non-covalent interactions) with the help of the Gaussian-09³⁵ program package. The Douglas–Kroll–Hess 2nd-order scalar relativistic calculations requesting a relativistic core Hamiltonian were carried out using DZP-DKH basis sets^36–40 for all atoms. The topological analysis of the electron density distribution with the help of the atoms-in-molecules (QTAIM) method developed by Bader⁴¹ has been performed by using the Multiwfn program (version 3.3.8).⁴²

We used the Chemcraft program (version 1.8)⁴³ for visualization of electrostatic surface potential distribution. The Hirshfeld molecular surfaces were generated by the CrystalExplorer 3.1 program^44,45 based on the results of the X-ray study. The normalized contact distances, d_norm,⁴⁶ based on Bondi's van der Waals radii,⁴⁷ were mapped into the Hirshfeld surfaces. In the color scale, negative values of d_norm are visualized by the red color indicating contacts shorter than the sum of van der Waals radii. The white color denotes intermolecular distances close to van der Waals contacts with d_norm equal to zero. In turn, contacts longer than the sum of van der Waals radii with positive d_norm values are colored with blue. The Cartesian atomic coordinates of model clusters are presented in Tables S3 and S4 (ESI†).

Results and discussion

General approach for verification of XB between organic and metal halides

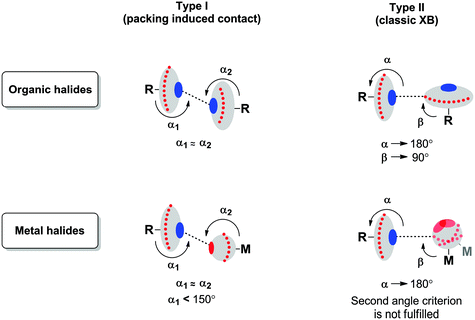
Two types of short halogen⋯halogen contacts are commonly discussed in the literature (Fig. 3).

Fig. 3 Illustration of the difference between carbon- (left) and metal-bound (right) halides.

Type I is a packing-induced contact (which is actually not an XB, see ref. 48), whereas type II is due to a classic XB because a halogen atom with a 90° angle provides its lone pair for interaction and the other one provides its σ-hole (or, in other words, an area of electropositive potential). According to the IUPAC definition,¹ XB is the real R–X⋯Y (X = halogen) contact, when, firstly, the interatomic distance between X and an appropriate Lewis base (Y = F, O, N, Cl, etc.) is less than the sum of their vdW radii and, secondly, the R–X⋯Y angle is close to 180°; exceptions from the linearity have been reviewed by Rissanen.⁴⁹

It is not surprising that metal halide species – when they are non-covalently linked to organic R–X halogen bond donors – exhibit certain deviations from linearity of the R–X⋯X–[M] fragment. Fig. 4 schematically illustrates the difference in ESPs between organic- and metal-bound halides.

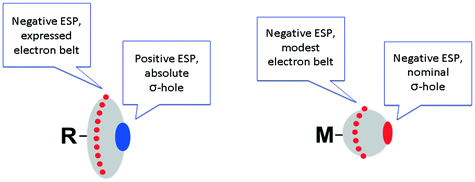Fig. 4 Schematic representation of different ESP distributions on the halogen atoms in organic (left) and metal halides (right).

In contrast to conventional organic XB donors, R–X, the ESP of the complexed halides, as, e.g., calculated by Brammer and co-workers,⁵⁰ is negative at both electron belt areas and also at the so-called σ-hole. This σ-hole is only nominal and its formulation has only relative, but not absolute sense. As an additional illustration (Fig. 5), we calculated the ESPs V_S(r) on the molecular vdW surfaces of CH₃I and cis-[PtI₂(NH₃)₂] taken as model systems (optimization in the gaseous phase at the M06/6-311++G** level of theory, quasi-relativistic Stuttgart pseudopotentials and appropriate contracted basis sets MWB60 and MWB46 were used on the platinum and iodine atoms, respectively).

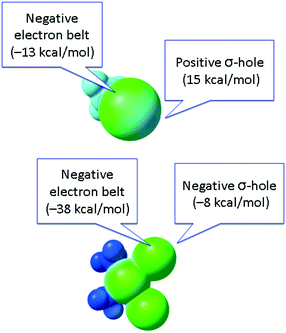Fig. 5 ESP distribution in the CH₃I (top) and cis-[PtI₂(NH₃)₂] (bottom) species. Green color – negative ESP, blue color – positive ESP.

It is clear that the organic halide has an expressed negative electron belt and deep positive σ-hole. In contrast, the ESP of the platinum-bound iodides is entirely negative, whereas the σ-hole is “positive” only relatively to the electron belt area rather than in its absolute value. Fig. 3 (bottom) illustrates the R–X⋯X–[M] bonding with particular emphasis on the possibility of deviation from linearity due to the flotation of X–[M] shown in Fig. 3 by the semitransparent species. Hence, the linearity of the R–X⋯X–[M] angle is not a univocal criterion for verification of the attractive XB interaction.

All these considerations point out to the need of certain theoretical calculations for reliable identification of non-covalent R–X⋯X–[M] interactions. In this work, we follow this approach for verification of XBs, viz. we applied the vdW IUPAC criterion for identification of possible halogen⋯halogen interactions, whereupon we conducted theoretical calculations irrespectively of the applicability of the angle IUPAC criterion.

XRD structure of the diiodomethane solvate featuring mixed XB/HB bonding

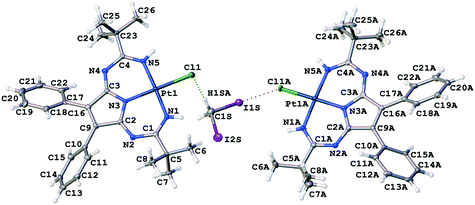
Complex 1 was prepared as previously reported³⁰via the metal-mediated coupling of two nitrile ligands in trans-[PtCl₂(NC^tBu)₂] and 2,3-diphenylmaleimidine. Crystals of 1·½CH₂I₂ were obtained by slow evaporation of a solution of 1 in CH₂I₂ in air at RT. The crystallographic data and processing parameters for 1·½CH₂I₂ are listed in Table S2 (ESI†); the plots for the structure and selected bond lengths can be found in Fig. 6 and Table 1, respectively.

Fig. 6 View of heterotrimeric cluster (1)₂·CH₂I₂ in 1·½CH₂I₂ with the atomic numbering scheme. The H₂C(I)–I⋯Cl–Pt XB and I₂C(H)–H⋯I–Pt HB are shown by dotted lines. Hereinafter, thermal ellipsoids are drawn with 50% probability.

Table 1 Selected bond lengths in two independent molecules of 1 (Fig. 6)

Molecule with Pt1 (left)		Molecule with Pt1A (right)
Bond	Length, Å	Bond	Length, Å
Pt1–Cl1	2.3232(11)	Pt1A–Cl1A	2.3374(11)
Pt1–N1	1.967(4)	Pt1A–N1A	1.966(3)
Pt1–N3	1.948(3)	Pt1A–N3A	1.948(4)
Pt1–N5	1.969(4)	Pt1A–N5A	1.968(4)
N1–C1	1.303(5)	N1A–C1A	1.304(6)
C1–N2	1.371(6)	C1A–N2A	1.357(6)
N2–C2	1.300(6)	N2A–C2A	1.309(5)
C2–N3	1.360(5)	C2A–N3A	1.366(6)
N3–C3	1.361(6)	N3A–C3A	1.365(5)
C3–N4	1.312(6)	C3A–N4A	1.303(6)
N4–C4	1.384(5)	N4A–C4A	1.366(6)
C4–N5	1.283(6)	C4A–N5A	1.306(6)

---

Previously, we reported two solvates 1·1¼CH₂Cl₂ and 1·1⅖CH₂Br₂, which demonstrated close cell parameters and similar packing features.²² We found the same heterotetrameric clusters (1)₂·(CH₂X₂)₂ (X = Cl, Br) held by two simultaneous H₂C(X)–X⋯Cl–Pt XBs and X₂C(H)–H⋯I–Pt HBs. These two clusters demonstrate the isostructural CH₂Cl₂/CH₂Br₂ exchange. Therefore, the next logical step was an attempt to use diiodomethane as a solvent and either an XB or a mixed XB/HB donor. The CH₂I₂ solvate, 1·½CH₂I₂, however, exhibits another packing type different from those of 1·1¼CH₂Cl₂ and 1·1⅖CH₂Br₂, but some similarities with the dichloromethane and dibromomethane solvates can be detected even in this case (for details, see Fig. S1 in the ESI†).

In 1·½CH₂I₂, isolated heterotrimeric clusters (1)₂·(CH₂I₂) (Fig. 6) are formed from two complex molecules and one solvent molecule linked together by the H₂C(I)–I⋯Cl–Pt XB and I₂C(H)–H⋯Cl–Pt HB. The corresponding parameters of both types of weak interactions are in accordance with the IUPAC definitions for XB¹ and HB.⁵¹ The I1S⋯Cl1A distance is less than Rowland's⁵²R_vdW(I) + R_vdW(Cl) sum [3.4071(12) vs. 3.79 Å]. The ∠(C1S–I1S⋯Cl1A) angle [173.11(13)°] is close to 180°, whereas the ∠(I1S⋯Cl1A–Pt1A) angle [108.83(4)°] is around 90°. All these mean that this interaction can be assigned to type II halogen⋯halogen contact, which is specific for XB.⁵¹ Theoretical calculations given in the next section fully supported our XRD-based conclusions.

The H1SA⋯Cl1 distance is less than the corresponding vdW sum (2.622 vs. 2.86 Å), and the ∠(C1S–H1SA⋯Cl1) angle (157.5°) is larger than 120°. The C1S⋯Cl1 separation is close to the corresponding vdW sum [3.538(5) vs. 3.53 Å] indicating that this HB should be treated as rather weak.

Two crystallographically independent molecules of 1 are almost the same (Table 1), and all the Pt–N bonds [1.948(4)–1.969(4) Å] as well as the C–N [1.357(6)–1.384(5) Å] and C=N [1.283(6)–1.312(6) Å] bonds in the PANT ligand are equal within 3σ. However, the Pt1A–Cl1A bond [2.3374(11) Å] in the halogen-bonded molecule is slightly longer than the Pt1–Cl1 distance [2.3232(11) Å] in the hydrogen-bonded molecule.

This difference can be explained by more effective electron density redistribution caused by XB than that caused by HB (Fig. 7). The same elongation on the Pt–Cl bonds was found in the previously reported trans-[PtCl₂(NCNR₂)₂] complexes linked with iodoform as an XB donor via C–I⋯Cl–Pt XBs.¹⁷

Fig. 7 The XB effect on the Pt–Cl bond length.

Halogen bond in the structure of VEMWOA

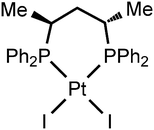
Although until now no XBs between diiodomethane and metal halide complexes have been reported, our inspection of the CCDC database verified the H₂C(I)–I⋯I–Pt XBs in the structure of VEMWOA,⁵³ which represents the platinum(II) associate [PtI₂{S,S-P̲(Ph)₂CH(Me)CH₂CH(Me)P̲Ph₂}]·⅓MeCN·⅓CH₂I₂ (2·⅓MeCN·⅓CH₂I₂) (Fig. 8).

Fig. 8 Graphical representation of the complex in 2·⅓MeCN·⅓CH₂I₂.

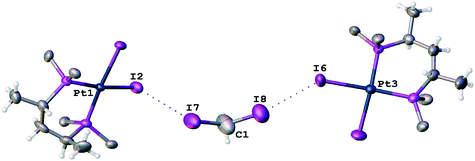
In the corresponding work,⁵³ it was pointed out that no anomalous van der Waals contacts were observed in 2·⅓MeCN·⅓CH₂I₂. By contrast, our inspection of this structure allows the identification of at least two H₂C(I)–I⋯I–Pt short contacts (Fig. 9; d(I8⋯I6) = 3.5865(11) Å, d(I7⋯I2) = 3.6501(12) Å), which are substantially less than the vdW sum⁵² (2R_vdW(I) = 4.06 Å).

Fig. 9 View of the H₂C(I)–I⋯I–Pt short contacts in VEMWOA. Phenyl rings are omitted for clarity.

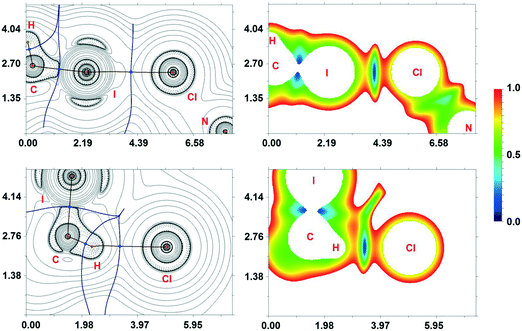
The I8⋯I6 contact should be treated as a type II inter-halogen interaction.⁴⁸ This can be attributed to the typical XB because the angle values around these atoms [159.0(4)° around I8 and 136.24(3)° around I6] fulfill the IUPAC criteria¹ and the difference between these two angles is more than 20°. However, the type of the second I7⋯I2 contact is not clear. The very similar angle values around the iodine atoms [153.2(4)° around I7 and 144.56(3)° around I2] led to the idea that this contact could be assigned to type I halogen⋯halogen contact caused by the crystal packing. We decided to clarify the nature of the I7⋯I2 contact by ESP distribution at 2, calculated and analyzed at the M06/DZP-DKH level of theory in the Multiwfn program.⁴² In 2, the surface maxima with the negative absolute value of V_S(r)_max (−18 kcal mol⁻¹) corresponding to “nominal σ-holes” (see above) were found on the iodine ligands (Fig. 10). The value of the I⋯I–Pt angle is acceptable for treatment of the iodide ligand as the nucleophilic partner in the non-covalent interaction. Taking into account the σ-hole on the diiodomethane I atom (Fig. 10, 23.1 kcal mol⁻¹), the C–I⋯I–Pt contact also belongs to XB in agreement with the IUPAC definition.¹

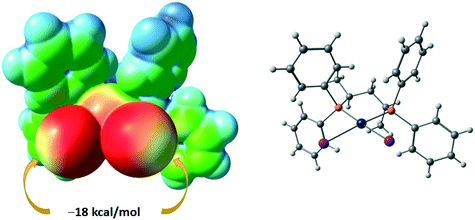Fig. 10 ESP distribution in 2 from the structure VEMWOA. Red color – negative ESP, blue color – positive ESP.

Theoretical consideration of XB in the diiodomethane solvates

The H₂C(I)–I⋯Cl–Pt XB and I₂C(H)–H⋯Cl–Pt HB were found in the crystal structure of 1·½CH₂I₂ through the single-crystal XRD experiment. As always in such cases, in addition to the structural analysis, a detailed computational study directed toward understanding the nature of these non-covalent interactions is desirable. This study is particularly important when metal-bound halides are involved in XB (see above).

In order to confirm or deny the hypothesis on the existence of these weak contacts in the solid state and to quantify their energies from a theoretical viewpoint, we carried out DFT calculations and performed topological analysis of the electron density distribution within the formalism of Bader's theory (QTAIM method)⁵⁴ for the (1)₂·(CH₂I₂) heterotrimeric cluster as a model system (Table 2). This approach has already been successfully used by our group in studies of different non-covalent interactions (e.g., hydrogen, halogen and chalcogen bonding, metallophilic interactions, stacking) and properties of coordination bonds in various transition metal complexes.^{17,22,55–61} The contour line diagrams of the Laplacian distribution ∇²ρ(r), bond paths, and selected zero-flux surfaces for intermolecular H⋯Cl HBs and I⋯Cl XBs are shown in Fig. 11. To visualize the studied non-covalent interactions, reduced density gradient (RDG) analysis⁶² was carried out, and RDG isosurfaces were plotted (Fig. 11).

Table 2 Values of the density of all electrons – ρ(r), Laplacian of electron density – ∇²ρ(r), energy density – H_b, potential energy density – V(r), and Lagrangian kinetic energy – G(r) (Hartree) at the bond critical points (3, −1), corresponding to intermolecular H⋯Cl HBs and I⋯Cl XBs in (1)₂·(CH₂I₂), bond lengths – l (Å), as well as energies for these contacts E_int (kcal mol⁻¹), defined by two approaches

Contact	ρ(r)	∇ ^2 ρ(r)	H b	V(r)	G(r)	E int	E int	l
a E int = −V(r)/2.^63 b E int = 0.429G(r).^64
H⋯Cl	0.011	0.037	0.001	−0.007	0.008	2.2	2.2	2.622
I⋯Cl	0.012	0.038	0.001	−0.008	0.009	2.5	2.4	3.407

---

Fig. 11 Contour line diagrams of the Laplacian distribution ∇²ρ(r), bond paths and selected zero-flux surfaces (left) and RDG isosurfaces referring to the non-covalent interactions (right) for the intermolecular H⋯Cl HBs and I⋯Cl XBs in (1)₂·(CH₂I₂). Bond critical points (3, −1) are shown in blue, while nuclear critical points (3, −3) are shown in pale brown. Length units – Å, RDG isosurface values are given in Hartree.

The same procedure was performed for cluster (2)₂·(CH₂I₂) from VEMWOA to study the intermolecular XBs in this system (Table S1, Fig. S2†).

The QTAIM analysis demonstrates the presence of appropriate bond critical points (BCPs; 3, −1) for the intermolecular H⋯Cl HBs and I⋯Cl XBs in (1)₂·(CH₂I₂) and the I⋯I XBs in (2)₂·(CH₂I₂). The low magnitude of the electron density (0.011–0.013 Hartrees), positive values of the Laplacian (0.037–0.041 Hartrees), and close-to-zero positive energy density (0.001 Hartrees) in these BCPs are typical for both HB and XB.^17,22,65,66 We have defined energies for these contacts according to the procedures proposed by Espinosa et al.⁶³ and Vener et al.⁶⁴ (Tables 2 and S1†) and one can state that the strength of these non-covalent interactions (2.2–2.8 kcal mol⁻¹) is comparable with those of weak hydrogen bonds following the classification of Jeffrey (“strong”: 40–15 kcal mol⁻¹, “moderate”: 15–4 kcal mol⁻¹, “weak”: <4 kcal mol⁻¹).⁶⁷ The balance between the Lagrangian kinetic energy G(r) and potential energy density V(r) at the BCPs (3, −1) reveals the nature of these interactions. If the ratio −G(r)/V(r) > 1 is satisfied, then the nature of the appropriate interaction is purely non-covalent, whereas in the case of −G(r)/V(r) < 1, some covalent component takes place.⁶⁸ Based on this criterion, we came to the conclusion that the covalent contribution is absent for intermolecular H⋯Cl HBs and I⋯Cl XBs in (1)₂·(CH₂I₂) and I⋯I XBs in (2)₂·(CH₂I₂). We additionally evaluated the magnitude of intermolecular interaction energies for HBs and XBs in (1)₂·(CH₂I₂) and (2)₂·(CH₂I₂) by the supermolecule method (E_int = E_AB − E_A − E_B, i.e. the total electronic energy of the complex subtracting the energies of the monomers) using the crystallographic coordinates. The obtained values of intermolecular interaction energies (E_int(H⋯Cl) = 6.7 kcal mol⁻¹, E_int(I⋯Cl) = 5.9 kcal mol⁻¹, E_int(I⋯I) = 2.1–3.6 kcal mol⁻¹) are higher than (for (1)₂·(CH₂I₂)) or comparable to (for (2)₂·(CH₂I₂)) those from QTAIM analysis. Thus, the QTAIM approach gives underestimated values of interaction energies for electrostatically favored HB and XB interactions.

Hirshfeld surface analysis of the crystal structures of 1·½CH₂I₂ and VEMWOA

The molecular Hirshfeld surface represents an area where molecules come into contact and its analysis gives the possibility of an additional insight into the nature of intermolecular interactions in the crystal state. For visualization, we have used a mapping of the normalized contact distance (d_norm); its negative value enables identification of molecular regions of substantial importance for detection of short contacts.

Fig. 12A depicts the Hirshfeld surface of the CH₂I₂ molecule in the solvate (1)₂·(CH₂I₂). In the Hirshfeld surface of CH₂I₂, the regions of intermolecular H⋯Cl and I⋯Cl contacts, visualized by large red circle areas, are seen near the hydrogen and iodine atoms, respectively. The following intermolecular contacts give the largest contributions to the Hirshfeld surface of CH₂I₂ in the solvate (1)₂·(CH₂I₂): I–H 66.9%, H–H 22.5%, Cl–H 3.4%, I–Cl 3.3%, H–C 2.2%; contributions of other intermolecular contacts are less than 1%.

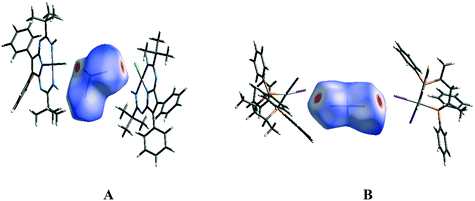Fig. 12 The Hirshfeld surfaces of the CH₂I₂ molecule in the solvates (1)₂·(CH₂I₂) (A) and VEMWOA (B) with the colored scale, which corresponds to values ranging from −0.2 Å (red) to 1.5 Å (blue).

Fig. 12B depicts the Hirshfeld surface of the CH₂I₂ molecule in VEMWOA. In the Hirshfeld surface of CH₂I₂, the regions of intermolecular I⋯I contacts, visualized by large red circle areas, are seen near the iodine atoms. The following intermolecular contacts give the largest contributions to the Hirshfeld surface of CH₂I₂: H–I 54.1%, H–H 20.8%, I–I 9.1%, C–H 7.9%, C–I 6.4%; contributions of other intermolecular contacts are less than 1%.

The Hirshfeld surface fingerprint plots (Fig. S2 and S3†) were generated using d_i (distance from the surface to the nearest atom in the molecule itself) and d_e (distance from the surface to the nearest atom in another molecule) as a pair of coordinates for each individual surface spot resulting in two-dimensional histograms. A color gradient in the plots ranging from blue to red represents the proportional contribution of contact pairs in the global surface.

Thus, the Hirshfeld surface analyses of 1·½CH₂I₂ and VEMWOA confirm that in the crystalline state CH₂I₂ behaves as an XB and HB donor.

Concluding remarks

In this work, we used multidisciplinary combined and complementary experimental and theoretical approaches that allow bypassing certain limitations of the XRD method in the studies of halogen bond systems. In particular, we succeeded in overcoming difficulties associated with the deviation from linearity of R–X⋯X–[M] linkage insofar as this deviation complicates the experimental identification of XBs in organic halide⋯metal-bound halide systems.

We found that a weak XB donor such as diiodomethane can still form a halogen bond with metal-bound halides and CH₂I₂ can serve as either an XB or a mixed XB/HB donor. All these non-covalent interactions in 1·½CH₂I₂ and VEMWOA were confirmed by Hirshfeld surface analysis, and their nature was investigated by DFT calculations and topological analysis of the electron density distribution within the formalism of Bader's theory (QTAIM method). The evaluated energies of the HBs (2.2 kcal mol⁻¹) and XBs (2.4–2.8 kcal mol⁻¹) again indicate their non-covalent character.

The results reported in this work can be used as a starting point for further studies of XBs in dihalomethane solutions, where they may be sufficiently strong to contribute, along with HBs, to the overall solvation. It is expected that all these findings can find an application in crystal engineering because they expand the arsenal of supramolecular organizations which may be useful for solvent storage⁶⁹ or separation⁷⁰ and also in physical chemistry as they contribute to the understanding of solvation with halomethanes. We hope that our results open up an avenue to the generation of other diiodomethane associates and studies in this direction are underway in our group.

Acknowledgements

The experimental part of this work was conducted in the framework of the Russian Science Foundation project (14-13-00060), whereas the theoretical part was performed under the Russian Foundation for Basic Research grant (16-33-00212). XRD studies were performed at the Center for X-ray Diffraction Studies of Saint Petersburg State University. The authors declare no competing financial interests.

References

1. G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713.
2. G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601.
3. L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Chem. Rev., 2015, 115, 7118–7195.
4. H. Wang, W. Z. Wang and W. J. Jin, Chem. Rev., 2016, 116, 5072–5104.
5. A. Mukherjee, S. Tothadi and G. R. Desiraju, Acc. Chem. Res., 2014, 47, 2514–2524.
6. K. B. Landenberger, O. Bolton and A. J. Matzger, J. Am. Chem. Soc., 2015, 137, 5074–5079.
7. V. V. Sivchik, A. I. Solomatina, Y.-T. Chen, A. J. Karttunen, S. P. Tunik, P.-T. Chou and I. O. Koshevoy, Angew. Chem., Int. Ed., 2015, 54, 14057–14060.
8. D. Bulfield and S. M. Huber, Chem. – Eur. J., 2016, 22, 14434–14450.
9. P. S. Ho, in Halogen Bonding I: Impact on Materials Chemistry and Life Sciences, Springer-Verlag Berlin, Berlin, 2014, pp. 241–276.
10. G. Cavallo, S. Biella, J. A. Lu, P. Metrangolo, T. Pilati, G. Resnati and G. Terraneo, J. Fluorine Chem., 2010, 131, 1165–1172.
11. S. V. Rosokha, I. S. Neretin, T. Y. Rosokha, J. Hecht and J. K. Kochi, Heteroat. Chem., 2006, 17, 449–459.
12. S. V. Rosokha, C. L. Stern and J. T. Ritzert, Chem. – Eur. J., 2013, 19, 8774–8788.
13. S. V. Lindeman, J. Hecht and J. K. Kochi, J. Am. Chem. Soc., 2003, 125, 11597–11606.
14. H. Bock and S. Holl, Z. Naturforsch., B: J. Chem. Sci., 2001, 56, 152–163.
15. H. G. Lohr, A. Engel, H. P. Josel, F. Vogtle, W. Schuh and H. Puff, J. Organomet. Chem., 1984, 49, 1621–1627.
16. P. V. Gushchin, G. L. Starova, M. Haukka, M. L. Kuznetsov, I. L. Eremenko and V. Y. Kukushkin, Cryst. Growth Des., 2010, 10, 4839–4846.
17. D. M. Ivanov, A. S. Novikov, I. V. Ananyev, Y. V. Kirina and V. Yu. Kukushkin, Chem. Commun., 2016, 52, 5565–5568.
18. S. V. Rosokha, J. Lu, T. Y. Rosokha and J. K. Kochi, Chem. Commun., 2007, 3383–3385.
19. S. V. Rosokha, C. L. Stern, A. Swartz and R. Stewart, Phys. Chem. Chem. Phys., 2014, 16, 12968–12979.
20. S. V. Rosokha and M. K. Vinakos, Cryst. Growth Des., 2012, 12, 4149–4156.
21. A. M. Afanasenko, M. S. Avdontceva, A. S. Novikov and T. G. Chulkova, Z. Kristallogr. - Cryst. Mater., 2016, 231, 435–440.
22. D. M. Ivanov, A. S. Novikov, G. L. Starova, M. Haukka and V. Y. Kukushkin, CrystEngComm, 2016, 18, 5278–5286.
23. W.-W. du Mont, V. Stenzel, J. Jeske, P. G. Jones, A. Sebald, S. Pohl, W. Saak and M. Baetcher, Inorg. Chem., 1994, 33, 1502–1505.
24. D. M. Ivanov, M. A. Kinzhalov, A. S. Novikov, I. V. Ananyev, A. A. Romanova, V. P. Boyarskiy, M. Haukka and V. Y. Kukushkin, Cryst. Growth Des., 2017, 17, 1353–1362.
25. F. M. A. Noa, S. A. Bourne and L. R. Nassimbeni, Cryst. Growth Des., 2015, 15, 3271–3279.
26. M. Podsiadlo and A. Katrusiak, CrystEngComm, 2008, 10, 1436–1442.
27. M. Podsiadlo, K. Dziubek, M. Szafranski and A. Katrusiak, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 1090–1098.
28. M. Podsiadlo and A. Katrusiak, J. Phys. Chem. B, 2008, 112, 5355–5362.
29. U. Geiser, S. K. Kumar, B. M. Savall, S. S. Harried, K. D. Carlson, P. R. Mobley, H. H. Wang, J. M. Williams, R. E. Botto, W. Liang and M. H. Whangbo, Chem. Mater., 1992, 4, 1077–1082.
30. D. M. Ivanov, P. V. Gushchin, A. S. Novikov, M. S. Avdontceva, A. A. Zolotarev, G. L. Starova, Y.-T. Chen, S.-H. Liu, P.-T. Chou and V. Yu. Kukushkin, Eur. J. Inorg. Chem., 2016, 2016, 1480–1487.
31. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.
32. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
33. CrysAlisPro, Agilent Technologies Ltd., Version 1.171.136.120 (release 127–106-2012).
34. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
35. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, in Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford, CT, 2010.
36. C. L. Barros, P. J. P. de Oliveira, F. E. Jorge, A. C. Neto and M. Campos, Mol. Phys., 2010, 108, 1965–1972.
37. F. E. Jorge, A. C. Neto, G. G. Camiletti and S. F. Machado, J. Chem. Phys., 2009, 130, 6.
38. A. C. Neto and F. E. Jorge, Chem. Phys. Lett., 2013, 582, 158–162.
39. C. L. Barros, P. J. P. de Oliveira, F. E. Jorge, A. C. Neto and M. Campos, Mol. Phys., 2010, 108, 1965–1972.
40. R. C. de Berredo and F. E. Jorge, J. Mol. Struct.: THEOCHEM, 2010, 961, 107–112.
41. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990.
42. T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592.
43. http://www.chemcraftprog.com.
44. S. K. Wolff, D. J. Grimwood, J. J. McKinnon, M. J. Turner, D. Jayatilaka and M. A. Spackman, CrystalExplorer (Version 3.1), University of Western Australia, 2012.
45. M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32.
46. J. J. McKinnon, D. Jayatilaka and M. A. Spackman, Chem. Commun., 2007, 3814–3816.
47. A. Bondi, J. Phys. Chem., 1964, 68, 441–451.
48. P. Metrangolo and G. Resnati, IUCrJ, 2014, 1, 5–7.
49. K. Rissanen, CrystEngComm, 2008, 10, 1107–1113.
50. L. Brammer, E. A. Bruton and P. Sherwood, Cryst. Growth Des., 2001, 1, 277–290.
51. E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenberg, P. Hobza, H. G. Kjaergaard, A. C. Legon, B. Mennucci and D. J. Nesbitt, Pure Appl. Chem., 2011, 83, 1637–1641.
52. R. S. Rowland and R. Taylor, J. Phys. Chem., 1996, 100, 7384–7391.
53. L. Jánosi, L. Kollár, P. Macchi and A. Sironi, J. Organomet. Chem., 2006, 691, 2846–2852.
54. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
55. A. S. Novikov, M. L. Kuznetsov and A. J. L. Pombeiro, Chem. – Eur. J., 2013, 19, 2874–2888.
56. V. N. Mikhaylov, V. N. Sorokoumov, K. A. Korvinson, A. S. Novikov and I. A. Balova, Organometallics, 2016, 35, 1684–1697.
57. T. V. Serebryanskaya, A. S. Novikov, P. V. Gushchin, M. Haukka, R. E. Asfin, P. M. Tolstoy and V. Yu. Kukushkin, Phys. Chem. Chem. Phys., 2016, 18, 14104–14112.
58. E. Andrusenko, E. Kabin, A. S. Novikov, N. A. Bokach, G. L. Starova and V. Yu Kukushkin, New J. Chem., 2017, 41, 316–325.
59. X. Ding, M. J. Tuikka, P. Hirva, V. Yu. Kukushkin, A. S. Novikov and M. Haukka, CrystEngComm, 2016, 18, 1987–1995.
60. E. S. Yandanova, D. M. Ivanov, M. L. Kuznetsov, A. G. Starikov, G. L. Starova and V. Yu Kukushkin, Cryst. Growth Des., 2016, 16, 2979–2987.
61. A. S. Mikherdov, M. A. Kinzhalov, A. S. Novikov, V. P. Boyarskiy, I. A. Boyarskaya, D. V. Dar'in, G. L. Starova and V. Yu Kukushkin, J. Am. Chem. Soc., 2016, 138, 14129–14137.
62. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
63. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173.
64. M. V. Vener, A. N. Egorova, A. V. Churakov and V. G. Tsirelson, J. Comput. Chem., 2012, 33, 2303–2309.
65. I. Rozas, I. Alkorta and J. Elguero, J. Phys. Chem. A, 1998, 102, 9925–9932.
66. I. Rozas, I. Alkorta and J. Elguero, J. Am. Chem. Soc., 2000, 122, 11154–11161.
67. T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76.
68. E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542.
69. C. B. Aakeröy, T. K. Wijethunga, J. Benton and J. Desper, Chem. Commun., 2015, 51, 2425–2428.
70. X. Q. Yan, Q. J. Shen, X. R. Zhao, H. Y. Gao, X. Pang and W. J. Jin, Anal. Chim. Acta, 2012, 753, 48–56.

---

Footnote

† Electronic supplementary information (ESI) available: Crystal data and structure refinement data. Cartesian atomic coordinates of model clusters. CCDC 1532142. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7ce00346c

---