Shaping particles by chemical diffusion and reaction

Abstract

Here, we report a general role of chemical diffusion and reaction in shaping particles. It is supposed that chemical diffusion and reaction play a role in shaping particles by changing the chemical distribution around the growth front of particles. Based on this understanding, three growth modes of particles are proposed in this paper, namely, reaction-limited mode, diffusion-limited mode, and reaction–diffusion balance mode. Silver particles are synthesized in different growth modes by various methods. No matter which method is employed, silver particles synthesized in the same mode have similar morphologies. To further generalize diffusion and reaction effects, copper and gold particles are synthesized. The morphological evolution of these two types of particles is similar to that of silver. These results indicate the general role of chemical diffusion and reaction in shaping particles, promising that a regulation on these two kinetic factors is a green and powerful technique for rational synthesis of materials.

---

1. Introduction

Rational synthesis of materials is a long-term dream of scientists and engineers, which attracts great attention in the communities of materials science, chemistry and physics,^1–4 since the functions and properties of materials are strongly dependent on their structures and morphologies. The equilibrium structures of materials are well described by thermodynamics, while the kinetic ones are difficult to predict, since the kinetic structures normally have the features of diversity, complexity, hierarchy and polymorphism.^5–11 One of the amazing kinetic structures is the dendritic structure which combines mathematic, aesthetic, and practical values due to its unique fractal morphology. Dendritic structures exhibit excellent performances in catalysis,¹² optics,¹³ magnetism,¹⁴ optoelectronics¹⁵ and sensors.¹⁶ Our previous work has specially reported that the dendritic particles present a remarkable surface enhanced Raman scattering (SERS) activity with a nearly 8 × 10⁴ times enhancement for Rhodamine 6G detection, due to their large surface areas and abundant “hot spots” from the gaps formed by the junctions of dendrites.¹⁷ The superhydrophobicity of a surface with silver dendritic structures was investigated and a maximal contact angle of 150.9° was achieved as a result of the porous and rough nature of dendritic morphologies.¹⁸

Different growth mechanisms have been proposed for the formation of dendritic structures, including the diffusion-limited aggregation model (DLA),¹⁹ interfacial wave theory,²⁰ vortex theory,^21,22 maximum entropy production principle (MEPP),²³ and Mullins–Sekerka (MS) instability theory.^24,25 Some of these models work well for certain cases, but the generality is still lacking so that a universal protocol for controllable synthesis of dendritic structures is highly desired. Unlike traditional ways using surfactants or templates to obtain particular structures, we put forward the strategy of shaping particles by controlling chemical diffusion and reaction rates. These two kinetic factors are generally involved in the bottom-up synthesis of materials, which refers to: (1) chemicals transport in the medium; (2) monomers meet and react to contribute to the growth of materials, respectively.²⁶ By adjusting the reaction and diffusion rates of chemicals, different shapes of calcium carbonates were synthesized.^27–29 Under conditions of quick reaction and diffusion limitation, snowflake-like calcium carbonate particles were synthesized for the first time.²⁷ By changing the diffusion of reactive ions, platinum particles switch from polyhedral shapes to porous dendritic spheres.³⁰ In the synthesis of silver particles, silver dendrites were largely formed in a specific reaction–diffusion range, which is independent of the preparation methods.^17,31,32 These studies confirmed the significance of chemical diffusion and reaction in shaping particles. However, our understanding on the mechanism of diffusion and reaction is still limited, which prevents the transfer of this new technique to other materials.

In our previous studies, we speculated that chemical diffusion and reaction determines the chemical distribution around the growth front of particles, which is the way in which chemical diffusion and reaction influence the shape development of particles. Based on this understanding, we proposed three growth modes of particles in this paper, namely, reaction limited mode, diffusion limited mode and balance mode of diffusion and reaction. Two different methods, namely, electrodeposition and solution-based reduction, are employed to synthesize silver particles. No matter which method is employed, similar morphologies of particles are obtained in the same growth mode. To further generalize the role of diffusion and reaction, copper and gold particles are also synthesized in different diffusion–reaction modes. The morphology evolution of these two particles is similar to that of silver, which indicates the general role of diffusion and reaction in shaping metal particles.

2. Experimental section

2.1 Chemicals

Silver nitrate (AgNO₃), potassium nitrate (KNO₃), sodium sulfate (Na₂SO₄), sodium chloride (NaCl), hydroxylamine (NH₂OH) and glycine (NH₂–CH₂–COOH) were obtained from Xilong Chemical Company. Sodium tetrachloroaurate dihydrate (NaAuCl₄·2H₂O) was provided by Aladdin Industrial Inc. Cupric sulfate pentahydrate (CuSO₄·5H₂O), n-propanol, glycine and glycerol were bought from Sigma-Aldrich. Indium tin oxide coated polyethylene terephthalate (ITO-PET) substrates, with a thickness of 0.127 mm (5 mil) and a surface resistivity of 60 Ω sq⁻¹, were also purchased from Sigma-Aldrich. All chemicals were of analytical grade and used without further purification. Deionized water from a Millipore system has a resistivity higher than 18 MΩ cm.

2.2 Synthesis of silver particles via solution-based reduction

The procedure for preparing silver particles is similar to ref. 17. In a typical experiment, 2 mL of silver nitrate (100 mM) and a defined amount of glycine were dissolved in 40 ml of glycerol–water solution followed by stirring for 10 minutes. Then a defined amount of hydroxylamine solution (200 mM) was added into the above mixture to initiate the reduction. The amounts of glycine and hydroxylamine were dependent on the reaction rate designed. The reduction lasted for 30 minutes in a water bath at 25 °C. To regulate the reduction rate, the concentrations of hydroxylamine and glycine were altered. To regulate the diffusion rate of chemicals, the volume ratios of glycerol (and later propanol) were changed and sonication was employed.

2.3 Synthesis of silver particles via electrochemical deposition

The procedure for preparing silver particles is similar to ref. 33. Electrochemical deposition was performed on an ITO-PET working electrode. Each ITO-PET substrate was cut into a 5 cm × 2 cm rectangle and immersed 2 cm deep into the electrolyte, i.e. an effective area of 4 cm². “Current-time” mode was used to achieve potentiostatic deposition (or constant-potential deposition) of silver, copper and gold particles. Different potentials (E_app) (vs. SCE) were applied on the working electrode to obtain various morphologies. Pulsed-potential deposition of silver was implemented using “differential pulse amperometry”. The pause-to-pulse ratio was fixed at 1, and the pulse time was set as 5, 0.5, and 0.05 s successively, i.e. the pulse frequency was 0.1, 1, and 10 Hz, respectively. The total time of each pulsed deposition was 1600 s. A potential of 0.3 V (vs. SCE) rather than an open circuit replaces the pause period to eliminate the anodic current as far as possible, when the potential was stopped.^34,35 Finally, the samples were dried in air.

2.4 Characterization on silver particles

The morphologies of silver products synthesized were characterized using a JSM-7001F thermal field scanning electron microscope (JEOL, Japan). Solution-reduction samples for SEM imaging were prepared by pipetting the product suspension onto an organic filter membrane. And samples from electrodeposition were characterized directly. The viscosity of the alcohol–water system was measured using a DMA5000-AMVn automatic falling ball viscometer (Anton Paar).

3. Results and discussion

Based on the difference in diffusion and reaction conditions, three growth modes of particles are proposed and the particle morphologies formed in each mode are shown in Fig. 1. In the case of slow reaction, the mass transport by diffusion is sufficient and the nucleus is fully surrounded by the bulk solution, as illustrated in Fig. 1a. Under this mode, the growth of particles is expected to follow a classic crystallization process via monomer deposition on the surface of the nuclei, forming thermodynamically favored structures. Since the reaction rate is limited, the particles grow slowly. When the nuclei have a chance to collide during crystallization, aggregation of these nuclei would occur to reduce the total surface energy. If the reaction is improved and the consumption of chemicals exceeds the diffusive transport, diffusion limitation is reached and a concentration gradient (in which the monomer concentration on the growth front of the nuclei is lower than that in the bulk^36–38) is generated around the nucleus obviously, as shown in Fig. 1b. Under a concentration gradient, dendritic structures are easily formed as depicted by the Mullins–Sekerka (MS) instability model.^24,25,33 In this case, the diffusion and reaction play a joint role to keep the delicate balance between chemical consumption and supplement, to maintain an appropriate concentration gradient. If the reaction tremendously overwhelms the diffusion of chemicals, a sparse or blank layer is formed around the nucleus, which results in a diffusion limited condition, as shown in Fig. 1c. Under this mode, the nucleus grows slowly due to the insufficient monomer supplement. In the following, we are going to evaluate the proposed growth modes in Fig. 1.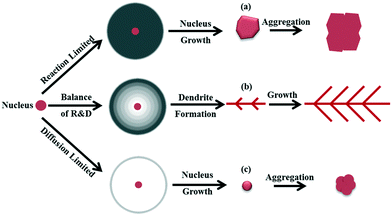

Fig. 1 Proposed growth modes (a–c) of particles under different diffusion and reaction conditions and the morphologies assumed to be formed in each growth mode.

In our previous papers,³³ the reaction–diffusion conditions have been quantitatively determined for the first time from the experimental aspect by employing the dimensionless Damköhler (Da) number, which is defined as the ratio of diffusion to reaction. Silver particles are synthesized by constant-potential electrodeposition reaction. The Da value is regulated by changing the potential applied. At the positive potential of 0.35–0.2 V, the reduction rate of silver ions is pretty small, which results in a relative large Da and a reaction limited condition, as shown in Fig. 2. Silver particles formed in this condition are big polyhedral particles with clear facets. A decrease in the potential leads to a quick decrease in the Da value, which results in diffusion limitation. At the potential of 0.1 V to −0.8 V, silver dendrites are largely formed. With a further decrease in the potential to −0.9 V and below, Da becomes extremely small, indicating a severely diffusion limited situation. Correspondingly, tiny particles are formed on the surface of the electrodes.

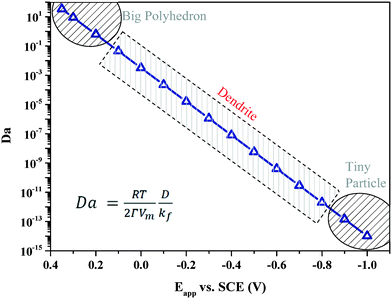Fig. 2 Silver particles synthesized at different Da values show three specific shapes. The ones synthesized at high Da values have big polyhedral shapes, while the ones at small Da values have tiny irregular shapes. In the middle range of Da values, silver dendrites are largely formed. The Da value represents the ratio of chemical diffusion (D) to reaction (k_f).³³

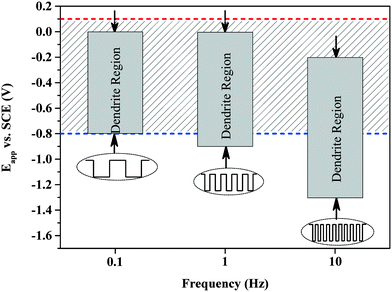
To determine the role of diffusion and reaction rates in dendritic structures, pulse potentials are employed to replace the constant potentials in the electrochemical synthesis of silver particles. Owing to the on and off modes of pulse potentials that do not favor the formation of a stable chemical concentration gradient around the growth front of particles, a quick and temporary concentration gradient can only form at a quick reaction. Therefore, with the increase in pulse frequency, a negative shift in dendritic formation range is observed, as shown in Fig. 3, which indicates that a quick reaction is necessary to establish a transitory concentration gradient in the pulse experiments.

Fig. 3 The potential range of dendrite formation in the case of pulsed-potential deposition at different frequencies (0.1, 1, 10 Hz). The hatched region between the red and blue dashed lines represents the existent range of dendrites under constant-potential deposition. The gray rectangles show that the dendrite formation regions in the pulsed-potential experiments shift to lower potentials with the increase in pulse frequencies.

To further testify the aforementioned modes, a solution-based reduction method is employed to synthesize silver particles via reduction of silver ions with hydroxylamine under continuous stirring. The reduction rate of silver ions is regulated by changing the concentration of hydroxylamine. By keeping the diffusion of silver ions unchanged, a regulation of the reduction rate is expected to switch the proposed growth modes. At very low concentration of hydroxylamine from 2.5 to 7.5 mM, irregular silver aggregates are formed, as shown in Fig. 4a. At the lowest concentration, some of the aggregates have smooth surfaces and clearly defined angles, which indicate that the growth of silver particles is dominated by thermodynamics. When the concentration of hydroxylamine is increased to 10 mM until 50 mM, silver dendrites are largely formed, as shown in Fig. 4b, which indicates that an increase in reaction rate leads to the formation of a concentration gradient around the growth front of particles. Further increasing the hydroxylamine concentration to 200 mM and above, the dendritic structures disappear while the spherical aggregates are formed, as shown in Fig. 4c, which indicates that an extremely quick reaction results in the disappearance of concentration gradient and the diffusion limited mode dominates the growth of silver particles.

Fig. 4 SEM images of silver particles synthesized in different growth modes: reaction limited (a), reaction–diffusion balance (b) and diffusion limited (c) modes, respectively. The relative magnitude of diffusion and reaction is regulated by the reaction rate via changing the reductant concentration. The scale bars represent 1 μm.

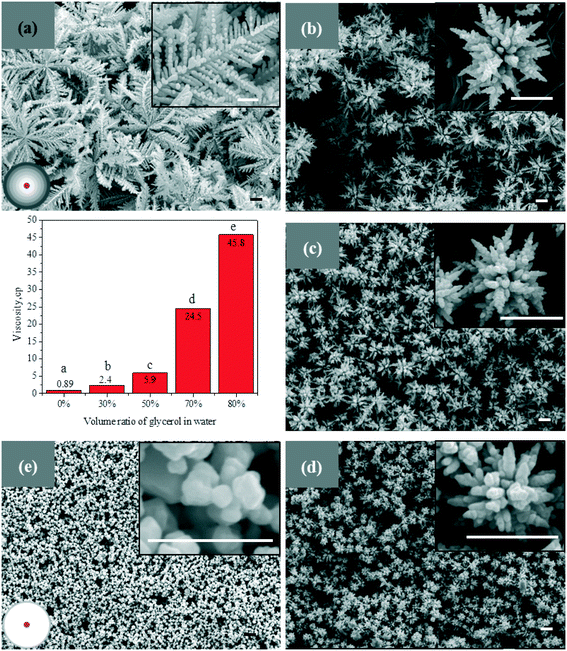
To examine the diffusion contribution on the proposed growth modes, we have synthesized silver particles at different viscosities of solvents, as the diffusion of chemicals is inversely proportional to viscosity, according to the Stokes–Einstein equation.³⁹ The solvents are composed of glycerol and water. The viscosity of solvents is regulated by changing the volume ratio of glycerol in water. Increasing the volume ratio of glycerol from 0% to 80%, the viscosity of the solvents increases from 0.89 cP to 45.8 cP, as shown by the bar graph in Fig. 5, which results in a remarkable reduction in chemical diffusion. The silver particles synthesized in each solvent are characterized by electron microscopy, as shown in Fig. 5. Leaf-like silver dendrites with a particle size of more than 10 μm are formed in a water solution without glycerol, as shown in Fig. 5a. When the volume ratio of glycerol is increased to 30%, dendritic flower-like structures are obtained, as shown in Fig. 5b. Increasing the volume ratio of glycerol to 50% or 70%, silver aggregates with predominantly dendritic structures are synthesized, as shown in Fig. 5c and d, respectively. Further increasing the volume ratio of glycerol to 80%, small crystals are largely formed, as shown in Fig. 5e. Except for the change in morphology, the size of silver particles decreases evidently with the increase in glycerol ratio. With the decrease in diffusion, the delivery of chemicals is delayed, which broadens the region of the concentration gradient, leading to a change of dendritic structures. Besides, owing to the restricted diffusion of chemicals in the viscous solution, the growth of each nucleus is limited. Therefore, small particles are formed under a diffusion limited condition, as shown in Fig. 5e. These small particles are stabilized by the high viscosity of the solvents. To further examine the diffusion contribution on the proposed modes, we employ ultrasound to improve the diffusion of silver ions in the solution. A reversible evolution trend, from small aggregates to dendrites, is also observed, as shown in Fig. S1.† Furthermore, to exclude the effect of solvent, glycerol is replaced by n-propanol to regulate the viscosity of the solution, and similar results are obtained, as shown in Fig. S2.†

Fig. 5 SEM images (a–e) of the silver particles synthesized in solvents with different viscosities (bar graph). With the increase of solvent viscosity, the dendritic particles change to small crystals as a result of the switch of growth modes from the reaction–diffusion balance mode to the diffusion limited mode. The scale bar in all images is 1 μm.

To further evaluate the general role of diffusion and reaction in shaping particles, other materials are prepared by the same electrochemical deposition method in different growth modes. First, copper particles are deposited by the constant-potential approach from the electrolytic mixture of 5 mM CuSO₄ and 100 mM Na₂SO₄ aqueous solution. Fig. 6 displays the copper morphologies synthesized under the potentials of −0.2 V to −0.9 V. Polyhedral particles are collected at −0.2 V and −0.3 V as a result of reaction limitation. Negatively shifting the applied potential, we observe ramifications on those particles, as shown in Fig. 6c and d. At −0.6 V, beautiful symmetrical dendritic structures appear, as shown in Fig. 6e. But when the potential is increased to −0.7 V, dendrites become very short and small. Only few dendritic shapes can be seen at −0.8 V, while they completely fade away at −0.9 V due to extremely limited diffusion. These results not only indicate that an increase in reaction rate leads to the formation of concentration gradient on the growth front of particles but also agree well with those obtained by the solution reduction method except that there is no obvious aggregation of small particles on the electrode at diffusion limitation. This is because the small particles adsorb on the surface of the electrode and they are not free to move and collide. Besides, gold particles are also synthesized by the same method in the potential range of 0.1 V to −1.4 V. The change in their morphologies with potentials is similar to those of copper and silver, as shown in Fig. S2,† which confirms that chemical diffusion and reaction have a general effect on shaping particles.

Fig. 6 The SEM images (a–h) of copper particles synthesized under different reaction conditions which are regulated by changing the applied potential. Dendritic structures emerge gradually and then fade away due to a switch from the reaction limited mode to the diffusion limited mode with the negative shift in the potential.

Although the change in morphologies of these three particles is similar, differences are also observed. For example, the formation regions of dendrites differ from each other, which is probably associated with their own redox standard potentials, 1.0, 0.7999, and 0.34 V (vs. NHE)⁴⁰ for AuCl₄⁻/Au, Ag⁺/Ag, and Cu²⁺/Cu, respectively. The more positive the standard electrode potential, the wider the range of dendritic formation expected. Therefore, gold has the broadest dendritic formation region while copper has the narrowest range. Moreover, small cubic crystals are formed on the surfaces of copper polyhedra due to the easy deposition on the vertical angle of the cube during secondary nucleation.⁴¹ And the surfaces of copper particles are much coarser than the other two, which may result from its higher surface energy than silver and gold,⁴² since it has been prove that a change in surface energy can convert dendritic growth to epitaxial growth.⁴³ In addition, leaf-like gold dendrites have three-fold symmetrical trunks with three groups of branches grown on the trunk, which are not observed in the other two metal systems. That is thought to be caused by preferential growth and symmetries of different crystals.⁴⁴ All the above possible reasons for morphological distinctions are supposed to be relevant to the intrinsic properties of materials. These intrinsic factors may interplay with reaction and diffusion, dominating the formation of diverse morphologies, which is expected to be discovered in the future study.

4. Conclusions

This paper indicated the general role of chemical diffusion and reaction in shaping particles. Different methods were employed to synthesize silver particles. No matter which method was employed, the reaction limitation resulted in the formation of polyhedral particles while the diffusion limitation led to the formation of small crystals. In the balance mode of diffusion and reaction, dendritic structures were largely synthesized, which were attributed to the establishment of a chemical concentration gradient around the growth front of particles. To further testify the generality of the diffusion and reaction effect, copper and gold particles were synthesized under different conditions of diffusion and reaction. The morphology evolution of these two particles with the change in diffusion and reaction is similar to that of silver particles. Therefore, the chemical distribution, which could be regulated by diffusion and reaction rates, plays an important role in the shape development of particles. Chemical distribution may collaborate or compete with other factors such as surface energy of crystals. A compromise between these factors is probably the dominant mechanism for the formation of diverse morphologies and structures of particles.

Author contribution statement

T. Yang and J. Liu conceived the experiment and contributed equally in this paper. T. Yang, J. Liu, J. Dai and Y. Han analyzed the results, and Y. Han proposed and supervised this study. All authors reviewed the manuscript.

Additional information

Competing financial interests: The authors declare no competing financial interests.

Acknowledgements

This study was supported by the Hundreds Talent Program from the Chinese Academy of Sciences and the project from the State Key Laboratory of Multiphase Complex Systems (MPCS-2014-D-05). The financial support from the National Natural Science Foundation of China (U1462130, 91534123) is warmly appreciated. Prof. Jinghai Li initiated this study and joined many discussion. We thank Prof. Helmuth Moehwald from Max Planck Institute of Colloids and Interfaces for fruitful discussions and revisions.

References

1. Y. N. Xia, Y. J. Xiong, B. Lim and S. E. Skrabalak, Shape-Controlled Synthesis of Metal Nanocrystals: Simple Chemistry Meets Complex Physics?, Angew. Chem., Int. Ed., 2009, 48, 60–103.
2. A. R. Tao, S. Habas and P. D. Yang, Shape control of colloidal metal nanocrystals, Small, 2008, 4, 310–325.
3. R. D. Braatz and S. Hasebe, Particle size and shape control in crystallization processes, AIChE Symposium Series, American Institute of Chemical Engineers, New York, 2002, pp. 307–327.
4. G. A. Somorjai and J. Y. Park, Colloid science of metal nanoparticle catalysts in 2D and 3D structures. Challenges of nucleation, growth, composition, particle shape, size control and their influence on activity and selectivity, Top. Catal., 2008, 49, 126–135.
5. E. V. Shevchenko, D. V. Talapin, N. A. Kotov, S. O'Brien and C. B. Murray, Structural diversity in binary nanoparticle superlattices, Nature, 2006, 439, 55–59.
6. S. C. Glotzer and M. J. Solomon, Anisotropy of building blocks and their assembly into complex structures, Nat. Mater., 2007, 6, 557–562.
7. L. Manna, E. C. Scher and A. P. Alivisatos, Synthesis of soluble and processable rod-, arrow-, teardrop-, and tetrapod-shaped CdSe nanocrystals, J. Am. Chem. Soc., 2000, 122, 12700–12706.
8. M. A. Snyder and M. Tsapatsis, Hierarchical nanomanufacturing: from shaped zeolite nanoparticles to high-performance separation membranes, Angew. Chem., Int. Ed., 2007, 46, 7560–7573.
9. L. Zhang, H. B. Wu, S. Madhavi, H. H. Hng and X. W. Lou, Formation of Fe₂O₃ microboxes with hierarchical shell structures from metal–organic frameworks and their lithium storage properties, J. Am. Chem. Soc., 2012, 134, 17388–17391.
10. A. Stein, F. Li and N. R. Denny, Morphological control in colloidal crystal templating of inverse opals, hierarchical structures, and shaped particles, Chem. Mater., 2008, 20, 649–666.
11. K. J. Kim and M. F. Doherty, Crystallization of selective polymorph using relationship between supersaturation and solubility, AIChE J., 2015, 61, 1372–1379.
12. F. Yang, K. Cheng, T. H. Wu, Y. Zhang, J. L. Yin, G. L. Wang and D. X. Cao, Dendritic palladium decorated with gold by potential pulse electrodeposition: enhanced electrocatalytic activity for H₂O₂ electroreduction and electrooxidation, Electrochim. Acta, 2013, 99, 54–61.
13. B. Q. Liu, X. P. Zhao, W. R. Zhu, W. Luo and X. C. Cheng, Multiple pass-band optical left-handed metamaterials based on random dendritic cells, Adv. Funct. Mater., 2008, 18, 3523–3528.
14. M. H. Cao, T. F. Liu, S. Gao, G. B. Sun, X. L. Wu, C. W. Hu and Z. L. Wang, Single-crystal dendritic micro-pines of magnetic α-Fe₂O₃: large-scale synthesis, formation mechanism, and properties, Angew. Chem., Int. Ed., 2005, 44, 4197–4201.
15. Q. T. Pan, K. Huang, S. B. Ni, Q. Wang, F. Yang and D. Y. He, Fabrication and photoluminescence properties of large-scale hierarchical CdS dendrites, Mater. Lett., 2007, 61, 4773–4776.
16. H. J. Yin, Z. Y. Chen, Y. M. Zhao, M. Y. Lv, C. A. Shi, Z. L. Wu, X. Zhang, L. Liu, M. L. Wang and H. J. Xu, Ag@Au core-shell dendrites: a stable, reusable and sensitive surface enhanced Raman scattering substrate, Sci. Rep., 2015, 5, 14502.
17. J. M. Liu, T. Yang, C. X. Li, J. H. Dai and Y. S. Han, Reversibly switching silver hierarchical structures via reaction kinetics, Sci. Rep., 2015, 5, 14942.
18. P. Che, W. Liu, X. X. Chang, A. H. Wang and Y. S. Han, Multifunctional silver film with superhydrophobic and antibacterial properties, Nano Res., 2015, 9, 442–450.
19. T. A. Witten and L. M. Sander, Diffusion-limited aggregation, a kinetic critical phenomenon, Phys. Rev. Lett., 1981, 47, 1400–1403.
20. J. J. Xu, Interfacial wave theory of pattern formation: selection of dendrite growth and viscous fingering in a Hele–Shaw flow, Springer Verlag, Berlin, Heidelberg, 1998.
21. V. Fleury, J.-N. Chazalviel and M. Rosso, Theory and experimental evidence of electroconvection around electrochemical deposits, Phys. Rev. Lett., 1992, 68, 2492–2495.
22. V. Fleury, J. H. Kaufman and D. B. Hibbert, Mechanism of a morphology transition in ramified electrochemical growth, Nature, 1994, 367, 435–438.
23. L. M. Martyushev and V. D. Seleznev, Maximum entropy production principle in physics, chemistry and biology, Phys. Rep., 2006, 426, 1–45.
24. W. W. Mullins and R. F. Sekerka, Morphological stability of a particle growing by diffusion or heat flow, J. Appl. Phys., 1963, 34, 323–329.
25. A. V. Avizienis, C. Martin-Olmos, H. O. Sillin, M. Aono, J. K. Gimzewski and A. Z. Stieg, Morphological transitions from dendrites to nanowires in the electroless deposition of silver, Cryst. Growth Des., 2013, 13, 465–469.
26. N. T. K. Thanh, N. Maclean and S. Mahiddine, Mechanisms of nucleation and growth of nanoparticles in solution, Chem. Rev., 2014, 114, 7610–7630.
27. H. Wang, Y. S. Han and J. H. Li, Dominant role of compromise between diffusion and reaction in the formation of snow-shaped vaterite, Cryst. Growth Des., 2013, 13, 1820–1825.
28. H. Wang, W. L. Huang and Y. S. Han, Diffusion–reaction compromise the polymorphs of precipitated calcium carbonate, Particuology, 2013, 11, 301–308.
29. H. Wang and Y. S. Han, A compromise between competing forces dominating the diversity of aragonite structures, CrystEngComm, 2014, 16, 1971–1977.
30. Y. Yang, H. Wang, Z. Ji, Y. S. Han and J. H. Li, A switch from classic crystallization to non-classic crystallization by controlling the diffusion of chemicals, CrystEngComm, 2014, 16, 7633–7637.
31. T. Yang, Y. S. Han and J. H. Li, Manipulating silver dendritic structures via diffusion and reaction, Chem. Eng. Sci., 2015, 138, 457–464.
32. W. Liu, T. Yang, C. X. Li, P. Che and Y. S. Han, Regulating silver morphology via electrochemical reaction, CrystEngComm, 2015, 17, 6014–6022.
33. T. Yang and Y. S. Han, Quantitatively relating diffusion and reaction for shaping particles, Cryst. Growth Des., 2016, 16, 2850–2859.
34. A. J. Bard and L. R. Faulkner, Electrochemical methods: fundamentals and applications, Wiley, New York, Chichester, Weinheim, Brisbane, Singapore, Toronto, 1980.
35. K. I. Popov, E. R. Stojilkovic, V. Radmilovic and M. G. Pavlovic, Morphology of lead dendrites electrodeposited by square-wave pulsating overpotential, Powder Technol., 1997, 93, 55–61.
36. B. Scharifker and G. Hills, Theoretical and experimental studies of multiple nucleation, Electrochim. Acta, 1983, 28, 879–889.
37. H. Liu and R. M. Penner, Size-selective electrodeposition of mesoscale metal particles in the uncoupled limit, J. Phys. Chem. B, 2000, 104, 9131–9139.
38. J. Ustarroz, J. A. Hammons, T. Altantzis, A. Hubin, S. Bals and H. Terryn, A generalized electrochemical aggregative growth mechanism, J. Am. Chem. Soc., 2013, 135, 11550–11561.
39. A. L. Kholodenko and J. F. Douglas, Generalized Stokes-Einstein equation for spherical particle suspensions, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 1081.
40. J. G. Speight, Lange's handbook of chemistry, McGraw-Hill, 2005.
41. R. Qiu, H. G. Cha, H. B. Noh, Y. B. Shim, X. L. Zhang, R. Qiao, D. Zhang, Y. Il Kim, U. Pal and Y. S. Kang, Preparation of dendritic copper nanostructures and their characterization for electroreduction, J. Phys. Chem. C, 2009, 113, 15891–15896.
42. L. Vitos, A. V. Ruban, H. L. Skriver and J. Kollar, The surface energy of metals, Surf. Sci., 1998, 411, 186–202.
43. T. Bian, H. Zhang, Y. Jiang, C. Jin, J. Wu, H. Yang and D. Yang, Epitaxial growth of twinned Au–Pt core–shell star-shaped decahedra as highly durable electrocatalysts, Nano Lett., 2015, 15, 7808–7815.
44. Y. Qin, Y. Song, N. J. Sun, N. N. Zhao, M. X. Li and L. M. Qi, Ionic liquid-assisted growth of single-crystalline dendritic gold nanostructures with a three-fold symmetry, Chem. Mater., 2008, 20, 3965–3972.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ce02068b

‡ The first two authors contributed equally in this paper.

---