Modeling the toxicity of chemical pesticides in multiple test species using local and global QSTR approaches

Abstract

The safety assessment processes require the toxicity data of chemicals in multiple test species and thus, emphasize the need for computational methods capable of toxicity prediction in multiple test species. Pesticides are designed toxic substances and find extensive applications worldwide. In this study, we have established local and global QSTR (quantitative structure–toxicity relationship) and ISC QSAAR (interspecies correlation quantitative structure activity–activity relationship) models for predicting the toxicities of pesticides in multiple aquatic test species using the toxicity data in crustacean (Daphnia magna, Americamysis bahia, Gammarus fasciatus, and Penaeus duorarum) and fish (Oncorhynchus mykiss and Lepomis macrochirus) species in accordance with the OECD guidelines. The ensemble learning based QSTR models (decision tree forest, DTF and decision tree boost, DTB) were constructed and validated using several statistical coefficients derived on the test data. In all the QSTR and QSAAR models, Log P was an important predictor. The constructed local, global and interspecies QSAAR models yielded high correlations (R²) of >0.941; >0.943 and >0.826, respectively between the measured and model predicted endpoint toxicity values in the test data. The performances of the local and global QSTR models were comparable. Furthermore, the chemical applicability domains of these QSTR/QSAAR models were determined using the leverage and standardization approaches. The results suggest for the appropriateness of the developed QSTR/QSAAR models to reliably predict the aquatic toxicity of structurally diverse pesticides in multiple test species and can be used for the screening and prioritization of new pesticides.

---

1. Introduction

Due to the global chemical revolution over the last few decades, the environment has been much exposed to diverse chemicals.¹ Unrestricted release of chemicals into the environment has contributed to severe pollution problems worldwide.² An increased use of agro-chemicals, pharmaceuticals, petrochemicals, and other industrial chemicals over the last few years has largely aggravated the chemical pollution problem.^3,4 Understanding the chemical toxicity to different species is becoming a point of focus in environmental toxicology research.^5,6 An effective environmental management must protect different living species from stresses arising from the chemicals released into the ecosystems.⁷ Subsequently, the regulatory agencies require a comprehensive toxicity data prior to the registration of the new chemicals for manufacture and use. Although, experimental protocols for toxicological evaluations of different chemicals have been developed by the industry and regulatory agencies, the toxicological screening of a large number of chemicals and understanding their complex cellular interactions require animal experimentation, which are unethical, time and cost intensive, and have difficulties in correlations/interpretations with the human system.⁸ Recently, the European Union REACH (Registration, Evaluation, Authorisation and Restriction of Chemicals) legislation requires toxicological hazard and risk assessments for all new and existing chemicals⁹ and advocates for the use of sufficiently validated computational prediction models based on QSAR (quantitative structure–activity relationship) to fill in the toxicity data gaps, and thus save time, money and help to reduce the numbers of animals used for experimental testing purposes.¹⁰ QSAR offers an in silico tool for the development of predictive models towards various activity and property endpoints for a series of chemicals using the response data that have been determined through experiments and molecular structure information derived computationally or sometimes from experiments.^11,12 The guidelines for the QSAR model development and validation proposed by the Organization for Economic Cooperation and Development (OECD) are expected to help increase the acceptability of QSAR models for regulatory purposes.¹³ Subsequently, a number of QSARs have been developed for the toxicity predictions of specific chemicals and are reported in the literature.^14–18 However, the majority of such reports concern with a single species toxicity analysis, whereas, for a comprehensive safety evaluation of chemicals, toxicity data in multiple test species of different trophic levels and complexities are needed. In toxicological evaluations of chemicals, the aquatic test system offers better and reliable options as it constitutes a chain of different trophic level species for toxicity assays and in addition, it is less cumbersome than other test methods. Aquatic toxicity is one of the most important parameters in the ecotoxicological risk assessment of chemicals.¹⁹

In aquatic toxicity studies, the crustacean models are generally chosen due to their ecological relevance, the availability of well-developed test protocols, and their established use in standard toxicity testing²⁰ of the crustaceans, Daphnia magna, mysid, scud, and pink shrimp which have been proposed for the regulatory testing of chemicals.^21,22Daphnia magna is widely used as a standard test organism in aquatic toxicology. It is an important primary consumer of primitive plant life and itself a major food source for vertebrate and invertebrate predators and has been used as a representative for other freshwater animals in the standard tests of toxicity²³ because of its high sensitivity, easy handling and high reproductive rate.²⁴ The Daphnia acute toxicity (48 h) test is used for short term toxicity (EC₅₀) assessment of chemicals.

Recently, a few studies^25–30 have reported QSTR models for the aquatic toxicity estimation of chemicals in multiple test species, however, no attempt has yet been made to develop QSTRs for the toxicological evaluation of pesticides in multiple crustacean test species. Local QSTR (L-QSTR) models based on mode of action (MOA),^31–34 and specific functional groups^35–39 have been proposed for toxicity assessment of chemicals. However, the application of such models is limited due to the pre-requirement of information on the MOA and functional groups (in the case of multiple groups) in the chemicals.⁴⁰ Recently, L-QSTR models based on toxicity data in a single test species and G-QSTR based on the combined toxicity data for different test species have been proposed.^29,40,41 Further, the interspecies correlation (ISC) based quantitative structure activity–activity relationships (QSAARs)^18,42–45 and global QSTR (G-QSTR) models have been proposed for toxicity prediction of chemicals in multiple species.²⁹ Global models have the advantage that they are applicable for large numbers of compounds across mechanisms of action and structure.^46,47 The ISC QSAAR extrapolates the data for one toxicity endpoint to those for another toxicity endpoint and can be used to determine the species-specific toxicity of a chemical, whereas, the G-QSTR model can simultaneously consider the toxicity end-point in multiple test species for model building and prediction.^46,47

In recent years, the artificial neural networks (ANNs) and support vector machines (SVMs) have emerged as the unbiased methods for predictive modeling. ANNs, although universal estimators, suffer from the problem of over-fitting of data. SVMs, known to overcome the problem of over-fitting, make use of limited data points in the training phase. In recent years ensemble learning (EL) methods⁴⁸ have emerged as unbiased tools for modeling the complex relationships between the independent and dependent variables.⁴⁹ These methods are designed to overcome the problems with weak predictors⁵⁰ and over-fitting the training data.⁵¹ Decision tree forest (DTF) and decision treeboost (DTB) implementing bagging and boosting techniques improve the accuracy of a predictive function.⁴⁹ These methods are inherently non-parametric statistical methods and make no assumption regarding the underlying distribution of the values of predictor variables and can handle numerical data that are highly skewed or multi-model in nature.^52,53

In this study, EL based local (L-QSTR) and global (G-QSTR) models were established for the aquatic toxicity predictions of structurally diverse pesticides in single and multiple crustacean test species in accordance with the OECD guidelines for QSAR modeling. The constructed QSTR models were rigorously validated using the internal and external validation procedures. Moreover, the ISC QSAAR models were also established using the toxicity data of pesticides in crustacean (D. magna) and fish (Oncorhynchus mykiss and Lepomis macrochirus) species. The applicability domains of the developed QSTR and ISC QSAAR models were defined using the leverage and standardization methods.

2. Materials and methods

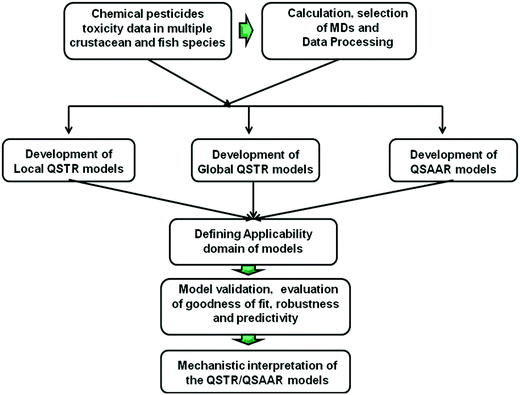
Here, QSTR models were constructed for predicting the toxicities of chemicals in single and multiple test species following the OECD guidelines¹³ for QSAR modeling. A schematic diagram showing the modeling steps is presented in Fig. 1.

Fig. 1 A flow chart showing the QSTR/QSAAR modeling procedure.

2.1 Datasets

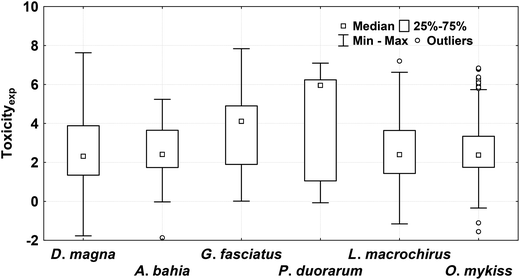
For the development of high quality QSAR models, high quality experimental data are essential.⁵⁴ The aquatic toxicity data of chemical pesticides on different crustacean species (Daphnia magna, Americamysis bahia, Gammarus fasciatus, and Penaeus duorarum) were collected from the OPP Pesticide Ecotoxicity Database.⁵⁵ This database contained well-defined experimental toxicity values of 3767 compounds in crustacean species. Here, 48-h EC₅₀ (ppm) toxicity in D. magna, and 96-h LC₅₀ (ppm) in the other three species were considered. The toxicity end-points were determined following the EPA guidelines (FIFRA 158.490). All the mixtures, duplicates, salts, and the compounds that have only qualitative end-point values were removed. Finally, a total of 445 pesticides (algaecide, fumigant, fungicide, growth regulator, herbicide, insecticide, microbiocide, miticide, molluscicide, nematicide, rodenticide, etc.) for D. magna were retained for the QSTR analysis. Further, the compounds that were common in other toxicity datasets were removed and chemicals that were uncommon in other species were retained for external validation. Accordingly, 43 pesticides in A. bahia, 15 in G. fasciatus, and 8 in P. duorarum test species were retained for multi-species QSTR analysis. For the development of interspecies QSAAR models, the pesticide toxicity data in fish was considered. Toxicity data of 318 pesticides in O. mykiss (96-h LC₅₀) and 294 in L. macrochirus (96-h LC₅₀) were taken. Prior to the QSTR modeling, the toxicity values were converted into the negative logarithmic scale. For different test species, the end-point toxicity values (pEC₅₀/pLC₅₀, mmol L⁻¹) ranged between −1.77 and 7.63 (D. magna), −1.87 and 5.24 (A. bahia), 0.01 and 7.84 (G. fasciatus), −0.07 and 7.10 (P. duorarum), −1.55 and 6.84 (O. mykiss), and −1.16 and 7.20 (L. macrochirus), respectively (Tables S1 and S2; ESI†). The Box–Whisker plots of the toxicities of pesticides in different test species considered here are given in Fig. 2.

Fig. 2 Box–Whisker plots of the toxicity of pesticides in different test species.

2.2 Molecular descriptors and data processing

For calculating the molecular descriptors (MDs), the SMILES (simplified molecular input line entry system) of the molecules were obtained using Chemspider.⁵⁶ The Chemopy program⁵⁷ was used to calculate the MDs. The program calculates 634 1D and 2D descriptors. These descriptors include the constitutional, connectivity, Basak, topology, Kappa, Buden, E-state, autocorrelation, molecular property, charge, and MOE-type descriptors. Relevant descriptors for QSTR analysis were selected using the model-fitting approach. The MDs with low variations (≤0.5) were excluded (380) from the pool. Finally, 254 descriptors were retained to undergo subsequent descriptor selection for QSTR modeling. Prior to the model construction, the toxicity datasets were split into the training (80%) and test (20%) subsets using the random distribution method. In this approach, the compounds are selected randomly with a uniform distribution and each sample (x) has an equal probability (p) of selection. For the training subset T_tr: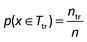 , where n and n_tr are the total number of samples in the complete and training (T_tr) sets. The random distribution method leads to a low bias of the model performance.^58,59 The relevant MDs and the optimal model parameters were determined using the training data through a 5-fold cross-validation (CV). The criterion of low root mean squared error (RMSE) was used to rank the contribution of the MDs in the current set. The lowest ranked descriptors (<5% contribution) were then removed²⁹ in the successive steps. The most significant descriptors were then retained and the corresponding prediction accuracies were computed. The descriptor selection process was performed separately for the local, global QSTR and QSAAR modeling. Finally the retained MDs for the QSTR and QSAAR models are presented in Table 1.

Table 1 Descriptors used in QSTR modeling

Descriptors	Models	Description
L-QSTR local QSTR models; G-QSTR global QSTR models; ISC QSAAR interspecies correlation models.
nta	L-QSTR	Number of atoms
TPSA	L-QSTR, G-QSTR	Topological polarity surface area
PEOEVSA13	L-QSTR, G-QSTR	MOE-type descriptors using partial charges and surface area contributions
Log P	L-QSTR, G-QSTR, ISC QSAAR	Log P value based on the Crippen method
Aweight	L-QSTR	Average atomic weight (not including H)
J	L-QSTR, G-QSTR	Balaban's J index
Hy	G-QSTR	Hydrophilic index

---

The structural diversity of the considered pesticide datasets was determined using the Tanimoto similarity index (TSI). It is a distance metric for the topology-based chemical similarity studies and calculates the Tanimoto similarity between the fingerprint of a chemical and a consensus fingerprint.⁶⁰ A good cut-off for biologically similar molecules is 0.7 or 0.8. In this study, the average TSI values of the pesticides in different toxicity datasets considered here were 0.025 (D. magna), 0.027 (A. bahia), 0.027 (G. fasciatus), 0.042 (P. duorarum), 0.010 (L. macrochirus), and 0.009 (O. mykiss), respectively. These values suggest that the considered pesticides in these datasets had a sufficiently high structural diversity.

2.3 QSTR analysis

Here, the EL-based L-QSTR and G-QSTR models were established for predicting the aquatic toxicities of structurally diverse chemical pesticides in different crustacean species (D. magna, A. bahia, G. fasciatus and P. duorarum). Further, the ISC based linear QSAAR models were also constructed using the aquatic toxicity data of crustacean (D. magna) and fish species. A brief account of these approaches is provided here.

2.3.1 EL-modeling methods. Ensemble learning (EL) is a machine learning paradigm where multiple learners are trained to solve the same problem. An ensemble contains a number of learners who are usually called base learners.⁶¹ The generalization ability of ensemble is usually much stronger than that of base learners. Ensemble learning is able to boost weak learners for making accurate predictions. The DTF and DTB are the ensembles of SDTs. The bagging technique implemented in DTF reduces the variance associated with prediction and improves the prediction accuracy. In this technique, several bootstrap samples are drawn from the data and prediction method is applied to each bootstrap sample and the results are combined to obtain the overall prediction.⁶² Theoretically, if a training set D consists of data {(X_i,Y_i), I = 1,2,⋯,n} where Y_i is the real-valued response and X_i is the p-dimensional predictor variable for the i^th instance, a predictor E(Y|X = x) = f(x) is denoted by C_n(x) = h_n (D₁, ⋯,D_n) (x), where h_n is the n^th hypothesis. Finally, the bagged predictor is obtained as, C_n;B(x) = E[D_n(x)].⁶³ In DTF, a number of independent trees are grown in parallel, and they do not interact until all of them have been built.⁶⁴

In DTB, the stochastic gradient boosting technique improves the prediction accuracy by applying the function repeatedly in a series.⁶⁵ For the overall prediction, boosting uses a weighted average of the results obtained by applying a prediction method to various samples. The DTB generates a series of trees with the output of one tree going into the next tree in the series. The DTB algorithm minimizes the loss function in the training set, {x,y}. After each iteration, F represents the sum of all trees built so far: F_m(x) = F_m−1(x) + Tree_m(x), where m is the number of trees in the model. The regularization parameter (number of iterations) is achieved by shrinkage through modifying the update rule as; F_m(x) = F_m−1(x) + νγ_mh_m(x), 0 < ν ≤ 1, where ν is the learning rate and h_m(x) is the base learner. The number and depth of each tree are the model parameters in DTF and DTB analyses. Here, the DTF and DTB approaches were used to develop nonlinear L-QSTR and G-QSTR models for toxicity prediction of pesticides in multiple crustacean test species.

2.3.2 Model validation. The robustness of the developed nonlinear QSTR and QSAAR models was verified by using different types of statistical validation metrics. Both the internal and external validation strategies were adopted. For internal validation, a 5-fold CV procedure was used, whereas the external validation was performed with the external test data, kept away during the training phase. Such test sets (when defined prior to analysis) are commonly accepted as the gold standard to assess the real predictivity of the QSAR model.⁶⁶ However, the external validation results of a QSAR model largely depend on the distribution of compounds in the training and test sets. A distribution of dissimilar compounds in the training and test sets may lead to poor external validation results. The validation strategies check the reliability of the developed models for their possible application on a new set of data and assess the confidence of such prediction.⁶⁷ Since, the main objective of the QSTR/QSAAR analysis here is to develop robust models that are capable of making accurate and reliable predictions of the toxicological effect of an unknown chemical in multiple test species, these were subsequently validated using the test set compounds for checking their predictive power. Accordingly, the external validation metrics, such as the CCC (concordance correlation coefficient), Q²_F1, Q²_F2, Q²_F3 and r²_m were taken into account.^68–73 The model fitness parameters R² and the root mean squared error (RMSE) were reported in connection with validation for the developed models. Further, the Y-randomization test was performed to evaluate any chance correlation among the data matrix. In this test, the dependent variable is randomly scrambled and a new model is developed using the original independent variable matrix.⁷⁴ A value of the coefficient of determination of the non-random model (R²) exceeding the average value for the random models (R²_r) disapproves the chance correlation probability. The extent of the difference in the values of R² and R²_r that signifies the reliability of the developed model was determined in terms of ^cR²_p.⁷⁵ The threshold value of ^cR²_p is 0.5 and a model exceeding this value might be not considered the outcome of mere chance only.

2.3.3 Applicability domain analysis. The applicability domain (AD) of a QSTR model should be defined before it is used for screening new chemicals. The AD is the physico–chemical, structural or biological space, on which the model (training) has been developed, and for which it is applicable to make predictions for new compounds.⁷⁶ The AD of the constructed QSTR/QSAAR models was defined using the leverage method, which is calculated as, h_i = x^T_i(X^TX)⁻¹x_i, where x_i is a row vector of MDs for a particular i^th compound and X is the n × m matrix of the m model MD values for the n training set compounds. The value of h_i greater than the critical h* value indicates that the structure of the compound substantially differs from those used for the calibration. The h* value can be calculated⁷⁶ as, , where p is the number of variables used in the model, and n is the number of training data. However, a major limitation of this method is that the value of h*, hence, the number of compounds within or out of the AD of a model would depend on the number of compounds in the training data. The AD of the QSTR models was also analyzed by the standardization approach.⁷⁷

3 Results and discussion

3.1 Local QSTR modeling

Here, EL-based L-QSTR models were constructed to predict the aquatic toxicities of diverse pesticides in D. magna using six descriptors (Table 1). A local model was constructed with toxicity data in a single crustacean species (D. magna) and applied to other crustacean species (A. bahia, G. fasciatus and P. duorarum). L-QSTR models were developed using the DTF and DTB algorithms. The optimal architectures and the model parameters of the two models for the D. magna toxicity data were determined using a 5-fold CV. The average RMSE in the training and CV data for the two models (DTF and DTB) were 0.49, 1.23 and 0.31, 1.24, respectively. In 5-fold Y-scrambling, the R² and ^cR²_p values were 0.005, 0.935 (DTF) and 0.004, 0.961 (DTB), respectively, which revealed that the original L-QSTR models are unlikely to arise as a result of chance correlation. The architectures and the optimal parameters of the constructed L-QSTR models determined through the internal and external validation are given in Table 2.

Table 2 Optimal parameters in L-QSTR and G-QSTR models

Model parameters	Local-QSTR models	Global-QSTR models
DTF-QSTR
Number of trees	200	245
Maximum depth of any tree in the forest	26	26
Average number of group splits in each tree	218.7	248.3
DTB-QSTR
Number of trees	405	404
Maximum depth of any tree in the series	11	11
Average number of group splits in each tree	580.0	593.9

---

The L-QSTR models were applied to the test data and yielded RMSE and R² values of 0.37, 0.941 (DTF) and 0.31, 0.958 (DTB), respectively. It is evident that the models yielded high correlations between the measured and the model predicted values of the endpoint toxicity both in the training and test data (Table 3). Fig. 3 shows the plot of the model predicted values of toxicity against the experimental values. As can be seen, the agreement between the measured and the predicted results across the entire range of values is excellent. A closely followed pattern of variation by the measured and model predicted values (Fig. 3) and reasonably low values of prediction errors (Table 3) suggest for a good-fit of the developed L-QSTR models to the datasets and for the adequacy of the selected models for predicting the toxicity of the pesticides. Both the DTF and DTB based L-QSTR models were applied to other three test species to predict the toxicities of pesticides. The results (Table 3) suggest that both the L-QSTR models successfully predicted the toxicities of the pesticides in all the three species. The high correlations (R²) between the measured and predicted toxicity values (Table 3) may be due to the high similarities of the training (TSI 0.026), test (TSI 0.021) and external test sets (0.027 A. bahia; 0.027 G. fasciatus; 0.042 P. duorarum) and the interpolation capacity (possible over-fitting) of the model.

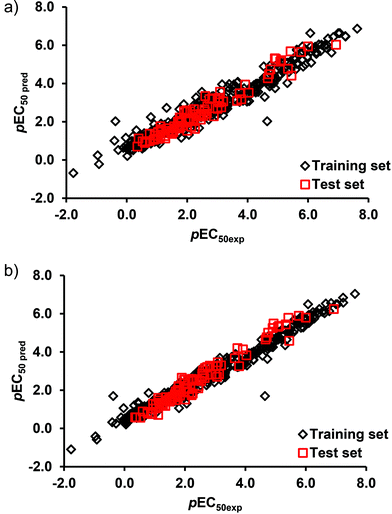Fig. 3 Plot of the measured and model predicted endpoint toxicity values of pesticides in the training and test sets of (a) DTF L-QSTR, and (b) DTB L-QSTR models.

Table 3 Performance parameters for the L-QSTR models in multiple crustacean test species

Model/data set	RMSE	R ^2	Q ^2F1	Q ^2F2	Q ^2F3	CCC	r ^2m
Coefficient threshold	—	0.5 (training)	0.7	0.7	0.7	0.85	0.65
		0.6 (test)
DTF L-QSTR
Training set	0.55	0.938	—	—	—	—	—
Test set	0.37	0.941	0.937	0.934	0.962	0.964	0.805
A. bahia	0.47	0.947	0.897	0.896	0.939	0.933	0.627
G. fasciatus	0.74	0.956	0.884	0.857	0.848	0.901	0.474
P. duorarum	0.95	0.971	0.909	0.885	0.747	0.922	0.584
DTB L-QSTR
Training set	0.43	0.963	—	—	—	—	—
Test set	0.31	0.958	0.956	0.955	0.974	0.977	0.906
A. bahia	0.23	0.987	0.974	0.974	0.985	0.985	0.862
G. fasciatus	0.44	0.983	0.958	0.948	0.945	0.969	0.746
P. duorarum	0.60	0.974	0.964	0.954	0.899	0.973	0.823

---

External validation coefficients (CCC, Q²_F1, Q²_F2, Q²_F3 and r²_m) were derived for the test data (D. magna) and other three species. The OECD principle 4 advocates for a rigorous validation of the constructed QSTR models prior to applying these for new chemicals. The values of these coefficients along with their respective thresholds^78,79 and the quality metric R² are given in Table 3. From the results, it is evident that the obtained values of the validation metrics for the developed L-QSTR models are in good agreement with the limit prescribed; demonstrating once again the high predictability of the L-QSTR models.

In the literature, there are some studies that reported linear QSAR models for pesticide toxicity prediction in Daphnia.^15,80–82 Although, it is difficult to perform an exact comparison of the present study with the previous ones due to the difference in the composition of the modeling and validation sets. These studies considered a limited number of compounds (n = 10–263) and reported the correlation (R²) values in the range of 0.590 and 0.895, which are lower to those achieved in our study.

3.2 Global QSTR modeling

The EL-based G-QSTR models (DTF and DTB) were constructed using the combined toxicity dataset of all the four crustacean test species (n = 511) and a set of five MDs commonly selected by two approaches. The constructed G-QSTR models thus have wider application domains both in terms of the chemicals and test species. Y-scrambling and external validation (test data) were performed to verify the chance correlation and applicability of the constructed G-QSTR models. In CV, the average RMSE in the training and CV data were 0.50, 1.28 (DTF) and 0.36, 1.29 (DTB), respectively. A low R² and high ^cR²_p values of 0.002, 0.931 (DTF) and 0.003, 0.961 (DTB), respectively in the Y-randomization test revealed that the original G-QSTR models disapproved the chance correlation probability. The statistical coefficients calculated for the test data are summarized in Table 4. The values of all the coefficients were above their respective thresholds.^78,79 The plot of the actual and G-QSTR model predicted toxicity values (Fig. 4) in each of the test species considered here suggested an excellent agreement between them. From the results, it is evident that the performances of both the G-QSTR models (DTF and DTB) are comparable. In the G-QSTR model, the high correlations (R²) between the measured and predicted toxicity values (Table 4) may be due to the high similarities of the compounds in the training (TSI 0.027) and test (TSI 0.024) sets.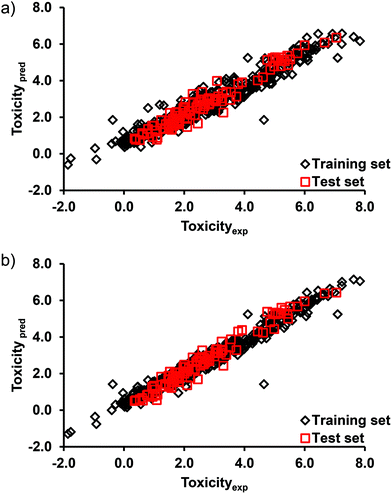

Fig. 4 Plot of the measured and model predicted endpoint toxicity values of pesticides in the training and test sets of (a) DTF G-QSTR, and (b) DTB G-QSTR models.

Table 4 Performance parameters for the G-QSTR models

Model/data set	RMSE	R ^2	Q ^2F1	Q ^2F2	Q ^2F3	CCC	r ^2m
DTF G-QSTR
Training set	0.57	0.932	—	—	—	—	—
Test set	0.38	0.943	0.939	0.939	0.960	0.967	0.824
DTB G-QSTR
Training set	0.41	0.962	—	—	—	—	—
Test set	0.31	0.960	0.959	0.959	0.973	0.980	0.930

---

An inter-comparison of the L-QSTR and G-QSTR models established in this study revealed that the performance of both these models were closely comparable and the two models successfully predicted the toxicities of pesticides having a huge diversity from the point of view of the chemical structure on different crustacean test species considered here (Tables 3 and 4). An excellent performance of the QSTR models here could further be attributed to the fact that both the EL methods (DTF and DTB) successfully captured the nonlinearities in the data. The bagging and boosting algorithms implemented in these models are known to improve the model accuracies.

3.3 QSAAR modeling

The QSAAR model extrapolate data for one toxicity endpoint to those for another toxicity endpoint and can be used to determine the species-specific toxicity of a chemical.⁴³ The QSAAR is a mathematical relationship between two different biological endpoints measured in the same species or the same endpoint in different species. This approach is widely used for the extrapolation of toxicological data from a surrogate species to a predicted species. In this study, it was investigated whether acute toxicity data for the invertebrate D. magna could be used to develop a model for making in vivo toxicity prediction to the vertebrate fish. The interspecies toxicity correlations were examined prior to the QSAAR modeling. A good interspecies correlation (R²) obtained in this study for D. magna to fish species (O. mykiss, 0.773; L. macrochirus, 0.795) seems to support the idea that one can use the toxicity data for one organism (D. magna) to predict the toxicity to another organism (fish). Here, we used the MLR technique to develop linear QSAAR models and to select the descriptor. The hydrophobicity has been identified as an important parameter to describe the toxicity of compounds to D. magna. The QSAAR models were established for the common pesticides in D. magna and two different fish species. Accordingly, MLR based QSAAR models were developed between D. magna and O. mykiss; D. magna and L. macrochirus. The common compounds in two fish species were 294 (L. macrochirus) and 318 (O. mykiss). The D. magna toxicity was considered as independent and those of other species (fish) were taken as the dependent variable. The respective linear equations (training) obtained were

pLC₅₀ (L. macrochirus) = 0.09 + 0.18 (Log P) + 0.67 (pEC₅₀D. magna); n = 235; R² = 0.831; RMSE = 0.65, F = 570.92; p < 0.00;

pLC₅₀ (O. mykiss) = 0.27 + 0.17 (Log P) + 0.67 (pEC₅₀D. magna); n = 254; R² = 0.813; RMSE = 0.65, F = 545.77; p < 0.00.

The developed ISC QSAAR models applied to the respective test data yielded R² and RMSE values of 0.68, 0.840 and 0.68, 0.826, respectively. The values of the statistical coefficients for the test set (Table 5) were above their respective thresholds (except for r²_m). The success of these QSAAR models may be attributed to a similar mode of action resulting in a similarity in the descriptor required to predict the toxicity in an organism. In the case of new pesticides that fit our defined selection criteria, the defined toxicological effects to D. magna and fish can be estimated using our developed models without any additional animal testing. Tremolada et al.⁸³ and Zvinavashe et al.¹⁵ developed QSAAR models for predicting the toxicities of pesticides in fish (O. mykiss and C. carpio) using D. magna toxicity data and reported R² of 0.59 (n = 267) and 0.94 (n = 9), respectively. In both the studies, simple toxicity–toxicity modes were constructed. However, both these studies considered lesser number of chemicals compared to the present report.

Table 5 Performance parameters for the QSAAR models

Data set/models	RMSE	R ^2	Q ^2F1	Q ^2F2	Q ^2F3	CCC	Q ^2m
QSAAR-1 interspecies QSAAR model for L. macrochirus; QSAAR-2 interspecies QSAAR model for O. mykiss.
QSAAR-1
Training set	0.65	0.831	—	—	—	—	—
Test set	0.68	0.840	0.831	0.831	0.818	0.900	0.636
QSAAR-2
Training set	0.65	0.813	—	—	—	—	—
Test set	0.68	0.826	0.817	0.817	0.794	0.894	0.598

---

3.4 Applicability of domain analysis

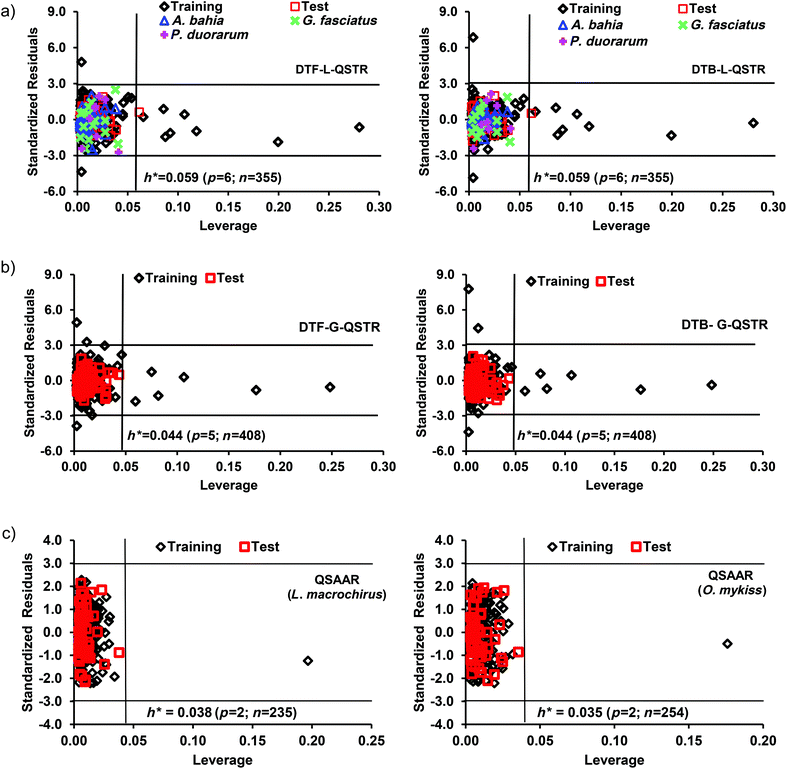
Here, the leverage and standardization methods were used to define the ADs of the developed L-QSTR, G-QSTR and QSAAR models and the corresponding Williams plots (Fig. 5) were used to detect the response outliers (standardized residuals >3) and the structurally influential chemicals in the model (h > h*) (in the training data). In both the DTF and DTB based L-QSTR models, there were totally 9 high leverage and 2 response outlier compounds detected, whereas in G-QSTR models, the number of such compounds were 7 and 3, respectively. On the other hand, there was a single high leverage compound (fenbutatin oxide) in both the QSAAR models. The structures of the outliers and structurally influential compounds in each model are presented in Table S3 (ESI†). Further, the outliers in the training, test and external datasets were identified using the standardization approach.⁷⁷ The analysis revealed that in the L-QSTR model fifteen compounds in the training, three in the test and one in the external dataset (A. bahia) were out of the AD. In G-QSTR, thirteen compounds in the training and four in the test set were out of the AD. In QSAAR models (L. macrochirus and O. mykiss), three and four compounds in training and one and two compounds in the test data were detected as the outliers (Table S4, ESI†). The anomalous behavior of the compounds outside the ADs of the models may be due to the fact that the set of the selected MDs could not capture some relevant structural features present in these molecules and that their biological mechanism is different from the remaining chemicals. However, the average predicted toxicity for the test molecules that are inside the AD is close to the average predicted toxicity of the molecules in the training set and the presence of the molecules inside or outside the AD reveals nothing regarding the difference or the correlation between the predicted/observed values of toxicity for molecules in the test set. For future predictions, the developed local, global and QSAAR models can be used to predict the toxicity of a new compound, if they locate in the AD of the respective model.

Fig. 5 Williams plot for the (a) L-QSTR, (b) G-QSTR, and (c) QSAAR models.

3.5 Mechanistic interpretation of QSTRs

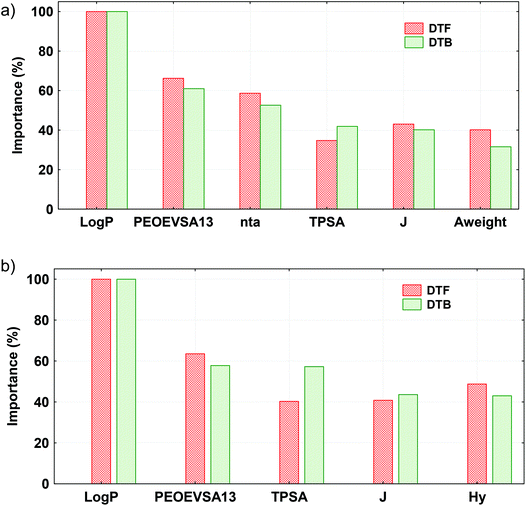
The principle 5 of the OECD guidelines requires that a QSAR model should be mechanistically interpretable. Here, totally seven MDs (nta, TPSA, Log P, Aweight, J, Hy and PEOEVSA13) were considered for developing the L-QSTR, G-QSTR, and QSAAR models. The contributions of the selected MDs in different QSTR models are presented in Fig. 6.

Fig. 6 Plots of the contributions of the MDs in (a) L-QSTR, and (b) G-QSTR models.

In the local and global QSTR models, Log P has the highest (100%) contribution followed by PEOEVSA13. Except TPSA and Hy, all the other MDs were positively correlated with the end-point. A positive relationship between the descriptor and the endpoint (pEC₅₀ or pLC₅₀) will mean its direct influence on the toxicity of the chemical, whereas a negative correlation would reveal an inverse effect on the toxicity. Log P is measure of the hydrophobicity of a chemical, reflecting the ability of a compound to form non-covalent interactions with its environment, to dissolve and persist in water or in a lipidic environment. A larger Log P indicates a stronger ability of a chemical to permeate the cell membrane of an organism and, therefore, to interact with its target in the organism.⁸⁴ PEOEVSA13, a MOE-type descriptor is calculated using partial charge and surface area contributions. These descriptors largely consist of physico–chemical properties, sub-divide surface areas, connectivity and shape indices, and atom and bond counts, featuring whole molecule properties.⁸⁵ TPSA is defined as the part of the surface area of the molecule associated with N, O, S and the H-bonded to any of these atoms.⁸⁶ It correlates well with the passive molecular transport through membranes and allows for the prediction of transport properties of chemicals.⁸⁷ Hy is a semi-empirical index related to the hydrophilicity of compounds based on count descriptors.⁸⁸ A negative correlation of Hy with toxicity suggests that the presence of hydrophilic groups (OH, SH, NH) in a molecule would result in a decrease of the toxicity. The nta and Aweight are constitutional descriptors and represent the total number of atoms and average atomic weight, respectively. This has a major role in defining the molecular density, molecular mass, rigidity and presence of individual atoms in the chemicals. The Balaban's J index represents branching in a molecule and a higher value of J indicates high branching in a compound.⁸⁹ The more branched molecules are less toxic, probably due to their lower membrane penetration ability.²⁴ To further investigate the relationships of the selected MDs with the end-point toxicity of pesticides, we selected a fraction (10%) of the compounds that exhibited the highest and lowest toxicities (pEC₅₀) in D. magna. For these compounds, the mean values of all the descriptors (expect TPSA, J and Hy) were high in high toxicity compounds and low in low toxicity compounds. The Box–Whisker plots of the MD values for the pesticides exhibiting low and high toxicities (10%) are shown in Fig. S1 (ESI†). Thus, it is clear that the selected descriptors have quantitative mechanistic relationships with the end-point properties investigated here.

In this study, QSTR models were constructed for predicting the toxicities of diverse chemical pesticides in multiple test species strictly in accordance with the OECD guideline for QSAR modeling for regulatory purposes.⁹⁰ Accordingly, for QSTR analysis, this study considered the databases reporting well-defined experimental values of the aquatic toxicities of diverse chemicals in crustacean and fish test species with experimental protocols. Further, we adopted an unambiguous and well established modeling procedure with clearly defined methodologies for the calculation and selection of MDs and data processing. The ADs of the developed QSTR models were adequately determined. Towards the statistical quality checks on the developed QSTR models, various stringent coefficients for model fitness, robustness, and validation metrics were computed, which were above their respective thresholds. Further, a convincing mechanistic interpretation of the models was offered and the relevance of the selected MDs in different aquatic toxicity QSTR models here was investigated.

4. Conclusions

For a comprehensive safety assessment of chemicals, toxicological profile data in multiple test species will be required. Experimental toxicity testing of chemicals in multiple species will be time and resource intensive. In this study, EL based QSTR and QSAAR models were developed for estimating the aquatic toxicities of diverse chemicals in multiple test species strictly in accordance with the OECD guidelines for QSAR modeling. Chemical pesticides toxicity dataset in crustacean and fish species was considered; local and global QSTR models were established using DTF and DTB modeling methods, whereas ISC QSAAR models were established to predict toxicity in fish with Daphnia toxicity data. Totally seven MDs were used and several statistical validation tests performed on the constructed QSTR/QSAAR models revealed a high predictivity for these models and rendered high statistical confidence. The performances of both the local and global QSTR models were excellent and comparable. The developed QSTR models in the present study performed better than those reported earlier for the prediction of the toxicities of pesticides. Excellent predictivity and generalization achieved for the QSTR models here may be due to their ability to capture the nonlinearities in the data. The proposed models will help in reducing the cost and number of animals in toxicity testing of chemicals and in generating reliable toxicity data in multiple test species to streamline the risk assessment process of diverse chemicals.

Acknowledgements

The authors thank the Director, CSIR-Indian Institute of Toxicology Research, Lucknow (India) for his keen interest in this work and providing all necessary facilities.

References

1. S. Pramanik and K. Roy, Predictive modeling of chemical toxicity towards Pseudokirchneriella subcapitata using regression and classification based approaches, Ecotoxicol. Environ. Saf., 2014, 101, 184–190.
2. H. Scherb and K. Voigt, Adverse genetic effects induced by chemical or physical environmental pollution, Environ. Sci. Pollut. Res., 2011, 18, 695–696.
3. J. R. Rohr, A. M. Schotthoefer, T. R. Raffel, H. J. Carrick, N. Halstead, J. T. Hoverman, C. M. Johnson, L. B. Johnson, C. Lieske, M. D. Piwoni, P. K. Schoff and V. R. Beasley, Agrochemicals increase trematode infections in a declining amphibian species, Nature, 2008, 455, 1235–1239.
4. A. G. Planson, P. Carbonell, E. Paillard, N. Pollet and J. L. Faulon, Compound toxicity screening and structure–activity relationship modeling in Escherichia coli, Biotechnol. Bioeng., 2012, 109, 846–850.
5. H. Azarbad, M. Niklinska, C. A. vanGestel, N. M. vanStraalen, W. F. Roling and R. Laskowski, Microbial community structure and functioning along metal pollution gradients, Environ. Toxicol. Chem., 2013, 32, 1992–2002.
6. S. Daouk, P. J. Copin, L. Rossi, N. Chevre and H. R. Pfeifer, Dynamics and Environmental risk assessment of the herbicide glyphosate and its metabolite AMPA in as mallvineyar driver of the Lake Geneva catchment, Environ. Toxicol. Chem., 2013, 32, 2035–2044.
7. B. J. Cardinale, D. J. Emmett, A. Gonzalez, D. U. Hooper, C. Perrings, P. Venail, A. Narwani, M. G. Mace, D. Tilman, D. A. Wardle, A. P. Kinzig, G. C. Daily, M. Loreau, J. B. Grace, A. Larigauderie, D. S. Srivastava and S. Naeem, Biodiversity loss and its impact on humanity, Nature, 2012, 486, 59–67.
8. A. Ahrens and T. P. Traas, Environmental exposure scenarios: development, challenges and possible solutions, J. Exposure Sci. Environ. Epidemiol., 2007, 17, S7–S15.
9. A. P. Worth, A. Bassan, J. DeBruijn, A. Gallegos-Saliner, G. Netzeva, G. Patlewicz, M. Pavan, I. Tsakovska and S. Eisenreich, The role of the European chemicals bureau in promoting the regulatory use of (Q)SAR methods, SAR QSAR Environ. Res., 2007, 18, 111–125.
10. European Commission, Directive 2006/121/EC of the European Parliament and of the Council of 18 December 2006 amending Council Directive 67/548/EEC on the approximation of laws, regulations and administrative provisions relating to the classification, packaging and labelling of dangerous substances in order to adapt it to Regulation (EC) no. 1907/2006 concerning the Registration, Evaluation, Authorisation and Restriction of Chemicals (REACH) and establishing a European Chemicals Agency. Off. J. Eur. Union (2006), L 396/850 of 30.12.2006, Office for Official Publications of the European Communities (OPOCE), Luxembourg.
11. K. Roy, S. Kar and R. N. Das, Understanding the Basics of QSAR for Applications in Pharmaceutical Sciences and Risk Assessment, Academic Press, London, UK, 2015, ISBN: 978-0-12-801505-6.
12. K. Roy, S. Kar and R. N. Das, A Primer on QSAR/QSPR Modeling Fundamental Concepts. Springer Briefs in Molecular Science, Springer Cham Heidelberg, New York, London, 2015,  DOI:10.1007/978-3-319-17281-1.
13. Organization for Economic Cooperation and Development (OECD). Guidance Document on the Validation of (Quantitative) Structure–activity Relationships [(Q)SAR] Models, ENV/JM/MONO 2 (2007), 2007, 1–154.
14. C.-P. Huang, Y.-J. Wang and C.-Y. Chen, Toxicity and quantitative structure−activity relationships of nitriles based on Pseudokirchneriella subcapitata, Ecotoxicol. Environ. Saf., 2007, 67, 439–446.
15. E. Zvinavashe, T. Du, T. Griff, H. H. van den Berg, A. E. Soffers, J. Vervoort, A. J. Murk and I. M. Rietjens, Quantitative structure–activity relationship modeling of the toxicity of organothiophosphate pesticides to Daphnia magna and Cyprinus carpio, Chemosphere, 2009, 75, 1531–1538.
16. V. Aruoja, M. Sihtmae, H.-C. Dubourguier and A. Kahru, Toxicity of 58 substituted anilines and phenols to algae Pseudokirchneriella subcapitata and bacteria Vibrio fischeri: Comparison with published data and QSARs, Chemosphere, 2011, 84, 1310–1320.
17. C. Bertinetto, C. Duce, R. Solaro, M. R. Tiné, A. Micheli, K. Héberger, A. Miličević and S. Nikolić, Modeling of the Acute Toxicity of Benzene Derivatives by Complementary QSAR Methods, MATCH, 2013, 70, 1005–1021.
18. S. Cassani, S. Kovarich, E. Papa, P. P. Roy, L. vanderWal and P. Gramatica, Daphnia and fish toxicity of (benzo)triazoles: validated QSAR models, and interspecies quantitative activity–activity modelling, J. Hazard. Mater., 2013, 258–259, 50–60.
19. A. A. Lagunin, A. V. Zakharov, D. A. Filimonov and V. V. Poroikov, A new approach to QSAR modelling of acute toxicity, SAR QSAR Environ. Res., 2007, 18, 285–298.
20. T. Verslycke, A. Ghekiere, S. Raimondo and C. Janssen, Mysid crustaceans as standard models for the screening and testing of endocrine-disrupting chemicals, Ecotoxicology, 2007, 16, 205–219.
21. EPA; US Environmental Protection Agency, Ecological Effects Test Guidelines, OPPTS 850.1010 Aquatic Invertebrate Acute Toxicity Test, Freshwater Daphnids, Prevention, Pesticides and Toxic Substances (7101), Washington, D.C. EPA 712-C-96-114, 1996.
22. US EPA; Marine Toxicity Identification Evaluation (TIE): Phase I Guidance Document. Office of Research and Development, EPA 600-R-96-054, September 1996.
23. OECD, Test No. 202: Daphnia sp. Acute Immobilisation Test, OECD Guidelines for the Testing of Chemicals, Section 2, OECD Publishing, Paris, France, 2004,  DOI:10.1787/9789264069947-en.
24. A. R. Katritzky, S. H. Slavov, I. S. Stoyanova-Slavova, I. Kahn and M. Karelson, Quantitative structure–activity relationship (QSAR) modeling of EC₅₀ of aquatic toxicities for Daphnia magna, J. Toxicol. Environ. Health, Part A, 2009, 72, 1181–1190.
25. K. P. Singh, S. Gupta and P. Rai, Predicting acute aquatic toxicity of structurally diverse chemicals in fish using artificial intelligence approaches, Ecotoxicol. Environ. Saf., 2013, 95, 221–233.
26. K. P. Singh, S. Gupta, A. Kumar and D. Mohan, Multispecies QSAR Modeling for Predicting the Aquatic Toxicity of Diverse Organic Chemicals for Regulatory Toxicology, Chem. Res. Toxicol., 2014, 27, 741–753.
27. K. P. Singh, S. Gupta and N. Basant, Predicting toxicities of ionic liquids in multiple test species – An aid in designing of green chemicals, RSC Adv., 2014, 4, 64443–64456.
28. K. P. Singh, S. Gupta and N. Basant, QSTR modeling for predicting aquatic toxicity of pharmacological active compounds in multiple test species for regulatory purpose, Chemosphere, 2015, 120, 680–689.
29. N. Basant, S. Gupta and K. P. Singh, Predicting toxicities of structurally diverse chemical pesticides in multiple aquatic test species using QSTR modeling approaches, Chemosphere, 2015, 139, 246–255.
30. N. Basant, S. Gupta and K. P. Singh, Predicting Toxicities of Diverse Chemical Pesticides in Multiple Avian Species Using Tree-Based QSAR Approaches for Regulatory Purposes, J. Chem. Inf. Model., 2015, 55, 1337–1348.
31. C. L. Russom, S. P. Bradbury, S. J. Broderius, D. E. Hammermeister and R. A. Drummond, Predicting modes of toxic action from chemical structure: Acute toxicity in the fathead minnow (Pimephales promelas), Environ. Toxicol. Chem., 1997, 16, 948–967.
32. H. Yuan, Y. Y. Wang and Y. Y. Cheng, Mode of action-based local QSAR modeling for the prediction of acute toxicity in the fathead minnow, J. Mol. Graphics Modell., 2007, 26, 327–335.
33. T. M. Martin, C. M. Grulke, D. M. Young, C. L. Russom, N. Y. Wang, C. R. Jackson and M. G. Barron, Prediction of Aquatic Toxicity Mode of Action Using Linear Discriminant and Random Forest Models, J. Chem. Inf. Model., 2013, 53, 2229–2239.
34. F. Lyakurwa, X. Yang, X. Li, X. Qiao and J. Chen, Development and validation of theoretical linear solvation energy relationship models for toxicity prediction to fathead minnow (Pimephales promelas), Chemosphere, 2014, 96, 188–194.
35. S. A. Kulkarni, D. V. Raje and T. Chakrabarti, Quantitative structure–activity relationships based on functional and structural characteristics of organic compounds, SAR QSAR Environ. Res., 2001, 12, 565–591.
36. A. A. Toropov and E. Benfenati, QSAR modeling aldehyde toxicity by means of optimization of correlation weights of nearest neighbouring codes, J. Mol. Struc.: THEOCHEM, 2004, 676, 165–169.
37. E. B. Martin Smiesko, Predictive models for aquatic toxicity of aldehydes designed for various model chemistries, J. Chem. Inf. Comput. Sci., 2004, 44, 976–984.
38. M. S. E. Benfenati, Thermodynamic descriptors derived from density functional theory calculations in predictions of aquatic toxicity, J. Chem. Inf. Model., 2005, 45, 378–389.
39. F. S. Lyakurwa, X. Yang, X. Li, X. Qiao and J. Chen, Development of in silico models for predicting LSER molecular parameters and for acute toxicity prediction to feathed minnow (Pimephales promelas), Chemosphere, 2014, 108, 17–25.
40. L. Sun, C. Zhang, Y. Chen, X. Li, S. Zhuang, W. Li, P. W. Lee and Y. Tang, In Silico prediction of chemical aquatic toxicity with chemicals category approaches and substructural alerts, Toxicol. Res., 2015, 4, 452–463.
41. S. Gupta, N. Basant and K. P. Singh, Predicting aquatic toxicities of benzene derivatives in multiple test species using local, global and interspecies QSTR modeling approaches, RSC Adv., 2015, 5, 71153–71163.
42. M. T. D. Cronin, Biological read-across: Mechanistically-based species-species and endpoint-endpoint extrapolations, in In Silico Toxicology: Principles and Applications, ed. M. T. D. Cronin and J. C. Madden, Royal Society of Chemistry, Cambridge, 2010, ch. 18, pp. 446–477.
43. A. Furuhama, K. Hasunuma and Y. Aoki, Interspecies quantitative structure–activity–activity relationships (QSAARs) for prediction of acute aquatic toxicity of aromatic amines and phenols, SAR QSAR Environ. Res., 2015, 26, 301–323.
44. R. N. Das, K. Roy and P. A. Popelier, Interspecies quantitative structure–toxicity–toxicity (QSTTR) relationship modeling of ionic liquids. Toxicity of ionic liquids to V. fischeri, D. magna and S. vacuolatus, Ecotoxicol. Environ. Saf., 2015, 122, 497–520.
45. K. Roy, R. N. Das and P. A. Popelier, Predictive QSAR modelling of algal toxicity of ionic liquids and its interspecies correlation with Daphnia toxicity, Environ. Sci. Pollut. Res., 2015, 22, 6634–6641.
46. M. T. D. Cronin, S. J. Enoch, M. Hewitt and J. C. Madden, Formation of Mechanistic Categories and Local Models to Facilitate the Prediction of Toxicity. Highlights of WC7 – part 3, ALTEX, 2009, 28, 45–49.
47. A. Bassan and A. P. Worth, The Integrated Use of Models for the Properties and Effects of Chemicals by means of a Structured Workflow, QSAR Comb. Sci., 2008, 27, 6–20.
48. T. H. Snelder, N. Lamouroux, J. R. Leathwick, H. Pella, E. Sauquet and U. Shanker, Predictive mapping of the natural flow regimes of France, J. Hydrol., 2009, 373, 57–67.
49. P. Yang, Y. H. Yang, B. B. Zhou and A. Y. Zomaya, A review of ensemble methods in bioinformatics, Curr. Bioinf., 2010, 5, 296–308.
50. T. Hancock, R. Put, D. Coomans, Y. Vander Heyden and Y. A. Everingham, Performance comparison of modern statistical techniques for molecular descriptor selection and retention prediction in chromatographic QSRR studies, Chemom. Intell. Lab. Syst., 2005, 76, 185–196.
51. T. G. Dietterich, Ensemble methods in machine learning, Lect. Notes Comput. Sci. Eng., 2000, 1857, 1–15.
52. J. Mahjoobi and A. Etemad-Shahidi, An alternative approach for the prediction of significant wave heights based on classification and regression trees, Appl. Ocean Res., 2008, 30, 172–177.
53. K. P. Singh, S. Gupta and P. Rai, Identifying pollution sources and predicting urban air quality using ensemble learning methods, Atmos. Environ., 2013, 80, 426–437.
54. M. T. D. Cronin and T. W. Schultz, Pitfalls in QSAR, J. Mol. Struct., 2003, 622, 39–51.
55. OPP Pesticide Ecotoxicity Database, 2014. Available at: http://www.ipmcenters.org/ecotox/ (accessed on October, 2014).
56. ChemSpider. http://www.chemspider.com (accessed on December, 2014).
57. The Chemopy program, http://www.scbdd.com/chemopy_desc/index/ (accessed on December, 2014).
58. S. Gupta, N. Basant and K. P. Singh, Estimating sensory irritation potency of volatile organic chemicals using QSARs based on decision tree methods for regulatory purpose, Ecotoxicology, 2015, 24, 873–886.
59. Z. Reitermanov , Data splitting, WDS'10 Proceedings of Contributed Papers, Part I, 2010, 31–36.
60. C. Y. Zhao, H. X. Zhang, X. Y. Zhang, M. C. Liu, Z. D. Hu and B. T. Fan, Application of support vector machine (SVM) for prediction toxic activity of different data sets, Toxicology, 2006, 217, 105–119.
61. H. Ishwaran and U. B. Kogalur, Consistency of random survival forests, Stat. Probab. Lett., 2010, 80, 1056–1064.
62. R. Pino-Mejias, M. D. Jimenez-Gamero, M. D. Cubiles-de-la-Vega and A. Pascual-Acosta, Reduced bootstrap aggregating of learning algorithms, Pattern Recognit. Lett., 2008, 29, 265–271.
63. P. Bühlmann and B. Yu, Analyzing bagging, Ann. Stat., 2002, 30, 927–961.
64. K. P. Singh, S. Gupta and D. Mohan, Evaluating influences of seasonal variations and anthropogenic activities on alluvial groundwater hydrochemistry using ensemble learning approaches, J. Hydrol., 2014, 511, 254–266.
65. J. H. Friedman, Stochastic gradient boosting, Comput. Stat. Data Anal., 2002, 38, 367–378.
66. R. Benigni, T. I. Netzeva, E. Benfenati, C. Bossa, R. Franke, C. Helma, E. Hulzebos, C. Marchant, A. Richard, Y. P. Woo and C. Yang, The expanding role of predictive toxicology: an update on the (Q)SAR models for mutagens and carcinogens, J. Environ. Sci. Health, Part C: Environ. Carcinog. Ecotoxicol. Rev., 2007, 25, 53–97.
67. K. Roy and A. S. Mandal, Development of linear and nonlinear predictive QSAR models and their external validation using molecular similarity principle for anti-HIV indolyl aryl sulfones, J. Enzyme Inhib. Med. Chem., 2008, 23, 980–995.
68. L. I. Lin, Assay validation using the concordance correlation coefficient, Biometrics, 1992, 48, 599–604.
69. L. M. Shi, H. Fang, W. Tong, J. Wu, R. Perkins, R. M. Blair, W. S. Branham, S. L. Dial, C. L. Moland and D. M. Sheehan, QSAR models using a large diverse set of estrogens, J. Chem. Inf. Comput. Sci., 2001, 41, 186–195.
70. G. Schuurmann, R. Ebert, J. Chen, B. Wang and R. Kuhne, External validation and prediction employing the predictive squared correlation coefficient test set activity mean vs training set activity mean, J. Chem. Inf. Model., 2008, 48, 2140–2145.
71. V. Consonni, D. Ballabio and R. Todeschini, Comments on the definition of the Q² parameter for QSAR validation, J. Chem. Inf. Model., 2009, 49, 1669–1678.
72. N. Chirico and P. Gramatica, Real external predictivity of QSAR models: how to evaluate it? Comparison of different validation criteria and proposal of using the concordance correlation coefficient, J. Chem. Inf. Model., 2011, 51, 2320–2335.
73. K. Roy, P. Chakraborty, I. Mitra, P. K. Ojha, S. Kar and R. N. Das, Some case studies on application of “r_m²” metrics for judging quality of quantitative structure–activity relationship predictions: Emphasis on scaling of response data, J. Comput. Chem., 2013, 34, 1071–1082.
74. C. Rücker, G. Rücker and M. Meringer, Y-Randomization and its variants in QSPR/QSAR, J. Chem. Inf. Comput. Sci., 2007, 47, 2345–2357.
75. I. Mitra, A. Saha and K. Roy, Exploring quantitative structure–activity relationship studies of antioxidant phenolic compounds obtained from traditional Chinese medicinal plants, Mol. Simul., 2010, 36, 1067–1079.
76. T. I. Netzeva, A. P. Worth, A. Aldenberg, R. Benigni, M. T. D. Cronin, P. Gramatica, J. S. Jaworska, S. Kahn, G. Klpoman and C. A. Marchant, et al., Current status of methods for defining the applicability domain of (quantitative) structure–activity relationship, ATLA, Altern. Lab. Anim., 2005, 33, 155–173.
77. K. Roy, S. Kar and P. Ambure, On a simple approach for determining applicability domain of QSAR models, Chemom. Intell. Lab. Syst., 2015, 145, 22–29.
78. A. Tropsha, A. Golbraikh and W. J. Cho, Development of kNN QSAR models for 3-arylisoquinoline antitumor agents, Bull. Korean Chem. Soc., 2011, 32, 2397–2404.
79. N. Chirico and P. Gramatica, Real external predictivity of QSAR models: Part 2. New intercomparable thresholds for different validation criteria and the need for scatter plot inspection, J. Chem. Inf. Model., 2012, 52, 2044–2058.
80. M. Vighi, M. M. Garlanda and D. Calamari, QSARs for toxicity of organophosphorous pesticides to Daphnia and honeybees, Sci. Total Environ., 1991, 109/110, 605–622.
81. A. A. Toropov and E. Benfenati, QSAR models for Daphnia toxicity of pesticides based on combinations of topological parameters of molecular structures, Chemosphere, 2003, 50, 403–408.
82. N. Amaury, E. Benfenati, E. Boriani, M. Casalengo, A. Chana, Q. Chaudhry, J. R. Chretien, J. Cotterill, F. Lemke and N. Piclin, et al., Results of DEMETRA models, in Quantitative structure–activity relationship (QSAR) for pesticide regulatory purposes, ed. E. Benfenati, Elsevier B.V., 2007, ch. 7, pp. 201–282.
83. P. Tremolada, A. Finizio, S. Villa, C. Gaggi and M. Vighi, Quantitative inter-specific chemical activity relationships of pesticides in the aquatic environment, Aquat. Toxicol., 2004, 67, 87–103.
84. D. X. Jiang, Y. Li, J. Li and G. X. Wang, Prediction of the aquatic toxicity of phenols to Tetrahymena pyriformis from molecular descriptors, Int. J. Environ. Res., 2011, 5, 923–938.
85. H. Sun, S. Shahane, M. Xia, C. P. Austin and R. Huang, Structure based model for the prediction of phospholipidosis induction potential of small molecules, J. Chem. Inf. Model., 2012, 52, 1798–1805.
86. P. Ertl, B. Rohde and P. Selzer, Fast Calculation of Molecular Polar Surface Area as a Sum of Fragment-Based Contributions and Its Application to the Prediction of Drug Transport Properties, J. Med. Chem., 2000, 43, 3714–3717.
87. A. Afantitis, G. Melagraki, P. A. Koutentis, H. Sarimveis and G. Kollias, Ligand – based virtual screening procedure for the prediction and the identification of novel b-amyloid aggregation inhibitors using Kohonen maps and Counter propagation Artificial Neural Networks, Eur. J. Med. Chem., 2011, 46, 497–508.
88. R. Todeschini, V. Consonni and R. Mannhold, in Handbook of Molecular Descriptors, ed. H. Kubinyi and H. Timmerman, Wiley-VCH, Weinheim, 2000.
89. M. Thakur, P. Makwane, A. Tiwari, L. Jain and A. Thakur, QSAR Study of PETT Derivatives: Role of Structural and Refractive Properties, International Conference on Emerging Trends in Computer and Image Processing (ICETCIP'2014) Dec. 15–16, 2014 Pattaya (Thailand), pp. 41–44.
90. N. Fjodorova, M. Novich, M. Vrachko, V. Smirnov, N. Kharchevnikova, Z. Zholdakova, S. Novikov, N. Skvortsova, D. Filimonov, V. Poroikov and E. Benfenati, Directions in QSAR Modeling for regulatory uses in OECD Member Countries, EU and in Russia, J. Environ. Sci. Health, Part C: Environ. Carcinog. Ecotoxicol. Rev., 2008, 26, 201–236.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5tx00321k

---