Perovskite ferroelectrics and relaxor-ferroelectric solid solutions with large intrinsic electrocaloric response over broad temperature ranges

Abstract

Electrocaloric materials have emerged as a viable technology for solid state heating/cooling and waste heat recovery applications. We determine here intrinsic electrocaloric (EC) entropy and temperature changes in perovskite ferroelectrics (FEs) using theoretical tools supported by experimentally measured heat capacities as a function of the applied electric field and temperature. A quantitative theoretical analysis of the thermal, pyroelectric and EC properties of representative ceramic FE systems is provided for BaTiO₃ and PbTiO₃ (PT) that display a weak and a strong first-order phase transformation to the FE state, and relaxor-FE xPb(Mg_l/3Nb_2/3)O₃–(1 − x)PbTiO₃ [xPMN−(1 − x)PT] solid solutions. Our results indicate that the intrinsic adiabatic temperature changes in relaxor-FEs are substantial. Temperature variations (related to reduced entropy) as high as 14 °C can be achieved with applied fields on the order of 1 MV cm⁻¹ at T ∼ 350 °C for (001) oriented 0.65PMN–0.35PT. Moreover, the EC response does not vary over a large temperature interval: 13 ± 1 °C for 200 < T < 600 °C. In PT, the adiabatic temperature change is approximately 28 °C for an applied field of 1 MV cm⁻¹, rivaling the best EC response observed in polymer FEs. This study provides the general methodology for theoretical analysis to both assess and guide the way in discovering newer high performance EC materials.

---

1. Introduction

Since the first observance nearly a decade ago of a giant electrocaloric (EC) effect in thin film ferroelectric PbZr_0.95Ti_0.05O₃ by Mischenko et al.,¹ the field of ferroelectric (FE) based solid state electrothermal interconversion has seen rapid advancement, significantly improving both the magnitude of usable EC adiabatic temperature change ΔT_EC, and the available cooling capacity as defined by an enthalpy (ΔH) or entropy (ΔS) variation: ΔH = ΔS·ΔT_EC.^2–5 Several materials systems have been proposed for use in electrothermal applications including FE/anti-FE ceramics in their single-crystal, bulk, and thin film forms, FE polymers/co-polymers/terpolymers, and liquid crystals.^6–13 There are also reports showing that relatively wide temperature range EC properties can be achieved in composites of ceramic and polymer relaxor FEs.¹⁴ These efforts have primarily been led through experimentation, augmented by expert intuition.¹⁵ The success of such an approach is demonstrated by the more than fourfold improvement in ΔT_EC with a concomitant increase in ΔH of similar magnitude.⁴ Fundamental enhancements in material properties of this kind directly impact system level performance and costs, reducing the effects of parasitic losses and potentially yielding system level performance competitive with vapor compression systems.⁷

Many applications of FEs, from random memory (FRAMs) devices,¹⁶ to piezoelectric actuators,^17,18 and pyroelectric infrared detectors,¹⁹ have all benefitted (and often been directed) by multi-scale theoretical approaches including ab initio and beyond first principles methods,^20,21 non-linear thermodynamics, and atomistic models.^22–24 Thus, it is compelling to employ similar methods as a means for understanding the material properties and discovering new materials systems for ECs. We present here a complete theoretical analysis of intrinsic adiabatic temperature changes in perovskite FEs using computational tools supported by carefully measured heat capacities²⁵ as a function of the applied electric field (E) and temperature (T). Specifically, thermal, pyroelectric and EC properties of prototypical FEs BaTiO₃ (BT) and PbTiO₃ (PT), and relaxor-FEs xPb(Mg_l/3Nb_2/3)O₃–(1 − x)PbTiO₃ [xPMN–(1 − x)PT] compounds are calculated. Two specific compositions of PMN–PT are chosen as representatives of a relaxor and a relaxor-FE solid solution, 0.90PMN–0.10PT and 0.65PMN–0.35PT, respectively. 0.90PMN–0.10PT is a relaxor composition that is far from the morphotropic phase boundary (MPB). 0.65PMN–0.35PT lies in close proximity of the MPB, where pseudo-rhombohedral, pseudo-monoclinic/orthorhombic, and pseudo-tetragonal phases can co-exist and phase transitions can be induced through applied electric and elastic fields.²⁶ This system is of particular interest because it displays a strong order–disorder and crystallographic phase transitions which couple with external stimuli. These particular characteristics are arguably at the core of the very large electromechanical response exhibited by xPMN–(1 − x)PT (with or without additional doping) which are used in high-strain actuators/transducers.²⁷ The very large electromechanical response has been attributed to the inherently (intrinsic) large piezoelectric response that stems from ionic displacements,²⁸ a large “extrinsic” contribution from highly adaptive nano- and mesoscale domain structures,²⁹ and a strong contribution from electrostriction.³⁰ A relatively large temperature change of ∼5 °C at an applied field difference of ∼900 kV cm⁻¹ and T = 75 °C has been reported for this solid solution for x = 0.90.²⁶

Our analysis is based on the thermodynamic methodology that is described in detail in the next section. This study uncovers two significant findings. Firstly, the intrinsic adiabatic temperature changes in relaxor-FEs are substantial and relatively temperature insensitive. ΔT_EC variations as high as 14 °C can be achieved with applied fields on the order of 1 MV cm⁻¹ at T ∼ 350 °C for (001) oriented 0.65PMN–0.35PT. This EC response does not vary over a large temperature interval: ΔT_EC = 13 ± 1 °C for 200 < T < 600 °C. Secondly, our studies indicate that one can find perovskite FEs with exceedingly large intrinsic EC effects. ΔT_EC is ∼28 °C in PT near its FE transition temperature for an applied field of 1 MV cm⁻¹, rivaling the best EC response observed in polymer FEs.^31,32 This is particularly important since only limited fundamental studies of the EC response exist in perovskite systems at high fields.^33,34 The overarching purpose of this study is to provide a theoretical framework by which new candidate materials can be assessed for their EC properties and to guide experimental research in exploiting the full potential of existing materials.

2. Methodology

2.1 Theoretical approach

We consider a monodomain single crystal FE in an unconstrained, unstressed state. We analyze PT, BT, 0.90PMN–0.10PT, and 0.65PMN–0.35PT that undergo a cubic (Pm3m) paraelectric (PE) to tetragonal (P4mm) FE transition at T_C. The components of the polarization vector P for the PE and the FE phases are P₁ = P₂ = P₃ = 0 and P₁ = P₂ = 0, P₃ = P ≠ 0, respectively. The volumetric (excess) free energy due to polarization is given by:

G(T,E,P) = G₀ + α₁P² + α₁₁P⁴ + α₁₁₁P⁶ − EP (1)

where G₀ is the free energy density of the (unpolarized) PE phase, and α₁, α₁₁, and α₁₁₁ are dielectric stiffness coefficients. α₁ is given by the Curie–Weiss law such that α₀ = (T − T_C)/(2ε₀C)⁻¹ where ε₀ is the permittivity of space and C is the Curie–Weiss constant. In eqn (1), E = (0,0,E₃ = E) is the applied electric field.

All thermodynamic properties and stiffness coefficients used in the computations are given in Table 1. For PMN–PT, we use Heitmann–Rossetti free energy potentials that were obtained using a combined phenomenological and topological analysis.³⁵ The free energy potentials are supplemented by experimental “hard-mode” contributions to heat capacity determined experimentally [see description below and ref. 36]. The equilibrium polarization P⁰ is then determined via solving the equation of state ∂G/∂P = 0.

Table 1 Property coefficients: property coefficients of BT, PT, 0.90PMN–0.10PT, and 0.65PMN–0.35PT. The data are compiled from ref. 18 and 23

Parameter/material	BT	PT	0.90PMN–0.10PT	0.65PMN–0.35PT
T C (°C)	121	475	38	159
α 1 (10^5 m F^−1)	3.76 (T − TC)	3.68 (T − TC)	1.81 (T − TC)	2.415 (T − TC)
α 11 (10^6 m^5 C^−2 F^−1)	3.6T–630	−146–0.38T	61.6–0.038T	28.9–0.038T
α 111 (10^9 m^8 C^−4 F^−1)	6.6	0.257	0.257	0.257
S 11 (10^12 m^2 N^−1)	8.3	7.7	0.018	0.31
S 12 (10^12 m^2 N^−1)	−2.73	−2.33	−0.63	−0.11
S 44 (10^12 m^2 N^−1)	9.22	8.77	−0.56	0.245
Q 11 (m^4 C^−2)	0.11	0.09	0.084	0.084
Q 12 (m^4 C^−2)	−0.034	−0.025	−0.025	−0.025
Q 44 (m^4 C^−2)	0.029	0.039	0.035	0.035
Hard mode CE (10^6 J g^−1 K^−1)	3.74	4	8(5 × 10^−9 × T^3 − 3 × 10^−6 × T^2 + 6 × 10^−4 × T + 0.31)	8(4 × 10^−9 × T^3 − 3 × 10^−6 × T^2 + 8 × 10^−4 × T + 0.3)

---

The two most important factors in determining the adiabatic temperature change ΔT_EC at a given T with an applied electric field difference ΔE = (E_b − E_a) are: the pyroelectric coefficient of the material, p, and the heat capacity at constant E, C^XS_E. The proper definitions of these quantities follow from the relevant Maxwell relations. At constant E, the excess entropy S^XS_E, the excess specific heat ΔC_E, and the pyroelectric coefficient p follow from:

ΔT_EC as result of a change in the electric field strength ΔE = E_b − E_a can then be calculated via: For all materials studied in this investigation, we estimate the absolute value of specific heat, C_E(T, E) by adding the computed zero-field values of the excess specific heat ΔC_E(T, E) from eqn (3) to the lattice or hard-mode contributions taken from the experimental values.

2.2 Experimental details

This study has benefited from a substantial series of test data from prior experimental results, detailed extensively in ref. 25 and 37–41. The (total) heat capacity at constant electric field E (C_E) was determined using either a high-resolution calorimeter described in ref. 25, 38 and 41, or a conventional Quantum Design Physical Properties Measurement System (PPMS) technique for all materials analyzed in this study except for PT. There is a quantitative and qualitative agreement between the calculated and measured heat capacities as discussed in ref. 37. The experimental values of C_E, which consists of the excess heat capacity due to the spontaneous polarization as given in eqn (3) and lattice (hard mode) contributions, allow us to evaluate the theoretical adiabatic temperature changes (ΔT_EC) with the application of an electric field difference ΔE [see eqn (5)].

In addition, there exists experimental data on ΔT_EC for 0.90PMN–0.10PT and 0.65PMN–0.35PT which were measured directly using the methods given in ref. 2 and 37–40. These experimental results provide us an opportunity to compare theoretical and experimental work, at least in the low electric field regime. The details of our previous work on 0.90PMN–0.10PT and 0.65PMN–0.35PT can be found in ref. 39. Briefly, the materials in that study were polished single crystals that are perpendicularly cut to the [110]. For direct EC measurements, a high-resolution calorimeter with small modifications to the experimental setup has been utilized to measure a sample temperature variation due to the EC when an external field was applied. A step voltage form is applied to all the samples by a high-voltage generator. The sample temperature was acquired by a small bead thermistor attached to the sample electrode. The surrounding bath temperature was stabilized by a temperature controller within 0.1 mK. In typical sequence the field was switched on to some level for 500 seconds and then switched off. During this time and additional 500 seconds after the switching off the field the relaxation of the sample's temperature was monitored. This allows detailed analysis of the amplitude of the EC temperature change induced by the electric field as described in details in ref. 2.

3. Analysis of results

3.1 Polarization, heat capacity, and pyroelectric coefficient

In Fig. 1, we plot the equilibrium (spontaneous) polarization P⁰ as functions of T and applied electric field E for PT, BT, 0.90PMN–0.10PT, and 0.65PMN–0.35PT. As expected, BT and PT display first-order phase transitions as described by the jump in P⁰ for E = 0 at the FE–PE transformation temperature T_C. In BT, this first-order phase transition is weaker compared to PT as characterized by the magnitude of the polarization jump at the respective T_Cs. An applied electric field in the direction of the spontaneous polarization “smears” the phase transformation and it destroys the discontinuities in thermodynamic properties that are a function of polarization at the phase transition temperature. For BT, a field as high as 20 kV cm⁻¹ is sufficient to wash out the first-order phase transition where as in PT, higher fields are required (E = 100 kV cm⁻¹). On the other hand, both PMN–PT compositions display a second-order phase transitions. Here, there is no discontinuity at T_C in the polarization response and the effect of the applied electric field is similar resulting in a smearing of the phase transformation.

Fig. 1 Theoretical polarization variations: temperature and electric field dependent polarization variations of (a) BT, (b) PT, (c) 0.90PMN–0.10PT, and (d) 0.65PMN–0.35PT (labels for (b), (c), and (d) are the same as (a)).

In Fig. 2 and 3 we plot the temperature dependence of the p and the C^XS_E for the four materials investigated for E = 0, 20, 100, and 1000 kV cm⁻¹. These parameters are defined through the Maxwell equations as described under “Materials and Methods” and are essentially partial derivatives of the polarization with respect to temperature. As such, near T_C, these quantities display a λ-type anomaly and this anomaly disappears with the application of an electric field in the direction of the equilibrium polarization. The behavior shown in Fig. 1–3 are expected responses and the relevant thermodynamic background can be found elsewhere.³⁶

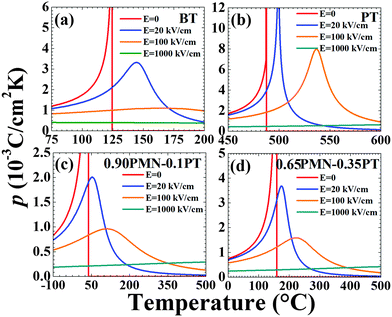Fig. 2 Theoretical pyroelectric behavior: pyroelectric coefficient, p, of (a) BT, (b) PT, (c) 0.90PMN–0.10PT, and (d) 0.65PMN–0.35PT as a function of temperature and applied electric field E.

Fig. 3 Theoretical heat capacity variations: excess heat capacity of (a) BT, (b) PT, (c) 0.90PMN–0.10PT, and (d) 0.65PMN–0.35PT as a function of temperature and applied electric field E (labels for (b), (c), and (d) are the same as (a)).

3.2 Adiabatic temperature change

It is necessary to experimentally determine or to be able to compute the reversible ΔT_EC near and away from the T_C as this is a critical parameter in the estimation of the system-level coefficients of performance. The temperature dependence of ΔT_EC as functions of T and ΔE are thus plotted in Fig. 4. For all four materials, the field change ΔE is taken relative to an initial bias of E_a = 50 kV cm⁻¹. Fig. 4a plots ΔT_EC as a function of applied field difference and temperature for BT. Near T_C (121 °C), ΔT_EC is computed to be 0.8, 2.8, 4.4, and 7.3 °C for ΔE = 50, 250, 500, and 1000 kV cm⁻¹. The experimental data points are taken from ref. 37 where ΔT_EC is obtained through direct high-resolution EC measurements for BT single-crystals oriented along the [001]. Although the applied fields are different and the initial fields are relatively small, ΔT_EC is larger compared to theoretical predictions (1.5 °C for ΔE = 28 kV cm⁻¹). We attribute this difference both due to extrinsic contributions to the EC effect, and the fact that we do not account for the non-zero entropy change between zero applied field and our lower bound value.

Fig. 4 Theoretical adiabatic temperature changes: EC adiabatic temperature change, ΔT_EC, of (a) BT, (b) PT, (c) 0.90PMN–0.10PT, and (d) 0.65PMN–0.35PT as a function of temperature for ΔE ranging from 50 to 1000 kV cm⁻¹. The initial (biasing field) E_a is taken as 50 kV cm⁻¹. Also shown are experimentally measured EC data points (solid symbols) in BT, 0.90PMN–0.10PT, and 0.65PMN–0.35PT samples (2, 33, 43).

For both 0.90PMN–0.10PT and 0.90PMN–0.35PT, the ΔT_EC responses are much broader and relatively less temperature sensitive as shown in Fig. 4c and d, respectively, compared to BT and PT. In the case of 0.90PMN–0.10PT, ΔT_EC = 0.8, 2.9, 4.9, and 8.8 °C for ΔE = 50, 250, 500, 1000 kV cm⁻¹, respectively, near its T_C of 38 °C. For 0.65PMN–0.35PT (T_C = 159 °C), the EC response is considerably larger; ΔT_EC = 1.6, 5.5, 8.5, and 13.1 °C for ΔE = 50, 250, 500, 1000 kV cm⁻¹, respectively. In the two PMN–PT systems (Fig. 4c and d), we found good agreement with directly measured EC data at lower fields (solid symbols). This difference can again be related to extrinsic contributions. Furthermore, experimentally, we start from zero field thus invoking the latent heat release (for fields below 14 kV cm⁻¹ which is critical field to induce the liquid–vapor type critical point in this system above which there is no contribution from a latent heat³⁹), which in turn enhances the EC effect in contrast to our calculation in which field change starts from 50 kV cm⁻¹. Thus, because essentially no latent heat is released and we probe only continuous variations of the total entropy (S) above the discontinuous jump in S our theoretical results are diminished compared to experiment.

For PT, the EC response near T_C = 490 °C is significantly larger, where ΔT_EC = 3.2, 15.0, 21.1, and 28.5 °C for ΔE = 50, 250, 500, and 1000 kV cm⁻¹ (Fig. 4b). We attribute this behavior to the more pronounced first-order phase transformation in PT compared to BT, as discussed in detail by Zhang et al.⁴² The “jump” in the polarization (and hence the entropy change) at T_C in PT is associated with the relatively large displacement of the Ti⁴⁺ ions with respect to the O²⁻ ions. In PT single crystals the eigenstrain at RT is as large as 3.67%.⁴³ The large intrinsic non-centrosymmetric displacement below T_C corresponds to a large entropy variation when compared to the non-polarized centrosymmetric PE phase. This displacement is considerably larger in PT compared to the BT and 0.90PMN–0.10PT and 0.65PMN–0.35PT (0.70%, 0.08%, and 1.30%, respectively, at RT^44–46) and this is the reason for the significantly larger ΔT_EC near their respective T_Cs.

4. Discussion

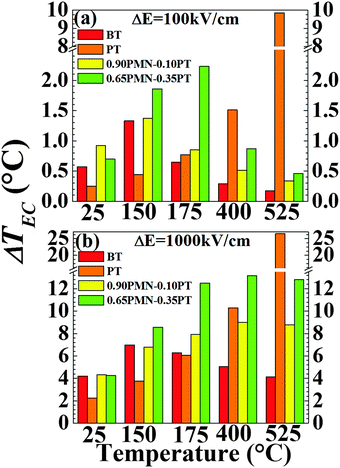
For E = 0, there is a λ-anomaly associated with the first-order FE to PE phase transformation, resulting in (theoretically) an infinitely large p and C^XS_E at the equilibrium transition temperature T_C. The application of high enough E along the polarization direction results in the smearing of the temperature dependence of p and C^XS_E as shown in Fig. 2 and 3 for all four materials. This results in the disappearance of well-defined maxima in these properties at sufficiently large electric fields: the maxima in p and C^XS_E shift to higher temperatures and are reduced in magnitude with an increase in E. Furthermore, these quantities become progressively less sensitive to temperature for larger fields. In the case of PT, however, owing to a much stronger first-order FE–PE phase change as defined by the jump in the spontaneous polarization at T_C (see Fig. 1), relatively higher electric fields are required to achieve the same effect. At lower field difference, all four materials show typical FE behavior such that there is an increase in the value ΔT_EC with operating temperature, up to a point around their respective T_C. There is a decrease in ΔT_EC beyond a maximum near the T_C with increasing temperature which is expected⁴² since the pyroelectric response for T > T_C for small electric fields is essentially given by the variation of the electric field induced polarization in the PE phase. For significantly higher fields, the EC response of PT and BT shows a maximum in ΔT_EC near T_C and a decrease for T > T_C. However, in the cases of 0.90PMN–0.10PT and 0.65PMN–0.35PT, ΔE = 1000 kV cm⁻¹ is sufficiently large to obscure the effect of the phase transition at T_C, at least for temperatures in which the material retains it ferroelectric properties. Such a difference in behavior can be assigned, at least in part, to the presence of a relaxor nature of the FE solid solutions, and the accompanying dispersion of the FE–PE transition.⁴⁷ Application of a large enough electric field can also be expected to result in a partial stabilization of the FE phase to slightly higher temperatures than T_C.⁴⁸ Also, as it can be seen in Fig. 5, both 0.90PMN–0.10PT and 0.65PMN–0.35PT have a relatively temperature insensitive ΔT_EC over a larger temperature range compared to PT and BT. The large peak in EC response of the PMN–PT composition corresponding to the MPB is similar to the previously calculated (and experimentally confirmed) peaks in the dielectric, piezoelectric and elastic compliance at the MPB for lead zirconate–lead titanate (PZT) solid solutions.³⁶ The enhancement in the properties are often attributed to the co-presence of two (or more) phases with differing polarization directions. This could be related to the disappearance of anisotropy contributions to the free energy and formation of nano-domains.^36,49

We note that the calculated values in this work are limited to intrinsic EC response. Effective functional responses in ferroic materials are due to both their intrinsic (lattice) and extrinsic nature which includes motion of domain walls, formation of phase boundaries, and local (defect) dipoles. While the amount of extrinsic contributions to the effective EC response has not been quantified, such data are indeed available for the dielectric response, and in part, also for the piezoelectric response of the materials considered here. In general, relaxor-FEs such as PMN–PT have been shown to exhibit enhanced extrinsic properties that can be as high as 30–80% of the total functional response in BT and PZT ceramics.⁵⁰ This contribution could be significantly larger in relaxor-PbTiO₃ near MPB single crystals, evaluated to be ∼300%.⁵¹ We can, therefore, expect that the overall EC response of these single crystals to be similarly augmented by the extrinsic contributions, and through domain wall engineering, i.e. creation of specific mobile (adaptive) domain architectures to further enhance entropy variations with an applied electric field. This enhancement should be more pronounced at relatively low initial biases. Finally, we show in Fig. 5 a more detailed comparison of the EC response of all four materials at five specific temperatures (T = 25, 150, 175, 400 and 525 °C) at an intermediate field of ΔE = 100 kV cm⁻¹ (Fig. 5a) and a relatively higher field of ΔE = 1000 kV cm⁻¹ (Fig. 5b). In both cases, E_a was taken to be 50 kV cm⁻¹.

Fig. 5 Theoretical adiabatic temperature change: comparative adiabatic temperature change, ΔT_EC, of BT, PT, 0.90PMN–0.10PT, and 0.65PMN–0.35PT at different working temperatures: (a) ΔE = 100 kV cm⁻¹ and (b) ΔE = 1000 kV cm⁻¹. The initial (biasing field) E_a is taken as 50 kV cm⁻¹.

5. Conclusions

In summary, we have calculated the EC temperature changes in BT, PT, 0.90PMN–0.10PT, and 0.65PMN–0.35PT over a wide range of temperatures. Large EC responses close to or exceeding 10 °C were found over a very broad temperature range exceeding several hundred degrees in case of BT, and two PMN–PT systems. In PT, a giant EC response of 28 °C at 1 MV cm⁻¹ is predicted. These adiabatic temperature changes correspond to significant entropy variations. For example, ΔS = −22.16 and −7.29 J kg⁻¹ K⁻¹ for PT and 0.65PMN–0.35PT, respectively for temperatures at which each material shows the maximum ΔT_EC (561 °C for PT and 253 °C for 0.65PMN–0.35PT). This is similar to some of the best EC responses experimentally observed at similar fields in polymeric FEs. It should be noted that ΔT_EC(ΔE) shows little saturation at large fields indicating that in these materials truly very large EC response is achievable.⁵² Therefore, it may prove optimal for application to operate these materials at large fields as demonstrated recently in thick films. Lastly, we note that many of the experimental studies of ceramic based materials have been performed on EC films clamped to a substantially thicker substrate. Considering that this two-dimensional clamping reduces all property coefficients including the pyroelectric and EC response,^42,53 our analysis provides a guide to the experimentalist and application community, in as much as it predicts that the highest EC responses will be best achieved by removing the constraints limiting the full performance of these materials.

Acknowledgements

Z. K. acknowledges support by the Slovenian Research Agency through Grant No. P1-0125 and J2-6779. N. B. G. gratefully acknowledges funding from the US National Science Foundation through grants DMR-1255379 and CMMI-1537262.

References

1. A. S. Mischenko, Q. Zhang, J. F. Scott, R. W. Whatmore and N. D. Mathur, Science, 2006, 311, 1270–1271.
2. Z. Kutnjak, B. Rožič and R. Pirc, Wiley Encyclopedia of Electrical and Electronics Engineering, 2015.
3. I. Takeuchi and K. Sandeman, Phys. Today, 2015, 68, 48.
4. S. P. Alpay, J. M. Mantese, S. Trolier-McKinstry, Q. Zhang and R. W. Whatmore, MRS Bull., 2014, 39, 1099–1111.
5. T. M. Correia, S. Kar-Narayan, J. S. Young, J. F. Scott, N. D. Mathur, R. W. Whatmore and Q. Zhang, J. Phys. D: Appl. Phys., 2011, 44, 165407.
6. S. G. Lu and Q. Zhang, Adv. Mater., 2009, 21, 1983–1987.
7. M. Valant, Prog. Mater. Sci., 2012, 57, 980–1009.
8. J. F. Scott, Annu. Rev. Mater. Res., 2011, 41, 229–240.
9. M. Ožbolt, A. Kitanovski, J. Tušek and A. Poredoš, Int. J. Refrig., 2014, 40, 174–188.
10. F.-C. Sun, A. M. Dongare, A. D. Asandei, S. P. Alpay and S. Nakhmanson, J. Mater. Chem. C, 2015, 3(32), 8389–8396.
11. V. F. Freitas, O. A. Protzek, L. A. Montoro, A. M. Gonçalves, D. Garcia, J. A. Eiras, R. Guo, A. S. Bhalla, L. F. Cótica and I. A. Santos, J. Mater. Chem. C, 2014, 2(2), 364–372.
12. J. Varghese, R. W. Whatmore and J. D. Holmes, J. Mater. Chem. C, 2013, 1(15), 2618–2638.
13. N. Bassiri-Gharb, Y. Bastani and A. Bernal, Chem. Soc. Rev., 2014, 43(7), 2125–2140.
14. Q. Li, G. Zhang, X. Zhang, S. Jiang, Y. Zeng and Q. Wang, Adv. Mater., 2015, 27, 2236–2241.
15. Y. Liu, I. C. Infante, X. Lou, L. Bellaiche, J. F. Scott and B. Dkhil, Adv. Mater., 2014, 26, 6132–6137.
16. R. Ramesh, S. Aggarwal and O. Auciello, Mater. Sci. Eng., R, 2001, 32, 191–236.
17. P. Yudin and A. Tagantsev, Nanotechnology, 2013, 24, 432001.
18. H. Khassaf, N. Khakpash, F. Sun, N. M. Sbrockey, G. S. Tompa, T. S. Kalkur and S. P. Alpay, Appl. Phys. Lett., 2014, 104, 202902.
19. F. Jin, G. W. Auner, R. Naik, N. W. Schubring, J. V. Mantese, A. B. Catalan and A. L. Micheli, Appl. Phys. Lett., 1998, 73, 2838–2840.
20. I. A. Kornev, L. Bellaiche, P.-E. Janolin, B. Dkhil and E. Suard, Phys. Rev. Lett., 2006, 97, 157601.
21. J. Lutsko, D. Wolf, S. Yip, S. Phillpot and T. Nguyen, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 11572.
22. S. R. Phillpot, S. B. Sinnott and A. Asthagiri, Annu. Rev. Mater. Res., 2007, 37, 239–270.
23. N. Khakpash, H. Khassaf, G. A. Rossetti Jr and S. P. Alpay, Appl. Phys. Lett., 2015, 106, 082905.
24. K. Bhattacharya and G. Ravichandran, Acta Mater., 2003, 51, 5941–5960.
25. N. Novak, G. Cordoyiannis and Z. Kutnjak, Ferroelectrics, 2012, 428, 43–48.
26. A. Mischenko, Q. Zhang, R. W. Whatmore and N. Mathur, Appl. Phys. Lett., 2006, 89, 242912.
27. Y. Zhang, G. Gao, H. L. Chan, J. Dai, Y. Wang and J. Hao, Adv. Mater., 2012, 24, 1729–1735.
28. L. Bellaiche and D. Vanderbilt, Phys. Rev. Lett., 1999, 83, 1347.
29. Y. Sato, T. Hirayama and Y. Ikuhara, Appl. Phys. Lett., 2012, 100, 172902.
30. V. Vikhnin, R. Blinc and R. Pirc, J. Appl. Phys., 2003, 93, 9947–9952.
31. S. G. Lu, B. Rozic, Q. M. Zhang, Z. Kutnjak, R. Pirc, M. Lin and L. Gorny, Appl. Phys. Lett., 2010, 97, 202901.
32. G. Zhang, Q. Li, H. Gu, S. Jiang, K. Han, M. R. Gadinski, M. A. Haque, Q. Zhang and Q. Wang, Adv. Mater., 2015, 27, 1450–1454.
33. I. Ponomareva and S. Lisenkov, Phys. Rev. Lett., 2012, 108, 167604.
34. R. Pirc, Z. Kutnjak, R. Blinc and Q. Zhang, Appl. Phys. Lett., 2011, 98, 1909.
35. A. A. Heitmann and G. A. Rossetti, J. Am. Ceram. Soc., 2014, 97, 1661–1685.
36. G. Akcay, S. P. Alpay, G. A. Rossetti Jr and J. F. Scott, J. Appl. Phys., 2008, 103, 024104.
37. N. Novak, Z. Kutnjak and R. Pirc, EPL, 2013, 103, 47001.
38. Z. Kutnjak, J. Petzelt and R. Blinc, Nature, 2006, 441, 956–959.
39. N. Novak, R. Pirc, M. Wencka and Z. Kutnjak, Phys. Rev. Lett., 2012, 109, 037601.
40. G. Sebald, L. Seveyrat, D. Guyomar, L. Lebrun, B. Guiffard and S. Pruvost, J. Appl. Phys., 2006, 100, 124112.
41. D. Guyomar, G. Sebald, B. Guiffard and L. Seveyrat, J. Phys. D: Appl. Phys., 2006, 39, 4491.
42. J. Zhang, A. A. Heitmann, S. P. Alpay and G. A. Rossetti Jr, J. Mater. Sci., 2009, 44, 5263–5273.
43. G. Shirane, H. Sadao and S. Kazuo, Phys. Rev., 1950, 80(6), 1105.
44. M. H. Frey and D. A. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(5), 3158.
45. J. C. Ho, K. S. Liu and I. N. Lin, J. Mater. Sci., 1993, 28(16), 4497–4502.
46. Z.-G. Ye, Y. Bing, J. Gao, A. A. Bokov, P. Stephens, B. Noheda and G. Shirane, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67(10), 104104.
47. A. A. Bokov and Z.-G. Ye, J. Adv. Dielectr., 2012, 2, 1241010.
48. L. Garten, P. Lam, D. Harris, J.-P. Maria and S. Trolier-McKinstry, J. Appl. Phys., 2014, 116, 044104.
49. D. Damjanovic, Appl. Phys. Lett., 2010, 97, 062906.
50. D. Damjanovic and M. Demartin, J. Phys.: Condens. Matter, 1997, 9, 4943.
51. D. Lin, S. Zhang, Z. Li, F. Li, Z. Xu, S. Wada, J. Luo and T. R. Shrout, J. Appl. Phys., 2011, 110, 084110.
52. S. Lu, B. Rožič, Q. Zhang, Z. Kutnjak, X. Li, E. Furman, L. J. Gorny, M. Lin, B. Malič and M. Kosec, Appl. Phys. Lett., 2010, 97, 162904.
53. J. Zhang, M. W. Cole and S. P. Alpay, J. Appl. Phys., 2010, 108(5), 054103.

---