High-energy density nanofiber-based solid-state supercapacitors

Abstract

We have developed binder-free solid-state electric double layer supercapacitors using freestanding porous carbon nanofiber electrodes fabricated using electrospinning and silica-based ionic liquid gel electrolytes. To ensure close electrode/electrolyte contact and efficient transport of ions for high power operation, we fabricated our electrodes by uniformly filling freestanding samples of porous carbon nanofiber mats with a blend of silica sol–gel precursor and ionic liquid electrolyte, which were then appropriately dried/gelled to form all-solid supercapacitors. Two different carbon nanofiber samples have been investigated with high specific surface areas of 1218 m² g⁻¹ and 2282 m² g⁻¹. The resulting solid-state supercapacitor can operate in a large voltage window of 3.5 V. We achieved specific capacitance (C_sp) and specific energy (E_cell, based on the mass of the two electrodes) of up to 144 F g⁻¹ and 61 W h kg⁻¹ respectively, rivaling that of lead-acid batteries, with a high active material (carbon only) loading of 3–5 mg cm⁻².

---

Introduction

High power density and long cycle life of supercapacitors in comparison to conventional batteries make supercapacitors propitious energy storage devices. Supercapacitors are ideal for applications that necessitate high power capability, such as rapid acceleration in electric vehicles, and long cycle lifetime in portable electronics. Energy is stored in supercapacitors in one of two ways; through ion adsorption and desorption at the electrode–electrolyte interface in electric double layer capacitors (EDLCs), or through rapid faradaic redox reactions in pseudocapacitors.^1,2 While the former provides higher power, but lower energy density, the latter provides higher energy density, but lower power.^2,3 To enhance the energy density of EDLCs, ionic liquids, particularly room-temperature ionic liquids (RTILs), have attracted immense attention due to their larger electrochemical potential window (up to 4 V).^4–9 In addition, RTILs offer the additional advantages of excellent thermal, electrochemical, and moisture stability. Development of all-solid state supercapacitors using ionic liquid-based electrolyte has also gained attention recently to eliminate the leakage and integrity problems inherent to liquid electrolyte EDLCs, while aiming to preserve their high energy density. However, current works with solid-state supercapacitors show limited voltage windows (typically up to 1 V) due to the choice of electrolyte used, and thus provide lower energy density (<10 W h kg⁻¹)^10–13 or have limited total cell capacitance and areal capacitance (20 mF cm⁻²) due to extremely low mass (<0.2 mg cm⁻²) and ultra-low thickness of electrodes (10–15 μm) used.^14–16 Such mass loading is more than an order of magnitude lower than that recommended for device testing and practical applications.¹⁷ Other works on solid-state supercapacitors tested the devices at high temperatures to enhance electrolyte conductivity, thereby failing to meet the practical operating conditions of supercapacitors in various applications¹¹ or show extremely resistive cyclic voltammetry behavior.¹⁸ It is of utmost importance to develop solid-state electrolytes that preserve the key properties of ionic liquids such as low charge transfer resistance, similar diffusion constant, and, more importantly, a high operating voltage.

The majority of electrodes today are carbon-based, created through the use of binding agents,¹⁶ spray deposition,^13,19 or using pre-purchased material such as nanofoam carbon paper.¹⁸ Other electrodes fabricated via deposition of carbon nanotubes (CNT) on office paper¹⁵ or bacterial nanocellulose paper¹⁴ have also been reported. Carbon nanofibers, as shown in this work, make excellent candidates for EDLC electrodes due to their high specific surface area, good electrical conductivity, controllable pore size and thickness, and most importantly their ability to be fabricated in a freestanding mat format, which can be heat-treated to form binder-free carbon electrodes with through-connected macropores for fast ion transport.^20,21–24

In this work, we demonstrate the first ever binder-free solid-state EDLC with energy density rivaling that of lead-acid batteries. In particular, the supercapacitor devices are developed using freestanding binder-free porous carbon nanofiber electrodes (fabricated using electrospinning) and silica-based ionic liquid gel electrolytes. To ensure close electrode/electrolyte contact and efficient transport of ions for high power operation, the electrodes were fabricated by uniformly filling freestanding samples of porous carbon nanofiber mats with a blend of silica sol–gel precursor and ionic liquid electrolyte, which were then appropriately dried/gelled to form all-solid supercapacitors. Two porous carbon nanofiber samples with high specific surface areas of 1218 m² g⁻¹ (PCNF) and 2282 m² g⁻¹ (A-PCNF) were incorporated as electrodes and their performance was investigated. The resulting solid-state supercapacitor achieved a high specific capacitance (C_sp) and specific energy (E_cell, based on the mass of the two electrodes) of up to 144 F g⁻¹ and 61 W h kg⁻¹ respectively, with a voltage window of 3.5 V and active material (carbon only) mass loading of 3–5 mg cm⁻². Such high energy density is comparable to that of lead-acid batteries.

Results and discussion

Briefly, polyacrylonitrile (PAN)/Nafion (30 : 70 wt%) blend was dissolved in dimethylformamide (DMF) (21 : 79 wt%) and electrospun onto grounded collectors. The fiber mat was then stabilized in air at 280 °C and then pyrolyzed at 800 °C in nitrogen to produce porous carbon nanofiber (PCNF) mat via simultaneous carbonization of PAN and decomposition of Nafion (to create through connected pores). To increase the surface area, further activation was conducted through soaking of PCNF mats in KOH solution (30 : 70 KOH : DI water wt%), and then heating to 800 °C in a flowing nitrogen environment to induce chemical etching of the carbon framework, producing micropores. The resultant nanofiber samples are referred to as activated porous carbon nanofibers (A-PCNF). Scanning electron microscope (SEM) image of the A-PCNF sample is shown in Fig. 1a. The overall fiber morphology remains intact after pyrolysis as well as after activation (see Fig. S1†). Fig. 1b and Table 1 show the pore size distribution data for PCNF and A-PCNF. Activation significantly increases the Brunauer, Emmett and Teller (BET) surface area from 1218 m² g⁻¹ (for PCNF) to 2282 m² g⁻¹ (for A-PCNF), while retaining the overall pore size distribution and a significant fraction of mesopores as seen in Fig. 1b, suggesting that activation not only creates additional micropores (as expected), but also etches the existing pores to form larger mesopores. The corresponding isotherms are shown in Fig. S2 in the ESI.†

Fig. 1 (a) SEM image of A-PCNF. (b) Pore size distribution for PCNF and A-PCNF. (c) Impedance spectra (IS) of the IL with 0.05 M iodine and 0.5 M lithium-iodide for characterization of solid-state electrolyte, with circuit fit lines. Insets: right – standard Randles circuit used for fitting the IS; left – picture of the ionic liquid electrolyte after gelation (using TMOS). (d) Top down SEM image of PCNF electrodes filled with IL-based solid electrolyte.

Table 1 BET analysis data of activated (A-PCNF) and non-activated (PCNF) samples

Samples	SSA (m^2 g^−1)	Subnanometer volume (cm^3 g^−1)	Cumulative pore volume (cm^3 g^−1)	Average pore size (nm)
PCNF	1218	0.24	0.72	1.88
A-PCNF	2282	0.49	1.24	1.80

---

The RTIL, 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide (EMIM TFSI), and sol–gel precursor, tetramethyl orthosilicate (TMOS), were well mixed before adding 0.1 M HCl to induce the reaction for formation of the solid state electrolyte. The minimal aqueous content (EMIM TFSI : TMOS : 0.1 M HCl: 1 g : 45 μL : 4.5 μL) required to sustain the condensation reaction for the solid state electrolyte is used, while also preserving the voltage window. TMOS is efficiently hydrolyzed in acidic conditions followed by condensation over a period of time resulting in the formation of Si–O–Si bonds.^25,26 After gelation, the features around 1020 cm⁻¹, 1100 cm⁻¹ and 442 cm⁻¹ observed in FTIR analysis (Fig. S3†) indicate Si–O–Si stretching vibrations and bending vibrations. A large broad band between 3600 and 3200 cm⁻¹ was attributed to the presence of the O–H stretching frequencies of the silanol groups. Pictures of gelled electrolyte are shown in Fig. S4† and the inset of Fig. 1c. Electrochemical impedance spectroscopy (EIS) was used to analyze the solid-state electrolyte properties before their inclusion in the devices. Fig. 1c shows the Nyquist plots of ionic liquid with and without gelation placed in between two symmetric platinum electrodes. Impedances of both devices follow the typical Warburg type diffusion and fit well with the standard Randles circuit. The circuit diagram is shown in the inset of Fig. 1c, where R_s is the lumped series resistance of the contacts, electrodes and electrolyte, R_ct is the charge transfer resistance, C_dl is the double layer capacitance, and Z_W is the Warburg impedance element. To account for the non-ideal behavior of capacitance, a constant phase element with the frequency exponent close to unity is used in place of the pure capacitor in this circuit. The R_s values with and without gelation are 23.0 Ω cm⁻² and 22.3 Ω cm⁻², showing almost no variation in the total series resistance. This is expected because the electrolyte thickness and electrode resistance are unchanged. After gelation, the R_ct values increase from the range of 1.5–4.0 Ω cm⁻² to 3.0–8.3 Ω cm⁻². This indicates that gelation increases the resistance of electron injection minimally at the electrode–electrolyte interface. On the other hand, the C_dl values remain close to ∼20 μF cm⁻² in both cases, showing that the thickness of the electrical double layer at the electrode–ion interface does not change with TMOS. The effective diffusion constant (D_eff) of the ions with and without gelation are 2.7 × 10⁻⁶ cm⁻² s⁻¹ and 1.6 × 10⁻⁶ cm⁻² s⁻¹ respectively obtained using Warburg impedance. These results indicate that ionic diffusion in the solid-state electrolyte is comparable to its liquid-state counterpart.

The dependence of conductivity on time and temperature of the electrolyte was also investigated (Fig. S5 and S6 and Tables S1 and S2†). The charge transfer resistance decreases as the temperature is increased from 295 K to 325 K, indicating elevated device performance at higher temperatures. Conductivity measurements over a two month time period showed that the charge transfer resistance drops after day 1, possibly due to increased electrode wetting. It then remains stable for 20 days before marginally increasing and stabilizing at 30 days. The preservation of key properties of ionic liquids upon gelation paves a path to obtain solid-state devices with superior performance.

Uniform distribution of the solid electrolyte throughout the electrodes was observed as seen in the SEM images of solid electrolyte PCNF electrodes shown in Fig. S7.† The electrolyte is uniformly gelled throughout the fiber mat, filling in the inter-fiber spacing with good interfacial contact. Energy-dispersive X-ray spectroscopy (EDS) mapping of elements C, Si, S, and F of a solid electrolyte PCNF electrode cross-section (Fig. S8 and S9†) confirmed the uniform distribution of the electrolyte components throughout the nanofiber electrode.

Electrochemical analysis of the PCNF electrodes was conducted with both liquid EMIM TFSI as the electrolyte (as control), and solid electrolyte. Fig. 2a shows the Nyquist plots generated using EIS. As seen in the figure, the x-intercept increases from 2.15 Ω cm⁻² for the control device to 10.09 Ω cm⁻² for the solid device, indicative of slightly larger electrolyte resistance in the solid state. This is expected due to the physical confinement of the ionic liquid in the solid-state device and also the lower adhesion of the solid electrolyte with the electrode pore surfaces compared to the liquid counterpart. Nevertheless, the resistance increase is minimal, suggesting the presence of a continuous ion pathway through the solidified electrolyte. Circuit fitting shows that the R_ct values for liquid and solid electrolytes are 0.13 Ω cm⁻² and 0.92 Ω cm⁻² respectively. This behavior is consistent with the findings from the platinum electrode test devices described earlier. The high frequency negative impedance values are accounted for by using a virtual inductance in series with the standard circuit. The inductance values for liquid and solid electrolytes are 1.36 μH cm⁻² and 1.24 μH cm⁻², respectively. The origin of this inductance is either due to measuring cable delay or the formation of a passive layer at the electrodes.

Fig. 2 (a) Nyquist plots of liquid and solid electrolyte devices assembled using PCNF electrodes. (b) Cyclic voltammetry of solid electrolyte PCNF device at various scan rates. (c) Galvanostatic charge–discharge curve for 1 A g⁻¹ current density. (d) Plot of specific capacitance against current density.

Cyclic voltammetry (CV) curves were obtained at various scan rates for the solid electrolyte devices (Fig. 2b). As shown in the figure, the PCNF solid device exhibits near-rectangular CV behavior even at a high scan rate of 100 mV s⁻¹, suggesting fast kinetics in the system. At a scan rate of 20 mV s⁻¹, the device shows a specific capacitance of 57 F g⁻¹, 75% of which is retained at 100 mV s⁻¹, again indicating fast ion transport through the gelled electrolyte embedded within the hierarchical pore structure of porous carbon nanofibers and low resistance. Galvanostatic charge–discharge tests were also conducted at various current densities and are shown in Fig. 2c and d.

Activated PCNF samples (A-PCNFs), with their higher porosity and specific surface area, were used as electrodes to further increase specific capacitance and energy density. Electrochemical tests were done with the same parameters used in testing the PCNF samples. The Nyquist plots in Fig. 3a show the impedance comparison for the A-PCNF solid and liquid electrolyte samples. Circuit fitting for these plots was done in a similar way as that of the non-activated samples. The series resistance increased from 7.41 Ω cm⁻² for the control sample to 10.11 Ω cm⁻² for the solid sample. The charge transfer resistance values showed small increase in the range of 1–3 Ω cm⁻² for both the control and solid samples. This indicates that the electron injection process at the interface is not adversely affected by the activation process. The inductance values were 1.36 μH cm⁻² and 1.31 μH cm⁻² for liquid and solid electrolyte. These values are nearly equal to those of non-activated samples. Cyclic voltammetry curves for the solid device under different scan rates are shown in Fig. 3b; they all exhibit the near-ideal rectangular behavior indicative of fast transport. It provides a capacitance of 144 F g⁻¹ (0.24 F cm⁻²), 123 F g⁻¹, 108 F g⁻¹ and 96 F g⁻¹ at 5, 20, 50 and 100 mV s⁻¹ scan rates, respectively, indicating large retention at high scan rates indicative of high power handling capability. For comparison, we have also included the CV curves at selected scan rates for the control liquid electrolyte samples in the ESI (Fig. S10†). Galvanostatic charge–discharge tests (Fig. 3) were conducted and a specific capacitance of 142 F g⁻¹ was obtained at a current density of 0.5 A g⁻¹. The device retained a capacitance of 97 F g⁻¹ at an order of magnitude higher current density of 5 A g⁻¹. Areal mass loading of our electrodes can be facilely tuned by modifying the nanofiber mat thickness through the amount of polymer solution being electrospun. Table 2 shows the areal capacitance corresponding to a range of electrode masses with a constant geometric diameter of 3/8′′. We observe an increase in areal capacitance of more than two-fold between 2.40 mg and 5.46 mg, with minimal variations between the related gravimetric specific capacitance values. Further experimentation is required to optimize gravimetric capacitance with areal capacitance.

Fig. 3 (a) Nyquist plots of liquid and solid electrolyte devices assembled using A-PCNF electrodes. (b) Cyclic voltammetry of solid electrolyte A-PCNF device at various scan rates. (c) Galvanostatic charge–discharge curves from 0.5 to 5 A g⁻¹ current density. (d) Plot of specific capacitance against current density.

Table 2 Areal and gravimetric specific capacitance with increasing electrode mass at a fixed scan rate of 20 mV s⁻¹. A constant 3/8′′ diameter electrode size was used, with increasing mass coming from electrode thickness

Total electrode mass (mg)	Gravimetric capacitance (F g^−1)	Areal capacitance (F cm^−2)
2.40	122.6	0.207
3.16	105.8	0.235
4.51	123.8	0.392
4.57	105.7	0.339
5.46	115.6	0.443

---

Through this work, we have been able to overcome several challenges in the current literature on solid-state supercapacitors, while developing a facile fabrication methodology with significantly fewer processing steps. With a 3.5 V potential window, the room temperature performance of the solid device in this work corresponds to an energy density of 61 W h kg⁻¹ at 5 mV s⁻¹ and 41 W h kg⁻¹ at 100 mV s⁻¹ (with a charge–discharge time of 35 seconds). Such energy density is comparable to that of lead acid batteries, while retaining the high power of supercapacitors. Moreover, with an appropriate electrode mass loading, we are able to achieve an areal capacitance of 443 mF cm⁻², which is several orders of magnitude higher than many of the previous works.^14–16

Experimental

Carbon nanofiber fabrication

Carbon nanofiber mats were fabricated using electrospinning followed by a heat treatment process. Polyacrylonitrile (PAN, Sigma-Aldrich) and Nafion (Ion Power) in 30 : 70 wt/wt ratio were mixed under low heat in N,N-dimethylformamide (DMF, Sigma-Aldrich) with a total solution concentration of 21 wt%. The resulting solution was drawn into a syringe and placed in an automatic pumping device located in a sealed chamber with a low-moisture environment. The pumping rate was set to 0.2 mL h⁻¹ at a distance of 7 inches from the aluminum foil collector plate with an applied voltage of 10–15 kV to form a stable jet.

The resultant nanofiber mat was separated from the aluminum foil and cut into smaller sections for heat treatment in a tube furnace, wherein the samples were first stabilized in air at 280 °C for five hours and then pyrolyzed in nitrogen at 1000 °C for one hour. The heat treatment converted PAN to carbon and decomposed out the Nafion to form PCNF. To fabricate A-PCNF to further increase specific surface area, PCNF samples were soaked in KOH solution (30 : 70 KOH : DI water wt%) overnight. They were then blotted with a sterile wipe to remove excess KOH and heated in nitrogen in the tube furnace at 800 °C for 30 minutes. The retrieved fibers were thoroughly washed in DI water with a few drops of HCl to remove any activation remnants. The fibers were then dried in a convection oven at 50 °C for a few hours.

Solid supercapacitor device fabrication

The sol–gel precursor/ionic liquid mixture was prepared by first mixing 1 g of EMIM TFSI with 45 μL of TMOS. 4.5 μL of 0.1 M HCl was then added to induce hydrolysis and was constantly stirred for a few minutes to form the final mixture. Electrochemical characterization (EIS) of IL-gels was performed with the addition of 0.05 M iodine and 0.5 M LI. Supercapacitor devices were made without the addition of these ions. PCNF or A-PCNF samples were punched into 3/8′′ (0.9525 cm) diameter electrodes and placed on either side of a Celgard 3501 separator. A 15 μL drop of the sol–gel precursor/ionic liquid mixture was placed in between each layer and the complete assembly was sandwiched between two smooth Teflon plates (see Fig. S11 in ESI†). The entire unit was then clamped shut and allowed to solidify in air for 5 hours. The unit was then opened and dried in a convection oven at 50 °C for 15 hours for complete solidification. The now-solid supercapacitor was then transferred into a glove box and placed in a Swagelok cell with stainless steel current collectors for electrochemical testing. A photograph of Swagelok cell is shown in Fig. S12.†

Structural and electrochemical characterization

The specific surface area (SSA) of the carbon nanofiber electrodes was measured using nitrogen sorption isotherms at 77 K (Autosorb-1, Quantachrome) and CO₂ sorption isotherms at 273 K (ASAP 2020, Micromeritics). Prior to the adsorption–desorption measurement, all samples were degassed at 200 °C under vacuum for 24 h to remove impurities. The pore size distribution (PSD) was calculated based on adsorption–desorption curves using the quenched solid density functional theory (QSDFT) with the assumption of slit-shaped pores. SEM (Zeiss Supra 50VP) was conducted for carbon nanofiber electrodes both before and after the solid electrolyte fill. Energy dispersive EDS was conducted for solid electrolyte-filled electrodes for elemental mapping.

As mentioned above, all cells were assembled in a glove box (MBraun) with water content below 1 ppm and were connected to the potentiostat (Gamry Reference 3000) through electrical feedthroughs for electrochemical measurements. Cyclic voltammetry was performed with various scan rates (from 5 mV s⁻¹ to 100 mV s⁻¹) in the voltage window from 0 to 3.5 V. The specific capacitance, C, and energy density, E, were evaluated using the following equations:

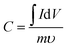where I is current response, m is mass of one electrode, and υ is scan rate. EIS was conducted in the frequency range from 100 kHz to 10 mHz with an alternating current amplitude of 10 mV at open circuit voltage. Note, C is calculated using the weight of one electrode and E is calculated for the device using the weight of both electrodes.

Galvanostatic charge/discharge was carried out at different current densities from 0.5 A g⁻¹ to 5 A g⁻¹ within the 3.5 V voltage window. The specific capacitance, C, was calculated by the following equation:

where I is the current, Δt is the discharging time, m is the total mass of the two carbon electrodes, and ΔV is the voltage window.

Conclusions

In summary, we have demonstrated the excellent performance of all-solid-state supercapacitors based on electrospun nanofiber electrodes and silica-based ionic liquid gel electrolytes. The electrodes are freestanding, thus eliminating the need for performance-inhibiting binders. The supercapacitor with an active material mass loading of 3–5 mg cm⁻² exhibits a specific capacitance of up to 144 F g⁻¹ (and 0.443 F cm⁻²) with a 3.5 V window corresponding to an energy density of 61 W h kg⁻¹, comparable to that of lead acid batteries. The device exhibits near rectangular cyclic voltammetry curves even at 100 mV s⁻¹, indicative of high power handling capability.

Acknowledgements

This work is supported by the National Science Foundation under grant numbers CBET-1150528, CBET-1236466 and the Los Alamos National Lab LDRD program. Authors would like to thank Richa Singhal for SEM/EDS imaging. The authors are grateful to Centralized Research Facility of Drexel University for instrumentation support.

References

1. G. P. Wang, L. Zhang and J. J. Zhang, Chem. Soc. Rev., 2012, 41, 797.
2. S. S. A. Hashmi, J. Solid State Electrochem., 2014, 18, 465.
3. Sellam and S. A. Hashmi, ACS Appl. Mater. Interfaces, 2013, 5, 3875.
4. M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621.
5. R. Y. Lin, P. L. Taberna, S. Fantini, V. Presser, C. R. Perez, F. Malbosc, N. L. Rupesinghe, K. B. K. Teo, Y. Gogotsi and P. Simon, J. Phys. Chem. Lett., 2011, 2, 2396.
6. E. Frackowiak, K. Metenier, V. Bertagna and F. Beguin, Appl. Phys. Lett., 2000, 77, 2421.
7. C. Kim, Y. I. Jeong, B. T. N. Ngoc, K. S. Yang, M. Kojima, Y. A. Kim, M. Endo and J. W. Lee, Small, 2007, 3, 91.
8. D. Carriazo, F. Pico, M. C. Gutierrez, F. Rubio, J. M. Rojo and F. del Monte, J. Mater. Chem., 2010, 20, 773.
9. Y. W. Zhu, S. Murali, M. D. Stoller, K. J. Ganesh, W. W. Cai, P. J. Ferreira, A. Pirkle, R. M. Wallace, K. A. Cychosz, M. Thommes, D. Su, E. A. Stach and R. S. Ruoff, Science, 2011, 332, 1537.
10. H. J. Fei, C. Y. Yang, H. Bao and G. C. Wang, J. Power Sources, 2014, 266, 488.
11. X. H. Liu, Z. B. Wen, D. B. Wu, H. L. Wang, J. H. Yang and Q. G. Wang, J. Mater. Chem. A, 2014, 2, 11569.
12. Y. X. Xu, Z. Y. Lin, X. Q. Huang, Y. Liu, Y. Huang and X. F. Duan, ACS Nano, 2013, 7, 4042.
13. J. Lee, W. Kim and W. Kim, ACS Appl. Mater. Interfaces, 2014, 6, 13578.
14. Y. J. Kang, S. J. Chun, S. S. Lee, B. Y. Kim, J. H. Kim, H. Chung, S. Y. Lee and W. Kim, ACS Nano, 2012, 6, 6400.
15. Y. J. Kang, H. Chung, C. H. Han and W. Kim, Nanotechnology, 2012, 23, 065401.
16. X. Yang, L. Zhang, F. Zhang, T. F. Zhang, Y. Huang and Y. S. Chen, Carbon, 2014, 72, 381.
17. M. D. Stoller and R. S. Ruoff, Energy Environ. Sci., 2010, 3, 1294.
18. J. J. Zhou, J. S. Cai, S. R. Cai, X. Y. Zhou and A. N. Mansour, J. Power Sources, 2011, 196, 10479.
19. G. P. Pandey, A. C. Rastogi and C. R. Westgate, J. Power Sources, 2014, 245, 857.
20. C. Tran and V. Kalra, J. Power Sources, 2013, 235, 289.
21. C. Tran, D. Lawrence, F. W. Rickey, C. Dillard, Y. Elabd and V. Kalra, Chem. Comm., 2015, 51, 13760.
22. R. Singhal and V. Kalra, J. Mater. Chem. A, 2015, 3, 377.
23. C. Tran, R. Singhal, D. Lawrence and V. Kalva, J. Power Sources, 2015, 293, 373.
24. F. W. Rickey, C. Tran, V. Kalva and Y. Elabd, J. Phys. Chem. C, 2014, 118, 21846.
25. G. Gupta, S. B. Rathod, K. W. Staggs, L. K. Ista, K. A. Oucherif, P. B. Atanassov, M. S. Tartis, G. A. Montano and G. P. Lopez, Langmuir, 2009, 25, 13322.
26. C. J. Brinker and G. W. Scherer, in Sol–Gel Science: The Physics and Chemistry of Sol–Gel Processing, Academica Press, Inc., New York, 1990, p. 212.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ta05552k

---