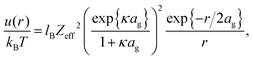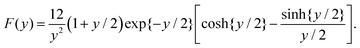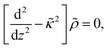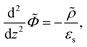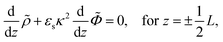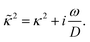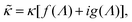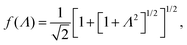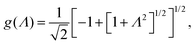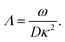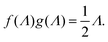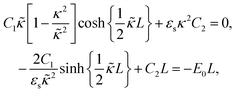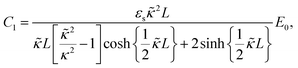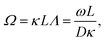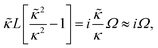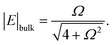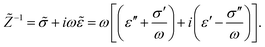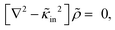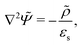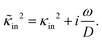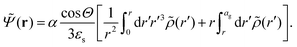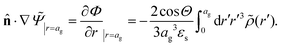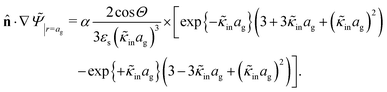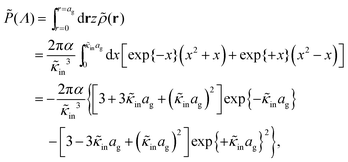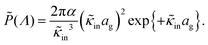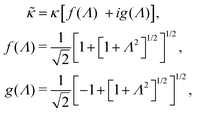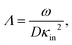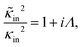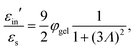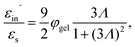Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dielectric spectroscopy of ionic microgel suspensions
P. S.
Mohanty
ab,
S.
Nöjd
a,
M. J.
Bergman
a,
G.
Nägele
cde,
S.
Arrese-Igor
f,
A.
Alegria
 fg,
R.
Roa
fg,
R.
Roa
 h,
P.
Schurtenberger
h,
P.
Schurtenberger
 a and
J. K. G.
Dhont
*cde
a and
J. K. G.
Dhont
*cde
aDivision of Physical Chemistry, Department of Chemistry, Lund University, Lund, Sweden
bSchool of Applied Sciences, KIIT University, Bhubaneswar 751024, India
cInstitute of Complex Systems ICS-3, Forschungszentrum Jülich GmbH, 52425 Jülich, Germany. E-mail: j.k.g.dhont@fz-juelich.de; Fax: +49-2461-612280; Tel: +49-2461-612160
dHeinrich-Heine Universität Düsseldorf, Department of Physics, D-40225 Düsseldorf, Germany
eJARA-SOFT, 52425 Jülich, Germany
fCentro de Física de Materiales (CSIC-UPV/EHU), Materials Physics Center, 20018 San Sebastián, Spain
gUniversidad del País Vasco (UPV/EHU), Departamento de Física de Materiales, 20080 San Sebastián, Spain
hSoft Matter and Functional Materials, Helmholtz-Zentrum Berlin, 14109 Berlin, Germany
First published on 24th October 2016
Abstract
The determination of the net charge and size of microgel particles as a function of their concentration, as well as the degree of association of ions to the microgel backbone, has been pursued in earlier studies mainly by scattering and rheology. These methods suffer from contributions due to inter-particle interactions that interfere with the characterization of single-particle properties. Here we introduce dielectric spectroscopy as an alternative experimental method to characterize microgel systems. The advantage of dielectric spectroscopy over other experimental methods is that the polarization due to mobile charges within a microgel particle is only weakly affected by inter-particle interactions. Apart from electrode polarization effects, experimental spectra on PNIPAM-co-AA [poly(N-isopropylacrylamide-co-acrylic acid)] ionic microgel particles suspended in de-ionized water exhibit three well-separated relaxation modes, which are due to the polarization of the mobile charges within the microgel particles, the diffuse double layer around the particles, and the polymer backbone. Expressions for the full frequency dependence of the electrode-polarization contribution to the measured dielectric response are derived, and a theory is proposed for the polarization resulting from the mobile charges within the microgel. Relaxation of the diffuse double layer is modeled within the realm of a cell model. The net charge and the size of the microgel particles are found to be strongly varying with concentration. A very small value of the diffusion coefficient of ions within the microgel is found, due to a large degree of chemical association of protons to the polymer backbone.
1 Introduction
Thermosensitive microgel particles are of fundamental and technological interest because of their unique response to various external parameters like temperature, ionic strength, pH, and electric fields, as well as their behaviour at high concentrations due to their soft interactions, deformability, and their ability to partially interpenetrate and to host small molecular species (many aspects of microgel systems are discussed, for example, in ref. 1–3). Microgel particles are thus foreseen to have a multitude of applications such as tunable micro-reactors, catalysts, drug-delivery vehicles, and functionalized colloids. In the present paper we focus on the response of such thermosensitive microgel particles to electric fields, which is important for their characterization and the prediction of structure formation under the action of an external electric field. We assess the possibilities of dielectric spectroscopy as a method to determine the net charge and size of microgel particles as a function of concentration, as well as the degree of association of protons to the polymer network. The advantage of dielectric spectroscopy over other methods is that the dielectric response due to polarization of mobile ions within the microgel particles is only indirectly affected by inter-particle interactions through, for example, shrinkage, pH changes, and electric fields generated by surrounding particles. Even at high concentrations, this polarization mode gives information about the state of single particles, without the direct interference of inter-particle interactions like in scattering and microscopy experiments. The electric-field induced polarization is at the origin their experimentally observed assembly into strings and several crystalline structures.4–6 A quantitative understanding of such field-induced transitions requires a theory for the field-induced charge distribution in- and around the microgel particles, which may be validated by means of dielectric spectroscopy. Dielectric spectroscopy can also be employed, for example, to study filtration processes of microgel suspensions, which is often used for their purification and removal of solvent. Knowledge of the electric response of these particles may be employed to study the temporal evolution of concentration profiles during filtration, as proposed in ref. 7, and may serve as an experimental technique to test models for microgel filtration.8 As the electric polarization is highly sensitive to interpenetration, dielectric spectroscopy is a method to probe whether interpenetration occurs.There are a limited number of experimental dielectric spectroscopy studies on dispersions of ionic microgel particles. Two dielectric relaxation modes are found in ref. 9 for various types of ionic PNIPAM microgels, which are attributed to relaxation mechanisms of the counter ions residing within the diffuse electric double layer outside the microgel matrix. Polarization due to mobile charges inside the microgel particles as a possible source for the observed dielectric relaxation has not been considered in this study. Dielectric spectroscopy has been used in ref. 10 and 11 to probe the coil–globule transition in PNIPAM microgel particles. In the swollen coiled state, dielectric spectra of the microgel particle suspensions are reported to resemble that of pure water. An additional relaxation process appears on collapse of the microgel particles to globules, which is attributed to the impermeability of the collapsed microgel for ions. This work has been extended in ref. 12 to very high frequencies, in the GHz range, where the water relaxation process within the microgel is probed. The non-Debye–Maxwell like relaxation of the water-orientational mode in the collapsed globular state is assumed to be due to hydrogen bonding of water with the polymer network, thus revealing in part the mechanism through which collapse occurs. At similar high frequencies, two relaxation processes have been observed in ref. 13, which are attributed to the reorientation of dipoles of the PNIPAM chains at 1 MHz and of solvent molecules at 10 GHz. Various solvents have been used to assess the importance of hydrogen bonding. Experiments on spherical polyelectrolyte brushes, which behave in many respects quite differently from thermosensitive gels, reveal a pronounced dielectric response at low frequencies, in the few tens of kHz range.14 This mode is due to polarization resulting from mobile charges within the brush, while the presence of the polymer network is held responsible for a reduced mobility of ions. In addition to microgel particles with a relatively homogeneous polymer network density, also particles with an inherently inhomogeneous network (PNIPAM/PAA SIPN microgels) have been studied by means of dielectric spectroscopy.15 The inhomogeneous network is composed of two interpenetrating networks, one of which is micro-phase separated into small compact domains. For the homogeneous particles a single relaxation mode is reported, while two relaxation modes are found for the inhomogeneous particles.
There are no electro-kinetic theories leading to explicit expressions for the polarization of ionic microgel particles in AC electric fields, including the polarization due to mobile ions within the gel matrix. The potential distribution and electrophoretic mobility of soft particles consisting of a charged polymer network and a core that is impenetrable for the ions are analyzed in detail in ref. 16 and 17. This work is limited to a DC electric field, and is therefore not applicable for the interpretation of dielectric spectra.
There is thus quite some uncertainty about the origin of the frequency dependent electric polarization modes of ionic microgel particles at low and intermediate frequencies. It is not known yet how to extract the net charge and size of microgel particles as a function of concentration from dielectric spectroscopy data. In addition, the correction of dielectric spectra for electrode polarization is often based on empirical approaches, and renders the interpretation of spectra for low frequencies uncertain. The aim of the present paper is therefore (i) to derive expressions for the polarization due to mobile charges within the microgel particles and for the full frequency dependence of the electrode-polarization contribution to dielectric spectra, (ii) to identify the various microgel relaxation modes that contribute to experimental spectra, and (iii) to extract the net charge and size of the particles as a function of their concentration, as well as the degree of dissociation/association of protons to the gel matrix. The determination of the net charge and size, and the degree of association, are quantities that are difficult to obtain from scattering and rheology experiments at higher concentrations, as inter-particle interactions have a strong effect on such experimental data. The polarization of mobile charges within the microgel particles, on the contrary, is only weakly affected by inter-particle interactions to within linear response to the external electric field.
This paper is structured as follows. A theory concerning the contribution of electrode polarization to experimental dielectric spectra is developed in Section 2. Section 3 discusses the polarization of microgel particles: a theory for the polarization due to mobile charges within the microgel matrix is given in Section 3.1, while the polarization of the electric double layer outside the microgel is discussed in Section 3.2 on the basis of a cell model, that accounts for the concentration dependent Debye length and the particle size and charge. The synthesis and characterization of the PNIPAM particles, as well as the dielectric spectroscopy equipment are introduced in Section 4. Experimental dielectric spectra at various microgel particle concentrations are presented in Section 5. The spectra are corrected for electrode polarization on the basis of the theory as developed in Section 2, while the remaining modes arising from the microgel particles are interpreted on the basis of the theories discussed in Section 3. The concentration dependence of the net charge and size of the microgel particles is extracted from the experiments, using the theories for electrode polarization and for the amplitude and characteristic frequency of the mode corresponding to polarization due to mobile charges within the microgel.
2 Electrode polarization
The apparent dielectric constant of the medium in which the microgel colloids are embedded (water plus possibly added ions) as measured by dielectric spectroscopy is relatively large at low frequencies due to the formation of electric double layers at the electrodes, even for the low ionic strength and the relatively large gap width of the dielectric cell. The apparent storage-permittivity diverges at zero frequency, as the charge that is applied to the electrodes by external means is fully compensated by the electric double layers. As a result of this charge compensation, the electric field strength for a DC experiment within the bulk of the medium, away from the double layers, is zero. The frequency dependent formation of double layers near the electrodes is commonly referred to “electrode polarization” (although “electrode de-polarization” would possibly be more accurate), or some times as “Maxwell–Wagner–Sillars interfacial polarization”. Dielectric measurements on suspensions of charged colloids are obviously affected by electrode polarization, and must be corrected to obtain reliable data corresponding to the polarization of the colloids themselves. There is a long history of attempts to describe the frequency dependence of the apparent dielectric constant as probed by dielectric spectroscopy due to electrode polarization (or more generally, “… the AC behaviour of solid or liquid materials containing charge carriers which can move freely within the material but can not leave it through the electrodes”18). Historical overviews can be found, for example, in ref. 19 and 20 (see their Section 2.1). The first attempts to describe electrode polarization (as well as developing theories for conductivity of semi-conductors) date back more than a century ago with the work of, for example, Wien,21 Warburg,22 Jaffé,23,24 and MacDonald18 (ref. 21–23 are written in German). More recent theories and experiments have been reported in ref. 20 and 25–28, with results that are partially at odds with each other, and where explicit results for the storage- and loss-permittivity are given only for small frequencies where ω ≪ Dκ2 (with ω the angular frequency, D the ion diffusion coefficient and κ−1 the Debye length). So far there are no explicit, real-valued expressions reported for the apparent loss- and storage-permittivities for arbitrary frequencies, which would allow a straightforward correction for electrode polarization. As will be seen later, it is essential to correct experimental data for the low ionic strengths used in the present study also for frequencies of the order of, and higher than Dκ2. This requires expressions for the apparent dielectric constant that are valid also for higher frequencies than Dκ2.An empirical electrode-polarization correction method that is sometimes used, is to fit the lower frequency contribution to experimental dielectric spectra to a form Aω−α, where ω is the frequency, and A and α are fitting parameters (see, for example, ref. 29 and 30). Extensive discussions of this empirical method can be found in ref. 31 and 32. Here we wish not to rely on an empirical approach for the description of electrode polarization, but will derive explicit expressions for the full frequency dependence from standard electro-kinetic equations.
In this section we discuss a theory for electrode polarization, based on the same standard electro-kinetic equations considered in the above mentioned recent literature, and assuming ideal electrodes which are accounted for by a no-flux boundary condition. Explicit expressions are derived for the apparent dielectric constants resulting from electrode polarization for arbitrary frequencies, which are compared to earlier reported expressions in the literature mentioned above. Furthermore, the theory is tested in Appendix C by measurements of the apparent dielectric constant of salt solutions at various concentrations, similar to what has been done in ref. 20, 24 and 26.
Consider a monovalent 1–1 salt solution confined between two flat electrodes which are separated by a distance L. A spatially homogeneous alternating electric field Eext = E0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos{ωt} in the z-direction is applied from the outside to the electrodes, where E0 is the field amplitude and ω the angular frequency. Within the overdamped limit, where the contribution of inertial forces can be neglected, the velocity of a uni-valent positively charged ion is equal to v+ = F/ξ where F is the total (non-inertial) force on the ion and ξ is the friction coefficient of the (solvated) ion with the surrounding solvent. The force along the z-direction on a positive ion consists of two parts, (i) the electric force −e∂Φ/∂z, with e > 0 the elementary charge and Φ the total potential, including the potential set up by the spatial distribution of ions and the field due to the externally applied charge to the electrodes, and (ii) the Brownian force −kBT∂
cos{ωt} in the z-direction is applied from the outside to the electrodes, where E0 is the field amplitude and ω the angular frequency. Within the overdamped limit, where the contribution of inertial forces can be neglected, the velocity of a uni-valent positively charged ion is equal to v+ = F/ξ where F is the total (non-inertial) force on the ion and ξ is the friction coefficient of the (solvated) ion with the surrounding solvent. The force along the z-direction on a positive ion consists of two parts, (i) the electric force −e∂Φ/∂z, with e > 0 the elementary charge and Φ the total potential, including the potential set up by the spatial distribution of ions and the field due to the externally applied charge to the electrodes, and (ii) the Brownian force −kBT∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ+/∂z, with kB Boltzmann's constant, T the temperature, and ρ+ the number concentration of positive ions. This leads to the well-known equation for the ion flux j+ = ρ+v+,
ρ+/∂z, with kB Boltzmann's constant, T the temperature, and ρ+ the number concentration of positive ions. This leads to the well-known equation for the ion flux j+ = ρ+v+,
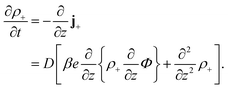 | (1) |
With the Poisson equation,
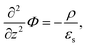 | (2) |
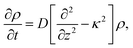 | (3) |
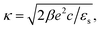 | (4) |
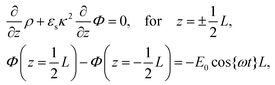 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos{ωt} is imposed to the electrodes.
cos{ωt} is imposed to the electrodes.
The set of eqn (2)–(5) is solved in Appendix A, which leads to explicit expressions for the measured, apparent dielectric constants εmed′ = εs + εep′ and εmed′′ = εep′′ for a medium consisting of a pure solvent with dielectric constant εs and the electrode-polarization contributions εep due to the presence of the 1–1 ions. For κL ≫ 1, the additive contributions due to electrode polarization are found to be equal to,
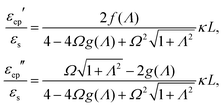 | (6) |
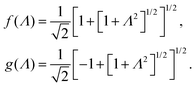 | (7) |
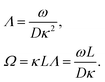 | (8) |
In case Λ ≪ 1 (that is, ω ≪ Dκ2), the above results for the dielectric constants reduce to,
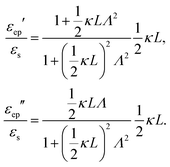 | (9) |
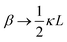 between the notation in ref. 20 and our notation), as well as those in eqn (2) and (3) in ref. 28 (with the same notation as in ref. 20, except that
between the notation in ref. 20 and our notation), as well as those in eqn (2) and (3) in ref. 28 (with the same notation as in ref. 20, except that 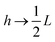 ). The expression (9) for the loss-permittivity also agrees with that found in eqn (48) in ref. 26, while that for the storage-permittivity in slightly different (the term
). The expression (9) for the loss-permittivity also agrees with that found in eqn (48) in ref. 26, while that for the storage-permittivity in slightly different (the term 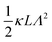 in the numerator of eqn (9) for εep′/εs is missing in ref. 26). The above expressions are at odds with those for the “blocking electrodes” in eqn (9) in ref. 27 (note the connection d → L, Λ → κ−1,
in the numerator of eqn (9) for εep′/εs is missing in ref. 26). The above expressions are at odds with those for the “blocking electrodes” in eqn (9) in ref. 27 (note the connection d → L, Λ → κ−1, 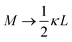 , and Ω → Λ between the notation in ref. 27 and our notation).
, and Ω → Λ between the notation in ref. 27 and our notation).
In the analysis of experimental dielectric data on suspensions of charged colloids, the dimensionless frequency Λ is not always small, so that the full expressions in eqn (6) must be used. These expressions have not been reported explicitly in literature before. Limiting expressions for the dielectric constant for small values of Λ are also derived in ref. 26, accounting in addition for the difference in the diffusion coefficients of both ion species. As shown in ref. 20, experiments on salt solutions with ion species with significantly different diffusion coefficients can be accurately described by the theory for frequencies for which Λ ≪ 1 when a “mean diffusion coefficient” is introduced.
Electrode polarization is affected by the presence of microgel particles, which enhances the ion concentrations stemming from their counterions. Section 5.1 quantifies these additional contributions to electrode polarization, which results in a method to obtain the net charge of the colloids. Electrode polarization is thus turned into a benefit for the characterization of microgel particles, instead of a phenomenon that is just an inconvenience that interferes with the determination of the dielectric properties of colloidal particles.
3 The polarizability of microgel particles
In the theory presented below we neglect the field-induced exchange of ions between the microgel and the surrounding solution. This is a reasonable approximation when there is a strong association of the mobile ions (H+-ions in our case) to the PNIPAM polymer backbone and/or when there is a considerable degree of Manning ion-condensation, although some leakage of ions will still occur.To within linear response to the external field, and with the neglect of leakage, the induced dipole moment is a linear superposition of the polarization resulting from motion of charges within the microgel particles, and those residing within the double layer outside the microgel. Analytical expressions for the contribution to the dielectric constant due to polarization stemming from the mobile ions within the microgel particle are derived in Section 3.1. Since there are no analytical results for the frequency dependent polarization of electric double layers, we use an existing cell model which describes, within a semi-quantitative accuracy, the polarization of possibly overlapping diffuse double layers at higher concentrations of microgel particles. This cell model will be discussed in Section 3.2.
3.1 Polarization due to charges within the microgel particle
The same electro-kinetic equations as used for the analysis of electrode polarization can be employed to describe the polarization of ions that are confined within the microgel particle. The description given below is coarse grained over distances of the order of the mesh-size of the microgel polymer network. The charge density, for example, is the average charge density within a volume element that contains many meshes of the polymer network. The inhomogeneous polymer density within a microgel particle can, in first approximation, be described through a core–shell structure, where the core is impenetrable for ions.35 Extending the calculations given below to include such a core, however, shows that the effect of the core on polarization is negligible, even for core diameters up to about 50% of the diameter of the microgel particle. We will therefore limit the discussion below to a quasi-homogeneous polymer network, which considerably simplifies the mathematics.Since the polarization of a microgel particle requires displacements of H+-ions over distances of the order of many meshsizes, ion transport is captured by a single, long-time diffusion coefficient that describes the motion of ions from one mesh to another. This diffusion coefficient involves the integration of complicated transport processes on very small length scales, like the parallel and perpendicular diffusion of an ion in the vicinity of a polymer strand, and the motion of an ion in the vicinity of a charge on the polymer backbone. Expressing the mesh-to-mesh diffusion coefficient in terms of these microscopic processes is a highly non-trivial problem in itself, which is beyond the scope of the present paper.
Let ρgel denote the number density of charges covalently bounded to the polymer backbone, within the same coarse-grained description as mentioned above. Note that −eρgel is the bare backbone charge density upon full dissociation, that is, it includes all negative charges on the backbone, irrespective of the degree of H+-bonding to the PNIPAM network. The above discussed approximation of a quasi-homogeneous network amounts to the neglect of ∇2ρgel against ∇2ρ+, with ρ+ the coarse-grained number density of H+-ions, including ions that are dissociated from the network and those that are associated. It is thus assumed that the inhomogeneity of the charge distribution of the mobile ions due to polarization is much more pronounced than the inhomogeneity of the fully charged polymer backbone. Such an approximation can not be made for star-like polymer brushes, which are inherently inhomogeneous both in polymer density and charge distribution.36 The theory presented below can, however, be extended to deal also with strongly inhomogeneous network densities (like those described in ref. 9). An analytical treatment is probably not feasible for these cases, so that polarizabilities have to be evaluated numerically, which has not been pursued so far.
The electric fields experienced by mobile ions within a microgel particle due to the surrounding particles (in the absence of the external field) may have an effect on the internal charge distribution within the gel matrix of a given particle. Since the Debye length (certainly at higher concentrations) is smaller than the radius of the microgel particles, and each particle is on average symmetrically surrounded by neighboring particles, the electric potential of the neighboring particles will be a smooth function of position within the main part of the microgel matrix. We will therefore neglect here the possibility of an inhomogeneous charge distribution resulting from inter-particle interactions. Taking such inter-particle polarization effects into account would certainly require a numerical approach.
A principle difference with the mathematical framework to describe electrode polarization is that on the right hand-side of eqn (3) there is now an additional convective contribution −∇·(vsρ+) to the flux of H+-ions, where vs is the local electro-osmotic flow velocity (the index “s” stands for solvent). However, to within linear response to the external electric field and for the homogeneous polymer network under consideration, bi-linear products of ρ, Ψ, vs, and E0 can be neglected, as all these variables are linear in the external-field amplitude (where ρ is the charge density, Ψ is the potential that arises from the polarization charges, and E0 is the amplitude of the external field). The convective contribution is such a bi-linear product. For the description of polarization of the double layer outside the microgel particle, the convective contribution can not be neglected, as the charge distribution within the double layer is inhomogeneous also without the external electric field. This renders the convective contribution within the diffuse double layer of first order in the external field strength. In that case the electro-kinetic equations couple to the Navier–Stokes equation that describes the solvent flow. Such a coupling is absent for the polarization resulting from mobile ions inside a homogeneous microgel, which renders an analytical treatment feasible. A second difference as compared to the electrode-polarization problem is that the immobile microgel backbone is charged, and thus contributes to the total charge density. The total charge density is now equal to,
| ρ = e[ρ+ − ρgel], | (10) |
Since within the Debye–Hückel approximation and within linear response, bi-linear products of ρ, Ψ, E0, and vs can be neglected in the electro-kinetic equation for ρ+, and assuming that |∇2ρ+| ≫ |∇2ρgel|, as discussed above, we are thus lead to the same electro-kinetic eqn (2) and (3) for the charge density (10) as for electrode polarization, but now in three dimensions,
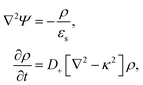 | (11) |
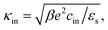 | (12) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) ·{∇ρ − εsκin2[E0 ·{∇ρ − εsκin2[E0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos{ωt} − ∇Ψ]} = 0, r ∈ ∂Vgel, cos{ωt} − ∇Ψ]} = 0, r ∈ ∂Vgel, | (13) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) is the unit normal vector to the boundary.
is the unit normal vector to the boundary.
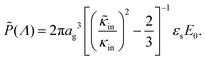
Note that cin is equal to the titration charge (the charge of the polymer backbone upon full dissociation of H+-ions) of a single microgel particle divided by its volume. As will be seen later, there is a large fraction of protons that is temporarily associated to the polymer backbone. The true Debye length within the gel matrix is therefore much larger than the bare inner-screening length, as will be discussed in Section 5.2.
The above electro-kinetic equations can be solved analytically (see Appendix B), leading to the following expressions for the additive increase of the dielectric constants due to polarization of the inner part of the microgel particles (the index “in” stands for “inside”),
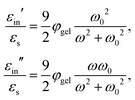 | (14) |
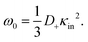 | (15) |
The same electro-kinetic equations used above can also be employed to describe the dielectric response of highly inhomogeneous networks (like the PNIPAM/PAA SIPN microgels15), and possibly include a boundary condition that allows for exchange of ions between the gel matrix and the solution. This can most probably only be done numerically.
3.2 Polarization of the diffuse double layer outside the microgel particle
For an isolated charged colloidal particle, three types of polarization-relaxation mechanisms related to the response of the electric double layer can be distinguished:(i) The first relaxation process is due to accumulation of ions on either side of the impenetrable colloidal core, as a result of ion fluxes induced by the electric field. When such field-induced ionic charges are mainly due to normal fluxes from the electrolyte solution to the surface, the dipole points in the opposite direction of the external electric field. This is in particular the case for uncharged colloids in a salt solution.37,38 On the contrary, if ion fluxes that are tangential to the colloidal surface are dominant, the induced dipole points in the same direction as the external electric field.39,40 The corresponding relaxation mechanism is commonly referred to as “concentration polarization”, “α-relaxation”, or “volume diffusion”. The characteristic frequencies for this mode can be estimated as follows.41,42 The relaxation of the dipole moment requires ions to diffuse from one side of the core to the other side, which corresponds to a distance πag, where ag is the radius of a particle. The time required to diffuse over that distance is (πag)2/D, where, as before, D is the ion-diffusion coefficient. The corresponding characteristic frequency ω0,cp = 2π/τ is thus of the order,
| ω0,cp ≈ 4D/(πag2). | (16) |
(ii) The remaining double-layer polarization mechanism is simply the electric-field induced distortion of the charge distribution within the double layer, other than that caused by concentration polarization. This includes double-layer deformation due to the electrophoretic motion of the colloid.43 The ions are now locally, on each side of the colloid, displaced over distances comparable to the Debye length. The corresponding relaxation frequency for this “ion-migration relaxation process” is thus of the order,
| ω0,im ≈ 4πDκ2, |
(iii) A third mechanism that is generally present is due to motion of charges along the surface of the colloid in case there is a mismatch in conductivity of the pure solvent (without ions) and the colloidal core. This so-called Maxwell–Wagner polarization44 does not play a role for the microgel particles. For very thin double layers, the above polarization mechanisms (i) and (ii) can be lumped into an effective surface conductivity. The resulting single relaxation mode is commonly referred to as the Maxwell–Wagner–O'Konski relaxation mode.45
An overview of the various polarization mechanisms for solid particles, as well as an introduction to dielectric spectroscopy, can be found in ref. 46.
Some of the experiments are performed at concentrations where the diffuse double layers overlap. We employ a cell model to describe their polarization. A cell model is developed in ref. 36 for a star-like polymer brush, and in ref. 47 for soft particles consisting of a core, impenetrable for ions, and a polymer shell. The latter of these cell models is relevant for the present work. It is found in ref. 47 that the numerical values for the dielectric response of soft and solid particles with the same charge (within the polymer network and on the particle surface, respectively) are typically a factor of two different, depending on the hydrodynamic penetration depth of the polymer network (the parameter 1/λ in ref. 47), which for PNIPAM networks is typically in the nanometer range.17 These differences apply to small values of the dielectric constant of the core-material of the particles, typically 2–5ε0, embedded in water (with a dielectric constant equal to 78ε0). Since the microgel particles contain a considerable fraction of water, the dielectric constant of their core material is much larger than such low values. For such much larger values of the dielectric constant of the core material, the difference in dielectric response between soft and solid particles is much less than the typical factor of two mentioned above. Furthermore, cell models are semi-quantitative (see, for example, ref. 48). It is therefore reasonable to use a cell model for solid particles to qualitatively describe the behaviour of soft particles. Such cell-model calculations are sufficiently discriminate to conclude that one of the experimentally found relaxation modes is due to the polarization of the diffuse double layer.
Our theoretical calculations are based on the cell model presented in ref. 49. In this approach, a representative spherical cell of radius b containing one spherical colloidal particle of radius a in its center is considered instead of the whole system. The cell radius b is such that the particle/cell volume ratio is equal to the particle volume fraction of the suspension, that is, φgel = (a/b)3. The standard boundary conditions at the particle's surface impose continuity of the electric potential, the discontinuity of the normal component of the electric field strength due to the surface-charge density (the dielectric constants of the solvent and the particle are taken equal, as discussed above), impenetrability of ions to the solid surface, and non-slip for the fluid flow. Hydrodynamic and electrical interactions between particles are modeled through boundary conditions at the cell outer boundary. On the outer surface of the cell, we use Kuwabara and Shilov–Zharkikh–Borkovskaya boundary conditions. The Kuwabara boundary condition50 for the fluid flow states that the radial component of the flow velocity v at the cell boundary is equal, but opposite in sign, to that of the electrophoretic velocity ve of the particle (with ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) the unit normal to the cell boundary),
the unit normal to the cell boundary),
v(r)·![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) |r=b = −ve· |r=b = −ve·![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) , , |
| ∇ × v(r)|r=b = 0. |
| Ψ0(r)|r=b − Ψ(r,t)|r=b = 〈E〉·r|r=b, |
| ni(r,t)|r=b = n0,i(r,t)|r=b, |
For the small net charge of the microgel particles and a Debye length of pure water, the above cell model predicts a single relaxation process corresponding to the double-layer polarization for all concentrations of microgel particles, to within numerical accuracy. The characteristic frequency of this mode complies with the frequency in eqn (16) for the concentration-polarization mode. The amplitude for the storage-permittivity is obtained as the difference between the zero-frequency and high-frequency values of the real part of the dielectric constant, while the characteristic frequency is obtained from the maximum slope of the dielectric constant as a function of frequency.
4 Particle synthesis and methods
Here we describe the synthesis and characterization of the ionic microgel particles, and the dielectric spectroscopy equipment.4.1 Synthesis and characterization of the PNIPAM-co-AA [poly(N-isopropylacrylamide-co-acrylic acid)] microgel particles
Negatively charged PNIPAM particles were synthesised by free-radical precipitation polymerization of 1.43 g re-crystallized N-isopropylacrylamide, NIPAM, where the remaining components in the reaction mixture in a round-bottom flask consist of 0.003 g sodium dodecyl sulfate as a pre-cursor stabiliser, 0.113 g of the cross-linker N,N′-methylenebis(acrylamide), 0.002 g polyfluor 570 methacryloxyethyl thiocarbonyl rhodamine B that was pre-dissolved in 10 ml water, and 0.08 g acrylic acid (99.5%) also pre-dissolved in 10 ml water. The reaction mixture was bubbled with argon for 20 min and thereafter kept under an argon atmosphere for the remaining time of the procedure. The reaction mixture was heated to 70 °C and 0.036 g potassium persulfate pre-dissolved in 5 g water was added to initiate the reaction. After four hours the reaction mixture was removed from the heater and left to cool down over night under constant stirring. The mixture was filtered and the particles were further cleaned by repeated centrifugation and redispersion steps. The purified particle solution was freeze dried in order to prepare samples with a well-controlled weight fraction of particles.The hydrodynamic radius and the size polydispersity were determined by a first order cumulant analysis of dynamic light scattering (DLS) correlation functions using a modulated 3D cross-correlated instrument at a wavelength of 660 nm (LS Instruments, Switzerland). Measurements were performed at 20 °C over an angular range of 30° ≤ θ ≤ 40°. The thus obtained hydrodynamic radius is equal to (578 ± 15) nm, with a size polydispersity as obtained from static light scattering of 7%. The a hydrodynamic radius is an intensity-weighted radius. The number-averaged radius that corresponds to this radius and polydispersity is (546 ± 15) nm.
The standard Zimm-plot procedure to obtain the molecular weight turned out to be quite inaccurate due to the large size of the microgel particles. Instead, an accurate value for the molecular weight can be obtained from confocal microscopy, by counting the number of particles within a given volume. In the confocal microscopy experiments, the number density of particles was obtained from the number of particles found in an analyzed volume using a Leica DMI6000 with a SP5 tandem scanner in the resonant mode (Leica, Germany) at an excitation wavelength of 543 nm. This was done for weight concentrations of 4.4 and 5.5 wt%. The molecular weight is found from measurements within five different regions to be equal to 2.20 × 1010 and 2.11 × 1010 g mol−1, respectively, with an estimated error of 7%. A quite accurate value of (2.16 ± 0.10) × 1010 g mol−1 for the molecular weight is thus obtained from microscopy. This molecular weight will be used to calculate number concentrations from concentrations in wt%.
The total bare charge of the particles was determined using conductometric titration (Probe Drum, Sweden, conductivity probe from Radiometer analytical, France), where 0.1 wt% particle solutions were fully de-protonated by addition of NaOH. The conductivity was thereafter monitored as a function of well-controlled additions of 0.1 M HCl. The obtained curves showed three distinct regions.54,55 First, a drop in conductivity due to the neutralization of excess NaOH. Second, the protonation of particle charges is manifested by an almost constant conductivity. Third, a linear rise in conductivity caused by the excess of HCl. The three distinct regions allow to determine the amount of HCl needed to neutralize the charges on the particles. The total charge per particle was thereafter calculated based on the number of particles in the titrated sample volume, using the molecular weight as determined from the number density obtained directly with confocal microscopy together with the number of protons present in the specific volume of HCl needed to neutralize all particle charges in the titrated sample volume. The total number of negatively charged groups on the PNIPAM network of a single microgel particle was accordingly determined to be (2.4 ± 0.2) × 107. This is the negative charge that a particle would obtain when it is fully de-protonated.
4.2 Dielectric spectroscopy measurements
A Novocontrol high-resolution dielectric analyzer (Alpha-S) was used to determine the complex dielectric permittivity over a wide frequency range 1–107 Hz. The applied (root-mean-squared) electric field strength is 155 V m−1. In the setup used, for each frequency, the impedance of a reference capacitor was compared with that of a parallel plate capacitor formed by two gold-plated electrodes (11 mm diameter). The measured values for the real and imaginary parts of the dielectric permittivity were subsequently calculated from the in-phase and out-phase sample cell capacitance. Measurements are performed at a temperature of 20 °C. A fixed distance of 6.45 mm between the flat electrodes was maintained by means a Teflon cylinder of suitable size, which was filled with the liquid material under investigation. The advantage of such a relatively large gap width is that the contribution of electrode polarization to measured dielectric spectra is diminished. The drawback is that the applied electric field strength where a linearized Poisson–Boltzmann approach to describe electrode polarization becomes invalid shifts to lower values, since for a given electric field strength the applied voltage increases linearly with the gap width.As is well-known, the experimentally measured in-phase dielectric constant (the storage-permittivity) εexp′ and the out-phase constant (the loss-permittivity) εexp′′ have a contribution from conductivity (see also Appendix A),
| εexp′ = ε′ − σ′′/ω, |
| εexp′′ = ε′′ + σ′′/ω, | (17) |
It is important to note that the apparent dielectric constant due to electrode polarization is additive to the dielectric contributions of the particles. The total, measured dielectric constant is thus equal to,
| εexp′ = εs′ + εep′ + εpar′, |
| εexp′′ = εs′′ + εep′′ + εpar′′ + σ0/ω, |
5 Experimental results for the storage-permittivity
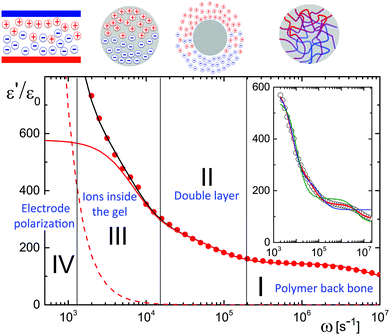
A typical experimental result for the frequency dependence of the storage-permittivity of a microgel dispersion in water is given in Fig. 1. In all experiments discussed here, the distance between the electrodes is 6.45 mm. Such a large gap width reduces the effect of electrode polarization to an extent that a meaningful determination of the contributions of the microgel particles can be deduced. Apart from the electrode-polarization contribution, there are three relaxation processes present: the regimes I, II, and III indicated in Fig. 1. Electrode polarization dominates in the low frequency regime IV. We therefore fitted spectra as a sum of the electrode-polarization contribution, using eqn (6)–(8), and a sum of three Debye–Maxwell contributions of the form Ãnω0,n2/(ω0,n2 + ω2), with Ãn the amplitude and ω0,n the characteristic relaxation frequency of the corresponding relaxation processes n = I, II or III of the microgel particles. Since the relaxation times of the three processes are well-separated, such a fit gives reliable values for both the amplitudes and the relaxation frequencies for the three Debye–Maxwell relaxation functions.The inset in Fig. 1 shows that the relaxation spectra can not be fitted with a sum of just two Debye–Maxwell contributions. The green curve is a least-square fit to two modes with a fixed base-line equal to that of pure water (which is 78ε0), while the blue curve is a fit with two modes where the base-line is a free fitting parameter. Obviously, two Debye–Maxwell contributions are not sufficient to describe the relaxation spectrum: the minimal value of the sum of squared residuals for two modes is more than ten times larger than for a fit to three modes (the red line in the inset and in the main figure).
As discussed in the second part of Appendix C, the large conductivity of salt solutions at low concentrations, as well as the dominant electrode polarization contribution to the out-phase measured dielectric response, renders the measurement of the loss-permittivity unfeasible. We therefore restrict the discussion to measurements of the storage-permittivity.
As the microgel particles enhance the ionic strength in the vicinity of the electrodes, the Debye length is used as a fitting parameter for the electrode-polarization contribution. The solid black line through the data points in Fig. 1 represents the fit result, while the dashed line is the contribution due to electrode polarization. The solid red line in Fig. 1 is the dielectric constant corrected for electrode polarization. Note that the contribution due to electrode-polarization is important up to frequencies where the slowest microgel particle relaxation process already decays. It is thus essential to correct the data for electrode polarization in order to extract meaningful results for all three relaxation processes, even for the large gap width of the dielectric sample cell that has been used.
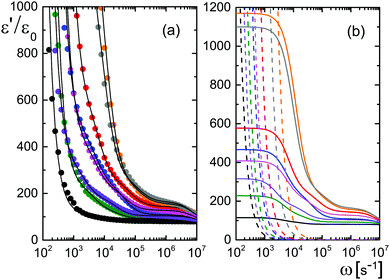
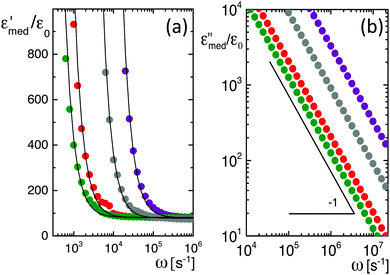
Data for several microgel particle concentrations and the corresponding fits are given in Fig. 2a. The contributions from electrode polarization are given in Fig. 2b as dashed lines, and the solid lines are the contributions from the microgel particles. The same color code is used as in Fig. 2a to label the various concentrations.
The amplitudes A = (ε0/εs) × Ã and characteristic frequencies for the three Debye–Maxwell modes are plotted in Fig. 3 as a function of the microgel particle concentration in terms of their weight percentage. The amplitudes of all three modes vary linearly with the microgel particle concentration at sufficiently low concentrations, which shows that these modes are indeed related to the polarization of the microgel particles.
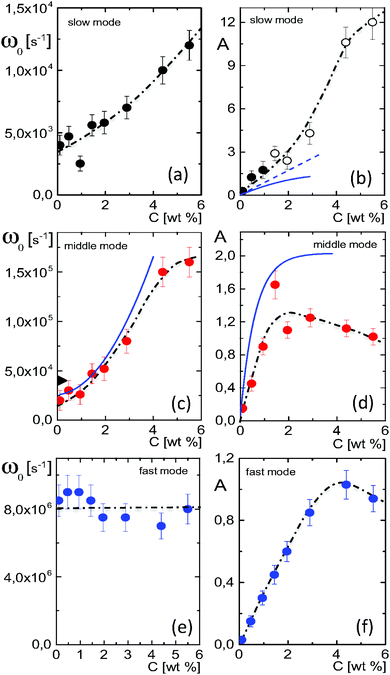 | ||
| Fig. 3 (a and b) The characteristic frequency and amplitude for the slow relaxing mode, respectively, as a function of the microgel particle concentration. The black dashed-dotted lines are guides-to-the-eye. Open symbols are used in (b) for data points that are unreliable due to failure of the linear Poisson–Boltzmann theory used to correct for electrode polarization. The blue lines in (b) correspond to the prediction in eqn (14): the dashed curve neglects shrinkage of the radius with increasing volume fraction, and the solid curve accounts for shrinkage. (c and d) The same for the middle mode. The blue solid lines are predictions by the cell model. The black, rotated triangle at zero concentration corresponds to the estimate in eqn (16) for the concentration-polarization mode. (e and f) The same as before, now for the fast mode. Note that the amplitudes are equal to A = (ε0/εs) × Ã, where à is the amplitude corresponding to the plots of ε′/ε0 in Fig. 1 and 2. | ||
In the following subsections we discuss the electrode-polarization contributions to the measured dielectric constant and the three microgel modes separately. The relaxation mode at high frequencies is in the frequency range where uncharged polymers are polarized, while the characteristic frequency of this mode is independent of the concentration. This mode is therefore attributed to the polarization of the PNIPAM polymer backbone. The intermediate mode relaxes at frequencies that are typical for double-layer polarization, with an amplitude that is in agreement with the prediction from the cell model. This mode is therefore attributed to double-layer polarization. The microgel-particle mode at low frequencies occurs in a frequency range that is well below the relaxation frequencies of double layers, with an amplitude that is much larger than for double-layer polarization. The amplitude is in accordance with the prediction for polarization due to mobile charges within the microgel. The slow mode is thus attributed to polarization due to mobile charges within the microgel. Both the well-separated relaxation frequencies as well as the quite different values of the amplitudes thus allow the unambiguous identification of the origin of the three relaxation modes. These features will be discussed in detail for each of the modes in the following subsections. The combined results from electrode polarization and the slow mode are used to obtain the concentration dependence of the radius and the net charge of the microgel particles as a function of concentration.
5.1 The contribution from electrode polarization
The very steep increase at low frequencies (the frequency range IV in Fig. 1) of the measured storage-permittivity with decreasing frequency is due to electrode polarization. The Debye length is the only fit parameter in eqn (6)–(8) for the contribution due to electrode polarization. As discussed before, the thus obtained apparent Debye length κ−1 depends on the concentration of microgel particles through the corresponding increase of the ion concentration near the electrodes. The concentration dependence of κ−1 is plotted in Fig. 4a. The Debye length at zero concentration is 210 ± 10 nm, which is in accordance with the calculated Debye length of 192 nm for water in atmospheric equilibrium with air (see Appendix D). It should be noted that Debye lengths that differ from those in the classic Debye–Hückel theory (where the ionic strength is given by the salt concentration outside the double layer) are introduced when describing interactions between charged colloids due to overlapping double layers.56–60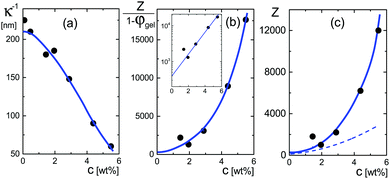 | ||
| Fig. 4 (a) The Debye length κ−1 as a function of the weight concentration, obtained from fits to the electrode-polarization equations. (b) The quantity Z/(1 − φgel) as a function of concentration obtained from eqn (18). The solid blue line corresponds to the blue curve in (a) according to eqn (18). The inset shows the extrapolation of this quantity to zero concentration. (c) The net charge as a function of concentration. The blue curve relates to the blue curve in (b) according to the volume fraction given in Fig. 5c. The dashed line is the effective charge that describes inter-particle interactions according to ref. 62. This is the charge that would be obtained from pair-correlation function measurements. | ||
The dependence of κ−1 on the microgel particle concentration can be obtained simply by adding the number of ions that result from the addition of microgel particles to the total ionic strength. The number of ions that are added to the solvent per microgel particle is equal to Z = |Q|/e, with Q the net charge of a microgel particle, while the available volume for the ions due to the presence of the microgel particles is reduced by a factor 1 − φgel, where φgel is the volume fraction of microgel particles. The ionic strength 2c in eqn (4) for the Debye length is thus increased due to the presence of the microgel particles by an amount Zcgel/(1 − φgel), where cgel is the number concentration of microgel particles, which is obtained from the molecular weight (as determined from confocal microscopy (see Section 4.1)) in terms of the weight concentration as cgel [microgel particles/m3] = 2.79 × 1017 × c [wt%]. The inverse Debye length as measured by electrode polarization is thus equal to,
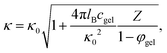 | (18) |
The quantity Z/(1 − φgel) obtained from the data in Fig. 4a is plotted in Fig. 4b. From an extrapolation of Z/(1 − φgel) to zero concentration (see the inset in that figure), the net charge is found to be equal to Z = 390 ± 100. As can be seen from this figure, however, the net charge increases quite strongly above weight fractions of about 2–3 wt%, quite independent of the precise concentration dependence of the volume fraction φgel. The variation of the net charge with weight concentration is given in Fig. 4c, where the volume fraction dependence on the weight concentration is taken from the analysis of the polarization mode from charges inside the particles, as discussed in the next subsection. Even at these higher concentrations, however, the net charge is always very small as compared to the total number of dissociable groups (the titration charge, which was found in Section 4.1 to be equal to 2.4 × 107 elementary charges). The small net charge at low concentrations is in accordance with the net charge of 190 as found in ref. 61 for similar microgel particles, but with a smaller degree of cross-linking (1.6 mol% instead of 5 mol%), and with a radius of 214 nm at very low concentrations. This led the authors of ref. 61 to conclude that “the vast majority of the interior counterions are condensed or at least one-dimensionally constrained on the polyelectrolyte chains, while only a small fraction is free to move three dimensionally in between the polymer chains”. This will be further discussed in some detail in the next subsection on the basis of the dielectric data obtained for the low-frequency mode. In ref. 61, the experimental structure factor is fitted to integral-equation theories to obtain the charge. A similar small charge of 400 is found for microgel particles with a hydrodynamic radius of 724 nm in ref. 4, by fitting pair-correlation functions as obtained by confocal microscopy to integral equation theory, and a charge of 300 is found in ref. 55 for particles with a radius of 160 nm at a volume fraction of 0.037 from a fit of the structure factor.
Note that the charges reported in ref. 4, 55 and 61, either from measurements of the pair-correlation function or the static structure factor, are “effective charges” that formally describe interactions between the microgel particles.56–60 As Denton has shown,57,62 based on linear response theory by modeling the microgel as a uniformly charged sphere that is permeable to the point-like assumed microions, the effective microgel pair-potential u(r) (with r the distance between the centers of the two particles) is given by a DLVO-Yukawa type potential of the standard form, for r > 2ag,
| Zeff = ZF(2κag), |
In the linear response treatment by Denton, only the mobile counterions are considered, without contributions from ions inside the microgel that are Manning-condensed on the polymer backbone. For the here considered microgels, Manning condensation does not occur, as will be discussed in detail in the next subsection. The effective charge based on the Denton model is plotted in Fig. 4c (the dashed line). At infinite dilution, the effective charge is found to be equal to 195 ± 60 elementary charges. The effective charge of 190 reported in ref. 61 is independent of the volume fraction, which, except for the largest concentration, is not larger than 0.21 (there is mistake in the calculation of the molar concentrations given in ref. 61; personal communication with Dr P. Holmqvist). The effective charge that we find is also reasonably constant for such low volume fractions (the volume fraction for our system at 1 wt% is about 0.15).
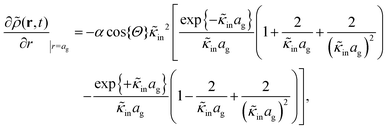
5.2 The low-frequency mode: polarization due to mobile ions within the microgel
The low-frequency mode in the frequency range III is due to polarization as a result of field-induced motion of ions within the microgel. As the number of H+-ions that is released on dissolving a microgel particle in water is very much smaller than the total number of dissociable protons within the microgel, the number concentration cin in eqn (12) for the bare inner-screening length is to a very good approximation equal to cin = Ztit/vp, with Ztit = (2.4 ± 0.2) × 107 the titration charge, and vp = (4π/3)ag3 the volume of a microgel particle, where ag is the geometrical radius of the particles (with the index “g” standing for gel). Since the radius at infinite dilution is equal to (546 ± 15) nm, the bare inner-screening length κin−1 given in eqn (12) is thus found to be equal to (1.7 ± 0.2) nm for very low concentrations. From the data in Fig. 3a for the characteristic frequency at zero concentration and eqn (15), we find a diffusion coefficient of D+ = (3.4 ± 0.4) × 10−14 m2 s−1, which is orders of magnitude smaller than the diffusion coefficient 9.3 × 10−9 m2 s−1 of H+-ions in water.There are three possible mechanisms that can lead to a reduction of the diffusion coefficient: hindrance of motion of the H+-ions by the polymer network, Manning-ion condensation that causes ions to move near to the polymer backbone which leads to an increased friction, and a high degree of association of H+-ions to the PNIPAM network that leads to a lower mobility as association leads to temporary immobilization. Since the mesh size of the network is estimated to be 30 nm, the reduced mobility due to the hindrance by the network for motion of the hydrated ions is expected to be moderate.63 The fraction of condensed ions can be estimated from the molecular weight of the microgel particles and the titration charge. The molecular weight of a NIPAM monomer is 113 g mol−1, while the contribution to the length of the PNIPAM chain per monomer is close to 0.30 nm. From the molecular weight of the PNIPAM particles of 2.16 × 1010 g mol−1 and the total charge of 2.4 × 107e (see Section 4.1), the line charge density is found to be equal to 0.36e nm−1. This value is below the critical value e/lB of the line charge density where Manning-condensation sets in (where lB = 0.74 nm is the Bjerrum length). Ion condensation can therefore not explain the strong reduction of the diffusion coefficient. We note that the role played by condensed ions in the dielectric response of highly charged, linear polyelectrolytes is still under debate (see ref. 64, where simulations are presented and an overview of the current understanding is given). The very small value of the diffusion coefficient is therefore attributed to the high degree of association of protons to the polymer backbone, possibly similar to the hydrogen bonding as described in ref. 65. Such a high degree of association has been suggested in ref. 55 and 61 to be responsible for the relatively small amount of ions that is released from within the microgel into the surrounding de-ionized water as compared to the total number of dissociable groups, that is, the titration charge. The reduction of the diffusion coefficient can be estimated by equating the electrochemical potential of dissociated H+-ions within the microgel with that of the ions in the solvent, outside the diffuse double layer. Using the Debye–Hückel expression for the potential within the gel, this leads to [H+]in = [H+]out![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp{ZlB/ao,g(1 + κ0ao,g)} = 1.76 × 1021 ions per m3, where [H+]in is the H+-ion concentration in dissociated form inside the microgel (not to be confused with cin, which also contains the number of temporarily associated ions), [H+]out is the concentration in water, ao,g = 546 nm is the particle radius at infinite dilution, and where κ0−1 = 210 nm is the Debye length. For infinite dilution we have [H+]out = 2.54 × 10−6 M as shown in Appendix D, which is the concentration in pure water including atmospheric carbon dioxide. Note that for larger particle concentrations the Hout+-concentration will be considerably higher. The above equation neglects the effect of confinement on the chemical potential of the dissociated ions by the polymer network, and is therefore only semi-quantitative. Since for low volume fractions we have Z = 390 (see Section 5.1) it is thus found from the titration charge and the radius of the microgel particles that the fraction of protons that is dissociated is approximately equal to [H+]in × (4π/3)ag3/Ztit = 5.0 × 10−5. From a two-state approximation where the diffusion coefficient is either equal to that of a freely diffusing H+-ion in dissociated form or equal to zero in the associated form, the average diffusion coefficient is thus estimated as 4.7 × 10−13 m2 s−1. This estimated value for the diffusion coefficient is of the same order of magnitude as the earlier experimentally determined diffusion coefficient at very high dilution of D+ = (3.4 ± 0.4) × 10−14 m2 s−1, which strongly suggests that the low value for the diffusion coefficient is indeed due to the high degree of association of H+-ions to the PNIPAM network.
exp{ZlB/ao,g(1 + κ0ao,g)} = 1.76 × 1021 ions per m3, where [H+]in is the H+-ion concentration in dissociated form inside the microgel (not to be confused with cin, which also contains the number of temporarily associated ions), [H+]out is the concentration in water, ao,g = 546 nm is the particle radius at infinite dilution, and where κ0−1 = 210 nm is the Debye length. For infinite dilution we have [H+]out = 2.54 × 10−6 M as shown in Appendix D, which is the concentration in pure water including atmospheric carbon dioxide. Note that for larger particle concentrations the Hout+-concentration will be considerably higher. The above equation neglects the effect of confinement on the chemical potential of the dissociated ions by the polymer network, and is therefore only semi-quantitative. Since for low volume fractions we have Z = 390 (see Section 5.1) it is thus found from the titration charge and the radius of the microgel particles that the fraction of protons that is dissociated is approximately equal to [H+]in × (4π/3)ag3/Ztit = 5.0 × 10−5. From a two-state approximation where the diffusion coefficient is either equal to that of a freely diffusing H+-ion in dissociated form or equal to zero in the associated form, the average diffusion coefficient is thus estimated as 4.7 × 10−13 m2 s−1. This estimated value for the diffusion coefficient is of the same order of magnitude as the earlier experimentally determined diffusion coefficient at very high dilution of D+ = (3.4 ± 0.4) × 10−14 m2 s−1, which strongly suggests that the low value for the diffusion coefficient is indeed due to the high degree of association of H+-ions to the PNIPAM network.
The effective inner-screening length, that is, the inverse Debye length corresponding to the true ionic strength within the gel matrix, is equal to (see eqn (12)),
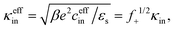 | (19) |
| ceffin = f+cin, | (20) |
The variation of the characteristic frequency with concentration in Fig. 3a is due to particle shrinkage on increasing their concentration. Shrinkage decreases the bare inner-screening length, since it leads an increase of the concentration of the total number of dissociable protons cin, and thereby increases the characteristic frequency (see eqn (12) and (15)). The diffusion coefficient D+ can also be a function of concentration due to the variation of the degree of association of H+-ions to the PNIPAM network upon particle shrinkage. In view of the above discussion, we thus write the diffusion coefficient as,
| D+ = f+D0+, | (21) |
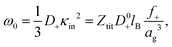 | (22) |
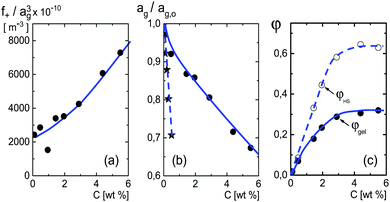 | ||
| Fig. 5 (a) The quantity f+/ag3 as a function of concentration, obtained from the experimental results in Fig. 3a and eqn (22). (b) The concentration dependence of the radius, as obtained from (a) with the neglect of the weak concentration dependence of f+. The starred data points are taken from ref. 61, for microgel particles with a considerably smaller cross-linking density. (c) The weight-concentration dependence of the volume fraction. The lower filled data points refer to the volume fraction of the microgel particles, while the upper open data points refer to the corresponding volume fraction of an equivalent hard-sphere system. The blue lines are guides-to-the-eye. | ||
The above discussed estimate of the fraction f+ of dissociated protons at low concentrations shows that f+ increases with increasing net charge. The estimate becomes inaccurate, however, for high volume fractions of microgel particles, since in case of strong double-layer overlap there is no region within the solvent anymore where the potential is zero, so that [H+]out in the earlier consideration becomes ill-defined. That f+ increases with increasing net charge is nevertheless expected to remain valid also for higher microgel particle concentrations. A higher concentration of dissociated mobile H+-ions within the microgel leads to an increased number of expelled ions, and hence to an increased net charge. Since the net charge increases with increasing concentration (see Section 5.1), f+ is thus expected to increase with increasing concentration. A lower limit for the microgel particle radius can therefore be obtained from Fig. 5a by assuming that f+ is constant, independent of concentration. The volume of a particle is thus seen from Fig. 5a to decrease by at most a factor of 3.5 from high dilution to 6 wt%. The corresponding volume fraction at this high concentration can be calculated from the connection between the number concentration cgel and the weight concentration of particles, as obtained from the molecular weight: cgel [microgel particles/m3] = 2.71 × 1017 × c [wt%]. It is thus found that the volume fraction is at least equal to 0.33 at 6 wt%. This seemingly low limiting volume fraction at high concentrations is either due to the long-ranged electrostatic forces with which surrounding particles act onto the covalently bounded negative charges on the backbone of each microgel particle, and/or the increased electro-osmotic pressure exerted by ions onto the microgel particle on increasing the concentration. The limiting volume fraction of 0.33 may seem small. However, the particles act as spheres with an effectively larger size due to the long-ranged electrostatic repulsive interactions, so that the corresponding “effective volume fraction” that accounts for the electrostatic interactions is quite high. The electrostatic forces keep the particles at distances significantly larger than the diameter of the microgel particles. This can be quantified by mapping the charged particles onto an equivalent hard-sphere system. A well-established method to map charged spheres onto an equivalent hard-sphere system is based on the Gibbs–Bogoliubov free energy variation67 with the Verlet–Weiss corrected Percus–Yevick pair-correlation function for hard spheres68,69 as an input. Minimizing the Gibbs–Bogoliubov free energy expression with respect to the hard-sphere diameter leads to equivalent hard-sphere volume fractions as plotted with a dashed line in Fig. 5c, which is seen to asymptote to about 0.64. Other more crude estimates of the equivalent hard-sphere volume fraction (for example based on an equivalent radius of ag + κ−1, or a diameter equal to the distance where the pair-potential energy equals the thermal energy kBT), give rise to similar large values for the volume fraction. When the equivalent hard-sphere volume fraction would have been as high as 0.70, say, this would imply an increase of f+ by about 10%. The variation of f+ with concentration is therefore weak as compared to that of the particle volume, which changes by a factor of 3.5. In the sequel we will therefore neglect the concentration dependence of f+, and set it equal to the value f+ = 3.7 × 10−6 at high dilution. This gives rise to the concentration dependence of the radius as plotted in Fig. 5b.
The starred data points in Fig. 5b for the radius dependence on concentration refer to a weaker crossed-linked microgel system:61 1.6 mol% instead of 5 mol%. As expected, the concentration dependence of the radius of these less cross-linked microgels is more pronounced. The ionic microgel particles with a cross-linking density of 0.36 mol% in ref. 70 with a hydrodynamic radius of 305 nm at infinite dilution shrink to 220 nm at a concentration of 2 wt%. The corresponding shrinkage lies in between that for the two microgels mentioned above, despite the much smaller cross-linking density. The Debye length outside these particles is much smaller due to the addition of NaOH, which leads to negligible electrostatic interactions, so that shrinkage is due to steric interactions and/or osmotic deswelling. For such much higher ionic strengths outside the particles, and thus a much smaller Debye length in the surrounding solvent, shrinkage due to inter-particle interactions only occurs at high volume fractions due to steric interactions, possibly in combination with variations in electro-osmotic pressure.66,70–72
There is as yet no theory that describes the combined effects of inter-particle interactions, osmotic pressure, network elasticity, self-electric network energy, as well as the association/dissociation equilibrium of protons to the polymer backbone on the shrinkage of ionic microgel particles.
The degree of softness of microgel particles may be used to tune their size by adding, for example, relatively small linear polymers. Such a polymer-induced shrinkage has been observed for star-polymers in ref. 73.
The amplitude of the slow mode is equal to (9/2)φgel, as predicted by the theory in Section 3.1 (see eqn (14)), up to large concentrations of microgel particles. The volume fraction at very low microgel particle volume concentrations can be obtained from the size of 546 nm and the molecular weight of 2.16 × 1010 g mol−1 (see Section 4.1) in terms of the weight concentration: φgel = 0.19 × c [wt%]. The dashed blue line in Fig. 3b corresponds to this relation which neglects particle shrinkage on increasing concentration, while the solid blue line corresponds to the volume fraction that includes shrinkage according to the data in Fig. 5b. The experimental values for the amplitudes in Fig. 3b imply unrealistically high volume fractions beyond concentrations of about 2 wt%. Such seemingly unrealistic large volume fractions can only occur when there is severe particle interpenetration. This would, however, lead to a decrease of the polarization amplitude, which is not observed in Fig. 3b. The above found maximum volume fraction of 0.33 confirms that no interpenetration occurs. The reason for the discrepancy between the experimental and predicted amplitudes is as follows. As discussed in Section 2, Appendix A and in ref. 20, the linearization of electro-kinetic equations fails for low frequencies in case there is a large effect of electrode polarization. As the effect of electrode polarization is very strong for the higher microgel particle concentrations (as can be seen from Fig. 2b), the corresponding amplitudes of the slow mode are therefore unreliable. For the highest concentration, the low-frequency plateau develops at a frequency of about 1 kHz, where the contribution to the measured dielectric constant from electrode polarization is as large as 3900ε0, for 2.89 wt% the corresponding contribution is 500ε0, and for c = 1.44 wt% about 50ε0. A reliable determination of the low-frequency plateau for larger microgel particle concentrations requires a non-linearized Poisson–Boltzmann approach, which has not been pursued yet, while quite accurate data are required to deal with the dominant and steeply rising electrode polarization contribution. The open symbols in Fig. 3b are used to indicate that these data points can not be reliably compared to the theory developed in this study. Note that, contrary to the plateau value, the characteristic frequency for the slow mode is reliable up to large particle concentrations, as the relaxation occurs at sufficiently high frequencies, where electrode polarization is much less pronounced.
The large amplitude of the low-frequency mode is also found for polyelectrolyte brushes, which is likewise attributed to polarization due to charges inside the brush.14 It is uncertain whether this high amplitude is also due to interference of electrode polarization. Contrary to the present ionic microgels, ion condensation on the polymer backbone is non-negligible for the polyelectrolyte brushes (about 65% of the mobile charges are estimated to be condensed), leading to a reduction of the ion mobility by a factor of approximately 1.5.
5.3 The middle-frequency mode: polarization of the diffuse electric double layer
The mode that relaxes at intermediate frequencies in the range II is due to polarization of the diffuse double layer outside the particles, within the solvent.For very low concentrations, where electric double layers do not overlap, an estimate for the relaxation time for concentration polarization is given is eqn (16) for ω0,cp. Using that D = 9.3 × 10−9 m2 s−1 and ag = 546 nm, it is found that ω0,dl = 4.0 × 104 Hz. This estimate is in reasonable agreement with the experimental value for the middle mode at zero concentration in Fig. 3c (the black tilted triangle at zero concentration indicates this value), and is very different from the characteristic frequencies for the two other modes.
What is not included in eqn (16) is the concentration dependence due to overlap of electric double layers. Already at a concentration of 1 wt%, the effective volume fraction corresponding to an effective radius of ag + κ−1 is about 0.3. This indicates that diffuse double layers already significantly overlap at that concentration. The cell model shows only a single relaxation mode which is well described by a Debye–Maxwell form. This single relaxation mode is due to concentration polarization, as discussed in Section 3.2. The solid blue lines in Fig. 3c and d for the characteristic frequency and amplitude, respectively, are based on the cell model described in Section 3.2. In view of the qualitative nature of the cell model for large concentrations, there is a reasonable agreement with the data for the middle mode. Note that the characteristic frequencies for the two other modes are more than an order of magnitude off from these theoretical predictions for double-layer polarization.
The significant increase of the characteristic frequency with increasing concentration is most probably due to the strong overlap of double layers: the exchange of ions between double layers of neighbouring particles in order for polarization to relax requires diffusive displacements over relatively small distances. This is also the reason why the amplitude exhibits a maximum as a function of concentration, as polarization charges from overlapping double layers tend to cancel. The decrease of the amplitude with increasing concentration is due to overlap of double layers, and not due to a low value of the dielectric constant of the core material of the microgel particles,49 since the microgel in the swollen state contains a large fraction of water.
We note that the a liquid-crystal phase transition occurs at about 4 wt%. For the two highest concentrations the system is therefore in a shear-molten crystalline state. This may have an effect on the polarization process of the double layers, while the two other modes are quite insensitive to structural ordering of surrounding particles.
5.4 The high-frequency mode: polarization of the polymer backbone
The relaxation process at high frequencies in the range I is attributed to dielectric polarization of the polymer backbone. The polarization process involves the polymer network itself, water molecules that are solvated to the polymer backbone, as well as ions that diffuse on small length scales in the vicinity of the network. The characteristic frequency for such polarization mechanisms are expected to be insensitive to the microgel particle concentration, which is indeed what is seen in Fig. 3e, contrary to the two slower modes. A similar relaxation process at such high frequencies (of about 3 × 107 Hz) is observed for linear-chain PNIPAM in ref. 12. This mode is only observed in the swollen state, and is attributed to the polarization due to the orientation of water molecules which solvate the polymer backbone.12 The high-frequency mode is in principle composed of several polarization mechanisms, as mentioned above. Since the amplitude of the high-frequency mode is quite small, it is not possible to distinguish within experimental error between the several relaxation modes that might contribute. Free-diffusive displacements of H+-ions over distances of the order of the mesh size (which is about 30 nm) corresponds to frequencies of the order 100 MHz. Even if the diffusion coefficient is a hundred times less than the free diffusion coefficient (due to interactions with the network) these processes will not contribute to the frequency range of mode II.6 Conclusions
Dielectric spectroscopy measurements on PNIPAM-co-AA [poly(N-isopropylacrylamide-co-acrylic acid)] microgel suspensions in de-ionized water are quantitatively interpreted on the basis of an improved theory for electrode polarization and a new model for the polarization of the ionic microgel particles. The microgel particles are 5% cross linked, and have a radius of 546 nm at infinite dilution.The experimental spectra reveal four distinct contributions to the storage-permittivity: a generic contribution from electrode polarization, and three modes stemming from polarization of the microgel particles. These modes relax at well separated frequencies, which allows for the determination of the amplitudes and the characteristic frequencies of each of them.
A theory is developed for electrode polarization for arbitrary frequencies, and for the polarization of the microgel particles due to the mobile charges within the gel matrix. Both theories are based on the linearized standard electro-kinetic equations of motion for ion concentrations. A cell model is employed to account for the relaxation process of the (overlapping) electric double layers that surround the microgel particles.
A fit of the experimental dielectric spectra for various microgel particle concentrations to the theory for electrode polarization and three additional Debye–Maxwell relaxation functions quantifies the amplitudes and characteristic frequencies of all modes as functions of the concentration.
The Debye length is the only fit parameter for the electrode polarization contribution. The Debye length decreases with increasing microgel concentration due to the increased ionic strength resulting from the microgel counter ions. This information is used to extract the net charge of the microgel particles as a function of their concentration. It is found that the net charge is approximately constant (390 elementary charges) up to volume fractions of about 0.15, and then quite steeply increases (up to 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 elementary charges) as the volume fraction reaches its maximum value of 0.33. The shrinkage of a microgel particle is due to the long-ranged electrostatic forces of surrounding particles acting on its backbone charges.
000 elementary charges) as the volume fraction reaches its maximum value of 0.33. The shrinkage of a microgel particle is due to the long-ranged electrostatic forces of surrounding particles acting on its backbone charges.
The relaxation mode at low frequencies is due to polarization of the microgel particles resulting from mobile charges within the gel matrix. This polarization mechanism is affected by particle interactions only indirectly through particle-interaction induced shrinkage and electric fields generated by surrounding particles. The shrinkage of particles increases the concentration of mobile ions within the microgel particles, leading to changes in their polarization. From the newly developed theory and the experimental characteristic frequencies, the concentration dependent size of the particles is determined. The size decreases quasi-linearly from 546 nm to 350 nm at the highest volume fraction. The volume fraction asymptotes to approximately 0.33, which corresponds to an equivalent hard-sphere volume fraction of 0.64. The diffusion coefficient of H+-ions within the microgel is found to be orders of magnitude smaller than the diffusion coefficient of protons in water. This is attributed to the high degree of association of protons to the polymer backbone, which also explains the very small net charge as compared to the bare (titration) charge. The concentration dependence of the amplitude of this relaxation mode is in accordance with theory only for quite small concentrations. For large concentrations, the experimental amplitudes are larger than their theoretically predicted values. This is a consequence of the failure of the linearized theory for the description of the electrode polarization contribution, in combination with it's dominant contribution and sensitive dependence on frequency. The concentration dependence of the volume fraction could be directly extracted from the amplitudes when a non-linear theory for electrode polarization is available, and with quite accurate data for the low frequencies where the plateau polarization for this mode is reached. The absence of a drop of the amplitude with increasing concentration indicates that there is no exchange of mobile charges between particles, and hence that there is no inter-particle interpenetration.
The mode at intermediate frequencies is due to double-layer polarization. The characteristic frequency at very low microgel particle concentration is in accord with the theoretical prediction corresponding to concentration polarization (some times also referred to as “α-relaxation” or “volume diffusion”). The concentration dependence of the amplitude and characteristic frequency of this mode is due to particle shrinkage, the change in the Debye length, as well as a strong double-layer overlap. There is a semi-quantitative agreement of the concentration dependence of the characteristic frequency and amplitudes with a cell model, where the volume fraction and the Debye length as determined from the characteristic frequency of the slow mode and electrode polarization are used as an input.
The characteristic frequency of the fast mode, due to polarization of the polymer backbone, is essentially independent of concentration, as the backbone properties are hardly affected by microgel particle crowding. The characteristic frequency of this mode is of the same order as found in earlier studies on polymer-backbone polarization.
Dielectric spectroscopy is thus shown to be a valuable experimental tool to determine the net charge and radius of microgel particles as a function of their concentration, as well as the degree of association of protons to the polymer backbone. The quantitative evaluation of experimental dielectric spectra requires theories for electrode polarization and the polarization of microgels due to mobile charges within the gel matrix. Dielectric spectroscopy can possibly play a future role to systematically study the behaviour of several types of ionic microgel particles, also as a function of temperature, including more complicated microgels like microgel particles where multivalent ferricyanides bind to several monovalent polymer charges, thus producing an apparent secondary network,74 and polyampholytic microgels.75
The present experiments have been performed at low ionic strength. For high ionic strengths, electrode polarization dominates up to higher frequencies so that the characterization of polarization due to mobile charges within the microgel may not be feasible. When at higher ionic strengths electrode polarization masks the internal polarization mode, only two microgel-particle modes can be experimentally probed, which correspond to electric double layer polarization and polarization of the polymer network. At higher pH, however, where the association of protons to the polymer network is less pronounced, the mode due to polarization of charges within the microgel shifts to higher frequencies. In such cases one may still resolve the internal polarization mode also at higher ionic strengths. For increasing pH, however, the internal mode may start to overlap with the double layer polarization mode in a way that they might not be distinguished anymore.
There are two improvements of the theories developed in this paper that may expand their applicability also to other types of microgel particles. First of all there is a generic need for an electrode-polarization theory based on non-linearized electro-kinetic equations. Secondly, the present theory is limited to quasi-homogeneous polymer networks. To extend the present theory to highly inhomogeneous microgel particles, the same electro-kinetic equations can be employed, which most probably can only be solved numerically.
Appendix A: solution of the electro-kinetic equations for electrode polarization and the resulting apparent dielectric constant
The solution to the system (2)–(5) is conveniently formulated in complex quantities. Let ρ′ and ρ′′ denote the in-phase and out-phase components of the charge density ρ, that is, ρ(r,t) = ρ′(r∣ω)cos{ωt} + ρ′′(r|ω)sin{ωt} (the notation ρ′(r∣ω) is used to indicate that ρ′(r) is parametrically depending on the frequency). Defining the complex charge density![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) = ρ′ − iρ′′, it is easily seen that the real part of
= ρ′ − iρ′′, it is easily seen that the real part of ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp{iωt} is equal to ρ′(r∣ω)cos{ωt} + ρ′′(r|ω)sin{ωt}. Similarly introducing the complex potential
exp{iωt} is equal to ρ′(r∣ω)cos{ωt} + ρ′′(r|ω)sin{ωt}. Similarly introducing the complex potential ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) , the system (2)–(5) is conveniently rewritten as,
, the system (2)–(5) is conveniently rewritten as,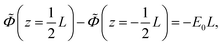 | (23) |
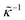 is equal to,
is equal to,Note that,
where,
with the dimensionless frequency Λ equal to,
Convenient relations in the evaluation of real and imaginary parts are,
| f2(Λ) − g2(Λ) = 1, |
Since the charge density is an odd function of z, the solution to the first equation of motion is,
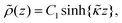 | (24) |
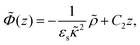 | (25) |
where the amplitude E0 is taken along the minus z-direction. The solutions to these equations are,
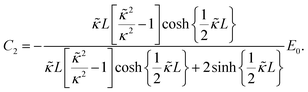 | (26) |
which is much larger than Λ for κL ≫ 1, we have,
provided that Λ ≪ 1. Within the bulk of the solution, away from the double layers at the electrodes, the charge density is zero, so that it follows from eqn (25) and (26) that the electric field strength in the bulk of the solution is equal to,
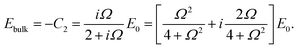 | (27) |
For large Ω we have Ebulk = E0, so that no electrode polarization occurs, while for Ω → 0 it is found that Ebulk = 0, so that the double layers at the electrodes completely screen the imposed field. Note that the bulk field strength is essentially equal to the applied field strength for Ω ≈ 10, which justifies the leading order expansion with respect to Λ = Ω/κL ≪ 1. Eqn (27) for the attenuation of the bulk field strength due to electrode polarization has been tested experimentally in ref. 76, where field-induced phase transitions have been probed as a function of the separation between the electrodes.
Due to the large contribution of electrode polarization to the dielectric constant, electrode polarization contributes up to much larger frequencies in dielectric experiments, such that Λ is not necessarily small.
The derivation of the relation of the above calculated charge density to the apparent dielectric constant needs some basic considerations on what is actually measured in a dielectric spectroscopy experiment. The suspension can be represented as an electric circuit of a capacitor in parallel with a resistor.46 The capacitor incorporates dielectric polarization at the electrodes, while the resistance accounts for the conductivity of the suspension. An oscillating voltage V = V0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos{ωt} with frequency ω is applied and the phase lag and amplitude of the resulting current is measured.
cos{ωt} with frequency ω is applied and the phase lag and amplitude of the resulting current is measured.
First consider the current jR through the Ohmic resistance, which is equal to jR = Z−1V0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos{ωt}, with Z = R the Ohmic resistance. Since for a parallel plate geometry the Ohmic resistance is proportional to the length L of the sample cell and inversely proportional to the area A of the electrodes, the specific conductance σ that is independent of the sample-cell geometry can be defined as Z−1 = σA/L, and hence jR = (A/L)σV0
cos{ωt}, with Z = R the Ohmic resistance. Since for a parallel plate geometry the Ohmic resistance is proportional to the length L of the sample cell and inversely proportional to the area A of the electrodes, the specific conductance σ that is independent of the sample-cell geometry can be defined as Z−1 = σA/L, and hence jR = (A/L)σV0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos{ωt}. This is most conveniently written in complex notation as follows. Define Ṽ = V0
cos{ωt}. This is most conveniently written in complex notation as follows. Define Ṽ = V0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp{iωt}. The applied potential is the real part of this complex-valued potential. Introducing the complex conductivity
exp{iωt}. The applied potential is the real part of this complex-valued potential. Introducing the complex conductivity ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) = σ′ − iσ′′, the real part of the complex-valued current
= σ′ − iσ′′, the real part of the complex-valued current ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) R = (A/L)
R = (A/L)![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) Ṽ is easily shown to be equal to (A/L)[σ′
Ṽ is easily shown to be equal to (A/L)[σ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos{ωt} + σ′′
cos{ωt} + σ′′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin{ωt}]V0, so that σ′ relates to the in-phase part of the current, and σ′′ to the out-phase part. We thus write for the current through the resistor,
sin{ωt}]V0, so that σ′ relates to the in-phase part of the current, and σ′′ to the out-phase part. We thus write for the current through the resistor,
![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) R = (A/L) R = (A/L)![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) Ṽ. Ṽ. |
Next consider the current jC that passes through the capacitor. Since the potential difference between the two parallel plates that constitute the capacitor is fixed, as it is applied by external means, the total charge on each of the plates at each instant of time is also fixed. The total charge is equal to the externally applied charge Qext on a given plate plus the charge Qpol due to polarization of the sample. Let Q0 denote the charge that corresponds to the given external potential when there is no polarization charge, that is, when there is vacuum between the two plates. To keep the potential fixed when polarization occurs, the externally applied charge must be enhanced by an amount equal to minus the polarization charge. Hence,
| Qext = Q0 − Qpol. | (28) |
Q0 = (A/L)ε0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos{ωt}V0, cos{ωt}V0, | (29) |
Qpol = −(A/L)[(ε′ − ε0)cos{ωt} + ε′′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin{ωt}]V0, sin{ωt}]V0, | (30) |
![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) ext = (A/L) ext = (A/L)![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) Ṽ, Ṽ, |
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) = ε′ − iε′′. The complex-valued current through the capacitor branch is thus equal to
= ε′ − iε′′. The complex-valued current through the capacitor branch is thus equal to ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) C = d
C = d![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) ext/dt, and hence,
ext/dt, and hence,![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) C = iω(A/L) C = iω(A/L)![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) Ṽ. Ṽ. |
The total current is the sum of ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) R and
R and ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) C,
C,
![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) = (A/L) = (A/L)![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif) −1Ṽ, −1Ṽ, |
This well-known result shows that the experimentally determined loss- and storage-permittivities are affected by the conductivity,
| εexp′ = ε′ − σ′′/ω, |
| εexp′′ = ε′′ + σ′/ω, |
There are two polarization mechanisms that need to be subtracted from the measured total dielectric constant in order to obtain the polarization contribution due to the microgel particles. First there is an in-phase contribution to the dielectric constant as a result of polarization of the pure solvent, and secondly there is an apparent polarization due to the accumulation of ions near the electrode. These two contributions comprise the dielectric response of a salt solution. The total polarization charge in eqn (30) for a salt solution can thus be written as a sum of the apparent contribution Qep from electrode polarization and the contribution Qs from the pure solvent,
| Qpol = Qep + Qs, |
Qep = −(A/L)[εep′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos{ωt} + εep′′ cos{ωt} + εep′′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin{ωt}]V0, sin{ωt}]V0, |
| Qs = −(A/L)(εs − ε0)cos{ωt}V0, | (31) |
The electrode polarization contribution can now be obtained from eqn (31) through the evaluation of the polarization charge due to the accumulation of ions near the electrodes. According to eqn (24) and (26), the electrode-polarization charge is equal to (where “ℜ” stands for “the real part of”),
 | (32) |
Appendix B: solution of the electro-kinetic eqn (11)–(13) for microgel particle polarization
The solution of the electro-kinetic eqn (11)–(13) for the microgel particle polarization due to the mobile ions inside the microgel matrix are again formulated in terms of complex quantities, as explained in Appendix A. The equation of motion and the boundary conditions in terms of the complex-valued quantities read,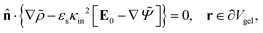 | (33) |
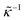 is equal to,
is equal to,The solution of the first differential equation in eqn (33) that is finite at the origin reads,
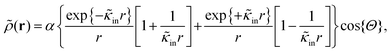 | (34) |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (r,t) ≡
(r,t) ≡ ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (r,t)/(α
(r,t)/(α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ)),
Θ)),It follows immediately that (with
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) the surface unit normal vector pointing outwards),
the surface unit normal vector pointing outwards),Evaluation of the integral leads to,
Using that,
the no-flux boundary condition at the periphery of the microgel particle gives,
For the highly charged and large microgel particles under consideration,
| κinag ≫ 1, | (35) |
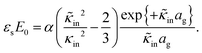 | (36) |
The complex-valued dipole moment ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) is, according to eqn (34), equal to (with
is, according to eqn (34), equal to (with 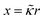 ),
),
From eqn (36) for α it thus follows that,
Using that,
where the dimensionless frequency Λ is defined as,
and hence,
it is readily found that the in-phase and out-phase part of the induced dipole moment,
| P(ω) = P′(ω)cos{ωt} + P′′(ω)sin{ωt}, |
Since the additive increment of the dielectric constant due to the particles is equal to εin = cgelP/E0, with cgel the number density of microgel particles, it is finally found that,
where φgel = (4π/3)cgelag3 is the volume fraction of microgel particles.
Appendix C: electrode polarization: some experiments on salt solutions
The apparent storage-permittivity of NaCl-solutions for various concentrations are shown in Fig. 6. There is a marked shift of the onset of electrode polarization towards larger frequencies on increasing the salt concentration, as also observed in ref. 20, 24 and 26. This is in accordance with the corresponding decreasing dimensionless frequencies in eqn (8) for a given applied frequency ω. There are three parameters that determine the dielectric constant: the gap width L, the ion diffusion coefficient D, and the Debye length κ−1. The gap width is fixed to 6.45 mm. The ion diffusion coefficient is taken equal to the average 1.5 × 10−9 m2 s−1 of those of Na+ and Cl−, which are respectively equal to 1.1 and 1.9 × 10−9 m2 s−1. Using these numerical values, the experimental data are fitted to eqn (6)–(8) with respect to the Debye length. The solid lines in Fig. 6a for the salt concentrations 0.030 (the green data points), 0.085 (red), 0.65 (grey), and 2.58 mM (purple) correspond to fitted Debye lengths of 55, 38, 12.5, and 5.8 nm, respectively. These results can be compared to the Debye lengths as calculated from eqn (4), from which is follows that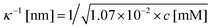 , where c [mM] is the concentration of neutral salt molecules in mM. This leads to calculated Debye lengths of 56, 33, 12.0, and 6.0 nm, respectively, which are in good agreement with those obtained from the fits.
, where c [mM] is the concentration of neutral salt molecules in mM. This leads to calculated Debye lengths of 56, 33, 12.0, and 6.0 nm, respectively, which are in good agreement with those obtained from the fits.
For the frequencies under consideration (less than 107 Hz), the out-phase conductivity is zero, while the in-phase conductivity is constant, being equal to its zero-frequency limit. According to eqn (17) there is thus a contribution to the experimentally determined loss-permittivity that varies inversely proportional to the frequency, and increases linearly with the salt concentration (for the low salt concentrations considered here). The same dependencies are also exhibited by the contribution from electrode polarization, as long as Ω > 10. For such frequencies it follows from eqn (9) that εep′′/ε0 = (εs/ε0)Dκ2/ω, while κ2 is proportional to the salt concentration. Both the apparent dielectric response due to electrode polarization as well as the conductivity contribution to the measured loss-permittivity thus exhibit the same frequency and salt-concentration dependence. These two contributions are therefore difficult to separate. The measured loss-permittivity is plotted in Fig. 6b on a double logarithmic scale for various salt concentrations, with the same color codes as in Fig. 6a. There is indeed a ∼ω−1 dependence. The contribution from conductivity and from electrode polarization are of the same order (the former can be estimated from the specific ion-conductivities, which are 5.0 × 10−3 S m2 mol−1 and 7.6 × 10−3 S m2 mol−1, for Na+-ions and Cl−-ions, respectively, from which it follows that σ′/ε0 [s−1] = 1.4 × 109 × c [mM]). These contributions to the loss-permittivity are very much larger than those to the storage-permittivity (compare Fig. 6a and b), and dominate the measured loss-permittivity of microgel suspensions. The loss-permittivity must therefore be obtained from the loss-permittivity through the Kramers–Kronig relations, as has been done, for example, in ref. 9.
Appendix D: ionic strength and conductivity of water in equilibrium with atmospheric carbon dioxide
The concentration of carbonic acid H2CO3 is directly proportional to the partial pressure pCO2 of gaseous CO2 in the air,| [H2CO3] = KCO2pCO2, | (37) |
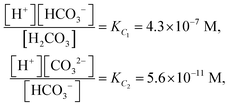 | (38) |
| [H+][OH−] = Kw = 10−14.0 M2, |
| 2[CO32−] + [HCO3−] + [OH−] = [H+]. | (39) |
From the above equations it is readily found that the H+-concentration is the solution of the cubic equation,
| [H+]3 − [H+](Kw + KC1KCO2pCO2) − 2KC1KC2KCO2pCO2 = 0. | (40) |
where the λ0X's are the single ion-conductivities of ion species X. The various concentrations can be expressed in terms of [H+] from eqn (37)–(39) as,
| [OH−] = Kw/[H+], |
| [HCO3−] = KC1KCO2pCO2/[H+], |
| [CO32−] = KC1KC2KCO2pCO2/[H+]2. |
The value of the constant KCO2pCO2 at atmospheric pressure has been determined in ref. 77 in connection to the ionic strength and pH of dispersions of fd-virus particles in low-concentration TRIS/HCL-buffers. It is found there from pH-measurements as a function of the TRIS/HCL-concentration that,
| KCO2pCO2 = 0.015 mM. |
| [H2CO3] + [HCO3−] + [CO32−] = HCO2pCO2, | (41) |
Comparing to eqn (37) thus leads to,
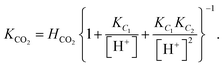 | (42) |
From the above results we obtain the following concentrations,
| [H+] = 2.54 × 10−6 M, [OH−] = 3.94 × 10−9 M, |
| [HCO3−] = 2.54 × 10−6 M, [CO32−] = 5.60 × 10−11 M. |
| I = 2.54 × 10−6 M, |
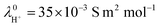 , and
, and 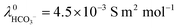 (ref. 78)),
(ref. 78)),| σw = (1.00 ± 0.10) × 10−4 S m−1. |
Acknowledgements
The authors thank Christopher Hirst for his assistance during the dielectric measurements, Jerome J. Crassous for his suggestion to determine the molecular weight from confocal microscopy, as well as a critical reading of the manuscript, and to Michel Cloitre and Alan Denton for very useful discussions. This work was supported by the Swiss National Science Foundation, the Swedish Research Council (Project 621-2011-4338), the science faculty of Lund University, the European Research Council (ERC-339678-COMPASS), and the Knut and Alice Wallenberg Foundation (project grant KAW 2014.0052). J. K. G. Dhont, G. Nägele, and R. Roa acknowledge support by the German Research Foundation (SFB 985, Functional Microgels and Microgel Systems, Project B6). The authors acknowledge financial support from the European Commission under the Seventh Framework Program by means of the grant agreement for the Integrated Infrastructure Initiative N. 262348, European Soft Matter Infrastructure (ESMI).References
- Microgel Suspensions: Fundamentals and Applications, ed. A. Fernández-Nieves, H. Wyss, J. Mattsson and D. A. Weitz, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2011 Search PubMed.
- Hydrogel Micro and Nanoparticles, ed. L. A. Lyon and M. J. Serpe, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2012 Search PubMed.
- P. J. Yunker, K. Chen, M. D. Gratale, M. A. Lohr, T. Still and A. G. Yodh, Rep. Prog. Phys., 2014, 77, 056601 CrossRef PubMed.
- P. S. Mohanty, A. Yethiraj and P. Schurtenberger, Soft Matter, 2012, 8, 10819 RSC.
- S. Nöjd, P. S. Mohanty, P. Bagheri, A. Yethiraj and P. Schurtenberger, Soft Matter, 2013, 9, 9199 RSC.
- P. S. Mohanty, P. Bagheri, S. Nöjd, A. Yethiraj and P. Schurtenberger, Phys. Rev. X, 2015, 5, 011030 Search PubMed.
- S. Bannwarth, T. Trieu, C. Oberschelp and M. Wessling, J. Membr. Sci., 2016, 503, 188 CrossRef CAS.
- R. Roa, D. Menne, J. Riest, P. Buzatu, E. K. Zholkovskiy, J. K. G. Dhont, M. Wessling and G. Nägele, Soft Matter, 2016, 12, 4638 RSC.
- J. Zhou, J. Wei, T. Ngai, L. Wang, D. Zhu and J. Shen, Macromolecules, 2012, 45, 6158 CrossRef CAS.
- M. Füllbrandt, R. von Klitzing and A. Schönhals, Soft Matter, 2012, 8, 12116 RSC.
- M. Füllbrandt, R. von Klitzing and A. Schönhals, Soft Matter, 2013, 9, 4464 RSC.
- M. Füllbrandt, E. Ermilova, A. Asadujjaman, R. Hölzel, F. F. Bier, R. von Klitzing and A. Schönhals, J. Phys. Chem. B, 2014, 118, 3750 CrossRef PubMed.
- S. Nakano, Y. Sato, R. Kita, N. Shinyashiki, S. Yagihara, S. Sudo and M. Yoneyama, J. Phys. Chem. B, 2012, 116, 775 CrossRef CAS PubMed.
- M. L. Jiménez, A. V. Delgado, S. Ahualli, M. Hoffmann, A. Witteman and M. Ballauff, Soft Matter, 2011, 7, 3758 RSC.
- M. Yang and K. Zhao, Soft Matter, 2016, 12, 4093 RSC.
- H. Ohshima, Sci. Technol. Adv. Mater., 2009, 10, 063001 CrossRef.
- K. Makino and H. Ohshima, Sci. Technol. Adv. Mater., 2011, 12, 023001 CrossRef.
- G. R. MacDonald, Phys. Rev., 1953, 92, 4 CrossRef.
- R. P. Buck, J. Electroanal. Chem., 1969, 23, 219 CrossRef CAS.
- A. D. Hollingsworth and D. A. Saville, J. Colloid Interface Sci., 2003, 257, 65 CrossRef CAS PubMed.
- M. Wien, Wied. Ann., 1896, 58, 37 CrossRef.
- E. Warburg, Drud. Ann., 1901, 6, 125 CAS.
- G. Jaffé, Ann. Phys., 1933, 408, 217 CrossRef.
- G. Jaffé and J. A. Rider, J. Chem. Phys., 1952, 20, 1077 CrossRef.
- P. A. Cirkel, J. P. M. van der Ploeg and G. J. M. Koper, Physica A, 1997, 235, 269 CrossRef CAS.
- C. Chassagne, D. Bedeaux, J. P. M. van der Ploeg and G. J. M. Koper, Colloids Surf., A, 2002, 210, 137 CrossRef CAS.
- G. Barbero and M. Scalerandi, J. Chem. Phys., 2012, 136, 084705 CrossRef CAS PubMed.
- A. D. Hollingsworth, Curr. Opin. Colloid Interface Sci., 2013, 18, 157 CrossRef CAS.
- W. Su, K. Zhao, J. Wei and T. Ngai, Soft Matter, 2014, 10, 8711 RSC.
- R. Roldán-Toro and J. D. Solier, J. Colloid Interface Sci., 2004, 274, 76 CrossRef PubMed.
- S. Emmert, M. Wolf, R. Gulich, S. Krohns, S. Kastner, P. Lunkenheimer and A. Loidl, Eur. Phys. J. B, 2011, 83, 157 CrossRef CAS.
- M. L. Jiménez, F. J. Arroyo, J. van Turnhout and A. V. Delgado, J. Colloid Interface Sci., 2002, 249, 327 CrossRef PubMed.
- H. Falkenhagen, Electrolytes, Oxford University, Oxford, 1934 Search PubMed.
- J. D. Ferry, J. Chem. Phys., 1948, 16, 737 CrossRef CAS.
- M. Stieger, W. Richtering, J. S. Pedersen and P. Lindner, J. Chem. Phys., 2004, 120, 6197 CrossRef CAS PubMed.
- S. Ahualli, M. Ballauff, F. J. Arroyo, A. V. Delgado and M. L. Jiménez, Langmuir, 2012, 28, 16372 CrossRef CAS PubMed.
- J. K. G. Dhont and K. Kang, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 33, 51 CrossRef CAS PubMed.
- J. Zhou and F. Schmid, Eur. Phys. J. E: Soft Matter Biol. Phys., 2013, 36, 33 CrossRef PubMed.
- C. Grosse and A. V. Delgado, Curr. Opin. Colloid Interface Sci., 2010, 15, 145 CrossRef CAS (with a Corrigendum in 2013, 18, 161).
- J. Zhou and F. Schmid, Eur. Phys. J.: Spec. Top., 2013, 222, 2911 CrossRef.
- E. H. B. DeLacey and L. R. White, J. Chem. Soc., Faraday Trans., 1981, 2(77), 2007 RSC.
- V. N. Shilov, A. V. Delgado, F. González-Caballero, J. Horno, J. J. López-García and C. Grosse, J. Colloid Interface Sci., 2000, 232, 141 CrossRef CAS PubMed.
- H. Zhao and H. H. Bau, J. Colloid Interface Sci., 2009, 333, 663 CrossRef CAS PubMed.
- K. W. Wagner, Arch. Electrotech., 1914, 2, 371 CrossRef.
- C. T. O'Konski, J. Phys. Chem., 1960, 64, 605 CrossRef.
- C. Grosse, Relaxation Mechanisms of Homogeneous Particles and Cells Suspended in Aqueous Electrolyte Solutions, in Surfactant Series: Interfacial Eletrokinetics and Electrophoresis, ed. A. V. Delgado, Marcel Dekker Inc., New York, 2002, vol. 106 Search PubMed.
- S. Ahualli, M. L. Jimenéz, F. Carrique and A. V. Delgado, Langmuir, 2009, 25, 1986 CrossRef CAS PubMed.
- P. J. Beltramo, R. Roa, F. Carrique and E. M. Furst, J. Colloid Interface Sci., 2013, 408, 54 CrossRef CAS PubMed.
- F. Carrique, F. J. Arroyo, M. L. Jiménez and A. V. Delgado, J. Chem. Phys., 2003, 118, 1945 CrossRef CAS.
- S. Kuwabara, J. Phys. Soc. Jpn., 1959, 14, 527 CrossRef.
- V. N. Shilov, N. I. Zharkikh and Y. B. Borkovskaya, Colloid J. USSR, 1981, 43, 434 Search PubMed.
- E. K. Zholkovskij, J. H. Masliyah, V. N. Shilov and S. Bhattacharjee, Adv. Colloid Interface Sci., 2007, 134, 279 CrossRef PubMed.
- C. Grosse, Colloids Surf., A, 2015, 467, 207 CrossRef CAS.
- I. Borukhov, D. Andelman, R. Borrega, M. Cloitre, L. Leibler and H. Orland, J. Phys. Chem. B, 2000, 104, 11027 CrossRef CAS.
- P. S. Mohanty and W. Richtering, J. Phys. Chem. B, 2008, 112, 14692 CrossRef CAS PubMed.
- D. Gottwald, C. N. Likos, G. Kahl and H. Löwen, J. Chem. Phys., 2005, 122, 074903 CrossRef CAS PubMed.
- C. N. Likos, in Part Three, Phase Behavior and Dynamics of Microgel Suspensions, Microgel Suspensions: Fundamentals and Applications, ed. A. Fernández-Nieves, H. Wyss, J. Mattsson and D. A. Weitz, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2011 Search PubMed.
- J. Riest, P. Mohanty, P. Schurtenberger and C. N. Likos, Z. Phys. Chem., 2012, 226, 711 CrossRef CAS.
- T. Colla, C. N. Likos and Y. Levin, J. Chem. Phys., 2014, 141, 234902 CrossRef PubMed.
- L. Belloni, J. Phys.: Condens. Matter, 2000, 12, R549 CrossRef CAS.
- P. Holmqvist, P. S. Mohanty, G. Nägele, P. Schurtenberger and M. Heinen, Phys. Rev. Lett., 2012, 109, 048302 CrossRef CAS PubMed.
- A. R. Denton, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 011804 CrossRef CAS PubMed (with an erratum in: A. R. Denton, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 049904(E) CrossRef ).
- K. Kang, A. Wilk, A. Patkowski and J. K. G. Dhont, J. Chem. Phys., 2007, 126, 214501 CrossRef PubMed.
- S. Fischer and R. R. Netz, Eur. Phys. J. E: Soft Matter Biol. Phys., 2013, 36, 117 CrossRef PubMed.
- K. Kratz, T. Hellweg and W. Eimer, Colloids Surf., A, 2000, 170, 137 CrossRef CAS.
- R. Borrega, M. Cloitre, I. Betremieux, B. Ernst and L. Leibler, Europhys. Lett., 1999, 47, 729 CrossRef CAS.
- J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids, Elsevier, 3rd edn, 2006 Search PubMed.
- L. Verlet and J.-J. Weis, Phys. Rev. A, 1972, 5, 939 CrossRef.
- D. Henderson, Condens. Matter Phys., 2009, 12, 127 CrossRef CAS.
- C. Pellet and M. Cloitre, Soft Matter, 2016, 12, 3710 RSC.
- M. Cloitre, R. Borrega, F. Monti and L. Leibler, C. R. Phys., 2003, 4, 221 CrossRef CAS.
- G. Romeo, L. Imperiali, J.-W. Kim, A. Fernández-Nieves and D. A. Weitz, J. Chem. Phys., 2012, 136, 124905 CrossRef PubMed.
- A. Wilk, S. Huissmann, E. Stiakakis, J. Kohlbrecher, D. Vlassopoulos, C. N. Likos, G. Meier, J. K. G. Dhont, G. Petekidis and R. Vavrin, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 32, 127 CrossRef CAS PubMed.
- S. Maccarrone, O. Mergel, F. A. Plamper, O. Holderer and D. Richter, Macromolecules, 2016, 49, 1911 CrossRef CAS.
- R. Schroeder, A. A. Rudov, L. A. Lyon, W. Richtering, A. Pich and I. I. Potemkin, Macromolecules, 2015, 48, 5914 CrossRef CAS.
- K. Kang and J. K. G. Dhont, Soft Matter, 2010, 6, 273 RSC.
- K. Kang, A. Wilk, A. Patkowski and J. K. G. Dhont, J. Chem. Phys., 2007, 126, 214501 CrossRef PubMed.
- D. M. Gray, A comprehensive look at conductivity measurement in steam and power generating waters, Mettler-Toledo Thornton, Inc., Presented at the 67th international water conference, Engineerings Society of Western Pennsylvania, Pittsburg, October 2006, IWC-06-29.
- T. S. Light, E. A. Kingman and A. C. Bevilacqua, The conductivity of low concentrations of CO2 dissolved in ultrapure water from 0–100 °C, Thornton Associates, Inc. 1432 Main Street Waltham, MA 02154, Paper presented at the 209th American Chemical Society National Meeting, Anaheim, CA, April 2–6, 1995.
| This journal is © The Royal Society of Chemistry 2016 |