DOI:
10.1039/C6SM01481J
(Paper)
Soft Matter, 2016,
12, 8155-8166
Stabilization of membrane necks by adhesive particles, substrate surfaces, and constriction forces
Received
27th June 2016
, Accepted 2nd August 2016
First published on 2nd August 2016
Abstract
Membrane remodelling processes involving the formation and fission of small buds require the formation and closure of narrow membrane necks, both for biological membranes and for model membranes such as lipid bilayers. The conditions required for the stability of such necks are well understood in the context of budding of vesicles with bilayer asymmetry and/or intramembrane domains. In many cases, however, the necks form in the presence of an adhesive surface, such as a solid particle or substrate, or the cellular cortex itself. Examples of such processes in biological cells include endocytosis, exocytosis and phagocytosis of solid particles, the formation of extracellular and outer membrane vesicles by eukaryotic and prokaryotic cells, as well as the closure of the cleavage furrow in cytokinesis. Here, we study the interplay of curvature elasticity, membrane-substrate adhesion, and constriction forces to obtain generalized stability conditions for closed necks which we validate by numerical energy minimization. We then explore the consequences of these stability conditions in several experimentally accessible systems such as particle-filled membrane tubes, supported lipid bilayers, giant plasma membrane vesicles, bacterial outer membrane vesicles, and contractile rings around necks. At the end, we introduce an intrinsic engulfment force that directly describes the interplay between curvature elasticity and membrane-substrate adhesion.
1 Introduction
In the absence of external forces, liquid droplets attain spherical shapes that minimize their surface area and, thus, their interfacial free energy for a given droplet volume. In contrast to droplets, lipid vesicles formed by biomimetic or biological membranes can attain a large variety of different shapes that minimize the membranes’ curvature energy for a given vesicle volume and membrane area. Particularly intriguing vesicle shapes are provided by two spheres connected by a narrow membrane neck that appears to be highly curved but does not contribute to the curvature energy of the vesicle membrane.1–4 Such necks are formed by membranes with uniform composition,1,5 by membranes with intramembrane domains,6–8 and by membranes exposed to optical tweezers.9 Furthermore, narrow membrane necks are also ubiquitous in biological cells. Indeed, such necks are observed prior to endo- and exocytosis,10,11 phagocytosis,12 cytokinesis,13 as well as autophagosome formation.14 In the latter processes, the neck formation is regulated by a complex network of proteins.15,16
The formation of membrane necks frequently occurs in the presence of adhesive particles or substrate surfaces, see Fig. 1. On the one hand, membranes can engulf adhesive nanoparticles and then form particle-filled buds, the size of which is determined by the particle size, as displayed in Fig. 1(a and b).17 These engulfment processes are essential for endocytosis and exocytosis by cellular membranes, can be used for drug delivery or medical imaging, and play an important role during viral infections. Analogous processes occur during phagocytosis of larger particles by specialized cells.
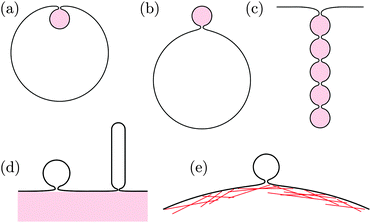 |
| | Fig. 1 Narrow membrane necks often form in the presence of adhesive particles or substrate surfaces: (a) endocytic and (b) exocytic engulfment of nanoparticles; (c) formation of necklace-like particle-filled tubes; (d) budding or tubulation of supported bilayers; and (e) formation of giant plasma membrane vesicles via chemically induced blebbing. In panels (a)–(c), the adhesive particles (pink) are located within the membrane buds and tubes. In panels (d) and (e), the membrane buds and tubes are not in direct contact with the adhesive substrates (pink) and the actin cortex. | |
On the other hand, the plasma membrane of eukaryotic cells, which is in permanent contact with the adhesive actin cortex, can form extracellular vesicles such as exosomes, ectosomes, and apoptotic bodies, the size of which can vary over a wide range from 30 nm to a couple of micrometers.18 During the formation of such a vesicle, the plasma membrane must detach from the actin cortex and bulge out towards the external medium until it forms a bud with a closed neck, which is eventually cleaved to release the vesicle. Particularly large cortex-free vesicles, so-called “giant plasma membrane vesicles”, are formed via chemically induced blebbing, see Fig. 1(e).19–22 A similar process is observed for Gram-negative bacteria during the secretion of “outer membrane vesicles”. These bacteria have a cell wall that consists of a peptidoglycan layer sandwiched between two lipid bilayers. During the secretion process, a large segment of the outer bilayer detaches from the peptidoglycan layer, bulges out towards the external medium, and forms a spherical vesicle that is released from the prokaryotic cell.23,24
The processes of endocytosis and exocytosis can be mimicked in model systems, such as lipid or polymer vesicles in contact with adhesive particles, and the formation and closure of a narrow membrane neck has been observed to occur spontaneously in these systems, without the help of complex protein machinery as in biological cells.25–29 Although not yet seen in experiments, particle-filled membrane tubes with narrow necks between the particles, see Fig. 1(c), have been predicted by numerical simulations.30–32 Furthermore, formation and closure of membrane necks in the presence of adhesion also occurs during the unbinding of supported lipid bilayers via budding or tubulation, see Fig. 1(d).33–37
In the absence of adhesion, the mechanisms for the formation and closure of membrane necks during budding have been understood for quite some time, and typically require either a strong bilayer asymmetry leading to a spontaneous curvature of the membrane,2,4 or phase separation in the membrane, giving rise to a line tension that contributes or even drives neck closure and budding.7,39 In ref. 17 we showed, in the context of particle engulfment, that the presence of an adhesive surface helps in stabilizing closed necks and described a novel stability condition for such necks. In the present paper, we will rederive this stability condition using a particular parametrization of the neck shape, which will allow us to examine the energetics and geometry of narrow necks in a systematic manner, as well as to extend the applicability of the stability condition to other cases of interest.
The paper is organized as follows. The spontaneous curvature model with adhesion is introduced in Section 2.1. In Sections 2.2 and 2.3, we describe in detail the numerical process used to find the minimum energy shapes of a vesicle in contact with an adhesive particle, while in Section 2.4 we present the analytical model used in the analysis of shapes with narrow necks. The predictions of the analytical model are then validated in detail by numerical calculations in Sections 3.1 and 3.2, focusing on the case of particle engulfment. In the remaining sections, we extend the application of the analytical model to particle-filled membrane tubes, budding of supported lipid bilayers from homogeneous and patterned substrates, giant plasma membrane and outer membrane vesicle formation, and narrow necks in the presence of externally applied constriction forces.
Throughout the paper, endocytic and exocytic engulfment will be discussed in parallel. In all equations, the upper and lower signs of the ± or ∓ symbols will correspond to endocytic and exocytic engulfment, respectively.
2 Theoretical description and methods
2.1 Spontaneous curvature model with adhesion
The membrane is treated as a smooth, continuous surface and is studied within the framework of the well-established spontaneous curvature model.2,40 Here, the membrane is described by two material parameters, namely its bending rigidity κ and its spontaneous curvature m. The bending energy of such a smooth membrane has the form| | 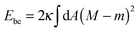 | (1) |
where M is the mean curvature at each point of the membrane, and the integral represents an area integral over the whole membrane surface of the vesicle. The mean curvature is taken to be positive (negative) if the membrane bulges towards the exterior (interior) compartment of the vesicle. We will only consider transformations that leave the topology of the vesicle unchanged, which implies that the area integral over the Gaussian curvature provides a shape-independent constant.40
The adhesive interaction with the particle is included via a contact potential, with adhesive energy per unit area W < 0 and the adhesion energy41
where
Abo is the area of the membrane segment bound to the particle. The total energy to be considered is then given by
2.2 Numerical minimization of total energy
Our aim is to calculate the minimum energy shapes of a vesicle with fixed area A and enclosed volume V, attached to a rigid spherical particle of radius Rpa. The wrapping angle ϕ, as described in Fig. 2, represents the reaction coordinate of the engulfment process. In the context of particle engulfment, this wrapping angle can vary continuously between ϕ = 0, corresponding to the non-adhering or free state of the particle, and ϕ = π, corresponding to the particle being completely engulfed. In this completely engulfed state, the membrane bound to the particle is connected to the mother vesicle by a closed neck. In the continuum model considered here, the closed neck has zero thickness.
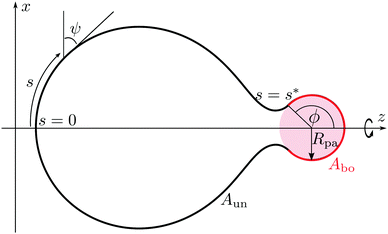 |
| | Fig. 2 Axisymmetric geometry and arc length parametrization of a vesicle in contact with a spherical particle (pink), used for the numerical minimization of the spontaneous curvature model with adhesion. The particle originates from the interior compartment corresponding to exocytic engulfment. The unbound part of the vesicle membrane (black), meets the bound part (red) smoothly at a certain wrapping angle ϕ. The bound part of the membrane has area Abo, whereas the unbound part has area Aun = A − Abo. | |
The bound segment of the vesicle membrane follows the contour of the particle, and thus assumes the shape of a spherical cap. This segment has the area
| | Abo = 2πRpa2(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ). ϕ). | (4) |
If we cut the spherical particle along the contact line, we obtain two spherical caps. The spherical cap adjacent to the bound membrane segment has the volume
| | 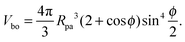 | (5) |
Furthermore, the combined bending and adhesion energy of the bound membrane segment is given by
| | Ebo = [4πκ(1 ± mRpa)2 − 2π|W|Rpa2](1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ). ϕ). | (6) |
The total energy
Eun of the unbound part of the membrane is equal to its bending energy
| | 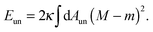 | (7) |
In order to find the shape of the unbound segment that minimizes
Eun, for a fixed value of
ϕ, and satisfies the constraints on the total membrane area and enclosed volume of the vesicle, we must minimize the shape functional
| | | F ≡ Eun + Σ(A − Abo) − ΔP(V ± Vbo) | (8) |
where
Σ and Δ
P are Lagrange multipliers for the area and volume constraints. The volume
V ±
Vbo is enclosed by the unbound membrane segment and the additional planar surface that spans the circular contact line.
Parametrizing the shape contour by its arc length s, see Fig. 2, the shape functional F becomes2
| | 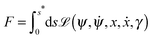 | (9) |
with the ‘Lagrangian’ function
| | 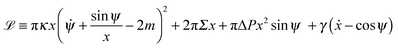 | (10) |
where
γ =
γ(
s) is a Lagrange multiplier function that serves to impose the geometrical constraint
ẋ = cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ
ψ, and the dot denotes a derivative with respect to the arc length
s.
We now put the first variation δF in (9) equal to zero and obtain the Euler–Lagrange equations of (10), which are identical to the shape equations for a free vesicle2 and have the form
| | 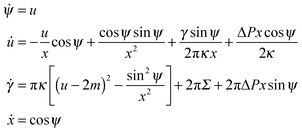 | (11) |
These equations are subject to the initial conditions
| | | ψ(0) = 0, u(0) = u0, γ(0) = 0, x(0) = 0. | (12) |
We can augment the system of equations in
(11) with the equations for the area and volume as given by
| | ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) = πx2sin = πx2sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ ψ | (13) |
with initial conditions
We then have a system of six first-order differential equations with six initial conditions. There are, however, four unknown parameters: Σ, ΔP, u0 and s*. These are used to satisfy the four boundary conditions
x(s*) = Rpasin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ ϕ |
at
s =
s*, which enforce the constraints in area and volume, and a smooth matching between the unbound and bound segment of the vesicle membrane.
The problem is thus well-posed, and can be solved using a non-linear shooting procedure. The numerical integration of eqn (11) and (13), with initial conditions in eqn (12) and (14), is performed using a Runge–Kutta method, while the search for the values of Σ, ΔP, u0 and s* that satisfy the boundary conditions in (15) is carried out using Newton's method. The case of a vesicle that can freely adjust its volume is included by setting ΔP = 0 in (11) and ignoring the boundary condition for the volume V(s*) in (15).
2.3 Parameters of the vesicle–particle system
The system depends on six parameters corresponding to three geometric parameters, namely the particle radius Rpa, the total membrane area A and enclosed volume V of the vesicle as well as three material parameters, namely the bending rigidity κ, the spontaneous curvature m and the adhesive strength |W|. However, choosing the bending rigidity κ as the basic energy scale and the vesicle size| | 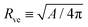 | (16) |
as the basic length scale, we can explore the whole parameter space via four dimensionless parameters as defined by| | rpa ≡ Rpa/Rve, v ≡ 3V/(4πRve3), ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ≡ mRve ≡ mRve | (17) |
andIf the solution contains no osmotically active solutes, the volume of the vesicle can adjust freely, and the three reduced parameters rpa, ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) and w completely define the system.
and w completely define the system.
The computation then proceeds as follows: for fixed values of rpa, ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) and v, the total energy of the system E(ϕ) as a function of ϕ is obtained from the bending energy Eun(ϕ) of the unbound membrane segment resulting from the shooting method, together with the bending and adhesive energies, Ebo(ϕ), of the particle-bound segment, given by (6), so that E(ϕ) ≡ Eun(ϕ) + Ebo(ϕ). Closed necks will be stable or unstable if E(ϕ) has a boundary minimum or maximum, respectively, at ϕ = π.
and v, the total energy of the system E(ϕ) as a function of ϕ is obtained from the bending energy Eun(ϕ) of the unbound membrane segment resulting from the shooting method, together with the bending and adhesive energies, Ebo(ϕ), of the particle-bound segment, given by (6), so that E(ϕ) ≡ Eun(ϕ) + Ebo(ϕ). Closed necks will be stable or unstable if E(ϕ) has a boundary minimum or maximum, respectively, at ϕ = π.
2.4 Analysis of narrow membrane necks
The limiting case of a particle close to complete engulfment with wrapping angle ϕ ≲ π, in which the bound part of the membrane is connected to the mother vesicle by a narrow neck, can be understood in the context of a specific shape parametrization that has been previously used for the budding of uniform membranes4 and of intramembrane domains.7,39 The corresponding shape contour is displayed in Fig. 3, and is divided into four regions I–IV. Region I is a hemisphere of radius R1 representing the least perturbed part of the vesicle. The neck is described by regions II and III, which correspond to unduloid segments. Region IV is a spherical cap of radius Rpa and aperture angle ϕ, representing the segment bound to the particle. Our model differs from the one in ref. 4 and 39 in that the aperture or wrapping angle ϕ can have any value in the range π/2 ≤ ϕ ≤ π, instead of being fixed to ϕ = π/2. This ϕ-range is essential in order to study necks in the presence of an adhesive particle.
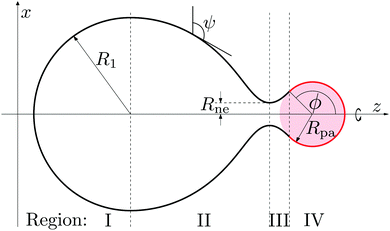 |
| | Fig. 3 Piece-wise parametrization for the shape contour of the vesicle membrane as used in the analytical study of narrow membrane necks for exocytic engulfment. All four membrane segments I, II, III, and IV have constant mean curvature. Segment I forms a hemisphere of radius R1, segments II and III represent two unduloidal segments connected by a neck of radius Rne, and segment IV is a spherical cap of radius Rpa and aperture angle ϕ. In the exocytic case depicted here, the spherical particle (pink) originates from the interior compartment. | |
Note that the piece-wise parametrization of the vesicle shape just described does not solve the shape equations as given by (11) and, thus, represents an approximation to the equilibrium shape of the vesicle. However, this parameterization leads to stability conditions for closed necks that are in excellent agreement with the lines of limit shapes as found numerically for the budding of uniform membranes2–4 and of intramembrane domains.7,39 This agreement implies that the parameterization correctly captures the asymptotic behavior of the system in the limit of small neck diameters. In general, the use of this piece-wise parametrization should always be scrutinized a posteriori by comparing its predictions with exact numerical results, see Section 3 below.
The shape contour of the unduloidal segment II can be parametrized by
| | 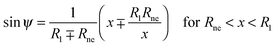 | (19) |
while the shape contour of the unduloidal segment III has the parametrization
| | 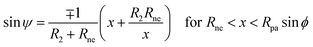 | (20) |
where
Rne is the radius of the neck connecting the two spherical caps,
R1 is the radius of the spherical cap representing the unperturbed part of the vesicle and
R2 is given by
| | 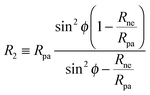 | (21) |
where
Rpa is the radius of the particle.
The total area, enclosed volume and bending energy of such a trial contour can be readily calculated analytically for given values of R1, Rne, Rpa and ϕ. We are, however, primarily interested in the limit of narrow necks which corresponds to the inequality
Inspection of
Fig. 3 shows that the neck radius
Rne tends to zero when the wrapping angle
ϕ tends to π. More generally, when the shifted angle
| | η ≡ π − ϕ with sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η = sin η = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ ϕ | (23) |
becomes small, the neck radius becomes small as well, with the condition
Rne <
Rpa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η
η or equivalently
ε < sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η
η being always satisfied during the closure of the membrane neck. We will thus consider an expansion in powers of
ε, taking into account that the dimensionless ratio sin
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η
η/
ε is of order one. The total membrane area of the trial contour is found to be
| | 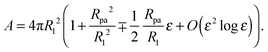 | (24) |
Because we will consider variations of the contour for fixed total area
A, the radius
R1 of the unperturbed part of the vesicle must obey the relation
| | 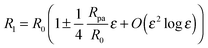 | (25) |
where
R0 is defined by 4π
R02 ≡
A − 4π
Rpa2, corresponding to the radius of the unbound part of the vesicle in the limit of a fully closed neck with
ε = 0. The total volume enclosed by the vesicle is
| | 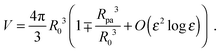 | (26) |
The contour parametrization used here does not allow us to keep both the total area and the enclosed volume constant at the same time. For this reason, we consider a shape ensemble of variable volume at constant osmotic pressure difference ΔP. The total energy to be considered is then composed of a bending term, an adhesion term and a pressure term and given by
In the exocytic case, the volume
V includes the volume of the particle, even if the latter is not accessible to the aqueous solution enclosed by the vesicle. However, including the particle volume in
V has no effect on the energy minimization, because it only adds the constant term −Δ
P(4π/3)
Rpa3 to the total energy, and this term is independent of the vesicle shape.
An expansion of the total energy in terms of the parameter ε then leads to the expression
| | 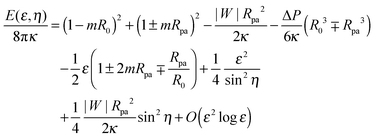 | (28) |
which depends on the neck radius
ε and the shifted wrapping angle
η. In order to compare the analytical theory with the numerical calculations, we need to find the optimal shape of the vesicle, and thus the optimal neck size
ε*, that minimizes the energy for a given wrapping angle
ϕ with small
η = π −
ϕ. Because the quadratic term in
ε in
eqn (28) is always positive, for a given value of
η, the energy will have a minimum at a finite positive value of
ε only if the linear term in
ε is negative, which implies the condition
| | 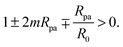 | (29) |
Indeed, if this condition is not satisfied, membrane buds of radius
Rpa or larger are stable even in the absence of the adhesive particle,
2,4 and our contour parametrization is no longer appropriate.
By imposing 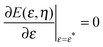 , we obtain the optimal neck size
, we obtain the optimal neck size
| | 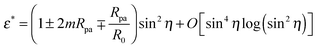 | (30) |
which, as expected, is small whenever sin
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η
η is small, and has a meaningful value only if the inequality
(29) is satisfied.
By substituting the value of ε* into (28), we obtain the total energy E(η) ≡ E(ε*, η) as a function of the shifted wrapping angle η. The difference in energy between a configuration with a narrow open neck and one with a closed neck δE(η) ≡ E(η) − E(0) is finally found to behave as†
| |  | (31) |
to first order in sin
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η
η with
η = π −
ϕ as in
(23). The energy difference δ
E(
η) represents the excess energy (or reversible work) necessary to open up the closed neck.
It is interesting to note that the pressure term −ΔPV does not contribute to the expression in (31) because it is of higher order in sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η. Alternatively, one could consider a shape ensemble in which the enclosed volume is kept constant, whereas the membrane area is variable at constant tension Σ, with a term ΣA added to the total energy. In the latter case, we similarly find that the tension only adds higher order terms in sin2
η. Alternatively, one could consider a shape ensemble in which the enclosed volume is kept constant, whereas the membrane area is variable at constant tension Σ, with a term ΣA added to the total energy. In the latter case, we similarly find that the tension only adds higher order terms in sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η to the energy, with eqn (30) and (31) remaining unaffected.
η to the energy, with eqn (30) and (31) remaining unaffected.
3 Neck stability for engulfed particles
3.1 Stability of closed necks for particle engulfment
We now proceed to compare the predictions of the analytical theory for narrow necks with numerical calculations. One of the most important consequences of eqn (31) is that completely engulfed particles with η = π − ϕ = 0 and a closed neck are (meta)stable only if the energy δE(η) increases with increasing η for small η, and unstable otherwise. Taking (31) together with the condition (29), we find that a closed neck adjacent to a completely engulfed particle is (meta)stable whenever| | 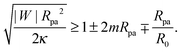 | (32) |
One limitation of the contour parametrization used in our analytical treatment is that the shape of the mother vesicle must be spherical with radius R0 in the limit of closed necks with Rne* = 0. This limiting geometry always applies to vesicles with a freely adjustable volume and ΔP = 0 but not to vesicles with fixed enclosed volume. In the latter case, the mother vesicle may display non-spherical shapes such as prolate or oblate shapes after the engulfment of the particle. In order to consider this more general situation, we can replace 1/R0 in (32) by the local mean curvature, M′, of the mother vesicle at the position of the neck. With a slight rearrangement of the different terms, we can rewrite the stability condition in the form
| | 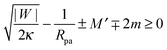 | (33) |
where the upper and lower signs of the ± and ∓ symbols correspond again to endocytic and exocytic engulfment, respectively, see
Fig. 1(a and b). The first term on the left hand side of
(33) is equal to the inverse of the adhesion length
RW defined by
| | 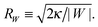 | (34) |
This length scale can vary from about 10 nm to a couple of microns as described in
ref. 17. The equality in
(33) represents the neck closure condition of a limit shape for which the open neck becomes closed.
The stability condition (33) was originally obtained in ref. 17, via a heuristic argument based on the continuity of the bending energy density across the neck, and was confirmed by extensive numerical calculations for vesicles with and without volume constraint. For planar membranes without spontaneous curvature, the condition (33) becomes simply |W| ≥ 2κ/Rpa2, which describes the numerical results in ref. 42 for the engulfment of particles by planar membranes with a fixed membrane tension. If we consider a non-adhesive particle with |W| = 0, the neck closure condition given by the equality in (33) becomes M′ + Mbo = 2m with the mean curvature Mbo ≡ ∓1/Rpa of the particle-bound membrane segment. The latter relation is identical with the ideal neck condition previously obtained2,4 for the budding of homogeneous vesicles. Eqn (33) is therefore a generalization of this neck condition to membranes interacting with adhesive surfaces.
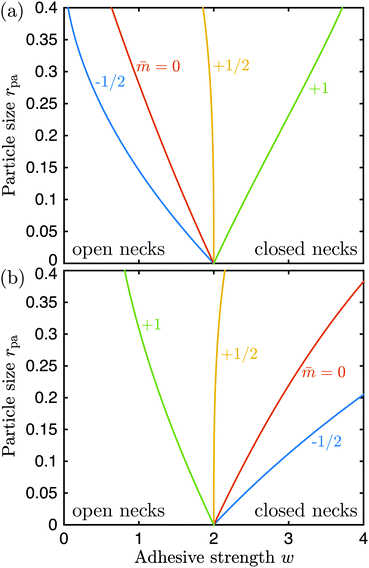
For the case of a pressureless vesicle with no volume constraint, the curvature of the (spherical) mother vesicle after complete engulfment is simply 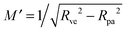 , where
, where 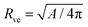 is now equal to the radius of the (spherical) vesicle before engulfment of the particle. In Fig. 4, we plot the neck closure condition (33) as a function of particle size rpa and adhesive strength w, for different values of the spontaneous curvature
is now equal to the radius of the (spherical) vesicle before engulfment of the particle. In Fig. 4, we plot the neck closure condition (33) as a function of particle size rpa and adhesive strength w, for different values of the spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) . Closed necks are stable and unstable for high and low values of the adhesive strength, respectively. The condition as given by eqn (33) has been quantitatively confirmed by numerical energy minimization for a large number of different parameter values. For endocytic engulfment, see Fig. 4(a), negative spontaneous curvatures favour the stability of closed necks, whereas positive spontaneous curvatures act to destabilize them. In contrast, for exocytic engulfment, closed necks are favoured by positive and suppressed by negative spontaneous curvatures, see Fig. 4(b).
. Closed necks are stable and unstable for high and low values of the adhesive strength, respectively. The condition as given by eqn (33) has been quantitatively confirmed by numerical energy minimization for a large number of different parameter values. For endocytic engulfment, see Fig. 4(a), negative spontaneous curvatures favour the stability of closed necks, whereas positive spontaneous curvatures act to destabilize them. In contrast, for exocytic engulfment, closed necks are favoured by positive and suppressed by negative spontaneous curvatures, see Fig. 4(b).
 |
| | Fig. 4 Neck closure condition for (a) endocytic and (b) exocytic engulfment of a spherical particle, as a function of adhesive strength w = |W|Rve2/κ and particle size rpa = Rpa/Rve. The different lines follow from (33) for different values of the spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = mRve. The vesicle can freely adapt its volume corresponding to the osmotic pressure difference ΔP = 0. = mRve. The vesicle can freely adapt its volume corresponding to the osmotic pressure difference ΔP = 0. | |
3.2 Energetics and geometry of neck opening
Using numerical computations, we now examine the expression (31) for the excess energy related to neck opening. In analogy to the derivation of eqn (33), we substitute 1/R0 in (31) by the local mean curvature M′ of the (non-spherical) mother vesicle which leads to| | 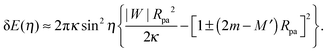 | (35) |
Eqn (35) implies that, to first order in sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η, the excess energy for neck opening depends only on the local mean curvature M′ of the membrane at the position of the neck, and is independent of the global shape of the vesicle.
η, the excess energy for neck opening depends only on the local mean curvature M′ of the membrane at the position of the neck, and is independent of the global shape of the vesicle.
We have validated eqn (35) by numerical energy minimization both for endocytic and exocytic engulfment, for vesicles with and without volume constraint, as well as for different spontaneous curvatures, particle sizes, and values of the adhesive strength. In all cases, eqn (35) provides the correct behaviour to first order in sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η. A few examples are displayed in Fig. 5(a). For sin2
η. A few examples are displayed in Fig. 5(a). For sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η = 0, corresponding to complete engulfment with ϕ = π, all numerical lines have a common tangent as given by eqn (35). In all cases, the numerical results are reasonably well approximated by the analytical line in the range 0 ≤ sin2
η = 0, corresponding to complete engulfment with ϕ = π, all numerical lines have a common tangent as given by eqn (35). In all cases, the numerical results are reasonably well approximated by the analytical line in the range 0 ≤ sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η ≤ 0.2, corresponding to π ≥ ϕ ≥ 0.85π.
η ≤ 0.2, corresponding to π ≥ ϕ ≥ 0.85π.
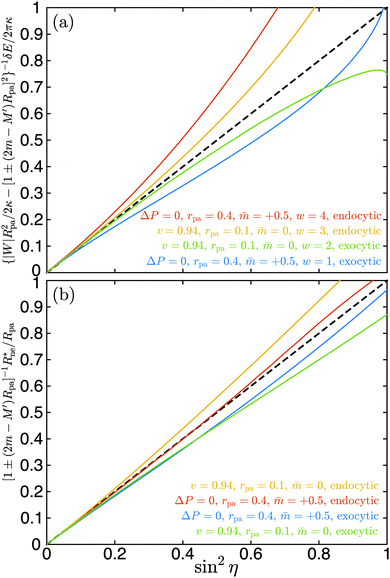 |
| | Fig. 5 (a) Excess energy δE for neck opening and (b) optimal neck radius Rne* as a function of sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η as obtained by numerical energy minimization. The shifted wrapping angle η = π − ϕ varies from η = 0 to η = π/2. The reduced volume v = 0.94 corresponds to prolate vesicles with fixed volume, the case ΔP = 0 to spherical vesicles with adjustable volume. Both endocytic and exocytic engulfment are considered for two particle sizes rpa = 0.1 and rpa = 0.4 as well as for two spontaneous curvatures η as obtained by numerical energy minimization. The shifted wrapping angle η = π − ϕ varies from η = 0 to η = π/2. The reduced volume v = 0.94 corresponds to prolate vesicles with fixed volume, the case ΔP = 0 to spherical vesicles with adjustable volume. Both endocytic and exocytic engulfment are considered for two particle sizes rpa = 0.1 and rpa = 0.4 as well as for two spontaneous curvatures ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 0 and = 0 and ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 0.5. In (a), a range of four different adhesive strengths w is examined. The scaling factors for the excess energy and the neck size, see lettering of the y-axes, correspond to eqn (35) and (36) respectively. As predicted by these equations, all lines have a common tangent at sin2 = 0.5. In (a), a range of four different adhesive strengths w is examined. The scaling factors for the excess energy and the neck size, see lettering of the y-axes, correspond to eqn (35) and (36) respectively. As predicted by these equations, all lines have a common tangent at sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η = 0, given by the black dashed line y = x. η = 0, given by the black dashed line y = x. | |
Another testable prediction of the analytical theory is the behaviour of the optimal neck size Rne* as a function of wrapping angle ϕ. Following (30), again replacing 1/R0 by M′ in order to generalize the result, and taking into account that ε* ≡ Rne*/Rpa we obtain
| | 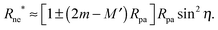 | (36) |
For small
η = π −
ϕ, the optimal radius of the neck depends only on the spontaneous curvature of the membrane, the particle size and the curvature of the mother vesicle at the position of the neck, irrespective of the global shape of the vesicle. We have also validated
eqn (36) by numerical energy minimization. Some examples are shown in
Fig. 5(b). As expected, all numerical lines have a common tangent at sin
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η
η = 0. In all cases tested, the numerical results are reasonably well approximated by
eqn (36) in the range 0 ≤ sin
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η
η ≤ 0.4, corresponding to π ≥
ϕ ≥ 0.78π.
3.3 Stability of particle-filled membrane tubes
It is not difficult to extend the analytical treatment described in Section 2.4, and in particular the stability condition for closed necks (33), to membrane necks that form between two adhesive particles when two or more such particles are collectively engulfed by a larger vesicle into a tube-like structure, see Fig. 1(c). In such a situation, endocytic engulfment leads to membrane in-tubes, whereas exocytic engulfment leads to membrane out-tubes. First, consider a neck that belongs to a membrane out-tube with positive mean curvature of the particle-bound membrane segments. If a particle of radius Rpa1 and adhesive strength |W1| is located on one side of the neck, and one of radius Rpa2 and adhesive strength |W2| on the other side, a closed neck between the two particles will be stable if| | 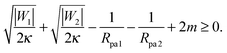 | (37) |
This relation implies that larger adhesive strengths, larger particles, and positive spontaneous curvatures favor the formation of closed necks for particle-filled out-tubes. Likewise, for a closed neck that belongs to a membrane in-tube with negative mean curvature of the particle-bound membrane segments, the stability relation for this neck is given by| | 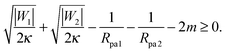 | (38) |
This relation implies that larger adhesive strengths, larger particles, and negative spontaneous curvatures favor closed necks for particle-filled in-tubes. If both particles are identical with radius Rpa1 = Rpa2 = Rpa and adhesive strength |W1| = |W2| = |W|, the stability conditions simplify and become| | 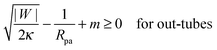 | (39) |
and| | 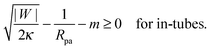 | (40) |
Particle-filled in- and out-tubes were first observed in simulations30,31 of vesicles interacting with several particles of identical size and adhesive strength. In ref. 32, the stability of such tubes was studied systematically for the case of a membrane without spontaneous curvature, and was found to be strongly dependent on the range of the adhesive potential between the particles and the membrane. As the range of the adhesive potential was decreased, tubes were found to be more and more necklace-like, with narrower and narrower membrane necks connecting adjacent engulfed particles, see Fig. 1(c). The stability limit of such necklace-like in-tubes was found numerically to approach |W| = 2κ/Rpa2, as predicted by eqn (40) with m = 0.
4 Closed necks and adhesive substrates
4.1 Budding and tubulation of supported bilayers
So far, we have focused on the case of a large vesicle engulfing a small particle. The analytical treatment in Section 2.4 and, in particular, the stability condition (33) for a closed neck are however equally valid in the case in which the particle is larger than the vesicle. One example, for which the neck stability becomes important, is the budding or tubulation of supported lipid bilayers, see Fig. 1(d). In this case, the planar substrate corresponds to the limit in which the particle size Rpa becomes infinite. The stability condition of the closed neck (33) then has the form| | 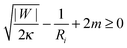 | (41) |
where Ri = Rbu or Rcy represents the radius of the spherical bud or the cylindrical tube respectively. The signs of the second and third term on the left hand side of (41) correspond to exocytic engulfment because the planar substrate corresponds to the limit of a large particle located within a somewhat larger vesicle.
Such budding and tubulation processes have been observed33–36 after asymmetric exposure of the supported membrane to ions or peptides that generate spontaneous curvature. Considering the energetic competition between bud or tube formation and adhesion, it was found in ref. 37 that the membrane will unbind from the adhesive substrate forming buds of radius Rbu = 1/m or cylindrical tubes of radius Rcy = 1/2m if the spontaneous tension 2κm2 exceeds the adhesive strength |W|. To extend this analysis, we now ask whether such budded or tubulated configurations are metastable for lower values of the spontaneous curvature, and could be obtained, e.g., via mechanical pulling.
In the case of spherical buds, the radius Rbu of the bud must satisfy the normal force balance equation ΔP = 2(Σ + 2κm2)/Rbu − 4κm/Rbu2, whereas in the case of a cylindrical tube, the cylinder radius Rcy must satisfy its corresponding normal balance equation ΔP = (Σ + 2κm2)/Rcy − κ/2Rcy3.37,38‡ In both cases, ΔP is the difference between the osmotic pressures in the interior and exterior solutions and Σ the membrane tension.
For a supported lipid bilayer, tangential force balance implies the mechanical tension Σ = |W| − 2κm2. Furthermore, if we include a water layer of finite thickness ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) W between the membrane and the substrate, the volume V ≈
W between the membrane and the substrate, the volume V ≈ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) WA for large A. Because the water layer thickness is determined by the molecular interactions between the membrane and the substrate, the volume V can no longer be varied independently of the area A and it becomes meaningless to include the Lagrange multiplier ΔP conjugate to the volume.
WA for large A. Because the water layer thickness is determined by the molecular interactions between the membrane and the substrate, the volume V can no longer be varied independently of the area A and it becomes meaningless to include the Lagrange multiplier ΔP conjugate to the volume.
Using ΔP = 0 and Σ + 2κm2 = |W| in the two normal force balance equations for a spherical bud and a cylindrical tube, we find Rbu = 2κm/|W| for the radius of the bud and 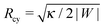 for the radius of the cylinder. Now, substituting the radius Ri in eqn (41) by these equilibrium values of Rbu and Rcy, we find the same stability relation
for the radius of the cylinder. Now, substituting the radius Ri in eqn (41) by these equilibrium values of Rbu and Rcy, we find the same stability relation
for the closed neck connecting spherical buds and cylindrical tubes to the supported bilayer.
In the case of cylindrical tubes, however, one also needs to consider the tangential force balance of the tube, that is, whether a tube will tend to grow indefinitely, whether there will be an equilibrium tube length, or whether the tube will shrink into a spherical bud. With ΔP = 0 and Σ + 2κm2 = |W|, and using the equilibrium value of the cylinder radius Rcy, tangential balance shows that cylindrical tubes will grow indefinitely (in practice, until all the supported bilayer has been transferred into the tube) if 2κm2>|W|, but will shrink into a spherical bud with radius Rbu = 2κm/|W| otherwise. This instability towards spherical buds is intrinsic to cylindrical tubes, and is independent of the stability of the closed neck connecting the tube to the supported bilayer.
In summary, we predict that budded states are unstable for 2κm2 < |W|/4, metastable in the interval |W|/4 ≤ 2κm2 ≤ |W|, and stable when 2κm2 > |W|. Cylindrical tubes, on the other hand, are unstable for 2κm2 ≤ |W|, but can grow if 2κm2 > |W|. It is also important to stress that, whereas the condition (42) and consequently these stability ranges depend on the particular choice of ΔP = 0 and Σ + 2κm2 = |W|, the stability condition (41) is independent of this choice. Therefore, even if in a given experimental system it were unclear whether these assumptions are correct, the condition (41) would remain valid and could be used to obtain lower bounds on the substrate adhesive strength or the membrane spontaneous curvature by simply measuring the bud or cylinder radius.
4.2 Budding of supported bilayers from patterned substrates
At first sight, eqn (41) and (42) seem to be incompatible. According to (41), and to the results on particle engulfment in Section 3, the adhesiveness of the substrate should contribute to the stability of closed necks; however, according to (42), substrate adhesiveness ultimately acts to destabilize closed necks. This puzzling contradiction is solved by noticing that, in the case of budding of a supported bilayer, adhesion acts in two opposing ways: locally, it acts to stabilize closed necks as dictated by (41); globally, it sets the membrane tension and thus the bud size Rbu = 2κm/|W|. This decrease in bud size with increasing substrate adhesion leads to an indirect destabilization of closed necks via(41).
These two effects can be disentangled by considering the budding of supported bilayers from patterned substrates, see Fig. 6. In this case, the substrate with ‘global’ adhesiveness |W| contains a chemically distinct surface domain that displays a different, ‘local’ adhesiveness |Wloc|. The stability condition for the closed neck connecting a spherical bud of radius Rbu to the supported bilayer within the surface domain is
| | 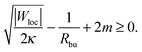 | (43) |
On the other hand, the membrane tension is still defined by the global substrate adhesiveness, with
Σ = |
W| − 2
κm2, and the equilibrium bud radius will therefore be
Rbu = 2
κm/|
W|, as in the case of a homogeneous substrate. As a consequence, a larger local adhesiveness |
Wloc| unequivocally increases the stability of buds within the surface domain.
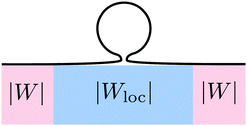 |
| | Fig. 6 Budding of a supported lipid bilayer from a patterned substrate. The substrate (pink region) with the ‘global’ adhesiveness |W| contains a chemically distinct surface domain (blue region) that displays a different, ‘local’ adhesiveness |Wloc|. The narrow neck that connects the spherical bud to the supported bilayer is located within the surface domain. | |
By substituting the equilibrium value of Rbu into (43), we can rewrite the neck stability condition as
| | 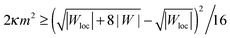 | (44) |
which directly shows that the stability of spherical buds is enhanced by an increase in local adhesiveness |
Wloc|. By setting |
Wloc| = |
W|, we recover the condition
(42) for homogeneous substrates. If |
Wloc| > |
W|, the threshold of spontaneous tension 2
κm2 at which buds become metastable is lowered, and can be made arbitrarily low as the local adhesiveness is increased. Indeed, for very large local adhesiveness |
Wloc| ≫ |
W| the stability condition
(44) behaves as 2
κm2 ≳ |
W|
2/|
Wloc|. Conversely, if the local adhesiveness is weaker than the global one, |
Wloc| < |
W|, the spontaneous tension threshold is raised. In the limit of a non-adhesive surface domain with |
Wloc| = 0, the stability condition
(44) becomes 2
κm2 ≥ |
W|/2.
Adhesive surface domains can thus be used to enhance the stability of spherical buds in supported bilayers. The threshold at which spherical buds become energetically favorable is still given by the global substrate adhesiveness, with 2κm2 > |W| as in ref. 37. Likewise, the stability of cylindrical tubes is still dictated by the global substrate adhesiveness, with tubes being unstable and shrinking for 2κm2 ≤ |W|, but growing for 2κm2 > |W|.
4.3 Giant plasma membrane vesicles
A similar budding geometry applies to the formation of giant plasma membrane vesicles (GPMVs) from cells via chemically induced blebbing. GPMVs are micrometer-sized spherical vesicles formed from the plasma membrane of eukaryotic cells that appear on the cell surface after treatment with a blebbing solution containing formaldehyde, dithiothreitol and Ca2+.19–22 In ref. 22, the mechanism of GPMV formation was studied in some detail. It was concluded that this blebbing solution causes a loss of membrane asymmetry and of actin cortex remodelling capabilities. As a consequence, the osmotic pressure can no longer be balanced by the cell cortex and blebs are formed. Before being cleaved off, the membrane will again form a narrow neck that must close in the presence of the adhesive cell cortex, see Fig. 1(e).
If the membrane asymmetry is lost as for the blebbing solution applied in ref. 22, the spontaneous curvature m vanishes. Using m = 0 in the exocytic version of the stability condition (33) and replacing 1/Rpa by the mean curvature Mcell of the cell at the position of the neck as well as M′ by the inverse radius 1/RGPMV of the spherical bleb, the stability condition for the closed neck of the bleb becomes
| | 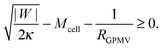 | (45) |
The bleb radius
RGPMV is controlled, in general, by a non-zero osmotic pressure difference between the inside and the outside of the cell, as well as by the cell membrane tension, both of which can be independently regulated by the cell and are not directly connected to the membrane-cortex adhesion |
W|.
43 For this reason, it is expected that membrane-cortex adhesion will always act to stabilize the closed neck connecting the GPMV to the cell membrane. If the adhesion between the membrane and the cortex is too low, such that
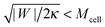
, the stability condition
(45) cannot be satisfied and GPMV formation is not possible. On the other hand, for given values of |
W| and
Mcell, this stability condition is equivalent to
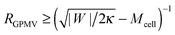
and, thus, provides a lower threshold value for the observable radii
RGPMV of fully-formed, spherical GPMVs.
4.4 Outer membrane vesicles secreted by bacteria
The stability condition for closed necks can also be applied to the secretion of outer membrane vesicles (OMVs) by Gram-negative bacteria. These bacteria have a cell wall that consists of a peptidoglycan layer sandwiched between two lipid bilayers. During the secretion process, a large segment of the outer bilayer detaches from the peptidoglycan layer, bulges out towards the external medium, and forms a spherical vesicle that is released from the prokaryotic cell.23 These vesicles have a variable radius between 25 and 125 nm, and their membranes are strongly asymmetric.23 As a consequence, the membrane spontaneous curvature m cannot be neglected and the stability condition (33) for a spherical, fully-formed OMV of radius ROMV becomes| | 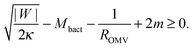 | (46) |
where |W| is the adhesive strength of the interaction between the peptidoglycan layer and the outer bilayer, and Mbact is the mean curvature of the outer bilayer membrane at the position of the closed neck. Eqn (46) shows that, for given values of Mbact and ROMV, the closed neck is stabilized by both the adhesive strength |W| and a positive spontaneous curvature m > 0. The spontaneous curvature has already been proposed to be a driving force for OMV formation.23,24 Our study shows that the adhesion of the membrane to the underlying peptidoglycan layer makes another important contribution to neck stability.
5 Neck stabilization by constriction forces
5.1 Externally applied constriction forces
In biological cells, many processes that involve the formation of membrane necks, such as particle endocytosis or exocytosis, involve proteins that generate constriction forces onto the necks,11 see Fig. 7. In the case of endocytosis, proteins such as dynamin16 or the ESCRT machinery15 are typically associated with such forces. In phagocytosis, a ‘purse string’ composed of actin and myosin motors is usually present around the neck.12
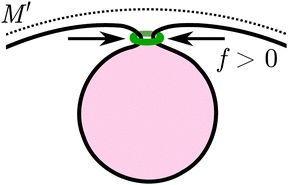 |
| | Fig. 7 Contractile ring (green), representing endocytosis-associated machinery, exerting a constriction force f > 0 perpendicular to the narrow membrane neck during particle engulfment. The mother membrane has mean curvature M′ at the position of the neck. | |
Externally applied constriction forces around a membrane neck can be easily included in the analytical treatment of Section 2.4, by simply adding the axi-symmetric term Ef = fRne to the total energy of the system as given by (27). Here, a positive value of f corresponds to a constriction force perpendicular to the neck while a putative negative value of f acts to widen the neck.
Including the additional energy term Ef = fRne in the computation of Section 2.4, we obtain the generalized stability condition
| | 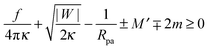 | (47) |
for a closed membrane neck. The upper and lower signs of the ± and ∓ symbols again apply to endocytic and exocytic engulfment, respectively, see
Fig. 1(a and b).
The generalized condition (47) implies that constriction forces with f > 0 promote the formation of closed necks. In particular, constriction forces generated, e.g., by active processes can be sufficient to close a neck even in the absence of any adhesive surface. Indeed, for |W| = 0, the condition (47) can be rewritten in the form
| | 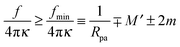 | (48) |
which defines the minimal constriction force
fmin necessary for neck closure. Such minimal constriction forces were numerically studied in
ref. 44, and we find that their numerical results are in complete agreement with the expression
(48) for
fmin.
It is also possible that constriction forces play a role in the budding of ‘empty’ vesicles in the presence of adhesive substrates, such as the actin cortex or the peptidoclycan layer as described in Sections 4.3 and 4.4. The corresponding stability conditions are obtained by adding the term f/4πκ to the left hand side of (45) and (46).
5.2 Intrinsic engulfment force
Additional insight into closed membrane necks can be obtained by rewriting eqn (47) in the alternative form f + feng ≥ 0 with the intrinsic engulfment force feng for neck closure defined by| | 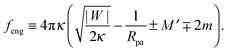 | (49) |
As before, the upper and lower signs of the ± or ∓ symbols correspond to endocytic and exocytic engulfment, respectively.
The stability condition (33) now has the simple form feng ≥ 0 corresponding to the neck closure condition feng = 0 and the closed neck condition feng > 0. Thus, even for f = 0, i.e., in the absence of externally applied constriction forces, the neck experiences the intrinsic engulfment force feng arising from the interplay of membrane-particle adhesion and curvature elasticity. This intrinsic force grows both with the adhesive strength and the particle size. It seems plausible to expect that such engulfment forces lower the barrier for the fission of the neck. Therefore, a larger value of feng should increase the probability for thermally-excited neck fission and vesicle cleavage.
6 Summary and conclusions
In this paper, we have shown that the presence of an adhesive surface strongly affects the stability of closed membrane necks. In the absence of an adhesive surface, previous research showed that closed necks could only be stable in membranes with bilayer asymmetry and/or intramembrane domains.2,4,7,39 Our analytical and numerical results reveal that membrane adhesion in itself is already sufficient to stabilize closed necks. Furthermore, we have derived precise stability conditions for several systems of experimental relevance: (i) endocytic and exocytic engulfment of particles by membranes, see eqn (33); (ii) necklace-like particle-filled membrane tubes, see eqn (37) and (38); (iii) budding and tubulation of supported lipid bilayers from homogenous substrates, see eqn (41) and (42), as well as from patterned substrates, see eqn (43) and (44); (iv) formation of giant plasma membrane vesicles via chemically induced blebbing, see eqn (45); (v) formation of outer membrane vesicles in Gram-negative bacteria, see eqn (46); and (vi) particle engulfment with externally applied constriction forces, see eqn (47). Finally, we showed that constriction forces can be sufficient to stabilize closed necks even in the absence of adhesion, see eqn (48), and introduced an intrinsic engulfment force that directly describes the effect of curvature elasticity and membrane-substrate adhesion on neck closure, see eqn (49). Whenever possible, we have validated the predictions of our analytical stability conditions against numerical results found in the literature.
Throughout the paper, we discussed the stability conditions for closed necks in the context of the spontaneous curvature model, which assumes that the area difference between the two leaflets of the membrane can change via lipid flip-flops. This assumption is valid for multi-component membranes containing sterols such as cholesterol because the latter molecules undergo fast flip-flops between the leaflets on the timescale of a second. For membranes containing only phospholipids, on the other hand, flip-flops occur much more slowly, and the area difference between the two leaflets has a certain preferred value on the typical timescales of experiments, a constraint that is incorporated in the area-difference-elasticity model.45 As discussed in ref. 46, the stability conditions for closed necks described here are also valid in the area-difference-elasticity model provided we replace the spontaneous curvature m by the effective spontaneous curvature meff ≡ m + π(κΔ/κ)(I0 − I)/A, where A is the membrane area, κΔ is a second bending rigidity,45 and 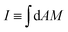 is the integrated mean curvature, which attains the value I0 when the area difference between the two leaflets is optimal. The parameter κΔ is a material parameter, the parameter I0 is determined by the preparation procedure and is, thus, difficult to control, while the integrated mean curvature I depends on the membrane shape, and thus on the size of the particles or membrane buds under consideration. These modified stability conditions can also be obtained directly from the analytical model in Section 2.4 by explicitly including the energetic contribution of the area difference elasticity in the total energy (27). In any case, we find that adhesive surfaces and constriction forces act to stabilize closed necks independently of the curvature model.
is the integrated mean curvature, which attains the value I0 when the area difference between the two leaflets is optimal. The parameter κΔ is a material parameter, the parameter I0 is determined by the preparation procedure and is, thus, difficult to control, while the integrated mean curvature I depends on the membrane shape, and thus on the size of the particles or membrane buds under consideration. These modified stability conditions can also be obtained directly from the analytical model in Section 2.4 by explicitly including the energetic contribution of the area difference elasticity in the total energy (27). In any case, we find that adhesive surfaces and constriction forces act to stabilize closed necks independently of the curvature model.
It seems appealing to generalize the stability condition (33), as well as the stability conditions described in Section 3.3, to the engulfment of non-spherical particles by simply substituting the inverse particle radius 1/Rpa by the local mean curvature Mpa that varies along the particle surface. This particle mean curvature is positive everywhere for convex particles, such as prolate or oblate ellipsoids; however, it can also be negative if the particle surface includes concave surface segments, e.g., around the poles of a discocyte-shaped particle. As a consequence of the variation of the particle mean curvature along the particle surface, the neck stability condition will change along the particle surface, which implies that the neck stability depends on the position of the neck. Therefore, the surface of a particle may exhibit two or more surface domains corresponding to stable and unstable necks. The latter conclusion can be scrutinized by numerical methods. As a first example, consider the engulfment of ellipsoidal particles by planar membranes with zero spontaneous curvature as studied in ref. 47, with prolate and oblate ellipsoids constrained to have their symmetry axis parallel and perpendicular to the membrane, respectively. In this numerical study, completely engulfed states with closed necks were found to be (meta)stable whenever |W| ≥ 2κMpa2, where Mpa was the mean curvature of the prolate and oblate ellipsoids at their equator and poles, respectively. These results are in complete agreement with the stability condition (33) when we put M′ = m = 0 and replace the inverse particle radius 1/Rpa by the local mean curvature Mpa of the particle surface.
The stability of closed necks as discussed here refers to their energetic stability against neck opening. A different question, which we hardly addressed here, is whether the closed neck will be stable against fission (or scission). Predicting whether the closed neck will break, leading to fission, or whether it will remain intact, leaving the topology of the membrane unchanged, lies beyond the realm of applicability for the continuum membrane model used here. As an example, our continuum model allows for the formation of infinitely narrow membrane necks, whereas the diameter of a real neck must exceed twice the membrane thickness ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) me ≃ 4–5 nm. In practice, the continuum model becomes inaccurate for neck sizes of the order of a few times the membrane thickness
me ≃ 4–5 nm. In practice, the continuum model becomes inaccurate for neck sizes of the order of a few times the membrane thickness ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) me, and corrections to the model will stabilize the neck size at a finite non-zero value, somewhat larger than
me, and corrections to the model will stabilize the neck size at a finite non-zero value, somewhat larger than ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) me. Understanding the fission step in detail requires modelling at the molecular level.48–50 In any case, our results provide a necessary condition for membrane fission, and will remain valid as long as the particles or membrane buds are large compared to the membrane thickness. It will also be interesting to see whether the intrinsic engulfment force as given by (49) can be related to the energy barrier for neck fission.
me. Understanding the fission step in detail requires modelling at the molecular level.48–50 In any case, our results provide a necessary condition for membrane fission, and will remain valid as long as the particles or membrane buds are large compared to the membrane thickness. It will also be interesting to see whether the intrinsic engulfment force as given by (49) can be related to the energy barrier for neck fission.
In experiments, the stability conditions described here can be used to estimate the adhesive strength of the membrane-surface interaction or the membrane spontaneous curvature, whenever fission or a closed neck are observed. Indeed, in most experiments the radii of the particles or curvature of the membranes involved can be measured optically. If the spontaneous curvature of the membrane is known, observation of a closed neck directly implies a minimal value of the adhesive strength via the stability conditions presented here. Conversely, if the adhesive strength is known, the stability conditions can be used to obtain a lower or upper estimate for the membrane spontaneous curvature. Furthermore, it will often be possible to directly observe the process of neck closure, and we can then use the equalities in the stability relations (33), (37), (38), (41), (43), (45) and (46) to obtain improved estimates for the different material parameters.
The stability condition for closed membrane necks in particle engulfment as given by eqn (33) has already proven useful in order to understand the size-dependence of endocytosis17 and the interaction of nanoparticles with membranes of complex shape.46 As shown here, analogous stability conditions are relevant for many different processes. As a consequence, adhesion should play an essential role in the formation and closure of narrow necks by biomimetic and biological membranes.
Acknowledgements
This study was supported by the German Research Foundation (DFG) via the IRTG 1524 and by the Federal Ministry of Education and Research (BMBF) via the consortium MaxSynBio.
References
- K. Berndl, J. Käs, R. Lipowsky, E. Sackmann and U. Seifert, Europhys. Lett., 1990, 13, 659–664 CrossRef.
- U. Seifert, K. Berndl and R. Lipowsky, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 1182–1202 CrossRef CAS.
- L. Miao, B. Fourcade, M. Rao, M. Wortis and R. K. P. Zia, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 6843–6856 CrossRef CAS.
- B. Fourcade, L. Miao, M. Rao, M. Wortis and R. K. P. Zia, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 5276–5286 CrossRef CAS.
- Y. Liu, J. Agudo-Canalejo, A. Grafmüller, R. Dimova and R. Lipowsky, ACS Nano, 2016, 10, 463–474 CrossRef CAS PubMed.
- R. Lipowsky, J. Phys. II, 1992, 2, 1825–1840 CrossRef CAS.
- F. Jülicher and R. Lipowsky, Phys. Rev. Lett., 1993, 70, 2964–2967 CrossRef PubMed.
- T. Baumgart, S. T. Hess and W. W. Webb, Nature, 2003, 425, 821–824 CrossRef CAS PubMed.
- R. Bar-Ziv and E. Moses, Phys. Rev. Lett., 1994, 73, 1392–1395 CrossRef PubMed.
- H. T. McMahon and J. L. Gallop, Nature, 2005, 438, 590–596 CrossRef CAS PubMed.
- J. H. Hurley, E. Boura, L.-A. Carlson and B. Różycki, Cell, 2010, 143, 875–887 CrossRef CAS PubMed.
- J. A. Swanson, M. T. Johnson, K. Beningo, P. Post, M. Mooseker and N. Araki, J. Cell Sci., 1999, 112, 307–316 CAS.
- I. Mendes Pinto, B. Rubinstein, A. Kucharavy, J. R. Unruh and R. Li, Dev. Cell, 2012, 22, 1247–1260 CrossRef CAS PubMed.
- R. Knorr, R. Lipowsky and R. Dimova, Autophagy, 2015, 11, 2134–2137 CrossRef CAS PubMed.
- J. H. Hurley and P. I. Hanson, Nat. Rev. Mol. Cell Biol., 2010, 11, 556–566 CrossRef CAS PubMed.
- S. M. Ferguson and P. De Camilli, Nat. Rev. Mol. Cell Biol., 2012, 13, 75–88 CAS.
- J. Agudo-Canalejo and R. Lipowsky, ACS Nano, 2015, 9, 3704–3720 CrossRef CAS PubMed.
- H. Kalra, G. P. C. Drummen and S. Mathivanan, Int. J. Mol. Sci., 2016, 17, 170 CrossRef PubMed.
- R. E. Scott, Science, 1976, 194, 743–745 CAS.
- T. Baumgart, A. T. Hammond, P. Sengupta, S. T. Hess, D. A. Holowka, B. A. Baird and W. W. Webb, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 3165–3170 CrossRef CAS PubMed.
- S. L. Veatch, P. Cicuta, P. Sengupta, A. Honerkamp-Smith, D. Holowka and B. Baird, ACS Chem. Biol., 2008, 3, 287–293 CrossRef CAS PubMed.
- H. Keller, M. Lorizate and P. Schwille, ChemPhysChem, 2009, 10, 2805–2812 CrossRef CAS PubMed.
- A. Kulp and M. J. Kuehn, Annu. Rev. Microbiol., 2010, 64, 163–184 CrossRef CAS PubMed.
- J. W. Schertzer and M. Whiteley, mBio, 2012, 3, e00297 CrossRef CAS PubMed.
- C. Dietrich, M. Angelova and B. Pouligny, J. Phys. II, 1997, 7, 1651–1682 CrossRef CAS.
- K. Jaskiewicz, A. Larsen, D. Schaeffel, K. Koynov, I. Lieberwirth, G. Fytas, K. Landfester and A. Kroeger, ACS Nano, 2012, 6, 7254–7262 CrossRef CAS PubMed.
- A. Meinel, B. Tränkle, W. Römer and A. Rohrbach, Soft Matter, 2014, 10, 3667–3678 RSC.
- R. Michel, E. Kesselman, T. Plostica, D. Danino and M. Gradzielski, Angew. Chem., Int. Ed., 2014, 53, 12441–12445 CAS.
- F. G. Strobl, F. Seitz, C. Westerhausen, A. Reller, A. A. Torrano, C. Bräuchle, A. Wixforth and M. F. Schneider, Beilstein J. Nanotechnol., 2014, 5, 2468–2478 CrossRef PubMed.
- A. H. Bahrami, R. Lipowsky and T. R. Weikl, Phys. Rev. Lett., 2012, 109, 188102 CrossRef PubMed.
- A. Šarić and A. Cacciuto, Phys. Rev. Lett., 2012, 109, 188101 CrossRef PubMed.
- M. Raatz, R. Lipowsky and T. R. Weikl, Soft Matter, 2014, 10, 3570–3577 RSC.
- Y. A. Domanov and P. K. J. Kinnunen, Biophys. J., 2006, 91, 4427–4439 CrossRef CAS PubMed.
- L. R. Cambrea and J. S. Hovis, Biophys. J., 2007, 92, 3587–3594 CrossRef CAS PubMed.
- A. Arouri, V. Kiessling, L. Tamm, M. Dathe and A. Blume, J. Phys. Chem. B, 2010, 115, 158–167 CrossRef PubMed.
- T. J. Pucadyil and S. L. Schmid, Biophys. J., 2010, 99, 517–525 CrossRef CAS PubMed.
- R. Lipowsky, Faraday Discuss., 2013, 161, 305–331 RSC.
- Z.-C. Ou-Yang and W. Helfrich, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 5280–5288 CrossRef CAS.
- F. Jülicher and R. Lipowsky, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 2670–2683 CrossRef.
- W. Helfrich, Z. Naturforsch., C: J. Biosci., 1973, 28, 693–703 CAS.
- U. Seifert and R. Lipowsky, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 42, 4768–4771 CrossRef CAS.
- M. Deserno, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 69, 031903 Search PubMed.
- J. Dai and M. P. Sheetz, Biophys. J., 1999, 77, 3363–3370 CrossRef CAS PubMed.
- B. Božič, J. Guven, P. Vázquez-Montejo and S. Svetina, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 052701 CrossRef.
- L. Miao, U. Seifert, M. Wortis and H.-G. Döbereiner, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 5389–5407 CrossRef CAS.
- J. Agudo-Canalejo and R. Lipowsky, Nano Lett., 2015, 15, 7168–7173 CrossRef CAS PubMed.
- S. Dasgupta, T. Auth and G. Gompper, Soft Matter, 2013, 9, 5473–5482 RSC.
- J. Shillcock and R. Lipowsky, Biophys. Rev. Lett., 2007, 2, 33–55 CrossRef CAS.
- A. Grafmüller, J. C. Shillcock and R. Lipowsky, Biophys. J., 2009, 96, 2658–2675 CrossRef PubMed.
- K. Yang and Y.-Q. Ma, Soft Matter, 2012, 8, 606–618 RSC.
Footnotes |
| † Here and below, the symbol ≈ stands for ‘asymptotically equal’. |
| ‡ The normal force balance equations for spheres and cylinders can be obtained in a simple manner by minimizing the bending energies of these shapes with respect to their radii.37 Alternatively, the same equations are obtained by specifying the Euler–Lagrange equation of the spontaneous curvature model38 to these shapes. |
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article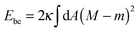
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ).
ϕ).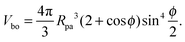
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ).
ϕ).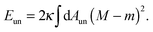
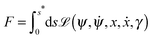
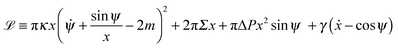
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ, and the dot denotes a derivative with respect to the arc length s.
ψ, and the dot denotes a derivative with respect to the arc length s.
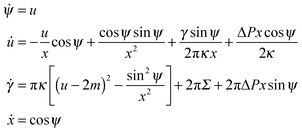
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) = πx2sin
= πx2sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ
ψ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ
ϕ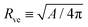
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ≡ mRve
≡ mRve![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) and w completely define the system.
and w completely define the system.
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) and v, the total energy of the system E(ϕ) as a function of ϕ is obtained from the bending energy Eun(ϕ) of the unbound membrane segment resulting from the shooting method, together with the bending and adhesive energies, Ebo(ϕ), of the particle-bound segment, given by (6), so that E(ϕ) ≡ Eun(ϕ) + Ebo(ϕ). Closed necks will be stable or unstable if E(ϕ) has a boundary minimum or maximum, respectively, at ϕ = π.
and v, the total energy of the system E(ϕ) as a function of ϕ is obtained from the bending energy Eun(ϕ) of the unbound membrane segment resulting from the shooting method, together with the bending and adhesive energies, Ebo(ϕ), of the particle-bound segment, given by (6), so that E(ϕ) ≡ Eun(ϕ) + Ebo(ϕ). Closed necks will be stable or unstable if E(ϕ) has a boundary minimum or maximum, respectively, at ϕ = π.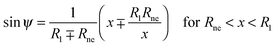
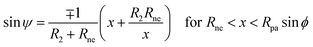
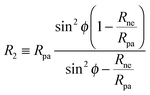
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η = sin
η = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ
ϕ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η or equivalently ε < sin
η or equivalently ε < sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η being always satisfied during the closure of the membrane neck. We will thus consider an expansion in powers of ε, taking into account that the dimensionless ratio sin2
η being always satisfied during the closure of the membrane neck. We will thus consider an expansion in powers of ε, taking into account that the dimensionless ratio sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η/ε is of order one. The total membrane area of the trial contour is found to be
η/ε is of order one. The total membrane area of the trial contour is found to be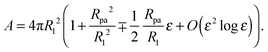
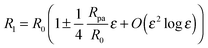
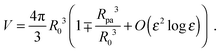
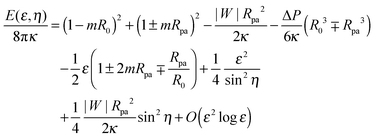
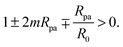
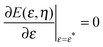 , we obtain the optimal neck size
, we obtain the optimal neck size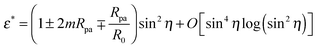
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η is small, and has a meaningful value only if the inequality (29) is satisfied.
η is small, and has a meaningful value only if the inequality (29) is satisfied.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η with η = π − ϕ as in (23). The energy difference δE(η) represents the excess energy (or reversible work) necessary to open up the closed neck.
η with η = π − ϕ as in (23). The energy difference δE(η) represents the excess energy (or reversible work) necessary to open up the closed neck.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η. Alternatively, one could consider a shape ensemble in which the enclosed volume is kept constant, whereas the membrane area is variable at constant tension Σ, with a term ΣA added to the total energy. In the latter case, we similarly find that the tension only adds higher order terms in sin2
η. Alternatively, one could consider a shape ensemble in which the enclosed volume is kept constant, whereas the membrane area is variable at constant tension Σ, with a term ΣA added to the total energy. In the latter case, we similarly find that the tension only adds higher order terms in sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η to the energy, with eqn (30) and (31) remaining unaffected.
η to the energy, with eqn (30) and (31) remaining unaffected.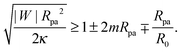
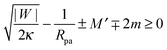
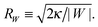
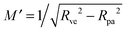 , where
, where 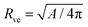 is now equal to the radius of the (spherical) vesicle before engulfment of the particle. In Fig. 4, we plot the neck closure condition (33) as a function of particle size rpa and adhesive strength w, for different values of the spontaneous curvature
is now equal to the radius of the (spherical) vesicle before engulfment of the particle. In Fig. 4, we plot the neck closure condition (33) as a function of particle size rpa and adhesive strength w, for different values of the spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) . Closed necks are stable and unstable for high and low values of the adhesive strength, respectively. The condition as given by eqn (33) has been quantitatively confirmed by numerical energy minimization for a large number of different parameter values. For endocytic engulfment, see Fig. 4(a), negative spontaneous curvatures favour the stability of closed necks, whereas positive spontaneous curvatures act to destabilize them. In contrast, for exocytic engulfment, closed necks are favoured by positive and suppressed by negative spontaneous curvatures, see Fig. 4(b).
. Closed necks are stable and unstable for high and low values of the adhesive strength, respectively. The condition as given by eqn (33) has been quantitatively confirmed by numerical energy minimization for a large number of different parameter values. For endocytic engulfment, see Fig. 4(a), negative spontaneous curvatures favour the stability of closed necks, whereas positive spontaneous curvatures act to destabilize them. In contrast, for exocytic engulfment, closed necks are favoured by positive and suppressed by negative spontaneous curvatures, see Fig. 4(b).
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = mRve. The vesicle can freely adapt its volume corresponding to the osmotic pressure difference ΔP = 0.
= mRve. The vesicle can freely adapt its volume corresponding to the osmotic pressure difference ΔP = 0.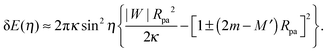
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η, the excess energy for neck opening depends only on the local mean curvature M′ of the membrane at the position of the neck, and is independent of the global shape of the vesicle.
η, the excess energy for neck opening depends only on the local mean curvature M′ of the membrane at the position of the neck, and is independent of the global shape of the vesicle.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η. A few examples are displayed in Fig. 5(a). For sin2
η. A few examples are displayed in Fig. 5(a). For sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η = 0, corresponding to complete engulfment with ϕ = π, all numerical lines have a common tangent as given by eqn (35). In all cases, the numerical results are reasonably well approximated by the analytical line in the range 0 ≤ sin2
η = 0, corresponding to complete engulfment with ϕ = π, all numerical lines have a common tangent as given by eqn (35). In all cases, the numerical results are reasonably well approximated by the analytical line in the range 0 ≤ sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η ≤ 0.2, corresponding to π ≥ ϕ ≥ 0.85π.
η ≤ 0.2, corresponding to π ≥ ϕ ≥ 0.85π.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η as obtained by numerical energy minimization. The shifted wrapping angle η = π − ϕ varies from η = 0 to η = π/2. The reduced volume v = 0.94 corresponds to prolate vesicles with fixed volume, the case ΔP = 0 to spherical vesicles with adjustable volume. Both endocytic and exocytic engulfment are considered for two particle sizes rpa = 0.1 and rpa = 0.4 as well as for two spontaneous curvatures
η as obtained by numerical energy minimization. The shifted wrapping angle η = π − ϕ varies from η = 0 to η = π/2. The reduced volume v = 0.94 corresponds to prolate vesicles with fixed volume, the case ΔP = 0 to spherical vesicles with adjustable volume. Both endocytic and exocytic engulfment are considered for two particle sizes rpa = 0.1 and rpa = 0.4 as well as for two spontaneous curvatures ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 0 and
= 0 and ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 0.5. In (a), a range of four different adhesive strengths w is examined. The scaling factors for the excess energy and the neck size, see lettering of the y-axes, correspond to eqn (35) and (36) respectively. As predicted by these equations, all lines have a common tangent at sin2
= 0.5. In (a), a range of four different adhesive strengths w is examined. The scaling factors for the excess energy and the neck size, see lettering of the y-axes, correspond to eqn (35) and (36) respectively. As predicted by these equations, all lines have a common tangent at sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η = 0, given by the black dashed line y = x.
η = 0, given by the black dashed line y = x.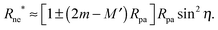
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η = 0. In all cases tested, the numerical results are reasonably well approximated by eqn (36) in the range 0 ≤ sin2
η = 0. In all cases tested, the numerical results are reasonably well approximated by eqn (36) in the range 0 ≤ sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η ≤ 0.4, corresponding to π ≥ ϕ ≥ 0.78π.
η ≤ 0.4, corresponding to π ≥ ϕ ≥ 0.78π.
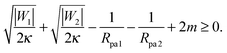
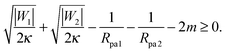
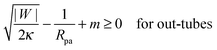
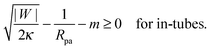
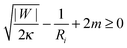
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) W between the membrane and the substrate, the volume V ≈
W between the membrane and the substrate, the volume V ≈ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) WA for large A. Because the water layer thickness is determined by the molecular interactions between the membrane and the substrate, the volume V can no longer be varied independently of the area A and it becomes meaningless to include the Lagrange multiplier ΔP conjugate to the volume.
WA for large A. Because the water layer thickness is determined by the molecular interactions between the membrane and the substrate, the volume V can no longer be varied independently of the area A and it becomes meaningless to include the Lagrange multiplier ΔP conjugate to the volume.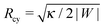 for the radius of the cylinder. Now, substituting the radius Ri in eqn (41) by these equilibrium values of Rbu and Rcy, we find the same stability relation
for the radius of the cylinder. Now, substituting the radius Ri in eqn (41) by these equilibrium values of Rbu and Rcy, we find the same stability relation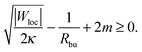
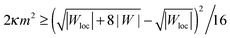
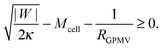
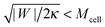 , the stability condition (45) cannot be satisfied and GPMV formation is not possible. On the other hand, for given values of |W| and Mcell, this stability condition is equivalent to
, the stability condition (45) cannot be satisfied and GPMV formation is not possible. On the other hand, for given values of |W| and Mcell, this stability condition is equivalent to 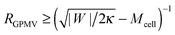 and, thus, provides a lower threshold value for the observable radii RGPMV of fully-formed, spherical GPMVs.
and, thus, provides a lower threshold value for the observable radii RGPMV of fully-formed, spherical GPMVs.
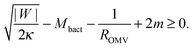
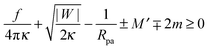
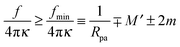
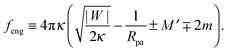
 is the integrated mean curvature, which attains the value I0 when the area difference between the two leaflets is optimal. The parameter κΔ is a material parameter, the parameter I0 is determined by the preparation procedure and is, thus, difficult to control, while the integrated mean curvature I depends on the membrane shape, and thus on the size of the particles or membrane buds under consideration. These modified stability conditions can also be obtained directly from the analytical model in Section 2.4 by explicitly including the energetic contribution of the area difference elasticity in the total energy (27). In any case, we find that adhesive surfaces and constriction forces act to stabilize closed necks independently of the curvature model.
is the integrated mean curvature, which attains the value I0 when the area difference between the two leaflets is optimal. The parameter κΔ is a material parameter, the parameter I0 is determined by the preparation procedure and is, thus, difficult to control, while the integrated mean curvature I depends on the membrane shape, and thus on the size of the particles or membrane buds under consideration. These modified stability conditions can also be obtained directly from the analytical model in Section 2.4 by explicitly including the energetic contribution of the area difference elasticity in the total energy (27). In any case, we find that adhesive surfaces and constriction forces act to stabilize closed necks independently of the curvature model.![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) me ≃ 4–5 nm. In practice, the continuum model becomes inaccurate for neck sizes of the order of a few times the membrane thickness
me ≃ 4–5 nm. In practice, the continuum model becomes inaccurate for neck sizes of the order of a few times the membrane thickness ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) me, and corrections to the model will stabilize the neck size at a finite non-zero value, somewhat larger than
me, and corrections to the model will stabilize the neck size at a finite non-zero value, somewhat larger than ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) me. Understanding the fission step in detail requires modelling at the molecular level.48–50 In any case, our results provide a necessary condition for membrane fission, and will remain valid as long as the particles or membrane buds are large compared to the membrane thickness. It will also be interesting to see whether the intrinsic engulfment force as given by (49) can be related to the energy barrier for neck fission.
me. Understanding the fission step in detail requires modelling at the molecular level.48–50 In any case, our results provide a necessary condition for membrane fission, and will remain valid as long as the particles or membrane buds are large compared to the membrane thickness. It will also be interesting to see whether the intrinsic engulfment force as given by (49) can be related to the energy barrier for neck fission.




