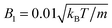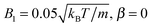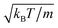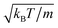DOI:
10.1039/C6SM01424K
(Paper)
Soft Matter, 2016,
12, 7372-7385
Modeling a spheroidal microswimmer and cooperative swimming in a narrow slit†
Received
21st June 2016
, Accepted 8th August 2016
First published on 8th August 2016
Abstract
We propose a hydrodynamic model for a spheroidal microswimmer with two tangential surface velocity modes. This model is analytically solvable and reduces to Lighthill's and Blake's spherical squirmer model in the limit of equal major and minor semi-axes. Furthermore, we present an implementation of such a spheroidal squirmer by means of particle-based mesoscale hydrodynamics simulations using the multiparticle collision dynamics approach. We investigate its properties as well as the scattering of two spheroidal squirmers in a slit geometry. Thereby we find a stable fixed point, where two pullers swim cooperatively forming a wedge-like conformation with a small constant angle.
1 Introduction
Living matter exhibits a broad spectrum of unique phenomena which emerge as a consequence of its active constituents. Examples of such systems range from the macroscopic scale of flocks of birds and mammalian herds to the microscopic scale of bacterial suspensions.1,2 Specifically, active systems exhibit remarkable nonequilibrium phenomena and emergent behavior like swarming,3–7 turbulence,6 and activity-induced clustering and phase transitions.8–21 The understanding of these collective phenomena requires the characterization of the underlying physical interaction mechanisms. Experiments and simulations indicate that shape-induced interactions, such as inelastic collisions between elongated objects or of active particles with surfaces lead to clustering, collective motion, and surface-induced aggregation.6,22–24 For micrometer-size biological unicellular swimmers, e.g., bacteria (E. coli), algae (Chlamydomonas), spermatozoa, or protozoa (Paramecium), hydrodynamic interactions are considered to be important for collective effects and determine their behavior adjacent to surfaces.1,25–30
Generic models, which capture the essential swimming aspects, are crucial in theoretical studies of microswimmers. On the one hand, they help to unravel the relevant interaction mechanisms and, on the other hand, allow for the study of sufficiently large systems. A prominent example is the squirmer model introduced by Lighthill31 and revised by Blake.32 Originally, it was intended as a model for ciliated microswimmers, such as Paramecia. Nowadays, it is considered as a generic model for a broad class of microswimmers, ranging from diffusiophoretic particles33–35 to biological cells and has been applied to study collective effects in bulk,36–42 at surfaces,36,43,44 and in a narrow slit.20
In its simplest form, a squirmer is represented as a spherical rigid colloid with a prescribed surface velocity.31,32,38 Restricting the surface velocity to be tangential, the spherical squirmer is typically characterized by two modes accounting for its swimming velocity and its force-dipole. The latter distinguishes between pushers, pullers, and neutral squirmers. The assumption of a spherical shape is adequate for swimmers like Volvox, however, the shape of bacteria such as E. coli or the time-averaged shape of cells such as Chlamydomonas is nonspherical. Hence, an extension of the squirmer concept to spheroidal objects is desirable. In 1977, Keller and Wu proposed a generalization of the squirmer model to a prolate-spheroidal shape, which resembles real biological microswimmers such as Tetrahymenapyriformis, Spirostomum ambiguum, and Paramecium multimicronucleatum.45 However, that squirmer model accounts for the swimming mode only and does not include a force-dipole mode. This is unfortunate, since the force-dipole mode determines swimmer–swimmer and swimmer–wall interactions.25,37,39,46 A route to incorporate the force-dipole mode into the spheroidal squirmer model was proposed in ref. 44. However, to the best of our knowledge, the resulting hydrodynamic model is not solvable analytically. In this article, we propose an alternative model for a spheroidal squirmer, taking into account both, a swimming and a force-dipole mode. The major advantage of our approach is that the flow field can be determined analytically (cf.Fig. 1).
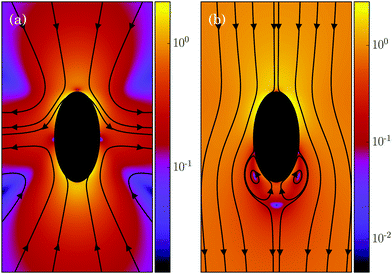 |
| | Fig. 1 Flow field of a spheroidal puller with β = 3, (a) in the laboratory frame, and (b) in the body-fixed frame. The magnitude of the velocity field is color coded logarithmically. | |
Various mesoscale simulation techniques have been applied to study the dynamics of squirmers embedded in a fluid, comprising Stokesian dynamics,39,40,43 the boundary-element method,38,44,46–48 the multiparticle collision dynamics (MPC) approach,20,37,49 lattice Boltzmann simulations,36,41,50 the smoothed profile method,42 and the force-coupling approach.51 In the following, we will apply the MPC method. MPC is a particle-based simulation technique which incorporates thermal fluctuations,52–54 provides hydrodynamic correlations,55,56 and is easily coupled with other simulation techniques such as molecular dynamics simulations for embedded particles.53,54 The method has successfully been applied in various studies of active systems underlining the importance of hydrodynamic interactions for microswimmers.1,20,24,28,37,53,57–65
Here, we implement our spheroidal squirmer model in MPC. More specifically, we study the resulting flow field and compare it with the theoretical prediction. Moreover, we present results for the cooperative swimming behavior of two spheroidal squirmers in a narrow slit. Two pullers exhibit a long-time stable configuration, where they swim together in a wedge-like conformation with a constant small angle due to the hydrodynamic interaction between the anisotropic squirmers as well as squirmers and walls. The cooperative and collective swimming motion of spheroidal squirmers in Stokes flow has been addressed in ref. 47 by an adopted boundary-element method. This approach neglects thermal fluctuations and tumbling of the squirmers completely; only hydrodynamic and excluded-volume interactions determine the squirmer motion. In contrast, our simulation approach includes thermal fluctuations, which affects the stability of the cooperative swimming motion due to the rotational diffusion of a spheroid.
2 Hydrodynamic model of a spheroidal squirmer
2.1 Spheroid geometry
We describe a nonspherical squirmer as a prolate spheroidal rigid body with a prescribed surface velocity usq. In Cartesian coordinates (x, y, z), the surface equation of a spheroid, or ellipsoid of revolution, is| | | (x2 + y2)/bx2 + z2/bz2 = 1, | (1) |
with bz and bx the semi-major and semi-minor axis, respectively, and bz ≥ bx (cf.Fig. 2). We denote half of the focal length by 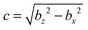 , which yields the eccentricity e = c/bz. Furthermore, we define a swimmer diameter as σ = 2bz. In terms of prolate (bz > bx) spheroidal coordinates (ζ, τ, φ), the Cartesian coordinates are given by
, which yields the eccentricity e = c/bz. Furthermore, we define a swimmer diameter as σ = 2bz. In terms of prolate (bz > bx) spheroidal coordinates (ζ, τ, φ), the Cartesian coordinates are given by| | 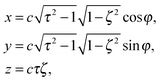 | (2) |
where −1 ≤ ζ ≤ 1, 1 ≤ τ ≤ ∞, and 0 ≤φ ≤ 2π. All points with τ = τ0 ≡ e−1 lie on the spheroid's surface. The intersection of the spheroid and a meridian plane, where φ is constant, is an ellipse. The normal n and tangent s to this ellipse are given by the unit vectors eτ and −eζ, respectively, which follow by partial derivative of eqn (2) with respect to the coordinates ζ and τ. For bx = bz, the spheroid becomes a sphere. The spherical coordinates| | (x, y, z)T = r(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, sin φ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, cos φ, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)T θ)T | (3) |
are obtained from eqn (2) for τ → ∞, cτ = r, and ζ = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. In this limit, the unit vectors turn into eτ → er and eζ → −eθ (cf.Fig. 2). The Lamé metric coefficients for prolate spheroidal coordinates are
θ. In this limit, the unit vectors turn into eτ → er and eζ → −eθ (cf.Fig. 2). The Lamé metric coefficients for prolate spheroidal coordinates are 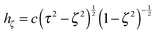 ,
, 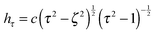 , and
, and 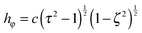 .
.
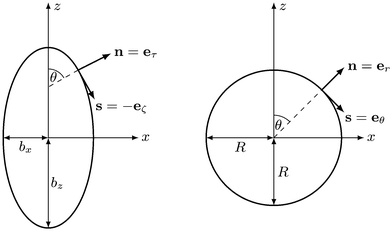 |
| | Fig. 2 Sketch of normal and tangent vectors of a spheroidal (left) and spherical (right) squirmer. In the squirmer model, self-propulsion (in z-direction) is achieved by a prescribed tangential surface velocity in direction of the tangent vector s. | |
2.2 Flow field
The squirmer is immersed in an incompressible low-Reynolds-number fluid, which is described by the incompressible Stokes equations| | | ηΔv − ∇p = 0, ∇·v = 0. | (4) |
Here, v(r) is the fluid velocity field, p(r) the pressure field at the position r, and η the viscosity. In an axisymmetric flow, the velocity field can be expressed by the stream function Ψ as66| | 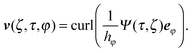 | (5) |
The stream function itself satisfies the equation66with the operator67| | 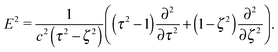 | (7) |
Each function Ψ in the kernel of E2 can be represented as67| | 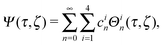 | (8) |
with constants cin and the functions
| Θ1n(τ,ζ) = Gn(τ)Gn(ζ), Θ2n(τ,ζ) = Gn(τ)Hn(ζ), |
| Θ3n(τ,ζ) = Hn(τ)Gn(ζ), Θ4n(τ,ζ) = Hn(τ)Hn(ζ). |
Here, Gn(x) and Hn(x) are Gegenbauer functions of the first and second kind, respectively (see Appendix B). The velocity components follow from the stream function via66| | 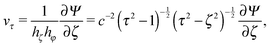 | (9) |
| | 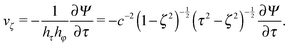 | (10) |
An important feature of a squirmer is the hydrodynamic boundary condition at its surface, which demands v(r) = usq. For the squirming velocity usq we propose
| | | usq = −B1(s·ez)s − B2ζ(s·ez)s | (11) |
| | 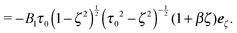 | (13) |
Here,
s is the tangent vector,
ez = (0, 0, 1)
T is the unit vector in
z-direction,
B1 and
B2 are the two surface velocity modes, and
β =
B2/
B1 (
cf.Fig. 2).
B1 determines the swimming velocity, while the
B2 term introduces a force-dipole, or pusher (
B2 < 0) and puller (
B2 > 0) mode. Note that the spherical squirmer introduced by Lighthill and Blake with modes
B1 and
B231,32 is recovered for the spherical limit of a spheroid, where
ζ → cos(
θ) =
n·
ez.
For B2 = 0, this model of a spheroidal squirmer was already introduced and analysed in ref. 45 and 68. An additional force-dipole mode has been introduced in ref. 44 and 47 as usq(ζ) = −B1s·ez(1 + βn·ez)s. However, we prefer the squirming velocity introduced in eqn (12), since it yields an analytically solvable boundary value problem for the Stokes equation. The two approaches provide a somewhat different flow field in the vicinity of the squirmer, but both yield the model of Lighthill and Blake in the limit of zero eccentricity.
In the swimmer's rest frame, and with eqn (12), the boundary value problem becomes
| | 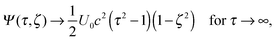 | (14) |
| | | Ψ(τ0,ζ) = 0 for all ζ, | (15) |
| | 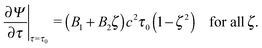 | (16) |
Eqn (14) implies a constant background flow
v = −
U0ez infinitely far from the squirmer,
eqn (15) guarantees
vτ = 0 at the spheroid surface, and
eqn (16) demands
vζ =
usq(
ζ)·
eζ. Due to linearity of the Stokes stream function
eqn (6), we can solve this boundary value problem for
B2 = 0 first, which yields the stream function
Ψ1. Subsequently we solve the problem
| | | Ψ(τ,ζ) converges for τ → ∞, | (17) |
| | | Ψ(τ0,ζ) = 0 for all ζ, | (18) |
| | 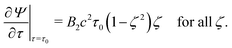 | (19) |
Eqn (17) imposes a vanishing velocity field infinitely far from the squirmer,
eqn (18) again guarantees
vτ = 0 at the spheroid surface, and
eqn (19) demands
vζ =
usq(
ζ,
B1 = 0)·
eζ. We denote the solution of the problem
eqn (17)–(19) by
Ψ2. Finally,
Ψ =
Ψ1 +
Ψ2 solves the initial problem
(14)–(16) for arbitrary
B1 and
B2.
The boundary value problem eqn (14)–(16) for B2 = 0 can be solved by the ansatz
| | | Ψ1(τ,ζ) = α1G2(τ)G2(ζ) + α2H2(τ)G2(ζ) + α3τ(1 − ζ2). | (20) |
Here, the third term is found by the separation ansatz
Ψ(
τ,
ζ) =
g(
τ)(1 −
ζ2) for
eqn (6).
Eqn (14) directly yields
α1 = −2
U0c2. The remaining coefficients
α2 and
α3 are determined by
eqn (15) and (16), keeping in mind that
B2 = 0. This yields
| | 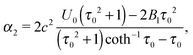 | (21) |
| | 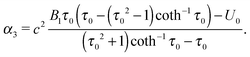 | (22) |
The boundary value problem
eqn (17)–(19) can be solved by the ansatz
| | | Ψ2(τ,ζ) = α4G3(τ)G3(ζ) + α5H3(τ)G3(ζ) + α6ζ(1 − ζ2). | (23) |
As before, the third term follows by a separation ansatz
Ψ(
τ,
ζ) =
g(
τ)
ζ(1 −
ζ2) for
eqn (6).
Eqn (17) yields
α4 = 0. The coefficients
α5 and
α6 are determined by
eqn (18) and (19) such that
| | 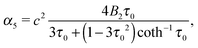 | (24) |
| | 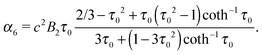 | (25) |
The total stream function
Ψ =
Ψ1 +
Ψ2 can be transformed to the laboratory frame (
cf.Fig. 1) by adding the background flow
v =
U0ez, which yields
| | 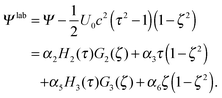 | (26) |
The force on the spheroid by the fluid follows from a multipole expansion,66,69 with a Stokeslet as the dominating contribution far away from a swimmer. Hence, for r → ∞ the stream function Ψlab has to be equal to the stream function of a Stokeslet,66 namely
| | 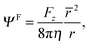 | (27) |
and, thus, the force on the spheroidal squirmer is given by
66| | 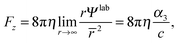 | (28) |
where
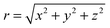
and
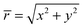
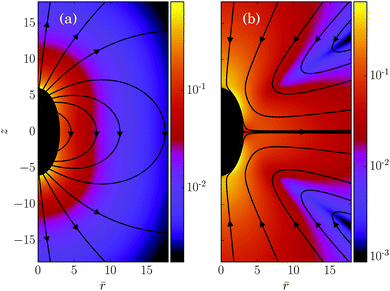
. As expected,
Ψ2 does not contribute to the force, since it assumes a constant value at infinity. Since a swimmer must be force free,
Fz = 0, which implies
α3 = 0. Then,
eqn (22) yields the swimming velocity of the squirmer (
τ0 = 1/
e)
| | | U0 = B1τ0(τ0 − (τ02 − 1)coth−1τ0), | (29) |
which was already found by Keller and Wu for the case
B2 = 0.
45 As a consequence,
α2 in
eqn (22) simply becomes
α2 = 2
B1c2τ0(
τ02 − 1). Examples of fluid velocity fields of a spheroidal squirmer are presented in
Fig. 1 and 3.
 |
| | Fig. 3 Fluid velocity fields of a spheroidal squirmer in the laboratory frame for (a) B1 = 1, B2 = 0, and (b) B1 = 0, B2 = 1. The corresponding stream function is given by eqn (26). The magnitude of the velocity field is color coded logarithmically. Note that the pusher velocity field with B1 = 0, B2 = −1 is not shown, since it follows from that of the puller with B1 = 0, B2 = 1 by inverting the arrows. | |
Far field.
The far field of a cylindrically symmetric microswimmer in terms of a multipole expansion is presented in ref. 48 and the ESI of ref. 70. To obtain the far field expansion of our spheroidal squirmer, we expand the stream function, eqn (26), in powers of 1/τ. Similarly, we determine the stream functions of the first few singularity solutions appearing in the multipole expansion (force dipole, force quadrupole, source dipole, rotlet dipole, etc.) and Taylor expand them in 1/τ. Note that we can omit the non-axisymmetric singularity solutions of the multipole expansion like the rotlet dipole (vRD), which is cylindrically symmetric but not axisymmetric (vRD·eφ ≠ 0). Equating the coefficients of (1/τ)n for n = 0, 1, 2, we find that the squirmer is well described in the far field by the flow fields of a force dipole, a source dipole, and a source quadrupole| | v(r) = κFDvFD(r) + κSDvSD(r) + κSQvSQ(r) + ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (r−5), (r−5), | (30) |
where| | 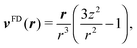 | (31) |
| | 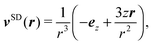 | (32) |
| | 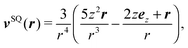 | (33) |
which decay like r−2, r−3, and r−4 for large r, respectively.48 The multipole coefficients are| | 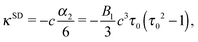 | (35) |
| | 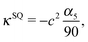 | (36) |
with the coefficients α5 and α6 of eqn (24) and (25). The values of the multipole coefficients in the spherical limit (bz → bx ≡ R, where R is the radius) follow from the above coefficients for τ0 → ∞, c → 0, and cτ0 = R as κFD = −B2R2/2, κSD = −B1R3/3, and κSQ = B2R4/6 as expected for a spherical squirmer.71
3 Multiparticle collision dynamics
Multiparticle collision dynamics (MPC) is a stochastic, particle-based mesoscale hydrodynamic simulation method.54 Thereby, a fluid is modeled by N point particles with equal mass m, undergoing subsequent streaming and collision steps. In the streaming step, the particle positions ri, i = 1,…,N, are updated according to| | | ri(t + h) = ri(t) + hvi(t), | (37) |
where vi are the particle velocities and h is denoted as collision time step. In the subsequent collision step, the particle velocities are changed by a stochastic process, which mimics internal fluid interactions. In order to define the local collision environment, particles are sorted into cells of a cubic lattice with lattice constant a. Different realizations for this stochastic process have been proposed.52,72,73 We employ the stochastic rotation dynamics (SRD) approach of MPC with angular momentum conservation (SRD+a),74,75 which updates the particle velocities in a cell according to| | 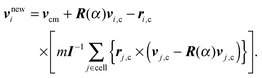 | (38) |
Here, ri,c = ri − rcm, where rcm is the center-of-mass position of the particles in the cell, and similarly, vi,c = vi − vcm, with the center-of-mass velocity vcm. R(α) is the rotation matrix, which describes a rotation around a randomly oriented axis by the angle α. The angle α is a constant, and the axis of rotation is chosen independently for each cell and time step. Finally, I is the moment-of-inertia tensor of the particles in the center-of-mass reference frame of the cell. Partition of the system into collision cells leads to a violation of Galilean invariance. To reestablish Galilean invariance, a random shift of the collision-cell lattice is introduced at every collision step.76,77
Since energy is not conserved in the collision step, we apply a cell level canonical thermostat at temperature T.78,79 The latter ensures Maxwell–Boltzmann distributed velocities. The MPC algorithm is embarrassingly parallel. Hence, we implement it on a Graphics Processing Unit (GPU) for a high performance gain.80
The following simulations are performed with the mean number of particles per collision cell 〈Nc〉 = 10, the rotation angle α = 130°, and the time step 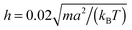 , which yields a fluid viscosity of
, which yields a fluid viscosity of 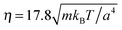 .
.
4 Implementation of a spheroidal squirmer in MPC
A spheroidal squirmer is a homogeneous rigid body characterized by its mass M, center-of-mass position C, orientation q, translational velocity U, and angular momentum l. Thereby, q = (q0,q1,q2,q3) is a rotation quaternion and can be related to the rotation matrix D, which transforms vectors from the laboratory frame to the body-fixed frame81 (see Appendix A (eqn (64))). We distinguish vectors in the laboratory frame and body-fixed frame by a superscript, i.e., vs is a vector in the laboratory (or space-fixed) frame whileis the corresponding vector in the body-fixed frame. For vectors in the laboratory frame, we will frequently omit the superscript. The orientation vector of a spheroid is e = DTeb = DT(0,0,1)T. The moment of inertia tensor in the body-fixed frame Ib is a constant diagonal matrix with diagonal elements Ix = (M/5)(bx2 + bz2) = Iy and Iz = (2M/5)bx2. When needed, the angular velocity is calculated as Ωs = DT(Ib)−1Dls.
For all simulations we choose a neutrally bouyant spheroid, i.e., M = ρ(4π/3)bzbx2, where ρ is the fluid mass density.
4.1 Streaming step
During the streaming step, a spheroid will collide with several MPC particles. Since the total change in (angular) momentum of a spheroid during one streaming step is small, we perform the collisions with MPC particles in a coarse-grained way.82
For the streaming step at time t, we determine the spheroid's position, velocity, orientation, and angular velocity at times t + h/2 and t + h, under the assumption that there is no interaction with MPC particles. However, steric interactions between spheroids, as well as spheroids and walls are taken into account as described in Section 4.3.
Subsequently, all MPC particles are streamed, i.e., their positions are updated according to ri(t + h) = ri(t) + hvi(t). Thereby, a certain fraction of MPC particles penetrates a spheroid. To detect those particles in an efficient way, possible collision cells intersected by the spheroid are identified first. For this purpose, we select all those cells, which are within a sphere of radius bz enclosing the spheroid instead of the spheroid itself, which is more efficient, since it avoids rotating candidate cells into the body-fixed frame during selection. A loop over all particles in respective collision cells identifies those particles, which are inside the spheroid and they are labeled with the spheroid index. Then, each particle i inside a spheroid at time t + h is moved back in time by half a time step and subsequently translated onto the spheroid's surface. The translation can be realized in different ways. One possibility is to construct a virtual spheroid with semi-axes ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) z,
z, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) x,
x, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) z/
z/![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) x = bz/bx and ri(t + h/2) on its surface. The particle is then translated along the normal vector of the virtual spheroid until it is on the real spheroid's surface. Alternatively, the difference vector ri(t + h/2) − C(t + h/2) can be scaled such that the particle position lies on the spheroid' surface. We tried both approaches and found no significant difference. Once the MPC particle at time t + h/2 is located on the spheroid's surface, the momentum transfer due to a bounce-back collision
x = bz/bx and ri(t + h/2) on its surface. The particle is then translated along the normal vector of the virtual spheroid until it is on the real spheroid's surface. Alternatively, the difference vector ri(t + h/2) − C(t + h/2) can be scaled such that the particle position lies on the spheroid' surface. We tried both approaches and found no significant difference. Once the MPC particle at time t + h/2 is located on the spheroid's surface, the momentum transfer due to a bounce-back collision
| | | Ji = 2m{vi − U − Ω × (ri − C) − DTubsq[D(ri − C)]} | (40) |
at time
t +
h/2 is determined, taking into account the squirmer surface fluid velocity
usq of
eqn (11).
83 Thereby, a useful identity to determine
s is given in eqn (8) of
ref. 45, and
ζ is given by
| | 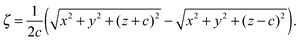 | (41) |
The velocity of the MPC particle is updated according to
vi′ =
vi −
Ji/
m. Subsequently, the position
ri(
t +
h) is obtained by streaming the MPC particle for the remaining time
h/2 with velocity
vi′,
i.e.,
ri(
t +
h) =
ri(
t +
h/2) +
hvi′/2.
As a consequence of the elastic collisions, the center-of-mass velocity and rotation frequency of a spheroid are finally given by
| | | U(t + h)′ = U(t + h) + J/M, | (42) |
| | | Ω(t + h)′ = Ω(t + h) + DT(Ib)−1DL, | (43) |
where
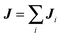
is total momentum transfer by the MPC fluid and
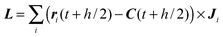
is the respective angular momentum transfer.
4.2 Collision step
In a first step, ghost particles are distributed inside each spheroid.82,84 The number density and mass are equal for ghost and fluid particles. The ghost particle positions rgi are uniformly distributed in the spheroid and their velocities are given by| | | vgi = U + Ω × (ri − C) + usq,i + vR,i. | (44) |
The Cartesian components of vR,i are Gaussian-distributed random numbers with zero mean and variance 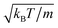 . The squirming velocity usq,i is determined by eqn (11), with the ghost particle position projected onto the spheroid's surface (cf. Section 4.1). As a result of MPC collisions, a spheroid's linear and angular momenta change by Jgi = m(
. The squirming velocity usq,i is determined by eqn (11), with the ghost particle position projected onto the spheroid's surface (cf. Section 4.1). As a result of MPC collisions, a spheroid's linear and angular momenta change by Jgi = m(![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) gi − vgi) and Lgi = (rgi − C) × Jgi, where
gi − vgi) and Lgi = (rgi − C) × Jgi, where ![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) gi and vgi are the ghost particle's velocity after and before the MPC collision. Hence, the spheroid velocity and angular velocity become
gi and vgi are the ghost particle's velocity after and before the MPC collision. Hence, the spheroid velocity and angular velocity become| | | Ω′ = Ω + RT(Ib)−1RLg. | (46) |
4.3 Rigid body dynamics for spheroids
During the streaming step, the spheroids move according to rigid-body dynamics, governed by85| | 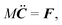 | (47) |
| | 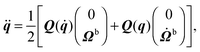 | (48) |
| | 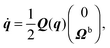 | (49) |
| | 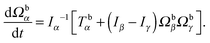 | (50) |
Here, Q(q) is defined in Appendix A (eqn (68)) and F and T are the force and torque acting on the spheroid. Forces and torques are derived from steric interaction potentials as presented in Appendix C. Eqn (50) are Euler's equations for rigid body dynamics and hold for (α, β, γ) = (x, y, z), (y, z, x), and (z, x, y). Whenever necessary, body-fixed and laboratory-frame quantities can be related by the rotation matrix D which is given in terms of the quaternion q in Appendix A (eqn (64)).
For the numerical integration of the equations of motion, the widely applied leap-frog method81 is not useful, since velocity, angular momentum, position, and orientation are required at the same point in time for the coupling to the MPC method. Hence, we employ the Verlet algorithm for rigid-body rotational motion proposed in ref. 85. Integration for a time step τ is performed as follows:
(i) Update C and q according to (cf.eqn (49) and (50))
| | 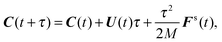 | (51) |
| | 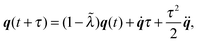 | (52) |
| | 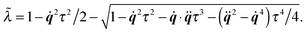 | (53) |
The parameter ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) is introduced to guarantee q2 = 1.
is introduced to guarantee q2 = 1.
(ii) Calculate forces and torques Fs(t + τ) and Ts(t + τ).
(iii) Update U and ls according to
| | 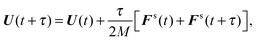 | (54) |
| | 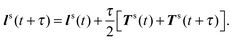 | (55) |
5 Simulations – thermal properties and flow field
5.1 Passive colloid
For the passive spheroidal colloid (B1 = B2 = 0), we perform equilibrium simulations and determine 〈Uα2〉 as well as 〈(Ωbα)2〉 for α ∈ {x, y, z}. Due to the equipartition of energy, we expect| | 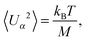 | (56) |
| | 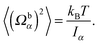 | (57) |
We fix the aspect ratio bz/bx = 2 and vary bx in the range bx ∈ [2a, 4a]. The simulation results agree very well with the theoretical values (56) and (57). As expected, the deviations from theory decrease with increasing spheroid size, due to a better resolution in terms of collision cells. In general, the relative error σr = (〈xtheo2〉 − 〈xsim2〉)/〈xtheo2〉 is larger for Ωbα than for Uα. We find the largest relative error for 〈(Ωbz)2〉, namely σr = 9.5%, 5.3%, and 3.1% for bx = 2a, 3a, and 4a. Hence, we choose the minor axis bx ≥ 3a in the following.
In addition, we determine the orientation correlation function 〈e(t)·e(0)〉. The theory of rotational Brownian motion86 predicts
| | | 〈e(t)·e(0)〉 = exp(−2D⊥Rt), | (58) |
where
DR = (2
D⊥R +
D∥R)/3,
D∥R =
kBT/
ξ∥,
D⊥R =
kBT/
ξ⊥, and
ξ∥ and
ξ⊥ are the parallel and perpendicular rotational friction coefficients of a prolate spheroid with respect to the major semi-axis; explicitly
69| | 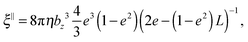 | (59) |
| | 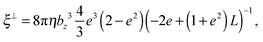 | (60) |
| | 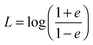 | (61) |
Simulation results for the orientational auto-correlation function are shown in
Fig. 4 for two spheroids of different eccentricity. The correlation functions decay exponentially. However, for the spheroid with the smaller eccentricity, we find a somewhat faster decay than predicted by theory, whereas good agreement is found for the larger spheroid. We attribute the difference to finite-size effects related to the discreteness of the collision lattice. For larger objects, discretization effects become smaller.
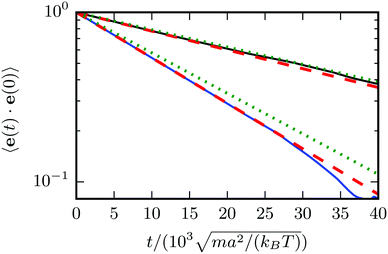 |
| | Fig. 4 Orientation correlation functions 〈e(t)·e(0)〉 for passive spheroids with bz = 6a, bx = 3a (bottom blue line) and bz = 9a, bx = 3a (top black line). The plot shows the simulation data (blue and black solid lines), an exponential fit to that data (red dashed), and the theoretical prediction according to eqn (58) (green dotted). | |
5.2 Squirmer
We determine the steady state swimming velocity of a squirmer via 〈e·U〉, which should be equal to U0 (cf.eqn (3)). Results for various eccentricities are displayed in Fig. 5. The velocity U0 increases with increasing eccentricity e in close agreement with the theoretical prediction of eqn (3). We confirm that the force-dipole parameter β does not affect the velocity of the squirmer, as long as the Reynolds number Re is low, i.e., Re = ρU0bz/η ≲ 0.1. We also determine the orientational correlation function and find that a squirmer exhibits the same orientational decorrelation as the corresponding passive particle (cf.Fig. 4).
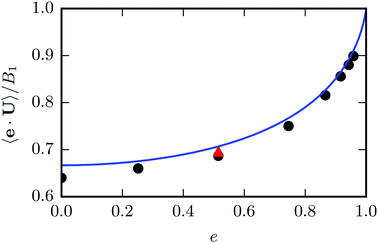 |
| | Fig. 5 Mean swimming velocity as function of the eccentricity e for a spheroidal squirmer with 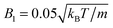 and B2 = 0. The solid line shows the theoretical prediction of eqn (3). Black dots are simulation results. The eccentricity was varied by changing bz and keeping bx = 3a constant. For the red triangle, we simulated a larger spheroid with bx = 6a, which shows a better agreement with theory. and B2 = 0. The solid line shows the theoretical prediction of eqn (3). Black dots are simulation results. The eccentricity was varied by changing bz and keeping bx = 3a constant. For the red triangle, we simulated a larger spheroid with bx = 6a, which shows a better agreement with theory. | |
Moreover, we calculate the flow field from the simulation data and compare it with the theoretical prediction. As shown in Fig. 6, the two fields are in close agreement. The two-dimensional flow field of the MPC fluid, averaged over the rotation angle φ, is determined at the vertices of a fine resolution mesh. The velocities at these vertices include averages over time of an individual realization as well as ensemble averages over various realizations. By the latter, we determine an estimate for the error of the mean velocity. The median (over vertices) of this error is approximately 5% for the parameters of Fig. 6(b) and 10% for that of Fig. 6(e). Note that we choose a smaller swimming mode B1 for the puller (Fig. 6(b)) than for the neutral squirmer (Fig. 6(e)). The reason is that the agreement with theory was not satisfactory for the puller with 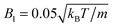 , which we attribute to a non-vanishing Reynolds number (Re ≈ 0.1) in the simulation. In Fig. 6(c) and (f), we observe lines of high relative errors (yellow in the color code). They appear because theory predicts v
, which we attribute to a non-vanishing Reynolds number (Re ≈ 0.1) in the simulation. In Fig. 6(c) and (f), we observe lines of high relative errors (yellow in the color code). They appear because theory predicts v![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) = 0 or vz = 0 for these lines, which is difficult to achieve in simulations. Hence, the overall agreement between simulations and theory is very satisfactory, and the implementation is very valuable for the simulation of squirmer–squirmer and squirmer–wall interactions, where the details of the flow field matter. For a benchmark of the code on a current GPU see Appendix D.
= 0 or vz = 0 for these lines, which is difficult to achieve in simulations. Hence, the overall agreement between simulations and theory is very satisfactory, and the implementation is very valuable for the simulation of squirmer–squirmer and squirmer–wall interactions, where the details of the flow field matter. For a benchmark of the code on a current GPU see Appendix D.
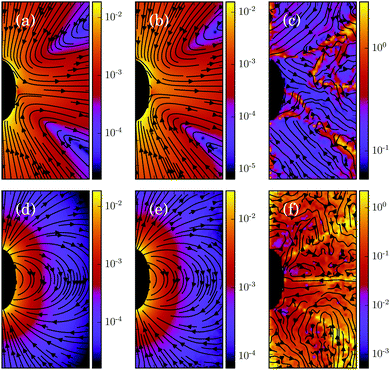 |
| | Fig. 6 Fluid flow fields of a spheroidal squirmer in the laboratory frame with bx = 3a, bz = 6a, 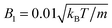 , and β = 3 (a–c), and with , and β = 3 (a–c), and with 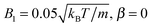 (d–f). The magnitude of the velocity field (in units of (d–f). The magnitude of the velocity field (in units of 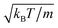 ) is color coded logarithmically. The plots (a) and (d) show theoretical results, (b) and (e) simulation results, and (c) and (f) relative errors. The relative error of the flow field is defined as Δvα = |vtheoα − vsimα|/[(|vtheoα| + |vsimα|)/2]. Note, due to the discrete representation of the velocity field, some streamlines end abruptly. ) is color coded logarithmically. The plots (a) and (d) show theoretical results, (b) and (e) simulation results, and (c) and (f) relative errors. The relative error of the flow field is defined as Δvα = |vtheoα − vsimα|/[(|vtheoα| + |vsimα|)/2]. Note, due to the discrete representation of the velocity field, some streamlines end abruptly. | |
6 Cooperative swimming in a narrow slit
We simulate the cooperative swimming behavior of two squirmers in a slit geometry. The slit is formed by two parallel no-slip walls located at y = 0 and y = Ly. The no-slip boundary condition is implemented by applying the bounce-back rule and ghost particles of zero mean velocity in the walls.84 Steric interactions between two squirmers and between a squirmer and a wall are taken into account by the procedure described in Appendix C. The initial positions and orientations of the two squirmers (i = 1, 2) are| | 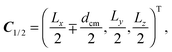 | (62) |
| | | e1/2 = (±cos(α0), 0, sin(α0))T. | (63) |
Here, dcm is the initial center-of-mass distance and α0 = (π − θ0)/2, where θ0 is the initial angle between e1 and e2. The swimming mode is chosen as 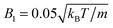 and the force dipole mode β ∈ {−4,0,4}. We choose dcm such that the squirmers are well separated and vary θ0. The squirmers major and minor axes are bx = 3a and bz = 6a, respectively, and the simulation box size is Lx = Lz = 15bz, and Ly = 7a. Note that Ly ≳ bx which keeps the swimming orientation essentially in the x–z plane.
and the force dipole mode β ∈ {−4,0,4}. We choose dcm such that the squirmers are well separated and vary θ0. The squirmers major and minor axes are bx = 3a and bz = 6a, respectively, and the simulation box size is Lx = Lz = 15bz, and Ly = 7a. Note that Ly ≳ bx which keeps the swimming orientation essentially in the x–z plane.
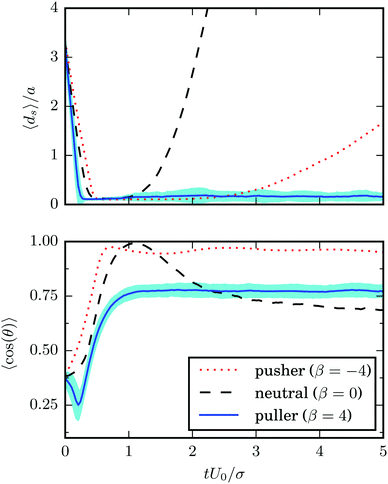
Results for the mean surface-to-surface distance between squirmers 〈ds〉 and the mean alignment 〈e1·e2〉 = 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉 are shown in Fig. 7 for pushers, pullers, and neutral swimmers with an initial angle θ0 = 3π/8. Due to the setup, the squirmers initially approach each other and collide at tU0/σ ≈ 0.5. The (persistence) Péclet number Pe = U0/(2D⊥Rσ) ≈ 60 is sufficiently high, such that the squirmer orientation has hardly changed before collision. When the neutral swimmers collide, they initially align parallel (cos
θ〉 are shown in Fig. 7 for pushers, pullers, and neutral swimmers with an initial angle θ0 = 3π/8. Due to the setup, the squirmers initially approach each other and collide at tU0/σ ≈ 0.5. The (persistence) Péclet number Pe = U0/(2D⊥Rσ) ≈ 60 is sufficiently high, such that the squirmer orientation has hardly changed before collision. When the neutral swimmers collide, they initially align parallel (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ ≈ 1 at tU0/σ ≈ 1 in Fig. 7), but their trajectories start to diverge immediately thereafter. Pushers remain parallel for an extended time window, which is expected as pushers are known to attract each other,37 but at tU0/σ ≈ 3 (cf.Fig. 7) their trajectories diverge as well. This is probably due to noise, since we observe several realizations where pushers remain parallel. Interestingly, pullers, which are known to repel each other when swimming in parallel,37 swim cooperatively and reach a stable orientation with 〈cos(θ)〉 ≈ 0.77 shortly after they collided (at tU0/σ ≈ 1). Thereby, their cooperative swimming velocity is about 0.8U0. The flow field of this stable state, determined by MPC simulations, is shown in Fig. 8. Note that the velocity field in the swimming plane is left-right symmetric, and that there is a stagnation point in the center behind the swimmers. Fig. 8 reveals that this point actually corresponds to a line normal to the walls. In ref. 87, it was shown that the flow field of a force dipole in a narrow slit exhibits a recirculating pattern with loops in a plane parallel to the walls88 and a parabolic flow profile perpendicular to them. Both features can be observed in Fig. 8. Fig. 9 shows that the fixed point of cooperatively swimming pullers is reached for nearly all simulated initial conditions θ0 ∈ (0, π/2). Only pullers that are nearly parallel initially (θ0 = π/8, cos
θ ≈ 1 at tU0/σ ≈ 1 in Fig. 7), but their trajectories start to diverge immediately thereafter. Pushers remain parallel for an extended time window, which is expected as pushers are known to attract each other,37 but at tU0/σ ≈ 3 (cf.Fig. 7) their trajectories diverge as well. This is probably due to noise, since we observe several realizations where pushers remain parallel. Interestingly, pullers, which are known to repel each other when swimming in parallel,37 swim cooperatively and reach a stable orientation with 〈cos(θ)〉 ≈ 0.77 shortly after they collided (at tU0/σ ≈ 1). Thereby, their cooperative swimming velocity is about 0.8U0. The flow field of this stable state, determined by MPC simulations, is shown in Fig. 8. Note that the velocity field in the swimming plane is left-right symmetric, and that there is a stagnation point in the center behind the swimmers. Fig. 8 reveals that this point actually corresponds to a line normal to the walls. In ref. 87, it was shown that the flow field of a force dipole in a narrow slit exhibits a recirculating pattern with loops in a plane parallel to the walls88 and a parabolic flow profile perpendicular to them. Both features can be observed in Fig. 8. Fig. 9 shows that the fixed point of cooperatively swimming pullers is reached for nearly all simulated initial conditions θ0 ∈ (0, π/2). Only pullers that are nearly parallel initially (θ0 = π/8, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ0 ≈ 0.92 in Fig. 9), repel each other such that they will not reach the fixed point. For Péclet numbers Pe < 60, the fixed point remains at 〈cos(θ)〉 ≈ 0.77. However, it becomes more likely for the swimmers to escape (or never reach) the fixed point.
θ0 ≈ 0.92 in Fig. 9), repel each other such that they will not reach the fixed point. For Péclet numbers Pe < 60, the fixed point remains at 〈cos(θ)〉 ≈ 0.77. However, it becomes more likely for the swimmers to escape (or never reach) the fixed point.
 |
| | Fig. 7 Average surface-to-surface distance ds and orientation of squirmers, where cos(θ) = e1·e2, as function of time. The solid blue, dashed black, and dotted red lines correspond to pullers β = 4, neutrals β = 0 and pushers β = −4. The standard deviation of the blue line (β = 4) is indicated by the cyan shaded region. | |
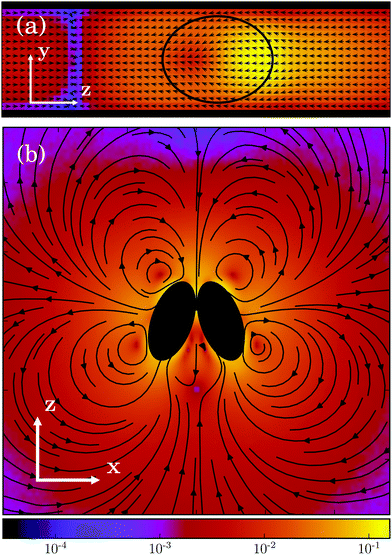 |
| | Fig. 8 Flow field of two cooperatively swimming pullers in the laboratory frame. The magnitude of the velocity field (in units of 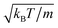 ) is color coded logarithmically. We denote the direction normal to the walls by y, the cooperative swimming direction by z, the remaining Cartesian axis by x, and choose the swimmers' center of mass as origin. Panel (a) shows the flow field at x = 0 in the zy-plane, while panel (b) shows the flow field at y = 0 in the xz-plane. The black elliptical shapes (“transparent”, solid) indicate the projection of the swimmers onto the considered plane. ) is color coded logarithmically. We denote the direction normal to the walls by y, the cooperative swimming direction by z, the remaining Cartesian axis by x, and choose the swimmers' center of mass as origin. Panel (a) shows the flow field at x = 0 in the zy-plane, while panel (b) shows the flow field at y = 0 in the xz-plane. The black elliptical shapes (“transparent”, solid) indicate the projection of the swimmers onto the considered plane. | |
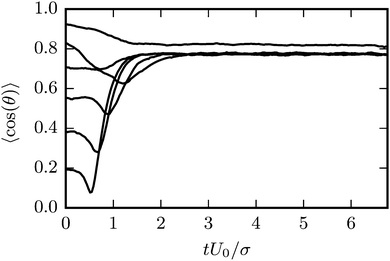 |
| | Fig. 9 Time dependence of the average alignment 〈e1·e2〉 = 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉 of two pullers with β = 4, bz/bx = 2 in a slit of height Ly = 7a, and various initial angles θ0 ∈ (0,π/2) (see ESI,† Movie beta 4). θ〉 of two pullers with β = 4, bz/bx = 2 in a slit of height Ly = 7a, and various initial angles θ0 ∈ (0,π/2) (see ESI,† Movie beta 4). | |
A detailed study reveals that the fixed point vanishes, when the walls are replaced by periodic boundary conditions (we use a cubic simulation box of length 10bz). This is even true when we apply three-dimensional periodic boundaries, but keep the wall potential implemented, i.e., the squirmers are still confined in a narrow slit of height 7a as before (the fluid simulation box is cubic with length 10bz). These observations are quantified in Fig. 10. Note that the slow increase of the average squirmer surface-to-surface distance in the case of a periodic system with wall potential is due to the fact that the pullers still swim together in several realizations. However, in these realizations they no longer swim in a plane as for the slit geometry, but rather show three-dimensional configurations with tilted major axes. Evidently, hydrodynamic interactions with the walls89 are essential for the swimmers' dynamics.
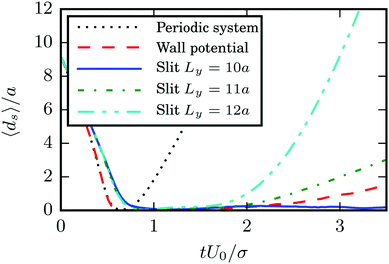 |
| | Fig. 10 Average surface-to-surface distance ds between two pullers with β = 4, bz = 6a, and bx = 3a as a function of time for various geometries. The distance ds increases rapidly after collision for squirmers in a cubic simulation box of side length 10bz with periodic boundary conditions (black dotted line). Trajectories still diverge, when a confining potential for the squirmers is present (red dashed line); for details see text. Squirmers confined in a slit of width Ly = 10a with no-slip walls swim together (blue solid line). However, their trajectories diverge for wide slits (Ly = 11a for the green dash-dotted line and Ly = 12a for the cyan dash-dot-dotted line). | |
In addition, we studied the swim behavior of spherical squirmers. Here, we observe diverging trajectories for all squirmer types, i.e., pushers, neutral squirmers, and pullers. Such diverging trajectories have already been reported in ref. 90 for spherical squirmers in bulk. In contrast, in ref. 91 a cooperative swimming mode for spherical squirmers has been observed (see Fig. 22(c) of ref. 91). However, this cooperative swimming—termed pair-swimming by the authors—is unstable to perturbations that displace one swimmer out of the swimming plane.91 Since our simulations and those of ref. 90 include thermal fluctuations, we consequently do not observe the cooperative swimming mode of ref. 91.
Hence, the stable close-by cooperative swimming of pullers is governed by the squirmer anisotropy, by the hydrodynamic interactions between them and, importantly, between pullers and confining surfaces.
This conclusion is in contrast to results presented in ref. 47, where a monolayer of spheroidal squirmers is considered, with their centers and orientation vectors fixed in the same plane, however, without confining walls. The study reports a stable cooperative motion for pullers with angles θ ∈ (0, π/2) by nearest-neighbor two-body interactions, where all angles between 0 and π/2 are stable. The difference to our study is that in ref. 47 cooperative features were extracted from a simulation of many swimmers, whereas we explicitly studied two swimmers. Furthermore our study explicitly models no-slip walls and includes thermal noise.
To shed light on the stability of the cooperative puller motion, we varied the puller strength β, the aspect ratio bz/bx, and the width of the slit Ly. Thereby, we started from our basic parameter set bx = 3a, bz = 6a, Ly = 7a, and β = 4. With decreasing β, the stable alignment disappears, i.e., the pullers' distance increases after collision (see ESI,† Movies beta 3 and beta 4). For increasing β the fixed point remains, but the value of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ decreases, i.e., the squirmers form a larger angle. With increasing wall separation, the fixed-point value of cos
θ decreases, i.e., the squirmers form a larger angle. With increasing wall separation, the fixed-point value of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ decreases, i.e., the angle between the swimmers increases. For Ly/bz ≳ 11/6, the mean distance between swimmers increases rapidly after collision (see Fig. 10). An increase of the aspect ratio bz/bx from 2 to 3 and 4 increases the fixed-point value of 〈cos
θ decreases, i.e., the angle between the swimmers increases. For Ly/bz ≳ 11/6, the mean distance between swimmers increases rapidly after collision (see Fig. 10). An increase of the aspect ratio bz/bx from 2 to 3 and 4 increases the fixed-point value of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉 from 0.77 to 0.84 and 0.88. The more elongated shape leads to a more parallel alignment of the squirmers. For bz/bx ≥ 2, the minimal value of β required to achieve cooperative motion depends weakly on the aspect ratio. In particular, for bz/bx = 2, 3, and 4, we find the minimal value β ≈ 3.5.
θ〉 from 0.77 to 0.84 and 0.88. The more elongated shape leads to a more parallel alignment of the squirmers. For bz/bx ≥ 2, the minimal value of β required to achieve cooperative motion depends weakly on the aspect ratio. In particular, for bz/bx = 2, 3, and 4, we find the minimal value β ≈ 3.5.
7 Summary and conclusions
We have introduced a spheroidal squirmer model, which comprises the swimming and force-dipole modes. It is a variation of previously proposed squirmer models. On the one hand, it includes the force-dipole mode as an extension to the model of ref. 45. On the other hand, it is an alternative approach compared to ref. 44 and 47, with the major advantage that our model allows for the analytical calculation of the flow field. In the present calculations we employed the Stokes stream function equation. Very recently a full set of solutions to Stokes' equations in spheroidal coordinates were given in ref. 92, which opens an alternative approach to derive the flow field for our choice of boundary conditions.
Furthermore, we have presented an implementation of our spheroidal squirmer in a MPC fluid. In contrast to other frequently employed simulation approaches, MPC includes thermal fluctuations. The comparison between the fluid flow profile of a squirmer extracted from the simulation data with the theoretical prediction yields very good agreement. As a consequence of the MPC approach with its discrete collision cells, the minor axis of the spheroid has to be larger than a few collision cells to avoid discretization effects. The analysis of the squirmer orientation correlation function shows that very good agreement between theory and simulations is already obtained for bz = 9a (major axis) and bx = 3a (minor axis).
To shed light on the cooperative swimming motion and on near-field hydrodynamic interactions, we investigated the collision of two spheroidal squirmers in a slit geometry. We found a stable stationary state of close-by swimming for spheroidal pullers, which is determined by hydrodynamic interactions between the anisotropic squirmers, and, even more important, by squirmers and surfaces. This stationary state disappears for low puller strengths and low eccentricities. We expect the stable close-by swimming of pullers to strongly enhance clustering in puller suspensions in narrow slits.
Our studies confirm that spheroidal squirmers can accurately be simulated by the MPC method. The proposed implementation opens an avenue to study collective and non-equilibrium effects in systems of anisotropic microswimmers. Even large-scale systems (103 to 104 swimmers) can be addressed by the implementation of MPC and the squirmer dynamics on current GPUs.
Appendix
A Quaternion matrices
The rotation matrix D introduced in eqn (39) is given in terms of the rotation quaternion q as| | 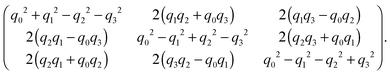 | (64) |
The matrix Q(q) in eqn (49) is given by| | 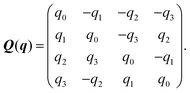 | (65) |
B Gegenbauer functions
For n ≥ 2 and x ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) the Gegenbauer functions of the first and second kind Gn and Hn, are defined in terms of the Legendre functions of the first and second kind Pn and Qn as67,93
the Gegenbauer functions of the first and second kind Gn and Hn, are defined in terms of the Legendre functions of the first and second kind Pn and Qn as67,93| | 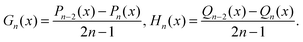 | (66) |
For n = 0, 1, they are defined as| | | G0(x) = −H1(x) = 1, G1(x) = H0(x) = −x. | (67) |
For the reader's convenience, we give the formula for the Gegenbauer functions of the first kind for n = 2, 3, and x ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif)
| | 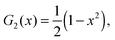 | (68) |
| | 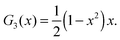 | (69) |
Furthermore, the Gegenbauer functions of the second kind for n = 2, 3, and x > 1 are given by| | 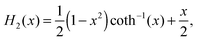 | (70) |
| | 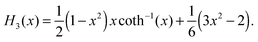 | (71) |
Here, we used coth−1(x) = ln([x + 1]/[x − 1])/2.
C Steric interactions
Here, we illustrate our implementation of the excluded-volume interactions between spheroids and walls following the approach provided in ref. 94.
The spheroid's surface in the laboratory frame is given by the quadratic form
| | 1 = ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (x) ≡ (x − C)TA(x − C), (x) ≡ (x − C)TA(x − C), | (72) |
where the orientation matrix
A can be expressed as
| | |
A
= (1 − eeT)/bx2 + eeT/bz2.
| (73) |
For the steric interactions, we introduce a virtual safety distance
dv, which is small compared to
bx and
bz. When computing steric interactions, we replace
bx and
bz by
bx +
dv and
bz +
dv, respectively. In this paper we used
dv = 0.05
a for all simulations.
C.1 Interaction between spheroids.
We introduce a repulsive interaction potential between spheroids to prevent their overlap. The potential is given by| | 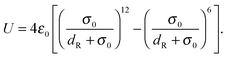 | (74) |
Here, σ0 and ε0 correspond to a length and energy scale, respectively. We choose ε0 = kBT and σ0 = 2dv. The directional contact distance dR between two spheroids, with orientation matrices A1, A2 and center positions C1, C2, is an approximation to their true distance of closest approach and is defined by| | | dR = R(1 − F(A1,A2)−1/2) | (75) |
Here, R = C2 − C1, R = |R|, and F(A1,A2) is the elliptic contact function, defined as94| | 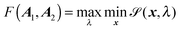 | (76) |
| | 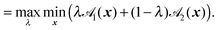 | (77) |
Minimization with respect to x demands ∇![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (x,λ) = 0, and hence,
(x,λ) = 0, and hence,| | | x(λ) = {λA1 + (1 − λ)A2}−1{λA1C1 + (1 − λ)A2C2}. | (78) |
The critical value λ = λc that maximizes ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (x(λ),λ) can be found by the root finding problem
(x(λ),λ) can be found by the root finding problem| | ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 1(x(λ)) − 1(x(λ)) − ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 2(x(λ)) = 0. 2(x(λ)) = 0. | (79) |
We implement Brent's root finding approach.95 The forces and torques arising from the potential (74) can be calculated analytically and are given by‡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 94
94| | 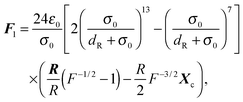 | (80) |
and| | 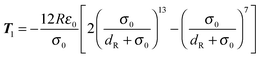 | (81) |
for the first spheroid, where Xc = 2λcA1(xc − C1). The force and torque on the second spheroid follow by Newton's action-reaction law, namely We restrict ourselves to short-range repulsive interactions by setting the potential U to a constant value for 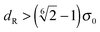 , which implies that F1 and T1 are zero for this range of dR values. Note that an upper bound to dR is R − 2bz, which means that two spheroids will not interact if
, which implies that F1 and T1 are zero for this range of dR values. Note that an upper bound to dR is R − 2bz, which means that two spheroids will not interact if 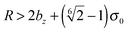 . This inequality is checked before a numerical calculation of dR is employed.
. This inequality is checked before a numerical calculation of dR is employed.
C.2 Interaction between a spheroid and a wall.
We assume that two parallel walls are positioned at y = 0, Ly, which—taking into account the safety distance dv—results in the effective wall positions y = dv and Ly − dv. We propose an interaction between a spheroid and a wall in the style of the spheroid–spheroid interaction presented in ref. 94. First, we find the point x on the spheroid's surface that is closest to a wall. For the wall at y = dv, this is achieved by minimizing the height h(x) = ey·x − dv under the constraint ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (x) = 1. Using the method of Lagrange multipliers, we have to minimize Λ(x,λ) = h(x) + λ(
(x) = 1. Using the method of Lagrange multipliers, we have to minimize Λ(x,λ) = h(x) + λ(![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (x) − 1). The necessary condition for a minimum ∂Λ/∂x = 0 yields
(x) − 1). The necessary condition for a minimum ∂Λ/∂x = 0 yields| | ey + λ∇![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (x) = ey + 2λA(x − C) = 0, (x) = ey + 2λA(x − C) = 0, | (85) |
and hence,
Substitution of
eqn (86) into
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif)
(
x) = 1 yields
| | 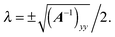 | (87) |
Finally, we obtain the point closest to the wall as
| | 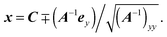 | (88) |
Here, the minus sign has to be chosen, which can be visualized by the example of a sphere of radius
R, for which
A =
R−21. This finally yields the height
| | 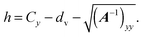 | (89) |
We employ the Lennard-Jones potential
| | 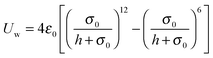 | (90) |
for a repulsive wall, and
Uw assumes a constant value for all
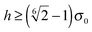
. We can derive the force
Fα = −
∂Uw/
∂Cα and torque
Tα = −
∂Uw/
∂ψα acting on the spheroid analytically. For the force, we find
| | 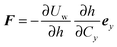 | (91) |
| | 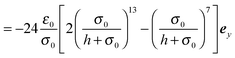 | (92) |
and for the torque
| | 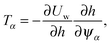 | (93) |
with
| | 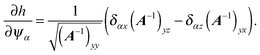 | (94) |
Here, we used the relation
| | 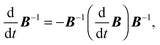 | (95) |
which holds for an invertible matrix
B =
B(
t) depending on a scalar parameter
t, and eqn (C9) from
ref. 94.
For the wall at y = Ly − dv, we have to minimize h(x) = Ly − dv − ey·x, with x on the spheroid's surface. This yields
| | | x = C + A−1ey[(A−1)yy]−1/2. | (96) |
The formulas for torque and force do not change, except that we have to insert
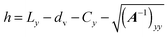
and need to change the sign of the force.
D Benchmark simulation
Computation time.
We perform benchmark simulations on an NVIDIA K80 GPU. First we determine the computation time for one MPC step in a periodic system, normalized by the number of fluid particles. We obtain approximately 4.5 nanoseconds per time step and particle, which is in accordance with the value of about 3 nanoseconds reported in ref. 80, since the extension to angular momentum conserving MPC roughly doubles the computation time, while the NVIDIA K80 is approximately twice as fast as the NVIDIA GTX580 employed in ref. 80.
Next, we perform a benchmark MPC simulation of many spheroidal squirmers with bx = 3a, bz = 6a in a narrow slit. The slit height and length are chosen as Ly = 7a and Lx = Lz = 600a, respectively. We vary the number Nsq of squirmers, i.e., the two-dimensional packing fraction Nsqπbxbz/(LxLz), and determine the computation time per MPC time step, normalized by the number of fluid and ghost particles. A simulation without squirmers takes approximately 4.9 nanoseconds per time step and particle. Hence, the addition of no-slip walls leads only to a minor increase in simulation time by approximately 10%. When spheroidal squirmers are introduced, the computation time increases linearly with the number of squirmers up to a value of 13.2 nanoseconds for the two-dimensional packing fraction 0.6, which corresponds to 3825 squirmers in our set-up. Similar values are found for smaller (Lx = Ly = 300a) and larger systems (Lx = Ly = 900a). The increase in computation time is mostly related to the squirmers' ghost particles. Unlike the fluid particles and the ghost particles for the no-slip walls, they are not spatially ordered in memory, which leads to a significantly lower processing speed (cf. Fig. 3 of ref. 80).
The steric interactions are computed sequentially on the CPU exploiting a cell-linked list.81 The computation time spent for the steric interactions increases linearly with Nsq. However, it only contributes by about 4% to the total simulation time for the considered set-up.
Memory limitations.
The size of the systems that can be studied with our code is limited by the available memory on the used GPU. Explicitly, the required memory to store fluid particle, collision cell, and spheroid properties are listed in Table 1.
Table 1 Memory requirement to store fluid particle, collision cell, and spheroid properties
| Memory usage per cell: |
| Particles per cell |
4 bytes |
| Random seed |
8 bytes |
| Cell energy/thermostat |
4 bytes |
| Center of mass velocity |
24 bytes |
| Rotation matrix |
24 bytes |
| Center of mass |
24 bytes |
| Inertia tensor |
48 bytes |
| Angular momentum |
24 bytes |
| Total per cell |
160 bytes |
|
|
| Memory usage per fluid particle: |
| Particle position (single precision) |
12 bytes |
| Particle velocity (double precision) |
24 bytes |
| Cell index |
4 bytes |
| Temporary memory for performance optimisation |
12 bytes |
| Total per particle |
52 bytes |
|
|
| Memory usage per spheroid: |
| Parameters describing current state |
296 bytes |
| Parameters describing state after half time step |
296 bytes |
| Total per spheroid |
592 bytes |
Compared to the number of fluid particles, the number of spheroidal squirmers is several orders of magnitude smaller and their impact on GPU memory usage is negligible. With a typical density of 〈Nc〉 = 10 particles per cell, the required GPU memory is 680 bytes per collision cell. Therefore, approximately 1.5 × 106 collision cells can be studied per 1 GB of GPU memory. Hence, the memory capacity of 4–12 GB of recent GPUs corresponds approximately to 6 × 106–2 × 107 collision cells. The volume of a spheroidal squirmer with bx = 3a, bz = 6a is equivalent to 226 cells. Assuming a 30% volume fraction of squirmers, memory limits the total number of squirmers to 8 × 103–2.4 × 104. Note that for systems of many squirmers, the time scales of interest can be very long. Hence, in applications, the considered system size has often to be smaller (≈103 squirmers) for acceptable total simulation times.
Acknowledgements
We thank A. Wysocki, A. Varghese, B. U. Felderhof, and A. J. T. M. Mathijssen for helpful discussions. Support of this work by the DFG priority program SPP 1726 on “Microswimmers – from Single Particle Motion to Collective Behaviour” is gratefully acknowledged.
References
- J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed.
- T. Vicsek and A. Zafeiris, Phys. Rep., 2012, 517, 71 CrossRef.
- M. F. Copeland and D. B. Weibel, Soft Matter, 2009, 5, 1174 RSC.
- N. C. Darnton, L. Turner, S. Rojevsky and H. C. Berg, Biophys. J., 2010, 98, 2082 CrossRef CAS PubMed.
- D. B. Kearns, Nat. Rev. Microbiol., 2010, 8, 634–644 CrossRef CAS PubMed.
- H. H. Wensink, J. Dunkel, S. Heidenreich, K. Drescher, R. E. Goldstein, H. Löwen and J. M. Yeomans, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14308 CrossRef CAS PubMed.
- J. D. Partridge and R. M. Harshey, J. Bacteriol., 2013, 195, 909 CrossRef CAS PubMed.
- J. Bialké, T. Speck and H. Löwen, Phys. Rev. Lett., 2012, 108, 168301 CrossRef PubMed.
- I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger and T. Speck, Phys. Rev. Lett., 2013, 110, 238301 CrossRef PubMed.
- B. M. Mognetti, A. Šarić, S. Angioletti-Uberti, A. Cacciuto, C. Valeriani and D. Frenkel, Phys. Rev. Lett., 2013, 111, 245702 CrossRef CAS PubMed.
- I. Theurkauff, C. Cottin-Bizonne, J. Palacci, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2012, 108, 268303 CrossRef CAS PubMed.
- Y. Fily, S. Henkes and M. C. Marchetti, Soft Matter, 2014, 10, 2132 RSC.
- X. Yang, M. L. Manning and M. C. Marchetti, Soft Matter, 2014, 10, 6477 RSC.
- J. Stenhammar, D. Marenduzzo, R. J. Allen and M. E. Cates, Soft Matter, 2014, 10, 1489 RSC.
- Y. Fily, A. Baskaran and M. F. Hagan, Soft Matter, 2014, 10, 5609 RSC.
- G. S. Redner, M. F. Hagan and A. Baskaran, Phys. Rev. Lett., 2013, 110, 055701 CrossRef PubMed.
- Y. Fily and M. C. Marchetti, Phys. Rev. Lett., 2012, 108, 235702 CrossRef PubMed.
- R. Großmann, L. Schimansky-Geier and P. Romanczuk, New J. Phys., 2012, 14, 073033 CrossRef.
- V. Lobaskin and M. Romenskyy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 052135 CrossRef PubMed.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2014, 112, 118101 CrossRef PubMed.
- A. Wysocki, R. G. Winkler and G. Gompper, EPL, 2014, 105, 48004 CrossRef.
- F. Peruani, A. Deutsch and M. Bär, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 030904 CrossRef PubMed.
- Y. Yang, V. Marceau and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 031904 CrossRef PubMed.
- J. Elgeti and G. Gompper, EPL, 2009, 85, 38002 CrossRef.
- A. P. Berke, L. Turner, H. C. Berg and E. Lauga, Phys. Rev. Lett., 2008, 101, 038102 CrossRef PubMed.
- E. Lauga and T. R. Powers, Rep. Prog. Phys., 2009, 72, 096601 CrossRef.
- E. Lauga, W. R. DiLuzio, G. M. Whitesides and H. A. Stone, Biophys. J., 2006, 90, 400 CrossRef CAS PubMed.
- J. Hu, A. Wysocki, R. G. Winkler and G. Gompper, Sci. Rep., 2015, 5, 9586 CrossRef PubMed.
- R. Di Leonardo, D. Dell'Arciprete, L. Angelani and V. Iebba, Phys. Rev. Lett., 2011, 106, 038101 CrossRef CAS PubMed.
- L. Lemelle, J.-F. Palierne, E. Chatre, C. Vaillant and C. Place, Soft Matter, 2013, 9, 9759 RSC.
- M. J. Lighthill, Commun. Pure Appl. Math., 1952, 5, 109–118 CrossRef.
- J. R. Blake, J. Fluid Mech., 1971, 46, 199–208 CrossRef.
- J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102 CrossRef PubMed.
- A. Erbe, M. Zientara, L. Baraban, C. Kreidler and P. Leiderer, J. Phys.: Condens. Matter, 2008, 20, 404215 CrossRef.
- G. Volpe, I. Buttinoni, D. Vogt, H. J. Kümmerer and C. Bechinger, Soft Matter, 2011, 7, 8810 RSC.
- I. Llopis and I. Pagonabarraga, J. Non-Newtonian Fluid Mech., 2010, 165, 946 CrossRef CAS.
- I. O. Götze and G. Gompper, EPL, 2010, 92, 64003 CrossRef.
- T. Ishikawa and M. Hota, J. Exp. Biol., 2006, 209, 4452–4463 CrossRef PubMed.
- T. Ishikawa and T. J. Pedley, J. Fluid Mech., 2007, 588, 399–435 Search PubMed.
- A. A. Evans, T. Ishikawa, T. Yamaguchi and E. Lauga, Phys. Fluids, 2011, 23, 111702 CrossRef.
- F. Alarcón and I. Pagonabarraga, J. Mol. Liq., 2013, 185, 56–61 CrossRef.
- J. J. Molina, Y. Nakayama and R. Yamamoto, Soft Matter, 2013, 9, 4923 RSC.
- T. Ishikawa and T. J. Pedley, Phys. Rev. Lett., 2008, 100, 088103 CrossRef PubMed.
- K. Ishimoto and E. A. Gaffney, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062702 CrossRef PubMed.
- S. R. Keller and T. Y. Wu, J. Fluid Mech., 1977, 80, 259–278 CrossRef.
- G.-J. Li and A. M. Ardekani, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 013010 CrossRef PubMed.
- K. Kyoya, D. Matsunaga, Y. Imai, T. Omori and T. Ishikawa, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 063027 CrossRef CAS PubMed.
- S. E. Spagnolie and E. Lauga, J. Fluid Mech., 2012, 700, 105–147 CrossRef.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2012, 108, 218104 CrossRef PubMed.
- I. Pagonabarraga and I. Llopis, Soft Matter, 2013, 9, 7174–7184 RSC.
- B. Delmotte, E. E. Keaveny, F. Plouraboué and E. Climent, J. Comput. Phys., 2015, 302, 524–547 CrossRef.
- A. Malevanets and R. Kapral, J. Chem. Phys., 1999, 110, 8605–8613 CrossRef CAS.
- R. Kapral, Adv. Chem. Phys., 2008, 140, 89–146 CrossRef CAS.
-
G. Gompper, T. Ihle, D. M. Kroll and R. G. Winkler, in Advanced Computer Simulation Approaches for Soft Matter Sciences III, ed. P. C. Holm and P. K. Kremer, Springer, Berlin, Heidelberg, 2009, pp. 1–87 Search PubMed.
- E. Tüzel, T. Ihle and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 056702 CrossRef PubMed.
- C.-C. Huang, G. Gompper and R. G. Winkler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 056711 CrossRef PubMed.
- S. Y. Reigh, R. G. Winkler and G. Gompper, Soft Matter, 2012, 8, 4363–4372 RSC.
- S. Y. Reigh, R. G. Winkler and G. Gompper, PLoS One, 2013, 8, e70868 CAS.
- G. Rückner and R. Kapral, Phys. Rev. Lett., 2007, 98, 150603 CrossRef PubMed.
- M. Yang and M. Ripoll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 061401 CrossRef PubMed.
- D. J. Earl, C. M. Pooley, J. F. Ryder, I. Bredberg and J. M. Yeomans, J. Chem. Phys., 2007, 126, 064703 CrossRef PubMed.
- J. Elgeti, U. B. Kaupp and G. Gompper, Biophys. J., 2010, 99, 1018–1026 CrossRef CAS PubMed.
- J. Elgeti and G. Gompper, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4470 CrossRef CAS PubMed.
- M. Theers and R. G. Winkler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 023012 CrossRef PubMed.
- J. Hu, M. Yang, G. Gompper and R. G. Winkler, Soft Matter, 2015, 11, 7843 RSC.
-
J. Happel and H. Brenner, Low Reynolds number hydrodynamics: with special applications to particulate media, Springer Science & Business Media, 1983 Search PubMed.
- G. Dassios and P. Vafeas, Phys. Res. Int., 2008, 2008, e135289 Search PubMed.
- A. M. Leshansky, O. Kenneth, O. Gat and J. E. Avron, New J. Phys., 2007, 9, 145 CrossRef.
-
S. Kim and S. J. Karrila, Microhydrodynamics: Principles and Selected Applications, Butterworth-Heinemann, 2013 Search PubMed.
- A. J. T. M. Mathijssen, D. O. Pushkin and J. M. Yeomans, J. Fluid Mech., 2015, 773, 498–519 CrossRef CAS.
- O. S. Pak and E. Lauga, J. Eng. Math., 2014, 88, 1–28 CrossRef.
- E. Allahyarov and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 036702 CrossRef CAS PubMed.
- H. Noguchi, N. Kikuchi and G. Gompper, EPL, 2007, 78, 10005 CrossRef.
- H. Noguchi and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 016706 CrossRef PubMed.
- M. Theers and R. G. Winkler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 033309 CrossRef PubMed.
- T. Ihle and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 020201 CrossRef CAS PubMed.
- T. Ihle and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 066705 CrossRef CAS PubMed.
- C. C. Huang, A. Chatterji, G. Sutmann, G. Gompper and R. G. Winkler, J. Comput. Phys., 2010, 229, 168–177 CrossRef CAS.
- C.-C. Huang, A. Varghese, G. Gompper and R. G. Winkler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 013310 CrossRef PubMed.
- E. Westphal, S. P. Singh, C. C. Huang, G. Gompper and R. G. Winkler, Comput. Phys. Commun., 2014, 185, 495–503 CrossRef CAS.
-
M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, Oxford, 1987 Search PubMed.
- J. T. Padding, A. Wysocki, H. Löwen and A. A. Louis, J. Phys.: Condens. Matter, 2005, 17, S3393 CrossRef CAS.
- M. T. Downton and H. Stark, J. Phys.: Condens. Matter, 2009, 21, 204101 CrossRef PubMed.
- A. Lamura, G. Gompper, T. Ihle and D. M. Kroll, EPL, 2001, 56, 319 CrossRef CAS.
- I. P. Omelyan, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 1169–1172 CrossRef CAS.
- L. D. Favro, Phys. Rev., 1960, 119, 53–62 CrossRef.
-
A. J. T. M. Mathijssen, A. Doostmohammadi, J. M. Yeomans and T. N. Shendruk, 2015, arXiv:1511.01859 [cond-mat, physics:physics].
- K. Drescher, J. Dunkel, L. H. Cisneros, S. Ganguly and R. E. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2011, 10940, 108 Search PubMed.
- J. d. Graaf, A. J. T. M. Mathijssen, M. Fabritius, H. Menke, C. Holm and T. N. Shendruk, Soft Matter, 2016, 12, 4704–4708 RSC.
- I. O. Götze and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041921 CrossRef PubMed.
- T. Ishikawa, M. P. Simmonds and T. J. Pedley, J. Fluid Mech., 2006, 568, 119–160 CrossRef.
-
B. U. Felderhof, 2016, arXiv:1603.08574 [physics].
-
Z. X. Wang and D. R. Guo, Special Functions, World Scientific, 1989 Search PubMed.
- L. Paramonov and S. N. Yaliraki, J. Chem. Phys., 2005, 123, 194111 CrossRef PubMed.
-
W. H. Press, Numerical Recipes 3rd Edition: The Art of Scientific Computing, Cambridge University Press, 2007 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm01424k |
| ‡ Note that eqn (54) of ref. 94 contains a typographical error. The factor 24 needs to be replaced by 12. |
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
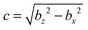 , which yields the eccentricity e = c/bz. Furthermore, we define a swimmer diameter as σ = 2bz. In terms of prolate (bz > bx) spheroidal coordinates (ζ, τ, φ), the Cartesian coordinates are given by
, which yields the eccentricity e = c/bz. Furthermore, we define a swimmer diameter as σ = 2bz. In terms of prolate (bz > bx) spheroidal coordinates (ζ, τ, φ), the Cartesian coordinates are given by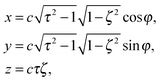
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, sin
φ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, cos
φ, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)T
θ)T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. In this limit, the unit vectors turn into eτ → er and eζ → −eθ (cf.Fig. 2). The Lamé metric coefficients for prolate spheroidal coordinates are
θ. In this limit, the unit vectors turn into eτ → er and eζ → −eθ (cf.Fig. 2). The Lamé metric coefficients for prolate spheroidal coordinates are 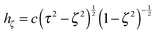 ,
, 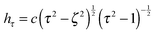 , and
, and 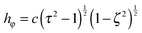 .
.
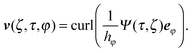
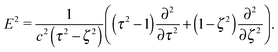
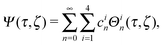
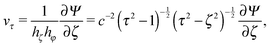
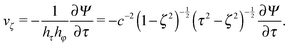
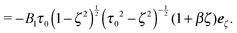
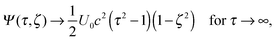
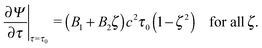
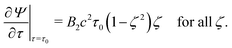
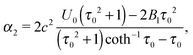
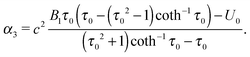
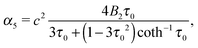
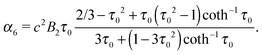
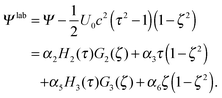
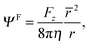
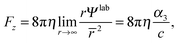
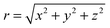 and
and 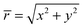 . As expected, Ψ2 does not contribute to the force, since it assumes a constant value at infinity. Since a swimmer must be force free, Fz = 0, which implies α3 = 0. Then, eqn (22) yields the swimming velocity of the squirmer (τ0 = 1/e)
. As expected, Ψ2 does not contribute to the force, since it assumes a constant value at infinity. Since a swimmer must be force free, Fz = 0, which implies α3 = 0. Then, eqn (22) yields the swimming velocity of the squirmer (τ0 = 1/e)
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (r−5),
(r−5),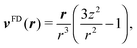
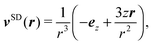
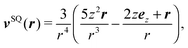
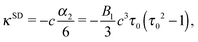
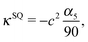
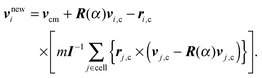
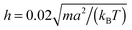 , which yields a fluid viscosity of
, which yields a fluid viscosity of 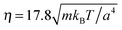 .
.![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) z,
z, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) x,
x, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) z/
z/![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) x = bz/bx and ri(t + h/2) on its surface. The particle is then translated along the normal vector of the virtual spheroid until it is on the real spheroid's surface. Alternatively, the difference vector ri(t + h/2) − C(t + h/2) can be scaled such that the particle position lies on the spheroid' surface. We tried both approaches and found no significant difference. Once the MPC particle at time t + h/2 is located on the spheroid's surface, the momentum transfer due to a bounce-back collision
x = bz/bx and ri(t + h/2) on its surface. The particle is then translated along the normal vector of the virtual spheroid until it is on the real spheroid's surface. Alternatively, the difference vector ri(t + h/2) − C(t + h/2) can be scaled such that the particle position lies on the spheroid' surface. We tried both approaches and found no significant difference. Once the MPC particle at time t + h/2 is located on the spheroid's surface, the momentum transfer due to a bounce-back collision
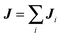 is total momentum transfer by the MPC fluid and
is total momentum transfer by the MPC fluid and 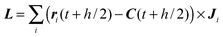 is the respective angular momentum transfer.
is the respective angular momentum transfer.
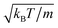 . The squirming velocity usq,i is determined by eqn (11), with the ghost particle position projected onto the spheroid's surface (cf. Section 4.1). As a result of MPC collisions, a spheroid's linear and angular momenta change by Jgi = m(
. The squirming velocity usq,i is determined by eqn (11), with the ghost particle position projected onto the spheroid's surface (cf. Section 4.1). As a result of MPC collisions, a spheroid's linear and angular momenta change by Jgi = m(![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) gi − vgi) and Lgi = (rgi − C) × Jgi, where
gi − vgi) and Lgi = (rgi − C) × Jgi, where ![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) gi and vgi are the ghost particle's velocity after and before the MPC collision. Hence, the spheroid velocity and angular velocity become
gi and vgi are the ghost particle's velocity after and before the MPC collision. Hence, the spheroid velocity and angular velocity become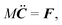
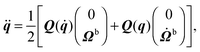
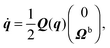
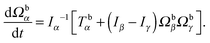
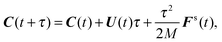
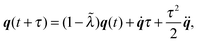
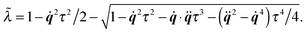
![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) is introduced to guarantee q2 = 1.
is introduced to guarantee q2 = 1.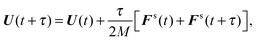
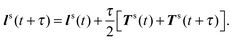
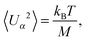
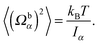
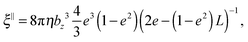
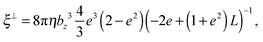
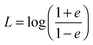


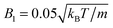 and B2 = 0. The solid line shows the theoretical prediction of eqn (3). Black dots are simulation results. The eccentricity was varied by changing bz and keeping bx = 3a constant. For the red triangle, we simulated a larger spheroid with bx = 6a, which shows a better agreement with theory.
and B2 = 0. The solid line shows the theoretical prediction of eqn (3). Black dots are simulation results. The eccentricity was varied by changing bz and keeping bx = 3a constant. For the red triangle, we simulated a larger spheroid with bx = 6a, which shows a better agreement with theory.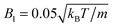 , which we attribute to a non-vanishing Reynolds number (Re ≈ 0.1) in the simulation. In Fig. 6(c) and (f), we observe lines of high relative errors (yellow in the color code). They appear because theory predicts v
, which we attribute to a non-vanishing Reynolds number (Re ≈ 0.1) in the simulation. In Fig. 6(c) and (f), we observe lines of high relative errors (yellow in the color code). They appear because theory predicts v![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) = 0 or vz = 0 for these lines, which is difficult to achieve in simulations. Hence, the overall agreement between simulations and theory is very satisfactory, and the implementation is very valuable for the simulation of squirmer–squirmer and squirmer–wall interactions, where the details of the flow field matter. For a benchmark of the code on a current GPU see Appendix D.
= 0 or vz = 0 for these lines, which is difficult to achieve in simulations. Hence, the overall agreement between simulations and theory is very satisfactory, and the implementation is very valuable for the simulation of squirmer–squirmer and squirmer–wall interactions, where the details of the flow field matter. For a benchmark of the code on a current GPU see Appendix D.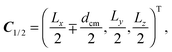
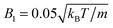 and the force dipole mode β ∈ {−4,0,4}. We choose dcm such that the squirmers are well separated and vary θ0. The squirmers major and minor axes are bx = 3a and bz = 6a, respectively, and the simulation box size is Lx = Lz = 15bz, and Ly = 7a. Note that Ly ≳ bx which keeps the swimming orientation essentially in the x–z plane.
and the force dipole mode β ∈ {−4,0,4}. We choose dcm such that the squirmers are well separated and vary θ0. The squirmers major and minor axes are bx = 3a and bz = 6a, respectively, and the simulation box size is Lx = Lz = 15bz, and Ly = 7a. Note that Ly ≳ bx which keeps the swimming orientation essentially in the x–z plane.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉 are shown in Fig. 7 for pushers, pullers, and neutral swimmers with an initial angle θ0 = 3π/8. Due to the setup, the squirmers initially approach each other and collide at tU0/σ ≈ 0.5. The (persistence) Péclet number Pe = U0/(2D⊥Rσ) ≈ 60 is sufficiently high, such that the squirmer orientation has hardly changed before collision. When the neutral swimmers collide, they initially align parallel (cos
θ〉 are shown in Fig. 7 for pushers, pullers, and neutral swimmers with an initial angle θ0 = 3π/8. Due to the setup, the squirmers initially approach each other and collide at tU0/σ ≈ 0.5. The (persistence) Péclet number Pe = U0/(2D⊥Rσ) ≈ 60 is sufficiently high, such that the squirmer orientation has hardly changed before collision. When the neutral swimmers collide, they initially align parallel (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ ≈ 1 at tU0/σ ≈ 1 in Fig. 7), but their trajectories start to diverge immediately thereafter. Pushers remain parallel for an extended time window, which is expected as pushers are known to attract each other,37 but at tU0/σ ≈ 3 (cf.Fig. 7) their trajectories diverge as well. This is probably due to noise, since we observe several realizations where pushers remain parallel. Interestingly, pullers, which are known to repel each other when swimming in parallel,37 swim cooperatively and reach a stable orientation with 〈cos(θ)〉 ≈ 0.77 shortly after they collided (at tU0/σ ≈ 1). Thereby, their cooperative swimming velocity is about 0.8U0. The flow field of this stable state, determined by MPC simulations, is shown in Fig. 8. Note that the velocity field in the swimming plane is left-right symmetric, and that there is a stagnation point in the center behind the swimmers. Fig. 8 reveals that this point actually corresponds to a line normal to the walls. In ref. 87, it was shown that the flow field of a force dipole in a narrow slit exhibits a recirculating pattern with loops in a plane parallel to the walls88 and a parabolic flow profile perpendicular to them. Both features can be observed in Fig. 8. Fig. 9 shows that the fixed point of cooperatively swimming pullers is reached for nearly all simulated initial conditions θ0 ∈ (0, π/2). Only pullers that are nearly parallel initially (θ0 = π/8, cos
θ ≈ 1 at tU0/σ ≈ 1 in Fig. 7), but their trajectories start to diverge immediately thereafter. Pushers remain parallel for an extended time window, which is expected as pushers are known to attract each other,37 but at tU0/σ ≈ 3 (cf.Fig. 7) their trajectories diverge as well. This is probably due to noise, since we observe several realizations where pushers remain parallel. Interestingly, pullers, which are known to repel each other when swimming in parallel,37 swim cooperatively and reach a stable orientation with 〈cos(θ)〉 ≈ 0.77 shortly after they collided (at tU0/σ ≈ 1). Thereby, their cooperative swimming velocity is about 0.8U0. The flow field of this stable state, determined by MPC simulations, is shown in Fig. 8. Note that the velocity field in the swimming plane is left-right symmetric, and that there is a stagnation point in the center behind the swimmers. Fig. 8 reveals that this point actually corresponds to a line normal to the walls. In ref. 87, it was shown that the flow field of a force dipole in a narrow slit exhibits a recirculating pattern with loops in a plane parallel to the walls88 and a parabolic flow profile perpendicular to them. Both features can be observed in Fig. 8. Fig. 9 shows that the fixed point of cooperatively swimming pullers is reached for nearly all simulated initial conditions θ0 ∈ (0, π/2). Only pullers that are nearly parallel initially (θ0 = π/8, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ0 ≈ 0.92 in Fig. 9), repel each other such that they will not reach the fixed point. For Péclet numbers Pe < 60, the fixed point remains at 〈cos(θ)〉 ≈ 0.77. However, it becomes more likely for the swimmers to escape (or never reach) the fixed point.
θ0 ≈ 0.92 in Fig. 9), repel each other such that they will not reach the fixed point. For Péclet numbers Pe < 60, the fixed point remains at 〈cos(θ)〉 ≈ 0.77. However, it becomes more likely for the swimmers to escape (or never reach) the fixed point.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉 of two pullers with β = 4, bz/bx = 2 in a slit of height Ly = 7a, and various initial angles θ0 ∈ (0,π/2) (see ESI,† Movie beta 4).
θ〉 of two pullers with β = 4, bz/bx = 2 in a slit of height Ly = 7a, and various initial angles θ0 ∈ (0,π/2) (see ESI,† Movie beta 4).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ decreases, i.e., the squirmers form a larger angle. With increasing wall separation, the fixed-point value of cos
θ decreases, i.e., the squirmers form a larger angle. With increasing wall separation, the fixed-point value of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ decreases, i.e., the angle between the swimmers increases. For Ly/bz ≳ 11/6, the mean distance between swimmers increases rapidly after collision (see Fig. 10). An increase of the aspect ratio bz/bx from 2 to 3 and 4 increases the fixed-point value of 〈cos
θ decreases, i.e., the angle between the swimmers increases. For Ly/bz ≳ 11/6, the mean distance between swimmers increases rapidly after collision (see Fig. 10). An increase of the aspect ratio bz/bx from 2 to 3 and 4 increases the fixed-point value of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉 from 0.77 to 0.84 and 0.88. The more elongated shape leads to a more parallel alignment of the squirmers. For bz/bx ≥ 2, the minimal value of β required to achieve cooperative motion depends weakly on the aspect ratio. In particular, for bz/bx = 2, 3, and 4, we find the minimal value β ≈ 3.5.
θ〉 from 0.77 to 0.84 and 0.88. The more elongated shape leads to a more parallel alignment of the squirmers. For bz/bx ≥ 2, the minimal value of β required to achieve cooperative motion depends weakly on the aspect ratio. In particular, for bz/bx = 2, 3, and 4, we find the minimal value β ≈ 3.5.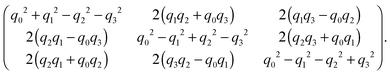
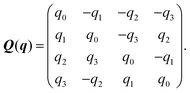
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) the Gegenbauer functions of the first and second kind Gn and Hn, are defined in terms of the Legendre functions of the first and second kind Pn and Qn as67,93
the Gegenbauer functions of the first and second kind Gn and Hn, are defined in terms of the Legendre functions of the first and second kind Pn and Qn as67,93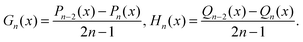
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif)
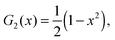
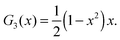
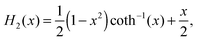
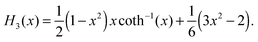
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (x) ≡ (x − C)TA(x − C),
(x) ≡ (x − C)TA(x − C),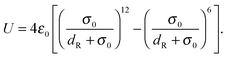
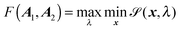
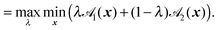
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (x,λ) = 0, and hence,
(x,λ) = 0, and hence,![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (x(λ),λ) can be found by the root finding problem
(x(λ),λ) can be found by the root finding problem![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 1(x(λ)) −
1(x(λ)) − ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 2(x(λ)) = 0.
2(x(λ)) = 0.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 94
94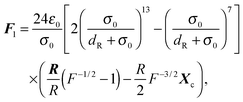
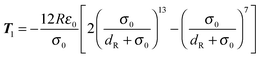
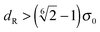 , which implies that F1 and T1 are zero for this range of dR values. Note that an upper bound to dR is R − 2bz, which means that two spheroids will not interact if
, which implies that F1 and T1 are zero for this range of dR values. Note that an upper bound to dR is R − 2bz, which means that two spheroids will not interact if 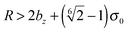 . This inequality is checked before a numerical calculation of dR is employed.
. This inequality is checked before a numerical calculation of dR is employed.
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (x) = 1. Using the method of Lagrange multipliers, we have to minimize Λ(x,λ) = h(x) + λ(
(x) = 1. Using the method of Lagrange multipliers, we have to minimize Λ(x,λ) = h(x) + λ(![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (x) − 1). The necessary condition for a minimum ∂Λ/∂x = 0 yields
(x) − 1). The necessary condition for a minimum ∂Λ/∂x = 0 yields![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (x) = ey + 2λA(x − C) = 0,
(x) = ey + 2λA(x − C) = 0,![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (x) = 1 yields
(x) = 1 yields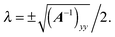
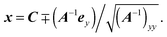
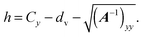
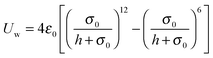
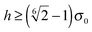 . We can derive the force Fα = −∂Uw/∂Cα and torque Tα = −∂Uw/∂ψα acting on the spheroid analytically. For the force, we find
. We can derive the force Fα = −∂Uw/∂Cα and torque Tα = −∂Uw/∂ψα acting on the spheroid analytically. For the force, we find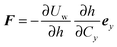
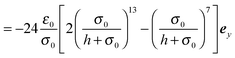
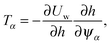
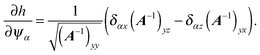
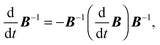
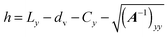 and need to change the sign of the force.
and need to change the sign of the force.