 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effects of confinement on pattern formation in two dimensional systems with competing interactions†
N. G.
Almarza‡
a,
J.
Pȩkalski
b and
A.
Ciach
b
aInstituto de Químca Física Rocasolano, CSIC, Serrano 119, E-28006 Madrid, Spain. E-mail: noe@ifqr.csic.es
bInstitute of Physical Chemistry, Polish Academy of Sciences, 01-224 Warszawa, Poland. E-mail: jpekalski@ichf.edu.pl; aciach@ichf.edu.pl
First published on 4th August 2016
Abstract
Template-assisted pattern formation in monolayers of particles with competing short-range attraction and long-range repulsion interactions (SALR) is studied by Monte Carlo simulations in a simple generic model [N. G. Almarza et al., J. Chem. Phys., 2014, 140, 164708]. We focus on densities corresponding to formation of parallel stripes of particles and on monolayers laterally confined between straight parallel walls. We analyze both the morphology of the developed structures and the thermodynamic functions for broad ranges of temperature T and the separation L2 between the walls. At low temperature stripes parallel to the boundaries appear, with some corrugation when the distance between the walls does not match the bulk periodicity of the striped structure. The stripes integrity, however, is rarely broken for any L2. This structural order is lost at T = TK(L2) depending on L2 according to a Kelvin-like equation. Above the Kelvin temperature TK(L2) many topological defects such as breaking or branching of the stripes appear, but a certain anisotropy in the orientation of the stripes persists. Finally, at high temperature and away from the walls, the system behaves as an isotropic fluid of elongated clusters of various lengths and with various numbers of branches. For L2 optimal for the stripe pattern the heat capacity as a function of temperature takes the maximum at T = TK(L2).
1 Introduction
Competing interactions, in particular short-range attraction and long-range repulsion (SALR), are present in many biological and soft matter systems1–4 as well as in magnetic films with competing ferromagnetic and dipolar forces.5,6 The repulsion is often of electrostatic origin, and the attraction between the particles comes from the van der Waals forces, or it is induced by the solvent. For example, the solvophobic attraction is present between globular proteins in water,2,7 or the depletion attraction is present between colloid particles when the solvent contains nonadsorbing polymer with small radius of gyration.2,4Despite the different origins of the SALR potential in the above examples, the structural and thermodynamic properties of the systems with competing interactions are very similar.5,8–18 Moreover, a self-assembly into patterns that are very similar to those observed in amphiphilic systems when the range of attraction is sufficiently large and the repulsion is sufficiently strong takes place.8–10 At sufficiently low temperature the following sequence of ordered phases was predicted for increasing volume fraction of particles by theory and simulation:10,18–23 spherical clusters, cylindrical clusters, gyroid network of particles, layers of particles, gyroid network of voids, cylindrical voids and finally spherical voids. Heating of the system first destroys the gyroid phase. Further increase of temperature leads to disordered distribution of the clusters or layers. At low volume fractions in the disordered cluster phase spherical clusters are present. Upon increase of the volume fraction the clusters become elongated and finally percolate.4,20 Much higher temperature is necessary for disassembly of the clusters. Structure factor, equation of state, specific heat etc. in the disordered cluster phase are significantly different than in the homogeneous fluid.24–27
In this work we focus on two dimensional (2D) patterns. Such patterns are formed in thin magnetic films,5,6 in thin layers of block-copolymers,28–30 by particles adsorbed at solid surfaces or at liquid interfaces,1,31,32 on elastic membranes or embedded in lipid bilayers.3,33 For increasing chemical potential of the particles, hexagonally ordered clusters, next stripes and finally hexagonally ordered voids occur for various versions of the SALR potential.11–17 The 2D self-assembly in continuous SALR models was studied by the density functional theory15 and by Monte Carlo (MC)12–14,34 methods. Recently lattice SALR models (LSALR) were introduced and studied in the mean-field approximation (MF) and by MC simulations.11,16,17,25 Here we investigate the effects of confinement between two parallel boundaries on the degree of order in monolayers of particles interacting through the SALR potential, using the lattice model.11,16
The effects of confinement on surfactant solutions were investigated experimentally and theoretically already long ago.35,36 Recently the attention focuses mainly on confined block-copolymers.37–40 The effects of confinement depend strongly on the surfactant concentration in the amphiphilic systems, or on the volume fraction of particles in the SALR systems. The confinement effects for different densities in 2D continuous SALR models were studied in ref. 15 and 34. In this work we limit ourselves to the lamellar or stripe phase. In the surfactant systems the parallel orientation of the lamellas was stable for any wall-separation for large-period phases.35,36 For phases with intermediate periods confined between weakly selective boundaries, parallel or perpendicular orientation of lamellas was found when the wall separation and the period of the bulk structure were or were not commensurate, respectively. In the case of thin lamellas and selective boundaries a zig-zag structure of layers was obtained in the case of the incommensurability.36
Slit-like confinement in the case of the 2D SALR system has been studied for rather thick stripes.14,15 Parallel orientation of layers was observed when the separation between the boundaries was commensurate with the bulk periodic structure. For incommensurate slit-widths, layers perpendicular to the boundaries for the whole slit or its central part were formed.14,15 This similarity between confined amphiphilic and SALR systems could be expected based on the similarity between properties of these systems in the bulk. By analogy, because in the amphiphilic systems thick and thin lamellas respond to confinement in a significantly different way, we may expect that the effects of confinement in the SALR system self-assembling into thick and thin stripes are different. However, in the case of thin stripes the effect of confinement has not been investigated yet.
The thickness of the stripes depends on the range of the attractive and the repulsive part of the potential. To study the effects of confinement in the case of thin stripes, we shall consider the 2D LSALR model introduced and studied in the bulk in ref. 11 and 16, since in this model thin stripes are formed. In ref. 11 a rather detailed phase diagram was obtained by MC simulations. It was found that at low temperature, T, the lamellar (L) phase with both orientational and translational order of stripes is stable for the reduced density ρ ∼ 1/2. This phase melts in two steps when heated. First the translational order is lost. The phase possessing only the orientational order was named “molten lamella” (ML). In the ML the translational order is lost due to topological defects, such as fracture, branching or junction of the stripes.29,30 The system is not isotropic, however. On the triangular lattice studied in ref. 11 the total length of stripe segments along the main lattice directions is not the same, i.e. there exists preferred orientation of the stripes. The unit vectors normal to the stripe segments are analogous to a discretized version of the director field in liquid crystals, therefore the ML phase is analogous to the nematic phase. Further heating leads to the transition from the ML to the isotropic fluid (F), when the separation between the topological defects becomes comparable with the period of the local lamellar order. In the F phase the total length of the stripe segments parallel to each principal lattice direction is the same. The transition between the ML and F phases was found to be continuous for a density interval centered at the reduced density ρ = 1/2 that is optimal for the lamellar structure.11 The line of continuous transitions terminates at two tricritical points, one with the density ρtcp ≈ 0.4, and the other one with ρtcp ≈ 0.6, where the transition becomes first-order.11 The ML phase is analogous to the nematic phase of stripes found in magnetic films.5 Recent studies of the 2D stripe-forming systems41 indicate that the transition between the anisotropic and isotropic phases can be of the second order for Coulomb-like repulsion, or of the Kosterlitz–Thouless type for dipolar interactions. Thus, the order of the transition depends on the range of the repulsion, and in general it is a very subtle issue. In this work we shall limit ourselves to ρ ∼ 1/2 in a system confined between two parallel boundaries, where no true phase transitions occur. The confined system is in contact with the bulk reservoir at fixed T and chemical potential.
Self-assembly into parallel stripes of particles might be a first step in the formation of ordered patterns of practical importance. From the point of view of some applications, it would be advantageous to have thin parallel self-assembled stripes without topological defects. In some other cases interconnected stripes forming porous structure would be preferable. The number of topological defects in the ML phase is significantly larger than in the L phase. Motivated by the phenomenon of capillary condensation in simple fluids, capillary lamellarization in surfactant solutions and capillary smectization in liquid crystals,42–44 we shall study if the ML structure can be transformed into the L structure by decreasing the separation between the boundaries at fixed temperature and chemical potential. We shall also investigate how the structural transformations are reflected in properties of thermodynamic functions such as the heat capacity and the solvation pressure.
In the next section the model and the simulation method are described, and the thermodynamic and structural functions are introduced. In Section 3 we present our results. The ground state (T = 0) is discussed in Section 3.1. Results for the heat capacity and the solvation pressure are described in Section 3.2. In Section 3.3 we discuss the structure. Typical configurations, and results for the density profiles across the slit and for the correlation function along the slit are presented for several values of T and for wall–wall separations L2 commensurate and incommensurate with the period of the bulk structure. Finally, the orientational order parameter as a function of T is obtained for a few values of L2. Section 4 contains our conclusions.
2 Model and simulation procedures
We consider a surface in equilibrium with a bulk reservoir and assume that the particles can occupy the sites of a triangular lattice with a lattice constant, σ, comparable with the diameter of the adsorbed particles. The lattice sites are denoted by x = x1e1 + x2e2 ≡ (x1,x2), where e1, e2 and e3 = e2 − e1 are the unit lattice vectors on the triangular lattice, i.e. |e1| = |e2| = |e1 − e2| = 1 (in σ-units), and xi are integer. We consider the triangular lattice, because it allows for close packing of the particles.We introduce the slit-like confinement by assuming that the particles are located between two lines parallel to e1, and separated by L2 layers of sites along the direction e2. Thus, 1 ≤ x2 ≤ L2. In the direction e1 we assume periodic boundary conditions (PBC). In simulations we assume 1 ≤ x1 ≤ L1, where L1 ≫ L2, and x1 = L1 + 1 is identified with x1 = 1. The system under consideration is shown in Fig. 1.
The interaction of the particles with the binding sites on a solid substrate, or with the lipids in the membrane plays analogous role as the chemical potential of the particles, and we introduce μ that is the sum of the binding energy and the chemical potential. We assume that the nearest-neighbors attract each other (SA), the interaction changes sign for the next-nearest neighbors, becomes repulsive for the third neighbors (LR), and vanishes for larger separations. The nearest-neighbor attraction is the standard assumption in the lattice-gas models. In the case of charged particles in electrolytes the assumed range of repulsion should be of order of the Debye screening length, 2.5σ ∼ λD. Since in various solvents with weak ionic strength λD ∼ 1–100 nm, the model is suitable for charged molecules, nanoparticles or globular proteins. The interaction between the occupied sites x and x + Δx of the form described above is given by
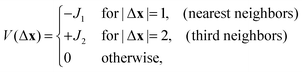 | (1) |
The thermodynamic Hamiltonian has the form
 | (2) |
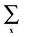 denotes the summation over all lattice sites, the microscopic density at the site x is
denotes the summation over all lattice sites, the microscopic density at the site x is ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (x) = 1(0) when the site x is (is not) occupied, and h denotes the interaction energy between the particle in the boundary layer and the confining wall.
(x) = 1(0) when the site x is (is not) occupied, and h denotes the interaction energy between the particle in the boundary layer and the confining wall.
The microscopic state of the whole system is specified by indicating which sites are occupied, and is denoted by {![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (x)}. The probability of a particular microscopic state has the form
(x)}. The probability of a particular microscopic state has the form
p[{![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (x)}] = Ξ−1 (x)}] = Ξ−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−βH[{ exp(−βH[{![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (x)}]), (x)}]), | (3) |
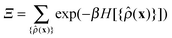 | (4) |
Ω = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ξ. Ξ. | (5) |
2.1 The ground state
In the previous work16 we determined the ground state (GS) of the model and the MF phase diagram. Later we computed11 the phase diagram by means of MC simulations for strong repulsion, J = 3. In this work we limit ourselves to J = 3, and to the chemical potential μ* = 6, for which the L phase is stable.11,16 In the most of the cases we shall assume h* = −1, which is a moderate wall–fluid interaction.The grand potential for T = 0 reduces to the minimum of the grand canonical Hamiltonian per site ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0 ≡ H[{
0 ≡ H[{![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (x)}]/(L1L2). The ground states for μ* = 6 and different wall–wall separations L2 and values of h* were computed as follows: for fixed values of μ*, L2, and h*, we consider different values of the lateral length L1, and determine by means of parallel tempering MC simulations their corresponding minima,
(x)}]/(L1L2). The ground states for μ* = 6 and different wall–wall separations L2 and values of h* were computed as follows: for fixed values of μ*, L2, and h*, we consider different values of the lateral length L1, and determine by means of parallel tempering MC simulations their corresponding minima, ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0(L1). The GS configuration and the GS energy, at the given conditions (μ*,L2,h*), are taken as those corresponding to the value L1 which minimizes
0(L1). The GS configuration and the GS energy, at the given conditions (μ*,L2,h*), are taken as those corresponding to the value L1 which minimizes ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 0.
0.
2.2 Thermodynamic properties
 | (6) |
| ωex ≡ (Ω − Ωbulk)/L1 = γ1 + γ2 + Ψ(L2), | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ξbulk is the grand potential of the bulk system with the same volume, i.e. with PBC in both directions, γi is the wall–fluid surface tensions at the i-th wall, and Ψ(L2) is the interaction between the confining walls per unit length induced by the confined fluid (solvation pressure). In order to compute Ψ(L2) we have applied the MC thermodynamic integration procedure for fixed chemical potential, which was previously used for the bulk system.11 The grand potential per lattice site was computed using the following relation
Ξbulk is the grand potential of the bulk system with the same volume, i.e. with PBC in both directions, γi is the wall–fluid surface tensions at the i-th wall, and Ψ(L2) is the interaction between the confining walls per unit length induced by the confined fluid (solvation pressure). In order to compute Ψ(L2) we have applied the MC thermodynamic integration procedure for fixed chemical potential, which was previously used for the bulk system.11 The grand potential per lattice site was computed using the following relation | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 results from the assumption that at infinite temperature our model acts like an ideal lattice gas. To obtain Ψ(L2) out of ωex = (Ω − Ωbulk)/L1, we note that these two quantities at fixed temperature differ only by a constant (see (7)). Since
2 results from the assumption that at infinite temperature our model acts like an ideal lattice gas. To obtain Ψ(L2) out of ωex = (Ω − Ωbulk)/L1, we note that these two quantities at fixed temperature differ only by a constant (see (7)). Since  , we have estimated the constant by the value of ωex for which the curve reaches a plateau.
, we have estimated the constant by the value of ωex for which the curve reaches a plateau.
2.3 Structural description
 | (9) |
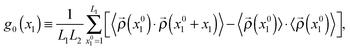 | (10) |
![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) (x01) ≡ (
(x01) ≡ (![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) (x01,1),…,
(x01,1),…,![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (x01,L2)), is a vector containing the densities of the sites belonging to a compact line of sites in the direction e2 (see Fig. 2), · is the standard scalar product, and 〈⋯〉 indicates an average over different system configurations. From g0(x1) we can define a normalized correlation function:
(x01,L2)), is a vector containing the densities of the sites belonging to a compact line of sites in the direction e2 (see Fig. 2), · is the standard scalar product, and 〈⋯〉 indicates an average over different system configurations. From g0(x1) we can define a normalized correlation function:| g(x1) ≡ g0(x1)/g0(0). | (11) |
 | (12) |
3 Results
3.1 The ground state
Long-range order of the system for given μ and L2 is found for T = 0. Before studying finite temperatures with thermally induced defects, we present how the bulk GS is modified in the slit confinement. Let us first briefly remind the GS in the bulk. For strong repulsion the energy in the bulk assumes a minimum when neither intra-cluster nor inter-cluster repulsion is present, and as many nearest-neighbors as possible are occupied. The energy competes with −μN, where N is the number of occupied sites. In this model the Hamiltonian takes the same value for straight stripes, and for zig-zag stripes that in one of the main lattice directions have the thickness 2.11,16 The segments of the zig-zag stripes can be parallel to two of the three main lattice directions. Thus, in the bulk the GS is strongly degenerated in the stability region of the L phase.If the confining surfaces strongly attract particles, then energetically favorable configurations have double layers (stripes) of particles adsorbed onto the walls. For fixed J the configuration of the particles between the adsorbed stripes will depend upon the distance between the confining walls, L2, and on the wall–fluid interaction h*.
If L2 = 4n + 2, where n is a positive integer, then the distance is commensurate with the period of the bulk structure and the straight lamella structure has the lowest energy. Note that in the case of the straight lamella structure no degeneracy of the GS is present. For L2 incommensurate with the period of the bulk structure geometrical defects appear in the stripes adsorbed at the walls (see Fig. 3 for h* = −1). The GS depends on both L2 and h*, and there are many GS configurations in the (L2,h*) plane. To fix attention we assume h* = −1, except from a few cases illustrating the effect of h*. We call the defects resulting from the incommensurability between the lamellar period and L2 at T = 0 “geometrical”, because the continuity of the stripe is not broken. The stripe next to the wall becomes locally thicker or thinner, or undulates to bypass a void at the wall. The first case can be seen for example in the first column in Fig. 3. The second and the third cases are shown in the two top panels in the third and the central column in Fig. 3, respectively. In order to avoid excess repulsion, the nearest stripe (second from the wall) has to bypass the defect. The turns of the nearest stripe entail turns of the other stripes inside the slit in such a way that it is energetically favorable to build a defect at the opposite wall. Such construction ensures that the distance between every two defects is the same, hence three consecutive defects in the e1 direction form an equilateral triangle (Fig. 4).
We found that for slit widths L2 > 13 the distance L2 determines the shape and the position of the defects, hence having L2 one can also tell the size of the unit cell in the e1 direction, L1, which is given by the following formula
We cannot tell, however, if for large wall–wall separations (e.g. L2 > 30) L1 is still determined uniquely by L2.
In contrast to the bulk, the segments of the lamella can be parallel not only to the two main lattice directions, but to all the three directions. Moreover, the presence of the confinement removes the degeneracy and the residual entropy of the GS.
In order to illustrate the effect of the wall–fluid interaction, we present in Fig. 5 the GS for L2 = 16 and the neutral, h* = 0, and strongly repulsive, h* = 3, boundaries. Note that the period in direction e1 is L1 = 12 for h* = −1 (see Fig. 3), and L1 = 16 for h* = 0 (see Fig. 5), but the general structure of the system is quite similar in the case of the attractive and neutral walls. In the case of strongly repulsive walls the particles are expelled from the bottom and top rows of the slit, and in the GS configuration four parallel straight stripes that do not interact with the walls occur (right panel of Fig. 5). Hence having the wall separation L2 = 4n one can remove the defects by changing the particle–wall interaction from attractive to strongly repulsive.
 | ||
| Fig. 5 Ground state configuration for L2 = 16 for different interactions with the walls. Left panel: h* = 0, right panel: h* = 3. | ||
We conclude that in the case of thin stripes the incommensurability between the slit width and the lamellar period leads to zig-zag or undulating stripes, and to a periodic order in the longitudinal direction. Very similar behaviour was found previously for thin lamellas in water–surfactant mixtures.36 The detailed shape of the undulating stripes and the geometrical defects at the near-surface layers both depend on the wall–wall separation, on the wall–fluid interactions and on the interparticle potential. For strong interparticle repulsion the continuity of the stripes is not broken at T = 0, i.e. the topological properties of the stripes do not change, when the wall–wall separation increases a little. With further increase of L2 a new stripe is introduced into the system.
3.2 Thermodynamics
 | ||
| Fig. 6 Reduced heat capacity, cμ*(T) ≡ cμ(T)/kB for μ* = 6 and h* = −1, and for different pore widths. cμ(T) exhibits two maxima for L2 > 30, and an inflection point for L2 = 30. | ||
We do not expect true thermodynamic phase transitions in slit systems at T* > 0, given the fact that the system is virtually macroscopic in only one direction of the space. However, in the 1D LSALR model pseudo-phase transitions were observed,25 and we can expect such pseudo-phase transitions, or crossovers between structures with different degree of order, in the 2D slit.
In the bulk, the continuous F–ML transition was found11 for μ* = 6 at T* ≃ 0.75 that is close to the location of the high-T maximum of cμ. On the other hand, MC simulations11 for L1 = L2 = 120 show that in the bulk the ML–L transition occurs at Tbulk* ≃ 0.25 that is much lower than the temperature at which cμ takes the low-T maximum for L2 ≤ 38. Note, however that in simple fluids the phenomenon of capillary condensation leads to the shift of the temperature at which the condensation occurs in thin capillaries.42 The thinner the capillary, the higher the temperature of the capillary condensation. The phenomenon is described by the Kelvin equation TK*(L2) = Tbulk* + a/L2, where Tbulk* is the transition temperature in the bulk, and a is associated with the difference in densities and entropy per particle in the coexisting phases.42,45 Similar behavior, i.e. capillary lamellarization or capillary smectization was observed in surfactant solutions or in liquid crystals.43,44
In order to verify if the low-T* maximum of the specific heat is associated with the capillary lamellarization, we plot in Fig. 7 the temperature Tmax*(L2) corresponding to the maximum of cμ. In addition, we plot the best fit of the data to the equation
| TK*(L2) = Tb* + a/L2. | (13) |
 | ||
| Fig. 7 Structure diagram based on the features of the heat capacity and particle distribution considerations. Symbols represent temperature corresponding to: (i) the low-T global maximum, cmaxμ (bullets), (ii) the high-T maximum or the inflection point of the heat capacity (small symbols connected by the dashed line), (iii) the boundary between the low-T and high-T regions where the structure does and does not dependent on the commensurability between the slit size and the period of the stipe pattern (big triangles). The reduced chemical potential and wall–fluid interaction are μ* = 6 and h* = −1, and the pore width is L2 = 4n + 2 with integer n (see Fig. 6). The solid line is the best fit to the Kelvin-like equation TK*(L2) (see (13)), where the fitting parameters are Tb* = 0.28 and a = 7.422. Note that Tb* is close to Tbulk* ≃ 0.25 associated with the transition between the L and ML phases in the unrestricted monolayer. The shaded region around TK*(L2) corresponds to the width of the peaks of cμ(T*), estimated based on temperatures for which cμ(T*) ≈ (cmaxμ + cpμ)/2, where cpμ is the high-temperature value of the heat capacity (the plateau in Fig. 6). L denotes the periodically ordered structure. ML and F are the anisotropic and isotropic structures without the periodic order respectively. | ||
The Kelvin-like equation was fitted to the maxima of the heat capacity only for L2 commensurate with the periodic structure, because in ref. 43 it was observed that the capillary lamellarization in surfactant mixtures is delayed if the slit width is incommensurate with the periodic structure. By analogy, deviations from (13) for incommensurate L2 are expected in the SALR system. We verified that the geometrical defects present for L2 incommensurate with the period of the striped structure influence the heat capacity too. For this reason we did not consider the values of L2 for which the simple eqn (13) cannot be valid.
 | ||
| Fig. 8 The effective wall–wall interaction potential as a function of the wall–wall separation, Ψ(L2), at temperature T* = 0.5 for L1 = 120, μ* = 6 and attractive walls with h* = −1. | ||
Since in a lattice model Ψ(L2) is meaningful only for integer L2, we did not try to fit Ψ(L2) to a smooth curve. In the 1D case the exact Ψ(L2) exhibits exponentially damped oscillations for large L2, and similar asymptotic behavior, i.e. exponentially damped oscillations for large L2, can be expected in this case. However, in 1D the asymptotic form of Ψ(L2) deviates significantly from the exact solution for relatively large L2, and by analogy we expect that for L2 < 30 no simple analytical formula can describe Ψ(L2) in Fig. 8.
At large separations L2 the interaction between the confining walls follows from the mismatch between L2 and the period of the periodic structure, therefore it should vanish in the absence of the periodic order, i.e. beyond the crossover between the L and ML or F structure. In particular, for T* = 0.5 from Fig. 8 we can estimate this range as ≃40, which is close to L2 ≃ 38 at the boundary of the shaded region in Fig. 7 for this temperature. We conclude that the range of Ψ(L2) increases significantly with decreasing temperature, and its very rough estimate is given by the high-T boundary of the shaded region in Fig. 7.
3.3 The structure
We are interested in the structure in the slit for temperatures below the first and above the second peak of the heat capacity, and between the two peaks. We shall verify if below the first and above the second peak the structure resembles the L and F phases, and if between the peaks the ML-like structure is present, as suggested by the thermodynamic considerations. | ||
| Fig. 10 Representative configurations of the system with attractive walls (h* = −1) and L1 = 120 for L2 = 30 (left column) and L2 = 32 (right column) and several temperatures. From top to bottom T* = 1.00, T* = 0.806, T* = 0.625, T* = 0.556, and T* = 0.403. The bottom panels correspond to temperature below the global maximum of the heat capacity, i.e. below T* = TK*(30) (see (13)). T* = 0.556 is slightly above TK*(30). Temperature at the central panels, T* = 0.625, is close to the minimum of the heat capacity. The two top panels correspond to temperature above the high-T maximum or the inflection point of cμ*, i.e. above the dashed line in Fig. 7. | ||
The above inspection of the representative configurations shows consistency of the thermodynamic and structural properties. Before looking at the structural functions, ρ(x2) and g(x1), let us consider a single line parallel to the boundary. To fix attention let us choose the 9th line from the bottom. At low T* it is completely filled with particles for L2 = 30, and there are alternating occupied and empty segments for L2 = 32, because of the stripe corrugation. The density averaged over the longitudinal direction for x2 = 9 is smaller for L2 = 32 than for L2 = 30. Further away from the boundary this difference in the average density increases. Moreover, for L2 = 32 the alternating occupied and empty segments along the direction e1 lead to an oscillating correlation function. The period of the oscillations at very low T* is determined by L2, as in the GS. For T* ≃ Tmax*(30) ≈ 0.53 the topological defects lead to additional alternating occupied and empty segments in each line parallel to the boundaries for L2 = 32, and to appearance of such segments for L2 = 30. The average length of the occupied and empty segments decreases with increasing temperature, because the number of the topological defects increases. This leads to smaller density averaged over the longitudinal direction in lines that were occupied at low T*, and to a smaller period of oscillations of the correlation function g(x1). The above qualitative observations concerning representative configurations are quantified in the functions representing the average structure in the transverse and in the longitudinal direction, and in the orientational order parameter discussed below.
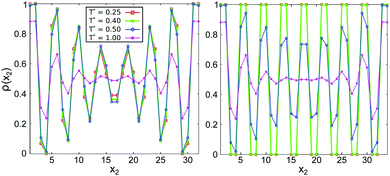 | ||
| Fig. 11 The density profiles in the direction perpendicular to the walls, averaged over the longitudinal direction (see (9)), for several temperatures. Left panel: L2 = 32, right panel: L2 = 34. The color code is the same in both panels. The walls are attractive with h* = −1. | ||
Interestingly, the density profiles averaged over the longitudinal direction resemble strongly the density profiles of the one-dimensional cluster phase.25
We have carried out a Fourier-like analysis of the correlation function g(x1). The Fourier integral applied to the lattice was taken as:
 | (14) |
In Fig. 13 we compare the correlation function g(x1) for L2 = 30 and L2 = 32 for temperatures that correspond to the L, ML and F pseudo-phases (see Fig. 7). As expected, in the L phase g(x1) quickly vanishes for L2 = 30, and for L2 = 32 exhibits damped oscillations with a very large decay length (see Fig. 12 for low T*). When the temperature approaches TK*(L2), damped oscillations are present in both cases, but the decay length and the period are both larger for L2 = 32, indicating that the corrugations induced by the size incommensurability are still important for T* = 0.55 that is slightly above TK*(L = 32). Near the temperature T* ≃ 0.6 the shape of g(x1) becomes nearly the same for L2 = 30 and L2 = 32. This close similarity remains present for higher temperatures, indicating that no trace of the L structure is left. The global correlation function in the ML and F pseudo-phases is not influenced by the changes of L2, as long as the same number of stripes is present between the walls.
 | ||
| Fig. 13 The correlation function g(x1) (see (10) and (11)) for L2 = 30 (solid lines) and L2 = 32 (dashed lines). The length of the system in the longitudinal direction in the MC simulations was L1 = 2520. Panels from (a) to (d) correspond to T* = 0.5, 0.55, 0.625 and 1 respectively. The thermodynamic considerations and Fig. 7, 10 and 11 indicate stability of the following phases: (i) for T* = 0.5 the L pseudo-phase when L2 ≤ 30, and the beginning of the L–ML crossover for L2 = 32, (ii) for T* = 0.55 the crossover between the L and ML pseudo-phases, (iii) for T* = 0.625 the ML pseudo-phase, and (iv) the F pseudo-phase for T* = 1. | ||
 | ||
| Fig. 14 The orientational OP OL computed for L1 = 180 and for the commensurate (L2 = 30, L2 = 34) and incommensurate (L2 = 32, L2 = 36) slit widths as a function of temperature. The thick solid line is the OL computed for the bulk system.11 | ||
For T* > 0.5 the OP shown in Fig. 14 differs significantly from the OP in the bulk. In the bulk OL(T*) very weakly decreases with temperature for T* < 0.725, and then decreases rapidly to zero with the inflection point at T* ≈ 0.75. In contrast, in the slit it decreases significantly for increasing T* when 0.5 < T* < 0.9, and for T* > 0.9 a slow decrease takes place. Comparison of Fig. 14 and 7 suggests that the OL(T*) starts to decrease when the crossover region between the L and ML structures is entered by heating the system. Thus, in contrast to the bulk, OL(T*) decreases with increasing temperature in the whole region that we identify with the ML pseudo-phase.
The confinement-reduced orientational order in the ML phase is counter-intuitive, and it is due to the definition of the order parameter. Our simulations in the bulk typically show stripes that consist of short segments parallel to two main lattice directions, and the number of lamellar segments in one of the main directions of the lattice is very small, which makes OL ≈ 1 (see (12)). In a slit, however, the geometrical defects in the near-boundary stripes induce a similar number of segments in directions e2, and e3; this number is smaller that the number or lamellar segments in direction e1, but by no means negligible, particularly for slit widths incommensurate with the lamellar periodicity. By visual inspection of Fig. 10 we can see that for T* ≥ 0.556 the stripes are parallel to the boundaries only close to the walls, whereas away from the boundaries the stripes consist of short segments parallel to different ei. It remains to be verified if in the off-lattice system the orientational order in the ML phase is reduced by confinement too.
Note that the OL(T*) lines computed for L2 and L2 + 2 coincide above certain temperature, in agreement with the identical shapes of the global correlation function g(x1) (see Fig. 13). This temperature is marked by big triangles in Fig. 7. This is another confirmation that the mismatch between L2 and the local lamellar period is irrelevant when there is no periodic order.
The ML–F phase transition in the bulk was identified with the inflection point of the OL(T*). The shape of OL in the slit is much different. There is no clearly distinguished temperature marking the transition between the anisotropic and isotropic structures when the OP changes gradually in a large temperature interval. We identify the pseudo phase transition between these phases in the slit with the second maximum of cμ, but in fact the crossover region between the two structures is very broad. The high-T plateau of the OL is reached at T* ≃ 1.4 that is much higher than in the system with PBC, i.e. at T* ≃ 0.8. This orientational ordering in the confined F-like structure is associated with the layering near the walls. As shown in Fig. 11, three maxima of the density profile in the transverse direction are present near each wall at T* = 1, and this periodic near-surface structure contributes to OL.
The pseudo-transition ML–F occurs at the temperature T* ≃ 0.7 that is somewhat lower than the temperature of the ML–F transition in the bulk, estimated as T* ≃ 0.75. Note that this transition in the bulk is continuous. An apparent continuous transition in a slit corresponds to the temperature at which the bulk correlation length and the slit width are comparable and it happens before the bulk transition occurs. Thus, lower temperature of the pseudo-transition in the slit agrees with the expected behavior.
4 Conclusions
Despite the fact that in a two-dimensional slit there are no true thermodynamic phase transitions, we have found significantly different structures for different parts of the temperature – slit width structure-diagram, (T*,L2). The structures with and without the periodic order lie on the low- and the high-temperature side of the Kelvin-like line T = TK(L2), respectively. Thus, the melting of the periodic lamellar structure occurs at the temperature that is much higher than in the unrestricted monolayer, and increases for decreasing L2.Importantly, in the periodic structure the stripes integrity is rarely broken. When the distance between the boundaries and the period of the structure are commensurate or incommensurate, the stripes are straight or show collective corrugation, respectively. In contrast, in the absence of the periodic order there are many topological defects. In this case changes of the distance between the boundaries from commensurate to incommensurate have no effect on the self-assembled structure.
Our results show that for T < TK(L2) the template in the form of parallel lines has a significant ordering effect on the structure occurring spontaneously on the length scale smaller than the wall separation. Thus, if ordered patters with few defects are needed, parallel boundaries such that T < TK(L2) should help. If isotropic or anisotropic porous medium is desired, then T > TK(L2) should be chosen. We have verified that the low-T maxima of the heat capacity measured for L2 commensurate with the period of the stripe pattern lie on the T = TK(L2) line, and that L2 at this line is comparable with the range of the solvation pressure. We hope that our findings can help in designing and interpreting experimental studies of systems self-assembling into stripe patterns in 2D.
5 Appendix
5.1 Grand canonical Monte Carlo simulation
We have extensively used the grand canonical Monte Carlo simulation through the paper. The elementary step for these simulations in our lattice system was:(i) Choosing randomly one of the sites, i of the system
(ii) Choose one of the two possible states for that site ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) i = 0,1:
i = 0,1:
with probabilities proportional to exp[−βhi(![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) i)], where hi includes the contributions of the site i to the Hamiltonian given in eqn (2).
i)], where hi includes the contributions of the site i to the Hamiltonian given in eqn (2).
We define a cycle as a number of elementary steps equal to the number of sites of the system.
5.2 Computation of the ground state configurations
In order to compute the ground state of the system, we have made use of the parallel tempering technique. In our procedure we considered typically nβ = 151 different values of the reverse temperature, β, as:| βk* = k × δβ*, with k = 0, 1, 2,…,nβ − 1, with δβ* = 0.10; |
After completion of each simulation cycle for all the nβ cases, we perform attempts of configuration interchange between (nβ − 1)/2 pairs of neighbor states, alternating between pairs (2k, 2k + 1) and (2k + 1, 2k + 2), with k = 0, 1,…,(nβ − 3)/2.
After a given number of simulation cycles (that depends on the system lengths), the energies of the lowest temperatures reach a clear plateau, with just occasional elementary excitations. The configurations in this region correspond to minimum energy for a given system size, given in terms of the lengths L2 (slit width), and L1 (length in the direction where periodic boundary conditions are applied).
The overall GS for a given slit width L2, is attained by considering the lateral length L1,min which minimizes H[{![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (x)}]/(L1L2). The result is checked by testing that the same minimum energy and configuration is obtained when considering L1 = 2L1,min.
(x)}]/(L1L2). The result is checked by testing that the same minimum energy and configuration is obtained when considering L1 = 2L1,min.
The required simulation lengths to achieve reliable estimates of the energy minima for each system size L1 × L2, ranges from ∼5 × 104 to ∼106 cycles. In general, more cycles are required as the slit width increases.
5.3 Thermodynamic properties
The thermodynamic properties were computed using the parallel tempering technique for systems with different slit widths: L2 = 2, 3, 4,…,40. We took for all the cases L1 = 120. For systems with L2 = 4n + 2 (with n being an integer number) we considered nβ = 401 values of the inverse temperature β, whereas for the other slit widths we took nβ = 501. In both cases the particular values of β are given βk* = kδβ*, with δβ* = 0.01 and k = 0, 1,…,nβ − 1.The simulations runs comprised typically 107 cycles of equilibration plus 107 cycles of sampling. These relative long simulations were required to get a reliable sampling of the properties at low temperature.
For the bulk system, whose properties were required to compute the solvation pressure, we used also the parallel tempering scheme on a system of 1202 sites, using nβ = 501, δβ* = 0.01, with about 3.2 × 106 cycles for equilibration, and equal simulation length for the sampling.
Replica exchanges were attempted for both, confined and bulk systems, every five simulation cycles following the same scheme described previously.
5.4 Correlation functions
The density profiles and the correlation functions presented in Section 3.3 were computed using standard GCMC simulations. In order to minimize the possible effects of the periodic boundary conditions, we considered large system size in the longitudinal direction, namely L1 = 2520.These simulations required some care to ensure that the systems were equilibrated before computing the correlation functions. The number of cycles to reach a good equilibration of the systems depends on the temperature and the slit width.
For L2 = 32 and T* ≤ 0.50, the simulation runs comprised ∼2 × 107 cycles of equilibration, and the same length for the sampling part. Shorter simulations (by one order of magnitude) could be used for T* > 0.50, and for L2 = 30 at all T*. Data for further computation of the correlation functions and the density profiles were collected from configurations every 103 cycles.
5.5 The orientational order parameter
The orientational order parameter is computed following the same strategies introduced in ref. 11. Firstly we establish which sets of triangles of occupied nearest-neighbor sites fulfill the definition of lamellar triangles as defined in ref. 11, and determine their corresponding orientation on the lamellar stripe. Then, we count how many lamellar triangles are oriented in each of the three main lattice directions.In order to focus on the ordering in the region not directly influenced by the presence of the walls, only sites with coordinates 2 < x2 < L2 − 1 are considered in the calculation.
The total length of so defined lemallar segments is S = S1 + S2 + S3, where Si is the number of lamellar triangles with orientation ei (see Fig. 1). The order parameter is defined as OL = 1 − 3 min (Si/S) as it was done in the bulk (ref. 11). If the three directions are almost equiprobable we will have OL ≈ 0, whereas if there is a preferential orientation for the lamellar stripes, OL will get a large value (relatively close to one) on approaching the ground state that will depend on the corrugation of the inner lamellar stripes for the corresponding slit width.
Acknowledgements
JP acknowledges the financial support by the National Science Center under Contract Decision No. DEC-2013/09/N/ST3/02551. JP received funding for the preparation of the doctoral dissertation from the National Science Center in the funding of PhD scholarships on the basis of the Decision No. DEC-2014/12/T/ST3/00647. AC acknowledges the financial support by the National Science Center grant 2015/19/B/ST3/03122. Financial support from the Dirección General de Investigación Cientfica y Técnica under Grant FIS2013-47350-C5-4-R is also acknowledged.References
- R. P. Sear and W. M. Gelbart, J. Chem. Phys., 1999, 110, 4582 CrossRef CAS.
- A. Stradner, H. Sedgwick, F. Cardinaux, W. Poon, S. Egelhaaf and P. Schurtenberger, Nature, 2004, 432, 492 CrossRef CAS PubMed.
- S. Rozovsky, Y. Kaizuka and J. T. Groves, J. Am. Chem. Soc., 2005, 127, 36 CrossRef CAS PubMed.
- A. I. Campbell, V. J. Anderson, J. S. van Duijneveldt and P. Bartlett, Phys. Rev. Lett., 2005, 94, 208301 CrossRef PubMed.
- D. G. Barci and D. A. Stariolo, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 075437 CrossRef.
- D. G. Barci, A. Mendoza-Coto and D. A. Stariolo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062140 CrossRef PubMed.
- A. Shukla, E. Mylonas, E. D. Cola, S. Finet, P. Timmins, T. Narayanan and D. I. Svergun, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 5075 CrossRef CAS PubMed.
- M. Seul and D. Andelman, Science, 1995, 267, 476 CrossRef CAS PubMed.
- A. Ciach, J. Pȩkalski and W. T. Góźdź, Soft Matter, 2013, 9, 6301 RSC.
- A. Ciach and W. T. Góźdź, Condens. Matter Phys., 2010, 13, 23603 CrossRef.
- N. G. Almarza, J. Pȩkalski and A. Ciach, J. Chem. Phys., 2014, 140, 164708 CrossRef CAS PubMed.
- A. Imperio and L. Reatto, J. Phys.: Condens. Matter, 2004, 18, S2319 Search PubMed.
- A. Imperio and L. Reatto, J. Chem. Phys., 2006, 124, 164712 CrossRef CAS PubMed.
- A. Imperio and L. Reatto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 040402 CrossRef PubMed.
- A. J. Archer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 031402 CrossRef PubMed.
- J. Pȩkalski, A. Ciach. and N. G. Almarza, J. Chem. Phys., 2014, 140, 114701 CrossRef PubMed.
- B. Chacko, C. Chalmers and A. J. Archer, J. Chem. Phys., 2015, 143, 244904 CrossRef PubMed.
- Y. Zhuang, K. Zhang and P. Charbonneau, Phys. Rev. Lett., 2016, 116, 098301 CrossRef PubMed.
- A. Ciach, W. T. Góźdź and A. Perera, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 021203 CrossRef PubMed.
- Y. Zhuang and P. Charbonneau, J. Phys. Chem. B, 2016, 120, 6178 CrossRef CAS PubMed.
- H. Shin, G. M. Grason. and C. D. Santangelo, Soft Matter, 2009, 5, 3629 RSC.
- B. A. Lindquist, R. B. Jadrich and T. M. Truskett, Soft Matter, 2016, 12, 2663 RSC.
- M. Edelmann and R. Roth, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2016, 93, 062146 CrossRef PubMed.
- A. Ciach and W. T. Gozdz, J. Phys.: Condens. Matter, 2016, 28, 244004 CrossRef CAS PubMed.
- J. Pȩkalski, A. Ciach and N. G. Almarza, J. Chem. Phys., 2013, 138, 144903 CrossRef PubMed.
- A. Ciach and W. T. Góźdź, J. Phys.: Condens. Matter, 2016, 28, 244004 CrossRef CAS PubMed.
- D. F. Schwanzer and G. Kahl, J. Phys.: Condens. Matter, 2010, 22, 415103 CrossRef PubMed.
- H. Hasegawa and T. Hashimoto, Polymer, 1992, 33, 475 CrossRef CAS.
- A. Horvat, G. J. A. Sevink, A. V. Zvelidovsky, A. Krekhov and L. Tsarkova, ACS Nano, 2008, 2, 1143 CrossRef CAS PubMed.
- M. R. Hammond, E. Cochran, G. H. Fredrickson and E. J. Kramer, Macromolecules, 2005, 38, 6575 CrossRef CAS.
- G. M. Whitsides and M. Boncheva, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4769 CrossRef PubMed.
- M. Rey, M. A. Fernández-Rodríguez, M. Steinacher, L. Scheidegger, K. Geisel, W. Richtering, T. M. Squires and L. Isa, Soft Matter, 2016, 12, 3545 RSC.
- A. Saric and A. Cacciuto, Soft Matter, 2013, 9, 6677 RSC.
- A. Imperio, L. Peatto and S. Zapperi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 021402 CrossRef PubMed.
- D. Antelmi, P. Kékicheff and P. Richetti, J. Phys. II, 1995, 5, 103–112 CrossRef CAS.
- M. Tasinkevych and A. Ciach, J. Chem. Phys., 2001, 115, 8705 CrossRef CAS.
- B. Yu, P. Sun, T. Chen, Q. Jin, D. Ding, B. Li and A.-C. Shi, Phys. Rev. Lett., 2006, 96, 138306 CrossRef PubMed.
- B. Yu, Q. Jin, D. Ding, B. Li and A.-C. Shi, Macromolecules, 2008, 41, 4042–4054 CrossRef CAS.
- P. Chi, Z. Wang, B. Li and A.-C. Shi, Langmuir, 2011, 27, 11683–11689 CrossRef CAS PubMed.
- S. Perkin and J. Klein, Soft Matter, 2013, 9, 10438 RSC.
- L. Nicolao, A. Mendoza-Coto and D. A. Stariolo, J. Phys.: Conf. Ser., 2016, 686, 012005 CrossRef.
- R. Evans, J. Phys.: Condens. Matter, 1990, 2, 8989 CrossRef.
- V. Babin, A. Ciach and M. Tasinkevych, J. Chem. Phys., 2001, 114, 9585 CrossRef CAS.
- D. de las Heras, E. Velasco and L. Mederos, Phys. Rev. Lett., 2005, 94, 017801 CrossRef CAS PubMed.
- A. Ciach, Prog. Colloid Polym. Sci., 2004, 129, 40 CAS.
- J. Pȩkalski, A. Ciach and N. G. Almarza, J. Chem. Phys., 2015, 142, 014903 CrossRef PubMed.
Footnotes |
| † Noé G. Almarza passed away unexpectedly during preparation of this manuscript for publication. This paper is dedicated to his memory. |
| ‡ Deceased. |
| This journal is © The Royal Society of Chemistry 2016 |







