Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Controlled capillary assembly of magnetic Janus particles at fluid–fluid interfaces†‡
Qingguang
Xie
 a,
Gary B.
Davies
b and
Jens
Harting
*ca
a,
Gary B.
Davies
b and
Jens
Harting
*ca
aDepartment of Applied Physics, Eindhoven University of Technology, P.O. Box 513, NL-5600MB Eindhoven, The Netherlands. E-mail: q.xie1@tue.nl
bInstitute for Computational Physics, University of Stuttgart, Allmandring 3, 70569 Stuttgart, Germany. E-mail: gbd@icp.uni-stuttgart.de
cForschungszentrum Jülich, Helmholtz Institute Erlangen-Nürnberg for Renewable Energy (IEK-11), Fürther Straße 248, 90429 Nürnberg, Germany. E-mail: j.harting@tue.nl
First published on 5th July 2016
Abstract
Capillary interactions can be used to direct assembly of particles adsorbed at fluid–fluid interfaces. Precisely controlling the magnitude and direction of capillary interactions to assemble particles into favoured structures for materials science purposes is desirable but challenging. In this paper, we investigate capillary interactions between magnetic Janus particles adsorbed at fluid–fluid interfaces. We develop a pair-interaction model that predicts that these particles should arrange into a side–side configuration, and carry out simulations that confirm the predictions of our model. Finally, we investigate the monolayer structures that form when many magnetic Janus particles adsorb at the interface. We find that the particles arrange into long, straight chains exhibiting little curvature, in contrast with capillary interactions between ellipsoidal particles. We further find a regime in which highly ordered, lattice-like monolayer structures form, which can be tuned dynamically using an external magnetic field.
I. Introduction
Colloidal particles absorb strongly at fluid–fluid interfaces because the attachment energy is much greater than the thermal energy.1 Particle properties such as weight,2 roughness,3 and shape anisotropy4 can deform the interface around the adsorbed particle. Recent studies have shown that external electric5 or magnetic fields6,7 can also cause particles to deform the interface. When interface deformations of individual particles overlap, the fluid–fluid surface area varies, leading to capillary interactions between the particles.8–11The shape of the interface deformations around individual particles characterises the capillary interaction modes that occur between the particles. The modes can be represented analytically as different terms in a multipolar expansion of the interface height around the particle:12 particle weight triggers the monopolar mode,13 external torques switch on the dipolar mode,6 and particle surface roughness and shape anisotropy activate the quadrupolar mode.14
The arrangement of many particles adsorbed at a fluid–fluid interface depends on both the dominant capillary interaction mode and how strongly an individual particle deforms the interface. The dipolar and quadrupolar modes are anisotropic, which allows the possibility of directed assembly. Varying both the dominant mode and/or the magnitude of the interface deformations can profoundly change the assembly behaviour of particles at interfaces. For example, Yunker et al.15 showed that switching spherical particles to ellipsoidal particles induces quadrupolar capillary interactions between the particles that inhibit the coffee-ring effect. However, these interactions depend only on particle properties and are therefore difficult to control on-the-fly assembly.
A desirable next step is to control the capillary strength or dominant capillary mode dynamically, allowing far greater control of the particle assembly process. Recently, Vandewalle et al.16 used heavy spherical particles with a magnetic dipole to tune the interplay between capillary attraction and magnetic repulsion. Applying an alternating magnetic field even causes the particles to swim across the interface, creating so-called magneto-capillary swimmers.
Recently, Davies et al.6,7 showed that the dipolar mode is a promising route to dynamically-controlled anisotropic assembly at an interface. They simulated ellipsoidal particles with a dipole moment parallel to the particle's long-axis and applied an external magnetic field normal to the interface. The dipole-field interaction causes the particles to tilt with respect to the interface, which deforms the interface, and the degree of deformation can be controlled by the dipole-field strength. They further demonstrated that one can switch off the capillary interactions altogether by causing the particles to flip into a vertical orientation with respect to the interface in which no interface deformations exist.
It is highly desirable to create ordered chains or crystals of particles at interfaces for materials science purposes. The structures created using both the dipolar mode and the quadrupolar mode tend to form open-chains with little long-range order.4,7 Xie et al.17 recently showed how to create tunable dipolar capillary interactions using spherical magnetic Janus particles adsorbed at fluid–fluid interfaces.
In this paper, we simulate the interaction between many such Janus-capillary particles at an interface, and find that we can create highly-ordered chains of particles. Additionally, we develop a theoretical model based on the superposition approximation describing capillary interactions between two particles, and measure the capillary forces between them, finding the results in good agreement with our theoretical model.
This paper is organised as follows: Section II briefly describes our simulation methods before we present our results in Section III, and Section IV concludes the article.
II. Simulation method
We use the lattice Boltzmann method (LBM) to simulate the motion of each fluid. The LBM is a local mesoscopic algorithm, allowing for efficient parallel implementations, and has demonstrated itself as a powerful tool for numerical simulations of fluid flows.18 It has been extended to allow the simulation of, for example, multiphase/multicomponent fluids19–21 and suspensions of particles of arbitrary shape and wettability.22–24We implement the pseudopotential multicomponent LBM method of Shan and Chen19 with a D3Q19 lattice25 and review some relevant details in the following. Two fluid components are modelled by the following evolution equation of each distribution function discretized in space and time according to the lattice Boltzmann equation:
fci(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) + + ![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) iΔt,t + Δt) = fci( iΔt,t + Δt) = fci(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t) + Ωci( ,t) + Ωci(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t), ,t), | (1) |
![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t) are the single-particle distribution functions for fluid component c = 1 or 2,
,t) are the single-particle distribution functions for fluid component c = 1 or 2, ![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) i is the discrete velocity in the ith direction, and
i is the discrete velocity in the ith direction, and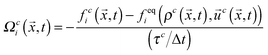 | (2) |
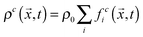 , where ρ0 is a reference density, and
, where ρ0 is a reference density, and 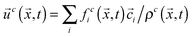 , respectively. Here, feqi(ρc(
, respectively. Here, feqi(ρc(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t),
,t),![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) c(
c(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t)) is a third-order equilibrium distribution function.27 When sufficient lattice symmetry is guaranteed, the Navier–Stokes equations can be recovered from eqn (1) on appropriate length and time scales.18 For convenience we choose the lattice constant Δx, the timestep Δt, the unit mass ρ0 and the relaxation time τc to be unity, which leads to a kinematic viscosity νc = ⅙ in lattice units.
,t)) is a third-order equilibrium distribution function.27 When sufficient lattice symmetry is guaranteed, the Navier–Stokes equations can be recovered from eqn (1) on appropriate length and time scales.18 For convenience we choose the lattice constant Δx, the timestep Δt, the unit mass ρ0 and the relaxation time τc to be unity, which leads to a kinematic viscosity νc = ⅙ in lattice units.
For fluids to interact, we introduce a mean-field interaction force between fluid components c and c′ following the Shan–Chen approach.19 The Shan–Chen LB method is a diffuse interface method, resulting in an interface width of ≈5Δx. The particle is discretized on the fluid lattice and coupled to the fluid species by means of a modified bounce-back boundary condition as pioneered by Ladd and Aidun.22,28,29 For a detailed description of the method including the extension to particles suspended in multicomponent flows, we refer the reader to the relevant literature.23,24,30–32
We perform simulations of two particles and multiple particles. For simulations between two particles, we place two particles along the x axis separated by a distance LAB. We fix the position and orientation of the particles and let the system equilibrate. We then measure the lateral forces on the particles as a function of tilt angle and bond angle, respectively. For simulations of multiple particles, we randomly distribute particles at the fluid–fluid interface, and let the system equilibrate. We note that there is no thermal coupling with the fluid and no fluctuating hydrodynamics involved in our simulation method. We then apply a magnetic field and analyse the results after the system reaches a steady-state.
III. Results and discussion
A. Pair interactions
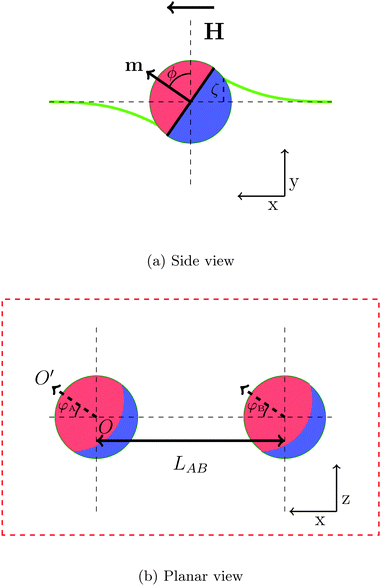
In order to gain insight into the behaviour of large numbers of magnetic Janus particles adsorbed at an interface interacting via capillary interactions, we first consider the interaction of two spherical Janus particles. Each particle comprises an apolar and a polar hemisphere of opposite wettability, with three-phase contact angles θa = 90° + β and θp = 90° − β, respectively, where β represents the amphiphilicity of the particle. Each particle has a magnetic moment m directed perpendicular to the Janus boundary, as illustrated in Fig. 1a.When a magnetic field directed parallel to the interface H is applied the particles experience a torque τ = m × H that causes them to rotate. The surface tension of the interface resists this rotation, and the particles tilt with respect to the interface. The tilt angle ϕ is defined as the angle between the particle dipole-moment m and the undeformed-interface normal.
As the particle tilts, it deforms the interface around it in a dipolar fashion:17 the interface is depressed on one side and elevated on the other, and the magnitude of these deformations are equal. The maximal deformation height of the interface, ζ, occurs at the surface of the particle.
The tilt angle therefore depends on the dipole-field strength Bm = |m|H|. For the purposes of our investigations, we assume that the external field strength is much greater than the magnitude of the dipole-moment, H ≫ m, such that the external field strength is the dominant contribution the dipole-field strength Bm ≈ H and we therefore neglect any magnetic dipole–dipole interactions between the particles.
Capillary interactions arise when the interface deformations caused by the tilting of one particle overlap with the interface deformations caused by the tilting of another particle. Like deformations attract, and unlike deformations repel.
To investigate the capillary interactions between two particles quantitatively, we define two bond angles φA, φB as the angle between the projection of orientation of the magnetic dipole on the undeformed interface and the centre–centre vector of particles, as shown in Fig. 1b. In this part of the paper, we study the interaction between two Janus particles with equal bond angles φ = φA = φB.
Fig. 2 shows how the interface deforms around two tilting Janus particles. In this representative system, the particles have equal tilt angles ϕ = 90° and bond angles φ = 0°. The yellow colour represents elevated regions, and the black colour represents depressed regions of the interface. In this configuration, the particles repel each other due to the unlike arrangement of their capillary charges. At a point equidistant between the two particles, the interface deformation is zero.
We have derived an expression for the interaction energy between two Janus particles interacting via capillary interactions of the kind described above. In this model, we assume that (i) the leading order deformation mode is dipolar (ii) the superposition approximation is valid (iii) interface deformations are small.12 The dipolar interaction energy for two Janus particles ΔE using cylindrical coordinates is
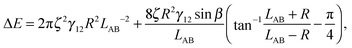 | (3) |
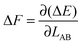 is therefore
is therefore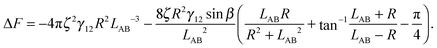 | (4) |
The maximal interface height ζ in eqn (4) depends on the tilt angle ϕ. In the case of a single Janus particle, the height of the contact line increases linearly for small tilt angles, and then reaches a constant value for large tilt angles, as we reported in our previous work.17 Interestingly, a hyperbolic tangent ζ = tanh(ϕ) approximates the variation of the contact line height ζ with tilt angle ϕ well.17 Therefore, eqn (4) can be written as a function of the tilt angle.
Assuming that the interface height ζ(ϕ) ∝ tanh![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,17 We compare the theoretical lateral capillary force eqn (4) (solid lines) to the measured lateral capillary force from our simulations (circles) in Fig. 3 for two different particle amphiphilicities β = 14° and β = 21°.
ϕ,17 We compare the theoretical lateral capillary force eqn (4) (solid lines) to the measured lateral capillary force from our simulations (circles) in Fig. 3 for two different particle amphiphilicities β = 14° and β = 21°.
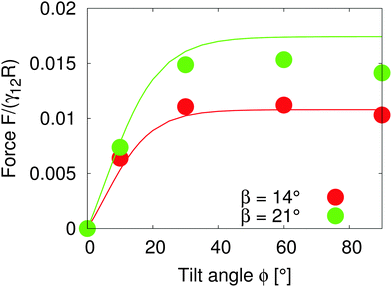 | ||
| Fig. 3 Lateral capillary force as a function of tilt angle for particles with amphiphilicities β = 14° (red) and β = 21° (green). The particles have equal bond angles φA = φB = 0. The solid line represents values from our theoretical model (eqn (4)), and the symbols are simulation data. The theoretical analysis agrees well with our simulation results in the limit of small interface deformations. | ||
We place two particles of radius R = 14 a distance LAB = 60 apart along the x-axis with total system size S = 1536 × 384 × 512. We fix the bond angle φ = 0° between the particles and measure the lateral force on the particles as the tilt angle varies.
Fig. 3 shows that the lateral capillary force increases as the amphiphilicity increases from β = 14° to β = 21° for a given tilt angle. For a given amphiphilicity, the capillary force increases with tilt angle up to tilt angles ϕ ≈ 30°. This is because the interface area increases for small tilt angles,17 which increases the interaction energy. As the tilt angle increases further ϕ > 30°, the capillary force tends to a nearly constant value, due to the fact that the maximal contact line height (and therefore the deformed interface area) also tends to a constant value.17
When comparing our theoretical model (solid lines) with simulation data (circles), we see that our model captures the qualitative features of the capillary interaction well, and quantitatively agrees with the numerical results for small tilt angles ϕ < 25° and small amphiphilicities β = 14°. The quantitative deviations at large tilt angles in the β = 21° case are due to the breakdown of various assumptions in the theoretical model, namely the assumption of small interface slopes, and of finite-size effects in our simulations. The important predictions of our model are that the capillary force between particles can be tuned by increasing the particle amphiphilicity and/or the particle tilt angle. Since the external field strength controls the tilt angle, this allows the tuning of capillary interactions using an external field.
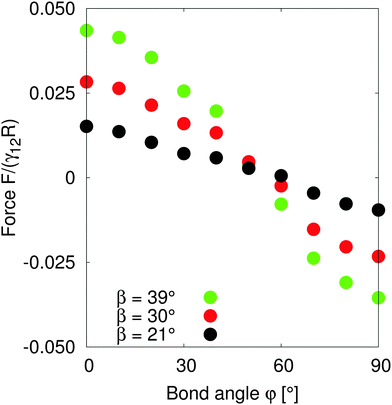
In order to understand the self-assembled structures of many-particles, it is required to consider the minimum energy orientation between two particles for a given tilt angle and separation. In the current case of equal bond angles φA = φB = φ, minimising the total interaction energy with respect to the bond angle using our theoretical model eqn (A10) indicates that the interaction energy decreases as the bond angle increases from φ = 0° to φ = 90° (as shown in Fig. 8 in Appendix A). This theoretical analysis predicts that bond angles φA = φB = 90° minimise the interaction energy, and that there is no energy barrier stopping the particles arranging into this configuration.
In order to test the predictions of our model, we performed simulations of two particles of radius R = 10 separated by a distance LAB = 40 along the x-axis with total system size S = 512 × 96 × 512. We fix the tilt angles ϕ = 90° and measured the lateral force on the particles as the bond angle varies. Fig. 4 shows that the capillary force is repulsive for bond angles φ < 50° and attractive for bond angles φ > 50°. There is maximal attractive force between two particles for φA = φB = 90°. The simulation results show that for these parameters, two Janus particles with equal bond angles φA = φB = φ = 90° minimises the interaction energy, agreeing with our theoretical predictions. Moreover, the lateral force decreases monotonically with increasing bond angle indicating that there is no energy barrier stopping the particles achieving the minimum energy state. Therefore, two Janus particles of the kind investigated in this paper interacting as capillary dipoles should rearrange into a configuration with φ = 90° bond angle.
B. Multiple particles
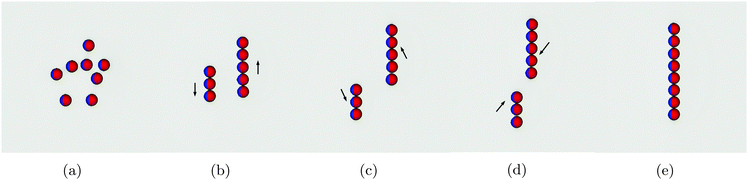
In this section we study the arrangement and many-body dynamics of multiple Janus particles adsorbed at a flat fluid–fluid interface. We start by simulating 8 Janus particles each of radius R = 10 adsorbed at an interface of area A = 2562.Fig. 5 shows simulation snapshots of the assembly process for this system. The particles start off randomly distributed with no external field applied (Fig. 5a). Once the external field is turned on, the particles arrange into two separate chains (Fig. 5b). Within each chain, the particles arrange side–side with bond angles φ = 90°, in agreement with our pair-interaction analysis. Between the chains, the particles in one chain arrange with particles in the other chain such that their bond angles are φ = 0°.
Once arranged into individual chains, the chains act as a composite unit and move relative to one another. First, they move in opposite directions, as indicated by the arrows in Fig. 5b. Once there is no end-end overlap of the chains, they begin to move towards one another (Fig. 5c and d) before finally assembling into a single chain in which all particles are arranged side–side with bond angles φ = 90° [Movie S1, ESI‡]. We need to reiterate that this assembly process occurs purely due to capillary interactions.
These results agree with our pair interaction analysis and suggest that short-range many-body effects are perhaps less relevant than in other capillary-interaction systems, in which many-body structures do not correspond with the predicted structures from pair-wise interactions alone.33,34
To investigate the assembly process further, we increase the number of particles on the interface. We define a surface fraction 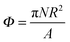 , where N is the total number of particles and A is the interface area before particles are placed at the interface.
, where N is the total number of particles and A is the interface area before particles are placed at the interface.
Fig. 6 shows the structure of particle monolayers with surface fraction Φ = 0.38 that form as we vary the dipole-field strength Bm. Initially, the particles are distributed randomly on the interface with no external field applied (Fig. 6a). We then apply an external magnetic field directed parallel to the interface that switches on capillary interactions, as described previously, and we then allow the system to reach a steady state.
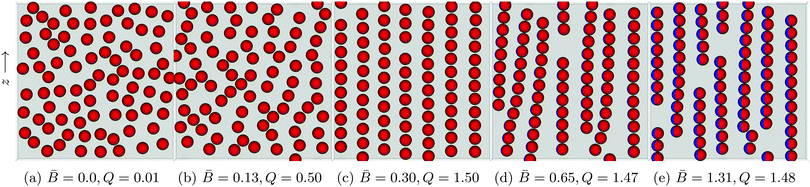 | ||
Fig. 6 Snapshots of self-assembled structures of a system with constant surface fraction Φ = 0.38 but varying dipole-field strength ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = Bm/πR2γ12. (a) No external field applied. The particles distribute randomly on the interface. (b) A small applied external field = Bm/πR2γ12. (a) No external field applied. The particles distribute randomly on the interface. (b) A small applied external field ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 0.13 shows the beginnings of chain formation but little global order. (c) Increase the dipole-field strength to = 0.13 shows the beginnings of chain formation but little global order. (c) Increase the dipole-field strength to ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 0.30 creates a highly ordered lattice structure. (d) As the field strength increases to = 0.30 creates a highly ordered lattice structure. (d) As the field strength increases to ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 0.65, the interparticle distance within a chain decreases and the chains act as a composite unit. Competing interactions with other chains causes chain bending and curving. (e) For = 0.65, the interparticle distance within a chain decreases and the chains act as a composite unit. Competing interactions with other chains causes chain bending and curving. (e) For ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 1.31 the chains exhibit less curvature due to the introduction of more defects in the system. The order parameter Q is computed using eqn (5). = 1.31 the chains exhibit less curvature due to the introduction of more defects in the system. The order parameter Q is computed using eqn (5). | ||
For a dipole-field strength of ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = Bm/πR2γ12 = 0.13 (Fig. 6b), we see some ordering, but no formation of distinct chains in which particles are aligned side–side. As we increase the dipole-field strength to
= Bm/πR2γ12 = 0.13 (Fig. 6b), we see some ordering, but no formation of distinct chains in which particles are aligned side–side. As we increase the dipole-field strength to ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 0.30 (Fig. 6c), the particles arrange into well-defined chains. For this dipole-field strength, the chains exhibit little bending or curvature. Within the chains, particles arrange with bond angles φ = 90°, and particles arrange with particles in other chains with bond angle φ = 0°, similar to the arrangements that we observed with 8 particles in Fig. 5. Due to the periodic boundary conditions of our simulations, we observe coexistence of hexagonal and rectangular particular arrangements with neighbouring particles in other chains. One can clearly observe a high degree of order for this field strength. We also notice that the particles within the chains maintain a clear separation between one another. Increasing the field strength further to
= 0.30 (Fig. 6c), the particles arrange into well-defined chains. For this dipole-field strength, the chains exhibit little bending or curvature. Within the chains, particles arrange with bond angles φ = 90°, and particles arrange with particles in other chains with bond angle φ = 0°, similar to the arrangements that we observed with 8 particles in Fig. 5. Due to the periodic boundary conditions of our simulations, we observe coexistence of hexagonal and rectangular particular arrangements with neighbouring particles in other chains. One can clearly observe a high degree of order for this field strength. We also notice that the particles within the chains maintain a clear separation between one another. Increasing the field strength further to ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 0.65 (Fig. 6d) and
= 0.65 (Fig. 6d) and ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 1.31 (Fig. 6e) reduces the inter-particle distance between particles within a particular chain, and the chains show a larger degree of bending and curvature.
= 1.31 (Fig. 6e) reduces the inter-particle distance between particles within a particular chain, and the chains show a larger degree of bending and curvature.
We suggest that the reason we observe a highly ordered lattice structure for dipole-field strength ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 0.30 (Fig. 6c) is due to the strength of capillary interactions for this dipole-field strength; particles are able to leave their chain and join other chains easily if it is energetically favourable [Movie S2, ESI‡]. In contrast, for higher dipole-field strengths
= 0.30 (Fig. 6c) is due to the strength of capillary interactions for this dipole-field strength; particles are able to leave their chain and join other chains easily if it is energetically favourable [Movie S2, ESI‡]. In contrast, for higher dipole-field strengths ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 0.65 (Fig. 6d) the capillary interactions between the particles are stronger, as evidenced by their smaller inter-particle separations within chains. Particles are more strongly bound to their initial chains, and chains essentially become self-contained. These chains interact with other chains as a composite unit, leading to the bending and the curving of the chains, but particles are not easily able to leave one chain and attach to another [Movie S3, ESI‡]. As the dipole-field strength increases yet further to
= 0.65 (Fig. 6d) the capillary interactions between the particles are stronger, as evidenced by their smaller inter-particle separations within chains. Particles are more strongly bound to their initial chains, and chains essentially become self-contained. These chains interact with other chains as a composite unit, leading to the bending and the curving of the chains, but particles are not easily able to leave one chain and attach to another [Movie S3, ESI‡]. As the dipole-field strength increases yet further to ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 1.31 (Fig. 6e), the chains exhibit less bending and curvature due to the introduction of more “defects” in the structure. Those appear due to the fact that there is more available interface area because of the smaller inter-particle separations.
= 1.31 (Fig. 6e), the chains exhibit less bending and curvature due to the introduction of more “defects” in the structure. Those appear due to the fact that there is more available interface area because of the smaller inter-particle separations.
Our results suggest that for intermediate dipole-field strengths there is a “sweet-spot” capillary interaction magnitude that allows the rearrangement of the particles into energetically favourable structures. For field strengths of this magnitude, it may be possible to create thermodynamically stable monolayers, as opposed to the meta-stable monolayers one usually observes in monolayers of particles interacting via capillary interactions.35
In order to characterize the straightness and order of the chains, we introduce a pair-orientation order parameter Q, defined as
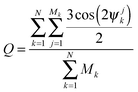 | (5) |
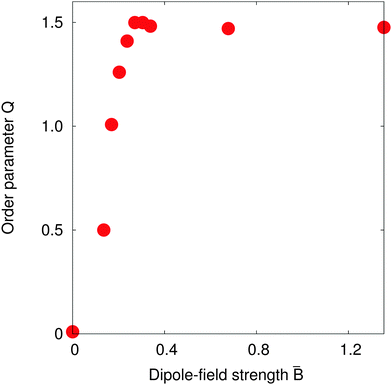
Fig. 7 shows the value of the order parameter Q as the dipole-field strength ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) increases. We see that the order parameter increases monotonically before reaching its maximum value Q = 1.5 at a dipole-field strength
increases. We see that the order parameter increases monotonically before reaching its maximum value Q = 1.5 at a dipole-field strength ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) ≈ 0.3. As the dipole-field strength increases further, the order parameter slightly decreases before reaching a constant value Q ≈ 1.47 for dipole-field strengths
≈ 0.3. As the dipole-field strength increases further, the order parameter slightly decreases before reaching a constant value Q ≈ 1.47 for dipole-field strengths ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) > 0.4. For these order parameter values, the particles within chains should be parallel with one another, which agrees with our observations in Fig. 6. Further, the maximum Q value we observe in Fig. 7 at dipole-field strength
> 0.4. For these order parameter values, the particles within chains should be parallel with one another, which agrees with our observations in Fig. 6. Further, the maximum Q value we observe in Fig. 7 at dipole-field strength ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 0.30 reconciles with our results in Fig. 6.
= 0.30 reconciles with our results in Fig. 6.
Fig. 7 suggests that the transition to a highly-ordered state is a smooth, second-order phase transition, rather than a first-order transition as observed with non-Janus ellipsoidal particles,6,7 due to the absence of any energy barrier separating particular particle configurations.
IV. Conclusion
We studied capillary interactions between magnetic spherical Janus particles both theoretically and numerically. Capillary interactions between magnetic spherical Janus particles are induced by applying a magnetic field parallel to the interface, which causes the particles to tilt and to deform the interface. We derived an analytical model for the interaction between two such particles using the superposition and small interface deformation approximations. Our model predicts that the strength of capillary interactions should rapidly increase for small particle tilt angles before reaching a constant value. It also predicts that a bond angle φ = 90° corresponding to the side–side configuration between two particles minimises the interaction energy between the particles, and that there is no energy barrier prohibiting the particles from achieving this configuration.We carried out lattice Boltzmann simulations of two Janus particles adsorbed at a fluid–fluid interface that confirmed our theoretical predictions. We then investigated the dynamics and steady-state behaviour of monolayers of Janus particles. Our simulations revealed interesting dynamical behaviour, namely that particles like to arrange in long, straight chains in the side–side configuration. However, if there are many particles on the interface, steric interactions lead to these chains bending and an increase in the number of defects in the monolayer.
Interestingly, we find that for intermediate dipole-field strengths a highly-ordered crystal-like arrangement of Janus particles is possible. This is because, for intermediate dipole-field strengths, the capillary interactions are weak, allowing particles to leave one chain and join another easily if it is energetically favourable to do so. In contrast, for high dipole-field strengths, capillary interactions are strong and particles are tightly bound to the chain that they initially join, leading to meta-stable structures.
Our results have implications for the directed self-assembly of particles adsorbed at fluid–fluid interfaces and the creation of ordered lattice structures of particle monolayers.
Appendix A: theoretical analysis of pair interactions
The interaction energy between two particles can be written as| ΔE = ΔEff + ΔEpf, | (A1) |
Firstly, we consider the interaction energy contributed by the deformed fluid–fluid interface. ΔEff can be written as ref. 12
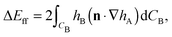 | (A2) |
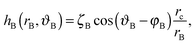 | (A3) |
We choose a local coordinate system (rB, ϑB) centered at particle B. In this coordinate particle A is located at (LAB, π). Therefore, hA in this local coordinate is transformed to
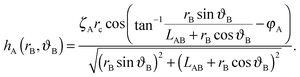 | (A4) |
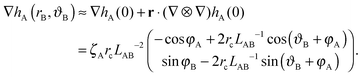 | (A5) |
ΔEff = 2πζAζBrc2LAB−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(φA + φB). cos(φA + φB). | (A6) |
Secondly we consider the interaction free energy contributed by the particle–fluid interface. Following the superposition approximation approach, we can write ΔEpf as
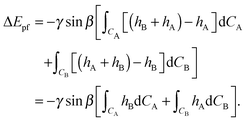 | (A7) |
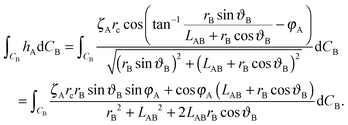 | (A8) |
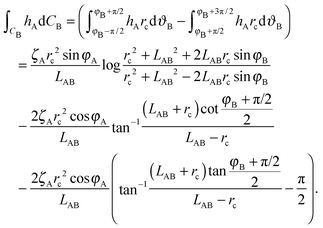 | (A9) |
Here we limit ourselves to discuss total energy for some special cases. By taking rc = R, in the case φA = φB = φ and ζA = ζB = ζ, we obtain
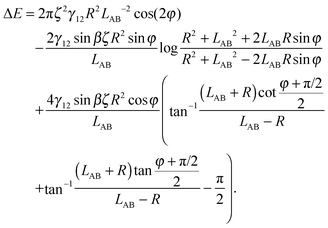 | (A10) |
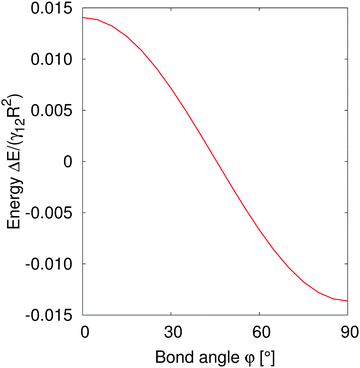 | ||
| Fig. 8 Normalized interaction energy ΔE/(γ12R2) as a function of bond angles of particles with amphiphilicity β = 21°. The two particles have a fixed tilt angle and a fixed pair separation LAB/R = 4. | ||
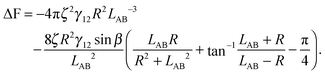
In the case φA = φB = 0° and ζA = ζB = ζ, the total interaction energy is
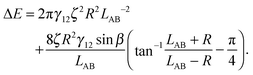 | (A11) |
 | (A12) |
Acknowledgements
Q. Xie and J. Harting acknowledge financial support from NWO/STW (STW project 13291). We thank the High Performance Computing Center Stuttgart and the Jülich Supercomputing Centre for the allocation of computing time.References
- B. P. Binks and P. D. I. Fletcher, Langmuir, 2001, 17, 4708 CrossRef CAS.
- D. Y. C. Chan, J. D. Henry and L. R. White, J. Colloid Interface Sci., 1981, 79, 410 CrossRef CAS.
- D. J. Adams, S. Adams, J. Melrose and A. C. Weaver, Colloids Surf., A, 2008, 317, 360 CrossRef CAS.
- J. C. Loudet, A. M. Alsayed, J. Zhang and A. G. Yodh, Phys. Rev. Lett., 2005, 94, 018301 CrossRef CAS PubMed.
- N. Aubry and P. Singh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 056302 CrossRef PubMed.
- G. B. Davies, T. Krüger, P. V. Coveney, J. Harting and F. Bresme, Soft Matter, 2014, 10, 6742 RSC.
- G. B. Davies, T. Krüger, P. V. Coveney, J. Harting and F. Bresme, Adv. Mater., 2014, 26, 6715 CrossRef CAS PubMed.
- B. Madivala, J. Fransaer and J. Vermant, Langmuir, 2009, 25, 2718 CrossRef CAS PubMed.
- B. J. Park, T. Brugarolas and D. Lee, Soft Matter, 2011, 7, 6413 RSC.
- E. P. Lewandowski, M. Cavallaro, L. Botto, J. C. Bernate, V. Garbin and K. J. Stebe, Langmuir, 2010, 26, 15142 CrossRef CAS PubMed.
- N. Aubry, P. Singh, M. Janjua and S. Nudurupati, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 3711 CrossRef CAS PubMed.
- D. Stamou, C. Duschl and D. Johannsmann, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 5263 CrossRef CAS.
- P. A. Kralchevsky and K. Nagayama, Langmuir, 1994, 10, 23 CrossRef CAS.
- L. Botto, L. Yao, R. L. Leheny and K. J. Stebe, Soft Matter, 2012, 8, 4971 RSC.
- P. J. Yunker, T. Still, M. A. Lohr and A. G. Yodh, Nature, 2011, 476, 308 CrossRef CAS PubMed.
- N. Vandewalle, N. Obara and G. Lumay, Eur. Phys. J. E: Soft Matter Biol. Phys., 2013, 36 Search PubMed.
- Q. Xie, G. B. Davies, F. Günther and J. Harting, Soft Matter, 2015, 11, 3581 RSC.
- S. Succi, The Lattice Boltzmann Equation for Fluid Dynamics and Beyond, Oxford University Press, 2001 Search PubMed.
- X. Shan and H. Chen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 1815 CrossRef.
- X. Shan and H. Chen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 2941 CrossRef CAS.
- H. Liu, Q. Kang, C. R. Leonardi, S. Schmieschek, A. Narvaez Salazar, B. D. Jones, J. R. Williams, A. J. Valocchi and J. Harting, Comp. Geosci., 2015 DOI:10.1007/s10596-015-9542-3.
- A. J. C. Ladd and R. Verberg, J. Stat. Phys., 2001, 104, 1191 CrossRef CAS.
- F. Jansen and J. Harting, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 046707 CrossRef PubMed.
- F. Günther, F. Janoschek, S. Frijters and J. Harting, Comput. Fluids, 2013, 80, 184 CrossRef.
- Y. H. Qian, D. D'Humières and P. Lallemand, Europhys. Lett., 1992, 17, 479 CrossRef.
- P. L. Bhatnagar, E. P. Gross and M. Krook, Phys. Rev., 1954, 94, 511 CrossRef CAS.
- H. Chen, S. Chen and W. H. Matthaeus, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45 CAS.
- C. K. Aidun, Y. Lu and E.-J. Ding, J. Fluid Mech., 1998, 373, 287 CrossRef CAS.
- J. Harting, S. Frijters, M. Ramaioli, M. Robinson, D. E. Wolf and S. Luding, Eur. Phys. J.: Spec. Top., 2014, 223, 2253–2267 CrossRef CAS.
- S. Frijters, F. Günther and J. Harting, Soft Matter, 2012, 8, 6542 RSC.
- S. Cappelli, Q. Xie, J. Harting, A. M. de Jong and M. W. J. Prins, N. Biotechnol., 2015, 32, 420 CrossRef CAS PubMed.
- T. Krüger, S. Frijters, F. Günther, B. Kaoui and J. Harting, Eur. Phys. J.: Spec. Top., 2013, 222(1), 177–198 CrossRef.
- G. B Davies and L. Botto, Soft Matter, 2015, 11, 7969 RSC.
- See ESI‡ for more details on many-body effects.
- F. Günther, S. Frijters and J. Harting, Soft Matter, 2014, 10, 4977 RSC.
- K. D. Danov and P. A. Kralchevsky, Adv. Colloid Interface Sci., 2010, 154, 91 CrossRef CAS PubMed.
Footnotes |
| † PACS Number: 47.11.–j, 47.55.Kf, 77.84.Nh. |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm01201a |
| This journal is © The Royal Society of Chemistry 2016 |