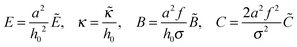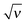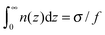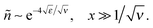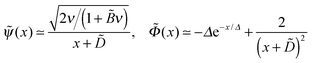Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Adsorption of flexible polyelectrolytes on charged surfaces
A. V.
Subbotin
a and
A. N.
Semenov
*b
aA. V. Topchiev Institute of Petrochemical Synthesis, Russian Academy of Sciences, Leninskii prosp. 29, Moscow, 119991, Russia. E-mail: subbotin@ips.ac.ru
bInstitut Charles Sadron, CNRS – UPR 22, Université de Strasbourg, 23 rue du Loess, 67034 Strasbourg Cedex 2, France. E-mail: semenov@unistra.fr
First published on 25th July 2016
Abstract
Adsorption of weakly charged polyelectrolyte (PE) chains from dilute solution on an oppositely charged surface is studied using the self-consistent mean-field approach. The structure of the adsorbed polymer layer and its excess charge are analyzed in the most important asymptotic and intermediate regimes both analytically and numerically. Different regimes of surface charge compensation by PE chains including partial and full charge inversion are identified and discussed in terms of physical parameters like the magnitude of specific short-range interactions of PE segments with the surface, solvent quality and ionic strength. The effect of excluded-volume monomer interactions is considered quantitatively both in the marginally good and poor solvent regimes.
1 Introduction
Let us consider a dilute solution of polyelectrolyte (PE) chains. In the presence of an oppositely charged surface the PE chains tend to form an adsorbed layer on it. Polyelectrolyte adsorption is an important phenomenon widely used for practical purposes including the stabilization of colloidal dispersions in numerous biological and industrial applications.1 The adsorbed layers are generically involved in many technologically important PE systems, including polyelectrolyte multilayers, vesicles, templates, etc. Understanding the structure of PE layers and the physics behind it is a challenging general problem.It is known that upon adsorption the total charge of the surface plus the adsorbed polymer can be opposite to the initial bare surface charge.2,3,5,7–9 This phenomenon, known as charge inversion, is important fundamentally and it seems to provide the driving force for the alternate adsorption of positively and negatively charged polymers, leading to the so-called PE multilayer formation.3,11,12 While the significance of this purely electrostatic driving force has been questioned since other more specific forces can (and often do) contribute to multilayer stability,10 the very fact that multilayers are typically and easily assembled by charged polymers points to the crucial role of electrostatic effects including the charge inversion phenomenon.
Adsorption of PEs on a charged surface was studied theoretically in ref. 6 for the case of constant surface potential and strongly repulsive short-range interactions of uncharged polymer segments with the surface (nonadsorbing surface). The problem was studied both numerically and by scaling analysis. The predictions6 concerning the polymer layer thickness and surface excess are generally in agreement with our results (see Discussion, Section 4.3). However, specifically the excess surface charge due to the adsorbed PE was not considered in ref. 6. The latter quantity was analysed by Joanny7 who developed a theory of polyelectrolyte adsorption from dilute solution on an oppositely charged surface based on a mean-field model rather similar to that adopted in ref. 6. The study7 was mainly focused on the ideal polymer regimes with insignificant non-Coulombic interactions between polymer segments, discussing briefly the effects of their 3-body excluded-volume interactions and non-electrostatic monomer/surface interactions; the effects of 2-body monomer interactions have not been discussed there. One aim of the present paper is to generalize the theory7 and to analyse the solvent quality and surface interaction effects in more detail. Another aim is to provide a more complete and quantitative analytical description of the charge inversion effect in the asymptotic regimes of low and high ionic strength and in other regimes. It was found7 that the excess charge of the adsorbed layer, σex, is inversely proportional to the Debye length rD at low salt concentration. However, this general relationship has not been fully justified and has been missing a proper prefactor. These gaps are also filled in our study.
PE adsorption and charge inversion phenomena have been studied theoretically more recently in ref. 4, 8 and 9. They used a mean-field approach similar to that of ref. 7, and altogether they generalized the theory to include the monomer and surface interactions. So why do we address the problem again? The point is that the results of ref. 8 and 9 seem to contradict each other: in ref. 8 a full charge inversion was not found (and it was concluded that multilayer formation must rely on non-electrostatic effects), while the regimes of full or even stronger overcharging are predicted in ref. 9. In both cases the results have been obtained mostly numerically: the analytical parts of these studies are more auxiliary and are not entirely satisfactory in our opinion (it was stated9 that their analytical approach involves ‘problematic’ approximations). To resolve the issue we considered the same simple mean-field model in a more analytical fashion which allows us to built a more complete picture of possible adsorption regimes and to quantitatively find the degree of overcharging (or undercharging) depending on the conditions. To facilitate this task we identified the basic reduced parameters characterizing the system. This allows us to systematically describe all the regimes in terms of a minimal set of essential parameters. For example, in the case of ideal polymer backbones and purely repulsive surfaces the adsorbed layer structure essentially depends on only one parameter, the reduced ionic strength ν.
The model, the basic mean-field equations, and the results of their numerical study highlighting the effects of ionic strength, polymer/surface and excluded-volume interactions on PE adsorption are presented in the next 2 sections. The main results are discussed in detail in Section 4 and the main conclusions are outlined in the last section.
2 Model and basic equations
In this paper we consider adsorbed layers of long weakly charged flexible PE chains (with a low fraction f ≪ 1 of positively charged units† and a large polymerization index N ≫ 1/f) in the regime of moderate polymer density in the layer (corresponding to semidilute solution). In this regime the excluded-volume interactions between polymer segments can be described in terms of virial coefficients B and C defining the relevant free energy densitywhere n is the concentration of monomer residues, kB is the Boltzmann constant, and T is the temperature. The corresponding chemical potential at distance z to the surface,
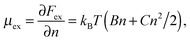 | (1) |
| n(z) → 0 at z → ∞. |
The surface is negatively charged with density −eσ, where σ is the number of −e charges per unit area. The volume density of charge is ρ = e(fn + c+ − c−), where c+ and c− are concentrations of small ions (in particular due to the added salt). In the mean-field approximation (adopted throughout the paper)
c± = cb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(∓Φ) exp(∓Φ) | (2) |
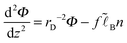 | (3) |
(
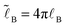 ,
,  is the Bjerrum length, and ε is the dielectric constant of the medium). It is assumed that ε does not significantly depend on polymer concentration since the latter is low (Cn2 ≪ 1): ε ≈ const.
is the Bjerrum length, and ε is the dielectric constant of the medium). It is assumed that ε does not significantly depend on polymer concentration since the latter is low (Cn2 ≪ 1): ε ≈ const.
Turning to the polymer concentration profile n(z) we note that it can be described within the mean-field ground-state dominance approximation13–16 since PE chains considered here are very long (polymerization index N → ∞) and flexible (with statistical segment as):
 | (4) |
 , and
, and| U = μex/(kBT) + fΦ |
Eqn (3) and (4) should be supplemented by the boundary conditions at the wall and at infinity. For the potential φ(z) they read
 | (5) |
The boundary condition for the order parameter ψ(z) at the wall is defined by the polymer/surface interactions. We will separate two cases, namely the case of a steric hard wall when the concentration of the polymer is zero on the surface and the boundary conditions are given by
| ψ|z=0 = 0, ψ|z=∞ = 0 | (6) |
 | (7) |
In the general case the solution of eqn (2)–(7) depends on the eigenvalue E correlating with the amount of the adsorbed polymer. The most stable polymer layer corresponds to the minimum of the free energy F including the conformational, electrostatic, ideal-gas and excluded-volume interaction terms given by (per unit surface area):
 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c+ + c−
c+ + c−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c− − (ln
c− − (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cb + 1)(c+ + c−) + 2cb is the reduced ideal-gas free energy density of small ions.
cb + 1)(c+ + c−) + 2cb is the reduced ideal-gas free energy density of small ions.
Eqn (2)–(8) can be rewritten in terms of the following non-dimensional variables:
where
 | (9) |
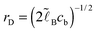 . The ratio of the two lengths defines the dimensionless ionic strength parameter ν = h02/rD2. Eqn (3) and (4) with boundary conditions (5) and (7) in the dimensionless form read:
. The ratio of the two lengths defines the dimensionless ionic strength parameter ν = h02/rD2. Eqn (3) and (4) with boundary conditions (5) and (7) in the dimensionless form read: | (10) |
 | (11) |
Eqn (11) can be solved in the general way yielding the following integral form
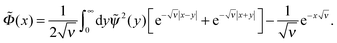 | (12) |
 | (13) |
Eqn (10) and (11) are formally equivalent to mechanical equations for a 2-dimensional classical particle (coordinates ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) ,
, ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) ) with anisotropic mass, mψ = 2, mΦ = −1 in the potential
) with anisotropic mass, mψ = 2, mΦ = −1 in the potential 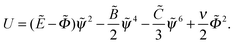 The ‘mechanical energy’ conservation law yields the following integral:
The ‘mechanical energy’ conservation law yields the following integral:
 | (14) |
Using boundary conditions at x → ∞ and extinction of the derivatives at x → ∞,  ,
,  , one finds I = 0. Using eqn (14) we obtain an additional condition at x = 0:
, one finds I = 0. Using eqn (14) we obtain an additional condition at x = 0:
 | (15) |
 | (16) |
![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 0 =
0 = ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (0),
(0), ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) 0 =
0 = ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) (0).
(0).
In the next two sections we consider the case of dominating electrostatic interactions (i.e., PE chains with negligible B and C interaction parameters).
3 Numerical results
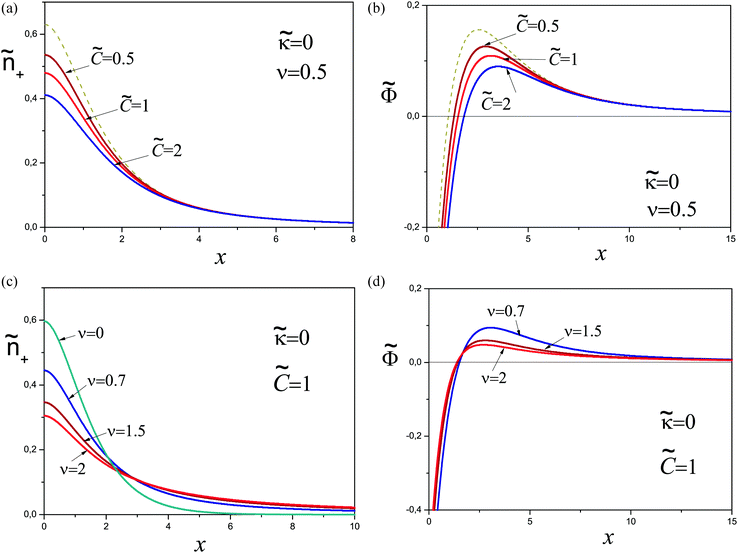
3.1 Repulsive hard wall
We start the analysis of polyelectrolyte layers with the case of a purely repulsive hard wall (κ = ∞) and no excluded-volume interactions. The system of eqn (10) and (11) is then written as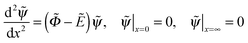 | (17) |
 | (18) |
This system was solved numerically. We start with the salt free case ν = 0. Since the electrical field at the infinity is zero, the adsorbed polyelectrolyte layer must completely screen the surface charge in this case. The reduced density profiles of charged monomers, ñ+(x) = ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 2(x), and the reduced potential
2(x), and the reduced potential ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) (x) are shown in Fig. 1. The potential monotonically increases from
(x) are shown in Fig. 1. The potential monotonically increases from ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) 0 ≈ 2.24 at the wall, and its main change occurs at x ∼ 3 corresponding to the length scale z ∼ 3h0. The adsorbed layer is localized near the wall at the same distance. At larger distances the polymer concentration and electric potential decay exponentially:
0 ≈ 2.24 at the wall, and its main change occurs at x ∼ 3 corresponding to the length scale z ∼ 3h0. The adsorbed layer is localized near the wall at the same distance. At larger distances the polymer concentration and electric potential decay exponentially: 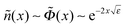 at x ≫1, where ε = −Ẽ0 ≈ 0.26 and subscript ‘0’ indicates that ν = 0.
at x ≫1, where ε = −Ẽ0 ≈ 0.26 and subscript ‘0’ indicates that ν = 0.
An added salt, ν > 0, screens the electrostatic interaction at 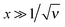 . Obviously, the length scales x ∼ 1 and
. Obviously, the length scales x ∼ 1 and  (that is h0 and rD) are well separated for ν ≪ 1. The adsorbed layer can be characterized by the excess charge σex which is the sum of the bare surface charge and the adsorbed layer charge:
(that is h0 and rD) are well separated for ν ≪ 1. The adsorbed layer can be characterized by the excess charge σex which is the sum of the bare surface charge and the adsorbed layer charge:
 | (19) |
The total mass of the adsorbed polymer layer and its free energy depend on the parameter Ẽ. As Ẽ is increased the free energy decreases and its minimum is attained at Ẽ = 0 corresponding to the saturated layer, see Fig. 2. In what follows we consider the saturated layers only, hence we set Ẽ = 0 for ν > 0. The density profiles of charged monomers and the potential profiles for different values of ν are shown in Fig. 3. In all cases the potential Φ passes through a maximum value. It means that the electric field changes its direction inside the layer. With increasing salt concentration the electrostatic attraction between the wall and the polyelectrolyte chains decreases, so the concentration of the polymer in the layer decreases as well. An adsorbed layer is not formed at all if the amount of salt is high enough: ν ≥ νc ≈ 0.78.
 | ||
| Fig. 3 Properties of saturated layers: concentration profiles of charged monomers (a) and the potential profiles (b) for different ν > 0. | ||
In Fig. 4 we show the plots of the surface potential ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) 0 and the reduced excess surface charge
0 and the reduced excess surface charge ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex = σex/σ as functions of ν. The surface potential increases monotonically with ionic strength, while the excess surface charge attains the maximum value (
ex = σex/σ as functions of ν. The surface potential increases monotonically with ionic strength, while the excess surface charge attains the maximum value (![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex ≈ 0.008) at ν ≈ 0.004. The adsorbed polymer layer overcharges the surface (i.e.,
ex ≈ 0.008) at ν ≈ 0.004. The adsorbed polymer layer overcharges the surface (i.e., ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex > 0) for ν < 0.015. However, the overcharging effect is very weak and occurs only at low ionic strength (for rD ≳ 8h0).
ex > 0) for ν < 0.015. However, the overcharging effect is very weak and occurs only at low ionic strength (for rD ≳ 8h0).
 | ||
Fig. 4 (a) The surface potential ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) 0 as a function of 0 as a function of  . (b) The excess charge . (b) The excess charge ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex as a function of ex as a function of  . Inset: . Inset: ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) exvs. ν for ν < 0.03. The dashed line represents the asymptotics for ν ≪ 1 according to eqn (20). exvs. ν for ν < 0.03. The dashed line represents the asymptotics for ν ≪ 1 according to eqn (20). | ||
Based on eqn (18) we established the asymptotic behavior of the potential ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) (x) at x ≫1 and ν ≪ 1 (cf. Section 4.2, eqn (28)). It implies that
(x) at x ≫1 and ν ≪ 1 (cf. Section 4.2, eqn (28)). It implies that
 | (20) |
3.2 Attractive wall
The system of eqn (10) and (11) for the adsorbing wall without volume interactions can be written as | (21) |
 | (22) |
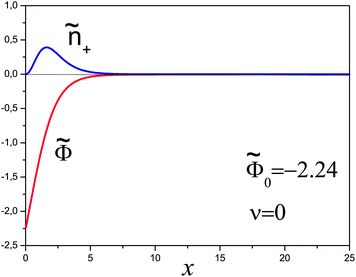
A series of profiles for the concentration of charged monomers and the electric potential are shown in Fig. 5–7 for  and different values of ν. In all cases the potential passes through a maximum whose height decreases with the ionic strength in the bulk solution, and so does the polymer concentration at κ > 0. By contrast, the surface potential increases as ν is increased (see Fig. 8a).
and different values of ν. In all cases the potential passes through a maximum whose height decreases with the ionic strength in the bulk solution, and so does the polymer concentration at κ > 0. By contrast, the surface potential increases as ν is increased (see Fig. 8a).
For any  the polymer layer is not formed for large enough ionic strength, ν ≥ νc; νc ≈ 1.35 for
the polymer layer is not formed for large enough ionic strength, ν ≥ νc; νc ≈ 1.35 for 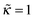 . This effect occurs because the electrostatic interaction is screened and the polymer/wall repulsion becomes dominant at high ionic strength.
. This effect occurs because the electrostatic interaction is screened and the polymer/wall repulsion becomes dominant at high ionic strength.
The degree of overcharging increases both with increasing polymer/wall attraction energy and ionic strength, see Fig. 8b. At low ionic strength (ν ≪ 1) the excess charge ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex shows the following asymptotic behavior:
ex shows the following asymptotic behavior:  (cf.eqn (29)), where ε is a function of
(cf.eqn (29)), where ε is a function of 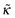 which is shown in Fig. 9.
which is shown in Fig. 9.
A detailed analysis of the excess charge and the polymer and electric potential profiles at high ionic strength (ν ≫1) is presented in Appendix B.
3.3 Effect of excluded-volume interactions
Let us turn to the effect of excluded-volume interactions of polymer segments on their adsorption. Below we consider only the most important case of an indifferent surface ( ) focusing on the regimes with negligible contribution of one of the virial coefficients:
) focusing on the regimes with negligible contribution of one of the virial coefficients: ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) = 0 or
= 0 or ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) = 0.
= 0.
We start with the case ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) = 0,
= 0, ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) ≠ 0. In Fig. 10 the density of polymer charge and potential profiles are shown. The adsorbed layer thickens with increasing attraction between the monomers or ionic strength. The excess charge also increases with the ionic strength. The plots of
≠ 0. In Fig. 10 the density of polymer charge and potential profiles are shown. The adsorbed layer thickens with increasing attraction between the monomers or ionic strength. The excess charge also increases with the ionic strength. The plots of ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex for different values of the second virial parameter are shown in Fig. 11. In the case of attractive interactions between monomers (
ex for different values of the second virial parameter are shown in Fig. 11. In the case of attractive interactions between monomers (![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) < 0) the system of eqn (10) and (11) has a well-defined stable solution if
< 0) the system of eqn (10) and (11) has a well-defined stable solution if ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) >
> ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) c(ν). For salt free conditions, the critical value of the second virial parameter is
c(ν). For salt free conditions, the critical value of the second virial parameter is ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) c ≈ −2.15 (for ν = 0). The excess charge monotonically decreases while B is passing from poor to good solvent conditions, and so does the reduced eigenvalue ε (cf.Fig. 12). At high ionic strength, ν ≫1, the critical excluded volume parameter is
c ≈ −2.15 (for ν = 0). The excess charge monotonically decreases while B is passing from poor to good solvent conditions, and so does the reduced eigenvalue ε (cf.Fig. 12). At high ionic strength, ν ≫1, the critical excluded volume parameter is ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) c ≃ −1/ν (cf. Appendix B and eqn (A3)).
c ≃ −1/ν (cf. Appendix B and eqn (A3)).
 | ||
Fig. 11 The excess charge as a function of  for different values of the second virial parameter for different values of the second virial parameter ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) and and ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) = 0. The dashed line corresponds to = 0. The dashed line corresponds to ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) = 0. = 0. | ||
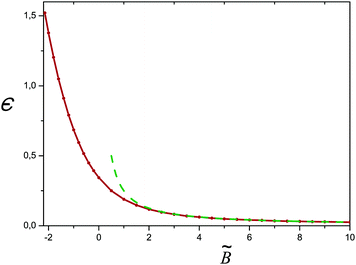 | ||
Fig. 12 The reduced eigenvalue ε for the salt free case (ν = 0) as a function of ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) = B/B0. The dashed curve shows the theoretical asymptotics according to eqn (C6). = B/B0. The dashed curve shows the theoretical asymptotics according to eqn (C6). | ||
Finally we address the effect of three-body interactions, ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) > 0. The profiles of ñ+(x) and
> 0. The profiles of ñ+(x) and ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) (x) obtained in this case using eqn (10) and (11) are shown in Fig. 13a–d. The dependence of the excess charge on the ionic strength is shown in Fig. 14. The degree of overcharging decreases as the third virial coefficient is increased;
(x) obtained in this case using eqn (10) and (11) are shown in Fig. 13a–d. The dependence of the excess charge on the ionic strength is shown in Fig. 14. The degree of overcharging decreases as the third virial coefficient is increased; ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex also decreases at high ionic strength for
ex also decreases at high ionic strength for ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) ≳ 0.5.
≳ 0.5.
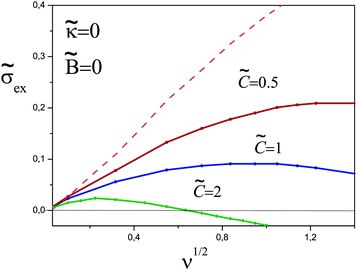 | ||
Fig. 14 The excess charge as a function of  for different values of the third virial parameter. The dashed line corresponds to for different values of the third virial parameter. The dashed line corresponds to ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) = 0. = 0. | ||
The reduced thickness ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) = h/h0 of the adsorbed layer is plotted in Fig. 15a as a function of the third virial parameter
= h/h0 of the adsorbed layer is plotted in Fig. 15a as a function of the third virial parameter ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) for the salt free case;
for the salt free case; ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) increases with
increases with ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) in accordance with analytical results (cf. Appendix C). The reduced eigenvalue ε (cf.Fig. 15b) monotonically decreases with
in accordance with analytical results (cf. Appendix C). The reduced eigenvalue ε (cf.Fig. 15b) monotonically decreases with ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) reflecting the similar behavior of σex.
reflecting the similar behavior of σex.
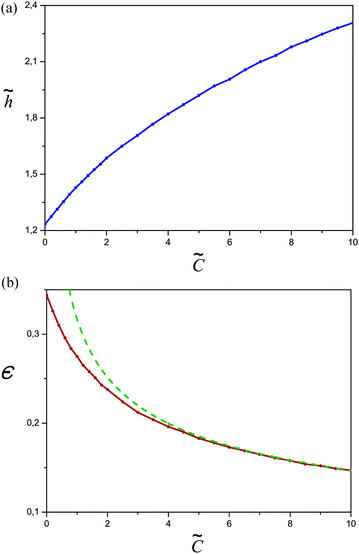 | ||
Fig. 15 (a) The reduced thickness of the adsorbed layer ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) (defined by the condition ñ( (defined by the condition ñ(![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ) = 0.5ñ(0)) as a function of ) = 0.5ñ(0)) as a function of ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) = C/C0 in the salt free case (ν = 0). (b) The reduced eigenvalue ε as a function of = C/C0 in the salt free case (ν = 0). (b) The reduced eigenvalue ε as a function of ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) . The dashed curve shows the theoretical asymptotics according to eqn (C9). . The dashed curve shows the theoretical asymptotics according to eqn (C9). | ||
4 Summary of the main results and discussion
4.1 The region of validity and essential variables
In this paper we considered the equilibrium structure of PE layers adsorbed on oppositely charged surfaces. The study concerns weakly charged PE chains, f ≪ 1, with very low bulk concentration (dilute solution). The weak charge condition is very important: it allows us to focus on the mean-field solution regime, where the existing well-established theoretical frameworks can be harnessed to cast quantitative results. In Appendix A we specify two main conditions of applicability of the mean-field approach demanding that concentration blobs are Gaussian (eqn (A1)) and electrostatic potential is low (eqn (A2)). It is only for f ≪ 1 that the two conditions are compatible defining a wide range of eligible surface charge densities (σ). Note that the second condition also ensures that electrostatic screening effects can be described by the mean field model (rD ≫![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) B): in fact, the relevant length-scale defining the characteristic Debye length rD is the adsorbed layer thickness h0 (cf.eqn (9)), which is much longer than
B): in fact, the relevant length-scale defining the characteristic Debye length rD is the adsorbed layer thickness h0 (cf.eqn (9)), which is much longer than  by virtue of eqn (9) and (A2), hence
by virtue of eqn (9) and (A2), hence  .
.
One focus of our study concerns charge inversion and the dependence of the excess charge eσex (that is, the total charge of the surface and adsorbed polymer) and of the layer thickness h on various parameters: bare surface charge eσ, ionic strength cb, fraction of charged units f, short-range specific attraction of the polymer backbone to the surface (its magnitude is characterized by the parameter κ), and virial parameters B and C. We quantitatively described (both numerically and analytically) the effect of monomer interactions considering both the regime where binary interactions (B) are dominating and the Θ-regime with significant 3-body interactions (C).
Both σex and h are generally related to the polymer adsorbance
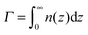 | (23) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n(z):
n(z):| σex = fΓ − σ, h = Γ/nmax. | (24) |
 (cf.eqn (9)) serves as a natural length-scale for the adsorption structure. Using this length we identified the following essential reduced parameters corresponding to the ionic strength, the monomer/surface and excluded-volume interactions:
(cf.eqn (9)) serves as a natural length-scale for the adsorption structure. Using this length we identified the following essential reduced parameters corresponding to the ionic strength, the monomer/surface and excluded-volume interactions:  where
where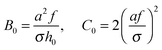 | (25) |
In addition to the Debye–Hückel (DH) approximation for monovalent ions (weak charge, Φ ≪ 1), we use the ground-state dominance (GSD) approximation to describe the chain statistics. The latter approximation is fully justified for very long (infinite) polymer chains considered in the present paper. In practice the chains are finite, and the GSD approximation is valid for N ≫N*, where N* ∼ h2/a2 is defined by the condition Rcoil = aN1/2 ≫h,14,16 meaning that the coil size (Gaussian gyration radius) Rcoil must well exceed the characteristic adsorbed layer thickness h. For example, h = h0 in the simplest case of no added salt, no specific monomer-wall attraction and no excluded-volume interactions, so the GSD condition then becomes7
It is also worth noting that the regime Rcoil ≫h is the most typical for high polymers: in the opposite case Rcoil ≪ h the polymer coils can be considered similarly to small multi-valent ions. In the latter regime (N ≪ N*) the PE chains are attracted less strongly to the substrate, so the adsorbance Γ typically decreases for shorter chains. The dependence of the PE adsorption profiles on the chain length (N) was analyzed in ref. 9 using the self-consistent field theory. The N-effect saturates for long chains in reasonable agreement with the theoretical criterion N ≫N* considered above.
4.2 The ground-state eigenvalue and the low-salt limit
The adsorbed layer structure (including the polymer profile n(z)) is defined by eqn (3) and (4) which involve a free parameter, the eigenvalue E. Below we discuss the general analytical results showing how E is related to the excess charge in the regime of low salt, rD ≫h. There is an important formal distinction between the case of no salt (cb ∝ ν = 0) and any finite ionic strength (ν > 0): as demonstrated below the ground-state eigenvalue E is negative in the former case, while E = 0 otherwise.For ν > 0, the free energy F of the adsorbed layer can be considered as a function of adsorbed amount Γ: F = F(Γ). The total free energy of the system (layer + bulk solution) is F(Γ) − μbΓ + const, where μb is the monomer chemical potential in the bulk solution (cf.eqn (1)):
The adsorbed layer is formed since the total free energy F(Γ) − μbΓ decreases with Γ at low Γ. The equilibrium state (saturated adsorbed layer) corresponds to the minimum of the total free energy, i.e.
 | (26) |
The situation for no salt (ν = 0) is different: here, F[n] is defined only for Γ = σ/f: F is infinite for any other Γ due to violation of the electroneutrality. Therefore F[n] has to be minimized under the side condition
(where λ is the Lagrange multilayer) and thus giving rise to Edwards equation (eqn (4)) with E = λ/(kBT) ≠ 0. The above equation formally implies that
 | (27) |
The following corollary can be deduced from the previous point: obviously Γ must tend to σ/f at ν → 0, that is, Γ is continuous at ν = 0, and so is the whole polymer profile n(z). By virtue of the Edwards equation (eqn (4)), the same statement applies to U(z) − E and fΦ(z) − E, where Φ = eφ/(kBT). Hence  , where subscript ‘0’ corresponds to ν = 0. Recalling also that Φ0(z) → 0 at z ≫h0, we find
, where subscript ‘0’ corresponds to ν = 0. Recalling also that Φ0(z) → 0 at z ≫h0, we find 
 for z ≫h0. In terms of reduced variables this gives
for z ≫h0. In terms of reduced variables this gives 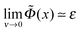 for x ≫1, where ε = −h02E0/a2,
for x ≫1, where ε = −h02E0/a2, ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) = φ/φ0,
= φ/φ0,  . Using eqn (11) and taking into account that
. Using eqn (11) and taking into account that ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (x) → 0 for x ≫1 we find the asymptotic behavior of the electrostatic potential at low salt concentrations:
(x) → 0 for x ≫1 we find the asymptotic behavior of the electrostatic potential at low salt concentrations:
 | (28) |
 | (29) |
The above result can also be rationalized in the following way: eqn (27) shows that ∂F/∂Γ = −kBT(a/h0)2ε is negative at Γ = Γ0 ≡ σ/f corresponding to exact charge compensation. Therefore, an increase of PE adsorbance (Γ > Γ0 leading to σex = f(Γ − Γ0) > 0) is favorable: F ≃ const − kBT(a/h0)2εσex/f for small σex. The energy penalty ΔFes to pay for this excess charge comes from the long-range electric field generated by σex at z ∼ rD ≫h0. Within the DH approximation its energy is  . Minimization of F + ΔFes then gives σex ≃ σεh0/rD, which is equivalent to eqn (29).
. Minimization of F + ΔFes then gives σex ≃ σεh0/rD, which is equivalent to eqn (29).
The reduced eigenvalue ε also defines the polymer density profile ñ(x) = ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (x)2 in the low salt regime. In the case of no salt (ν = 0) we find that ñ(x) decays exponentially at large distances:
(x)2 in the low salt regime. In the case of no salt (ν = 0) we find that ñ(x) decays exponentially at large distances:
![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (x)2 can be obtained using eqn (17) with Ẽ = 0 and
(x)2 can be obtained using eqn (17) with Ẽ = 0 and ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) (x) defined in eqn (28):
(x) defined in eqn (28):Thus, ñ decays exponentially for
 (i.e., for the range h0 ≪ z ≪ rD of real distances z to the surface), and then saturates at a very low level:
(i.e., for the range h0 ≪ z ≪ rD of real distances z to the surface), and then saturates at a very low level:The saturation plateau stays until exponentially long distances, for
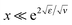 , and it is followed by a power-law decay at even larger distances.
, and it is followed by a power-law decay at even larger distances.
4.3 The Θ-solvent regime: ionic strength and specific polymer/surface interaction effects
For sterically repulsive surfaces and negligible excluded-volume interactions (B = C = 0), the only essential parameter is ν = h02/rD2. In this case the low-salt asymptotics, eqn (20), is applicable only for very low ν < 10−3. The excess charge eσex is positive for ν < 0.015, but its value does not exceed 1% of the surface charge: σex/σ < 1%. For ν > 0.015, the adsorbed layer enters the charge undercompensation regime (σex < 0), and the PE charge disappears completely (σex = −σ) at ν = νc ≈ 0.78. The PE layer is not formed at all for ν > νc. The adsorbed layer thickness stays nearly the same, h ∼ h0 at 0 < ν < 0.6: it is the layer concentration that decreases significantly with ν in this regime. Closer to νc the adsorbed layer is characterized by 2 length scales: h0 (for the proximal region where n(z) is increasing) and h (the layer thickness), the latter is diverging at νc. Note that the ionic strength for the adsorption cutoff, , is proportional to (σf)2/3, so the cutoff ionic strength increases with the polymer charge density (f) in agreement with experimental data.23
, is proportional to (σf)2/3, so the cutoff ionic strength increases with the polymer charge density (f) in agreement with experimental data.23
It is remarkable that the adsorption criterion ν < νc can be rewritten as
rD3σf![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) B/as2 > const B/as2 > const |
The revealed significant decrease of PE adsorbance Γ and of the excess PE charge σex with addition of salt (beyond a very low threshold, ν > 0.004, corresponding to rD < 16h0) is in agreement with the numerical results of ref. 8. We also agree with ref. 8 on the very low degree of overcharging in the case of strongly repulsive surfaces. However, our results do not confirm the linear scaling of σex with the bare surface charge σ stated in ref. 8 for the electrostatically dominated regime. Rather, we analytically predict σex ∝ σ2/3 at very low ionic strength (rD > 20h0) in agreement with our numerical results and with the scaling result of ref. 7.
At the scaling level our results for the layer thickness and the amount of adsorbed polymer for ν ≪ 1,  and Γ ∼ σ/f, are in agreement with the scaling eqn (11) and (13) of ref. 6 (note their notations p = f, D ∼ h and the reduced surface potential |ys| ∼ σh
and Γ ∼ σ/f, are in agreement with the scaling eqn (11) and (13) of ref. 6 (note their notations p = f, D ∼ h and the reduced surface potential |ys| ∼ σh![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) B). On the other hand, the results of ref. 6 in the high salt limit contradict our prediction of no adsorption for ν > νc in the case of sterically repulsive surface (we believe that the origin of this discrepancy lies in the approximate nature of the second term in their eqn (14) which seems to be reasonable for an indifferent rather than for a repulsive surface).
B). On the other hand, the results of ref. 6 in the high salt limit contradict our prediction of no adsorption for ν > νc in the case of sterically repulsive surface (we believe that the origin of this discrepancy lies in the approximate nature of the second term in their eqn (14) which seems to be reasonable for an indifferent rather than for a repulsive surface).
Following Joanny7 we distinguish the important regime of an indifferent surface where short-range attractive and repulsive interactions of PE segments with the surface are balanced (κ = 0). In this case the relative excess charge ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex = σex/σ always increases with ionic strength (ν), see Fig. 8b. We identified analytically the following asymptotic behaviors of the excess charge (cf. Appendix B):
ex = σex/σ always increases with ionic strength (ν), see Fig. 8b. We identified analytically the following asymptotic behaviors of the excess charge (cf. Appendix B):
 ) we find the full dependence on ν:
) we find the full dependence on ν: | (30) |
 | ||
Fig. 16 The dependence of 1 − ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) exvs. exvs. for an indifferent surface (κ = 0): analytical interpolation, eqn (30) (solid line); numerical results based on eqn (21), (22) and (19) (dashed line). for an indifferent surface (κ = 0): analytical interpolation, eqn (30) (solid line); numerical results based on eqn (21), (22) and (19) (dashed line). | ||
Returning to the scaling level in the high salt regime (ν ≫1), our results for the layer thickness and the total polymer adsorbance,  and Γ = (σ + σex)/f ∼ 2σ/f (cf. Appendix B, eqn (B3) and (B4)), are consistent with eqn (15) and (17) of ref. 6.
and Γ = (σ + σex)/f ∼ 2σ/f (cf. Appendix B, eqn (B3) and (B4)), are consistent with eqn (15) and (17) of ref. 6.
The effect of polymer/surface interactions (κ) can be gathered from Fig. 8b: surface repulsion suppresses PE adsorption, leading to a smaller or negative σex, and a somewhat thicker but more dilute adsorbed layer. Quite naturally, attractive surface (κ < 0) enhances PE adsorption, so the adsorbed layer becomes thinner and denser in this regime. These conclusions are backed by our analytical results described below (cf. Appendix B): in the high salt regime, ν ≫1 (i.e. rD ≪ h0), the layer is characterized by 2 length-scales: short, the Debye screening length rD, and long, D ∼ D0 ≡ h03/rD2 defining the layer thickness h ≃ D. The effective extrapolation length D is defined more precisely in eqn (B5) (note that ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) = D/h0):
= D/h0):
 | (31) |
Turning to the excess charge in the high salt regime (ν ≫1), we find that
| σex/σ ≃ −1 + 2D0/D ≃ 1 − 3ν−1.5 − 2κh0ν(1 − 2ν−1.5). | (32) |
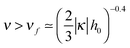 for |κ| ≪ 1/h0.
for |κ| ≪ 1/h0.
At low ionic strength, ν ≪ 1, the excess charge is small unless the surface is strongly attractive, κ < 0, |κh0| ≫1. In this regime the polymer density profile is nearly exponential, n(z) ∝ exp(−2z/h). The layer thickness and the excess charge are
 | (33) |
 . Thus, the full charge inversion is possible even for ν ≪ 1 in the case of specific affinity of PE segments to the surface suggesting that PE multilayers can be stable in the low-salt regime. This conclusion is not in disagreement with experiments.3,11,17
. Thus, the full charge inversion is possible even for ν ≪ 1 in the case of specific affinity of PE segments to the surface suggesting that PE multilayers can be stable in the low-salt regime. This conclusion is not in disagreement with experiments.3,11,17
4.4 The effect of binary interactions
Qualitatively, the effect of excluded-volume interactions (B) is similar to that of polymer/surface interactions (κ): the excess charge decreases in the marginal solvent conditions (B > 0) and increases as the solvent gets poor (B < 0) as illustrated in Fig. 11.The effect of B in the marginal solvent and low salt conditions is analyzed in detail in Appendix C. The main results for B ≫B0 and ν ≪ B0/B are outlined below: the adsorbed layer structure is characterized by 3 length-scales: z* = h0x* = h0(B0/B)1/4, 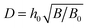 and
and  . Its effective thickness is
. Its effective thickness is  . The polymer density shows significant changes associated with the first two lengths, z* and D. The electrostatic potential profile φ(z) involves the two longer lengths, D and rD:
. The polymer density shows significant changes associated with the first two lengths, z* and D. The electrostatic potential profile φ(z) involves the two longer lengths, D and rD:
 and
and 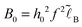 . As in the other weak adsorption regimes, the potential here changes sign being negative at z ∼ D and positive at z ∼ rD ≫D. The excess surface charge (cf.eqn (C7)) is positive and low, σex ≪ σ:
. As in the other weak adsorption regimes, the potential here changes sign being negative at z ∼ D and positive at z ∼ rD ≫D. The excess surface charge (cf.eqn (C7)) is positive and low, σex ≪ σ:| σex ≃ a2f/(4BrD), B ≫B0, ν ≪ B0/B, κh0 > −0.5B/B0 | (34) |
 | (35) |
As discussed in Appendix C, σex and h are also nearly independent of the monomer/surface interactions as long as κ > 0 or |κh0| < 0.5B/B0. For strongly attractive surface, κ < 0,  and
and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) ≫1, we obtain
≫1, we obtain
 | (36) |
In the high salt regime, ν ≫1, the effect of excluded-volume parameter ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) is quantitatively equivalent to the effect of monomer/surface interactions
is quantitatively equivalent to the effect of monomer/surface interactions  provided that both parameters are sufficiently small,
provided that both parameters are sufficiently small, ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) ≪ 1/ν and
≪ 1/ν and  (cf.eqn (B8)). For
(cf.eqn (B8)). For  , the excess charge
, the excess charge ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex shows a maximum as a function of ionic strength (ν). Such behavior was observed for cationic PEs adsorbed on silica surfaces.23,25 Conversely, for
ex shows a maximum as a function of ionic strength (ν). Such behavior was observed for cationic PEs adsorbed on silica surfaces.23,25 Conversely, for  , a monotonic increase of
, a monotonic increase of ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex and full charge inversion are predicted at high ν.
ex and full charge inversion are predicted at high ν.
To better illustrate the effect of solvent conditions for ν ≫1 let us consider the case of an indifferent surface (κ = 0) and |![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) | ≪ 1 in more detail. Here the excess charge is (cf.eqn (B6)):
| ≪ 1 in more detail. Here the excess charge is (cf.eqn (B6)):
 | (37) |
![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) −1(1 − 3
−1(1 − 3![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 3/2) ≡ νinv. In this range of ionic strength the excess charge first increases and then decreases with ν showing a maximum
3/2) ≡ νinv. In this range of ionic strength the excess charge first increases and then decreases with ν showing a maximum ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex ≃ 1 − 4.61
ex ≃ 1 − 4.61![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 3/5 at ν ≃ (4
3/5 at ν ≃ (4![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) /9)−2/5 corresponding to a partial charge inversion. The surface charge is undercompensated at a larger ionic strength:
/9)−2/5 corresponding to a partial charge inversion. The surface charge is undercompensated at a larger ionic strength: ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex < 0 at ν > νinv. This regime is entered as soon as the Debye length becomes short enough, rD < h*, where the length h* is defined in eqn (35).
ex < 0 at ν > νinv. This regime is entered as soon as the Debye length becomes short enough, rD < h*, where the length h* is defined in eqn (35).
In poor solvent conditions, B < 0, the excess charge always increases with ν. A full charge reversal (σex > σ) occurs for ν > νf with
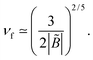 | (38) |
Based on the analytical results for ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex in low and high salt limits (cf.eqn (37)) we propose an analytical interpolation (of Padé type with variable
ex in low and high salt limits (cf.eqn (37)) we propose an analytical interpolation (of Padé type with variable 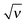 ) valid for any ionic strength ν (for κ = 0 and |
) valid for any ionic strength ν (for κ = 0 and |![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) | ≪ 1):
| ≪ 1):
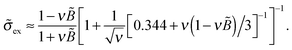 | (39) |
4.5 Further remarks
We established that the excess charge in the low-salt regime (rD ≫h0) is always positive and obeys the general equation (eqn (29)). This result can be compared with the scaling relation| σex/σ ∼ h/rD | (40) |
The excess charge σex predicted in Appendix C for C ≫C0 at low ionic strength (ν ≪ 1) scales as σex ∝ C−1/3 (cf.eqn (C10)). It is remarkable that the asymptotic analytical equations (eqn (C10) and (C9)) are quantitatively valid for C/C0 ≳ 4 as evidenced by the excellent agreement between the numerical and analytical results in this range (cf.Fig. 15b).
In this study we considered weakly charged polyelectrolytes with a small fraction f of charged units. One possible realization is a copolymer with neutral units and a small fraction f of charged units. A more common case is a homopolymer with weakly dissociated groups: each unit of the chain can be charged with probability f. Our theory is applicable in both cases. Note that in the latter case the PE charge is not necessarily constant: it depends on the electric potential. However, for weak potentials required by the DH approximation this dependence can be neglected.
The results on charge inversion considered in this paper may provide some basis for understanding the structure of PE multilayers (PEMs),3,11,12 but we do not claim a direct relevance of the adsorption results to PEMs. For example, the full charge inversion regime does not necessarily imply that PEM formation is mainly driven electrostatically. We believe however that the quantitative model of PE adsorption considered in this paper and the approach taken to analyse it can be usefully applied to study PEM structure. It is a challenging task to quantitatively assess the role of electrostatic interactions in different regimes of PEM formation. We presume that these interactions always contribute to PEM stability. In fact, as was correctly pointed out in ref. 7, even in the regime of charge undercompensation the electrostatic potential outside the last sublayer of PEM is attractive for the new-coming PE chains forming yet another sublayer. We verified that this feature is generally valid in all the regimes.
5 Conclusions
1. The adsorbed PE layer structure and charge compensation effect can be described in terms of the minimal set of the following reduced variables reflecting a self-similar structure of flexible PE chains:![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) = h/h0,
= h/h0, ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex = σex/σ,
ex = σex/σ,  ,
, 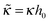 ,
, ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) = B/B0, and
= B/B0, and ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) = C/C0, where h is the layer thickness, σex = fΓ − σ is the excess charge (in units of proton charge e and per unit area), ν is the reduced ion strength, κ is the magnitude of specific short-range monomer/surface repulsion (attraction in the case κ < 0),
= C/C0, where h is the layer thickness, σex = fΓ − σ is the excess charge (in units of proton charge e and per unit area), ν is the reduced ion strength, κ is the magnitude of specific short-range monomer/surface repulsion (attraction in the case κ < 0),  is the characteristic electrostatic thickness,
is the characteristic electrostatic thickness, 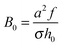 , and
, and  . The reduced parameters depend on the bare surface charge σ: ν ∝ σ−2/3,
. The reduced parameters depend on the bare surface charge σ: ν ∝ σ−2/3,  ,
, ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) ∝ σ2/3, and
∝ σ2/3, and ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) ∝ σ2.
∝ σ2.
The following main regimes are distinguished based on the reduced excess charge, ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex, of the PE layer:
ex, of the PE layer: ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex = −1, no PE layer is formed (the adsorbed charge fΓ = 0), −1 <
ex = −1, no PE layer is formed (the adsorbed charge fΓ = 0), −1 < ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex < 0 charge undercompensation, 0 <
ex < 0 charge undercompensation, 0 < ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex < 1 partial (incomplete) charge inversion,
ex < 1 partial (incomplete) charge inversion, ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex = 1 full charge inversion, and
ex = 1 full charge inversion, and ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex > 1 charge inversion with amplification.
ex > 1 charge inversion with amplification.
2. It is found that in the low salt regime (rD ≫h0) the PE charge always overcompensates the initial surface charge, and that the excess charge ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex is inversely proportional to rD. We established the general asymptotic relation
ex is inversely proportional to rD. We established the general asymptotic relation ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex ≃ εh0/rD, where ε is the reduced ground-state eigenvalue involved in the Edwards eqn (4), for ν = 0. We calculated ε analytically in a number of important asymptotic regimes (for
ex ≃ εh0/rD, where ε is the reduced ground-state eigenvalue involved in the Edwards eqn (4), for ν = 0. We calculated ε analytically in a number of important asymptotic regimes (for 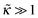 , for
, for ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) ≫1 and any κ, and for
≫1 and any κ, and for ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) ≫1) and numerically in intermediate regimes.
≫1) and numerically in intermediate regimes.
For strongly repulsive surfaces we predict the overcharging regime (σex > 0) in a very narrow range of low ionic strength, the degree of overcharging being always very small: ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex < 0.01. We also obtained an analytical expression, eqn (B6), for the excess charge in the high salt regime, ν ≫1, and we quantitatively considered the effect of excluded-volume monomer interactions both in the marginally good and poor solvent regimes. All our analytical and numerical results point to the following general trends: excess charge always increases as the solvent quality decreases (lower or negative B), or as the uncharged surface becomes less repulsive or more attractive for PE segments (lower or negative κ).
ex < 0.01. We also obtained an analytical expression, eqn (B6), for the excess charge in the high salt regime, ν ≫1, and we quantitatively considered the effect of excluded-volume monomer interactions both in the marginally good and poor solvent regimes. All our analytical and numerical results point to the following general trends: excess charge always increases as the solvent quality decreases (lower or negative B), or as the uncharged surface becomes less repulsive or more attractive for PE segments (lower or negative κ).
3. The dependence of the excess charge on the ionic strength (parameter ν) is more complicated. As is follows from eqn (29)![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex always increases at low ν. Its further behavior depends on the parameters κ and B:
ex always increases at low ν. Its further behavior depends on the parameters κ and B:
(i) At κ > 0 (repulsive surface) and B > 0 (marginal solvent) ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex varies with ν in a nonmonotonic way reaching maximum (
ex varies with ν in a nonmonotonic way reaching maximum (![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex)max, 1 > (
ex)max, 1 > (![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex)max > 0, at some ν = νmax, then decreasing down to
ex)max > 0, at some ν = νmax, then decreasing down to ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex = −1 at ν = νc. The adsorbed layer disappears at ν > νc. Such behavior of the PE adsorbance Γ (nonmonotonic dependence of Γ = σ(1 +
ex = −1 at ν = νc. The adsorbed layer disappears at ν > νc. Such behavior of the PE adsorbance Γ (nonmonotonic dependence of Γ = σ(1 + ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex)/f on the amount of added NaCl followed by adsorption cutoff) has been observed experimentally for cationic PEs on silica surfaces.23,25 For strongly repulsive surfaces νmax is small, so both the surface coverage Γ and excess charge σex mostly decrease with ionic strength (see the dashed curve and the curve for
ex)/f on the amount of added NaCl followed by adsorption cutoff) has been observed experimentally for cationic PEs on silica surfaces.23,25 For strongly repulsive surfaces νmax is small, so both the surface coverage Γ and excess charge σex mostly decrease with ionic strength (see the dashed curve and the curve for  in Fig. 8b) in agreement with experimental data on adsorption of weakly charged polycations on mica.26
in Fig. 8b) in agreement with experimental data on adsorption of weakly charged polycations on mica.26
(ii) For κ > 0 and B < 0 (poor solvent), σex monotonically increases with ν diverging at the bulk stability threshold ν → νmax ≃ 1/|![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) |, if
|, if 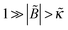 . In the opposite case,
. In the opposite case,  , the behavior of
, the behavior of ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex is nonmonotonic again like in regime (i).
ex is nonmonotonic again like in regime (i).
(iii) For κ < 0 (attractive surface) and B < 0, both the excess charge and surface coverage increase monotonically with ionic strength. Such behavior is typically observed for PEs adsorbed onto oppositely charged surfaces with some nonelectrostatic affinity for the polymer.27–30
(iv) Finally, for κ < 0 and B > 0, the excess charge increases, reaches a maximum and then decreases down to a plateau value if  , while
, while ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex monotonically increases up to the plateau at high ionic strength in the opposite case,
ex monotonically increases up to the plateau at high ionic strength in the opposite case,  .
.
The predicted tendencies are in agreement with experimental results22 showing a decrease of polymer adsorbance Γ ∝ 1 + ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex with ionic strength cb at a low fraction of charged polymer units (f = 1%) and an increase of Γ with cb at higher f = 13% and 30%. (Note that
ex with ionic strength cb at a low fraction of charged polymer units (f = 1%) and an increase of Γ with cb at higher f = 13% and 30%. (Note that 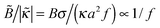 , hence a transition from the regime
, hence a transition from the regime 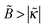 to
to  is expected as f is increased.)
is expected as f is increased.)
4. Concerning the effect of surface charge σ on charge inversion, we find that normally the reduced excess charge ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex decreases as σ is increased. This is always true for indifferent or attractive surfaces. However, in the case of repulsive surfaces (κ > 0) the excess charge can increase with σ at low σ, so
ex decreases as σ is increased. This is always true for indifferent or attractive surfaces. However, in the case of repulsive surfaces (κ > 0) the excess charge can increase with σ at low σ, so ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex can show a maximum as a function of σ. Such behavior in the regime
ex can show a maximum as a function of σ. Such behavior in the regime  , ν ≫1 is implied in eqn (B8).
, ν ≫1 is implied in eqn (B8).
5. In Θ-solvent conditions the full (or stronger) charge inversion (σex ≥ σ) is expected only with some specific attraction of polymer to the surface (κ < 0, |κ| ≥ |κ|f, where 1/|κ| = d is the surface extrapolation length). The critical surface attraction parameter |κ|f always decreases with salt addition following the scaling law |κ|f ∝ rD5 at high ionic strength (ν ≫1, rD ≪ h0). More precisely, |κ|f ≃ 1.5rD5/h06, and so critical attraction strength increases with bare surface charge: |κ|f ∝ σ2 for ν ≫1. In low salt conditions (ν ≪ 1, rD ≫h0) the magnitude of critical attraction increases significantly: |κ|f ∼ ν−1/4/h0. It is shown however (see Section 4.4) that in poor solvent conditions (B < 0) the full charge inversion can be achieved even in the case of repulsive surfaces (κ > 0). This conclusion is in agreement with the numerical results of ref. 9.
6. The surface layer structure is generally characterized by multiple essentially different length-scales including the PE layer mean thickness h (cf.eqn (24)) and the Debye length rD. In the case of low ionic strength (long rD) and significant excluded-volume interactions (![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) ≫1 corresponding to high enough surface charge σ) the third length z* ∼ h0
≫1 corresponding to high enough surface charge σ) the third length z* ∼ h0![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) −1/4 emerged (z* ≪ h ≪ rD). In Θ-solvent conditions with
−1/4 emerged (z* ≪ h ≪ rD). In Θ-solvent conditions with ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) ≫1 (this again corresponds to sufficiently high σ) two extra lengths are involved: the proximal decay length z* ∼ h0
≫1 (this again corresponds to sufficiently high σ) two extra lengths are involved: the proximal decay length z* ∼ h0![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) −1/6 showing how fast the effect of surface interactions fades off away from the surface, and the distal decay length ξ ∼ h0
−1/6 showing how fast the effect of surface interactions fades off away from the surface, and the distal decay length ξ ∼ h0![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 1/6 characterizing the decrease of polymer density in the region h < z ≲ rD. The characteristic lengths then form the following sequence: z* ≪ ξ ≪ h ≪ rD.
1/6 characterizing the decrease of polymer density in the region h < z ≲ rD. The characteristic lengths then form the following sequence: z* ≪ ξ ≪ h ≪ rD.
We also established (both numerically and analytically) that the adsorbed layer thickness h always increases with ionic strength. This conclusion is in agreement with experimental data.25–27
Appendix A: marginal solvent and other conditions
Below we outline the regimes of validity for the main approximations used in the paper.(1) Gaussian chains and weak fluctuation effects: this approximation effectively means that the relevant chain fragment (of size comparable with the adsorbed layer thickness h) is not swollen by monomer interactions. For rD ≫h we distinguish electrostatic and excluded-volume contributions to the interactions. Electrostatic interactions do not affect much chain conformations on the length-scales h shorter than the electrostatic blob size18 : h ≪ ξe. With h ∼ h0, where h0 is the characteristic thickness (defined in eqn (9)) in the low-salt regime, we thus get
: h ≪ ξe. With h ∼ h0, where h0 is the characteristic thickness (defined in eqn (9)) in the low-salt regime, we thus get
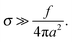 | (A1) |
 , where
, where 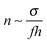 is the typical concentration in the layer. With
is the typical concentration in the layer. With  (corresponding to significant binary monomer interactions) the marginal solvent condition becomes σ ≫f/(63/2a2) which virtually coincides with condition (A1).
(corresponding to significant binary monomer interactions) the marginal solvent condition becomes σ ≫f/(63/2a2) which virtually coincides with condition (A1).
In the high salt regime (rD ≪ h) electrostatic interactions are equivalent to excluded volume with B ∼ B0/ν (where ν = h02/rD2), and the layer thickness is h ∼ h0ν, so the marginal solvent condition (n ≫B/as6) again reduces to eqn (A1). (Note: for higher ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) = B/B0, i.e.
= B/B0, i.e. ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) ν ≫1, the marginal solvent condition is stronger:
ν ≫1, the marginal solvent condition is stronger: 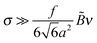 .)
.)
(2) The Debye–Hückel (DH) approximation: it is hinged on low electric potential, Φ ≪ 1. For rD ≫h (low salt)  , so using eqn (9) we get
, so using eqn (9) we get
 | (A2) |
(3) In the case of attractive monomer interactions, B < 0, the total excluded volume Btot = B + Bes, where  is the effective additional excluded volume due to the Coulomb repulsion of charged units. The solution stability then demands that |B| < Bes, which is equivalent to
is the effective additional excluded volume due to the Coulomb repulsion of charged units. The solution stability then demands that |B| < Bes, which is equivalent to
|![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) |ν < 1 |ν < 1 | (A3) |
Appendix B: theory of PE adsorption at high ionic strength
Here we consider the adsorption profiles and excess charge for ν ≫ 1 at different excluded volumes and surface repulsion parameters,![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) and
and 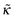 . We start with the simplest case
. We start with the simplest case ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) = 0,
= 0,  (ideal backbones, indifferent surface).
(ideal backbones, indifferent surface).
In this case reduced eqn (4) and boundary conditions are
![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) ′′ = ′′ = ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) , , ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) ′′ = − ′′ = −![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 2 + ν 2 + ν![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) , x > 0, , x > 0, | (B1) |
![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) ′ = 1, ′ = 1, ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) ′ = 0 at x = 0 ′ = 0 at x = 0 | (B2) |
![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) ) in a standard way yielding (cf.eqn (12))
) in a standard way yielding (cf.eqn (12))where
 is the reduced Debye length. The above expression was substituted for
is the reduced Debye length. The above expression was substituted for ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) (x) in the first eqn (B1), and the latter equation was solved in a perturbative way (with a small parameter Δ) to yield
(x) in the first eqn (B1), and the latter equation was solved in a perturbative way (with a small parameter Δ) to yieldwhere the effective extrapolation length
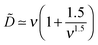 | (B3) |
 | (B4) |
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ex ≡ σex/σ = −1 +
ex ≡ σex/σ = −1 + ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) p and
p and  is the reduced charge of the adsorbed PE layer). The first term (=1) is the limiting value obtained by Joanny,7 and the second term is the main correction. Our analysis shows that other corrections are subdominant (∼1/ν3). This result indicates that σex/σ < 1, so full charge inversion does not occur in this regime (charge inversion is incomplete).
is the reduced charge of the adsorbed PE layer). The first term (=1) is the limiting value obtained by Joanny,7 and the second term is the main correction. Our analysis shows that other corrections are subdominant (∼1/ν3). This result indicates that σex/σ < 1, so full charge inversion does not occur in this regime (charge inversion is incomplete).
The case of arbitrary κ and B can be considered in a similar way. The result is:
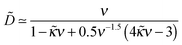 | (B5) |
 | (B6) |
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) > 0, which is true for
> 0, which is true for  . For larger
. For larger  , the surface is too repulsive and no adsorption layer is formed, hence σex = −σ in this case. In the case of poor solvent, B < 0, another restriction, eqn (A3), is applicable.
, the surface is too repulsive and no adsorption layer is formed, hence σex = −σ in this case. In the case of poor solvent, B < 0, another restriction, eqn (A3), is applicable.
The full charge inversion (σex = σ) is thus predicted for
 | (B7) |
![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) < (
< (![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) )f. On the other hand, eqn (B6) points to charge undercompensation (σex < 0) for a large enough excluded volume parameter
)f. On the other hand, eqn (B6) points to charge undercompensation (σex < 0) for a large enough excluded volume parameter ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) .
.
For small interaction parameters  , eqn (B6) simplifies as
, eqn (B6) simplifies as
 | (B8) |
Appendix C: the effect of excluded-volume interactions in the low salt regime
For ν = 0, the basic equations are![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) ′′ = (ε + ′′ = (ε + ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) ) )![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) + + ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 3, 3, ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) ′′ = − ′′ = −![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 2 2 | (C1) |
 | (C2) |
![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) = B/B0 is the reduced excluded volume and ε is an important free parameter, the reduced eigenvalue characterizing the fundamentally interesting case of no salt (see Section 4.2 for more details). The effect of B is negligible if
= B/B0 is the reduced excluded volume and ε is an important free parameter, the reduced eigenvalue characterizing the fundamentally interesting case of no salt (see Section 4.2 for more details). The effect of B is negligible if ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) ≪ 1. Below we consider the opposite regime,
≪ 1. Below we consider the opposite regime, ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) ≫ 1, where the adsorbed layer structure is defined by electrostatic and excluded-volume interactions. Their balance demands that
≫ 1, where the adsorbed layer structure is defined by electrostatic and excluded-volume interactions. Their balance demands that![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) = − = −![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 2, 2, ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) ′′ = − ′′ = −![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 2 2 |
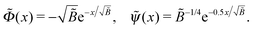 | (C3) |
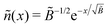 , so the reduced thickness of the adsorbed layer is
, so the reduced thickness of the adsorbed layer is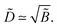 | (C4) |
 with ε = 1/(4
with ε = 1/(4![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) ) ≡ ε*. What happens if
) ≡ ε*. What happens if 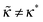 ? In this case a mismatch between the asymptotic solution, eqn (C3), and the actual boundary condition for ψ gives rise to a perturbation of both functions (ψ and Φ) at short distances x ≲ 1/
? In this case a mismatch between the asymptotic solution, eqn (C3), and the actual boundary condition for ψ gives rise to a perturbation of both functions (ψ and Φ) at short distances x ≲ 1/![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 1/4 ≡ x*. For
1/4 ≡ x*. For  and for
and for  , the resultant
, the resultant ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (x) involves 2 length-scales, x* and
(x) involves 2 length-scales, x* and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) , x* ≪
, x* ≪ ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) :
:where x0 is defined by the boundary condition (cf. the second eqn (C2)), and i = 1 for κ > κ*, i = −1 for κ < κ*. (The effect of κ on the electrostatic potential
![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) (x) is negligible in the specified region of κ.)
(x) is negligible in the specified region of κ.)
For x ≫ x*, the effect of the boundary condition  becomes exponentially weak, and for that reason ε stays extremely close to ε*. A more detailed analysis shows that ε ≃ ε* with an exponentially small error (ln|ε − ε*| < −23/2
becomes exponentially weak, and for that reason ε stays extremely close to ε*. A more detailed analysis shows that ε ≃ ε* with an exponentially small error (ln|ε − ε*| < −23/2![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) 3/4 for
3/4 for ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) ≫ 1) if
≫ 1) if  .
.
The opposite case 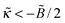 corresponds to very strongly attractive surfaces; in this case
corresponds to very strongly attractive surfaces; in this case  . The polymer density profile in this regime is
. The polymer density profile in this regime is
 | (C5) |
 ,
, 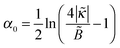 .
.
Thus, we get the following general result:
 | (C6) |
 | (C7) |
So far we considered the effect of 2-body excluded-volume interactions (B), neglecting 3-body interactions (C) for simplicity. This assumption requires that Bn ≫ Cn2. With n = n0ñ, B = B0![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) ,
,  ,
, 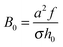 , and ñ ∼
, and ñ ∼ ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) −0.5 (see eqn (C3) above) this condition for
−0.5 (see eqn (C3) above) this condition for ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) ≫ 1 becomes
≫ 1 becomes
The effect of 3-body interactions is analyzed below in the low-salt theta-solvent conditions (B = 0). The reduced 3rd virial parameter is ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) = Cσ2/(2a2f2). The effect of C is negligible if
= Cσ2/(2a2f2). The effect of C is negligible if ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) ≪ 1, i.e. if
≪ 1, i.e. if
![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) ′′ = (ε + ′′ = (ε + ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) ) )![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) + + ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 5, 5, ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) ′′ = − ′′ = −![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 2, 2, ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) ′ = 1. ′ = 1. | (C8) |
![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) at x = 0, since it nearly does not affect either the profiles or the eigenvalue ε, as it follows from our above analysis of the case
at x = 0, since it nearly does not affect either the profiles or the eigenvalue ε, as it follows from our above analysis of the case ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) ≫ 1. (The boundary condition
≫ 1. (The boundary condition  reflecting specific polymer/surface interactions generates a perturbation of polymer density on a short length-scale x* ∼
reflecting specific polymer/surface interactions generates a perturbation of polymer density on a short length-scale x* ∼ ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) −1/6.)
−1/6.)
Using the same sort of approximation as before we arrive at equations
![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) = − = −![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) ñ2, ñ2, ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) ′′ = −ñ ′′ = −ñ |
![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 2. Their solution is
2. Their solution is![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) (x) = − (x) = −![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) 0(1 − x/ 0(1 − x/![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) )4, ñ(x) = ñ0(1 − x/ )4, ñ(x) = ñ0(1 − x/![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) )2 )2 |
Thus, the polymer concentration profile shows parabolic dependence on x in this case.
Both functions ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) (x) and ñ(x) vanish at x >
(x) and ñ(x) vanish at x > ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) within the approximation used above. In reality these functions do not vanish completely, but rather are small in this region (
within the approximation used above. In reality these functions do not vanish completely, but rather are small in this region (![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) ≪
≪ ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) 0, ñ ≪ ñ0), showing exponential decay:
0, ñ ≪ ñ0), showing exponential decay:
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) , for |x −
, for |x − ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) | ≲
| ≲ ![[small xi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e119.gif) , where
, where  is the edge decay length. The result is
is the edge decay length. The result isε ≃ 0.317/![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 1/3, 1/3, ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) ≫ 1 ≫ 1 | (C9) |
![[small xi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e119.gif) ∼
∼ ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 1/6. The corresponding excess charge at low ionic strength is
1/6. The corresponding excess charge at low ionic strength is | (C10) |
Acknowledgements
We acknowledge the partial support from the International Research Training Group (IRTG) “Soft Matter Science: Concepts for the Design of Functional Materials”.References
- D. H. Napper, Polymer Stabilization of Colloidal Dispersions Academic, London, 1983 Search PubMed.
- Y. Lvov, G. Decher, H. Haas, H. Möhwald and A. Kalachev, Physica B, 1994, 198, 89 CrossRef CAS.
- G. Decher, Science, 1997, 277, 1232 CrossRef CAS.
- R. R. Netz and D. Andelman, Phys. Rep., 2003, 380, 1–95 CrossRef CAS.
- U. Voigt, V. Khrenov, K. Tauer, M. Halm, W. Jaeger and R. von Klitzing, J. Phys.: Condens. Matter, 2003, S15, 213 CrossRef.
- I. Borukhov, D. Andelman and H. Orland, Macromolecules, 1998, 31, 1665 CrossRef CAS.
- J.-F. Joanny, Eur. Phys. J. B, 1999, 9, 117 CrossRef CAS.
- A. Shafir and D. Andelman, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 061804 CrossRef PubMed.
- Q. Wang, Macromolecules, 2005, 38, 8911 CrossRef CAS.
- A. Shafir and D. Andelman, Eur. Phys. J. E: Soft Matter Biol. Phys., 2006, 19, 155 CrossRef CAS PubMed.
- G. Decher and B. J. Schlenoff, Multilayer Thin Films. Wiley-VCH, Weinheim, 2003 Search PubMed.
- J. F. Quinn, A. P. R. Johnston, G. K. Such, A. N. Zelikin and F. Caruso, Chem. Soc. Rev., 2007, 36(5), 707–718 RSC.
- S. F. Edwards, Proc. Phys. Soc., London, 1965, 85, 613 CrossRef CAS.
- I. M. Lifshitz, A. Y. Grosberg and A. R. Khokhlov, Rev. Mod. Phys., 1978, 50, 683 CrossRef CAS.
- P.-G. de Gennes, Scaling Concepts in Polymer Physics, Cornell Univ. Press, Ithaca, 1979 Search PubMed.
- A. Grosberg and A. Khokhlov, Statistical Physics of Macromolecules, American Institute of Physics, New York, 1994 Search PubMed.
- K. Tang and N. A. M. Besseling, Soft Matter, 2016, 12, 1032 RSC.
- P.-G. de Gennes, P. Pincus, F. Brochard and R. M. Velasco, J. Phys., 1976, 37, 1461 CAS.
- A. R. Khokhlov, Polymer, 1978, 19, 1387 CrossRef CAS.
- D. Schaefer, J. F. Joanny and P. Pincus, Macromolecules, 1980, 13, 1280 CrossRef CAS.
- A. N. Semenov and A. A. Shvets, Soft Matter, 2015, 11, 8863 RSC.
- G. Durand, F. Lafuma and R. Audebert, Prog. Colloid Polym. Sci., 1988, 76, 278 CAS.
- N. Hansupalak and M. M. Santore, Langmuir, 2003, 19, 7423 CrossRef CAS.
- M. Muthukumar, J. Chem. Phys., 1987, 86, 7230 CrossRef CAS.
- S. C. Liufu, H. N. Xiao and Y. P. Li, J. Colloid Interface Sci., 2005, 285, 33 CrossRef CAS PubMed.
- O. J. Rojas, P. M. Claesson, D. Muller and R. D. Neuman, J. Colloid Interface Sci., 1998, 205, 77 CrossRef CAS PubMed.
- T. Sennerfors, D. Solberg and F. Tiberg, J. Colloid Interface Sci., 2002, 254, 222 CrossRef CAS PubMed.
- T. Cosgrove, T. M. Obey and B. Vincent, J. Colloid Interface Sci., 1986, 111, 409 CrossRef CAS.
- E. Kokofuta and K. Takahashi, Macromolecules, 1986, 19, 351 CrossRef.
- M. Kawaguchi, H. Kawaguchi and A. Takahashi, J. Colloid Interface Sci., 1988, 124, 57 CrossRef CAS.
- A. N. Semenov, J. Bonet-Avalos, A. Johner and J. F. Joanny, Macromolecules, 1996, 29, 2179 CrossRef CAS.
Footnotes |
| † The positive sign is chosen just to be specific. |
| ‡ The result E = 0 is strictly valid only for N → ∞. For finite chains it is replaced by E ≃ −(1/N)ln(nmax/nb).31 |
| This journal is © The Royal Society of Chemistry 2016 |