DOI:
10.1039/C6SM01094F
(Paper)
Soft Matter, 2016,
12, 8495-8505
Dynamics of self-propelled filaments pushing a load†
Received
10th May 2016
, Accepted 1st August 2016
First published on 1st August 2016
Abstract
Worm-like filaments, which are propelled by a tangential homogeneous force along their contour, are studied as they push loads of different shapes and sizes. The resulting dynamics is investigated using Langevin dynamics simulations. The effects of size and shape of the load, propulsion strength, and thermal noise are systematically explored. The propulsive force and hydrodynamic friction of the load cause a compression in the filament that results in a buckling instability and versatile motion. Distinct regimes of elongated filaments, curved filaments, beating filaments, and filaments with alternating beating and circular motion are identified, and a phase diagram depending on the propulsion strength and the size of the load is constructed. Characteristic features of the different phases, such as beating frequencies and rotational velocities, are demonstrated to have a power-law dependence on the propulsive force.
1 Introduction
Self-propelled filaments are of fundamental importance for natural and artificial active matter. One of the most prominent examples from biology are actin filaments and microtubules on motility assays.1 In addition to playing a decisive role for the mechanical behavior of the cell cytoskeleton,2 these filaments are ideal for the study of collective phenomena and non-equilibrium statistical mechanics.3–10 Finally, microtubules are the major constituent of cilia, the hair-like structures that serve inter alia as the propulsive component of most eukaryotic cells.1 Artificial filament-like active matter can either be synthesized directly from biological filaments, such as artificially bundled microtubules that show beating motion when clamped to a wall,11 or from the assembly of Janus colloids to a propelled chain.12–16 A unifying feature of active filaments is that their physical behavior is governed by their slender body, their deformability, and their ability to buckle under a compressive load.
Theoretical studies of active filaments have hitherto concentrated on filaments that are either freely swimming17–22 or clamped or pinned at the leading tip22–26 (where the tip of a clamped filament does not have rotational or translational degrees of freedom, while the tip of a pinned filament is fixed in its position but is free to rotate). For unconstrained swimmers, analytic theory and Brownian dynamics simulations show that colored noise leads to super-diffusive filament motion and stronger bending of the filament.20 Spontaneous symmetry breaking in worm-like chains of stresslets results in predominantly translational or rotational motion.19 Finally, Brownian dynamics simulations reveal that tangentially self-propelled filaments swim approximately along the contour of an infinite chain of equal bending rigidity and, in two dimensions, can wind into spirals for sufficiently strong propulsion and low bending rigidity.17 When clamped or pinned, self-propelled filaments buckle at sufficiently strong propulsion forces as revealed by analytic23,24 and computational25,26 studies; clamped filaments display a beating motion, and pinned filaments a spontaneous rotational motion.
The motion of a self-propelled filament pushing a load in a viscous fluid is studied here. The load – a rigid body of finite size – acts as a translational and rotational hydrodynamic resistance. This study thereby closes the gap between the two extremes of freely swimming filaments that move without additional hydrodynamic resistance, and pinned or clamped filaments, which correspond to filaments pushing either infinite translational and zero rotational hydrodynamic resistance (pinned) or infinite translational and infinite rotational hydrodynamic resistance (clamped). We find that the filament motion is decisively controlled by the size and shape of the rigid body, as well as the active propulsion force. A new type of motion of alternating beating and rotational swimming is observed in addition to the sperm-like beating and rotational phases known for clamped and pinned filaments. This beating motion is due to a mechanical instability. Although it is geometrically similar to the flagellar beat of sperm, it does not contribute to the swimmer propulsion, in contrast to sperm where it is essential. Thus, our model is well suited to describe the motion of semi-flexible filaments on motility assays and of self-propelled chains of colloids, but has no direct relation to sperm or bacteria swimming.
2 Model and methods
2.1 Self-propelled filament
We study worm-like filaments that are connected to either a rigid rod or a hexagon in two dimensions with the filament being propelled with a constant force acting tangentially in the direction of the rigid body, as shown in Fig. 1. The filament, which is also referred to as the tail, is discretized into a chain of NF beads. The rigid body, also referred to as the head or the load, is discretized into NB beads. The motion of the beads is described by the Langevin equation| | 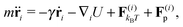 | (1) |
where ![[r with combining umlaut]](https://www.rsc.org/images/entities/b_char_0072_0308.gif) i and ṙi are the first and second time derivative of the position ri of bead i, m is the mass of the beads, γ is the friction coefficient with the solvent, U is the configurational potential,
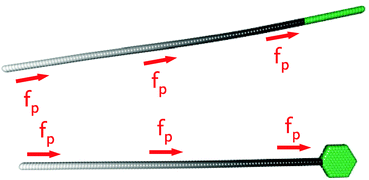
i and ṙi are the first and second time derivative of the position ri of bead i, m is the mass of the beads, γ is the friction coefficient with the solvent, U is the configurational potential, 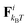 is the thermal noise force that acts on particle i, and F(i)p is the propulsive force.
is the thermal noise force that acts on particle i, and F(i)p is the propulsive force.
 |
| | Fig. 1 Simulation model. The active force acts tangentially along all bonds in the worm-like filament of length L, which is discretized into NF beads (grayscale). The color gradient indicates the force direction. The rigid, passive body (green) is either a rod composed of NR beads or a (filled) hexagon composed of NH beads. | |
The configurational potential
| | | U = Ubond + Uangle + UEV, | (2) |
is composed of a spring contribution
| | 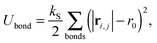 | (3) |
that acts between all neighboring beads in the filament and the beads that connect the filament and the rigid body, a bending energy
| | 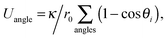 | (4) |
that acts between all groups of three adjacent beads in the tail and the first beads of the head, and a volume-exclusion interaction
| | 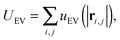 | (5) |
| | 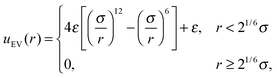 | (6) |
that acts on beads separated by three or more bonds, where
r0 is the equilibrium distance between bonded beads,
kS is a spring constant,
ri,j is the vector between two beads
i and
j,
κ is the bending rigidity,
θ is the angle between three subsequent beads, and
σ and
ε are the bead diameter and the characteristic volume exclusion interaction energy. The self-propulsion acts tangentially along all bonds in the tail
| | 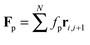 | (7) |
with a force per unit length
fp. The drag force −
γṙi and the thermal force
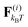
act on all beads. The thermal force is modeled as white noise with zero mean and variance 2
kBTγ/Δ
tS, where Δ
tS is the time step, as described in
ref. 27. Note that hydrodynamic interactions are not included in our model (free-draining approximation), which is a reasonable simplification for systems like filaments on molecular motor carpets. The relevance of hydrodynamic interactions for the motion of rods and filaments, in particular near surfaces, has been discussed in
ref. 28–32.
The rigid rod is composed of NR beads on a line with spacing r0. The (filled) hexagon is composed of NH beads that are positioned on a hexagonal lattice with a spacing of r0. The crucial feature of these bodies is their resistance to translational and rotational motion. The resistance to translational motion is
and
for the rod and hexagon. The resistance to rotational motion around the center of gravity of the rigid body is
| | 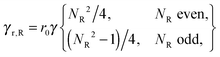 | (10) |
for the rod. For the hexagon,
| | 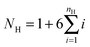 | (11) |
and
| | 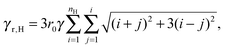 | (12) |
where
nHr0 is the edge length of the hexagon, from which it follows that
especially for large
NH. Comparison of
eqn (8)–(10) and (13) thus shows that the rod has much stronger resistance to rotational motion for equal translational resistance.
The Langevin equation is used to facilitate Verlet integration33,34 instead of Euler integration, which allows a much larger time step ΔtS and therefore provides faster computations. m and γ are selected such that viscous drag dominates over inertia even at short timescales, such that the behavior of the system is close to overdamped. To ensure that inertia has a negligible effect, simulations at selected conditions are rerun with an increased friction coefficient. Equal observations for the measured quantities show that inertia has no significant impact on the results presented here. The rigidity of the head is ensured by combining all forces inside the rod or hexagon to a single force and torque that acts on the center of mass and integrating the velocities and positions of the head beads as a single entity.
The system can be described by three dimensionless numbers. The flexure number
| | 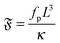 | (14) |
is the ratio of propulsive forces to bending rigidity,
| | 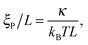 | (15) |
is the ratio of the persistence length
ξP to the filament length
L. And finally, the ratio of the translational hydrodynamic friction of the filament
γF to the translational hydrodynamic friction of the rigid body
γB is
| | 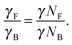 | (16) |
We study systems in which
kS is sufficiently large that the bond length is almost constant, that the local curvature is sufficiently small to ensure validity of the worm-like chain description, and that the thickness of the chain has negligible impact on the results. The three dimensionless numbers specified above therefore provide a complete characterization of the system.
Simulation parameters and results are reported in dimensionless form, where length is measured in units of the filament length L, energy is measured in the units of κ/L, and time is measured as the viscous relaxation time of the first bending mode of a filament35
| | 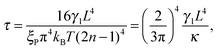 | (17) |
where we have introduced the friction per unit length
γl =
γNF/
L and employed
n = 2 for the first bending mode. Fixed parameters in the simulations are Δ
tS = 2.466 × 10
−4τ,
m = 12.159
τ2κ/
L3,
m/
γ = 0.0247
τ,
NF = 100,
kS = 2 × 10
7κ/
L3,
r0 =
σ =
L/
NF, and
ε = 0.5
κ/
L. Different values of
γF/
γB are examined by selecting
NR ∈ {5,10,15,20,30,40,60,120,240} and
NH ∈ {7,19,37,61,91,127,169,217,271}, which corresponds to the hexagonal edge lengths
nH ∈ {1,2,3,4,5,6,7,8,9}. Additional simulations were run with a clamped filament corresponding to an infinitely large load or
γF/
γB = 0. The propulsion force
fp was varied to sample flexure numbers in the range 0 ≤
![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif)
≤ 10
5. The effect of thermal noise was studied by running simulations at two different temperatures
kBT ∈ {0.0005,0.5}
κ/
L, corresponding to
ξP/
L ∈ {2000,2}. Thermal energy has a negligible impact for the simulations at the lower temperature.
Unless mentioned explicitly in the following, simulations were started with straight filament configuration and equilibrated for 1232.825τ. Subsequent simulations for collecting data for ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) ≤ 5000 were run for 123282.5τ at low temperatures and 246565τ at high temperatures. Bead coordinates were stored every 0.616τ. For
≤ 5000 were run for 123282.5τ at low temperatures and 246565τ at high temperatures. Bead coordinates were stored every 0.616τ. For ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) > 5000, simulations were run 20 times shorter and data was collected 20 times more frequently. All simulations were performed with the LAMMPS molecular simulation package36 with in-house modification to describe the self-propulsion. Additional simulations to study the impact of a distinct bending rigidity of the link between the filament and the load are presented in the ESI.†
> 5000, simulations were run 20 times shorter and data was collected 20 times more frequently. All simulations were performed with the LAMMPS molecular simulation package36 with in-house modification to describe the self-propulsion. Additional simulations to study the impact of a distinct bending rigidity of the link between the filament and the load are presented in the ESI.†
2.2 Curvature analysis with principal component analysis
Principal component analysis37 (PCA) of the local curvature c is employed to characterize the filament motion. PCA is effectively a coordinate transformation to a coordinate system in which the data is uncorrelated. This new coordinate system is spanned by the eigenvectors ψi of the covariance matrix of the data in the initial coordinate system. ψi are also referred to as modes. The magnitude of the data in the new coordinate system is denoted by the amplitudes λi of each mode. The unentered PCA is employed, in which the entries of the covariance matrix are computed aswhere ci and cj are the local curvatures at the beads i and j and the angular brackets denote a time average. The eigenvectors are ranked by the size of the eigenvalues, which are equal to the average square of the amplitudes of the data in the new coordinate system. Therefore, they are ordered by their importance to describe the filament motion. If few eigenvalues dominate, the overall behavior of the system can be approximated by the dynamics of these eigenmodes only. Note that for the chosen bending potential and small local curvatures, the total bending energy of the filament is| | 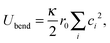 | (19) |
where the sum is over all angles in the filament. The representation| | 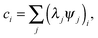 | (20) |
where the sum is over all eigenmodes, and the property that the eigenmodes are normalized and orthogonal, yields| | 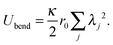 | (21) |
The bending energy of a single mode is thus 1/2κr0λj2. The amplitudes therefore have a strong physical interpretation and meaning.
3 Results
Depending on the strength of propulsion, size and shape of the load (a rod or a hexagon), and thermal energy, the motion of the filament can be subdivided into the four characteristic regimes shown in Fig. 2. In the elongated phase that is observed for low propulsion strengths, the filament is almost straight. Above a critical self-propulsion force, the filament buckles under the compressive load that results from the balance of self-propulsion and viscous drag. For strong self-propulsion, the filament enters the beat phase. Here, the motion is dominated by a sperm-like beating pattern, as observed for self-propelled clamped filaments.26 At large temperatures (ξp/L = 2), this beating pattern can be interrupted by spontaneous, short-lived circular swimming motion in the beat-and-circle regime. Filaments at intermediate propulsion strength, and attached to sufficiently large hexagonal heads, buckle into a monotonically curved shape. As a consequence, the filaments swim in a circle, as previously observed for self-propelled, asymmetric rigid bodies.38,39 The swimming direction in this rotation phase spontaneously changes between clockwise and counter-clockwise rotation, especially at large thermal noise.
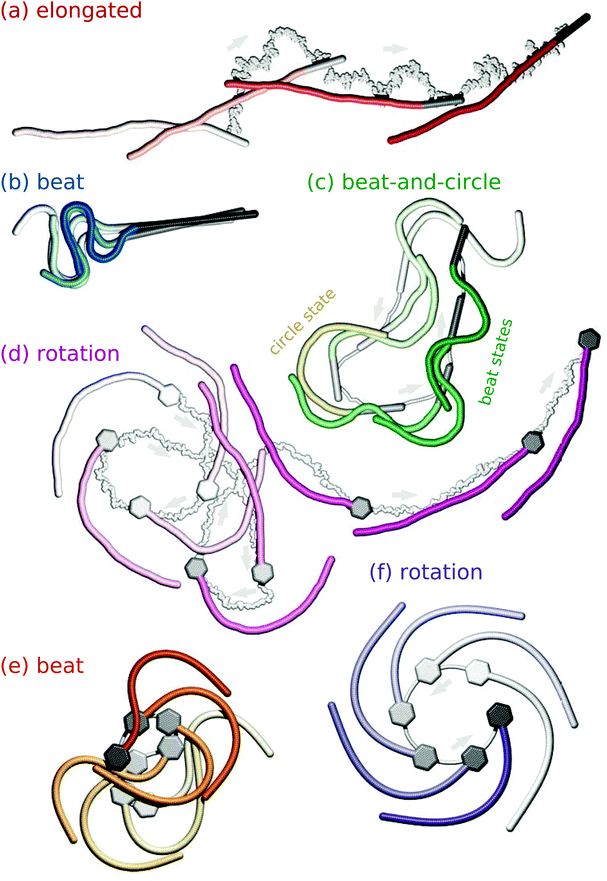 |
| | Fig. 2 Sequence of filament snapshots from the different regimes. Time increases from transparent to opaque. The gray lines are the trajectories of the center of mass of the rigid body. (a) Filament attached to a rod-shaped load in the elongated phase with ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) = 50, ξP/L = 2, and γF/γB = 5. (b) Filament attached to a rod-shaped load in the beat phase with = 50, ξP/L = 2, and γF/γB = 5. (b) Filament attached to a rod-shaped load in the beat phase with ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) = 5000, ξP/L = 2, and γF/γB = 1.67. (c) Filament attached to a rod-shaped load in the beat-and-circle regime with = 5000, ξP/L = 2, and γF/γB = 1.67. (c) Filament attached to a rod-shaped load in the beat-and-circle regime with ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) = 5000, ξP/L = 2, and γF/γB = 5. (d) Filament with a hexagonal head in the rotation phase with = 5000, ξP/L = 2, and γF/γB = 5. (d) Filament with a hexagonal head in the rotation phase with ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) = 250, ξP/L = 2, and γF/γB = 1.64. (e) Filament with a hexagonal head in the beat phase at low thermal noise with = 250, ξP/L = 2, and γF/γB = 1.64. (e) Filament with a hexagonal head in the beat phase at low thermal noise with ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) = 1000, ξP/L = 2000, and γF/γB = 1.1. (f) Filament with a hexagonal head in the rotation phase at low thermal noise with = 1000, ξP/L = 2000, and γF/γB = 1.1. (f) Filament with a hexagonal head in the rotation phase at low thermal noise with ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) = 150, ξP/L = 2000. Videos from all regimes are available in the ESI.† = 150, ξP/L = 2000. Videos from all regimes are available in the ESI.† | |
Criteria to identify the different phases and delineate phase boundaries, based on the principal component analysis, are developed in Section 3.1. These criteria are employed to construct phase diagrams in Section 3.2. This information paves the way for a more detailed description of the filament dynamical properties presented Section 3.3. The various time scales examined in this description are summarized in Table 1.
Table 1 Description of characteristic times and angular velocities
|
τ
|
Time unit defined in eqn (17) |
|
τ
b
|
Lifetime of the beat state in the beat-and-circle regime |
|
τ
c
|
Lifetime of the circle state in the beat-and-circle regime |
|
τ
r
|
Lifetime of persistent swimming in the same direction in the rotation phase |
|
ω
b
|
Angular velocity of the beating motion |
|
ω
e
|
Angular velocity of the end-to-end vector |
|
ω
c
|
Average angular velocity of the end-to-end vector in the circle state |
|
ω
r
|
Angular velocity of the rotation phase |
3.1 Phase description and identification
3.1.1 Elongated phase.
In the elongated phase, the filament shape is nearly straight, and deviations are dominated by thermal noise. Because of the large stiffnesses ξP/L ∈ {2,2000} examined here, the filament is only weakly deformed by the thermal forces. The average bending energy is approximately equal in all modes ψi and satisfies the equipartition theorem. The amplitudes are uncorrelated and show Gaussian behavior, as shown in Fig. 3(a). For sufficiently strong propulsion, but still in the elongated regime, the time-autocorrelation functions| | 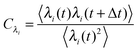 | (22) |
of the amplitudes λ1 and λ2 show regular oscillations around zero. However, λ1 and λ2 are so small that strong deformations or even oscillations are not visible in real space. Linear stability analysis40 of the overdamped equations of motion of a perfectly aligned filament attached to a rod reveals the reason for the onset of oscillations in the elongated phase. For sufficiently strong propulsion, the aligned filament turns from a stable node, where all eigenvalues of the Jacobian matrix are real and negative (with the exception of the eigenvalue of zero that corresponds to the Goldstone modes that has to exist for our model), to a stable focus, where the real parts of the eigenvalues are negative but at least one pair of complex conjugated eigenvalues with a non-zero imaginary part exists. Thus, this kind of oscillations are not enough to indicate the presence of beating motion.
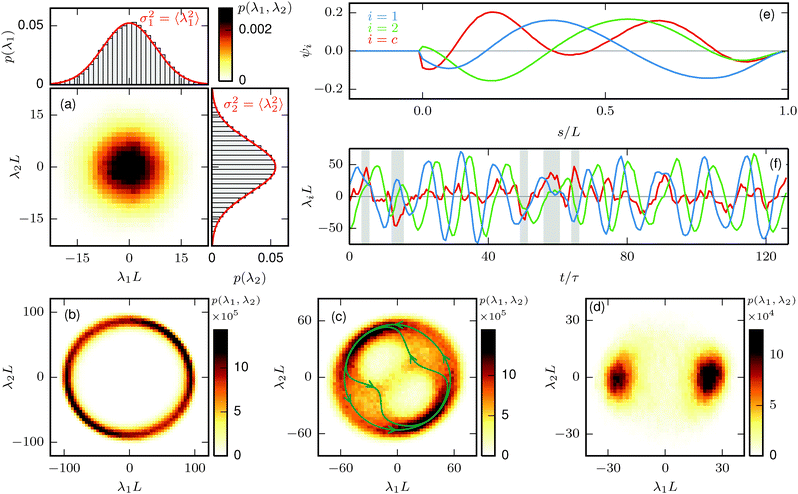 |
| | Fig. 3 Shape characterization obtained from principal component analysis (PCA). Histograms of λ1 and λ2 for (a) the elongated phase, (b) the beat phase, (c) the beat-and-circle regime, and (d) the rotation phase, with the same parameters as in Fig. 2(a)–(d). The peaks in quadrant I and III in (b) clearly demonstrate that the angular phase velocity is dependent on the phase angle for the beat phase. The green arrows in (c) sketch typical amplitude evolutions in the λ1–λ2 plane. Crossing the circle via the bridge in (c) is the absolute exception and a change of rotation direction is impossible. (e–f) Eigenmodes and time evolution of the amplitudes for parameters from the beat-and-circle regime with equal simulation parameters as in (c). Circle states are marked by the gray background color. | |
3.1.2 Buckling.
A buckling criterion can be used to separate the elongated (non-buckled) phase from the other (buckled) phases (beat, beat-and-circle, and rotation phases).
In the elongated phase, the modes amplitude λi are statistically independent and Gaussian distributed. Therefore, the sum of the normalized squares of the first two eigenvalues,
| | 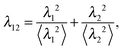 | (23) |
follows a Rayleigh distribution,
| | f(λ12) = λ12/σr2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−λ122/2σr2), exp(−λ122/2σr2), | (24) |
with scale parameter
σr = 1.
In contrast, for the buckled filaments, the first two amplitudes λ1, λ2 show non-Gaussian behavior (see Fig. 3(b)–(d)). The deviation of the probability density p(λ12) from the Rayleigh distribution f(λ12),
| | 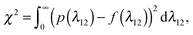 | (25) |
can therefore be used to detect filament buckling. The integral is evaluated from density distributions discretized into bins of width Δ
λ12 = 0.1.
3.1.3 Beat phase.
In the beat phase, the filament is buckled and performs a sperm-like beat pattern. The structure is dominated by two eigenmodes whose amplitudes oscillate at the same frequency and form a limit cycle in the λ1–λ2 plane, as shown in Fig. 3(b). The time-autocorrelation functions of the amplitudes λ1 and λ2 show strong and persistent oscillations. In terms of stability analysis, the transition from the elongated phase to the beat phase corresponds to a Hopf bifurcation, in which the real value of the pair of eigenvalues with the non-zero imaginary part becomes positive and the stable focus becomes an unstable focus.
Thus, the beat phase is characterized by a buckled filament, with periodic oscillations in the autocorrelation function Cλ1. The oscillation criteria is met if there is at least one statistically significant minimum (3-σ environment) below zero in Cλ1.
3.1.4 Beat-and-circle regime.
Sufficiently strong thermal fluctuations can interrupt the regular beat. The filament enters the beat-and-circle regime. This manifests itself in principal component space by a decay of the amplitudes of the beating modes λ1 and λ2 and the increase of the amplitude λc of the circle mode ψc as shown in Fig. 3(f). The circle mode is defined as the mode whose squared amplitudes λi2 show maximal negative correlation with λ12 + λ22. Most often it is ψ3, but sometimes ψ4. The filament is defined as being in a circle state when λc2 is the largest amplitude. The filament is mostly bent into the same direction in the circle mode ψc, as shown in Fig. 3(e), which results in the circular motion of the filament.
3.1.5 Rotation phase.
The rotation phase only appears for filaments pushing a hexagonal load. The filament buckles and gives rise to motion on a circle. The filament shape is dominated by the first principal mode ψ1 only. In contrast to the beat phase, there are no oscillations in the autocorrelation function of λ1. There is thus no periodic oscillation in the system, even if the direction of rotation changes occasionally.
The region of stability of the rotation phase in the phase diagram is characterized by the lack of filament oscillations (equivalent to the absence of oscillations in Cλ1 (cf. Section 3.1.1)), but the existence of rotational motion. The criterion for the existence of circular swimming motion is a significant minimum below zero (3-σ environment) in the time-autocorrelation function
| | | Cte = 〈te(t)te(t + Δt)〉 | (26) |
of the end-to-end vector
te from the leading tip of the load to the free end of the filament.
3.2 Phase diagram
Phase diagrams can now be constructed on the basis of the criteria described in Section 3.1. A filament is buckled when the distribution of the first two eigenmodes is non-Gaussian; it is elongated otherwise. A buckled filament is in the beat phase if oscillations in Cλ1 are observable; it is in the rotation phase if oscillations in Cλ1 are not observable but oscillations in Cte do exist. The beat-and-circle state is not a distinct phase, but a region within the phase diagram in which oscillations in Cλ1 are visible. The importance of the circle motion in this regime is characterized by the fraction Pλc of states in which the circle mode dominates.
The phase diagrams are depicted in Fig. 4. The filament attached to a rod at low temperature (ξp/L = 2000) (cf.Fig. 4(a)) shows the simplest phase behavior; the elongated and the beating phases are separated by a sharp boundary, where χ2 steeply increases. This boundary moves to larger values of ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) for decreasing rod length. Simulation results and stability analysis are in excellent agreement. Note that in the elongated phase, oscillations in Cλ1 appear already before the transition to the beat phase, when the stability analysis predicts that the stable node turns into a stable focus (light gray line in Fig. 4(a)); however, the oscillation amplitude is too small to result in any visible patterns in the filament structure (as discussed in Section 3.1.1).
for decreasing rod length. Simulation results and stability analysis are in excellent agreement. Note that in the elongated phase, oscillations in Cλ1 appear already before the transition to the beat phase, when the stability analysis predicts that the stable node turns into a stable focus (light gray line in Fig. 4(a)); however, the oscillation amplitude is too small to result in any visible patterns in the filament structure (as discussed in Section 3.1.1).
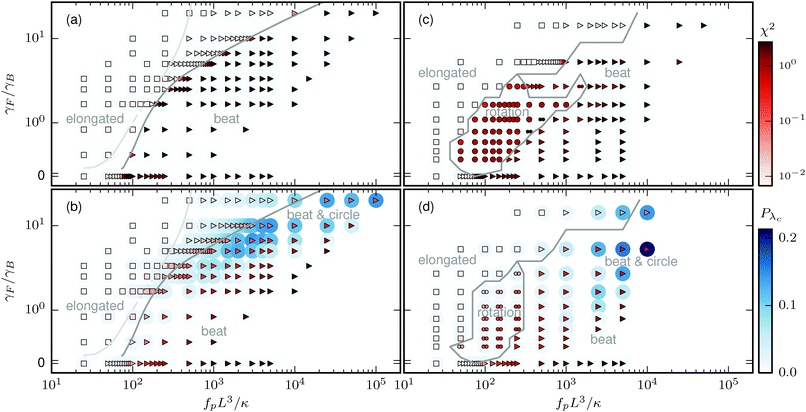 |
| | Fig. 4 Phase diagram as a function of head size over filament length γF/γB and flexure number ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) = fpL3/κ. (a) Filament with rod-shaped load at low temperature (ξP/L = 2000). (b) Filament with rod-shaped load at high temperature (ξP/L = 2). (c) Filament with hexagonal head at low temperature (ξP/L = 2000). (d) Filament with hexagonal head at high temperature (ξP/L = 2). Symbols: triangles for oscillations in Cλ1, circles for permanent rotation, double-circles for rotation with alternating directions, squares for non-rotating and non-oscillating states. The gray lines for (c) and (d) are phase boundaries and are guides to the eye. The gray line for (a) and (b) labels the transition from a stable focus to an unstable focus in the stability analysis. The light gray line labels the transition from a stable node to a stable focus. The line is dotted where the transition from a node to a focus is interpolated because it could not be determined accurately due to numeric difficulties. Pλc is the fraction of states in which the circle mode ψc dominates, and χ2 measures the deviation of Gaussian behavior of λ1 and λ2. = fpL3/κ. (a) Filament with rod-shaped load at low temperature (ξP/L = 2000). (b) Filament with rod-shaped load at high temperature (ξP/L = 2). (c) Filament with hexagonal head at low temperature (ξP/L = 2000). (d) Filament with hexagonal head at high temperature (ξP/L = 2). Symbols: triangles for oscillations in Cλ1, circles for permanent rotation, double-circles for rotation with alternating directions, squares for non-rotating and non-oscillating states. The gray lines for (c) and (d) are phase boundaries and are guides to the eye. The gray line for (a) and (b) labels the transition from a stable focus to an unstable focus in the stability analysis. The light gray line labels the transition from a stable node to a stable focus. The line is dotted where the transition from a node to a focus is interpolated because it could not be determined accurately due to numeric difficulties. Pλc is the fraction of states in which the circle mode ψc dominates, and χ2 measures the deviation of Gaussian behavior of λ1 and λ2. | |
The phase diagram for the filament attached to a rod at elevated temperatures (ξp/L = 2) is more complex (see Fig. 4(b)). The transition between the elongated phase and the beat phase is at the same position, in agreement with the observation that thermal energy has only a weak effect on buckling transitions for filaments with ξP/L ≥ 2 for similar systems.41 The transition in the values of χ2 is less sharp, though. In addition to the pure beating motion for long rods, the phase diagram has a region in which the circle swimming mode is of significant importance. The transition from the purely beating to the beat-and-circle region is smooth.
The filament attached to a hexagonal head displays three different behaviors. The elongated phase is approximately in the same region of parameter space as for the rod-shaped load. Differently to rods, there is the rotation phase at intermediate propulsive strength. Notable differences for the filament attached to the hexagonal head at low temperatures (Fig. 4(c)), compared to the same filament at high temperatures (Fig. 4(d)) are: first, the rotation phase takes a smaller fraction of the phase diagram, and second, at high temperatures the rotation mode always shows spontaneous switching between clockwise and counter-clockwise rotation, whereas a change of the rotation direction rarely occurs at low temperatures. This is a result of the increased thermal energy that occasionally kicks the buckled filament over the energy barrier separating the clockwise and counter-clockwise rotation. The transition from the rotation phase to the beating phase can be explained noting that, at low ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) and high temperature, the “energy” barrier between clockwise and counter-clockwise rotations is strongly reduced, leading to fast thermal jumps over the barrier.
and high temperature, the “energy” barrier between clockwise and counter-clockwise rotations is strongly reduced, leading to fast thermal jumps over the barrier.
3.3 Phase dynamics
3.3.1 Bending energy.
The bending energy stored in the first mode is shown in Fig. 5. In the elongated phase (at low propulsion), the bending energy in the modes is not affected by activity but is controlled by thermal noise only. Because of the equivalence of (squared) amplitudes and bending energies, the amplitudes follow the equipartition theorem| | 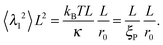 | (27) |
In the beat phase (strong propulsion), the bending energies in the first mode ψ1 show linear dependence on the propulsion force fp. Moreover, when plotted over a rescaled flexure number| | 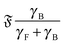 | (28) |
as in Fig. 5, the observations for different temperatures and head sizes and shapes collapse onto a single curve. The term γB/(γF + γB) is motivated by a consideration of the effective forces on the beads in a comoving reference frame. The straight filament moves with a velocityIn the comoving reference frame, part of the driving force is balanced by friction. The effective force on each bead remaining for buckling is then| | 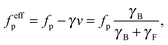 | (30) |
which justifies the rescaled flexure number (28). An interesting feature of the rotation phase at intermediate propulsions (Fig. 5(b)) is that the bending energies collapse onto a single line for different head sizes and temperatures, and that the dependence on the self-propulsion is weak.
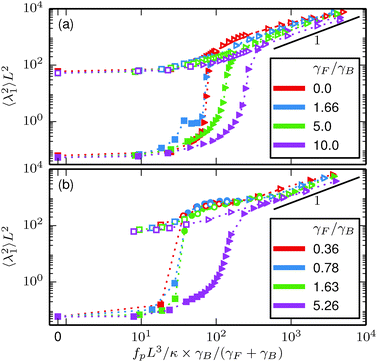 |
| | Fig. 5 Average amplitude of the dominating mode ψ1 for (a) the rod swimmer and (b) the hexagon swimmer. Triangles indicate measurable oscillations in Cλ1, circles indicate the rotation phase, and squares non-oscillating and non-rotating filaments. Closed symbols are for the low temperature (ξP/L = 2000) and open symbols for the high temperature (ξP/L = 2). Note that the scaling lines in (a) and (b) are depicted at identical coordinates. | |
3.3.2 Beat phase: angular beating frequency.
The angular frequency of the beating pattern ωb is determined by fitting the autocorrelation function Cλ1 with a damped oscillation| | ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) λ1 = cos(ωbΔt)exp(−Δt/τbd), λ1 = cos(ωbΔt)exp(−Δt/τbd), | (31) |
where τbd is a characteristic decay time. When plotted over the flexure number ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) , the frequency ωb, for the rod head, approximately collapses onto a single line (Fig. 6(a)). The thermal energy and the rod length have a rather weak effect. The scaling ωb ∝
, the frequency ωb, for the rod head, approximately collapses onto a single line (Fig. 6(a)). The thermal energy and the rod length have a rather weak effect. The scaling ωb ∝ ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) 4/3 results from a balance of the energy input in the system by the propulsive force and the dissipation of energy through friction with the solvent, as shown in ref. 26. Note that the same scaling is approximately valid also for oscillations in the elongated phase (for fpL3/κ ≲ 300). For the filament attached to a hexagonal head (Fig. 6(b)), the effect of size of the load is more important than for rod-shaped loads, which is apparent from that data for different friction ratios γF/γB do not collapse onto a single curve.
4/3 results from a balance of the energy input in the system by the propulsive force and the dissipation of energy through friction with the solvent, as shown in ref. 26. Note that the same scaling is approximately valid also for oscillations in the elongated phase (for fpL3/κ ≲ 300). For the filament attached to a hexagonal head (Fig. 6(b)), the effect of size of the load is more important than for rod-shaped loads, which is apparent from that data for different friction ratios γF/γB do not collapse onto a single curve.
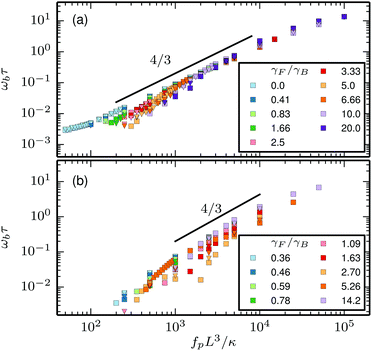 |
| | Fig. 6 Angular frequency of the beating filament ωb for (a) the rod swimmer and (b) the hexagon swimmer. Squares indicate low temperature (ξP/L = 2000) and triangles high temperature (ξP/L = 2). | |
3.3.3 Beat-and-circle regime: state characteristics and angular velocity.
Histograms of the lifetime of the beat and circle states, τb and τc, respectively, were computed for ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) = 5000, γF/γB = 10, and ξP/L = 2. Very short-lived states, with a lifetime of 3 or less snapshots, were ignored in the analysis.
= 5000, γF/γB = 10, and ξP/L = 2. Very short-lived states, with a lifetime of 3 or less snapshots, were ignored in the analysis.
As shown in Fig. 7(a), the histogram of τb decays exponentially with half life ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) b, where the bar indicates an average over all individual uninterrupted beat states. This suggests that the onset of circular motion is controlled by an underlying Poisson process, that – since the beat-and-circle motion only occurs at high temperatures – is activated by thermal noise.
b, where the bar indicates an average over all individual uninterrupted beat states. This suggests that the onset of circular motion is controlled by an underlying Poisson process, that – since the beat-and-circle motion only occurs at high temperatures – is activated by thermal noise.
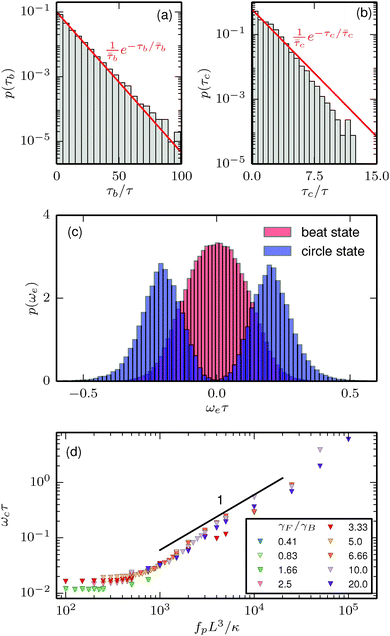 |
| | Fig. 7 Histograms of the lifetime of (a) the beat state τb and (b) the circle state τc, in the beat-and-circle regime. (c) Histogram of the instantaneous rotational velocity ωe of the end-to-end vector separated into beat-and-circle states. Note that both curves are normalized separately. (d) Average angular velocity ωc of the end-to-end vector in the circle state. The data from (a) to (c) is for the rod swimmer at ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) = 5000, γF/γB = 0.1, and ξP/L = 2. = 5000, γF/γB = 0.1, and ξP/L = 2. | |
The lifetime of the circle state on the other hand, shows deviations from the exponential decay for large τc (see Fig. 7(b)). At large τc, the measured histogram decays more quickly than the exponential fit, i.e., the circular swimming state is short-lived. As a result of the short lifetime, the overall rotation angle of the end-to-end vector in an uninterrupted circle state is typically less than π/3 for any simulation. This suggests that the circle motion in the beat-and-circle regime is an unstable transient state. This is also confirmed by numerous trials with different starting configurations of the rod swimmer that failed to reproduce a circle-swimming agent at low temperatures (ξp/L = 2000).
The instantaneous angular rotation velocity ωe of the swimmer is approximated using the symmetric derivative of the orientation of the end-to-end vector from subsequent snapshots. As shown in Fig. 7(c), the histogram of ωe shows a broad peak centered around zero for the beat state. In contrast, p(ωb) has a minimum at ωe = 0 for the circle state and has two peaks for positive and negative rotation. This confirms that the circle state corresponds to predominantly rotational motion.
The average rotation velocity in the circle state 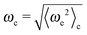 , where averaging is done over circle states only, is depicted in Fig. 7(d) for the rod swimmer as a function of the flexure number
, where averaging is done over circle states only, is depicted in Fig. 7(d) for the rod swimmer as a function of the flexure number ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) . The data collapse to a single line. Below
. The data collapse to a single line. Below ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) ≈ 103, where the circular state rarely occurs (cf.Fig. 4(b)), ωc shows no dependence on the flexure number. Above
≈ 103, where the circular state rarely occurs (cf.Fig. 4(b)), ωc shows no dependence on the flexure number. Above ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) ≈ 103, the rotational velocity of the circle state increases linearly with the self-propulsion force, which is a simple consequence of the linearly increased swimming velocity.
≈ 103, the rotational velocity of the circle state increases linearly with the self-propulsion force, which is a simple consequence of the linearly increased swimming velocity.
3.3.4 Rotation phase: persistence and angular velocity.
The change of rotational direction occurs most frequently for the hexagon swimmer with ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) = 250, γF/γB ≈ 2.7, and ξP/L = 2. The histogram of the lifetime of the direction of the rotation states for these parameters is shown in Fig. 8(a). The criterion that λ1 falls below
= 250, γF/γB ≈ 2.7, and ξP/L = 2. The histogram of the lifetime of the direction of the rotation states for these parameters is shown in Fig. 8(a). The criterion that λ1 falls below 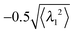 or grows above
or grows above 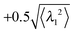 is employed as criterion for change of the rotation direction. The measured histogram of τr accurately matches an exponential decay with half-life
is employed as criterion for change of the rotation direction. The measured histogram of τr accurately matches an exponential decay with half-life ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) r, which suggests that the change of rotation direction is again a thermally activated Poisson process.
r, which suggests that the change of rotation direction is again a thermally activated Poisson process.
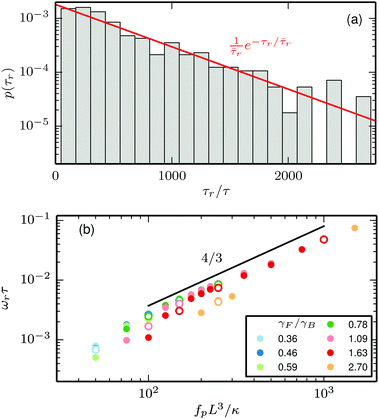 |
| | Fig. 8 (a) Histogram of the lifetime of the persistence of the direction of the rotational swimming τr for ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) = 250, γF/γB ≈ 2.7, and ξP/L = 2. (b) Average rotation velocity. Filled symbols correspond to low temperature (ξP/L = 2000), open symbols correspond to high temperature (ξP/L = 2). = 250, γF/γB ≈ 2.7, and ξP/L = 2. (b) Average rotation velocity. Filled symbols correspond to low temperature (ξP/L = 2000), open symbols correspond to high temperature (ξP/L = 2). | |
The angular velocity of the rotational swimming ωr is computed from a fit of the functional form
| | ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) t = [1 − b + b t = [1 − b + b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωrΔt)]exp(−Δt/τrd), cos(ωrΔt)]exp(−Δt/τrd), | (32) |
with the parameter
b and the characteristic decay time
τrd to the time-autocorrelation function of the end-to-end unit vector. As shown in
Fig. 8(b), the angular rotation velocity scales with the self-propulsion as
fp4/3, which is in agreement with observations for the rotation velocity of self-propelled, pinned filaments.
26 Thermal energy has a subordinate impact on the rotation velocity. The effect of the size of the hexagon is also small, except for simulations with the smallest head.
4 Summary and discussion
Buckling instabilities caused by compressive loads give rise to a versatile phase behavior for self-propelled filaments pushing finite-sized rigid bodies, including elongated, rotating, beating, and beat-and-circle motion. The phase diagram has been constructed for varying propulsion force, and size and shape of the rigid head. The physical nature of the various states has been examined. It is shown that the beating and rotation states are stable buckled states, and that the transition from beat to circle swimming as well as the change of the rotational direction are thermally-activated Poisson processes. In contrast, the circle motion in the beat-and-circle regime is an unstable transient state. The circle state is a well-defined perturbation of the regular beating pattern that is caused by an interplay of activity and thermal noise.
A power-law dependence on the propulsive force fp is observed for various characteristic filament quantities. In particular, it is demonstrated that the bending energy in the filament in the beating phase and the angular velocity in the circle state scale linearly with fp, and that the beating frequency and the angular velocity in the rotation phase have a power-law dependence on fp with exponent of 4/3.
Due to the clear separation of noise- and buckling-induced dynamics, simulations at low temperature (ξp/L = 2000) are well suited to gain a deeper understanding of the mechanical properties of self-propelled filaments pushing a load. Because of the high persistence length and small diffusion, however, the observations at reduced temperatures are related primarily to quasi-macroscopic systems, for which thermal fluctuations are irrelevant. In contrast, the behavior at elevated temperatures (ξp/L = 2) is tightly connected to microscopic systems, with a pronounced role of thermal fluctuations. In particular, our model with ξp/L = 2 corresponds to an actin filament with a length of about 8 μm. On a dense carpet of myosin, flexure numbers up to ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) ≈ 5000 are possible,17,24 which suggests that all our observed phases and regimes should be reproducible in motility assays.
≈ 5000 are possible,17,24 which suggests that all our observed phases and regimes should be reproducible in motility assays.
The beat-and-circle dynamics observed at high temperatures correspond to irregular switching between predominantly rotational and predominantly translational motion. This unsteady behavior results from the interplay of thermal noise and activity causing spontaneous excitation of a higher mode. Thermal noise can thus lead to well defined switching dynamics – which, in our model, is the spontaneous increase of the amplitude λc of the circle mode ψc, and the simultaneous decay of the amplitudes of the beating modes. This raises the questions whether excitations caused by an interplay of activity and thermal noise are a generic feature that can also be observed experimentally.42
The rotational motion observed for the filament attached to a hexagon at intermediate propulsion strength and the circle motion in the beat-and-circle regime at strong propulsion both correspond to predominantly rotational motion. Yet, to avoid confusion between these two states, it should be noticed that their physical causes are different. The rotation motion is a stable state caused by a buckling instability and shows persistent rotational swimming, where alteration of the rotation direction is possibly. In contrast, the circle motion of the beat-and-circle regime is an unstable, short-lived transient state.
Our study gives a glimpse of the wealth of phenomena that can occur for filaments pushing finite loads. The results show that the shape of the head – or more precisely, the ratio of translational to rotational hydrodynamic resistance – has a critical impact on the phase behavior. Only two different shapes were examined here, however, which essentially differ in their rotational and translational friction coefficients. Furthermore, the loads were always attached with a linker of the same bending rigidity as the bending rigidity within the filament. In the ESI,† we show that more flexible linkers significantly favor rotating states. Similarly, an asymmetric attachment of the filament also breaks the left/right symmetry and thereby favors rotating states. Finally, even filaments with the lowest bending rigidity considered (ξP/L = 2) are still rather stiff. Investigation of lower bending rigidities, which can occur for chains of colloids or longer filaments, can be expected to show substantially different behaviors.
We have focused on the behavior of self-propelled filaments in two dimensions, relevant in particular for filaments near surfaces. In three dimensions, a self-propelled filament has additional degrees of freedom, which can give rise to new dynamic regimes. For example, the beating motion could turn into a rotational motion of helical filament shapes.43 Finally, the dynamic modes of the freely-swimming filament provide an interesting possibility to study of the effect of external forces or stimuli on the “self-generated” sperm-like beat, as well as the dynamics of spontaneous synchronization and collective behavior of many self-propelled filaments.
Acknowledgements
The authors gratefully acknowledge financial support by the Deutsche Forschungsgemeinschaft through the priority program SPP 1726 on “Microswimmers”, financial support for J. J. through the International Helmholtz Research School IHRS-Biosoft, and a computing-time grant on the supercomputer JURECA at Jülich Supercomputing Centre (JSC).
References
- J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed.
- O. C. Rodriguez, A. W. Schaefer, C. A. Mandato, P. Forscher, W. M. Bement and C. M. Waterman-Storer, Nat. Cell Biol., 2003, 5, 599–609 CrossRef CAS PubMed.
- T. Vicsek and A. Zafeiris, Phys. Rep., 2012, 517, 71–140 CrossRef.
- M. Abkenar, K. Marx, T. Auth and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062314 CrossRef PubMed.
- S. J. DeCamp, G. S. Redner, A. Baskaran, M. F. Hagan and Z. Dogic, Nat. Mater., 2015, 14, 1110–1115 CrossRef CAS PubMed.
- T. Sanchez, D. T. N. Chen, S. J. DeCamp, M. Heymann and Z. Dogic, Nature, 2012, 491, 431–434 CrossRef CAS PubMed.
- V. Schaller and A. R. Bausch, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4488–4493 CrossRef.
- V. Schaller, C. Weber, E. Frey and A. R. Bausch, Soft Matter, 2011, 7, 3213–3218 RSC.
- V. Schaller, C. Weber, C. Semmrich, E. Frey and A. R. Bausch, Nature, 2010, 467, 73–77 CrossRef CAS PubMed.
- Y. Sumino, K. H. Nagai, Y. Shitaka, D. Tanaka, K. Yoshikawa, H. Chaté and K. Oiwa, Nature, 2012, 483, 448–452 CrossRef CAS PubMed.
- T. Sanchez, D. Welch, D. Nicastro and Z. Dogic, Science, 2011, 333, 456–459 CrossRef CAS PubMed.
- Y. Sasaki, Y. Takikawa, V. S. R. Jampani, H. Hoshikawa, T. Seto, C. Bahr, S. Herminghaus, Y. Hidaka and H. Orihara, Soft Matter, 2014, 10, 8813–8820 RSC.
- P. J. Vach and D. Faivre, Sci. Rep., 2015, 5, 9364 CrossRef CAS PubMed.
- F. Martinez-Pedrero, A. Ortiz-Ambriz, I. Pagonabarraga and P. Tierno, Phys. Rev. Lett., 2015, 115, 138301 CrossRef PubMed.
- F. Li, D. P. Josephson and A. Stein, Angew. Chem., Int. Ed., 2011, 50, 360–388 CrossRef CAS PubMed.
- J. Zhang, E. Luijten and S. Granick, Annu. Rev. Phys. Chem., 2015, 66, 581–600 CrossRef CAS PubMed.
- R. E. Isele-Holder, J. Elgeti and G. Gompper, Soft Matter, 2015, 11, 7181–7190 RSC.
-
Z. Farkas, I. Derényi and T. Vicsek, Structure and Dynamics of Confined Polymers, Springer, Netherlands, 2002, vol. 87, pp. 327–332 Search PubMed.
- G. Jayaraman, S. Ramachandran, S. Ghose, A. Laskar, M. S. Bhamla, P. B. S. Kumar and R. Adhikari, Phys. Rev. Lett., 2012, 109, 158302 CrossRef PubMed.
- A. Ghosh and N. S. Gov, Biophys. J., 2014, 107, 1065–1073 CrossRef CAS PubMed.
- A. Kaiser, S. Babel, B. ten Hagen, C. von Ferber and H. Löwen, J. Chem. Phys., 2015, 142, 124905 CrossRef PubMed.
- A. Laskar and R. Adhikari, Soft Matter, 2015, 11, 9073–9085 RSC.
- K. Sekimoto, N. Mori, K. Tawada and Y. Toyoshima, Phys. Rev. Lett., 1995, 75, 172–175 CrossRef CAS PubMed.
- L. Bourdieu, T. Duke, M. Elowitz, D. Winkelmann, S. Leibler and A. Libchaber, Phys. Rev. Lett., 1995, 75, 176–179 CrossRef CAS PubMed.
- A. Laskar, R. Singh, S. Ghose, G. Jayaraman, P. B. S. Kumar and R. Adhikari, Sci. Rep., 2013, 3, 1964 Search PubMed.
- R. Chelakkot, A. Gopinath, L. Mahadevan and M. F. Hagan, J. R. Soc., Interface, 2014, 11, 20130884 CrossRef PubMed.
- B. Dünweg and W. Paul, Int. J. Mod. Phys. C, 1991, 02, 817–827 CrossRef.
- M. T. Downton and H. Stark, J. Phys.: Condens. Matter, 2009, 21, 204101 CrossRef PubMed.
- I. O. Götze and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041921 CrossRef PubMed.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2014, 112, 118101 CrossRef PubMed.
- J. Elgeti and G. Gompper, EPL, 2009, 85, 38002 CrossRef.
- K. Drescher, J. Dunkel, L. H. Cisneros, S. Ganguly and R. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10940–10945 CrossRef CAS PubMed.
- W. C. Swope, H. C. Andersen, P. H. Berens and K. R. Wilson, J. Chem. Phys., 1982, 76, 637–649 CrossRef CAS.
- M. Tuckerman, B. J. Berne and G. J. Martyna, J. Chem. Phys., 1992, 97, 1990–2001 CrossRef CAS.
- L. Harnau, R. G. Winkler and P. Reineker, J. Chem. Phys., 1996, 104, 6355 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
-
I. Jolliffe, Principal component analysis, Wiley Online Library, 2002 Search PubMed.
- S. van Teeffelen and H. Löwen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 020101 CrossRef PubMed.
- F. Kümmel, B. ten Hagen, R. Wittkowski, I. Buttinoni, R. Eichhorn, G. Volpe, H. Löwen and C. Bechinger, Phys. Rev. Lett., 2013, 110, 198302 CrossRef PubMed.
-
S. H. Strogatz, Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering, Westview press, 2014 Search PubMed.
- K. Baczynski, R. Lipowsky and J. Kierfeld, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 76, 1–9 Search PubMed.
- D. Takagi, A. B. Braunschweig, J. Zhang and M. J. Shelley, Phys. Rev. Lett., 2013, 110, 038301 CrossRef PubMed.
- R. Chelakkot, R. G. Winkler and G. Gompper, Phys. Rev. Lett., 2012, 109, 178101 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Videos of swimming filaments of all observed phases. Simulation results for distinct (reduced) bending rigidity of the link between the filament and the load. See DOI: 10.1039/c6sm01094f |
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article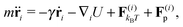
![[r with combining umlaut]](https://www.rsc.org/images/entities/b_char_0072_0308.gif) i and ṙi are the first and second time derivative of the position ri of bead i, m is the mass of the beads, γ is the friction coefficient with the solvent, U is the configurational potential,
i and ṙi are the first and second time derivative of the position ri of bead i, m is the mass of the beads, γ is the friction coefficient with the solvent, U is the configurational potential, 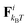 is the thermal noise force that acts on particle i, and F(i)p is the propulsive force.
is the thermal noise force that acts on particle i, and F(i)p is the propulsive force.
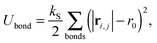
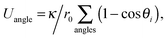
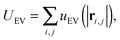
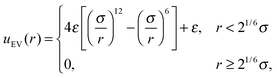
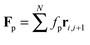
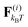 act on all beads. The thermal force is modeled as white noise with zero mean and variance 2kBTγ/ΔtS, where ΔtS is the time step, as described in ref. 27. Note that hydrodynamic interactions are not included in our model (free-draining approximation), which is a reasonable simplification for systems like filaments on molecular motor carpets. The relevance of hydrodynamic interactions for the motion of rods and filaments, in particular near surfaces, has been discussed in ref. 28–32.
act on all beads. The thermal force is modeled as white noise with zero mean and variance 2kBTγ/ΔtS, where ΔtS is the time step, as described in ref. 27. Note that hydrodynamic interactions are not included in our model (free-draining approximation), which is a reasonable simplification for systems like filaments on molecular motor carpets. The relevance of hydrodynamic interactions for the motion of rods and filaments, in particular near surfaces, has been discussed in ref. 28–32.
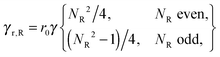
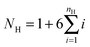
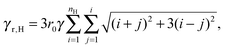
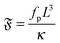
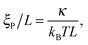
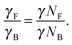
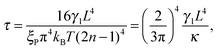
![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) ≤ 105. The effect of thermal noise was studied by running simulations at two different temperatures kBT ∈ {0.0005,0.5}κ/L, corresponding to ξP/L ∈ {2000,2}. Thermal energy has a negligible impact for the simulations at the lower temperature.
≤ 105. The effect of thermal noise was studied by running simulations at two different temperatures kBT ∈ {0.0005,0.5}κ/L, corresponding to ξP/L ∈ {2000,2}. Thermal energy has a negligible impact for the simulations at the lower temperature.
![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) ≤ 5000 were run for 123282.5τ at low temperatures and 246565τ at high temperatures. Bead coordinates were stored every 0.616τ. For
≤ 5000 were run for 123282.5τ at low temperatures and 246565τ at high temperatures. Bead coordinates were stored every 0.616τ. For ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) > 5000, simulations were run 20 times shorter and data was collected 20 times more frequently. All simulations were performed with the LAMMPS molecular simulation package36 with in-house modification to describe the self-propulsion. Additional simulations to study the impact of a distinct bending rigidity of the link between the filament and the load are presented in the ESI.†
> 5000, simulations were run 20 times shorter and data was collected 20 times more frequently. All simulations were performed with the LAMMPS molecular simulation package36 with in-house modification to describe the self-propulsion. Additional simulations to study the impact of a distinct bending rigidity of the link between the filament and the load are presented in the ESI.†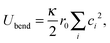
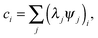
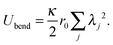

![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) = 50, ξP/L = 2, and γF/γB = 5. (b) Filament attached to a rod-shaped load in the beat phase with
= 50, ξP/L = 2, and γF/γB = 5. (b) Filament attached to a rod-shaped load in the beat phase with ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) = 5000, ξP/L = 2, and γF/γB = 1.67. (c) Filament attached to a rod-shaped load in the beat-and-circle regime with
= 5000, ξP/L = 2, and γF/γB = 1.67. (c) Filament attached to a rod-shaped load in the beat-and-circle regime with ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) = 5000, ξP/L = 2, and γF/γB = 5. (d) Filament with a hexagonal head in the rotation phase with
= 5000, ξP/L = 2, and γF/γB = 5. (d) Filament with a hexagonal head in the rotation phase with ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) = 250, ξP/L = 2, and γF/γB = 1.64. (e) Filament with a hexagonal head in the beat phase at low thermal noise with
= 250, ξP/L = 2, and γF/γB = 1.64. (e) Filament with a hexagonal head in the beat phase at low thermal noise with ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) = 1000, ξP/L = 2000, and γF/γB = 1.1. (f) Filament with a hexagonal head in the rotation phase at low thermal noise with
= 1000, ξP/L = 2000, and γF/γB = 1.1. (f) Filament with a hexagonal head in the rotation phase at low thermal noise with ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) = 150, ξP/L = 2000. Videos from all regimes are available in the ESI.†
= 150, ξP/L = 2000. Videos from all regimes are available in the ESI.†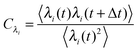

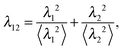
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−λ122/2σr2),
exp(−λ122/2σr2),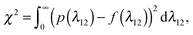
![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) for decreasing rod length. Simulation results and stability analysis are in excellent agreement. Note that in the elongated phase, oscillations in Cλ1 appear already before the transition to the beat phase, when the stability analysis predicts that the stable node turns into a stable focus (light gray line in Fig. 4(a)); however, the oscillation amplitude is too small to result in any visible patterns in the filament structure (as discussed in Section 3.1.1).
for decreasing rod length. Simulation results and stability analysis are in excellent agreement. Note that in the elongated phase, oscillations in Cλ1 appear already before the transition to the beat phase, when the stability analysis predicts that the stable node turns into a stable focus (light gray line in Fig. 4(a)); however, the oscillation amplitude is too small to result in any visible patterns in the filament structure (as discussed in Section 3.1.1).![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) and high temperature, the “energy” barrier between clockwise and counter-clockwise rotations is strongly reduced, leading to fast thermal jumps over the barrier.
and high temperature, the “energy” barrier between clockwise and counter-clockwise rotations is strongly reduced, leading to fast thermal jumps over the barrier.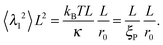
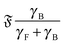
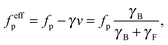
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) λ1 = cos(ωbΔt)exp(−Δt/τbd),
λ1 = cos(ωbΔt)exp(−Δt/τbd),![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) , the frequency ωb, for the rod head, approximately collapses onto a single line (Fig. 6(a)). The thermal energy and the rod length have a rather weak effect. The scaling ωb ∝
, the frequency ωb, for the rod head, approximately collapses onto a single line (Fig. 6(a)). The thermal energy and the rod length have a rather weak effect. The scaling ωb ∝ ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) 4/3 results from a balance of the energy input in the system by the propulsive force and the dissipation of energy through friction with the solvent, as shown in ref. 26. Note that the same scaling is approximately valid also for oscillations in the elongated phase (for fpL3/κ ≲ 300). For the filament attached to a hexagonal head (Fig. 6(b)), the effect of size of the load is more important than for rod-shaped loads, which is apparent from that data for different friction ratios γF/γB do not collapse onto a single curve.
4/3 results from a balance of the energy input in the system by the propulsive force and the dissipation of energy through friction with the solvent, as shown in ref. 26. Note that the same scaling is approximately valid also for oscillations in the elongated phase (for fpL3/κ ≲ 300). For the filament attached to a hexagonal head (Fig. 6(b)), the effect of size of the load is more important than for rod-shaped loads, which is apparent from that data for different friction ratios γF/γB do not collapse onto a single curve.
![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) = 5000, γF/γB = 10, and ξP/L = 2. Very short-lived states, with a lifetime of 3 or less snapshots, were ignored in the analysis.
= 5000, γF/γB = 10, and ξP/L = 2. Very short-lived states, with a lifetime of 3 or less snapshots, were ignored in the analysis.
![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) b, where the bar indicates an average over all individual uninterrupted beat states. This suggests that the onset of circular motion is controlled by an underlying Poisson process, that – since the beat-and-circle motion only occurs at high temperatures – is activated by thermal noise.
b, where the bar indicates an average over all individual uninterrupted beat states. This suggests that the onset of circular motion is controlled by an underlying Poisson process, that – since the beat-and-circle motion only occurs at high temperatures – is activated by thermal noise.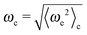 , where averaging is done over circle states only, is depicted in Fig. 7(d) for the rod swimmer as a function of the flexure number
, where averaging is done over circle states only, is depicted in Fig. 7(d) for the rod swimmer as a function of the flexure number ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) . The data collapse to a single line. Below
. The data collapse to a single line. Below ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) ≈ 103, where the circular state rarely occurs (cf.Fig. 4(b)), ωc shows no dependence on the flexure number. Above
≈ 103, where the circular state rarely occurs (cf.Fig. 4(b)), ωc shows no dependence on the flexure number. Above ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) ≈ 103, the rotational velocity of the circle state increases linearly with the self-propulsion force, which is a simple consequence of the linearly increased swimming velocity.
≈ 103, the rotational velocity of the circle state increases linearly with the self-propulsion force, which is a simple consequence of the linearly increased swimming velocity.![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) = 250, γF/γB ≈ 2.7, and ξP/L = 2. The histogram of the lifetime of the direction of the rotation states for these parameters is shown in Fig. 8(a). The criterion that λ1 falls below
= 250, γF/γB ≈ 2.7, and ξP/L = 2. The histogram of the lifetime of the direction of the rotation states for these parameters is shown in Fig. 8(a). The criterion that λ1 falls below 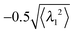 or grows above
or grows above 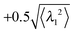 is employed as criterion for change of the rotation direction. The measured histogram of τr accurately matches an exponential decay with half-life
is employed as criterion for change of the rotation direction. The measured histogram of τr accurately matches an exponential decay with half-life ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) r, which suggests that the change of rotation direction is again a thermally activated Poisson process.
r, which suggests that the change of rotation direction is again a thermally activated Poisson process.
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) t = [1 − b + b
t = [1 − b + b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωrΔt)]exp(−Δt/τrd),
cos(ωrΔt)]exp(−Δt/τrd),![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) ≈ 5000 are possible,17,24 which suggests that all our observed phases and regimes should be reproducible in motility assays.
≈ 5000 are possible,17,24 which suggests that all our observed phases and regimes should be reproducible in motility assays.





