 Open Access Article
Open Access ArticleCharacterization of the diffusive dynamics of particles with time-dependent asymmetric microscopy intensity profiles†
Maria A.
Vorontsova
a,
Peter G.
Vekilov
*ab and
Dominique
Maes
*c
aDepartment of Chemical and Biomolecular Engineering, University of Houston, Houston, Texas 77204, USA. E-mail: vekilov@uh.edu
bDepartment of Chemistry, University of Houston, Houston, Texas 77204, USA
cStructural Biology Brussels, SBB, Vrije Universiteit Brussel, 1050 Brussels, Belgium. E-mail: dommaes@vub.ac.be
First published on 26th July 2016
Abstract
We put forth an algorithm to track isolated micron-size solid and liquid particles that produce time-dependent asymmetric intensity patterns. This method quantifies the displacement of a particle in the image plane from the peak of a spatial cross-correlation function with a reference image. The peak sharpness results in subpixel resolution. We demonstrate the utility of the method for tracking liquid droplets with changing shapes and micron-size particles producing images with exaggerated asymmetry. We compare the accuracy of diffusivity determination with particles of known size by this method to that by common tracking techniques and demonstrate that our algorithm is superior. We address several open questions on the characterization of diffusive behaviors. We show that for particles, diffusing with a root-mean-square displacement of 0.6 pixel widths in the time between two successive recorded frames, more accurate diffusivity determinations result from mean squared displacement (MSD) for lag times up to 5 time intervals and that MSDs determined from non-overlapping displacements do not yield more accurate diffusivities. We discuss the optimal length of image sequences and demonstrate that lower frame rates do not affect the accuracy of the estimated diffusivity.
1. Introduction
Diffusive dynamics constitute an important part of processes of interest in fields ranging from biotechnology1–7 and cell biology8–13 to fluid mechanics14,15 and colloid science.16,17 Understanding the role of diffusion in natural and engineered processes requires methods to quantify the motion of micron and submicron particles in complex media.18,19 Recent technological developments in time-lapse microscopy have greatly improved the imaging field. Nowadays, one can monitor the dynamics of single particles (spheres, living cells, protein complexes, viruses, etc.) with unprecedented detail and single particle tracking (SPT) has provided important insights into particle properties, their interactions with other particles and the environment, and the mechanisms that drive particle motion, and in this way have helped to understand numerous physical and biological processes.2,11–13Over the years several computer algorithms for particle tracking from a sequence of microscopic images have been developed.20–22 On each image, particles are identified and the coordinates of their centers are determined, resulting in a time series of positions. General tracking methods deal with cases in which the intensity profile of a particle is radially symmetric. As such the center is allocated to the point of maximum intensity or the intensity centroid. More sophisticated techniques use a variety of fitting algorithms to provide sub-pixel resolution of the particle coordinates. As the peak of the point spread function of a diffraction-limited spot can, in most cases, be approximated by a Gaussian function, many fitting algorithms use Gaussian profiles.23–25 The radial centering technique uses the direction of the gradient in a radially symmetric intensity pattern to identify the intensity center.26,27 This technique does not employ iterative nonlinear fitting and is faster than fitting algorithms.
Several recently studied systems appear to challenge even advanced particle tracking algorithms. For instance, in images of micron-size liquid droplets the recorded intensity patterns are asymmetric and fluctuate with a characteristic time comparable to their diffusion time. Another example comes from particle tracking by oblique illumination microscopy, a method that records the intensity scattered from submicron and micron-size particles28–30 in which the identification of the particle center is hampered by the asymmetry of the scattered intensity pattern. To quantify the diffusive motion for such particles and droplets, here we put forth a fast and easy to implement SPT algorithm. We employ a local spatial cross-correlation function to identify the displacement of a particle between two frames.31,32 We implement radial centering26,27 of the computed cross-correlation functions to evaluate the travelled distance with sub-pixel resolution. In its current implementation, the method is only applicable to relatively dilute solutions since it requires non-overlapping trajectories of the tracked particles. Importantly, the proposed algorithm does not rely on the identification of the particle center in any single image, but reconstructs the particle trajectory from the displacements between pairs of images.
We demonstrate that particle tracking by this method enables an accurate characterization of the dynamic behavior of single particles. We employ the proposed algorithms to obtain trajectories of submicron and micron-size particles and droplets of protein dense liquid. From the recorded trajectories, we evaluate the diffusion coefficient of spherical latex particles of known size, using least squares fits of the mean square displacement as a function of time,33–37 and compare its value to the diffusivity determined by dynamic light scattering. We use the correspondence between the two values as a quantitative indicator of the performance of the method. Applying this criterion, we demonstrate that the proposed cross-correlation method yields a more accurate estimate of particle diffusivity than several common tracking methods.
2. Methods
2.1 Materials
The spatial cross-correlation method of single particle tracking was tested using aqueous solutions of model spherical and rod-like particles. We used spherical particles of three different diameters: 0.1 and 1.0 μm, supplied by OptiLink™, and 0.424 μm, from Seradyne. The particles had carboxylate-modified surfaces to provide surface charge that impedes aggregation. We used gold rod-like particles of 0.1 μm diameter and 1.0 μm length (Nanopartz™ Inc., US). The concentrations of the particles were chosen so that their trajectories did not overlap within the longest data collection time. The highest volume fraction was 10−8, employed for the smallest 0.1 μm spheres to improve their visibility. These low concentrations minimized particle interactions, eliminated particle aggregation, and ensured that only self-diffusivity and convection contributed to particle motion.Two protein solutions were tested in our work. Glucose isomerase (Microcrystal Oy, Helsinki, Finland) solution was prepared at a concentration of 90 mg ml−1 in 100 mM Na-HEPES (N-2-hydroxyethylpiperazine-N-2-ethanesulfonic acid, Fisher, US) buffer at pH = 7.0 containing 200 mM MgCl2 (Fisher, US). Lysozyme powder (Affymetrix, US) was dissolved in 20 mM HEPES buffer at pH 7.8 and dialyzed over two days. Tested solutions contained 20 mg ml−1 lysozyme and 15% v/v ethanol (Fisher, US). Both protein solutions were aged for 1–2 weeks prior to the experiments to ensure large cluster size in the range 1–2 μm.38
2.2 Oblique illumination microscopy (OIM) and dynamic light scattering (DLS)
OIM data were collected employing a Nanosight TM microscope setup, Fig. 1, discussed in ref. 28 and 30. We used a green laser with wavelength λ = 532 nm as a light source and captured data from a solution volume of 120 × 80 × 5 μm3 (width × length × height). We used two cameras: sCMOS, operating at 25 frames s−1, supplied by Nanosight, and Cooke Edge 4.2 with an adjustable frame rate. The Cooke Edge 4.2 camera was used at 50 frames s−1. Slower frame rates (25, 10 and 5 s−1) were obtained from the original movies by removing a corresponding number of frames. In the object plane, the width of one pixel is 330 nm.Dynamic light scattering data were collected using an ALV goniometer equipped with a He–Ne laser (632.8 nm) and an ALV-5000/EPP Multiple tau Digital Correlator (ALV-GmbH, Langen, Germany). The intensity correlation functions were acquired for 60 s at 90°; for details see ref. 28 and 30.
2.3 Centering and tracking algorithms
All tracking algorithms were implemented in MATLAB (version 2013a, MathWorks). No background correction was applied to the images. All images were cropped to the region containing the particle of interest.(1) The coordinates of the intensity centroid (xc, yc) were determined as
 | (1) |
 | (2) |
(2) The Gaussian center was determined as the maximum (xc,yc) of the Gaussian profile
 | (3) |
(3) The radial centering technique relies on the fact that in a radially-symmetric intensity pattern the intensity gradient at any point is directed towards the center of the tracked particle. We followed the procedure by Parthasarathy26,27 and used the MATLAB code published in the ESI of ref. 26.
3. Results and discussion
3.1 The challenges of tracking micron-size droplets and particles
The current particle tracking methods may break down when the particle images vary in shape and intensity during monitoring. The variation may reflect deformations of liquid droplets and cells driven by Brownian collisions with the solvent molecules, and rotation of particles with anisotropic shapes or non-uniform optical properties. Asymmetric illumination may exaggerate the shape variations of particles with minor deviations from sphericity, which expose different sides to the beam as they undergo rotational diffusion.As examples of time-dependent intensity patterns, here we use images of diffusing solid spheres, rods, and liquid droplets obtained with oblique illumination dark-field microscopy, sometimes referred to as Brownian microscopy or Nanosight technology.28,30,38–41 In this technique, solution samples are held in a thin cuvette under a microscope, Fig. 1. The illuminating beam extends at an angle with the microscope optical axis, adjusted to avoid the microscope objective lens. Light scattered from particles in the viewfield is captured by the objective lens and recorded using a video camera. The reliance on scattered light offers several important advantages. First, particles with refractive indices close to that of the solution and with sizes smaller than the diffraction limit are detectable. Second, owing to stronger scattering, reflected in the Rayleigh law, larger particles produce stronger signals and can be detected on a background of smaller scatterers. Lastly, particles out of the image plane are detectable, leading to better population statistics.
To produce time-dependent asymmetric scattered intensity patterns with oblique illumination microscopy, we use spherical particles with near-micron diameters (these particles are too small for continuous monitoring with bright-field microscopy), which produce asymmetric intensity patterns because of the asymmetric illumination. To test the performance of commonly used tracking algorithms (intensity maximum (IM), radial centering (R), intensity centroid (IC), and Gaussian centering (G), described in detail in the Materials and Methods section), we monitor the diffusive motion of four classes of particles. We use spherical latex particle with diameters 0.1, 0.424 and 1 μm and gold nanorods with 1 μm length and 100 nm diameter.
The selection of images in Fig. 2a, in which we have indicated the particle centers identified by each of the four techniques, reveals that the IM, R, and G algorithms yield consistent results for the submicron size particles: the center locations are identical and the particle trajectories, displayed in Fig. 2b, similar. The IC method misjudges the center locations owing to the low-intensity of the scattered pattern. The accuracy of this method depends heavily on the background estimation and can be improved by background correction, but this drastically increases the expended computational time.31 The Gaussian centering method failed to converge for the intensity patterns of 0.424 and 1.0 μm particles, comprising several concentric rings.
Where applicable, these methods produce disparate center locations and trajectories for spheres of diameter 0.424 and 1.0 μm and for 1 μm long nanorods. Inspection of the images in Fig. 2a suggests that the errors of the tested methods are rooted in the lack of radial symmetry of the intensity patterns, accompanied by fast changes in the location of the intensity maxima.
3.2 The spatial cross-correlation (SCC) method
We propose to quantify the displacement of single particles using the spatial cross-correlation function of an image, taken at time t, with a reference image. Because the spatial cross-correlation has a single sharp quasi-centrosymmetric peak, the movements of the particles can be studied by tracking the intensity maximum of the spatial cross correlation function. The algorithm is illustrated in Fig. 3. To calculate the cross-correlation function of the images shown in Fig. 3a, we first compute their spatial fast Fourier transforms (FFTs); their respective amplitudes and phases are displayed in Fig. 3b. We then compute the product of the FFT of an image with the complex conjugate of the reference image (the FFT of the reference image is multiplied with its own complex conjugate, resulting in a phase uniformly equal to zero). The respective products are displayed in Fig. 3c.Inverting the FFT of the products yields the cross-correlation function of the two images, or the autocorrelation function of the reference image (Fig. 3d). The displacement of the intensity maximum of the cross-correlation function from that of the autocorrelation function of the reference image is taken as a measure of the displacement vector  of the tracked particle between the two images. In Fig. 3e we superimpose the reference and the target images and position the tail of the displacement vector
of the tracked particle between the two images. In Fig. 3e we superimpose the reference and the target images and position the tail of the displacement vector  at the apparent center of the reference image. As evidence of the reliability of the SCC method, the vector head points to the center of the target image.
at the apparent center of the reference image. As evidence of the reliability of the SCC method, the vector head points to the center of the target image.
To achieve subpixel resolution, we apply radial centering26,27 in the vicinity of the cross-correlation maximum, where this function is quasi radially symmetric. The radial centering technique uses the fact that the orientation of the gradient at any point on a radially symmetric intensity pattern is in the direction of the intensity center. Furthermore, in cases where the shape of the intensity profile changes drastically within a sequence of images, resulting in a decaying peak of the spatial cross-correlation function, a second reference image may be selected. Thus, if for the first group of k images image 1 is used as a reference, for images numbered k + 1 through 2k, we use image k as a reference. To choose k, we note that large k values bring down the signal-to-noise ratio since they correspond to longer particle displacement. On the other hand small values of k result in a higher and narrower peak of the spatial cross-correlation function, conducive to more accurate localization.
Note that the choice of a reference image, 1 in Fig. 3, is arbitrary and can be changed at any moment of particle tracking. Re-selection of the reference image allows for the elimination of the effects of the rotation of strongly asymmetric particles or the changing shape of liquid droplets on the tracking of their translations. If a rod-like particle rotates with a characteristic time shorter than the chosen translational lag times, or if a liquid particle changes shape with a similarly short characteristic time, the rotation and shape change, respectively, will average out and not affect the determination of the particle trajectory. If the two characteristic times, however, are comparable or longer than the monitored lag times, the resulting evolution of the speckle pattern will induce a gradual decay of the maximum intensity of the cross-correlation function. This intensity decay can be used as an indication for a change in the reference image with respect to which the translational motions of the studied particle are computed.
In its current version, the SCC method is applicable to relatively dilute solutions and suspensions, which produce sequences of images that can be cropped so that a single particle is left in them. In the next step we will consider solutions at higher concentrations resulting in images displaying several particles. The cross correlation function of pairs of such images will display several peaks. Displacements of all imaged particles between successive images will be computed from the shifts of the peaks corresponding to each particle in the cross correlation function.
3.3 Applicability of the SCC method to tracking liquid clusters and asymmetric objects
Liquid droplets of near micron size present additional challenges for tracking owing to the variability of their shape and the intensity patterns. We compare the trajectories determined from the image sequences of mesoscopic protein-rich clusters that exist in solutions of numerous proteins42–45 and are liquid.29,46,47 Evidence for several systems suggests that they may serve as precursors to the nucleation of crystals and other solid aggregates.29,48–50 The protein liquid clusters may relate to the non-membrane bound compartments (nucleoli, centrosomes, Cajal bodies, etc.) in several organisms.51–54 The clusters of the proteins lysozyme and glucose isomerase (GI) change shape in the course of their tracking, which leads to asymmetric and variable patterns of scattered intensity, Fig. 4a. As a result, the radial centering technique, the most advanced of the currently available options, overestimates the shifts of the particle center, Fig. 4a, and produces an exaggerated particle trajectory, Fig. 4b.In Fig. 4b we compare the trajectories of liquid droplets of variable shape resulting from the SCC method to those produced by radial centering. Similarly, in Fig. 3b we plot the SCC trajectories of spherical particles of three sizes and nanorods. For these five classes of diffusing objects, the SCC trajectories are more compact. In view of the unrealistic shifts of the droplet centers identified by radial centering in the images in Fig. 4a, and by the other three tracking methods in Fig. 3a, we conclude that the SCC trajectories are better fits to the actual particle motions. The proposed SCC method is robust: cross-correlation functions of overexposed images, such as the ones in Fig. 4a and Movies I and II (ESI†), possess sharp intensity peaks that allow accurate determination of the particle displacement.
3.4 The accuracy of the spatial cross-correlation algorithm
To test the accuracy of the SCC algorithm, we employ it to evaluate the diffusion coefficient D of single spherical particles with known diameter, suspended in a solvent with known viscosity, and compare the resulting D with the value determined by dynamic light scattering.46 We monitor latex particles of 1 μm diameter freely diffusing in water and construct projections of their trajectories in the image plane. The diffusivity of such particles is (4.51 ± 0.18) × 10−13 m2 s−1 (the error range was evaluated from ten-fold repetition of the determination) and their characteristic diffusion time τD, corresponding to the average time required to diffuse across the particles' diameter, equals 0.37 s. We quantify the mobility of a particle from its net displacement over n steps in terms of the mean squared displacement (MSD) denoted as . In current diffusivity evaluators,33–37 a time series of positions of a particle
. In current diffusivity evaluators,33–37 a time series of positions of a particle ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 0(x0,y0),
0(x0,y0), ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1(x1,y1),…,
1(x1,y1),…,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) N(xN,yN) is used to evaluate its displacements along the x and y coordinate axes, Δxi and Δyi. The SCC method yields displacements with respect to the center of a reference image Δ
N(xN,yN) is used to evaluate its displacements along the x and y coordinate axes, Δxi and Δyi. The SCC method yields displacements with respect to the center of a reference image Δ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(Δxi,Δyi). Assuming
i(Δxi,Δyi). Assuming ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 0(x0,y0) = (0,0) yields
0(x0,y0) = (0,0) yields ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i = Δ
i = Δ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i. From these,
i. From these, | (4) |
We evaluate D as the slope of the correlation between 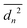 and the duration tn of n steps. We compute tn = nt, where t is the time between two consecutive images in the sequence, from which the displacement is computed. With this, D is the slope of the relation
and the duration tn of n steps. We compute tn = nt, where t is the time between two consecutive images in the sequence, from which the displacement is computed. With this, D is the slope of the relation
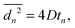 | (5) |
Besides evaluating the accuracy of the SCC algorithm, we use data on the diffusive motion of known particles to address several outstanding questions related to the characterization of diffusive dynamics. These are: (1) the utility of one-dimensional particle displacement data. (2) The significance of using non-overlapping n step sets for MSD determination. (3) The optimal values of the duration over which particle displacement should be averaged, the number of points included in the least-squares fit,35,37,56–59 the frequency of particle localization, and the length of particle monitoring. In addition, we test the relative accuracy of two diffusivity estimators, the least squares method, discussed above, and the maximum likelihood estimator, based on the mean displacement over the shortest captured time interval.
Often, projections of Brownian trajectories on a single dimension are used to determine the diffusivity from  , where
, where  or
or 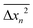 . To address the validity of this data reduction scheme, we compute the mean squared displacements along the x and y axes, respectively, as
. To address the validity of this data reduction scheme, we compute the mean squared displacements along the x and y axes, respectively, as
 | (6a) |
 | (6b) |
 | (7) |
In Fig. 5a we display the projection in the plane of the image of the trajectory of a latex particle with diameter 1 μm. The particle coordinates with respect to the center of the autocorrelation function of the first image were evaluated using the SCC method from 5000 images collected at constant Δt = 20 ms. This Δt is 20-fold shorter than the characteristic diffusion time of the particle τD. The corresponding root-MSD between two successive frames is 190 nm, equal to 0.57 pixel widths. The particle trajectory is highly asymmetric, suggesting the presence of a strong drift roughly parallel to the x axis. The MSDs  over tn = nΔt from 0 to 100 s, computed using eqn (4) are displayed in Fig. 5b. The MSD values increase monotonically with tn for tn < 48 s and then decrease and reach values close to zero. This nonlinear behavior is far from the straight line predicted by the Einstein relation.60–62 Similar behaviors were reported by Vestergaard et al.37 They are a consequence of the high correlations of the displacements at longer times and of the limited statistics provided by data of a single particle. The points in the curve have a statistical uncertainty that increases with n (the point at t = 100 s is not even an average value, but corresponds to a single data point).
over tn = nΔt from 0 to 100 s, computed using eqn (4) are displayed in Fig. 5b. The MSD values increase monotonically with tn for tn < 48 s and then decrease and reach values close to zero. This nonlinear behavior is far from the straight line predicted by the Einstein relation.60–62 Similar behaviors were reported by Vestergaard et al.37 They are a consequence of the high correlations of the displacements at longer times and of the limited statistics provided by data of a single particle. The points in the curve have a statistical uncertainty that increases with n (the point at t = 100 s is not even an average value, but corresponds to a single data point).
 | ||
Fig. 5 Evaluation of the accuracy of the SCC method. (a) Trajectory of a 1 μm latex sphere determined by the SCC method from a sequence of images recorded at 50 frames s−1 for 100 s. (b) Mean squared displacement (MSD)  , calculated from the trace in (a) using eqn (4), as a function of the corresponding lag time tn. (c) Diffusivities D obtained as the slope of linear fits of , calculated from the trace in (a) using eqn (4), as a function of the corresponding lag time tn. (c) Diffusivities D obtained as the slope of linear fits of  in (b) as a function of the highest lag time tn included in the fit. Only tn < 20 s, shaded in gray in (b), were considered. The horizontal red line marks the value of the particle diffusivity measured by DLS, D = 4.51 × 10−13 m2 s−1. Horizontal stripes in shades of green denote deviations by 10, 20 and 30% from the DLS value. (d) The diffusivities D of 20 particles, identical to the one traced in (a), were determined by the method illustrated in (a–c) with fits to single-particle in (b) as a function of the highest lag time tn included in the fit. Only tn < 20 s, shaded in gray in (b), were considered. The horizontal red line marks the value of the particle diffusivity measured by DLS, D = 4.51 × 10−13 m2 s−1. Horizontal stripes in shades of green denote deviations by 10, 20 and 30% from the DLS value. (d) The diffusivities D of 20 particles, identical to the one traced in (a), were determined by the method illustrated in (a–c) with fits to single-particle  correlations with highest fitted tn varying from 0.02 to 20s. The relative frequencies of the obtained D-values falling within 10, 20 and 30% of the DLS value are plotted as a function of the highest tn used in the determination. correlations with highest fitted tn varying from 0.02 to 20s. The relative frequencies of the obtained D-values falling within 10, 20 and 30% of the DLS value are plotted as a function of the highest tn used in the determination. | ||
The particle diffusivity, D, values evaluated from the MSDs in Fig. 5b, are displayed in Fig. 5c. We determined each D value by a least-squares fit of the  data ranging from the lowest tn = 0.02 to a highest tn varying from 0.04 to 20 s, and plotted the resulting D as a function of the highest tn used in the fit. The upper limit of the highest tn range, 20 s, was chosen somewhat arbitrarily to evaluate the effects of longer tn on the D determination. Evidence presented below suggests that the accuracy of D determination decreases monotonically at tn > 5 s, significantly shorter than the chosen limit, and no peculiarities occur near this limit.
data ranging from the lowest tn = 0.02 to a highest tn varying from 0.04 to 20 s, and plotted the resulting D as a function of the highest tn used in the fit. The upper limit of the highest tn range, 20 s, was chosen somewhat arbitrarily to evaluate the effects of longer tn on the D determination. Evidence presented below suggests that the accuracy of D determination decreases monotonically at tn > 5 s, significantly shorter than the chosen limit, and no peculiarities occur near this limit.
We compared these D values to the results of the determination by DLS, carried out in a solution identical to the one characterized in Fig. 5a and b. DLS yields the autocorrelation function g2 of the scattered light. The function g2 identifies the characteristic time of decay of the scattered intensity, which, in Newtonian solutions, equals the characteristic diffusion time tp of the suspended particles. The diffusivity is determined as the product (q2tp)−1, where q is the scattering wave vector. In general, the D values in Fig. 5c deviate from the DLS value (4.51 ± 0.18) × 10−13 m2 s−1. At lag times tn < 1 s, the deviation is <10%. The best correspondence is achieved at tn near 1 s. At lag times longer than this, the deviation increases and reaches up to 30%. At lag times >10 s, the deviation decreases and reaches below 10% at tn = 18 s.
To evaluate the statistical significance of the observations on the accuracy of the diffusivity determination at different lag time ranges, observed in Fig. 5c, we carried out identical determinations with a total of 20 particles. We divided the diffusivities determined in each tn range in four groups: those that are within, respectively, 10, 20, and 30% of the DLS value, and those that deviate by more than 30% from it. Clearly, the diffusivities in the first group are a subset of those in the second, and the latter are a subset of the 30% group. In Fig. 5d we plot the number of diffusivities in each group scaled with the total number of tested particles (this ratio is equal to the relative frequency of the respective deviations from the DLS value) as a function of the upper limit of the tn range.
The data in Fig. 5d reveal that for lag times shorter than 3 s about half of the tested particles yielded diffusivities within 10%, and about 85%, within 30%, of the DLS value. These data allow for the evaluation of the quality of the procedures for the determination of D. Thus, D values determined over shorter lag time ranges are more accurate. This may appear counterintuitive since fewer data points seem to produce a better result. In fact, even the shortest MSD,  , represents an average over the entire particle trajectory. To understand these observations, we note that recent theoretical analyses59 demonstrated that the ratio
, represents an average over the entire particle trajectory. To understand these observations, we note that recent theoretical analyses59 demonstrated that the ratio
 | (8) |
3.5 Comparison with other methods of particle tracking
We compare the performance of the SCC method to those of the intensity maximum and radial centering26,27 techniques of particle tracking. The lack of convergence of the Gaussian profile fitting algorithm precludes tests of this method. Using these three methods, we process sequences of 5000 images for 20 particles of diameter 1 μm taken at a rate of 50 frames s−1. From the resulting trajectories we computed the MSDs and from those values we evaluated the diffusivities for different lag time ranges tn, as illustrated in Fig. 5.The first three columns in Fig. 6 demonstrate that a greater number of particles yield diffusivities closer to the DLS value with the SCC method than with the intensity maximum or radial centering methods.
As expected, the radial centering technique produces more accurate D estimates than the intensity maximum method. In addition, the two older techniques exhibit frequency maxima at lag times of several seconds. These maxima contradict the predictions of the theoretical analysis35,59 of diffusivity determination from particle trajectories and the contradiction suggests inaccurate identification of the particle coordinates, similar to the sequence illustrated in Fig. 2. A closer inspection of the SCC data at short lag times in the semi-logarithmic plots in Fig. 7a reveals that diffusivities evaluated from MSD correlations with lag times of about 0.1 s (5 fitting points) are more accurate than those with the shorter tested lag times, 0.02 s (1 fitting point resulting in the Maximum Likelihood Estimate of D), 0.04 s, etc. This slight discord with the theoretical prediction is due to the finite accuracy of particle tracking by the SCC method. The theoretical root-mean-square displacement of the particle during this optimal lag time of 0.1 s is 429 nm, corresponding to 1.3 pixels.
The data in the rightmost column represent MSDs computed from independent displacements using eqn (7) and SCC-produced trajectories to evaluate the diffusivity of individual particles. The frequency dependencies on the lag time are noisier, reflecting noisier dn2(tn) correlations that are likely due to significantly reduced statistics.55 The numbers of particles yielding diffusivities closer to the DLS value with this method is comparable to the numbers of particle processed with the “classical” SCC method with overlapping displacements. This similarity suggests that the use of independent displacements does not produce a significant advantage.55
The diffusivities reflected in the statistics in Fig. 6 were computed from two-dimensional displacements in the image plane (bottom row) and from displacements exclusively along the x or y axes (top and middle row, respectively). The quality of the diffusivity data evaluated from trajectories identified by the intensity maximum technique does not appear to display significant differences between the three methods to compute displacements. The radial centering technique produces highest data quality with two-dimensional displacements. The higher accuracy of the SCC method allows finer distinctions. While the diffusivities evaluated from the two-dimensional data are more accurate (the initial values of the 10, 20, and 30% curves are higher, and the areas under them are greater) than those evaluated from x-data, the diffusivities evaluated from the displacements along the y axis are even more accurate (e.g., 75% of the particles yield diffusivities within 10% of the DLS value). Examination of the trajectories of the 20 particles revealed that they are similar to those in Fig. 5a and exhibit significant drift nearly parallel to the x-direction. The inability to accurately account for this drift biases the displacements in the x-direction, and by inclusion, the two-dimensional displacements. The displacements in the y direction are relatively free from such bias.
3.6 The length of the movie and the frame rate
The length of a time series of images of a particle may be limited owing to factors such as limited fluorescence time or departure from the field of view. Shorter image sequences may lead to poorer statistics and reduced accuracy of determination. The data in Fig. 7a characterize the quality of the diffusivity evaluated with an increasing number of frames from 50 to 5000 recorded at a rate of 50 frames s−1. The data demonstrate that sequences of 1000 images lead to more accurate diffusivity determinations than those of 50, 100, 250 or 500 images. The recording of 1000 images takes 20 s, equal to 54 τD; the corresponding two-dimensional root-MSD is 6 μm or 18 pixel widths. Extending the sequence length to 2500 and 5000 images does not improve the determination accuracy. Best results are obtained with lag times up to 0.1 s corresponding to five fitting points irrespective of the length of the sequence.Slower frame rates ensure longer displacements between two successive images resulting in a high signal to noise ratio of the particle trajectory and should induce more accurate diffusivity data. On the other hand, with a fixed image sequence length, slower frame rates extend the duration of data acquisition and enhance the effects of drift, vibrations, temperature variations and other destructive factors. To evaluate the effects of frame rates on the quality of the diffusivity data, we compare the accuracy of diffusivity determinations from image sequences collected with frame rates varying from 5 to 50 frames s−1. The time interval between two successive frames ranges from 200 to 20 ms with a corresponding two-dimensional root-MSD ranging from 1.8 to 0.57 pixel widths. The data in Fig. 7b demonstrate that the frame rate does not affect the accuracy of diffusivity determinations. We conclude that we do not need the better signal to noise ratio of a coarser sampling, a testament to the high accuracy of the SCC tracking method.
4. Conclusions
We have developed a new method to track the diffusive motions of single particles producing intensity patterns that vary over a timescale comparable to that of diffusion. The method constructs particle trajectories in the image plane from the displacements of the peak of the cross-correlation function of an image with respect to a reference image.We demonstrate the utility of the method for tracking liquid droplets with changing shapes and micron-size particles producing images with exaggerated asymmetry. We evaluate the accuracy of the method by comparing the diffusivity of particles of known size determined by this method to the value determined by dynamic light scattering. We compare the results with the intensity maximum and radial centering methods. We show that the diffusivity evaluations using trajectories determined using the spatial-cross-correlation (SCC) method are significantly closer to the expected value than those determined using the intensity maximum or radial centering methods.
We address several open questions on the characterization of diffusive behaviors. We show that in the presence of a drift, one dimensional trajectories in the direction perpendicular to the dominant convective flow yield more accurate diffusivity values. We show that MSDs determined from non-overlapping displacements do not yield more accurate diffusivities than methods employing overlapping displacements. We show that for particles diffusing with a root-mean-square displacement of 0.6 pixel widths in the time interval between two successive frames, more accurate diffusivity determinations result from mean squared displacement (MSD) for lag times equal to five time intervals.
We show that sequences of 1000 images lead to more accurate diffusivity determinations than those of 50, 100, 250 or 500 images. Extending the sequence length to 2500 and 5000 images does not improve the determination accuracy. We show that with constant movie length, larger frame rates do not affect the accuracy of diffusivity determinations.
We envision the applicability of the SCC tracking method to all classes of objects with variable image shapes: cells, liquid droplets, particles of anisotropic shapes or optical density,64,65 particles with non-uniform fluorescent labeling, and others. If an anisotropic particle rotates with a characteristic time shorter than the chosen translational lag times, or if a liquid particle changes shape with a similarly short characteristic time, the rotation and shape change, respectively, will average out and will not affect the speckle pattern. If the two characteristic times are comparable or longer than the monitored lag times, the resulting evolution of the speckle pattern will induce a gradual decay of the maximum intensity of the cross-correlation function. This intensity decay can be used as an indication for a change in the reference image with respect to which the sequence of cross-correlation functions is computed. A thorough benchmarking against these more complex particles will be performed in a forthcoming paper.
Acknowledgements
We thank M. Giglio for important recommendations and discussions, J. C. Conrad for helpful suggestions on the tests of the SCC method. PGV gratefully acknowledges the support of the Francqui Foundation for his stay at VUB as a Francqui International Professor during part of this work. Funding was provided by BelSPO (ESA-Prodex AO-2004-070) to DM, NSF (Grants MCB-1244568 and MCB-1518204) and NASA (Grants NNX14AE79G and NNX14AD68G) to PGV.References
- J. N. Wilking, V. Zaburdaev, M. De Volder, R. Losick, M. P. Brenner and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 848–852 CrossRef CAS PubMed.
- V. Filipe, R. Poole, M. Kutscher, K. Forier, K. Braeckmans and W. Jiskoot, Pharm. Res., 2011, 28, 1112–1120 CrossRef CAS PubMed.
- P. G. Vekilov, W. Pan, O. Gliko, P. Katsonis and O. Galkin, in Lecture Notes in Physics, vol. 752: Aspects of Physical Biology: Biological Water, Protein Solutions, Transport and Replication, ed. G. FranzeseM. RubiSpringer, Heidelberg, 2008, pp. 65–95 Search PubMed.
- A. Parodi, S. G. Haddix, N. Taghipour, S. Scaria, F. Taraballi, A. Cevenini, I. K. Yazdi, C. Corbo, R. Palomba, S. Z. Khaled, J. O. Martinez, B. S. Brown, L. Isenhart and E. Tasciotti, ACS Nano, 2014, 8, 9874–9883 CrossRef CAS PubMed.
- Q. Xu, N. J. Boylan, J. S. Suk, Y.-Y. Wang, E. A. Nance, J.-C. Yang, P. J. Mcdonnell, R. A. Cone, E. J. Duh and J. Hanes, J. Controlled Release, 2013, 167, 1–9 CrossRef PubMed.
- W. G. Kreyling, S. Hirn, W. Möller, C. Schleh, A. Wenk, G. Celik, J. Lipka, M. Schäffler, N. Haberl, B. D. Johnston, R. Sperling, G. Schmid, U. Simon, W. J. Parak and M. Semmler-Behnke, ACS Nano, 2014, 8, 222–233 CrossRef CAS PubMed.
- S. Barua and S. Mitragotri, ACS Nano, 2013, 7, 9558–9570 CrossRef CAS PubMed.
- C. P. Brangwynne, G. H. Koenderink, F. C. Mackintosh and D. A. Weitz, Trends Cell Biol., 2009, 19, 423–427 CrossRef CAS PubMed.
- Y. Guo, S. Jangi and M. A. Welte, Mol. Biol. Cell, 2005, 16, 1406–1416 CrossRef CAS PubMed.
- K. Barlan, M. J. Rossow and V. I. Gelfand, Curr. Opin. Cell Biol., 2013, 25, 483–488 CrossRef CAS PubMed.
- B. L. Haas, J. S. Matson, V. J. DiRita and J. S. Biteen, Molecules, 2014, 19, 12116–12149 CrossRef PubMed.
- E. P. Perillo, Y. L. Liu, K. Huynh, C. Liu, C. K. Chou, M. C. Hung, H. C. Yeh and A. K. Dunn, Nat. Commun., 2015, 6, 7874 CrossRef CAS PubMed.
- X. Michalet, F. F. Pinaud, L. A. Bentolila, J. M. Tsay, S. Doose, J. J. Li, G. Sundaresan, A. M. Wu, S. S. Gambhir and S. Weiss, Science, 2005, 307, 538–544 CrossRef CAS PubMed.
- D. Boucher, Z. Deng, T. Leadbeater, R. Langlois, M. Renaud and K. E. Waters, Miner. Eng., 2014, 62, 120–128 CrossRef CAS.
- B. Rabencov, J. Arca and R. van Hout, Int. J. Multiphase Flow, 2014, 62, 110–122 CrossRef CAS.
- H. E. Pace, N. J. Rogers, C. Jarolimek, V. A. Coleman, E. P. Gray, C. P. Higgins and J. F. Ranville, Environ. Sci. Technol., 2012, 46, 12272–12280 CrossRef CAS PubMed.
- T. Turiv, A. Brodin and V. G. Nazarenko, Condens. Matter Phys., 2015, 18, 23001 CrossRef.
- K. He, M. Spannuth, J. C. Conrad and R. Krishnamoorti, Soft Matter, 2012, 8, 11933–11938 RSC.
- M. S. Safari, M. A. Vorontsova, R. Poling-Skutvik, P. G. Vekilov and J. C. Conrad, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 042712 CrossRef PubMed.
- N. Chenouard, I. Smal, F. de Chaumont, M. Maska, I. F. Sbalzarini, Y. H. Gong, J. Cardinale, C. Carthel, S. Coraluppi, M. Winter, A. R. Cohen, W. J. Godinez, K. Rohr, Y. Kalaidzidis, L. Liang, J. Duncan, H. Y. Shen, Y. K. Xu, K. E. G. Magnusson, J. Jalden, H. M. Blau, P. Paul-Gilloteaux, P. Roudot, C. Kervrann, F. Waharte, J. Y. Tinevez, S. L. Shorte, J. Willemse, K. Celler, G. P. van Wezel, H. W. Dan, Y. S. Tsai, C. O. de Solorzano, J. C. Olivo-Marin and E. Meijering, Nat. Methods, 2014, 11, 281–289 CrossRef CAS PubMed.
- E. Meijering, O. Dzyubachyk and I. Smal, Methods Enzymol., 2012, 504, 183–200 Search PubMed.
- M. J. Saxton, Nat. Methods, 2014, 11, 247–248 CrossRef CAS PubMed.
- C. Kural, H. Kim, S. Syed, G. Goshima, V. I. Gelfand and P. R. Selvin, Science, 2005, 308, 1469–1472 CrossRef CAS PubMed.
- Z. Y. Liang, N. Xu, Y. H. Guan, M. Xu, Q. H. He, Q. D. Han, Y. Y. Zhang and X. S. Zhao, Biochem. Biophys. Res. Commun., 2007, 353, 231–237 CrossRef CAS PubMed.
- V. Levi and E. Gratton, Cell Biochem. Biophys., 2007, 48, 1–15 CrossRef CAS PubMed.
- R. Parthasarathy, Nat. Methods, 2012, 9, 724–726 CrossRef CAS PubMed.
- R. Parthasarathy, Biophys. J., 2012, 102, 202a CrossRef.
- Y. Li, V. Lubchenko and P. G. Vekilov, Rev. Sci. Instrum., 2011, 82, 053106 CrossRef PubMed.
- D. Maes, M. A. Vorontsova, M. A. C. Potenza, T. Sanvito, M. Sleutel, M. Giglio and P. G. Vekilov, Acta Crystallogr., Sect. F: Struct. Biol. Commun., 2015, 71, 815–822 CrossRef CAS PubMed.
- M. A. Vorontsova, H. Y. Chan, V. Lubchenko and P. G. Vekilov, Biophys. J., 2015, 109, 1959–1968 CrossRef CAS PubMed.
- M. K. Cheezum, W. F. Walker and W. H. Guilford, Biophys. J., 2001, 81, 2378–2388 CrossRef CAS PubMed.
- R. Besseling, L. Isa, E. R. Weeks and W. C. K. Poon, Adv. Colloid Interface Sci., 2009, 146, 1–17 CrossRef CAS PubMed.
- D. Boyer, D. S. Dean, C. Mejia-Monasterio and G. Oshanin, Eur. Phys. J.: Spec. Top., 2013, 216, 57–71 CrossRef.
- E. Kepten, I. Bronshtein and Y. Garini, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 052713 CrossRef PubMed.
- X. Michalet and A. J. Berglund, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 061916 CrossRef PubMed.
- M. J. Saxton, Biophys. J., 1997, 72, 1744–1753 CrossRef CAS PubMed.
- C. L. Vestergaard, P. C. Blainey and H. Flyvbjerg, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 022726 CrossRef PubMed.
- Y. Li, V. Lubchenko, M. A. Vorontsova, L. Filobelo and P. G. Vekilov, J. Phys. Chem. B, 2012, 116, 10657–10664 CrossRef CAS PubMed.
- V. Filipe, A. Hawe and W. Jiskoot, Pharm. Res., 2010, 27, 796–810 CrossRef CAS PubMed.
- B. Anderson, M. H. Rashid, C. Carter, G. Pasternack, C. Rajanna, T. Revazishvili, T. Dean, A. Senecal and A. Sulakvelidze, Bacteriophage, 2011, 1, 86–93 CrossRef PubMed.
- I. Montes-Burgos, D. Walczyk, P. Hole, J. Smith, I. Lynch and K. Dawson, J. Nanopart. Res., 2010, 12, 47–53 CrossRef.
- M. A. Vorontsova, D. Maes and P. G. Vekilov, Faraday Discuss., 2015, 179, 27–40 RSC.
- P. G. Vekilov and M. A. Vorontsova, Acta Crystallogr., Sect. F: Struct. Biol. Cryst. Commun., 2014, 70, 271–282 CrossRef CAS PubMed.
- M. Sleutel and A. E. Van Driessche, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E546–553 CrossRef CAS PubMed.
- F. Zhang, F. Roosen-Runge, A. Sauter, R. Roth, M. W. A. Skoda, R. M. J. Jacobs, M. Sztucki and F. Schreiber, Faraday Discuss., 2012, 159, 313–325 RSC.
- W. Pan, O. Galkin, L. Filobelo, R. L. Nagel and P. G. Vekilov, Biophys. J., 2007, 92, 267–277 CrossRef CAS PubMed.
- O. Gliko, N. Neumaier, W. Pan, I. Haase, M. Fischer, A. Bacher, S. Weinkauf and P. G. Vekilov, J. Am. Chem. Soc., 2005, 127, 3433–3438 CrossRef CAS PubMed.
- T. E. Williamson, A. Vitalis, S. L. Crick and R. V. Pappu, J. Mol. Biol., 2010, 396, 1295–1309 CrossRef CAS PubMed.
- P. G. Vekilov, Soft Matter, 2010, 6, 5254–5272 RSC.
- O. Galkin, W. Pan, L. Filobelo, R. E. Hirsch, R. L. Nagel and P. G. Vekilov, Biophys. J., 2007, 93, 902–913 CrossRef CAS PubMed.
- P. Li, S. Banjade, H.-C. Cheng, S. Kim, B. Chen, L. Guo, M. Llaguno, J. V. Hollingsworth, D. S. King, S. F. Banani, P. S. Russo, Q.-X. Jiang, B. T. Nixon and M. K. Rosen, Nature, 2012, 483, 336–340 CrossRef CAS PubMed.
- C. P. Brangwynne, J. Cell Biol., 2013, 203, 875–881 CrossRef CAS PubMed.
- S. C. Weber and C. P. Brangwynne, Curr. Biol., 2015, 25, 641–646 CrossRef CAS PubMed.
- A. A. Hyman, C. A. Weber and F. Jülicher, Annu. Rev. Cell Dev. Biol., 2014, 30, 39–58 CrossRef CAS PubMed.
- H. Qian, M. P. Sheetz and E. L. Elson, Biophys. J., 1991, 60, 910–921 CrossRef CAS PubMed.
- X. Michalet, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041914 CrossRef PubMed.
- X. Michalet, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 059904 CrossRef.
- D. Boyer and D. S. Dean, J. Phys. A: Math. Theor., 2011, 44, 335003 CrossRef.
- D. Boyer, D. S. Dean, C. Mejia-Monasterio and G. Oshanin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 060101 CrossRef PubMed.
- A. Einstein, Ann. Phys., 1905, 17, 549–560 CrossRef CAS.
- A. Einstein, Ann. Phys., 1906, 19, 371–381 CrossRef CAS.
- A. Einstein, in Einstein, Collected Papers, ed. R. Fürth, 1926, reprinted 1956, vol. 2, pp. 170–182, 206–122 Search PubMed.
- D. S. Martin, M. B. Forstner and J. A. Käs, Biophys. J., 2002, 83, 2109–2117 CrossRef CAS PubMed.
- S. M. Anthony and S. Granick, Langmuir, 2009, 25, 8152–8160 CrossRef CAS PubMed.
- S. M. Anthony, M. Kim and S. Granick, Langmuir, 2008, 24, 6557–6561 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm00946h |
| This journal is © The Royal Society of Chemistry 2016 |








