Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
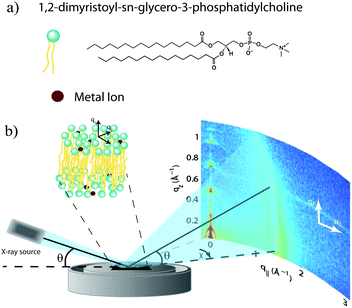
Swelling of phospholipid membranes by divalent metal ions depends on the location of the ions in the bilayers†
Richard J.
Alsop
,
Rafaëla
Maria Schober
and
Maikel C.
Rheinstädter
*
Department of Physics and Astronomy, McMaster University, ABB-241, 1280 Main Street West, Hamilton, Ontario L8S 4M1, Canada. E-mail: rheinstadter@mcmaster.ca; Fax: +1-(905)-546-1252; Tel: +1-(905)-525-9140-23134
First published on 29th June 2016
Abstract
The Hofmeister series illustrates how salts produce a wide range of effects in biological systems, which are not exclusively explained by ion charge. In lipid membranes, charged ions have been shown to bind to lipids and either hydrate or dehydrate lipid head groups, and also to swell the water layer in multi-lamellar systems. Typically, Hofmeister phenomena are explained by the interaction of the ions with water, as well as with biological interfaces, such as proteins or membranes. We studied the effect of the divalent cations Mg2+, Ca2+, Fe2+, and Zn2+ on oriented, stacked, phospholipid bilayers made of dimyristoylphosphatidylcholine (DMPC). Using high-resolution X-ray diffraction, we observed that the cations lead to a swelling of the water layer between the bilayers, without causing significant changes to the bilayer structure. The cations swelled the bilayers in different amounts, in the order Fe2+ > Mg2+ > Ca2+ > Zn2+. By decomposing the total bilayer electron density into different molecular groups, Zn2+ and Ca2+ were found to interact with the glycerol groups of the lipid molecules and cause minor swelling of the bilayers. Mg2+ and Fe2+ were found to position near the phosphate groups and cause a strong increase in the number of hydration water molecules. Our results present a molecular mechanism-of-action for the Hofmeister series in phospholipid membranes.
1. Introduction
Metal ions are ubiquitous in biology. Mono- and divalent ions, such as Na+, K+ and Ca2+, exist at high concentrations and play important roles in the regulation of cell polarization and action potentials.1 In addition, divalent metals such as Mg2+, Zn2+, and Fe2+ exist in trace amounts and are important to specific enzymatic reactions.1 The interaction of ions with membranes also influences biological function. For example, adsorption of ions to the membrane changes the membrane dipole potential and influences nerve cell action potentials.2,3 As well, zinc is believed to protect against lipid peroxidation by out-competing free-radicals for lipid binding sites.4The lipid bilayer is a biological interface, which is susceptible to perturbations by ions that typically bind to membranes through interactions with the polar head groups.5–7 Once bound, ions reduce the membrane dipole potential,3,8 as well as influence head group hydration.9,10 In multilamellar membranes, ions cause an increase in, or swelling of, the inter-lamellar water layer.11–13
The extent of membrane perturbation by a specific ion is not exclusively determined by ion charge. For example, Ca2+ is observed to bind more strongly to DPPC (dipalmitoylphosphatidylcholine) membranes compared to Mg2+.7 In addition, at low concentrations, KBr was found to cause greater swelling in multilamellar vesicles than KCl.12,13 Binder and Zschörnig observed that while Ca2+ and Mg2+ increased the lipid head group hydration, Zn2+ decreased hydration.14
The Hofmeister series describes specific ion effects in solution, which are not exclusively explained by ion charge.1 For example, zinc is the only divalent metal used in the so-called “Zinc-finger” protein motif. Specific ion interactions with proteins, polymers, and in bulk solution are best explained by the ion entropies and enthalpies of hydration, which are in turn explained by ion size, polarizability, as well as charge. As atomic radii are determined by the number of electron shells and the shell/proton ratio, ions with identical charge could have very different Hofmeister effects. However, not all Hofmeister effects are explained by interactions with water. Ion-interactions with the biological interface often influence the observed effects.15
The physical mechanism for the diverse effects of ions on lipid bilayers is not well understood. To precisely quantify the effect of salts on the lipid bilayer, we used X-ray diffraction to study oriented DMPC multi-bilayers prepared with the divalent metal ions Ca2+, Mg2+, Fe2+, and Zn2+. Changes to bilayer spacing and in-plane molecular order were detected by 2-dimensional diffraction, and the position of the ions in the bilayers determined from reconstructed electron density profiles. We observe strong bilayer swelling, which is dependent on the binding position of the ion in the membrane. Our results suggest that the membrane specific effects depend intimately on the binding site of the ion in the bilayer.
2. Materials and methods
2.1. Preparation of the highly-oriented multi-lamellar membrane complexes
Highly oriented, multi-lamellar membranes were prepared on polished 1 × 1 cm2 silicon wafers. The wafers were first pre-treated by sonication in dichloromethane (DCM) at 310 K for 25 minutes to remove all organic contamination and create a hydrophobic substrate. After removal from the DCM post-sonication, each wafer was thoroughly rinsed three times by alternating with ∼50 mL of ultra pure water (18.2 MΩ cm) and methanol. This treatment renders the surface of the wafers hydrophobic.1,2-Dimysteroyl-sn-glycero-3-phosphocholine (DMPC) was obtained from Avanti polar lipids and dissolved in ultra-pure water to form multi-lamellar vesicles. The lipid solution, which is initially milky and opaque, is sonicated using a tip sonicator (Branson SLPt) until small unilamellar vesicles are formed and the solution turns translucent. ZnCl2, MgCl2, CaCl2 (all from Caledon Laboratories) and FeCl2 (Sigma Aldrich) were dissolved in ultra-pure water at mM concentrations. Note that at these low concentrations, and in the absence of added acid or peroxide, Fe2+ is not expected to oxidize to Fe3+.16 The lipid and salt solutions were then mixed in the appropriate ratios to achieve the desired molecular concentrations.
A tilting incubator was heated to 343 K and the solutions were placed inside to equilibrate. 80 μL of lipid solution was deposited on each wafer. The solvent was then allowed to slowly evaporate for ∼10 minutes while gently rocked, such that the lipid solution spread evenly on the wafers. Samples were then placed in a sealed container containing an open vial of ultra pure water and incubated for 24 hours at 303 K. This procedure results in highly oriented, multi-lamellar membrane stacks and a uniform coverage of the silicon wafers. About 3000 highly oriented stacked membranes with a total thickness of ∼10 μm are produced using this protocol. The high sample quality and high degree of order are prerequisites to determine the in-plane and out-of-plane structures of the membranes separately, but simultaneously.
2.2. X-ray diffraction experiment
Out-of-plane and in-plane X-ray scattering data were obtained using the Biological Large Angle Diffraction Experiment (BLADE) in the Laboratory for Membrane and Protein Dynamics at McMaster University. BLADE uses a 9 kW (45 kV, 200 mA) CuKα Rigaku Smartlab rotating anode at a wavelength of 1.5418 Å. Both the source and the detector are mounted on moveable arms such that the membranes remain horizontal during measurements. Focussing, multilayer optics provide a high intensity parallel beam with monochromatic X-ray intensities up to 1010 counts per (s mm2). This beam geometry provides the optimal illumination of the membrane samples to maximize the scattered signal. By using highly-oriented stacks, the in-plane (q‖) and out-of-plane (qz) structures of the membranes could be determined independently. A sketch of the scattering geometry is depicted in Fig. 1(b).The X-ray diffraction experiments determine three pieces of information relevant to the molecular structures of the membranes. Firstly, out-of-plane diffraction scans permit the reconstruction of electron density profiles, which were used to determine the detailed structure of the lipid bilayer perpendicular to the membrane plane. Secondly, in-plane scattering measurements at higher q‖ values allow for the study of organization of the lipid molecules in the plane of the membranes, as detailed in, e.g., Barrett et al.17 Thirdly, scans performed at low q‖ and low qz were used to measure the degree of orientation of the bilayers in the stack.
2.3. Out-of-plane structure and electron densities
The out-of-plane membrane electron density, ρ(z), can be approximated by a 1-dimensional Fourier analysis:17,18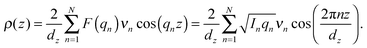 | (1) |
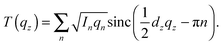 | (2) |
The calculated electron densities, ρ(z), which are initially on an arbitrary scale, were transformed into an absolute scale. The curves were vertically shifted to fulfil the condition ρ(0) = 0.22 e− Å−3 (the electron density of a CH3 group) in the center of a bilayer. The curves were then scaled until the total number of electrons 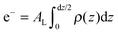 across a membrane leaflet agrees with the total number of electrons of a DMPC molecule with nw water molecules and the contribution of the metal ion. AL is the area of a lipid molecule. No further modification is made to the electron densities after this scaling is applied. nW for a pure DMPC membrane under the conditions of the experiment (T = 28° and 50% RH) was chosen to be 7, in agreement with ref. 19 and 20.
across a membrane leaflet agrees with the total number of electrons of a DMPC molecule with nw water molecules and the contribution of the metal ion. AL is the area of a lipid molecule. No further modification is made to the electron densities after this scaling is applied. nW for a pure DMPC membrane under the conditions of the experiment (T = 28° and 50% RH) was chosen to be 7, in agreement with ref. 19 and 20.
The volume per DMPC lipid (VL) can be modelled using:
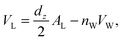 | (3) |
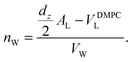 | (4) |
2.4. Real-space modelling of electron density profiles
To determine the changes to the bilayer structure induced by the presence of metal ions along the z-axis, electron density profiles were decomposed using a composite model. The specific models used for the lipid component groups are those used by Klauda et al.23 Atoms from the DMPC molecules were distributed between five component groups representing distinct portions of the bilayer. These regions are (1) the terminal CH3 groups at the end of the lipid chains, for both lipids in the bilayer, found at the center of the bilayer (CH3); (2) the CH2 groups composing the hydrocarbon core of the lipid molecule (CH2); (3) the glycerol moiety in the head group (GC); and (4) the phosphate group in the head group (P). An additional function is added to describe the hydration water layer and the choline group of the lipid (BC). The functions describe a full bilayer, i.e. two leaflets.The CH3 groups at the center are described by a Gaussian distribution, ρCH3(z):
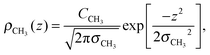 | (5) |
The tail group region is described by the same function as Klauda et al.:
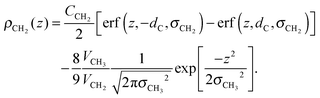 | (6) |
A set of two Gaussian peaks (one for each leaflet) is used to describe the GC groups:
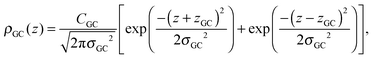 | (7) |
A set of two Gaussian peaks are used to describe the phosphate (P) group of the lipid molecules:
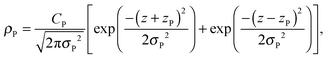 | (8) |
The final distribution used describes the choline group, combined with the water layer between leaflets, ρBC(z), which is determined from the free volume assumption. The summed probability of observing a lipid molecule at z, P(z), is determined by ref. 23
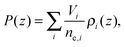 | (9) |
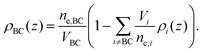 | (10) |
For membranes prepared using metal ions, an additional density term, ρm(z), must be added to include the divalent cations. The ion density is modelled as a Gaussian distribution centered at zm with width σm, and height given by the number Cm. All ions are assumed to partition into the lipid unit cell, therefore Cm is normalized such that Cm × AL = ne,m, where ne,m = (the number of electrons on a single ion) × (ion molar concentration). As chloride ions are oxidized in solution to become chlorine gas,24 only the cations are included in the electron density:
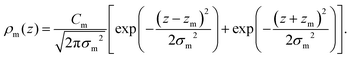 | (11) |
| ρ(z) = ρCH3(z) + ρCH2(z) + ρGC(z) + ρP(z) + ρH2O(z) + ρm(z). | (12) |
Additional relevant structural properties can be calculated from the fits. The head group–head group distance is calculated from the positions of the phosphate (zp) and glycerol, (zGC):
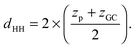 | (13) |
| dB′ = 2(dC + 9 Å) | (14) |
| dW′ = ½(dz − dB′). | (15) |
3. Results
3.1. Two-dimensional X-ray diffraction
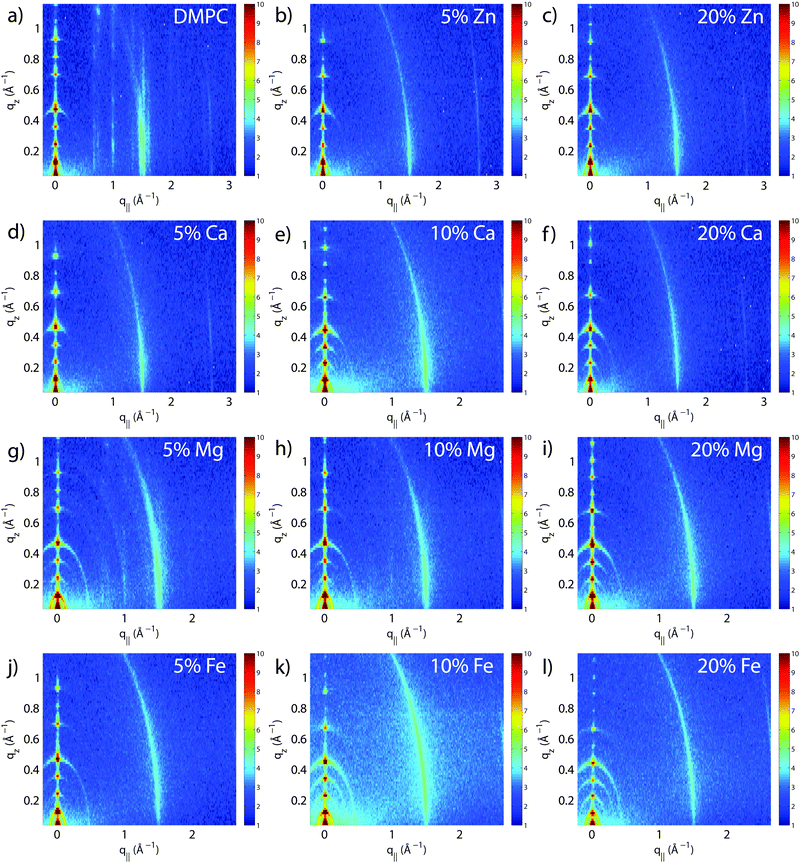
The molecular structure of the membrane complexes was studied using high-resolution X-ray diffraction imaging, as depicted in Fig. 1. By using oriented samples, the in-plane (q‖) and out-of-plane (qz) structures were determined separately but simultaneously. All membranes were incubated for 24 h at T = 30 °C and then scanned at a temperature of T = 28 °C and 50% relative humidity (RH). Similar to protein crystallography, this dehydrated state suppresses thermal fluctuations, increases the number of higher order Bragg peaks, and thereby enhances structural features, allowing for a high structural resolution.26 In addition, this dehydrated state permits sensitivity to subtle changes in hydration caused by ions.Fig. 2 shows 2-dimensional reciprocal space maps for all samples in this study. Measurements are taken for −0.3 Å−1 < q‖ < 3 Å−1 and 0 Å−1 < qz < 1.1 Å−1. Pure DMPC membranes are shown in Fig. 2(a). The observed scattering shows a number of well-defined intensities along both qz and q‖ axes, indicative of lamellar bilayers with strong in-plane ordering. The pattern is typical for DMPC membranes in the well-ordered gel phase.17,27
The peaks are best indexed by orthorhombic unit cells to describe the head group and lipid tail organization in the plane of the bilayers, as described, e.g., by Barrett et al.,17 with AL = 40.5 Å2. The sample with 5 mol% Mg2+ in Fig. 2(g) shows a qualitatively similar pattern, indicating that small amounts of Mg2+ do not lead to significant changes to the in-plane membrane structure. All other samples displayed in Fig. 2 show a single in-plane feature at q‖ = 1.5 Å−1, only.
The area per lipid molecule can be determined from the in-plane diffraction data, when assuming that the lipid tails form a densely packed structure with hexagonal symmetry (planar group p6), as reported from, e.g., neutron diffraction.28 In the absence of fluctuations (in gel phase lipid bilayers), the area per lipid molecule can be determined from the position of the in-plane Bragg peak at qT to 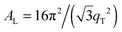 .17,29,30 The distance between two acyl tails is determined to be
.17,29,30 The distance between two acyl tails is determined to be 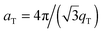 , with the area per lipid simplified to
, with the area per lipid simplified to 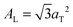 . Values of AL are listed in Table 1. The area per lipid for pure DMPC and DMPC + 5 mol% Mg was determined from the lattice parameters of the corresponding orthogonal head group lattice.
. Values of AL are listed in Table 1. The area per lipid for pure DMPC and DMPC + 5 mol% Mg was determined from the lattice parameters of the corresponding orthogonal head group lattice.
| Sample | d z (Å) | A L (Å2) | n W | H |
|---|---|---|---|---|
| DMPC | 54.4 ± 0.1 | 40.5 ± 0.2 | 7.0 ± 0.3 | 0.968 ± 0.004 |
| 5 mol% Zn2+ | 55.4 ± 0.1 | 41.1 ± 0.2 | 8.2 ± 0.2 | 0.962 ± 0.003 |
| 20 mol% Zn2+ | 55.2 ± 0.1 | 41.1 ± 0.1 | 8.1 ± 0.2 | 0.962 ± 0.002 |
| 5 mol% Ca2+ | 54.8 ± 0.1 | 41.1 ± 0.1 | 7.8 ± 0.3 | 0.964 ± 0.003 |
| 10 mol% Ca2+ | 57.4 ± 0.1 | 41.1 ± 0.1 | 9.6 ± 0.2 | 0.963 ± 0.003 |
| 20 mol% Ca2+ | 57.2 ± 0.1 | 41.1 ± 0.1 | 9.4 ± 0.2 | 0.958 ± 0.003 |
| 5 mol% Mg2+ | 54.7 ± 0.1 | 40.6 ± 0.3 | 7.3 ± 0.3 | 0.957 ± 0.004 |
| 10 mol% Mg2+ | 55.1 ± 0.1 | 41.1 ± 0.1 | 8.0 ± 0.2 | 0.951 ± 0.005 |
| 20 mol% Mg2+ | 56.7 ± 0.1 | 41.1 ± 0.1 | 9.1 ± 0.2 | 0.942 ± 0.004 |
| 5 mol% Fe2+ | 54.7 ± 0.1 | 41.1 ± 0.1 | 7.7 ± 0.2 | 0.954 ± 0.005 |
| 10 mol% Fe2+ | 56.9 ± 0.1 | 41.1 ± 0.1 | 9.1 ± 0.2 | 0.935 ± 0.007 |
| 20 mol% Fe2+ | 60.8 ± 0.1 | 41.1 ± 0.1 | 11.8 ± 0.2 | 0.92 ± 0.01 |
To determine the degree of orientation of membranes in the stack, the intensity as a function of the meridional angle δ was determined. δ is defined as the angle relative to the qz axis. The intensity, I(δ), was integrated around the fourth Bragg peak, at Q ≈ 0.45 Å−1, from 10° < δ < 40°. δ < 10° was not used in order to avoid contributions from incoherent scattering.31 The fourth Bragg peak was chosen as incoherent contributions were weaker than the first Bragg peak, while coherent contributions were stronger than peaks two and three.
I(δ) was fit with a Gaussian distribution centered at δ = 0, which was then used to calculate the degree of orientation using Hermans orientation function:
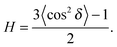 | (16) |
3.2. Out-of-plane diffraction
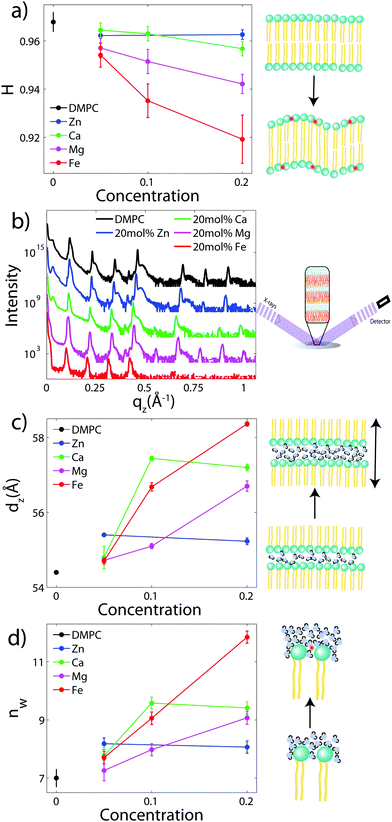
To determine the out-of-plane structure of the bilayer stack, the 2-dimensional data in Fig. 2 were cut along the qz direction. Out-of-plane reflectivities for selected samples are shown in Fig. 3(b). Up to 12 evenly spaced diffraction peaks are observed for pure DMPC bilayers, indicative of a well-ordered lamellar structure. Note that not all diffraction orders are necessarily observed for the different samples as the scattering intensity depends on the form factor of the bilayers. The dz-spacing between two neighboring membranes in the stack was determined from the distance between the Bragg reflections (dz = 2π/Δqz) along the out-of-plane axis, qz. The measured lamellar spacing, dz, for the pure DMPC was determined to be 54.4 Å, in agreement with previous reports.17,21,27 Lamellar patterns were observed for all membrane complexes in this study.The presence of ions caused significant increases in the lamellar spacing, dz, as shown in Fig. 3(c). dz increased to 55.2 Å, 57.2 Å, 56.7 Å, and 60.8 Å for 20 mol% Zn2, Ca2+, Mg2+ and Fe2+, respectively. While Mg2+ and Fe2+ caused monotonic increases in dz, a plateau in dz was observed for Ca2+ and Zn2+, as reported previously for Ca2+.11,32 Salts have been shown previously to increase the lamellar spacing of multi-lamellar membrane samples.11–13
The number of water molecules per lipid, nW, was determined using eqn (4), and the results are shown in Fig. 3(d). In general, the addition of salts leads to a strong increase in nW from 7 for DMPC to 11.8 for Fe2+. Only a minor increase to 8.2 was observed for Zn2+.
3.3. Analysis of electron density profiles
To determine detailed changes to the lipid structure caused by divalent salts in the membrane, electron density profiles (EDPs) of the membranes, ρ(z), were assembled by Fourier synthesis of the observed lamellar Bragg peaks. ρ(z) for a pure DMPC membrane is shown in Fig. 4(a). The profile corresponds to a lipid bilayer in the gel state with both chains in an all-trans configuration, as reported previously.17,27,33 The electron rich phosphorous group in the head region can be identified by the absolute maximum in the electron density at z ∼ 20 Å. ρ(z) monotonically decreases to the bilayer center at z = 0 where CH3 groups reside in the center with ρ(0) = 0.22 e− Å−3. The phases, vn, were determined using the T(qz) function (eqn (2)), and are shown in the ESI,† in Fig. S1.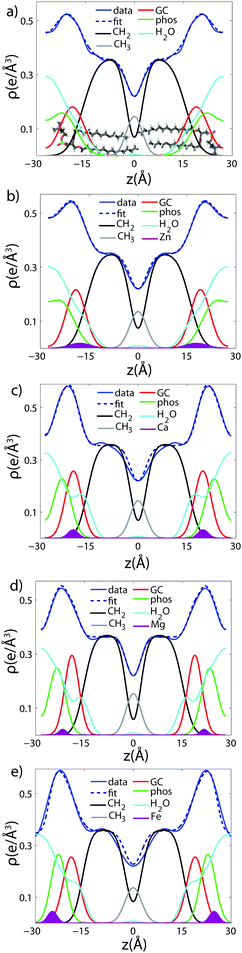 | ||
| Fig. 4 Fits of the component group model to the electron density profiles of (a) pure DMPC, as well as membranes with 20 mol% (b) Zn2+ (c) Ca2+ (d) Mg2+ and (e) Fe2+. | ||
As introduced above, the bilayer was described by a set of atomic component groups, as suggested by Klauda et al.23 Separate functions were used to describe electron density contributed by the terminal methyl group, the CH2 lipid chains, the glycerol group, the phosphate group, the water/choline layer, and the divalent metal ion. The model was applied to the pure DMPC bilayer profile, as well as the bilayers with 20 mol% ions. The results are shown in Fig. 4, and the fitting parameters written in Table 2.
| Sample | d HH (Å) | d B′ (Å) | d W′ (Å) | σ CH3 (Å) | σ CH2 (Å) | d C (Å) | σ GC (Å) | z GC (Å) | σ P (Å) | z P (Å) | z m (Å) | σ m (Å) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tristram-Nagle | 40.6 | 48.3 | 7.3 | — | — | 15.15 | — | — | — | — | — | — |
| DMPC | 40.6 ± 1 | 49.8 ± 1 | 2.5 ± 1 | 2.44 ± 0.01 | 2.98 ± 0.4 | 15.7 ± 0.1 | 3.1 ± 0.1 | 18.3 ± 0.1 | 3.6 ± 0.1 | 22.4 ± 0.1 | — | — |
| 20% Zn2+ | 42.2 ± 1 | 49.8 ± 1 | 2.7 ± 1 | 2.58 ± 0.01 | 3.1 ± 0.40 | 15.9 ± 0.1 | 3.0 ± 0.20 | 19.1 ± 0.1 | 3.9 ± 0.50 | 23.3 ± 0.1 | 17.9 ± 0.7 | 3.2 ± 1 |
| 20% Ca2+ | 43.0 ± 1 | 49.2 ± 1 | 4 ± 1 | 2.43 ± 0.01 | 2.4 ± 0.2 | 15.6 ± 0.1 | 2.52 ± 0.2 | 19.8 ± 0.1 | 2.73 ± 0.3 | 23.3 ± 0.2 | 19.9 ± 3 | 1.5 ± 1 |
| 20% Mg2+ | 42.2 ± 1 | 48.7 ± 1 | 4.2 ± 1 | 2.28 ± 0.01 | 2.5 ± 0.1 | 15.2 ± 0.1 | 2.20 ± 0.1 | 18.8 ± 0.1 | 2.51 ± 0.1 | 23.4 ± 0.1 | 21.7 ± 0.5 | 1.1 ± 0.2 |
| 20% Fe2+ | 42.0 ± 0.1 | 49 ± 1 | 5.88 ± 1 | 2.56 ± 0.01 | 2.16 ± 0.38 | 15.6 ± 0.2 | 2.55 ± 0.27 | 19.0 ± 0.2 | 2.34 ± 0.3 | 22.9 ± 0.1 | 24.8 ± 2 | 1.4 ± 1 |
Fig. 4(a) illustrates the model fit to the DMPC bilayer. The experimentally determined EDP for DMPC is well fit by five functional groups. The parameters extracted from the model agree well with those determined by Klauda et al. for fluid phase DMPC membranes. As our membrane samples are in the dehydrated gel phase, there are, however, some differences. For example, the hydrocarbon chain length was found to be dC = 12.3 Å in hydrated DMPC, whereas we measure straighter chains with dC = 15.6 Å, due to the well packed chains in the gel phase. However, this is in close agreement with the measurements of the fully hydrated gel phase, where dC = 15 Å.21 The positions of zGC and zp were found to increase accordingly. In addition, the widths of the head group interfaces, σp, σGC, and σCH2, were larger than previously reported results, likely due to inter-head group interactions in the dehydrated phase.34
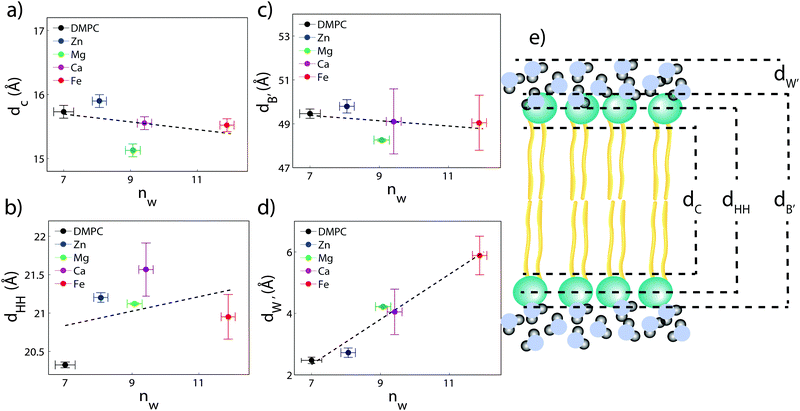
The composite model was used to fit DMPC membranes containing divalent metal ions at a concentration of 20 mol% in order to determine the position of the ion and observe changes to the bilayer caused by the metal. An additional density term was included to capture the position of the metal (Fig. 4(b)–(e)), with the fitting parameters in Table 2. In general, the width of the head group region decreases at high ion concentration, corresponding to the increase in hydration. Structural parameters from the fits are shown in Fig. 5 as a function of nW for the various ions. While parameters such as dC and dB′ are not strongly affected by nW (∼1 Å), there is a large increase in dW′ observed with increasing nW.
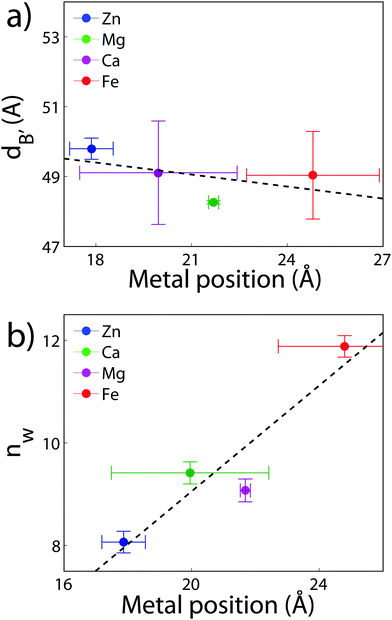
The position of the metal ion is determined by fitting ρm(z) to the electron density profiles. For all four metals studied, the ion is found in the head group region of the DMPC bilayers. The position varies from |z| = 17.9 Å for Ca2+, to |z| = 24.8 Å for Fe2+. As shown in Fig. 6(b), there is a correlation between the position of the ion in the membrane and the number of water molecules in the bilayer. The further the ion resides in the membrane center, the greater the number of water molecules. However, as shown in Fig. 6(a), there is no influence of dB′ on the head group position, further illustrating that the ions do not significantly impact the bilayer structure.
4. Discussion
4.1. The effect of divalent ions on multilamellar DMPC membranes
The structure of oriented DMPC membranes containing the divalent cations Mg2+, Ca2+, Fe2+, and Zn2+ was determined by high resolution X-ray diffraction. In general, the ions caused significant swelling or an increase in dz by increasing the number of water molecules, nW. Recruitment of water is associated with increased bilayer bending. Modelling of reconstructed electron densities revealed that the degree of swelling caused by the ions is related to the position of the ion in the bilayer.The DMPC membranes were studied in their gel phase at 50% RH and T = 28 °C. We measure dC = 15.6 Å and AL = 40.6 Å2 in the gel phase, in agreement with previous reports.17,21 While studying ion-membrane interactions in the dehydrated gel phase permitted greater structural information leading to a precise localization of the ions, we note that lipid interactions in the dehydrated state may be different compared to the fully hydrated, fluid phase. Increased inter-bilayer interactions in the gel phase (characterized by increased σP) may result in altered ion–membrane interactions.
In gel phase DMPC membranes, each lipid is in contact with 7 water molecules, as determined previously by X-ray reflectivity.19 In this dehydrated state, there are significant head group interactions between adjacent bilayers in the stack, resulting in overlap with the electron density between two bilayers at |z| = dz/2.26,34,35 Consequently, the electron density profile of our pure DMPC membrane at |z| = dz/2 is not that of pure water (0.33 e− Å−3), but instead increased to 0.45 e− Å−3. The bilayer overlap leads to increased uncertainty in the position of the head group, which is captured by the increased head group width in our component group model. The width of the phosphate group, σP, for example, increased from 2.37 Å to 5.00 Å for the gel phase. We note that in fluid phase bilayers, nW increases to ∼25 water molecules36 in fully hydrated bilayers. The area per lipid increases to 65 Å2 while dC decreases to 12.3 Å.23
With the addition of cations to the bilayers in this study, nW increases to a maximum of 11.8 Å for 20 mol% Fe2+. However, no significant increases in AL or decreases in dC are observed, suggesting that the increased hydration does not change the lipid structure of the gel phase and also does not induce a transition into the fluid phase. In addition, the increased water between the layers results in decreased head group interactions, with σP ∼ 3.3 Å for 20 mol% Fe2+. A shoulder in the water density profile, ρBC, is observed within the bilayer for profiles with water (Fig. 4), suggesting that additional hydration water molecules may also partition deep into the membrane.
A comment is in order: our model assumes a constant volume-per-DMPC, VDMPCL. From our experiments, we observe that the area per lipid and the steric width of the bilayer, dB′, do not change significantly in the presence of ions. dB′ varies by ∼5%, indicative of a variation in VDMPCL of 5%, and equivalent to nW changing by ∼1 water molecule. We argue that this small change does not significantly influence our results and interpretation. In addition, the physical presence of the ions is not expected to add significant volume, as the largest ion, Zn2+, is 6 Å3 in volume, only. Therefore, we believe that fixed VDMPCL is a reasonable assumption.
4.2. The effect of the ion position on bilayer swelling
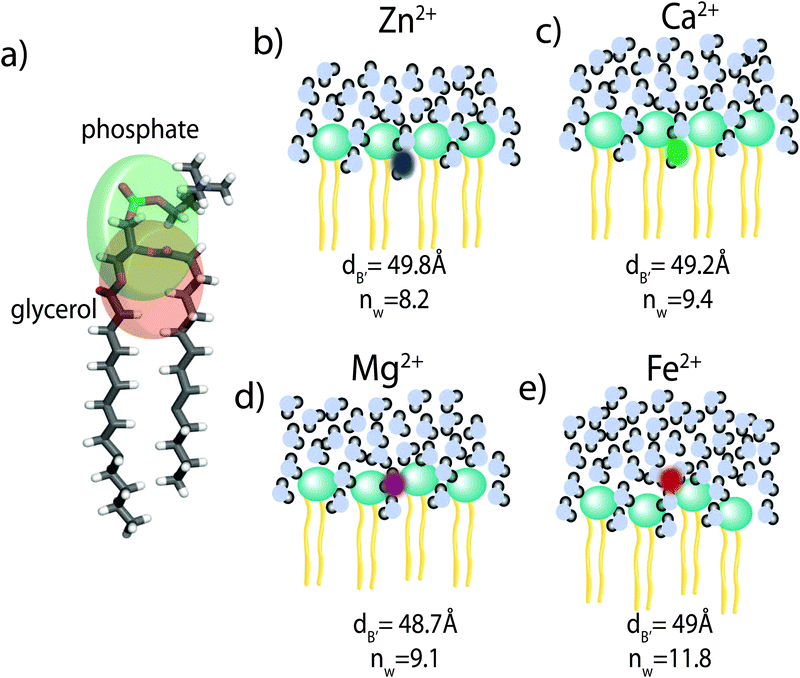
Using a component group model to fit the bilayer electron density profiles, the position of the cations, zm, was determined. The position was different for the different ions studied: Ca2+ and Zn2+ were found to bind closer to the glycerol group (zm ∼ 17 Å), while Mg2+ and Fe2+ were observed closer to the phosphate group (zm ∼ 19–21 Å), as depicted in Fig. 7.When binding to zwitterionic lipids, such as DMPC, a cation may interact with the negatively charged phosphate group or coordinate with the oxygens of the carbonyl group deeper in the bilayer.14 The binding position is dependent on the size of the ion, as well as the chemistry of the ion–oxygen bond. For example, Binder et al. found that the 3d10 electron of Zn2+ binds covalently to the electronegative oxygens on the carboyl group, binding the ion to the lipid.37 In addition, while Ca2+ coordinates and binds electrostatically with oxygens on four adjacent lipid molecules, Mg2+ binds closer to the phosphate group and coordinates with water-oxygens.9 In agreement with the above literature, we observe that Zn2+ and Ca2+ are adjacent to the glycerol group and Mg2+ is close to the phosphate group.9,37 Fe2+, being smaller than Mg2+, resides even further from the glycerol group (Fig. 7(b)–(e)).
In our component group model, the electron distribution of the ion is modelled as a Gaussian with the position and width determined by the least squares fitting procedure. In addition, we determine the steric membrane width, dB′, (see Table 2) for our membrane samples with high ion concentration. Using these measurements, the fraction of ions bound to the head groups (z < dB′) and the fraction outside the lipid bilayer (z > dB′) is calculated. For Zn2+, Ca2+, and Mg2+, a negligible fraction of the ion is found outside the bilayer suggesting that these metals bind 100% to our membranes. Also from this calculation 60% of Fe2+ sits outside the bilayer and in the water layer.
An ion interacting with the dehydrated DMPC membranes could swell the bilayers by two mechanisms: For one, an ion could globally alter the energetics of bilayer interactions in the lamellar stack, thereby increasing the equilibrium water thickness. The thickness of the water layer in the bilayer stack is determined by the balance of (1) a repulsive entropic force caused by bilayer undulations, (2) an attractive van-der-Waals interaction between adjacent bilayers, and (3) a short range, repulsive force caused by steric water interactions.12
Monovalent ions have previously been shown to increase the water layer by screening the van-der-Waals attraction in oriented bilayer and multilamellar vesicle systems.11–13 Petrache, Nagle et al. and Petrache, Zemb et al. studied the monovalent salts KCl and KBr in multilamellar membrane samples using X-ray diffraction.12 The authors demonstrate that the salts screen the van-der-Waals interaction, resulting in a swelling of the water layer between bilayers, while not influencing the lipid structure. Cations also bind to the polar lipid head groups, reducing the dipole potential,3 suggesting that cations that bind closer to the phosphate group are more effective at reducing the van-der-Waals force.
As a second mechanism for swelling the bilayer, the ion could directly recruit water from the vapour phase to the lipid interface, causing local regions of high water density and an increase in the width of the water layer.14 An ion, which resides deeper in the lipid heads, is unable to coordinate and recruit as many waters as an ion which is closer to the water layer.9
While the exact swelling mechanism (local water recruitment or global changes to bilayer energetics) cannot be resolved from our experiments, swelling of the water layer between the bilayers is clearly dependent on the ion and, specifically, the binding position of the ion, in the order of Fe2+ > Mg2+ > Ca2+ > Zn2+.
The results present a potential mechanism-of-action for the so-called Hofmeister series in lipid membranes. The Hofmeister series was initially used to describe the ability of various ions to either enhance the dissolution (“salt-in”) or precipitation (“salt-out”) of ions.1 Ions are often sorted into water-structure-breakers (chaotropes) or water-structure-makers (kosmotropes). The cations studied here are all known as chaotropes.15 However, the exact ordering of the Hofmeister series varies based on the system in question, and typically depends on physiochemical interactions between the ions and the interface in question.15 In our experiments, the ion effects depend on the position of the ion in the membrane.
5. Conclusion
We investigated the effect of the divalent metal ions Mg2+, Ca2+, Fe2+ and Zn2+ on phospholipid bilayers made of dimyristoylphosphatidylcholine (DMPC) using high resolution X-ray diffraction. All cations in this study were found to partition in the head group region of the bilayers and lead to swelling of the bilayers. The location of the cations in the bilayers was determined from electron densities and all ions were found to reside at z-values of 15.9 Å < |z| < 21.4 Å away from the bilayer center. Through a component analysis, we show that the increase in lamellar spacing is not caused by an increase in the membrane thickness, however, by an increase of the water layer thickness, i.e., an increase in the number of water molecules bound per lipid molecule.The cations swelled the bilayers in different amounts, in the order Fe2+ > Mg2+ > Ca2+ > Zn2+, corresponding to a Hofmeister series in phospholipid membranes. There is a correlation between the ion's location and the swelling: the metal ions which attract more hydration water molecules bind further away from the bilayer center.
Acknowledgements
This research was funded by the Natural Sciences and Engineering Research Council of Canada (NSERC), the National Research Council Canada (NRC), the Canada Foundation for Innovation (CFI) and the Ontario Ministry of Economic Development and Innovation. R.J.A. is the recipient of an NSERC PGSD scholarship, M.C.R. is the recipient of an Early Researcher Award of the Province of Ontario and a University Scholar Award from McMaster University. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.References
- P. Lo Nostro and B. W. Ninham, Hofmeister phenomena: an update on ion specicity in biology, Chem. Rev., 2012, 112, 2286–2322 CrossRef CAS PubMed.
- A. L. Hodgkin and P. Horowicz, The effect of nitrate and other anions on the mechanical response of single muscle fibres, J. Physiol., 1960, 153, 404–412 CrossRef CAS.
- R. J. Clarke and C. Lüpfert, Influence of anions and cations on the dipole potential of phosphatidylcholine vesicles: a basis for the Hofmeister effect, Biophys. J., 1999, 76, 2614–2624 CrossRef CAS PubMed.
- A. W. Girotti, J. P. Thomas and J. E. Jordan, Inhibitory effect of zinc(II) on free radical lipid peroxidation in erythrocyte membranes, J. Free Radicals Biol. Med., 1985, 1, 395–401 CrossRef CAS.
- B. Klasczyk, V. Knecht, R. Lipowsky and R. Dimova, Interactions of alkali metal chlorides with phosphatidylcholine vesicles, Langmuir, 2010, 26, 18951–18958 CrossRef CAS PubMed.
- R. A. Böckmann and H. Grubmüller, Multistep binding of divalent cations to phospholipid bilayers: a molecular dynamics study, Angew. Chem., Int. Ed., 2004, 43, 1021–1024 CrossRef PubMed.
- L. J. Lis, W. Lis, V. A. Parsegian and R. P. Rand, Adsorption of divalent cations to a variety of phosphatidylcholine bilayers, Biochemistry, 1981, 20, 1771–1777 CrossRef CAS PubMed.
- J. N. Sachs, H. Nanda, H. I. Petrache and T. B. Woolf, Changes in phosphatidylcholine headgroup tilt and water order induced by monovalent salts: molecular dynamics simulations, Biophys. J., 2004, 86, 3772–3782 CrossRef CAS PubMed.
- J. Yang, C. Calero, M. Bonomi and J. Mart, Specific ion binding at phospholipid membrane surfaces, J. Chem. Theory Comput., 2015, 11, 4495–4499 CrossRef CAS PubMed.
- D. Uhrková, N. Kučerka, J. Teixeira, V. Gordeliy and P. Balgavy, Structural changes in dipalmitoylphosphatidylcholine bilayer promoted by Ca2+ ions: a small-angle neutron scattering study, Chem. Phys. Lipids, 2008, 155, 80–89 CrossRef PubMed.
- G. Pabst, A. Hodzic, J. Štrancar, S. Danner, M. Rappolt and P. Laggner, Rigidification of neutral lipid bilayers in the presence of salts, Biophys. J., 2007, 93, 2688–2696 CrossRef CAS PubMed.
- H. I. Petrache, S. Tristram-Nagle, D. Harries, N. Kučerka, J. F. Nagle and V. A. Parsegian, Swelling of phospholipids by monovalent salt, J. Lipid Res., 2006, 47, 302–309 CrossRef CAS PubMed.
- H. I. Petrache, T. Zemb, L. Belloni and V. A. Parsegian, Salt screening and specific ion adsorption determine neutral-lipid membrane interactions, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 7982–7987 CrossRef CAS PubMed.
- H. Binder and O. Zschörnig, The effect of metal cations on the phase behavior and hydration characteristics of phospholipid membranes, Chem. Phys. Lipids, 2002, 115, 39–61 CrossRef CAS PubMed.
- W. Kunz, Specific ion effects in colloidal and biological systems, Curr. Opin. Colloid Interface Sci., 2010, 15, 34–39 CrossRef CAS.
- W. Stumm and G. F. Lee, Oxygenation of ferrous iron, Ind. Eng. Chem., 1961, 53, 143–146 CrossRef CAS.
- M. A. Barrett, S. Zheng, G. Roshankar, R. J. Alsop, R. K. Belanger, C. Huynh, N. Kučerka and M. C. Rheinstädter, Interaction of aspirin (acetylsalicylic acid) with lipid membranes, PLoS One, 2012, 7, e34357 CAS.
- T. Adachi, A new method for determining the phase in the X-ray diffraction structure analysis of phosphatidylcholine:alcohol, Chem. Phys. Lipids, 2000, 107, 93–97 CrossRef CAS PubMed.
- E. Nováková, K. Giewekemeyer and T. Salditt, Structure of two-component lipid membranes on solid support: an X-ray reflectivity study, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 051911 CrossRef PubMed.
- H. Dies, L. Toppozini and M. Rheinstädter, The interaction between amyloid-β peptides and anionic lipid membranes containing cholesterol and melatonin, PLoS One, 2014, 9, e99124 Search PubMed.
- S. Tristram-Nagle, Y. Liu, J. Legleiter and J. F. Nagle, Structure of gel phase dmpc determined by X-ray diffraction, Biophys. J., 2002, 83, 3324–3335 CrossRef CAS PubMed.
- M. Wiener, R. Suter and J. Nagle, Structure of the fully hydrated gel phase of dipalmitoylphosphatidylcholine, Biophys. J., 1989, 55, 315–325 CrossRef CAS PubMed.
- J. B. Klauda, N. Kučerka, B. R. Brooks, R. W. Pastor and J. F. Nagle, Simulation based methods for interpreting X-ray data from lipid bilayers, Biophys. J., 2006, 90, 2796–2807 CrossRef CAS PubMed.
- E. W. Lim, Longman Effective Guide to O Level Chemistry, Pearson Education South Asia, 2007 Search PubMed.
- N. Kučerka, S. Tristram-Nagle and J. F. Nagle, Structure of fully hydrated fluid phase lipid bilayers with monounsaturated chains, J. Membr. Biol., 2006, 208, 193–202 CrossRef PubMed.
- K. Hristova and S. H. White, Determination of the hydrocarbon core structure of fluid dioleoylphosphocholine (dopc) bilayers by X-ray diffraction using specific bromination of the double-bonds: effect of hydration, Biophys. J., 1998, 74, 2419–2433 CrossRef CAS PubMed.
- R. J. Alsop, M. A. Barrett, S. Zheng, H. Dies and M. C. Rheinstädter, Acetylsalicylic acid (asa) increases the solubility of cholesterol when incorporated in lipid membranes, Soft Matter, 2014, 10, 4275–4286 RSC.
- C. L. Armstrong, D. Marquardt, H. Dies, N. Kučerka, Z. Yamani, T. A. Harroun, J. Katsaras, A.-C. Shi and M. C. Rheinstädter, The observation of highly ordered domains in membranes with cholesterol, PLoS One, 2013, 8, e66162 CAS.
- T. T. Mills, G. E. S. Toombes, S. Tristram-Nagle, D.-M. Smilgies, G. W. Feigenson and J. F. Nagle, Order parameters and areas in fluid-phase oriented lipid membranes using wide angle X-ray scattering, Biophys. J., 2008, 95, 669–681 CrossRef CAS PubMed.
- M. Barrett, S. Zheng, L. Toppozini, R. Alsop, H. Dies, A. Wang, N. Jago, M. Moore and M. Rheinstädter, Solubility of cholesterol in lipid membranes and the formation of immiscible cholesterol plaques at high cholesterol concentrations, Soft Matter, 2013, 9, 9342–9351 RSC.
- M. S. Jablin, K. Akabori and J. F. Nagle, Experimental support for tilt-dependent theory of biomembrane mechanics, Phys. Rev. Lett., 2014, 113, 248102 CrossRef CAS PubMed.
- D. Uhrková, J. Teixeira, A. Lengyel, L. Almásy and P. Balgavy, Formation of unilamellar dipalmitoylphosphatidylcholine vesicles promoted by Ca2+, J. Spectrosc., 2007, 21, 43–52 CrossRef.
- R. J. Alsop, C. L. Armstrong, A. Maqbool, L. Toppozini, H. Dies and M. C. Rheinstädter, Cholesterol expels ibuprofen from the hydrophobic membrane core and stabilizes lamellar phases in lipid membranes containing ibuprofen, Soft Matter, 2015, 11, 4756–4767 RSC.
- S. Tristram-Nagle and J. F. Nagle, Lipid bilayers: thermodynamics, structure, fluctuations, and interactions, Chem. Phys. Lipids, 2004, 127, 3–14 CrossRef CAS PubMed.
- R. J. Mashl, H. L. Scott, S. Subramaniam and E. Jakobsson, Molecular simulation of dioleoylphosphatidylcholine lipid bilayers at differing levels of hydration, Biophys. J., 2001, 81, 3005–3015 CrossRef CAS PubMed.
- J. F. Nagle and S. Tristram-Nagle, Structure of lipid bilayers, Biochim. Biophys. Acta, 2000, 1469, 159–195 CrossRef CAS.
- H. Binder, K. Arnold, A. Ulrich and O. Zschörnig, Interaction of zn 2+ with phospholipid membranes, Biophys. Chem., 2001, 90, 57–74 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm00695g |
| This journal is © The Royal Society of Chemistry 2016 |