Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Bistable self-assembly in homogeneous colloidal systems for flexible modular architectures†
G.
Steinbach
*ab,
D.
Nissen
c,
M.
Albrecht
c,
E. V.
Novak
d,
P. A.
Sánchez
 e,
S. S.
Kantorovich
de,
S.
Gemming
ab and
A.
Erbe
*b
e,
S. S.
Kantorovich
de,
S.
Gemming
ab and
A.
Erbe
*b
aInstitute of Physics, Technische Universität Chemnitz, 09107 Chemnitz, Germany. E-mail: gabi.steinbach@physik.tu-chemnitz.de
bHelmholtz-Zentrum Dresden-Rossendorf, Bautzner Landstraße 400, 01328 Dresden, Germany. E-mail: a.erbe@hzdr.de
cInstitute of Physics, University of Augsburg, 86159 Augsburg, Germany
dUral Federal University, Lenin av. 51, 620000, Ekaterinburg, Russia
eUniversity of Vienna, Sensengasse 8, 1090, Vienna, Austria
First published on 21st January 2016
Abstract
This paper presents a homogeneous system of magnetic colloidal particles that self-assembles via two structural patterns of different symmetry. Based on a qualitative comparison between a real magnetic particles system, analytical calculations and molecular dynamics simulations, it is shown that bistability can be achieved by a proper tailoring of an anisotropic magnetization distribution inside the particles. The presented bistability opens new possibilities to form two-dimensionally extended and flexible structures where the connectivity between the particles can be changed in vivo.
Introduction
Colloidal self-assembly is widely used to systematically study building principles of structures of various complexities. One especially interesting example for complex structures is given by modular architectures. They are prevalent in natural materials on the microscale1,2 and occur in numerous biological systems.3 Commonly, such structures form by self-assembly of modular units into larger structures, for example tissues,4,5 leading to complex designs with variable functionalities. In nature, high flexibility and variability in the design is obtained by exploiting self-organization processes, which depend on diverse, often interrelated, physical and chemical mechanisms. The longstanding quest for the replication6 of such structures, based on self-assembly of artificially fabricated constituents, is impeded by the difficulty to imitate those naturally occurring structural processes. This can be tackled by developing artificial, self-organizing systems that also provide large flexibility in their design. For a controlled artificial self-assembly it is important to formulate basic, simple building principles and to prove that the latter can determine the formation of complex and flexible structures.Following the idea of ‘colloidal Lego’,7,8 one simple approach for flexible modular design is to create colloids that can connect to each other in multiple ways, leading to various assembly patterns (minimum two) with different symmetry. To date, in most cases of directional self-assembly, colloidal particles can be bound together in only one specific position and orientation, which is set by the interactions at the contact points between the particles.9–12 For example, extensively studied ferromagnetic particles, which can be approximated by point dipoles,13–17 form exclusively linear structures due to the dominating head-to-tail minimum of the dipolar potential. Thus, the interparticle interaction defines only one specific type of connection based on which clusters can grow. In order to obtain more than one type of connection, non-uniform systems with at least two different types of particles have been used in previous reports.18–20 Here, we present a novel approach in which a single type of colloidal particle self-assembles through two symmetrically distinct types of connections, thus providing the system with a structural bistability. Flexibility/variability of this system stems from the fact that there coexist two almost equiprobable self-assembly scenarios. We show that these scenarios can be realized by magnetic particles with a permanent, anisotropic magnetization distribution, as the latter leads to essential deviations from the interaction landscape of particles that can be approximated by a single point dipole. In contrast to the approach of combining heterogeneous particles, the presence of a bistability in the system allows us to control the ratio between the available distinct connections by tuning the properties of a single type of colloid.
In particular, the system presented here exhibits a bistability already in clusters of three particles. We observed two stable states with distinct topologies: one cluster type is compact and has zero net magnetic moment, whereas the other one has the shape of a staggered chain, with a net magnetization perpendicular to the chain. The interconversion between those two stable states can be realized by applying external magnetic field pulses. Following the experimental observations, we develop a simplified model of spheres containing three point dipoles, which represent the magnetization distribution in the particles. We show, analytically and by molecular dynamics simulations, that the proposed model reproduces both stable configurations observed in the experimental system. Additionally, this model allows for the derivation of general design rules for the magnetization distribution inside the particles, which enables controlled tuning of the connection patterns. The detailed investigation of the stable connectivity between three particles provides a basis for the description of two-dimensionally extended self-assembled structures based on those connection patterns.
Results and discussion
Experimental investigations
In the present study, we investigate silica particles (Fig. 1a), hemispherically covered with a ferromagnetic thin film (see Experimental details), in the following denoted as cap. Colloids built in this way are examples of so-called Janus particles,7,21 with two hemispheres distinct in chemical and/or physical properties. In our case, the cap has a magnetic anisotropy that points perpendicular to the particle surface.22 Such a particle exhibits a rotational magnetization distribution with a net magnetic moment pointing perpendicular to the Janus interface (Fig. 1b). In solution, the colloidal particles sediment and form quasi-2D assemblies due to their magnetostatic interaction. Via video microscopy, we access the information on spatial and magnetic configurations of assembled clusters. The latter is extracted from the orientation of the caps, which coincides with the orientation of the net magnetic moments of the particles. The component of the magnetic orientation that lies in the assembly plane (Fig. 1b) is visualized by the optical contrast between the transparent, uncapped hemisphere and the opaque, capped hemisphere. The projected area of the uncapped hemisphere serves as measure for the magnetic orientation that lies perpendicular to the assembly plane.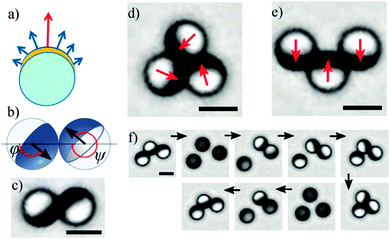 | ||
| Fig. 1 Sketches and microscopy images of self-assembled structures from magnetic Janus particles. (a) Cross section sketch of a silica sphere with hemispherical metal coverage (yellow arc). The arrows indicate the magnetization distribution. (b) Sketch of two particles in contact, displaying the cap (dark blue) and the net magnetic moment (black arrow), which has an in-plane orientation measured by the angles φ and ψ. (c) The two-particle cluster exhibits a staggered antiparallel magnetic alignment. Three particles can assemble in two different structures, (d) a compact cluster, where the magnetic moments (red arrows) form a flux-closure ring or (e) a staggered cluster with antiparallel magnetic moments. (f) Image sequence showing the interconversion between both three-particle configurations by applying short pulses of external magnetic fields (at 2nd and 7th image) perpendicular to the image plane (see Movie, ESI†) (scale bar: 5 μm). | ||
In our system, the self-assembly of two particles always results in a dumbbell structure (Fig. 1b and c), characterized by the antiparallelly aligned caps φ − ψ = 180°, with angles φ and ψ defining the net magnetization direction of the first and the second particle, respectively. This remarkable magnetic feature of staggered antiparallel orientation has been presented before23 and is a consequence of the hemispherical metal coverage, by which the center of mass of the magnetic cap deviates from the geometric center of the particles.24 In order to explain this configuration, a model of so-called shifted-dipole particles (1sd-particles) has been introduced.23,25 In this model, every particle contains a dipole that is shifted radially away from its center. It has been shown that two interacting 1sd-particles reproduce the dumbbell shown in Fig. 1b and c. A similar model was used to describe the self-assembly of spherical colloids with embedded off-centred magnetic cubes.26
Unexpectedly, during the self-assembly of three capped particles, two different stable cluster structures are observed. First, the particles can form a compact, equilateral triangle (Fig. 1d) with a three-fold rotational symmetry. Here, each pair of caps encloses an angle of φ − ψ = 120°. The caps form a flux-closure ring, which results in a vanishing net magnetic moment of the cluster. The transparent hemisphere of each particle is maximally visible, indicating that the particle-particle interaction favors an in-plane orientation. Second, three particles can form a staggered chain with mirror symmetry (Fig. 1e). Here, particles in contact exhibit an antiparallel cap orientation. Such a cluster has a net magnetic moment that points perpendicular to the particle chain. Thus, the staggered cluster aligns in an external magnetic field, provided that the field strength is relatively weak and does not distort the cluster structure. If stronger external fields are applied, the caps align with the field and eventually the cluster structure is altered. This can be used to transform one structure into another, as is described below and depicted in the image sequence in Fig. 1f. A magnetic field, which is applied perpendicular to the layer of colloids, forces the individual particles to rotate such that the caps point perpendicular to the image plane. The dominating dipole interaction between coaligned side-by-side dipoles leads to a strong repulsion and, thus, separation of the particles. Releasing the field results in reorientation and subsequent recombination of the particles. During the application of successive magnetic field pulses, any of the two cluster types (6th and 9th image of Fig. 1e) can form (see Movie, ESI†), provided that sufficient time between the pulses is allowed for cluster recombination. This suggests that both clusters are metastable and their energies are of a similar order of magnitude. After the field is released, the formation of one of the states instead of the other one depends on the relative orientations and positions of the particles before recombination and is, therefore, strongly influenced by thermal fluctuations and external factors such as magnetic fields. For example, if weak in-plane fields are applied during the recombination process of three particles, we primarily observed staggered configuration.
Analytic investigations
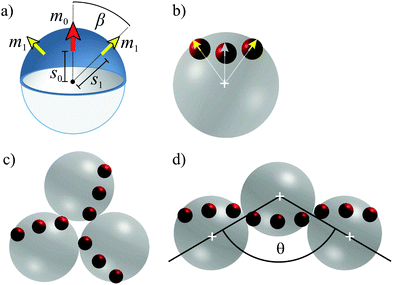
The staggered cluster is not found with the 1sd-particle model and only three-fold rotationally symmetric rings are observed.25,27 This suggests that the metallic cap is not adequately approximated by a single shifted dipole. Therefore, based on the form of the magnetization distribution of the cap (Fig. 1a), we introduce additional anisotropy by assigning each particle three point dipoles (Fig. 2a), which are shifted radially outwards (3sd-particles). Such a 3sd-particle carries a central dipole moment with shift s0 and magnitude m0, and two further dipoles on two opposite sides of the central one with equal shift s1 and magnitude m1. We denote the angle between each of the side dipoles and the central one as β.It is important to note that the discrepancy between the rotational symmetry, which is attributed to the capped particles, and the mirror symmetry of the proposed model has no qualitative relevance for the present study. It has been previously shown28 that for a monolayer of strongly interacting dipolar particles, the magnetic flux does not, on average, fluctuate out of the plane of the particle assembly. Since we restrict our study to two-dimensional particle assemblies, all three dipoles of each particle will lie in this plane. As the model breaks rotational symmetry in the direction perpendicular to this plane, we do not expect qualitative differences between the results of our analytical investigations and the experimental observations.
In comparison with the 1sd-particle model, where the dipole shift s0 is the only parameter, the increased number of parameters in the 3sd-particle model results in a more complex interaction energy landscape and potentially causes richer assembly behavior. In the following, we show step by step how the individual parameters impact the three-particle configurations, and extract suitable values for the parameters that match the capped particles. As a starting point, we made several assumptions listed below. First, the previously reported comparison between simulations of the 1sd-model24,25,27 and artificially grown compact clusters of the capped particles23 suggests a dipole shift of s0 = 0.6, where s0/1 is measured in units of the particle radius. We can use this value here since the side dipoles only cause a perturbation of the energy landscape. Second, analytic investigations revealed that the configurations of three-particle clusters of 3sd-particles qualitatively do not depend on the absolute values of the dipoles, but only on their ratio m1/m0. We can assume that m1/m0 = 0.5 since the thickness t of the cap at intermediate angles β of the side dipoles is approximately half the thickness tmax at the top of the cap, which varies as t(γ) = tmax![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ with the angle γ measured with respect to its symmetry axis. With these starting values, it is possible to determine suitable values for s1 and β in the model by comparing our experimental observations with analytical calculations and numerical simulations using the 3sd-particle model.
γ with the angle γ measured with respect to its symmetry axis. With these starting values, it is possible to determine suitable values for s1 and β in the model by comparing our experimental observations with analytical calculations and numerical simulations using the 3sd-particle model.
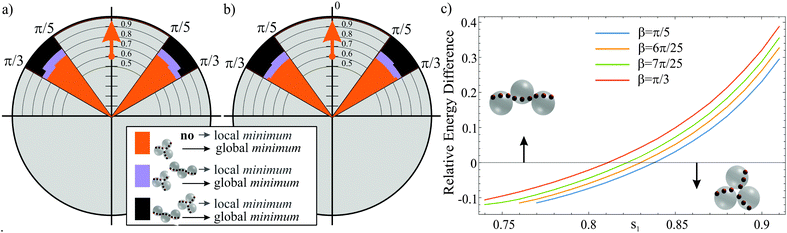
By energy minimization of the analytical interaction potential between 3sd-particles (Fig. 2b), we identify all stable configurations of three-particle clusters for a range of the parameters s1 and β. The configuration space is depicted in Fig. 3a as polar plot, where the central dipole is drawn as an orange arrow. Below a critical value of s1, which is around 0.76 for the examined range of β, only a triangle with the central dipoles forming a flux-closure ring (Fig. 2c) is found to be stable. Larger values of s1 result in two energy minima, which correspond to the ring and the staggered chain with antiparallel orientation of the central dipoles (Fig. 2d). The critical value of s1 increases only slightly with decreasing β (Fig. 3a). The impact of the magnitudes of the dipoles has been examined by recalculating the configuration space with m1/m0 = 1 (Fig. 3b). From the comparison between configuration spaces, we can derive that by increasing or decreasing m1/m0 moderately, the critical value of s1 (above which coexistence occurs) slightly decreases or increases, respectively. In any case, the side dipoles must always be shifted further off-center than the central dipole (s1 > s0) to ensure the coexistence of two stable three-particle configurations. From the configuration space it can be concluded that, in this 3sd-particle model, one can observe the coexistence of the two the stable configurations if the parameters are chosen appropriately.
The influence of s1 and β within the coexistence space is scrutinized in the following for the case m1/m0 = 0.5. With increasing s1 the global energy minimum switches from the ring (Fig. 3a, blue regime) to the staggered chain (black regime). More specifically, the relative difference of the energy between both states can be tuned gradually by s1 (Fig. 3c). Which of both states is the global minimum depends on the sign of the energy difference. This implies that the stability of the ring can be reduced in favor of the staggered chain primarily by increasing s1. Fig. 3c shows that the variation of β results in only a small and consistent vertical shift of the energy difference. Therefore, s1 acts as major tuning parameter for the energy landscape. Based on Fig. 3a, we can conclude that the modeling of the presented capped particles requires a value of s1 > 0.76.
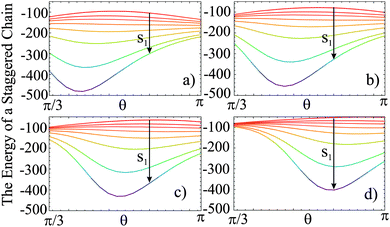
In the next step, we investigate the influence of s1 and β on the structure of the three-particle clusters. While the ring has a unique structure, the staggered chain can assume different shapes by varying the stagger angle θ (Fig. 2d). A systematic understanding is gained by calculating the energy of the staggered chain versus the stagger angle θ for various values of the shift s1 and the angle β, which is presented in Fig. 4. It can be seen that for s1 < 0.76 no energy minimum exists for a staggered configuration. For larger values of s1 a minimum is found which increases in depth with increasing shift. This is consistent with the conclusions that we have drawn from Fig. 3. Further, it can be seen that for a fixed value of β (in each plot), the stagger angle, at which the energy exhibits a minimum, decreases only slightly with increasing s1. In contrast, increasing β (among the four plots) results in a significant variation of the stagger angle.
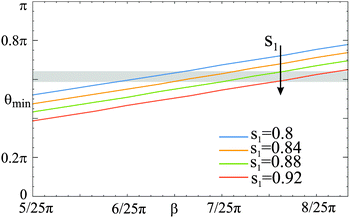
The linear dependence of θ on β in the equilibrium configuration is visualized in Fig. 5 for suitable values of s1. Here, varying s1 causes only small vertical shifts of the linear function. Thus, in a staggered configuration, θ is predominantly affected by β. The comparison of Fig. 5 and the experimentally obtained staggered chains allows for the extraction of suitable values of β. For the capped particles, we find experimental values in the range of 21π/36 < θ < 23π/36. In Fig. 5, this range is marked by a semi-transparent grey vertical bar. Taking into account that s1 > 0.76, we can derive suitable values of β = [6π/25…8π/25]. Based on this range, an upper limit of s1 can be determined from Fig. 3c. The relative energy difference should be small since both three-particle structures are of comparable energy as derived from their field-induced interconversion (Fig. 1f). Assuming a maximum relative energy difference of 10% and β = [6π/25…8π/25] gives an upper limit of s1 < 0.86.
So far, we have demonstrated by analytical calculations that the proposed 3sd-particle is a suitable model to explain the coexistence of two distinct self-assembly patterns exhibited by three capped colloids. Clearly, the model is not limited to the presented capped particles, but can also be transferred to other variants with a fixed anisotropic magnetization distribution. One alternative is given by Janus-like magnetic hydrogel particles29 with anisotropic distribution of magnetic nanoparticles.30–34 We anticipate that, by using this model, general design recommendations can be derived on how to tune the magnetization distribution in order to provide a bistability of three-particle configurations. Moreover, the results obtained here evidence that a magnetic particle with anisotropic magnetization distribution can be sectioned into regions with broadly similar net magnetic anisotropy direction, and that the regions can be effectively approximated by a single point dipole. The finite number of dipole interactions between particles enables an analytic description. The magnetic center of mass of these regions is determined by the shift parameters s0 and s1 and the net magnetization in these regions is given by the parameters m0 and m1. The introduced angle β corresponds to the spreading of the magnetic material in the particle.
Generalization and simulations
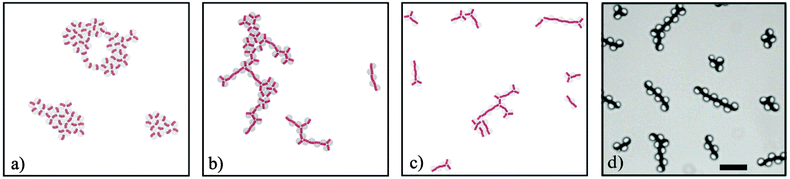
In fact, from Fig. 3 and 4 we learn that, in order to obtain a bistability of compact and staggered local conformations, one needs a sufficiently broad magnetization distribution (large β) that is anisotropic (s0 not equal to s1). The relative probability for a staggered or compact three-particle cluster to form (i.e., the ratio between the two free energies), can be controlled by changing s1. By increasing s1, the staggered configuration is preferred, whereas the decrease of s1 leads to the dominance of compact clusters. As a logical consequence, compact structures become the only stable state if the magnetically functionalized volume shrinks (β → 0) or if the magnetization distribution is rather uniform, such that the shift on the sides is not large enough (s1 ≤ s0). In addition, if β → 0, s0,1 → 0 linear head-to-tail structures would form in the system. To test the consequences of the relative energy on self-assembled structures by varying s1, we have performed extensive simulations of larger 3sd-particle systems and summarize prototypical clusters in Fig. 6. While the uniqueness of the ring as a stable state results in the formation of rather compact clusters (Fig. 6a, s1 is small), the aggregates become more open if the stability of the second, staggered configuration is increased (Fig. 6b and c, intermediate and large s1). The stagger angle θ is growing with β, as predicted analytically (Fig. 4). Even though in the experiment we cannot directly access the energies of the three particle clusters, by looking at the simulation snapshots, on the basis of qualitative visual resemblance with large clusters of capped particles (Fig. 6d) we can speculate that the system of capped colloids corresponds to the case depicted in Fig. 6c, i.e. the energy of the staggered three-particle cluster is lower than that of a compact ring. For a quantitative analysis, one has to compare the ratio between the staggered and the compact connections of all three-particle subunits in clusters obtained from the simulations and the digital microscopy images. The evaluation of such a quantitative analysis is not straightforward. The occurrence of one or the other assembly pattern is not a purely stochastic property that is determined by the energy ratio of both patterns, but also strongly depends on the relative positions, distance and orientations of the particles prior to the assembly. The quantitative analysis, thus, requires an extensive and separate study of the cluster structure as function of the starting configuration and the particle density. This remains an open task for continuing investigations.Methods
Experimental details
A dense suspension of silica spheres with a diameter of d = 4.54 ± 0.45 μm is dropped on a pretreated glass substrate. Via self-assembly, the particles arrange in densely packed two-dimensional arrays upon slow evaporation of the suspension solvent under ambient conditions. A metallic multi-layer sequence consisting of Pd(1.1 nm)/[Co(0.28 nm)/Pd(0.9 nm)]8/Pd(3.0 nm)/Ta(3.0 nm) is evaporated onto the particle array via magnetron sputter deposition.22 Deposition normal to the substrate leads to a uniform, hemispherical coverage of each particle with the metallic film. Film deposition leads to a thickness variation of the particle of less than 0.2%, justifying the assumption that capped particles are still spherical. The magnetic caps have to be magnetically saturated after film deposition to ensure the single-domain state as sketched in Fig. 1a.The coated particles are re-suspended in distilled water via sonication. A droplet of 1.5 μl of this particle suspension is enclosed between two glass slides and sealed with UV glue to prevent evaporation of the solvent. Due to the density mismatch the particles sediment. To test the stability of the suspension, we have first examined demagnetized particles. They form a stable dispersion in water without coagulation and, thus, the particles do not require any further surface preparation for stabilization. This further proves that the presented agglomeration of magnetically saturated particles primarily results from magnetostatic interactions and other sources such as attractive electrostatic interactions can be neglected. The sample cell is studied via video microscopy (Leica DMI3000B transmission light microscope). The cap orientation is resolved via digital image analysis with an uncertainty of less than 3°. An electromagnetic coil for the alignment of the capped particles is mounted parallel to the sample cell.
Analytical approach
To calculate the interaction energy of two 3sd-particles, and to analyze the global and local minima in the systems of three 3sd-particle configurations, we construct analytical expressions. For two particles, the general form of the interaction potential can be written as: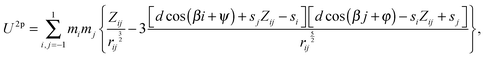 | (1) |
| Zij = cos(φ − ψ − β(i−j)); |
rij = d2 + si2 + sj2 − 2sisjZij − 2d[si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(βi + ψ) − sj cos(βi + ψ) − sj![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(βj + φ)] cos(βj + φ)] |
For three particles, the situation is more complex and we used the following approach for finding a ground state based on ref. 16, 25 and 28: we first performed molecular dynamics simulations to define the ground-state candidates, which turned out to be a linear chain, a staggered chain and a ring; then, using the reduced phase space, we could analytically obtain the energies for these candidates and pinpoint the lowest one. These analytic expressions for the energies are provided in the ESI.†
Computer simulation details
The numerical investigations consist of three sets of equilibrium molecular dynamics simulations carried out with the simulation package ESPResSo.35 In all cases, a Langevin thermostat is chosen, with the value of the reduced temperature set to T* = 1. The usage of this thermostat allows us to avoid the explicit simulation of the carrier fluid. In this approach, the effects of the thermal fluctuations of the carrier fluid on the colloidal particles are treated as stochastic terms added to the translational and rotational equations of motion (for details, see works24,36 and references therein). During the simulations, we impose a quasi-2d geometry by keeping the positions of the centers of all real particles and virtual sites coplanar, laying in the XY plane. Accordingly, all translations and rotations are limited to the latter plane. Finally, besides the dipolar magnetic interactions, the real particles interact between them with a soft core steric repulsion, given by a WCA potential.37 In the present study, we do not apply any external magnetic fields, as the subject deserves a separate investigation. With these common ingredients, we simulate three different systems. First, we obtain the equilibrium configurations of systems of two and three 3sd-particles under open boundary conditions, calculating the magnetic interactions by direct sum. These simulations provide us with the ground state candidates and make the analytical calculations feasible. In the second case, we perform the same kind of simulations for 3sd-particles, whose centers of mass are fixed at a given θ (Fig. 2d), and only their rotations are allowed. In this way, we check the analytical results shown in Fig. 4 for the optimal opening of the staggered configuration. Finally, we simulate the self-assembly of large systems of 3sd-particles. In this case, in order to mimic a pseudo-infinite system, we impose lateral periodic boundaries. For efficient calculations of the magnetic interactions under periodic boundaries in slab geometry, we chose the dipolar-p3m algorithm and dipolar layer corrections.36,38 We simulate systems with different 3sd-particle ground states, as shown in Fig. 3a. In this way, we check how the equilibrium self-assembly can be tuned through modifying the parameters of the colloidal cap. The results are presented in the main section (Fig. 6).Conclusions
In summary, we have shown that a homogeneous system of colloidal particles that exhibit rotationally symmetric, anisotropic magnetization distribution is a suitable system for flexible self-assembly on the microscale. Experimentally, we have studied the self-assembly of three magnetic microspheres with hemispherical magnetic coverage and discovered two symmetrically distinct connection patterns. We have demonstrated that these two assembly scenarios are a result of two almost equiprobable connection patterns that are an inherent property of the particle system. Further, we have introduced an analytical and simulation model of a 3sd-particle, a spherical particle with three shifted dipoles. Based on analytical calculations and molecular dynamics simulations of three interacting 3sd-particles, we have explained that the observed connection patterns originate from the shape of the magnetization distribution. The observations can be generalized to Janus-like particles that exhibit such an anisotropic magnetization distribution. Open, extended two-dimensional structures can self-assemble via only one type of interactions (e.g. magnetostatic interactions), because of the coexistence of a linear and a rotational connection pattern. This opens up unprecedented perspectives in the self-assembly of microstructures and shows that such a bistability leads to a drastic increase in the variety of the cluster structures.Beyond this flexibility, the instantaneous control over the ratio between both existing assembly patterns might be desirable. Here, one possibility to interconvert between both assembly patterns of the three-particle clusters has been presented. We are currently investigating the possibilities to control the relative occurrence of both assembly patterns. This can be realized by imprinting a certain spatial and directional distribution of the single particle suspension by, e.g., external magnetic fields or geometric confinements.
Acknowledgements
These investigations have been partially supported by the Austrian Research Fund (FWF): START-Projekt Y 627-N27 and the German Research Foundation (DFG, Grant No. ER 341/9-1, AL 618/11-1 and FOR 1713 GE 1202/9-1). Authors are grateful to the Ural Federal University stimulating programme. S. S. K. is supported by RFBR mol-a-ved 15-32-20549. E. V. N. acknowledges the support of President RF Grant No. MK-5216.2015.2. The authors were partially supported by the Ministry of Education and Science of the Russian Federation (Contract 02.A03.21.000, Project 3.12.2014/K) and ETN-COLLDENSE (H2020-MCSA-ITN-2014, Grant No. 642774). Computer simulations were performed at the Vienna Scientific Cluster (Austrian universities consortium for High Performance Computing). We thank Joe Donaldson for fruitful discussions and Michaela McCaffrey for linguistic suggestions.References
- G. P. Wagner, M. Pavlicev and J. M. Cheverud, Nat. Rev. Genet., 2007, 8, 921 CrossRef CAS PubMed.
- J. Clune, J. B. Mouret and H. Lipson, Proc. R. Soc. B, 2013, 280, 20122863 CrossRef PubMed.
- A. Hintze and C. Adami, PLoS Comput. Biol., 2008, 4, e23 Search PubMed.
- P. Zorlutuna, N. E. Vrana and A. Khademhosseini, IEEE Rev. Biomed. Eng., 2013, 6, 47 CrossRef PubMed.
- P. Lenas, F. P. Luyten, M. Doblare, E. Nicodemou-Lena and A. E. Lanzara, Artif. Organs, 2011, 35, 656 CrossRef PubMed.
- A. M. Kushner and Z. B. Guan, Angew. Chem., Int. Ed., 2011, 50, 9026 CrossRef CAS PubMed.
- J. Zhang, E. Luijten and S. Granick, Annu. Rev. Phys. Chem., 2015, 66, 581 CrossRef CAS PubMed.
- S. Sacanna, M. Korpics, K. Rodriguez, L. Colon-Melendez, S. H. Kim, D. J. Pine and G. R. Yi, Nat. Commun., 2013, 4, 6 Search PubMed.
- D. Heinrich, A. R. Goni, A. Smessaert, S. H. L. Klapp, L. M. C. Cerioni, T. M. Osan, D. J. Pusiol and C. Thomsen, Phys. Rev. Lett., 2011, 106, 208301 CrossRef CAS PubMed.
- Q. Chen, S. C. Bae and S. Granick, Nature, 2011, 469, 381 CrossRef CAS PubMed.
- A. B. Pawar and I. Kretzschmar, Macromol. Rapid Commun., 2010, 31, 150 CrossRef CAS PubMed.
- A. Kaiser, K. Popowa and H. Lowen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 012301 CrossRef PubMed.
- S. K. Smoukov, S. Gangwal, M. Marquez and O. D. Velev, Soft Matter, 2009, 5, 1285 RSC.
- J. Yan, S. C. Bae and S. Granick, Adv. Mater., 2015, 27, 874 CrossRef CAS PubMed.
- J. Yan, K. Chaudhary, S. C. Bae, J. A. Lewis and S. Granick, Nat. Commun., 2013, 4, 1516 CrossRef PubMed.
- V. Danilov, T. Prokopyeva and S. Kantorovich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 17 CrossRef PubMed.
- B. Ren, A. Ruditskiy, J. H. Song and I. Kretzschmar, Langmuir, 2012, 28, 1149 CrossRef CAS PubMed.
- H. Schmidle, S. Jager, C. K. Hall, O. D. Velev and S. H. L. Klapp, Soft Matter, 2013, 9, 2518 RSC.
- A. B. Pawar, I. Kretzschmar, G. Aranovich and M. D. Donohue, J. Phys. Chem. B, 2007, 111, 2081 CrossRef CAS PubMed.
- X. Zhang, Z. Meng, J. Ma, Y. Shi, H. Xu, S. Lykkemark and J. Qin, Small, 2015, 11, 3666 CrossRef CAS.
- A. Walther and A. H. E. Müller, Chem. Rev., 2013, 113, 5194 CrossRef CAS PubMed.
- M. Albrecht, G. H. Hu, I. L. Guhr, T. C. Ulbrich, J. Boneberg, P. Leiderer and G. Schatz, Nat. Mater., 2005, 4, 203 CrossRef CAS PubMed.
- L. Baraban, D. Makarov, M. Albrecht, N. Rivier, P. Leiderer and A. Erbe, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 031407 CrossRef PubMed.
- S. Kantorovich, R. Weeber, J. J. Cerda and C. Holm, J. Magn. Magn. Mater., 2011, 323, 1269 CrossRef CAS.
- S. Kantorovich, R. Weeber, J. J. Cerda and C. Holm, Soft Matter, 2011, 7, 5217 RSC.
- A. I. Abrikosov, S. Sacanna, A. P. Philipse and P. Linse, Soft Matter, 2013, 9, 8904 RSC.
- M. Klinkigt, R. Weeber, S. Kantorovich and C. Holm, Soft Matter, 2013, 9, 3535 RSC.
- T. A. Prokopieva, V. A. Danilov, S. S. Kantorovich and C. Holm, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031404 CrossRef PubMed.
- C. H. Chen, R. K. Shah, A. R. Abate and D. A. Weitz, Langmuir, 2009, 25, 4320 CrossRef CAS PubMed.
- C. H. Chen, A. R. Abate, D. Y. Lee, E. M. Terentjev and D. A. Weitz, Adv. Mater., 2009, 21, 3201 CrossRef CAS.
- A. K. F. Dyab, M. Ozmen, M. Ersoz and V. N. Paunov, J. Mater. Chem., 2009, 19, 3475 RSC.
- K. P. Yuet, D. K. Hwang, R. Haghgooie and P. S. Doyle, Langmuir, 2010, 26, 4281 CrossRef CAS PubMed.
- L. R. Shang, F. Q. Shangguan, Y. Cheng, J. Lu, Z. Y. Xie, Y. J. Zhao and Z. Z. Gu, Nanoscale, 2013, 5, 9553 RSC.
- L. B. Zhao, L. Pan, K. Zhang, S. S. Guo, W. Liu, Y. Wang, Y. Chen, X. Z. Zhao and H. L. W. Chan, Lab Chip, 2009, 9, 2981 RSC.
- H. J. Limbach, A. Arnold, B. A. Mann and C. Holm, Comput. Phys. Commun., 2006, 174, 704 CrossRef CAS.
- J. J. Cerda, V. Ballenegger, O. Lenz and C. Holm, J. Chem. Phys., 2008, 129, 234104 CrossRef PubMed.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237 CrossRef CAS.
- A. Brodka, Chem. Phys. Lett., 2004, 400, 62 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Analytic expression for the energies of three 3sd-particles. Movie: field-induced transformation between staggered and compact three-particle cluster. See DOI: 10.1039/c5sm02899j |
| This journal is © The Royal Society of Chemistry 2016 |