Open Access Article
Open Access ArticleImidazolium-based anion exchange membranes for alkaline anion fuel cells: elucidation of the morphology and the interplay between the morphology and properties†
Yue
Zhao
*a,
Kimio
Yoshimura
a,
Hideyuki
Shishitani
b,
Susumu
Yamaguchi
b,
Hirohisa
Tanaka
b,
Satoshi
Koizumi
*c,
Noemi
Szekely
d,
Aurel
Radulescu
d,
Dieter
Richter
e and
Yasunari
Maekawa
*a
aQuantum Beam Science Center (QuBS), Japan Atomic Energy Agency (JAEA), 1233 Watanuki-machi, Takasaki, Gunma 370-1292, Japan. E-mail: zhao.yue@jaea.go.jp; maekawa.yasunari@jaea.go.jp
bDaihatsu Motor Co., Ltd., Ryuo Gamo, Shiga 520-2593, Japan
cDepartment of Engineering, Ibaraki University, Hitachi 316-8511, Japan. E-mail: skoizumi@mx.ibaraki.ac.jp
dForschungszentrum Jülich GmbH, Jülich Centre for Neutron Science @ MLZ, Lichtenbergstraße 1, D-85747 Garching, Germany
eJülich Centre for Neutron Science & Institute for Complex Systems, Forschungszentrum Jülich GmbH, D-52425 Jülich, Germany
First published on 30th November 2015
Abstract
We investigated the morphology and swelling behavior of a new graft-type of anion exchange membrane (AEM) containing 2-methylimidazolium groups by using a contrast variation small angle neutron scattering (SANS) technique. These AEMs were prepared by radiation-induced grafting of 2-methyl-1-vinylimidazole and styrene into poly(ethylene-co-tetrafluoroethylene) (ETFE) films and subsequent N-alkylation with methyliodide, and possessed both high alkaline durability and high conductivity. Our results showed that the crystalline lamellar and crystallite structures originating from the pristine ETFE films were more or less conserved in these AEMs, but the lamellar d-spacing in both dry and wet membranes was enlarged, indicating an expansion of the amorphous lamellae due to the graft chains introduced in the grafting process and the water incorporated in the swelling process. For the first time, the swelling behavior of the AEMs was studied quantitatively in various water mixtures of water and deuterated water with different volume ratios (contrast variation method), and the morphology of these membranes was elucidated by three phases: phase (1) crystalline ETFE domains, which offer good mechanical properties; phase (2) hydrophobic amorphous domains, which are made up of amorphous ETFE chains and offer a matrix to create conducting regions; phase (3) interconnected hydrated domains, which are composed of the entire graft chains and water and play a key role in promoting the conductivity.
I. Introduction
In a previous study, we reported the synthesis and characterization of a series of newly developed imidazolium cation based anion exchange membranes (AEMs) made by radiation-induced grafting of 1-vinylimidazole and styrene into poly(ethylene-co-tetrafluoroethylene) (ETFE) films, and followed by N-alkylation with methyliodide.1 These AEMs were characterized to be terpolymers, and showed better alkaline durability in 1 M KOH at 80 °C. Most lately, we have further modified the grafted imidazole group to 2-methyl-1-vinylimidazole, and the resultant AEMs (hereafter named 2Me-AEM) exhibit even higher ion conductivity (>100 mS cm−1) and longer alkaline durability, owing to the fact that the methyl protecting group at the 2-imidazole position prevents ring-opening degradation. 2Me-AEM with an IEC (ion exchange capacity) of 1.82 mmol g−1 shows the best well-balanced properties required for fuel cell applications. All these findings, on the one hand, are a result of the sample preparation procedure of the radiation grafting method and the introduction of alkylimidazolium cations as an anion conducting group, and on the other hand, are believed to be controlled by the microphase separated structures of the membranes in the hydrated state, the precise manifestation of which was unclear. In this work, we aim to advance the work, elucidate the morphology of these 2Me-AEMs and understand the structure related unique properties such as the mechanical properties and the anion conductivity.Due to the growing concerns about the depletion of petroleum based energy resources and climate change, polymer electrolyte membrane fuel cell (FC) technologies have received much attention in recent years owing to their high efficiencies and low emission.2–12 Among them, hydrogen-type FCs which use proton exchange membranes (PEMs) have been heavily studied due to their features of low operating temperature, high current density and fast start-ups.10–12 However, PEM-FCs need to work in a highly acidic environment to promote high proton conductivity, which requires the consumption of acid-resistant precious metal catalysts and is expensive. In order to solve this problem, an alkaline anion exchange membrane fuel cell (AEM-FC) is a good solution, in which oxygen reduction reaction kinetics at the cathode is much more facile than in PEM-FCs under alkaline conditions, potentially allowing the use of inexpensive, non-noble metal catalysts such as nickel, cobalt or iron particles for the cathode and nickel for the anode.13–15
Although AEM-FCs exhibit the above potential advantages, the biggest challenge in developing AEM-FCs is to fabricate an AEM with high ion conductivity and mechanical stability without chemical deterioration at elevated pH and temperatures. So far, most strategies have focused on synthesizing new thermally and chemically durable fluorinated and aromatic polymers.16–18 For the first time, our group tried to develop a new type of 2Me-AEM by radiation grafting of imidazole/styrene on mechanically tough poly(ethylene-co-tetrafluoroethylene) (ETFE) films.1,19 There have been intensive reports including our previous studies20–22 on the radiation grafting technique, which has been successfully applied for the preparation of PEMs, where grafts containing an ion-conducting group (i.e. sulfonic acid) grafted onto fluorinated polymer films such as cross-linked polytetrafluoroethylene (cPTFE), ETFE, and poly(vinylidene fluoride) (PVDF) or fully aromatic hydrocarbon polymers such as poly(ether ether ketone).20–29 Therefore, we believe that this technique may allow the introduction of a large amount of grafts containing ion-conducting groups into the AEMs, and thus the resultant AEMs are expected to possess both high ion conductivity and good mechanical properties.
It is generally accepted that the properties of membranes derive from the microphase separation of a hydrophilic ionic material from a hydrophobic substance. Therefore, to design new AEMs, one should not only consider the architecture of the molecule itself, but also understand the microphase separation structures of membranes, such as the crystalline domains, the formation of conducting regions, and the distribution of ionic groups and water in the conducting regions. The morphology of the crystalline domains for polystyrene-grafted PEMs prepared by the radiation grafting technique has been intensively investigated using differential scanning calorimetry (DSC), X-ray diffraction (XRD) and small-angle scattering methods.20–29 For instance, the crystallinity of the grafted films was found to decrease with an increase in the grafting degree by many researchers in different fluoropolymer bases.27–29 In our previous work, we studied the hierarchical structure of PEMs consisting of poly(styrenesulfonic acid) and the PTFE base by using small angle neutron scattering (SANS) and small-angle X-ray scattering (SAXS) methods. The structure of these PEMs was characterized as being composed of conducting layers (graft domains) in lamellar stacks with 48–57 nm spacing on the surface of 480 nm diameter crystallites and ultrasmall structures with 1.7 nm correlation distance of sulfonic acid groups in the conducting layers.20,21 Most recently, we investigated the hierarchical structures of graft-type ETFE-based PEMs by using the Ultra-SAXS technique, and found that when the IEC is low, the conducting graft domains are around the ETFE lamellar crystals, however, when the IEC is high, new amorphous hydrated and crystallite network domains are formed independently.22
According to the previous studies on graft-type PEMs, ETFE was regarded as the most promising base material because of its well-balanced properties. Thus, we selected ETFE as the base material to develop a new type of imidazolium cation-grafted AEM.1 These AEMs, on the one hand, are expected to form interconnected hydrophilic microdomains with ion transport channels, swelling in water to promote the ion conductivity; and on the other hand, their hydrophobic crystalline domains originating from pristine ETFE membranes are expected to provide mechanical strength and restrict the dimensional changes upon swelling.
In this paper, we focus on the elucidation of the morphology of 2Me-AEMs by using the contrast variation SANS method. Note that this is the first study on graft-type AEM material prepared by the radiation grafting technique, and for the first time, we employ the contrast variation SANS method to quantitatively analyze the structure of these AEMs.
II. Experimental
II-1. Sample preparation and characterization
2Me-AEMs were prepared by radiation-induced grafting of 2-methyl-1-vinylimidazole and styrene into poly(ethylene-co-tetrafluoroethylene) (ETFE) films followed by N-alkylation with methyliodide. The molecular structure is schematically shown in Scheme 1. The sample preparation process is briefly described below: firstly, pristine ETFE membranes with a thickness of 50 μm (Asahi Glass Co. Ltd., mass density (dETFE) = 1.75 g cm−3, crystallinity (Xc) = 0.32) were irradiated by a 60Co γ-ray source (JAEA Takasaki, Gunma, Japan) with a total dose of 50 kGy under an argon atmosphere; secondly, these pre-irradiated membranes were immersed in an argon-purged monomer mixture solution of 2-methyl-1-vinylimidazole and styrene (9/1 v/v) to obtain grafted-ETFE membranes; finally, grafted-ETFE membranes were immersed in a 1 M 1,4-dioxane solution of methyliodide and then soaked in a hydrochloric acid solution followed by a sodium bicarbonate solution to afford N-alkylated 2Me-AEMs. Note that the counter-ions in the AEMs have been converted from iodide to bicarbonate forms in the final step to prevent degradation, which is often observed with the hydroxide form. The details of the radiation grafting method and preparation conditions can be found elsewhere.1,19 The ion exchange capacity of the 2Me-AEMs was determined by standard back-titration analysis.1 Because of the best performance in the direct hydrazine hydrate fuel cell test, the structure of 2Me-AEMs with an IEC of 1.82 mmol g−1 is targeted to be comprehensively studied in the following sections.The grafting degree (GD) of these 2Me-AEMs (IEC ∼ 1.82 mmol g−1) is 91%, estimated by eqn (1)
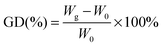 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 36. Thus, the mass density of the grafts (dgraft) can be calculated to be ∼0.98 g cm−3 on the basis of the reported mass densities of polystyrene and poly(N-vinylimidazole) homo-polymers being 1.05 and 0.95 g cm−3, respectively.
36. Thus, the mass density of the grafts (dgraft) can be calculated to be ∼0.98 g cm−3 on the basis of the reported mass densities of polystyrene and poly(N-vinylimidazole) homo-polymers being 1.05 and 0.95 g cm−3, respectively.
Fully water-swollen membranes were simply prepared by immersing the dry 2Me-AEMs into water at 25 °C. The water-uptake U is determined by the weight measurements using eqn (2) below.
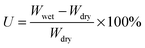 | (2) |
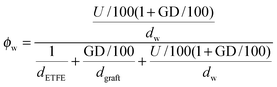 | (3) |
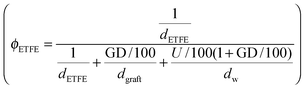 and grafts
and grafts  in the wet state can be deduced as well. Thus, the volume fraction of crystalline ETFE (ϕcry_ETFE) and amorphous ETFE (ϕamo_ETFE) can be estimated by considering Xc: ϕcry_ETFE = Xc × ϕETFE and ϕamo_ETFE = (1 − Xc) × ϕETFE, respectively. Furthermore, according to the ratio of 2-methyl-1-vinylimidazole to styrene units (64
in the wet state can be deduced as well. Thus, the volume fraction of crystalline ETFE (ϕcry_ETFE) and amorphous ETFE (ϕamo_ETFE) can be estimated by considering Xc: ϕcry_ETFE = Xc × ϕETFE and ϕamo_ETFE = (1 − Xc) × ϕETFE, respectively. Furthermore, according to the ratio of 2-methyl-1-vinylimidazole to styrene units (64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 36) on the grafts, the volume fraction of imidazole (ϕim) and styrene (ϕst) segments can also be roughly estimated to be ϕim = 0.64 × ϕgraft and ϕst = 0.36 × ϕgraft, respectively. The volume fraction of each component in the fully water-swollen AEMs is summarized in Table 1.
36) on the grafts, the volume fraction of imidazole (ϕim) and styrene (ϕst) segments can also be roughly estimated to be ϕim = 0.64 × ϕgraft and ϕst = 0.36 × ϕgraft, respectively. The volume fraction of each component in the fully water-swollen AEMs is summarized in Table 1.
| cry_ETFE | amo_ETFE | St | Im | Water | |
|---|---|---|---|---|---|
| b (×10−10 cm−2) | 2.23 | 2.0 | 1.415 | 1.123 | Variable |
| ϕ (%) | 7.55 | 16.05 | 13.82 | 24.58 | 38 |
Note that we also prepared 2Me-AEMs having an Im/St ratio of ca. 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 with GDs of 30, 46 and 120% by the same procedure as 2Me-AEM with a GD of 91% mentioned above to investigate the effect of GDs on the electrochemical properties and hierarchical structures. The preparation and characterization of these membranes will be reported in detail elsewhere for discussion of the fuel cell performance and durability of the 2Me-AEMs.
35 with GDs of 30, 46 and 120% by the same procedure as 2Me-AEM with a GD of 91% mentioned above to investigate the effect of GDs on the electrochemical properties and hierarchical structures. The preparation and characterization of these membranes will be reported in detail elsewhere for discussion of the fuel cell performance and durability of the 2Me-AEMs.
II-2. Small-angle neutron scattering (SANS) measurement
SANS measurements were performed mainly on a KWS-2 SANS diffractometer operated by Juelich Centre for Neutron Science at the neutron source Heinz Maier-Leibnitz (FRM II reactor) in Garching, Germany.30 The incident neutron beam at KWS-2 was monochromatized with a velocity selector to have the average wavelength (λ) of 5 Å with a wavelength resolution of Δλ/λ = 20%. The scattering patterns were collected using a two-dimensional scintillation detector, and circularly averaged to obtain scattering intensity profiles as a function of q, where q is the scattering vector, defined by q = (4π/λ)sin(θ/2), with λ and θ being the wavelength of the neutron and the scattering angles, respectively. Some of the SANS measurements were also done on the IBARAKI Materials Design Diffractometer (iMATERIA) at the Japan Proton Accelerator Research Complex (J-PARC), Japan,31 where the SANS instrument has four detector banks and covers a wide q range from 0.02 to 40 Å−1 with gradually changing resolution. The obtained scattering profiles were corrected for the instrument background, detector sensitivity, and scattering from the empty cell, and finally calibrated to an absolute scale (cm−1) using a Plexiglas secondary standard. The scattering intensity profile of each water mixture of H2O and D2O was measured in a quartz cell with a thickness of ∼0.5 mm, and used to estimate the incoherent scattering intensity for each water-swollen membrane with respect to its thickness. The estimated incoherent scattering intensity was subtracted from the absolute scattering intensity of each profile. All of the measurements were done at 25 ± 0.5 °C.II-3. Electrochemical impedance spectroscopy
In-plane anionic conductivity was calculated using electrochemical impedance spectroscopy (EIS) to measure membrane resistance. The membrane was mounted in a four-electrode test cell, with platinum electrodes that are separated by a constant distance l. Impedance spectra were obtained over a frequency range of 1 Hz to 10 kHz. EIS data were collected using a LCR meter (HIOKI 3522).1 All the AEMs were fully hydrated in nitrogen-saturated deionized water, and the conductivity measurements under fully hydrated conditions were carried out in a beaker filled with nitrogen-saturated deionized water at 60 °C. The ionic conductivity σ (mS cm−1) of a given membrane can be calculated from σ = l/(S × R) × 103, where l is the distance between two electrodes (cm), S is the cross-section area of the membrane (cm2), and R is the membrane resistance (Ω).III. Results
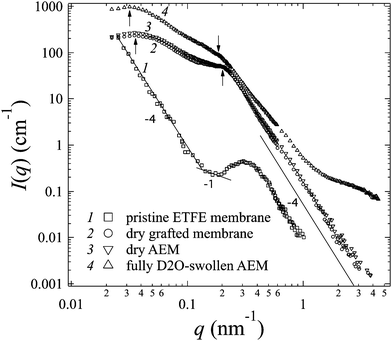
III-1. Grafting, alkylation and swelling effects on the morphology of the membranes
After grafting and alkylation, the ion conducting groups in AEMs are formed. When such a dry AEM is immersed in water, the hydrophilic chains with imidazolium cation groups can absorb water and form interconnected ion channels in hydrated regions, where the ions are capable of being transported, and hence the ion conductivity is created. In order to improve the ion transport efficiency, the understanding of the grafting, alkylation and swelling effects on the morphology of the membranes is very crucial. In this section, we compare the SANS profiles of the dry pristine ETFE membranes (profile 1, squares), dry grafted-ETFE membranes (profile 2, circles), dry 2Me-AEMs (profile 3, down-triangles) and AEMs equilibrated in D2O (profile 4, up-triangles) in Fig. 1, and report how the morphology of the membranes changes during these processes.Both the intensity and the shape of the profiles varied significantly upon grafting. Before grafting, the scattering intensity, I(q), of profile 1 is relatively weak compared to that of profile 2 and the other profiles, however, a clear upturn in the small q range at q < 0.2 nm−1 and a profound scattering maximum at q = 0.31 nm−1 are observed, indicating the typical crystalline ETFE lamellar structure with a d-spacing (=2π/q) of 20.0 nm as shown in Fig. 2(a). This result is very much consistent with the previously reported data measured by the SAXS method.22,32,33
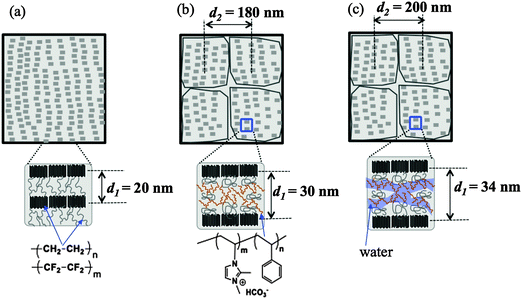 | ||
| Fig. 2 Schematic illustrations of the morphology of (a) dry pristine ETFE membranes; (b) dry grafted ETFE membranes or AEMs; (c) AEMs equilibrated in water. | ||
After grafting, profile 2 shows two broad scattering maxima: one maximum appears at q1 = 0.21 nm−1 (d1 = 2π/q1 ∼ 30 nm), corresponding to the low-q shift of the crystalline peak observed in profile 1. This larger d-spacing indicates the expansion of the lamellar stacks compared to that in the pristine ETFE membranes due to the incorporation of the graft chains in the lamellar amorphous domains; the other maximum which appears at q2 = 0.035 nm−1 (d2 = 2π/q2 ∼ 180 nm) represents the average distance between two grains, which are composed of crystalline ETFE regions and graft chains incorporated with amorphous ETFE regions as shown in Fig. 2(b). Note that Tap et al.22 even found an ambiguous peak in the ultra-small angle range at qs ∼ 0.006 nm−1 (ds ∼ 1050 nm) for the polystyrene grafted ETFE films, and they attributed d2 and ds to the short and long periods of the crystallites. Since the same pristine ETFE material and similar grafting procedures were used in this study, a related peak around qs might also exist though this q-range that was not covered in the current SANS experiment.
It should also be noted that though the crystalline peaks in profile 2 (profiles 3 and 4 as well) are broad, they can certainly be identified. Generally, semicrystalline polymers34–36 like poly(ether ether ketone) (PEEK), with a low grafting or sulfonation degree,37 usually exhibit clear scattering maxima attributed to crystalline domains. The crystallinity index decreases with the sulfonation degree significantly. For instance, sulfonated PEEK membranes are reported to be amorphous when the sulfonation degree is over 50%.38 Similarly, the broadening of crystalline peaks in profiles 2–4 supports the idea that the grafted ETFE membranes and AEMs have lower crystallinity than pristine ETFE membranes. This conclusion is confirmed by DSC measurement. Surprisingly, the crystalline structure is conserved in the grafted ETFE and AEMs even when the grafting degree is as high as 91%. Previous studies on ETFE-based PEMs prepared by the radiation technique also showed the conservation of the crystalline structure when the grafting degree is above 100%.22 All these results proved that the irradiation grafting method is an efficient way to maintain the inherent characteristics of the substrates such as the crystallinity index and hence the mechanical strength, which offers new opportunities for material development.
According to the scattering theory,39I(q) of the membranes is proportional to the square of the scattering contrast, which is the difference in the scattering length density (SLD) between crystalline and amorphous domains. Hence the weaker I(q) of profile 1 in comparison to that of profile 2 reveals a smaller scattering contrast between the ETFE crystalline regions and amorphous regions than that between the ETFE crystalline regions and graft incorporated amorphous regions. In order to verify this point, we should estimate SLD of each component in the membrane theoretically as below.
SLD of a molecule of i atoms is related to its molecular structure and may be readily calculated from the simple expression given by 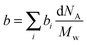 where bi is the scattering length of the ith atom, d is the mass density of the scattering body, Mw is the molecular weight, and NA is the Avogadro constant.39 Thus, SLD of imidazole (bim) and styrene (bst) segments on graft chains, and amorphous ETFE chains (bamo_ETFE) is calculated to be 1.123, 1.415 and 2.0 (×1010 cm−2), respectively.40 SLD of crystalline ETFE (bcry_ETFE) cannot be theoretically estimated so far, because their mass density is unknown, which heavily depends on the crystallinity and crystallization process in the membrane processing. However, a relatively high value of bcry_ETFE compared to bamo_ETFE is expected due to the larger mass density of crystalline ETFE than that of amorphous ETFE though they have the same chemical structure. Obviously, the incorporation of graft chains may decrease the average SLD of amorphous regions (bamo) and hence increase the scattering contrast between crystalline ETFE and amorphous regions, which explains the enhanced scattering intensity of the grafted membranes. The SLD value of each component is also listed in Table 1. Note that bcry_ETFE can be experimentally deduced by the contrast variation SANS method, which will be further discussed in Section IV-1 in conjunction with Fig. 6.
where bi is the scattering length of the ith atom, d is the mass density of the scattering body, Mw is the molecular weight, and NA is the Avogadro constant.39 Thus, SLD of imidazole (bim) and styrene (bst) segments on graft chains, and amorphous ETFE chains (bamo_ETFE) is calculated to be 1.123, 1.415 and 2.0 (×1010 cm−2), respectively.40 SLD of crystalline ETFE (bcry_ETFE) cannot be theoretically estimated so far, because their mass density is unknown, which heavily depends on the crystallinity and crystallization process in the membrane processing. However, a relatively high value of bcry_ETFE compared to bamo_ETFE is expected due to the larger mass density of crystalline ETFE than that of amorphous ETFE though they have the same chemical structure. Obviously, the incorporation of graft chains may decrease the average SLD of amorphous regions (bamo) and hence increase the scattering contrast between crystalline ETFE and amorphous regions, which explains the enhanced scattering intensity of the grafted membranes. The SLD value of each component is also listed in Table 1. Note that bcry_ETFE can be experimentally deduced by the contrast variation SANS method, which will be further discussed in Section IV-1 in conjunction with Fig. 6.
The upturn at q < 0.2 nm−1 in profile 1 reflects the large length scale morphology of the pristine ETFE sample. We notice that I(q) and q follow power-law functions in different q-ranges: at q < 0.14 nm−1, a typical Porod law for smooth surfaces is observed, i.e. I(q) ∼ q−4,41 which is due to the scattering from the smooth surface of the crystallites or grains; at 0.14 nm−1 < q < 0.2 nm−1, a power law shows I(q) ∼ q−1, indicating that the crystalline lamellar domains are rod-like, within which the typical lamellar periodical spacing was found to be 20 nm as we have mentioned above. Note that though the q-region where the power law exponent of −1 was observed is narrow, it shows a common characteristic for fluoropolymer membranes. The same change in the power law exponent from −1 to −4 with an increase in q was reported by Song et al. for the pure ETFE film using the SAXS method.29 Very similar patterns in the SANS profiles were also found in other fluoropolymer films such as PTFE and poly(tetrafluoroethylene-co-hexafluoropropylene) (FEP).21,27
It should be noted that the Porod law is observed in high-q regions of the profiles for both pristine membranes and grafted membranes, arising from the sharp interface between amorphous and crystalline lamellae. This Porod region is also found to shift toward the low-q range in the grafted membranes, evidencing the expansion of the amorphous lamellae due to the grafting effect.
In addition to the change in I(q) described above in (1), we also observe the following changes in the shape of profile 4 arising from the swelling effects: (2) the two broad peaks shift more toward the low-q range at q1 = 0.185 nm−1 and q2 = 0.0315 nm−1, revealing the further expanded lamellar d-spacing (d1) of 34 nm, and the inter-grain distance (d2) of 200 nm in the presence of water. Unlike in the alkylation process, the expansion of both d1 and d2 upon swelling is obvious, indicating that the incorporation of water in the hydrophilic graft domains does enlarge the total lamellar spacing as shown in Fig. 2(c). (3) Contrary to all the other three profiles, profile 4 shows a clear deviation from the Porod law at q > 1.4 nm−1, at the length scale within the amorphous lamellae. It indicates the excess scattering arising from the hydrated ion channels composed of hydrophilic graft chains and water. This excess scattering intensity varies when the water solvent is changed from pure D2O to partially deuterated water, due to the changeable scattering contrast between the water and hydrophilic graft chains. We will discuss these results further in conjunction with contrast variation SANS results in Sections III-2 and IV.
III-2. Polymer-solvent contrast variation
In this section, contrast variation SANS measurements on the AEMs, which are equilibrated in water mixtures of water (H2O) and deuterated water (D2O) with different volume fractions of D2O, fD2O, were performed.Note that the SLD of the water mixture (bw) is a function of fD2O given by
| bw = bD2OfD2O + bH2O (1 − fD2O) | (4) |
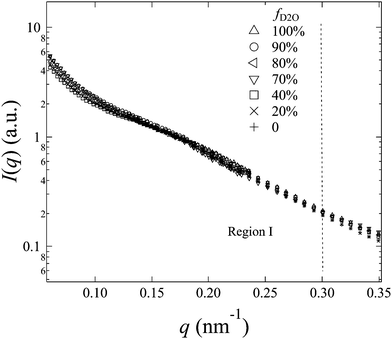
The representative scattering profiles of AEMs swollen in different water mixtures are shown in Fig. 3. Apparently, both the intensity and shape of the profiles change as a function of fD2O. Since the structure of the AEM itself is believed to be invariant whether the solvent is water or deuterated water, the apparent change in the profiles at different scattering contrasts reflects either all or partial structure information of the membranes. According to the shape of the profiles and the dependency of the scattering intensity on fD2O, the scattering profiles are classified into two q-regions: q-region I (q < 0.3 nm−1) and q-region II (q > 0.3 nm−1).
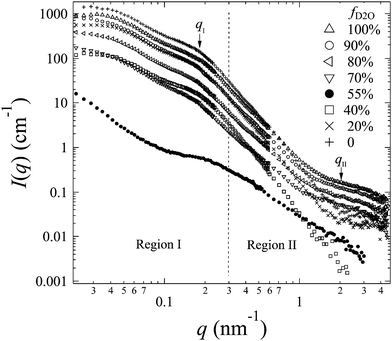 | ||
| Fig. 3 SANS profiles (symbols) obtained from 2Me-AEMs equilibrated in a water mixture with different representative fD2O. | ||
In q-region I, I(q) decreases with the increasing fD2O up to 55% and then increases again from 55 to 100%. The two typical crystalline peaks representing the crystalline structure of the membranes are clearly observed in all profiles, except for that at fD2O = 55%. At fD2O = 55%, the crystalline peaks are invisible, indicating that the crystalline domains have been matched with the hydrated regions, namely, approaching the matching point of m1. To quantitatively determine the matching point of m1, the scattering maxima at qI (=0.185 nm−1), I(qI), was plotted as a function of fD2O for all contrasts in Fig. 4a. m1 at which a minimum I(qI) shows up has been thus determined to be 55%. The schematic illustration of the phase matching at m1 is shown in the inset of Fig. 4a. The hydrated regions and crystalline ETFE regions are painted in the same color, demonstrating that the two phases have the same SLD, and there is no scattering contrast between them. Thus the AEM at m1 is apparently a two-phase system composed of the hydrated phase (together with the crystalline ETFE phase) and the hydrophobic amorphous phase.
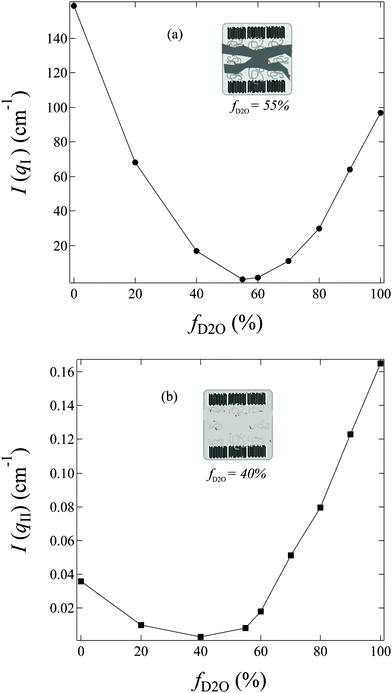 | ||
| Fig. 4 f D2O dependence of (a) the scattering maximum at qI (=0.185 nm−1), I(qI); (b) the scattering intensity at qII (=2.0 nm−1), I(qII), observed for AEMs swollen in water mixtures shown in Fig. 3. Inset of (a): schematic illustration for phase matching at m1. Inset of (b): schematic illustration for phase matching at m2. | ||
In region II, I(q) decreased with increasing fD2O up to 40% and then increased again when fD2O increases from 40 to 100%. The excess scattering in a high-q range are clearly observed in all profiles, except for that at fD2O = 40%, indicating the formation of hydrated regions in the water-swollen AEMs. However, it is invisible at fD2O = 40%, instead, a Porod law behavior is clearly observed, indicating that the amorphous hydrophobic domains have been matched with the hydrated regions, namely, approaching the matching point of m2. To determine m2, the apparent excess scattering intensity at a characteristic qII (=2.0 nm−1), I(qII), was plotted as a function of fD2O for all contrasts in Fig. 4b. m2 at which a minimum I(qII) shows up has been thus determined to be close to 40%. The schematic illustration of the phase matching at m2 is shown in the inset of Fig. 4b. The hydrated regions and hydrophobic amorphous regions are painted in the same color, demonstrating that the scattering contrast between these two phases is very small, namely, the whole amorphous regions are forming one phase. Thus the AEM at m2 is apparently a two-phase system composed of the crystalline ETFE phase and the entire amorphous phase.
IV. Discussion
IV-1. Determination of the components of the hydrated regions
From the contrast variation results in Fig. 3, we noticed that all the profiles in region I, except for the profile at the matching point of m1 (fD2O = 55%), seemed to be very similar to each other. When we normalized the scattering profiles to be superposed around the typical crystalline peak at qI (=0.185 nm−1), I(q) depends only on the contrast factor as clearly seen in Fig. 5. Accordingly, the system can be analyzed as a two-phase system, composed of crystalline ETFE domains and amorphous domains. The entire amorphous domains are regarded as one phase, consisting of hydrated regions and hydrophobic regions, both of which contribute to the total scattering intensity. Note that the deviations in high-q region II due to scattering from the microphase separated structures within the amorphous lamellae were ignored in this section, but will be discussed in detail in later Section IV-4.For a two-phase system, the scattering intensity at qI, I(qI), which is experimentally readable, is proportional to the square of scattering contrast (Δb2) between the ETFE crystallites phase (bcry_ETFE) and the entire amorphous phase (bamo), and is given by
| I(qI) ∼ (bcry_ETFE − bamo)2 | (5) |
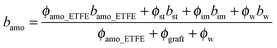 | (6) |
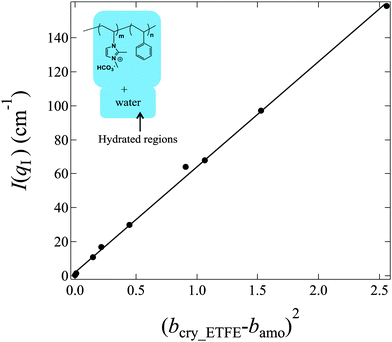
In contrast to bamo, it is difficult to determine bcry_ETFE theoretically, however, we have experimentally found that at the matching point m1 (fD2O = 55%), bcry_ETFE ≈ bhydra, where bhydra is the averaged SDL of the hydrated regions. The estimation of bhydra at m1 offers a way to quantitatively determine bcry_ETFE. To estimate bhydra, we have to know the components of hydrated regions. Only if we find the correct composition in the hydrated region, the plot of I(qI) as a function of (bcry_ETFE − bamo)2 in eqn (5) will give a linear relationship. Based on this strategy, we successfully determined that the hydrated regions are composed of the entire graft chains and water as shown in the inset of Fig. 6, and bcry_ETFE is 2.23 × 1010 cm−2 (listed in Table 1). A good linear relationship between I(qI) and (bcry_ETFE − bamo)2 is shown in Fig. 6, verifying not only the correctness of bcry_ETFE but also the components of the hydrated regions. The model analysis with various components of the hydrated regions can be found in the ESI,† in conjunction with Fig. S1–S3.
IV-2. Morphology of amorphous ETFE domains
Since the hydrated regions are made of the entire graft chains and water, the matching at m1 (fD2O = 55%) makes hydrophobic amorphous ETFE domains the only visible component. Thus, the scattering profile at m1, Im1(q), represents the morphology of the hydrophobic amorphous ETFE chains. We extract Im1(q) and plot it in Fig. 7a.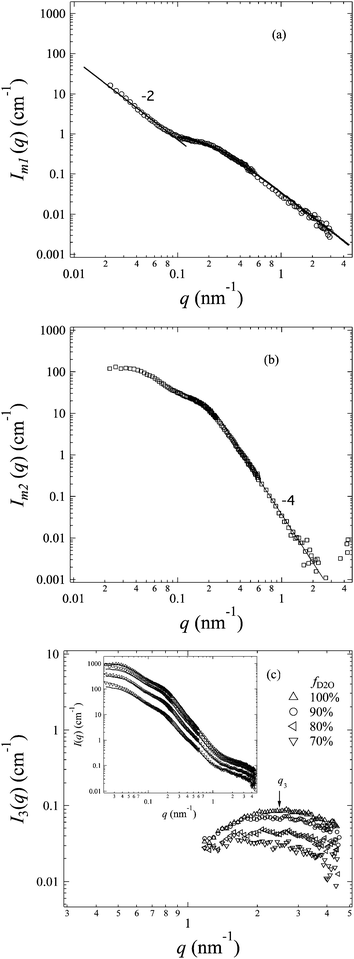 | ||
| Fig. 7 (a): SANS profile of amorphous ETFE domains (profile at the matching point of m1). The best-fitted curve based on eqn (7) in the high-q range (q > 0.09 nm−1) is shown in the figure by a solid line, and the straight line in the low-q range (q < 0.09 nm−1) is also drawn to guide the readers' eye; (b): SANS profile of crystalline ETFE domains (profile at the matching point of m2); (c): SANS profiles of the hydrated domains, I3(q), at fD2O > 55%. Inset of (c): the comparison between the profiles at fD2O > 55% (symbols) and the theoretical curves (solid lines) based on eqn (10) through all q-ranges. | ||
At q > 0.09 nm−1, the scattering profile can be well fitted by the Debye function for random polymer coils as shown in eqn (7) below
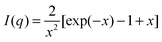 | (7) |
At q < 0.09 nm−1, I(q) and q follow a power law function as I(q) ∼ q−2, seemingly indicating a lamellar structure, though no typical lamellar periodical peaks were observed at qI in the profile. Note that the lamellar signature arising from the amorphous lamellar frame is always there, but apparently hidden by the tricky contrast matching technique.
IV-3. Morphology of crystalline ETFE domains
At m2 (fD2O ∼ 40%), the hydrated regions almost match the amorphous ETFE domains, and thus the entire amorphous phase roughly has the same SLD, which makes the system automatically be simplified to a two-phase system: the crystalline ETFE phase, and the amorphous phase which include all components such as graft chains, amorphous ETFE and water. The profile at m2, Im2(q), has been extracted and shown in Fig. 7b. It reflects the morphology of the crystalline ETFE domains. Since the scattering patterns of the hydrated regions in the amorphous lamellae have been hidden under this matching condition, a typical Porod law in the high-q range is clearly observed, indicating the sharp interface between the crystalline ETFE domains and amorphous domains. The extracted profile for the crystalline structures of ETFE under the matching condition is quite similar to the SAXS profiles of ETFE-PEMs with grafting degrees of 79–117%, in which amorphous hydrated and crystallite network domains appeared by graft-polymerization-induced phase transition of grafted ETFE.22 It should be noted that ETFE-PEM and AEM exhibit a quite similar crystalline morphology although they are composed of different types of graft polymers (cation and anion conducting groups).IV-4. Morphology of hydrated regions in the amorphous lamellae
Taking advantage of the contrast matching technique, we have successfully elucidated the morphologies of the crystalline ETFE domains (phase 1) by the profile Im2(q) and the hydrophobic amorphous ETFE domains (phase 2) by the profile Im1(q). The only unclear domains left here are the hydrated regions (phase 3), which are found to be composed of entire graft chains and water, and have clear excess scattering in the high-q range. In this section, we shall extract the excess scattering of these hydrated regions and elucidate their morphology in the amorphous phase.For the current three-phase AEM system, there is inhomogeneity within the individual phases, due to the atomic nature of the material and to the density fluctuations at all size scales arising from thermal motions of atoms. Thus, the total scattering intensity from such a system can be expressed by39
| I(q) = I0(q) + I1(q) + I2(q) + I3(q) + I12(q) + I13(q) + I23(q) | (8) |
| I(q) = I1(q) + I2(q) + I3(q) | (9) |
| I(q) = (AIm2(q) + BIm1(q)) + I3(q) | (10) |
| f D2O | 70% | 80% | 90% | 100% |
|---|---|---|---|---|
| A | 0.7 | 2.1 | 4.2 | 7 |
| B | 2.0 | 3.5 | 5.6 | 8.2 |
The excess scattering intensity of phase 3, I3(q), can be deduced from eqn (10) for each profile at fD2O > 55%. We plot I3(q) as a function of fD2O in Fig. 7c. Note that I3(q) for the profiles at fD2O ≤ 20% are too weak to be extracted accurately, and thus not shown in the figure.
A broad scattering maximum around q3 ∼ 2.5 nm−1 commonly shows up in I3(q) profiles in Fig. 7c, indicating the density fluctuations of the graft chains present in the hydrated regions within the amorphous phase. According to the scattering theory, the scattering maximum at q3, I(q3), should be proportional to the square of the scattering contrast between graft chains (bgraft) and water, given by
| I(q3) ∼ (bgraft − bw)2 | (11) |
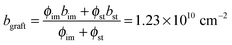 , and bw can be estimated by eqn (4). We plot I(q3) versus (bgraft − bw)2 for all I3(q) profiles at fD2O > 55% in Fig. 8, and a good linear relationship is clearly observed, evidencing that I3(q) profiles reflect the density fluctuations of the graft chains in the hydrated regions.
, and bw can be estimated by eqn (4). We plot I(q3) versus (bgraft − bw)2 for all I3(q) profiles at fD2O > 55% in Fig. 8, and a good linear relationship is clearly observed, evidencing that I3(q) profiles reflect the density fluctuations of the graft chains in the hydrated regions.
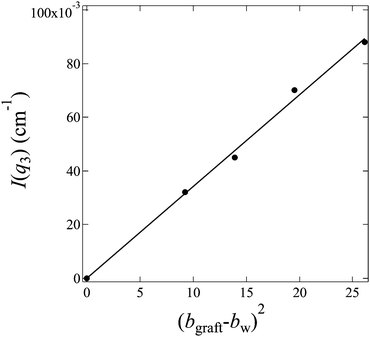 | ||
| Fig. 8 Plot of I(q3) versus (bgraft − bw)2 for profiles of hydrated regions shown in Fig. 7 (c) according to eqn (11). | ||
IV-5. GD dependence of the structure and properties
In order to investigate the GD dependence of the structure and the properties of the membranes, SANS measurements were also performed for grafted-ETFE membranes with a GD of 30, 46 and 120% and the corresponding AEMs with IECs of 0.95, 1.26 and 2.15 mmol g−1, respectively (see SANS profiles in Fig. S6 in the ESI†). Though the shape of the scattering profiles is hardly changed in comparison with that of the membranes with a GD of 91%, the lamellar d-spacing varies significantly with the GD and water uptake in the membranes. In Fig. 9a, the GD dependence of the lamellar period, d1, for both grafted-ETFE membranes and AEMs equilibrated in deuterated water at 25 °C is plotted. Additionally, the corresponding water uptake, U, for AEMs in the bicarbonate form is also plotted as a function of the GD in the inset of Fig. 9a. A rapid increase in d1 with the increase of GD up to 46% is clearly observed for both membranes, and then d1 changes steadily with the further increase in the GD. This is probably because at the early stage of graft polymerization, most graft chains were created within the lamellar stacks, while for higher GDs, graft chains were mainly generated outside of the lamellar stacks due to the confined space. Thus, at the later stage of polymerization, d1 of the grafted-ETFE membranes does not change obviously though the GD continuously increases. This phenomenon was also observed in the ETFE and PTFE based PEMs prepared by the radiation grafting method, though the transition point of the GD, at which the lamellar d-spacing stopped increasing, changes, depending on the stiffness of the base film and the chemical structure of the grafts.20–22 The increase in the GD definitely leads to the increase in U due to the more incorporation of hydrophilic imidazole groups. However, when the creation of the graft chains within lamellar stacks stopped, the water adsorption within the lamellar stacks would be restricted, too. Hence, the d1 of AEMs also reaches a constant level, very similar to the case of grafted-ETFE membranes, though U gradually increases at higher GD levels (>40%).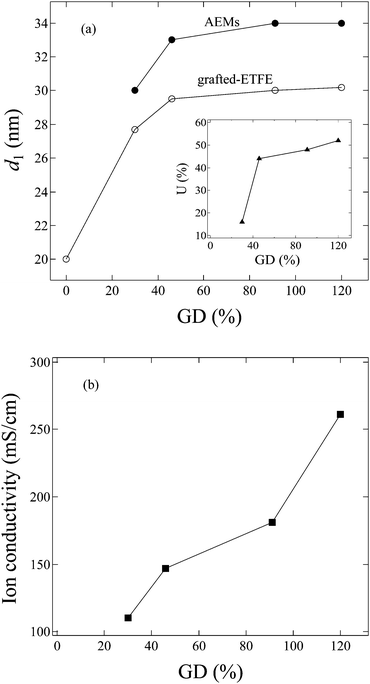 | ||
| Fig. 9 GD dependence of (a) the lamellar period (d1), and the inset of (a) water uptake (U); (b) ion conductivity in 1.0 M KOH at 60 °C. | ||
The hydroxide conductivity of these AEMs was measured in 1.0 M KOH solution at 60 °C, and plotted as a function of the GD in Fig. 9b. High hydroxide conductivities over 100 mS cm−1 are observed for all of these AEMs. Generally, conductivities of ca. 100 mS cm−1 are the required level for high current density cell output.43,44 So far, the conductivity of the AEMs in the present study has been the best in comparison with that of the recently reported AEMs formed by either poly(phenylene oxide) tethered with cationic alkyl side chains,44 ionic liquid block copolymers,45,46 the block copolymer of polybutadiene-b-poly(4-methylstyrene)47 or the polymer blends of the block copolymer of poly(vinylbenzyl chloride)-b-polystyrene and poly(2,6-dimethyl-1,4-phenylene oxide).48Fig. 9b shows that the hydroxide conductivity increases with increasing GDs. However, higher GDs over 100% usually result in too high a water uptake, which causes poor stability and alkaline durability in real fuel cell operation. The AEMs with GD = 120% were proved to be mechanically weak and have poor fuel cell performance, though their conductivity is higher than that of the 2Me-AEM (GD = 91%, IEC = 1.82 mmol g−1).
IV-6. Interplay between the morphology and properties of AEMs
Let us next consider the interplay between the morphology and the properties of the AEMs. According to the discussion above, the interconnected hydrated regions in the AEMs do exist, which are believed to play a key role in improving the ion conductivity of the membrane. 2Me-AEMs, which have the best well-balanced properties required for fuel cell applications, exhibit a relatively high IEC value (1.82 mmol g−1) in comparison with that of the Nafion® membrane (0.91 mmol g−1),49 revealing a larger density of ionic groups in AEMs.50,51 This result is consistent with the SANS analysis in the sections above, which shows more pronounced hydrophilic/hydrophobic microphase separation than Nafion due to the incorporation of whole polymer grafts with the water comprising the hydrated regions. On the one hand, this leads to the high ion diffusion and water transport; on the other hand, the high ion exchange capacity leads to excessive swelling of polymers upon hydration. However, the crystalline domains, consisting of crystalline and amorphous lamellae, originating from the substrate, can be conserved by preparation steps and water absorption; hence the concomitant loss of mechanical properties is restricted.V. Conclusions
In summary, for the first time, we employed the contrast variation small angle neutron scattering technique to quantitatively investigate the morphology of the new graft-type AEMs: 2Me-PEM, composed of poly(dimethyl-vinylimidazole-co-styrene) copolymer chains grafted onto poly(ethylene-co-tetrafluoroethylene) films via the radiation-induced grafting method. These AEMs were found to more or less conserve the crystalline lamellae and crystallite structures from the pristine ETFE material, and hence possess good mechanical properties and alkaline durability. After swelling in water, the interconnected hydrated conducting regions in the amorphous domains were formed, evidenced by the excess scattering in the high-q range, and responsible for the high ion conductivity through the membranes. The contrast variation SANS studies on the AEMs, equilibrated in various water mixtures of water and deuterated water with different volume ratios, concluded that there exist three phases in these AEMs: phase (1) crystalline ETFE domains; phase (2) hydrophobic amorphous ETFE domains; and phase (3) interconnected hydrated domains, composed of the entire graft chains and water.Acknowledgements
This work was partially supported by the Advanced Low Carbon Technology Research and Development Program (ALCA) from the Japan Science and Technology Agency (JST).Notes and references
- K. Yoshimura, H. Koshikawa, T. Yamaki, H. Shishitani, K. Yamamoto, S. Yamaguchi, H. Tanaka and Y. Maekawa, J. Electrochem. Soc., 2014, 161, F889 CrossRef.
- W. Vielstich, A. Lamm and H. Gasteiger, Handbook of Fuel Cells: Fundamentals, Technology, Applications, John Wiley, 2004 Search PubMed.
- S. G. Chalk, J. F. Miller and F. W. Wagner, J. Power Sources, 2000, 86, 40 CrossRef.
- G. Cacciola, V. Antonucci and S. Freni, J. Power Sources, 2001, 100, 67 CrossRef CAS.
- P. Costamagna and S. Srinivasan, J. Power Sources, 2001, 102, 253 CrossRef CAS.
- A. F. Ghenciu, Curr. Opin. Solid State Mater. Sci., 2002, 6, 389 CrossRef.
- S. Gamburzev and A. J. Appleby, J. Power Sources, 2002, 107, 5 CrossRef CAS.
- V. Mehta and J. S. Cooper, J. Power Sources, 2003, 114, 32 CrossRef CAS.
- H. A. Gasteiger and J. E. Panels, J. Power Sources, 2004, 127, 162 CrossRef CAS.
- M. Z. Jacobson, W. G. Colella and D. M. Golden, Science, 2005, 308, 1901 CrossRef CAS PubMed.
- J. H. Wee, Renewable Sustainable Energy Rev., 2007, 11, 1720 CrossRef CAS.
- Y. Wang, K. Chen, J. Mishler, S. C. Cho and X. C. Adroher, Appl. Energy, 2011, 88, 981 CrossRef CAS.
- A. Serov and C. Kwak, Appl. Catal., B, 2010, 98, 1 CrossRef CAS.
- K. Asazawa, K. Yamada, H. Tanaka, A. Oka, M. Taniguchi and T. Kobayashi, Angew. Chem., Int. Ed., 2007, 46, 8024 CrossRef CAS PubMed.
- J. R. Varcoe and R. C. T. Slade, Fuel Cells, 2005, 5, 187 CrossRef CAS.
- J. Pan, C. Chen, L. Zhuang and J. Liu, Acc. Chem. Res., 2011, 45, 473 CrossRef PubMed.
- G. Couture, A. Alaaeddine, F. Boschet and B. Ameduri, Prog. Polym. Sci., 2011, 36, 1521 CrossRef CAS.
- G. Merle, M. Wessling and K. Nijmeijer, J. Membr. Sci., 2011, 377, 1 CrossRef CAS.
- H. Koshikawa, K. Yoshimura, W. Ainnananchi, T. Yamaki, M. Asano, K. Yamamoto, S. Yamaguchi, H. Tanaka and Y. Maekawa, Macromol. Chem. Phys., 2013, 214, 1756 CrossRef CAS.
- H. Iwase, S. Sawada, T. Yamaki, S. Koizumi, M. Ohnuma and Y. Maekawa, Macromolecules, 2012, 45, 9121 CrossRef CAS.
- H. Iwase, S. Sawada, T. Yamaki, Y. Maekawa and S. Koizumi, Int. J. Polym. Sci., 2011, 1 CrossRef.
- T. D. Tap, S. Sawada, K. Hasegawa, Y. Yoshimura, M. Oba, M. Ohnuma, Y. Katsumura and Y. Maekawa, Macromolecules, 2012, 47, 2373 CrossRef.
- N. Li, T. Yan, Z. Li, T. T. Albrecht and W. H. Binder, Energy Environ. Sci., 2012, 5, 7888 CAS.
- N. Li, Q. Zhang, C. Wang, Y. M. Lee and M. D. Guiver, Macromolecules, 2012, 45, 2411 CrossRef CAS.
- F. Zhang, H. Zhang and C. Qu, J. Mater. Chem., 2011, 21, 12744 RSC.
- H. Zhang and P. Shen, Chem. Rev., 2012, 112, 2780 CrossRef CAS PubMed.
- K. Mortensen, U. Gasser, S. A. Guersel and G. G. Scherer, J. Polym. Sci., Polym. Phys. Ed., 2008, 46, 1660 CrossRef CAS.
- M. M. Nasef and E. A. Hegazy, Prog. Polym. Sci., 2004, 29, 499 CrossRef CAS.
- J. M. Song, B. S. Ko, J. Y. Sohn, Y. C. Nho and J. Shin, Radiat. Phys. Chem., 2014, 97, 374 CrossRef CAS.
- A. Radulescu, V. Pipich, H. Frielinghaus and M. S. Appavou, J. Phys.: Conf. Ser., 2012, 351, 012026 CrossRef.
- T. Ishigaki, A. Hoshikawa, M. Yonemura, T. Morishima, T. Kamiyama, R. Oishi, K. Aizawa, T. Sakuma, Y. Yomota, M. Arai, M. Hayashi, K. Ebata, Y. Takano, K. Komatsuzaki, H. Asano, Y. Takano and T. Kasao, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 21, 189 CrossRef.
- K. Jokela, R. Serima, M. Torkkeli, F. Sundholm, T. Kallio and G. Sundholm, J. Polym. Sci., Polym. Phys. Ed., 2002, 40, 1539 CrossRef.
- S. Balog, U. Gasser, K. Mortensen, L. Gubler, G. G. Scherer and H. B. Youcef, Macromol. Chem. Phys., 2010, 211, 635 CrossRef.
- M. Reitman, D. Jaekel, R. Siskey and S. M. Kurtz, Morphology and Crystalline Architecture of Polyaryletherketones, in PEEK Biomaterials Handbook, ed. S. M. Kurtz, Elsevier Press, New York, 2012, ch. 4, p. 49 Search PubMed.
- T. W. Giants, IEEE Trans. Dielectr. Electr. Insul., 1994, 1, 991 CrossRef CAS.
- O. Dupont, A. M. Joneas, B. Nysten, R. Legras, P. Adriaensens and J. Gelan, Macromolecules, 2000, 33, 562 CrossRef CAS.
- G. Gebel, Macromolecules, 2013, 46, 6057 CrossRef.
- V. Di Noto, M. Piga, G. A. Giffin and G. Pace, J. Membr. Sci., 2012, 390–391, 58 CrossRef CAS.
- See for example, R. J. Roe, Methods of X-ray and neutron scattering in polymer science, Oxford Uni. Press, New York, 2000 Search PubMed.
- Since the ratio of ET to FE in the commercial ETFE membranes is 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the SLD of the amorphous ETFE (bamo_ETFE) can be calculated by the volume averaged SLD of amorphous ET (bamo_ET) and amorphous FE (bamo_FE) as follows:
1, the SLD of the amorphous ETFE (bamo_ETFE) can be calculated by the volume averaged SLD of amorphous ET (bamo_ET) and amorphous FE (bamo_FE) as follows: 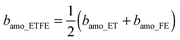 . The mass density of amorphous ET (damo_ET) and FE (damo_FE) is generally assumed to be 0.86 and 2.0 g cm−2, respectively. Thus bamo_ET and bamo_FE are theoretically calculated to be −0.306 and 4.33 (×1010 cm−2), respectively. Hence bamo_ETFE is estimated to be 2.0 × 1010 cm−2. Similarly, SLD of D2O and H2O is theoretically calculated to be 6.34 and −0.56 (×1010 cm−2), respectively, the values of which will be used in the following sections to discuss the matching point.
. The mass density of amorphous ET (damo_ET) and FE (damo_FE) is generally assumed to be 0.86 and 2.0 g cm−2, respectively. Thus bamo_ET and bamo_FE are theoretically calculated to be −0.306 and 4.33 (×1010 cm−2), respectively. Hence bamo_ETFE is estimated to be 2.0 × 1010 cm−2. Similarly, SLD of D2O and H2O is theoretically calculated to be 6.34 and −0.56 (×1010 cm−2), respectively, the values of which will be used in the following sections to discuss the matching point. - G. Porod, Kolloid-Z., 1951, 124, 83 CrossRef.
- A. Oshima, S. Ikeda, T. Seguchi and Y. Tabata, Radiat. Phys. Chem., 1997, 50, 519 CrossRef CAS.
- J. R. Varcoe, P. Atanassov, D. R. Dekel, A. M. Herring, M. A. Hickner, P. A. Kucernak, W. E. Mustain, K. Nijmeijer, K. Scott, T. W. Xu and L. Zhuang, Energy Environ. Sci., 2014, 7, 3135 CAS.
- H. S. Dang and P. Jannasch, Macromolecules, 2015, 48, 5741 CrossRef.
- Y. Ye, S. Sharick, E. M. Davis, K. I. Winey and Y. A. Elabd, ACS Macro Lett., 2013, 2, 575 CrossRef CAS.
- K. M. Meek, S. Sharick, Y. S. Ye, K. I. Winey and Y. A. Elabd, Macromolecules, 2015, 48, 4850 CrossRef CAS.
- Y. F. Li, Y. Liu, A. C. Jackson, F. L. Beyer, S. Seifert, A. M. Herring and D. M. Knauss, Macromolecules, 2015, 48, 6523 CrossRef CAS.
- Y. F. Li, A. C. Jackson, F. L. Beyer and D. M. Knauss, Macromolecules, 2014, 47, 6757 CrossRef CAS.
- K. A. Mauritz and R. B. Moore, Chem. Rev., 2004, 104, 4535 CrossRef CAS PubMed.
- O. Diat and G. Gebel, Nat. Mater., 2008, 7, 13 CrossRef CAS PubMed.
- G. Gebel and J. Lambard, Macromolecules, 1997, 30, 7914 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm02724a |
| This journal is © The Royal Society of Chemistry 2016 |