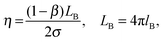Assessment of micro-polarity anisotropy as a function of surfactant packing in sodium dodecyl sulphonate–hexane reverse micelles†
Xin
Peng
ab,
Xing-Zhong
Yuan
b,
P.
Somasundaran
c and
Partha
Patra
 *c
*c
aNational and Local United Engineering Laboratory for New Petrochemical Materials and Fine Utilization of Resources, Key Laboratory of Resource Fine-Processing and Advanced Materials of Hunan Province and Key Laboratory of Chemical Biology and Traditional Chinese Medicine Research (Ministry of Education of China), College of Chemistry and Chemical Engineering, Hunan Normal University, Changsha, 410081, P. R. China
bCollege of Environmental Science and Engineering, Hunan University, Changsha 410082, P. R. China
cLangmuir Center for Colloid and Interface Science, Columbia University, New York, 10027, USA. E-mail: pp2295@columbia.edu
First published on 30th September 2015
Abstract
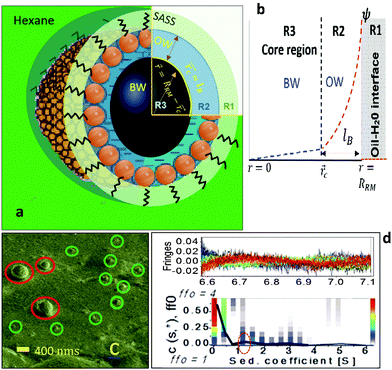
The micro-polarity anisotropy behaviour across the aqueous phase of a SDS (sodium dodecyl sulphonate)–hexane reverse micelle (RM) relies on the SDS packing in the oil–water interfacial self-assembled surfactant structure of the RM.
Reverse micelle (RM) systems are advantageous for a number of processes such as nanoparticle synthesis1 and the liquid–liquid extraction of enzymes.2 The effectiveness of these processes relies on the micro-polarity anisotropy (MPA) of the aqueous phase of a RM. The MPA of a RM varies according to its water
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) surfactant (ω0) ratio.3 A reliable estimate of MPA is critical to predict and regulate the enzyme activity in RMs.4,5 The common approaches assess MPA(
surfactant (ω0) ratio.3 A reliable estimate of MPA is critical to predict and regulate the enzyme activity in RMs.4,5 The common approaches assess MPA(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) (
) (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) – the radial distance, Fig. 1) in terms of the microstructural characteristics of water in RMs6 and the electrostatic potential distribution (ψ(
– the radial distance, Fig. 1) in terms of the microstructural characteristics of water in RMs6 and the electrostatic potential distribution (ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )) across the aqueous phase (Fig. 1b).7,8 Spectroscopy studies and molecular dynamic simulations reveal that, in terms of the micro-polarity attributes, the RM aqueous phase comprises at least two spatially separable regions (Fig. 1a and b), the interfacial region (ordered water) and the core region (bulk water).6,9 The ψ(
)) across the aqueous phase (Fig. 1b).7,8 Spectroscopy studies and molecular dynamic simulations reveal that, in terms of the micro-polarity attributes, the RM aqueous phase comprises at least two spatially separable regions (Fig. 1a and b), the interfacial region (ordered water) and the core region (bulk water).6,9 The ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) profile that exemplifies the MPA results from the oil–water interfacial charge density levels (per volume of water in a RM) of the surfactant head groups, and the distributional aspects of the counter ions in the aqueous phase. The ψ(
) profile that exemplifies the MPA results from the oil–water interfacial charge density levels (per volume of water in a RM) of the surfactant head groups, and the distributional aspects of the counter ions in the aqueous phase. The ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) profiles exhibit an exponential form (Fig. 1b).6–9 For the aqueous phases in the vicinity of the surfactant-stabilized oil–water interfaces, the ψ profile is attributed to the surfactant chemistries. The ψ profile for these interfacial systems is developed as per the electrical double layer (EDL) models.10–13 Conversely, as the volume of the confined (nano-sized) aqueous phase of a RM is much lower, the EDL characteristics are governed by the interfacial charge density levels (per RM water content), which decrease as the ω0 values become higher. The charge density level, even at a particular ω0 value, could vary depending on the degree of surfactant packing (inter-surfactant distances) in the self-assembled surfactant structure (SASS) of a RM.14 Thus, the EDL characteristics that determine the MPA are attributed to the surfactant-types and -density/packing in a SASS.7,8 We assessed the MPA(
) profiles exhibit an exponential form (Fig. 1b).6–9 For the aqueous phases in the vicinity of the surfactant-stabilized oil–water interfaces, the ψ profile is attributed to the surfactant chemistries. The ψ profile for these interfacial systems is developed as per the electrical double layer (EDL) models.10–13 Conversely, as the volume of the confined (nano-sized) aqueous phase of a RM is much lower, the EDL characteristics are governed by the interfacial charge density levels (per RM water content), which decrease as the ω0 values become higher. The charge density level, even at a particular ω0 value, could vary depending on the degree of surfactant packing (inter-surfactant distances) in the self-assembled surfactant structure (SASS) of a RM.14 Thus, the EDL characteristics that determine the MPA are attributed to the surfactant-types and -density/packing in a SASS.7,8 We assessed the MPA(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) as a function of surfactant density/packing in the SASSs for the SDS (sodium dodecyl sulphonate)–hexane RMs.15
) as a function of surfactant density/packing in the SASSs for the SDS (sodium dodecyl sulphonate)–hexane RMs.15
The RMs were devised by adding desired amounts of water to SDS–hexane solutions (ESI,† 1). Cryo-SEM (ESI,† 2) images indicated that the RM sizes were <50 nm (ω0 ≈ 24; Fig. 1c). Analytical ultra-centrifuge (AUC) studies (ESI,† 2) reveal the RMs as spherical in shape (Fig. 1d). The RMs with ω0 in the range of 5 to 25 were spherical and of sizes in the range of 10 to 50 nm. For ESR studies (ESI,† 1), a 16-DSA (16-DOXYL-stearic acid) probe containing the NO˙ radical was added to the RM samples in desired amounts. The hyperfine splitting constant (aN) – MPA(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), and the rotational correlation time (τc) – surfactant packing in the SASS, were estimated for these RM systems. The application of the ESR technique is a reliable option as the energy absorbance value of a probe with free radicals, which can locate in the aqueous and SASS regions, allows concurrent estimation of the MPA and SASS packing aspects. The microstructural aspects of RM water were studied using IR (attenuated total reflection-infrared) spectroscopy (ESI,† 1).
), and the rotational correlation time (τc) – surfactant packing in the SASS, were estimated for these RM systems. The application of the ESR technique is a reliable option as the energy absorbance value of a probe with free radicals, which can locate in the aqueous and SASS regions, allows concurrent estimation of the MPA and SASS packing aspects. The microstructural aspects of RM water were studied using IR (attenuated total reflection-infrared) spectroscopy (ESI,† 1).
We compartmentalize a RM's environment into three spatially segregated and sequentially placed regions (Fig. 1a and b), and the MPA(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) of these regions was assessed in terms of their contribution to the RM's ψ(
) of these regions was assessed in terms of their contribution to the RM's ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) profile. The non-linear Poisson–Boltzmann description of the ψ(
) profile. The non-linear Poisson–Boltzmann description of the ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) profile that associates these three regions is:
) profile that associates these three regions is:
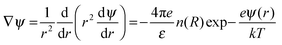 | (1) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) for a RM can be written as:
) for a RM can be written as: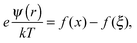 | (2) |
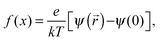 | (3) |
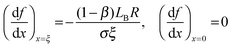 .
.
The ξ term is dependent on the association coefficient of the counter ions, given as β.10,19 The parameters that allow differentiation of the ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) profile for the regions R2 and R3 are:
) profile for the regions R2 and R3 are:
For RRM ≤ lB, ψ decreases in an exponential manner from the interface to the core, and a plateau region of the ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) profile is absent. For RRM ≫ lB, the plateau part of the ψ(
) profile is absent. For RRM ≫ lB, the plateau part of the ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) profile represents the
) profile represents the ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ≈ 0 − (RRM − lB) region (R3). And, this plateau region changes minimally with increase in RM sizes, as the micro-polarity contributions are due to the bulk-type water therein. In order to gain insights into how the ψ(
≈ 0 − (RRM − lB) region (R3). And, this plateau region changes minimally with increase in RM sizes, as the micro-polarity contributions are due to the bulk-type water therein. In order to gain insights into how the ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) profiles differentiate for the RMs of different sizes, the responses of the NO˙ of 16-DSA in RMs of different sizes were determined. These responses were in terms of the energy absorbance values of the NO˙ in the aqueous phases of the RMs. We define the NO˙ radical (in a RM) system as a π-electron system; m π electrons and n core atoms; m + n = N. The charge and position vectors of the jth particle in this system are ej and rj, ρπr is the π-electron density, and QHCH is the σ–π parameter. The hyperfine splitting value, aHr, for a hydrogen-bonded carbon atom (rth carbon atom) of 16-DSA is:
) profiles differentiate for the RMs of different sizes, the responses of the NO˙ of 16-DSA in RMs of different sizes were determined. These responses were in terms of the energy absorbance values of the NO˙ in the aqueous phases of the RMs. We define the NO˙ radical (in a RM) system as a π-electron system; m π electrons and n core atoms; m + n = N. The charge and position vectors of the jth particle in this system are ej and rj, ρπr is the π-electron density, and QHCH is the σ–π parameter. The hyperfine splitting value, aHr, for a hydrogen-bonded carbon atom (rth carbon atom) of 16-DSA is:
| aHr = QHCHρπr and ρπr = ckr2 | (4) |
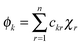 | (5) |
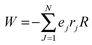 , where R is the electric field of the RM aqueous phase, and as per the counter ion density levels in the R2 and R3 regions, and the charge density (surfactant head groups) levels in the R2 region. If NO˙ radicals reside in a spherical RM having an isotropic solvent (relative permittivity εr) with a point dipole at the core as pr, the Block Walker reaction field RR16 for NO˙ is:
, where R is the electric field of the RM aqueous phase, and as per the counter ion density levels in the R2 and R3 regions, and the charge density (surfactant head groups) levels in the R2 region. If NO˙ radicals reside in a spherical RM having an isotropic solvent (relative permittivity εr) with a point dipole at the core as pr, the Block Walker reaction field RR16 for NO˙ is:RR = (pr/RRM3)(ε![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) ) | (6) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) acting on the NO˙ radicals. We determined the aN values for RMs of different sizes. The changes in the micro-polarity of the
) acting on the NO˙ radicals. We determined the aN values for RMs of different sizes. The changes in the micro-polarity of the ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) = 0 − (RRM − lB) region (bulk water) are negligible as a function of the RRM values (ω0 levels).8,16 Thus, the aN values vary as per the micro-polarity aspects of the R2 region. Therefore, the aN values, as a function of RRM, provide a measure of how aN would be as a function of
= 0 − (RRM − lB) region (bulk water) are negligible as a function of the RRM values (ω0 levels).8,16 Thus, the aN values vary as per the micro-polarity aspects of the R2 region. Therefore, the aN values, as a function of RRM, provide a measure of how aN would be as a function of ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) for a RM. We developed the ‘aNvs. ω0’ correlation, which is representative of the aNvs.
for a RM. We developed the ‘aNvs. ω0’ correlation, which is representative of the aNvs. ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) for the SDS RMs.
for the SDS RMs.
Due to the non-polarity attribute of the R1 region, the aN values for this region are negligible in comparison to those for the R2 and R3 regions. The rotational coefficient τc is particularly pronounced for the non-polar R1 region. Thus, the changes in aN for the R1 region, and τc for the R2 and R3 regions, as a function of ω0, are negligible. The aN and τc values can be accounted as:
| 〈Δτc〉 = p1〈Δτc〉 + p2+3〈Δτc〉 ≈ p1〈Δτc〉 | (7) |
| 〈ΔaN〉 = p1〈ΔaN〉 + p2+3〈ΔaN〉 ≈ p2+3〈ΔaN〉 | (8) |
The 〈aN〉 vs. ω0(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) profile was considered to assess the MPA(
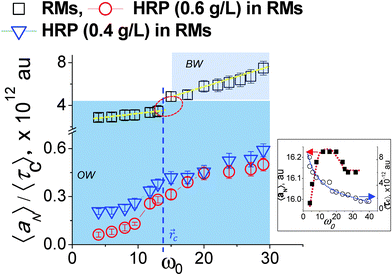
) profile was considered to assess the MPA(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) of a RM of a particular size.17Fig. 2 (inset) shows that this profile exhibits a maxima. The lower 〈aN〉 values are observed as
) of a RM of a particular size.17Fig. 2 (inset) shows that this profile exhibits a maxima. The lower 〈aN〉 values are observed as ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) → RRM (interface) and
→ RRM (interface) and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) → 0 (core). The lower 〈aN〉 value at the ω0 ≈ 5 level justifies highly ordered forms of water in the R2 region, and presumably due to the relative population of the head groups and the counter ions across the interfacial region being significantly higher. Across the 5 < ω0 < 10 range, the 〈aN〉 values are higher with ω0, which is due to the increase in the volume of the R2 region having less ordered forms of water (in comparison to the highly ordered region at ω0 ≈ 5). The drop in the 〈aN〉 vs.
→ 0 (core). The lower 〈aN〉 value at the ω0 ≈ 5 level justifies highly ordered forms of water in the R2 region, and presumably due to the relative population of the head groups and the counter ions across the interfacial region being significantly higher. Across the 5 < ω0 < 10 range, the 〈aN〉 values are higher with ω0, which is due to the increase in the volume of the R2 region having less ordered forms of water (in comparison to the highly ordered region at ω0 ≈ 5). The drop in the 〈aN〉 vs. ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) profile beyond the maxima, at the ω0 > 10 levels, is due to the increase in the bulk-type water content of the R3 region. At ω0 ≫ 10 levels, the bulk water content is higher, and the plateau region of the aNvs.
profile beyond the maxima, at the ω0 > 10 levels, is due to the increase in the bulk-type water content of the R3 region. At ω0 ≫ 10 levels, the bulk water content is higher, and the plateau region of the aNvs. ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) profile mostly accounts for the micro-polarity of the bulk-type water in the R3 region. Though these inferences that are made from the aNvs.
profile mostly accounts for the micro-polarity of the bulk-type water in the R3 region. Though these inferences that are made from the aNvs. ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (ω0) profile provide an assessment of the MPA(
(ω0) profile provide an assessment of the MPA(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), these inferences are based on the assumption that: the surfactant charge density levels in the SASSs, as per ω0 levels, exhibit a linear relationship. The surfactant density level, according to the Debye–Stokes–Einstein equation is:
), these inferences are based on the assumption that: the surfactant charge density levels in the SASSs, as per ω0 levels, exhibit a linear relationship. The surfactant density level, according to the Debye–Stokes–Einstein equation is:
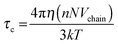 | (9) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ). We considered a normalized value of 〈aN〉 as 〈aN〉/〈τc〉, which accounts for the variability associated with the degree of surfactant-packing in the SASSs for different ω0 levels.
). We considered a normalized value of 〈aN〉 as 〈aN〉/〈τc〉, which accounts for the variability associated with the degree of surfactant-packing in the SASSs for different ω0 levels.
The 〈aN〉/〈τc〉 vs. ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (ω0) profile was examined to study the MPA(
(ω0) profile was examined to study the MPA(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ). The slopes of this profile, (Δ(〈aN〉/〈τc〉)/Δ
). The slopes of this profile, (Δ(〈aN〉/〈τc〉)/Δ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), provide a direct estimate of how the MPA(
), provide a direct estimate of how the MPA(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) varies as per the differences in the packing attributes of the SASSs. The slope value was higher at the ω0 > 15 levels, than that at the ω0 < 10 levels (Fig. 2, dotted lines). At the ω0 < 10 levels, the lower slope value is due to the ordered form of water in the R2 region, which could be interpreted from the aNvs.
) varies as per the differences in the packing attributes of the SASSs. The slope value was higher at the ω0 > 15 levels, than that at the ω0 < 10 levels (Fig. 2, dotted lines). At the ω0 < 10 levels, the lower slope value is due to the ordered form of water in the R2 region, which could be interpreted from the aNvs. ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (ω0) profile as well Fig. 2 (inset). At ω0 > 15 levels, RRM ≫ lB, the higher slope value is due to the plateau region of the ψ(
(ω0) profile as well Fig. 2 (inset). At ω0 > 15 levels, RRM ≫ lB, the higher slope value is due to the plateau region of the ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) profile that represents the bulk water in the region |
) profile that represents the bulk water in the region |![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) | ≤ 0 − (R − lB). Instead of the plateau region, as seen in the 〈aN〉 vs.
| ≤ 0 − (R − lB). Instead of the plateau region, as seen in the 〈aN〉 vs. ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (ω0) profile, a higher slope value is seen for the 〈aN〉/〈τc〉 vs.
(ω0) profile, a higher slope value is seen for the 〈aN〉/〈τc〉 vs. ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (ω0) profile as τc decreases with increase in ω0 – decrease in the SASS volume. A non-linearity in the 〈aN〉/〈τc〉 vs.
(ω0) profile as τc decreases with increase in ω0 – decrease in the SASS volume. A non-linearity in the 〈aN〉/〈τc〉 vs. ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (ω0) profile – the deviation shown in a circle in Fig. 2 – demonstrates that the aqueous phase constitutes two spatially segregated regions, having markedly different micro-polarity behaviour. This non-linearity in the 〈aN〉/〈τc〉 vs.
(ω0) profile – the deviation shown in a circle in Fig. 2 – demonstrates that the aqueous phase constitutes two spatially segregated regions, having markedly different micro-polarity behaviour. This non-linearity in the 〈aN〉/〈τc〉 vs. ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (ω0) profile is pronounced at a critical distance,
(ω0) profile is pronounced at a critical distance, ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) c, and demarcates the two regions of a RM. Such a demarcation is the maxima (Fig. 2 (inset)) in the 〈aN〉 vs.
c, and demarcates the two regions of a RM. Such a demarcation is the maxima (Fig. 2 (inset)) in the 〈aN〉 vs. ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (ω0) profile; the degree of surfactant packing in SASSs is not considered in making this demarcation. Thus, the 〈aN〉/〈τc〉 vs.
(ω0) profile; the degree of surfactant packing in SASSs is not considered in making this demarcation. Thus, the 〈aN〉/〈τc〉 vs. ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (ω0) profile allows to reliably demarcate the two spatially separable R2 and R3 regions for SDS–hexane RMs,
(ω0) profile allows to reliably demarcate the two spatially separable R2 and R3 regions for SDS–hexane RMs, 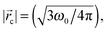 ω0 ≈ 12. Though here, the slope values were similar across the ω0 < 10 and ω0 > 15 ranges, it could well be possible that the slope values could vary significantly due to marked differences in the SASS packing aspects.10
ω0 ≈ 12. Though here, the slope values were similar across the ω0 < 10 and ω0 > 15 ranges, it could well be possible that the slope values could vary significantly due to marked differences in the SASS packing aspects.10
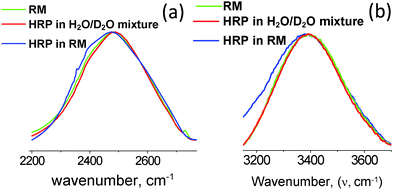
The 〈aN〉/〈τc〉 vs. ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) profiles were developed for the RMs (ω0 levels) having HRP enzymes at different concentration levels. In comparison to the 〈aN〉/〈τc〉 values for the RMs alone, the 〈aN〉/〈τc〉 values were significantly lower for RMs having HRP enzymes (Fig. 2). The lower values of 〈aN〉/〈τc〉 are due to the HRP-concentration dependent micro-polarity attributes. The differences in the slope values were almost an order of magnitude less with HRP in the RMs (Fig. 2), which strongly suggested that the RM water exhibits an ordered form not only in the R2 region but in the R3 region as well. Wherein, the bulk-type water is in negligible amounts in RMs having HRP enzymes. In order to examine the microstructural aspects of the ordered form of water, we studied the O–H/O–D stretching vibration spectroscopic (ATR-IR) absorbance line shapes. In terms of the HRP structural dynamics, there were significant conformational changes of the HRP enzymes in the RMs (ESI,† 4). The amide I peak of HRP in RMs shifted to lower frequencies, and suggested the transformation of the α-helix structures of HRP to β-sheet types. Based on the negligible changes in the amide III peak positions and shapes, the possibilities of HRP denaturation in the RMs were eliminated. In terms of the microstructural features of water, for the RM of the ω0 ≈ 20 level, the blue shifts of the OD- and OH-bands positions (Fig. 3a and b) were prominent for RMs with HRP. These shifts confirmed the ordered forms of water in the R2 and R3 regions. This ordered forms of water could be ascribed to the 〈aN〉/〈τc〉 values. In the cases where other shapes of RM are possible and, depending whether the RMs coalesce, the slope values are likely to be different. It would be interesting to see how the 〈aN〉/〈τc〉 vs.
profiles were developed for the RMs (ω0 levels) having HRP enzymes at different concentration levels. In comparison to the 〈aN〉/〈τc〉 values for the RMs alone, the 〈aN〉/〈τc〉 values were significantly lower for RMs having HRP enzymes (Fig. 2). The lower values of 〈aN〉/〈τc〉 are due to the HRP-concentration dependent micro-polarity attributes. The differences in the slope values were almost an order of magnitude less with HRP in the RMs (Fig. 2), which strongly suggested that the RM water exhibits an ordered form not only in the R2 region but in the R3 region as well. Wherein, the bulk-type water is in negligible amounts in RMs having HRP enzymes. In order to examine the microstructural aspects of the ordered form of water, we studied the O–H/O–D stretching vibration spectroscopic (ATR-IR) absorbance line shapes. In terms of the HRP structural dynamics, there were significant conformational changes of the HRP enzymes in the RMs (ESI,† 4). The amide I peak of HRP in RMs shifted to lower frequencies, and suggested the transformation of the α-helix structures of HRP to β-sheet types. Based on the negligible changes in the amide III peak positions and shapes, the possibilities of HRP denaturation in the RMs were eliminated. In terms of the microstructural features of water, for the RM of the ω0 ≈ 20 level, the blue shifts of the OD- and OH-bands positions (Fig. 3a and b) were prominent for RMs with HRP. These shifts confirmed the ordered forms of water in the R2 and R3 regions. This ordered forms of water could be ascribed to the 〈aN〉/〈τc〉 values. In the cases where other shapes of RM are possible and, depending whether the RMs coalesce, the slope values are likely to be different. It would be interesting to see how the 〈aN〉/〈τc〉 vs. ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (ω0) profile could be applicable for RM–enzyme systems to study the dependency of the MPA(
(ω0) profile could be applicable for RM–enzyme systems to study the dependency of the MPA(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) on the surfactant-packing in a SASS with surfactants of different chemistries.
) on the surfactant-packing in a SASS with surfactants of different chemistries.
Acknowledgements
Support from the NSF I/UCR Center for Particulate and Surfactant Systems is acknowledged. The authors are thankful to Dr William Rice at the New York Structural Biology Center for the Cryo-SEM studies and Dr Jun Wu for Analytical Ultra centrifuge studies.Notes and references
- J. Eastoe, M. J. Hollamby and L. Hudson, Recent advances in nanoparticle synthesis with reversed micelles, Adv. Colloid Interface Sci., 2006, 128, 5–15, DOI:10.1016/j.cis.2006.11.009.
- M. Dekker, et al., Enzyme Recovery by Liquid-Liquid-Extraction Using Reversed Micelles, Chem. Eng. J. Biochem. Eng. J., 1986, 33, B27–B33, DOI:10.1016/0300-9467(86)80050-8.
- P. L. Luisi, Enzymes Hosted in Reverse Micelles in Hydrocarbon Solution, Angew. Chem., Int. Ed. Engl., 1985, 24, 439–450, DOI:10.1002/anie.198504393.
- A. Dasgupta, D. Das and P. K. Das, Reactivity of trypsin in reverse micelles: neglected role of aggregate size compared to water-pool components, Biochimie, 2005, 87, 1111–1119, DOI:10.1016/j.biochi.2005.05.006.
- E. P. Melo, M. R. Aires-Barros and J. M. Cabral, Reverse micelles and protein biotechnology, Biotechnol. Annu. Rev., 2001, 7, 87–129 CAS.
- D. E. Moilanen, E. E. Fenn, D. Wong and M. D. Fayer, Water dynamics in large and small reverse micelles: From two ensembles to collective behavior, J. Chem. Phys., 2009, 131, 014704, DOI:10.1063/1.3159779.
- D. Bratko, A. Luzar and S. H. Chen, Electrostatic Model for Protein Reverse Micelle Complexation, J. Chem. Phys., 1988, 89, 545–550, DOI:10.1063/1.455443.
- F. Akoum and O. Parodi, Electrostatic Interactions inside the Aqueous Core of Spherical Reversed Micelles (L2-Phase), J. Phys. (Paris), 1985, 46, 1675–1681, DOI:10.1051/jphys:0198500460100167500.
- R. Biswas, J. Furtado and B. Bagchi, Layerwise decomposition of water dynamics in reverse micelles: A simulation study of two-dimensional infrared spectrum, J. Chem. Phys., 2013, 139, 144906, DOI:10.1063/1.4824446.
- R. Vacha and S. Roke, Sodium dodecyl sulfate at water-hydrophobic interfaces: a simulation study, J. Phys. Chem. B, 2012, 116, 11936–11942, DOI:10.1021/jp304900z.
- R. Vacha, et al., The Orientation and Charge of Water at the Hydrophobic Oil Droplet-Water Interface, J. Am. Chem. Soc., 2011, 133, 10204–10210, DOI:10.1021/Ja202081x.
- D. Das, S. Roy, R. N. Mitra, A. Dasgupta and P. K. Das, Head-group size or hydrophilicity of surfactants: the major regulator of lipase activity in cationic water-in-oil microemulsions, Chemistry, 2005, 11, 4881–4889, DOI:10.1002/chem.200500244.
- A. Dasgupta, D. Das, R. N. Mitra and P. K. Das, Surfactant tail length-dependent lipase activity profile in cationic water-in-oil microemulsions, J. Colloid Interface Sci., 2005, 289, 566–573, DOI:10.1016/j.jcis.2005.03.083.
- D. Kurad, G. Jeschke and D. Marsh, Lipid membrane polarity profiles by high-field EPR, Biophys. J., 2003, 85, 1025–1033, DOI:10.1016/S0006-3495(03)74541-X.
- A. L. Creagh, J. M. Prausnitz and H. W. Blanch, Structural and Catalytic Properties of Enzymes in Reverse Micelles, Enzyme Microb. Technol., 1993, 15, 383–392, DOI:10.1016/0141-0229(93)90124-K.
- H. Block and S. M. Walker, Modification of Onsager Theory for a Dielectric, Chem. Phys. Lett., 1973, 19, 363–364, DOI:10.1016/0009-2614(73)80380-X.
- H. Caldararu, A. Caragheorgheopol, M. Vasilescu, I. Dragutan and H. Lemmetyinen, Structure of the Polar Core in Reverse Micelles of Nonionic Poly(Oxyethylene) Surfactants, as Studied by Spin-Probe and Fluorescence Probe Techniques, J. Phys. Chem., 1994, 98, 5320–5331, DOI:10.1021/J100071a024.
- M. P. Pileni, Reverse Micelles as Microreactors, J. Phys. Chem., 1993, 97, 6961–6973, DOI:10.1021/J100129a008.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm01950h |
| This journal is © The Royal Society of Chemistry 2016 |