 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Monte Carlo study of the frame, fluctuation and internal tensions of fluctuating membranes with fixed area
Hayato
Shiba†
a,
Hiroshi
Noguchi
a and
Jean-Baptiste
Fournier
*b
aInstitute for Solid State Physics, University of Tokyo, Chiba 277-8581, Japan
bLaboratoire Matière et Systèmes Complexes (MSC), UMR 7057 CNRS, Université Paris Diderot, F-75205, Paris, France. E-mail: jean-baptiste.fournier@univ-paris-diderot.fr
First published on 22nd January 2016
Abstract
Three types of surface tensions can be defined for lipid membranes: the internal tension, σ, conjugated to the real membrane area in the Hamiltonian, the mechanical frame tension, τ, conjugated to the projected area, and the “fluctuation tension”, r, obtained from the fluctuation spectrum of the membrane height. We investigate these surface tensions by means of a Monge gauge lattice Monte Carlo simulation involving the exact, nonlinear, Helfrich Hamiltonian and a measure correction for the excess entropy of the Monge gauge. Our results for the relation between σ and τ agrees well with the theoretical prediction of [J.-B. Fournier and C. Barbetta, Phys. Rev. Lett., 2008, 100, 078103] based on a Gaussian approximation. This provides a valuable knowledge of τ in the standard Gaussian models where the tension is controlled by σ. However, contrary to the conjecture in the above paper, we find that r exhibits no significant difference from τ over more than five decades of tension. Our results appear to be valid in the thermodynamic limit and are robust to changing the ensemble in which the membrane area is controlled.
1 Introduction
A few decades of research has clarified that lipid bilayers can be treated as sheets obeying the continuum curvature/tension elasticity formulated by Helfrich.1 Characterising membrane elastic constants in numerical simulations has become an important issue due to the increase in computational power and development of simulation methods. Starting with the seminal work of ref. 2, a growing number of research papers are dedicated to the determination of bending rigidity,3–12 Gaussian modulus,13 and surface tension,7,8,11,14,15 from molecular simulation of all-atom systems to coarse-grained models.A number of questions have been raised regarding the definition of membrane surface tension. When a thermally fluctuating flexible membrane is stretched by a moderate lateral tension, the membrane extends its projected area by suppressing its transverse fluctuation.16 This leads to multiple definitions of membrane tension: (i) “internal tension”, σ, conjugated to the real area A in the membrane Hamiltonian, (ii) mechanical “frame tension”, τ, conjugated to the projected area Ap,17 and (iii) “fluctuation tension”, r, associated to the lowest-order wavevector dependence of the inverse fluctuation spectrum. The latter two are directly experimentally measurable.18
Some discussions on the difference between these surface tensions have been lasting for more than a decade. First of all, it is well accepted that σ and τ are intrinsically different, because σ is a microscopic parameter belonging to the effective Hamiltonian while τ is a macroscopic observable integrating the local stress tensor over all the membrane fluctuations. Based on free-energy calculations and stress tensor averages, the difference between σ and τ has been estimated within the Gaussian approximation.14,19,20 Note that the validity of this estimation was questioned by Schmid.21 It is also well accepted that σ and r are different, because r is actually the renormalised version of σ (at the Gaussian level they are equal). The relationship between r and τ has been much debated. Several authors have argued theoretically,5,15,22,23 or observed in numerical simulations,2–4,7,8,15,21,24–28 that r matches the mechanical frame tension τ. Other authors have observed a difference between r and τ, either in numerical simulations11,14,20,29 or experiments.18
These questions should be carefully revisited with the help of extensive, large-scale numerical simulations. A complication has to do with the equivalence of ensembles in the thermodynamic sense, as in the simulations found in the literature, either the areas A and Ap or their conjugated tensions σ and τ are fixed. Different ensembles are only equivalent in the thermodynamic limit of infinite membranes, A → ∞ at fixed A/N, with N the total number of degrees of freedom. It is therefore very important to check the convergence of the numerical results with system size. In another recent simulation,30r was claimed to deviate from τ for τ < 0 and to coincide with τ for τ > 0. It is thus interesting to study how r behaves when τ assumes positive values very close to zero, for which the system undergoes large fluctuations. Let us stress that investigating several orders of magnitude of τ is important, because membrane tension can experimentally vary over more than five decades.31
In this paper, we investigate the differences between the three surface tensions, σ, τ and r, over several decades of τ, by means of Monte Carlo simulations of a lattice membrane system in the Monge gauge. In the lattice model, the internal tension σ and the frame tension τ can be controlled and short range fluctuations generated by molecular or particle protrusions, which make accurate estimations of r difficult, are not present. However, a measure correction is required to cure the excess entropy due to the unidirectional lattice-site motions implied by the Monge gauge. We also employ exact nonlinear expressions to calculate the membrane’s curvature and area. We find that σ differs from τ at small positive frame tensions, while they match at moderate and high frame tensions. Our results for σ − τ agree well with the prediction of ref. 20 based on a Gaussian approximation, although our simulation investigates regimes where the Gaussian approximation is far from being justified. We find also that r and τ match, within the accuracy of our simulation, over more than five decades, even in the limit of very small frame tensions. These relationships remain in the thermodynamic limit and seem not to depend on the ensemble in which the real area A is controlled (see Appendix A).
Our paper is organised as follows. In Section 3, we detail our lattice membrane model and the Monte Carlo simulation framework that realises an equilibrium ensemble for fixed τ and σ. In this framework, the average of the real membrane area, 〈A〉, is kept constant by adjusting σ while τ is varied. We also perform our simulation in the equilibrium ensemble for fixed τ and A. This is discussed in Appendix A. In the thermodynamic limit of large systems, we thus simulate a membrane with fixed real area subjected to a variable frame tension. In Section 3, we numerically determine and we compare the three tensions σ, τ and r. We give our conclusions in Section 4.
2 Model and method
2.1 Stress-controlled ensemble
Let us consider an incompressible, fluctuating lipid membrane with a fixed area A = A0, corresponding to a fixed number of lipids. We assume that it is attached to a deformable frame, of variable area Ap, that exerts onto the membrane a fixed tension τ. The Hamiltonian of the system is thus given by1 | (1) |
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) has been neglected, according to the Gauss–Bonnet theorem, which is correct for fixed angular boundary conditions or periodic boundary conditions along the frame.32
has been neglected, according to the Gauss–Bonnet theorem, which is correct for fixed angular boundary conditions or periodic boundary conditions along the frame.32
We use the Monge representation, in which the membrane shape is describe by its height z = h(x,y) above the plane of the frame. Note that this parametrisation does not require the membrane deformation to be small. The only restriction is that overhangs are forbidden, since the function h is single valued. In this representation, the total curvature H is exactly given by33
 | (2) |
Because it is quite difficult to work with a fixed area A = A0, we change ensemble in order to control the conjugated internal tension σ, instead of the membrane area A. In the thermodynamic limit, the two ensembles are expected to be equivalent. Indeed, as shown in Appendix A, we find quantitatively similar results in the ensemble in which the real area A is almost prescribed by means of a quadratic potential. In this stress-controlled ensemble, the modified Hamiltonian weighting the membrane fluctuations is given by
 | (3) |
2.2 Lattice model
In order to implement the membrane fluctuations numerically, we introduce a Nx × Ny lattice on the plane (x,y) of the frame, with lattice spacing a. The height of the membrane surface is defined by hij on each lattice site, with 1 ≤ i ≤ Nx and 1 ≤ j ≤ Ny. In the reminder of this paper, we take . Furthermore, we adopt periodic boundary condition. Thus the projected area is given by Ap = Na2.
. Furthermore, we adopt periodic boundary condition. Thus the projected area is given by Ap = Na2.
Importantly, because the number of lipids is fixed while the frame area Ap is variable, we take N constant but a variable. In other words, in our simulation the lattice spacing is not fixed. We stress, however, that a always remains uniform over the lattice: it is the overall lattice spacing that changes. Therefore the projection over the reference plane of the vertices always maps onto a square grid of finite spacing and the vertices can never overlap. Note that a similar lattice membrane model (with fixed spacing and the Gaussian approximation) has been employed for Monte Carlo simulation in order to investigate inclusions effects.34
Monte Carlo simulations are performed with the lattice heights {hij} and the lattice spacing a as dynamical variables. Special care is required, however, for the sampling of the height variables. In the Monge gauge, each site can only fluctuate in the z direction, whereas in the physical gauge, because the membrane is fluid, the relevant fluctuations occur by local displacements along the membrane’s normal. In order to avoid an artificial entropy increase of the states where the membrane is tilted, the naive measure  , where δ0 is a quantum of height fluctuations, must be transformed to
, where δ0 is a quantum of height fluctuations, must be transformed to
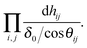 | (4) |
 . In this way, the quantum height displacement in the normal direction is always δ0. Equivalently, we can keep the naive measure dN[h] and add to the Hamiltonian the following correction term:
. In this way, the quantum height displacement in the normal direction is always δ0. Equivalently, we can keep the naive measure dN[h] and add to the Hamiltonian the following correction term: | (5) |
The partition function in the stress-controlled ensemble introduced above is given by
 | (6) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ′ =
′ = ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) * +
* + ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) corr. Metropolis sampling is employed.35 In each Monte Carlo step, N trial moves of the height of a random site are attempted. The change of a (hence Ap) is attempted every 5 Monte Carlo steps. The amplitudes of the hij and Ap changes are adjusted so that the rejection rate lies in the range 40–60%. Both A and Ap change during the simulations. However, for a given Monte Carlo run at a specified value of τ, the internal tension σ is adjusted in order for the average of the membrane area 〈A〉 to have the specific value A0, fixed once for all.
corr. Metropolis sampling is employed.35 In each Monte Carlo step, N trial moves of the height of a random site are attempted. The change of a (hence Ap) is attempted every 5 Monte Carlo steps. The amplitudes of the hij and Ap changes are adjusted so that the rejection rate lies in the range 40–60%. Both A and Ap change during the simulations. However, for a given Monte Carlo run at a specified value of τ, the internal tension σ is adjusted in order for the average of the membrane area 〈A〉 to have the specific value A0, fixed once for all.
In our simulation, the real area A of the membrane is calculated as follows. The local area associated to a site P(i, j) is obtained as one half of the total area of the four triangles [APB], [BPC], [CPD] and [DPA] built from the neighbouring sites of coordinates:
| A(i + 1, j), B(i, j + 1), C(i − 1, j), D(i, j − 1). | (7) |
 | (8) |
Simulation are carried out at least for 107 steps after the initial relaxation. The statistical errors are calculated from four or more independent runs.
2.3 Dimensionless units and orders of magnitudes
Since our simulated membrane has a prescribed average area A0 and a fixed number N of degrees of freedom, we can picture each degree of freedom as a patch of lipids of fixed average area a02 = A0/N. In the following we are going to nondimensionalise the lengths by a0 (the size of a degree of freedom in the membrane) and the energies by kBT = 4 × 10−21 J (room temperature energy). In other words, we shall set a0 = kBT = 1. Hence, all tensions will be given in units of kBT/a02. As previously discussed, we shall thus adjust σ for each τ in order to have systematically 〈A〉 = N, in dimensionless units.Let us estimate tension scale kBT/a02. In principle, we are free to choose the linear size a0 of the lipid patches that constitute our degrees of freedom. It is convenient, however, to choose the smallest possible size, in order to allow for all possible fluctuations and to avoid using renormalised elastic constants. Owing to the level of coarse-graining of our simulation, in which the bilayer membrane of real thickness ≈5 nm is treated as a mathematical surface, it is natural to think of the lipid patches as regions of typical size, e.g. a0 ≈ 20 nm. Then, the natural unit of tension in our simulation is kBT/a02 ≈ 10−5 J m−2. The tension mechanically imposed on ordinary vesicle membranes, in experiments, are in the range of 10−7 to 10−2 J m−2, where the smallest value corresponds to floppy vesicles and the largest value corresponds to the lytic tension.36 We shall therefore have τ span the range 10−2–103 in dimensionless units. Let us stress that this corresponds to five orders of magnitude.
In our simulation, we choose a specific value of the bending rigidity corresponding to κ = 10 kBT, i.e., κ = 10 in dimensionless units. We shall consider membrane sizes corresponding to N = 400, 1600, 6400 and 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600. With the value of a0 given above, this corresponds to membrane of linear dimension
600. With the value of a0 given above, this corresponds to membrane of linear dimension  , 800 nm, 1.6 μm and 3.2 μm, respectively. These values are quite small if one thinks of macroscopic experiments, but they are reasonably large on the biological scale. Because of the change of ensemble that we have performed, we shall check the convergence of our results with increasing N.
, 800 nm, 1.6 μm and 3.2 μm, respectively. These values are quite small if one thinks of macroscopic experiments, but they are reasonably large on the biological scale. Because of the change of ensemble that we have performed, we shall check the convergence of our results with increasing N.
In Fig. 1, a simulation snapshot for N = 6400 is shown in the tensionless state τ = 0.
3 Results
3.1 Frame tension and internal tension
From now, unless otherwise specified, all quantities will be given in dimensionless units (see Section 3.3). We investigate here the relationship between σ and τ. As explained above, we place ourselves in the (σ,τ) ensemble; however, for every imposed frame tension τ, we determine the internal tension σ that achieves 〈A〉 = N. Our simulated membrane thus effectively has a constant real area (up to fluctuations that become irrelevant in the thermodynamic limit). Simulations in the (A,τ) ensemble, where A is nearly fixed by means of a steep quadratic potential, are discussed in Appendix A.The determined values of σ are plotted in Fig. 2a against the frame tension for different system sizes: N = 400, 1600, 6400 and 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600. For any value of τ we find σ > τ. Data for both positive and negative frame tensions are displayed together as a function of |τ|: the upper branch corresponds to τ > 0 and the lower branch corresponds to τ < 0. Note that for τ > 0 the difference between σ and τ is sizeable only for small values of the frame tension. For τ = 0 we find that the residual internal tension is equal to σ0 ≃ 0.500 ± 0.001, where the error bar takes into account the determinations using different values of N. In other words, the residual tension turns out to be fairly independent of system size.
600. For any value of τ we find σ > τ. Data for both positive and negative frame tensions are displayed together as a function of |τ|: the upper branch corresponds to τ > 0 and the lower branch corresponds to τ < 0. Note that for τ > 0 the difference between σ and τ is sizeable only for small values of the frame tension. For τ = 0 we find that the residual internal tension is equal to σ0 ≃ 0.500 ± 0.001, where the error bar takes into account the determinations using different values of N. In other words, the residual tension turns out to be fairly independent of system size.
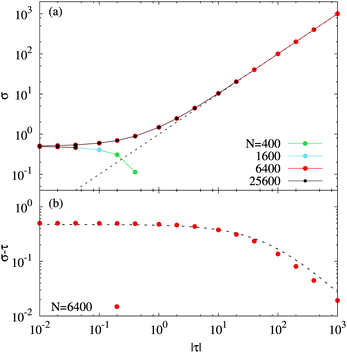 | ||
Fig. 2 (a) The values of σ corresponding to the prescribed average membrane area 〈A〉 = N are plotted against |τ|, for system sizes N = 400, 1600, 6400 and 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600. The upper (resp. lower) branch displays the data for τ > 0 (resp. τ < 0). For τ < 0 the data points are plotted up to the buckling transition. The dotted line indicates σ = τ (for τ > 0). (b) The red points show the difference σ − τ as a function of τ > 0 for N = 6400; the black dashed line shows the best fit to the theoretical Gaussian prediction eqn (9) and (10). 600. The upper (resp. lower) branch displays the data for τ > 0 (resp. τ < 0). For τ < 0 the data points are plotted up to the buckling transition. The dotted line indicates σ = τ (for τ > 0). (b) The red points show the difference σ − τ as a function of τ > 0 for N = 6400; the black dashed line shows the best fit to the theoretical Gaussian prediction eqn (9) and (10). | ||
When τ decreases below some negative threshold τb < 0, the membrane buckles either into the x or the y direction: the average membrane shape undergoes a transition from flat to non-flat through a symmetry breaking (like a rod under compression). Note that the membrane height function remains single valued although it acquires a bimodal distribution. The absolute value |τb| of the buckling threshold decreases as the system size N gets larger. In the lower branch, the data points for |τ| > |τb|, in the buckling state, are eliminated from the plots in Fig. 2a. It is notable that the condition σ < 0 is not required for the buckling transition. We also simulated our lattice model in the (Ap,σ) ensemble, i.e. with constant lattice spacing a and freely changing membrane area A. We found that the membrane buckles then at σ = 0. These results suggest that σ is not the mechanical force that drives membrane buckling.
In ref. 20, the difference between the tensions σ and τ was calculated within the Gaussian approximation, yielding
 | (9) |
 | (10) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600. Here, only positive values of τ are displayed: the downwards divergence of the curves associated to the plain circles corresponds to τ → 0. The system size dependence is marked for small sizes, but the data appears to converge to a universal thermodynamic limit at large system sizes. Finite size effects are more or less irrelevant for N ≥ 6400.
600. Here, only positive values of τ are displayed: the downwards divergence of the curves associated to the plain circles corresponds to τ → 0. The system size dependence is marked for small sizes, but the data appears to converge to a universal thermodynamic limit at large system sizes. Finite size effects are more or less irrelevant for N ≥ 6400.
3.2 Fluctuation tension
We now discuss the fluctuation tension r. It is derived from the spectrum density, assumed to take the standard form:33 | (11) |
In estimating these quantities using simulation results, it is crucially important to consider large-scale fluctuations. However, because we always treat finite-size systems, the wavevector spectrum is limited, which results in systematic deviations. Previously, two of the present authors have addressed in detail the question of the estimation of the bending rigidity from simulation data.8 For a planar membrane, the correct value of the bending rigidity can be determined uniquely by first estimating the rigidity κrvia a fit of the inverse spectrum (rq2 + κrq4)/(kBT) in the wavevector range  , then by extrapolating the results to the limit qcut → 0, where qcut is a varying upper fitting wavevector limit. Note that because the projected area Ap fluctuates, there is some ambiguity regarding the definition of the quantified wavevectors. As discussed in Appendix C, our results are not sensitive to those details. This procedure has been carried out for the present system. We find that the value of κr coincides with the bare value κ, up to our numerical precision. This result makes sense because renormalisation group calculations predict
, then by extrapolating the results to the limit qcut → 0, where qcut is a varying upper fitting wavevector limit. Note that because the projected area Ap fluctuates, there is some ambiguity regarding the definition of the quantified wavevectors. As discussed in Appendix C, our results are not sensitive to those details. This procedure has been carried out for the present system. We find that the value of κr coincides with the bare value κ, up to our numerical precision. This result makes sense because renormalisation group calculations predict
 | (12) |
The correct value of the fluctuation tension r can be estimated likewise in the limit qcut → 0. For finite values of qcut, we find that r is overestimated but converges in the limit qcut → 0 to a well defined value. The corresponding extrapolation is performed by using a quadratic function of qcut. The fitting was performed in the range 0.015 ≤ (qcut/π)2 < 0.15.
Fig. 4 shows the values of the fluctuation tension r. We find that r is fairly close to τ for all the investigated values of τ, as indicated in Fig. 4a. In Fig. 4b, the difference r − τ is plotted against τ. For large system sizes, N = 6400 and 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600, we observe a small deviation between r and τ; however, as discussed in Appendix B, we believe that this deviation is smaller than a possible systematic error arising from the measure correction.
600, we observe a small deviation between r and τ; however, as discussed in Appendix B, we believe that this deviation is smaller than a possible systematic error arising from the measure correction.
 | ||
Fig. 4 (a) Plot of τ, r, and σ as a function of excess area (A − Ap)/A for N = 6400, which roughly corresponds to the thermodynamic limit. The data for τ and σ are the same as in Fig. 3, and r is plotted with the error bars. As for the statistical errors in (A − Ap)/A, they are small, within the symbol marks. (b) The difference between r and τ, normalised by σ, is plotted against τ for N = 1600, 6400, and 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600. The convergence of the data with increasing N indicates that the thermodynamic limit is reached for N = 6400. 600. The convergence of the data with increasing N indicates that the thermodynamic limit is reached for N = 6400. | ||
3.3 Comparison with the Gaussian approximation
In the present work, all the nonlinearities of the problem have been taken into account: (i) the nonlinear expression of the membrane elementary area dA (ii) the nonlinear expression of the membrane bending energy density H2dA, and (iii) the nonlinear measure correction![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) corr dealing with the excess entropy of the Monge gauge. The Gaussian approximation, which is frequently used in basic calculations, consists in replacing the bending energy density H2dA by HL2dAp, where HL = hxx + hyy is the Laplacian approximation of the mean-curvature and dAp the projected elementary area, and in neglecting the entropy measure correction
corr dealing with the excess entropy of the Monge gauge. The Gaussian approximation, which is frequently used in basic calculations, consists in replacing the bending energy density H2dA by HL2dAp, where HL = hxx + hyy is the Laplacian approximation of the mean-curvature and dAp the projected elementary area, and in neglecting the entropy measure correction ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) corr. Indeed, at quadratic order, the measure correction becomes
corr. Indeed, at quadratic order, the measure correction becomes 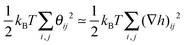 , which is of no consequences as it simply redefines the tunable parameter σ. In this subsection, we investigate how these two Gaussian approximations affect the surface tensions. First, we make the Laplacian approximation, i.e., H2dA is replaced by HL2dAp in eqn (1), and we keep the entropy correction term
, which is of no consequences as it simply redefines the tunable parameter σ. In this subsection, we investigate how these two Gaussian approximations affect the surface tensions. First, we make the Laplacian approximation, i.e., H2dA is replaced by HL2dAp in eqn (1), and we keep the entropy correction term ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) corr. The corresponding results are denoted by the subscript EL in Fig. 5. Then we also remove the entropy correction term. The corresponding calculations are denoted by the subscript L.
corr. The corresponding results are denoted by the subscript EL in Fig. 5. Then we also remove the entropy correction term. The corresponding calculations are denoted by the subscript L.
We find that the internal tension σ is not changed by these modifications. However, rEL and rL are significantly different from r, as shown in Fig. 5. Using the Laplacian approximation while keeping the entropy correction term results in a fluctuation tension rEL about three times larger than σ. Further removing the entropy correction yields a tension rL very close to σ, in agreement with the well-known coincidence of r and σ at the Gaussian level. Therefore, the effects of the measure correction and of the nonlinear curvature are opposite to each other: the former raises the value of r, the latter lowers it. Both of these effects need to be taken into account for a faithful description of the membrane fluctuations beyond the level of the Gaussian approximation. The estimated r deviates from the true value if either of them is missing.
4 Conclusions
In this paper, we have examined the various surface tensions of membranes: frame tension τ, internal tension σ, and renormalised “fluctuation” tension r. We have compared them quantitatively using a Monte Carlo simulation with control over both τ and σ, the latter being slaved to the former in order to keep the average membrane area 〈A〉 constant. We have also validated our results in the conjugated ensemble where the real membrane area A is fixed (Appendix A). We have investigated large systems in order to reach the thermodynamic limit. Our model being a lattice model instead of a particle-based model, protrusion effects and other artificial elements are eliminated. Gaussian approximation artefacts are also excluded because curvatures and areas are computed with exact formulas (although we employ the Monge gauge) and because we have corrected the excess entropy associated with the measure of the Monge gauge. Moreover, because our simulated membrane does not exhibit rupture at extremely large τ, all tensions from vanishingly small to very high can be investigated.There have been two findings in our results. The first is that the residual internal tension σ0 = σ − τ remains finite at large N (large systems). While it is well known that σ and τ are different, we have confirmed that the theoretical (albeit Gaussian) estimation of ref. 20 predicts correctly and quantitatively the difference σ − τ from vanishingly small frame tensions to very large frame tensions.
The renormalised “fluctuation” tension r has also been investigated, and compared with the other two tensions. We conclude r ≃ τ within an accuracy of 0.1kBT/a2 (estimated ≃ 10−6 J m−2), which is consistent with the proposition of ref. 22.
Note finally that the shape of the buckled membrane, described by elliptic functions, breaks the symmetry between the x and y directions and yields an anisotropy in the frame tension.9 How exactly the thermal fluctuations of the membrane modify the mechanical buckling transition should be investigated in further studies.
Appendix
A Simulation with nearly constant real area
In the body of this paper, the real area A of the membrane is not fixed, but its average value 〈A〉 is controlled by the parameter σ (much as the average number of particles in a grand-canonical ensemble is controlled by the chemical potential). In principle, we have checked the validity our results by studying the thermodynamic limit of increasing system sizes. It is nonetheless interesting to test our results by working in the ensemble in which the area A is prescribed. This is the purpose of the present Appendix.While it is very difficult to prescribe exactly the membrane area, because it is difficult to identify the sampling condition that satisfies this constraint, one can easily almost prescribe the area by using a quadratic potential of tunable strength KA. We thus worked with the Hamiltonian
 | (13) |
We have performed the corresponding Monte Carlo simulations exactly in the same manner as in the body of the paper. Fig. 6 shows the result of these additional simulations, for KA = 1, 10 and 100, with N = 6400, and compares them with the results of Fig. 4. With increasing KA, the standard deviation of the real area decreases: 0.01%, 0.001%, and 0.0003%, for KA = 1, 10, and 100, respectively.
 | ||
| Fig. 6 The deviation of the fluctuation tension r from the frame tension τ is plotted in the form (r − τ)/σ. The red points are pasted from Fig. 4b for comparison. The results for three values of KA (=1, 10, and 100) are shown by using symbols and error bars of different colours. For all the plotted data, the system size is N = 6400. Although we normalise the data by σ, no estimate is available in the present simulation; therefore, we use the values of Fig. 4a as substitutes. | ||
B Entropy correction for membrane tilt
To check the reliability of the measure correction![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) corr, eqn (5), we performed simulations in which the entire membrane is tilted by an angle θa. The periodic boundary condition along the x direction is modified to h(Nx, j) = h(0, j) + Nxa
corr, eqn (5), we performed simulations in which the entire membrane is tilted by an angle θa. The periodic boundary condition along the x direction is modified to h(Nx, j) = h(0, j) + Nxa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θa. The x side length of the lattice is changed to a
θa. The x side length of the lattice is changed to a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θa in order to maintain a square grid in the tilted projected plane. The height spectrum is calculated for the tilted plane, of normal vector (−sin
θa in order to maintain a square grid in the tilted projected plane. The height spectrum is calculated for the tilted plane, of normal vector (−sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θa, 0, cos
θa, 0, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θa). The fluctuation tension r increases with increasing θa (see Fig. 7), while σ is independent of θa. This implies that the excess entropy associated with the membrane tilt in the Monge gauge is not completely removed. However, the deviation is small for small θa, and the overestimation of r is less than 0.1 for θa < 0.1π. In our simulation, at τ = 0 we obtain 〈cos
θa). The fluctuation tension r increases with increasing θa (see Fig. 7), while σ is independent of θa. This implies that the excess entropy associated with the membrane tilt in the Monge gauge is not completely removed. However, the deviation is small for small θa, and the overestimation of r is less than 0.1 for θa < 0.1π. In our simulation, at τ = 0 we obtain 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θij〉 = 0.98, i.e., the mean angle is 0.066π. We conclude that the obtained values of r are reliable within the accuracy of 0.1 (in dimensionless units).
θij〉 = 0.98, i.e., the mean angle is 0.066π. We conclude that the obtained values of r are reliable within the accuracy of 0.1 (in dimensionless units).
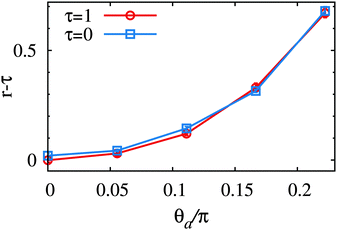 | ||
| Fig. 7 Dependence of the fluctuation tension r for a membrane whose projected plane is entirely tilted by the angle θa, for τ = 0 and τ = 1, at N = 6400. | ||
C Definition of the spectrum wavevectors
In Section 3.2, the renormalised tension r is calculated by fitting the height spectrum 〈|h(q)|2〉. We use a sequence of instantaneous height configurations, and we perform averages after the simulation finishes. Because the projected area Ap changes during the simulations, the wavevectors on the reciprocal lattice are not fixed. They are given by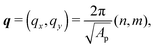 | (14) |
 . Here, b = 1.2 is taken) and over all the height configurations.
. Here, b = 1.2 is taken) and over all the height configurations.
We have confirmed the robustness of our estimation of r, by using a different set of wavevectors, defined by
 | (15) |
Acknowledgements
The authors thank F. Schmid and H. Diamant for their comments. This work was supported by the Core-to-Core Program “Non-equilibrium dynamics of soft matter and information” by the Japan Society for Promotion of Science (JSPS) and also by a Grant-in-Aid for Scientific Research on Innovative Areas “Synergy of Fluctuation and Structure: Foundation of Universal Laws in Nonequilibrium Systems” (Grant No. 25103010). Numerical calculations were partly carried out on SGI Altix ICE 8400EX System at ISSP, University of Tokyo.References
- W. Helfrich, Z. Naturforsch., 1973, 28c, 693–703 Search PubMed
.
- R. Goetz, G. Gompper and R. Lipowsky, Phys. Rev. Lett., 1999, 82, 221–224 CrossRef CAS
.
- E. Lindahl and O. Edholm, Biophys. J., 2000, 79, 426–433 CrossRef CAS PubMed
.
- W. K. Den Otter and W. J. Briels, J. Chem. Phys., 2003, 118, 4712–4720 CrossRef CAS
.
- O. Farago and P. Pincus, J. Chem. Phys., 2004, 120, 2934–2950 CrossRef CAS PubMed
.
- V. A. Harmandaris and M. Deserno, J. Chem. Phys., 2006, 125, 204905 CrossRef PubMed
.
- H. Noguchi and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 021903 CrossRef PubMed
.
- H. Shiba and H. Noguchi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031926 CrossRef PubMed
.
- H. Noguchi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 061919 CrossRef PubMed
.
- M. Hu, P. Diggins IV and M. Deserno, J. Chem. Phys., 2013, 138, 214110 CrossRef PubMed
.
- P. Tarazona, E. Chacón and F. Bresme, J. Chem. Phys., 2013, 139, 094902 CrossRef PubMed
.
- M. C. Watson, A. Morriss-Andrews, P. M. Welch and F. L. H. Brown, J. Chem. Phys., 2013, 139, 084706 CrossRef PubMed
.
- M. Hu, J. J. Briguglio and M. Deserno, Biophys. J., 2012, 102, 1403–1410 CrossRef CAS PubMed
.
- A. Imparato, J. Chem. Phys., 2006, 124, 154714 CrossRef PubMed
.
- O. Farago, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 051914 CrossRef PubMed
.
- J. B. Fournier, A. Ajdari and L. Peliti, Phys. Rev. Lett., 2001, 86, 4970–4973 CrossRef CAS PubMed
.
- F. David and S. Leibler, J. Phys. II, 1991, 1, 959–976 CrossRef CAS
.
- K. Sengupta and L. Limozin, Phys. Rev. Lett., 2010, 104, 088101 CrossRef PubMed
.
- O. Farago and P. Pincus, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 11, 399–408 CrossRef CAS PubMed
.
- J.-B. Fournier and C. Barbetta, Phys. Rev. Lett., 2008, 100, 078103 CrossRef PubMed
.
- F. Schmid, EPL, 2011, 95, 28008 CrossRef
; Comment: J.-B. Fournier, EPL, 2012, 97, 18001 CrossRef
; Reply: F. Schmid, EPL, 2012, 97, 18002 CrossRef
.
- W. Cai, T. C. Lubensky, P. Nelson and T. Powers, J. Phys. II, 1994, 4, 931–949 CrossRef CAS
.
- H. Diamant, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 061123 CrossRef PubMed
.
- S. J. Marrink and A. E. Mark, J. Phys. Chem. B, 2001, 105, 6122–6127 CrossRef CAS
.
- Z. J. Wang and D. Frenkel, J. Chem. Phys., 2005, 122, 234711 CrossRef PubMed
.
- G. Brannigan and F. L. H. Brown, Biophys. J., 2006, 90, 1501–1520 CrossRef CAS PubMed
.
- B. West, F. L. H. Brown and F. Schmid, Biophys. J., 2009, 96, 101–115 CrossRef CAS PubMed
.
- J. Neder, B. West, P. Nielaba and F. Schmid, J. Chem. Phys., 2010, 132, 115101 CrossRef PubMed
.
- J. Stecki, J. Chem. Phys., 2006, 125, 154902 CrossRef CAS PubMed
.
- Y. Y. Avital and O. Farago, J. Chem. Phys., 2015, 142, 124902 CrossRef PubMed
.
- E. Evans and W. Rawicz, Phys. Rev. Lett., 1990, 64, 2094–2097 CrossRef CAS PubMed
.
-
B. S. Buchin, Lectures on Differential Geometry, World Scientific, Singapore, 1980 Search PubMed
.
-
S. A. Safran, Statistical thermodynamics of surfaces, interfaces, and membranes, Addison-Wesley, Massachusetts, 1994 Search PubMed
.
- T. R. Weikl, Europhys. Lett., 2001, 54, 547–553 CrossRef CAS
.
-
D. P. Landau and K. Binder, A Guide to Monte Carlo Simulations in Statistical Physics, Cambridge University Press, Cambridge, 3rd edn, 2009 Search PubMed
.
- W. Rawicz, K. C. Olbrich, T. McIntosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339 CrossRef CAS PubMed
.
Footnote |
| † Present address: Institute for Materials Research, Tohoku University, Sendai 980-8577, Japan. |
| This journal is © The Royal Society of Chemistry 2016 |



