Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Critical nucleation mesh-size of coarsening transient colloidal networks
Florian Johannes
Maier
and
Thomas Martin
Fischer
Experimentalphysik V, University of Bayreuth, 95440 Bayreuth, Germany. E-mail: Florian-Johannes.Maier@uni-bayreuth.de
First published on 22nd October 2015
Abstract
Isotropic magnetic field modulations cause the formation and coarsening of transient two dimensional paramagnetic colloidal networks. We show that the virgin transient network consists of sub- and supercritical meshes. In the initial coarsening process subcritical meshes shrink while supercritical meshes grow. While the coarsening is a truly non-equilibrium process, the critical nucleation size is independent of transport coefficients and can be theoretically described by the competition of first order long range collective dipolar interactions and short range second order dipolar pair correlations.
1 Introduction
The equilibrium formation of modulated phases with a characteristic length scale of modulation is known to arise via the competition of long- and short range interactions.1 One prominent example of such modulated phases are quasi two dimensional coexistence structures of dipolarly interacting phases which occur in thin low-coercivity perpendicular magnetic films,2 Langmuir monolayers3,4 and coexisting nonmagnetic and magnetic fluids.5 It is an interesting question whether analogues of such modulated phases could also occur as a transient metastable state in an evolving non-equilibrium system. A wet foam is a typical non-equilibrium structure that occurs via nucleation droplets and coarsens via Ostwald ripening6,7 with the larger droplets growing on expense of the smaller ones. The behavior of paramagnetic beads in an isotropically fluctuating external magnetic field8–10 bares many similarities with both the structure modulated phases and with the coarsening behavior of non-equilibrium foams. The similarities arise since time averaged and non-time averaged dipolar interactions determine the dynamics of these colloids in similar ways as in modulated equilibrium phases. It has been shown9 that isotropic external field fluctuations favor the formation of locally uniaxial structures and disfavor isotropic arrangements. Chains having a prolate uniaxial anisotropy require less beads and are the structures that due to kinetic reasons form first. Membranes having an oblate uniaxial anisotropy are more stable, however they require a larger amount of beads and therefore only form after chains have been formed. The result of the coexistence of membranes and chains is a transient network. The question we try to understand with this work is, whether the length scale of the transient network structure is truly dynamic or whether it can be determined solely using energetic arguments like in dipolar equilibrium foams.11The problem has been pioneered by Martin and coworkers.8 One observation is the collective nature of the interactions causing a pair of beads to interact quite differently in the presence of other beads. The subtle effects of third and other beads on the pair interaction of a pair of beads renders the theoretical description in terms of single particle interactions quite complex. Contrary to the work of Martin and the work of Babic and Dobnikar,9 we use a continuum description of the arrangement of the beads, that treats a close packed membrane as conserved area of homogeneous susceptibility. In this treatment the driving forces are line tensions arising at the boundary of the membrane,3,4 while the resulting motion is that of an incompressible probably viscoelastic10 two dimensional fluid.
2 Experimental
We followed the method of Babic et al.9 to create transient networks in a semi-dilute suspension of superparamagnetic spherical colloids (Dynabeads M-270, diameter 2.8 μm). The colloids are dispersed on top of a glass substrate, where they sediment to form a two dimensional dispersion above the glass surface. A cover slip placed on spacer particles of diameter 9.6 μm created a sample of known thickness allowing for at most two superparamagnetic beads to hop on top of each other. A magnetic field normal to the glass surface induces a repulsion that causes a structure of well separated beads on the surface to build up. Two pairs of coils oriented along the x and y direction and one single coil oriented along z direction arranged around the sample provide the possibility to produce time dependent magnetic fields of arbitrary orientation. At t = 0 we switch on a back and forth precessing field of the formHext(t) = Hext(cos(φ(t))![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ,sin(φ(t)) ϑ,sin(φ(t))![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ,cos ϑ,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ) ϑ) | (1) |
3 Results
Fig. 1 shows a two dimensional ensemble of paramagnetic colloids right before (t = −1 s) and after (t = 0.8 s + n·10 s, n = 0, 1, 2, 3, 4) switching on the dynamic time reversal invariant magnetic field modulation12 of eqn (1). For negative times (t < 0), the ensemble consists of a two dimensional dispersed collection of individual, well separated colloidal particles at an area fraction of Φ = 0.44. After switching on the modulation (t > 0), within less than a second a virgin colloidal network forms in the focal plane of the microscope that then (t > 0.8 s) coarsens over time. It is the coarsening of the 2D-network that we intend to describe and understand with the current manuscript. To analyze the coarsening dynamics, we extract the centers of the positions of each colloidal particle in every frame of the recorded video and mark the excluded area of each particle by a solid black circle of radius a = 1.4 μm, such that particles with distances closer than d < 2.8 μm cause a connected excluded area, while particles separated more than d > 2.8 μm will result in two separate excluded areas. Free area A that is fully enclosed by excluded area is denoted as a mesh of the network if it exceeds the area A > 2.4 μm2. The free area of a triangle of three connected colloidal particles is smaller than this threshold. A free area below the size of A < 2.4 μm2 is hence called an interstitial.In Fig. 2 we plot the number of meshes n in the field of view of the microscope as a function of time. The number of meshes n rapidly increases during the nucleation process (0 < t < 2 s) of the network, reaching a maximum after about two seconds. Afterwards the coarsening process begins and the number of meshes decreases exponentially (solid line in Fig. 1) with a decay time of τ = 35 s.
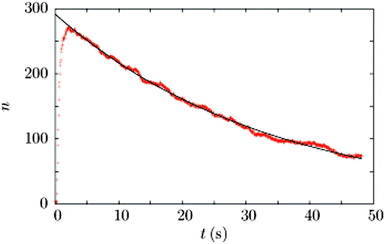 | ||
| Fig. 2 Time evolution of the number of meshes n (red datapoints). The solid black line is a fit to the falling part of the curve, using an exponential decay with time constant τ = 35 s. | ||
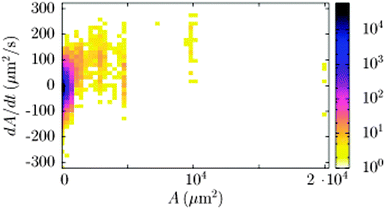
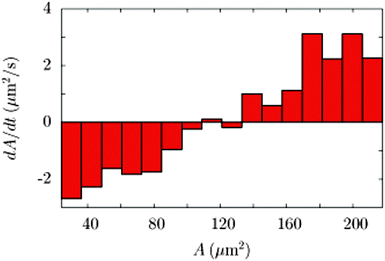
The area of an individual mesh can change with time. In Fig. 3 we show the occurrence of meshes of a size A having a growth rate dA/dt. There is a broad distribution of growth rates for small sized meshes. The distribution somewhat narrows for larger meshes and peaks at positive growth rates. The mean growth rate as a function of the size of the mesh is depicted in Fig. 4. On average, sub-critical meshes below the critical mesh-size Ac = 120 μm2 shrink and super-critical meshes above the critical mesh-size grow. The dividing mesh size separating growing from shrinking meshes is corresponding to an area having the capacity of incorporating roughly 20 colloidal particles.
The fate of sub-critical meshes is to collapse into a cluster, reducing the number of persisting meshes. On the time scale of the experiments, coalescences of super-critical meshes are very rare. Coalescence processes of super-critical meshes are important on much larger time scales. The focus of the current work is not the formation of the finally stable membrane where coalescence processes dominate, but the coarsening of the virgin network, where sub-critical mesh collapse processes are more important.
4 Discussion
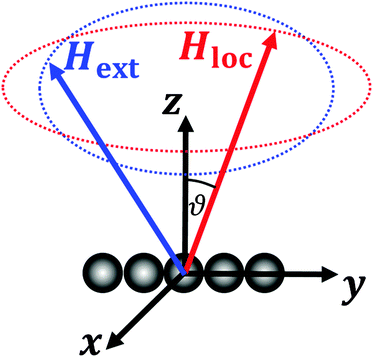
The coarsening dynamics happens via the disappearance of meshes. In the time frame investigated, the overwhelming amount of disappearances of meshes occurs via the collapse of small size meshes into clusters. The growth direction of the structures depends on their local anisotropies which cause local anisotropies of the magnetic field. We can describe the relation between the local and the external magnetic field using the demagnetization tensor. Only the anisotropic traceless part of the demagnetization tensor leads to a non-vanishing time average of the dipole interaction of a particle at this particular location with its surroundings. Whether this interaction is attractive or repulsive is determined by the sign of the eigenvalue of the traceless part of the demagnetization tensor. The demagnetization tensor in turn is a function of the local particle structure. Since the sum of all eigenvalues of the traceless part of the demagnetization tensor vanishes, there may be only one or two not three attractive directions. In a purely paramagnetic system a pair of particles causes a demagnetization field that tilts the local field with respect to the external field slightly toward the connecting line between the particles (Fig. 5). This tilt turns the initially indifferent dipole interactions slightly attractive in the direction along the connecting line. A self-consistent feedback loop amplifies the growth along the chain axis.The chain structure of the paramagnetic system is metastable. A paramagnetic particle adsorbing sideways onto a paramagnetic chain might alter the local magnetic field orientation such that instead of tilting the local field with respect to the external field toward the chain axis, the local field is tilted now toward the plane defined by the chain axis and the additional particle. This leads to the attraction of further paramagnets to the structure in the plane of adsorption. Chains cross linked with paramagnets will grow into a two dimensional membrane from the cross links. The eigenvalue of the traceless part of the demagnetization tensor along the adsorption direction (sideways, perpendicular to the chain) changes sign upon the adsorption. A transition from uniaxial prolate growth along the chain to planar oblate growth in the plane of adsorption occurs. The instability of chains to the sideways adsorption of paramagnetic particles causes the transient character of the network. The network starts to grow the finally stable membrane from the paramagnetic cross links.
We hence understand that the transient network structure arises because chains in the network are metastable structures, that transform into the final membrane by having to pass a saddle point in the energy landscape. The passing probability of such a saddlepoint is a kinetically determined quantity that cannot be computed solely using the energy landscape in conformational space. One might think that also the critical nucleation size of a mesh is such a kinetic quantity. We will show that this is not the case. The final membranous structure can be considered as one final node of the network surrounded by the last and biggest mesh. It is therefore clear that the meta-stability of the network and the stable membrane is the reason why the number of meshes decreases.
If the interactions were short range the system should be described macroscopically similar to other coarsening short range interacting systems. In two dimensional short range systems the line tension between the dense and the diluted phase is an intensive materials parameter independent of the shape of the structure. In long-range interacting system with super extensive line energy13 the line tension is not a material parameter and depends on the shape of the whole structure. In short-range case the bulk and line free energy of the system compete and give rise to an Ostwald ripening system with large sized meshes growing on the expense of smaller sized meshes, thereby increasing the dividing length scale between growing meshes and disappearing meshes as a function of time. Instead the system looks more like a nucleating system, with a critical size of nucleated meshes that shrink if they are below the critical nucleation size and grow via Ostwald-ripening once beyond the critical nucleation size.
In the paramagnetic colloidal system, dipole interactions between paramagnetic particles are long range interactions.13 The far field of a dipole decays with the third power of the inverse distance from the particle. The isotropic modulation of the external field lets the time average of the dipolar interactions vanish in an isotropic surrounding with only the correlations of the dipolar interactions surviving. The surviving correlated interactions are isotropic and similar to van der Waals interactions that decay with the sixth power of the inverse distance from the particle and they are thus short range.13 This behavior has been pointed out for our colloidal system in the work of Martin et al.8 From the short range van der Waals type of interactions one would expect the coarsening to follow an Ostwald ripening process. However, the surroundings only appear isotropic on length scales larger than the meshes, such that differently oriented long range dipolar interactions survive the time averaging procedures on those mesoscopic length scales.
We believe that the surviving long-range interactions on the mesoscopic scale cause the broad distribution of growth rates seen in Fig. 3, since there is a broad range of different particle surroundings of both prolate and oblate anisotropy. The competition of isotropic second order short range interactions with the long range time averaged dipolar pair interactions in the presence of an anisotropic arrangement of other colloidal particles causes a characteristic length scale. We test this idea by computing the time averaged energy (that we have regularized on the length scale 2a of the diameter of the beads to mimic the hard core repulsion part of the interactions) for a model mesh surrounded by particles having an excluded area A.
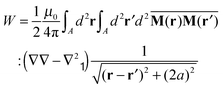 | (2) |
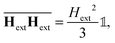 | (3) |
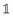 is the unit tensor in three dimensions). The flatness of the ring allows us to approximate the internal magnetic field of the ring as
is the unit tensor in three dimensions). The flatness of the ring allows us to approximate the internal magnetic field of the ring as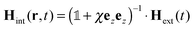 | (4) |
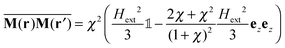 | (5) |
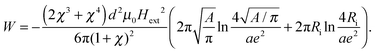 | (6) |
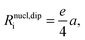 | (7) |
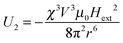 | (8) |
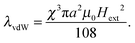 | (9) |
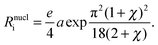 | (10) |
The major cause for the length scale of the network therefore is the competition of time averaged dipolar interactions surviving in the anisotropic surroundings of the two dimensional network with the short range isotropic second order pair interactions.
The dynamics of the transient network coarsening, however, is not only determined by energetic effects as suggested by Osterman et al.9 but also influenced by thermal fluctuations. In particular, the sideways adsorption of the first paramagnetic particle to a paramagnetic chain is associated with a change in sign of the eigenvalue of the traceless part of the demagnetization tensor. The chain switches from repelling the adsorbing particle to attracting the adsorbing particle. On energetic grounds one passes a saddle point of the energy landscape in conformational space. This corresponds to an activated process that would not occur without thermal fluctuations. It would also not occur with patchy particles15 whose bond energy is independent of the presence of other beads. Besides the energetic conditions Brownian fluctuations are playing an important role. The activation energies at the saddle point are proportional to the square of the magnetic moment of the particles and thus scale with the sixth power of the radius. We expect that the activation energy of larger particles can no longer be overcome such that the sideways adsorption of a particle to a chain does not occur. If on the other hand the particles are small also the desorption of a previously sideways adsorbed particle becomes possible. At fixed magnetic field there should be a window of particle sizes for which transient networks occur. At a fixed size of particles on the other hand we have to adapt the magnetic field amplitude accordingly to get a high activation barrier of desorption but a low activation barrier for adsorption. In this way the mobilities of the particles would not only set the timescale with which one passes a certain pathway but also choose a particular conformational pathway into the final equilibrium respectively non-equilibrium structure.
5 Conclusions
The competition of the long-range dipolar pair interaction renormalized by the presence of other particles creating an anisotropic surroundings with the short-range isotropic second order dipolar pair correlations defines a dividing length scale. Meshes smaller than this length are below the critical nucleation mesh size and hence shrink, while larger meshes grow on the expense of subcritical meshes. The Ostwald ripening on the scale of seconds and minutes is governed by this dynamics. Only a few processes of coalescence of meshes contribute to the coarsening in this regime. The coarsening is a dynamic process, while the critical nucleation mesh-size is determined by purely energetic reasons.Acknowledgements
We thank Ingrid Bauer and Dani de las Heras and Matthias Schmidt for stimulating discussion.References
- M. Seul and D. Andelman, Domain shapes and patterns – the phenomenology of modulated phases, Science, 1995, 267(5197), 476–483 CrossRef CAS PubMed.
- A. Hubert and R. Schäfer, Magnetic domains, the analysis of magnetic microstructures, Springer, Berlin, Heidelberg, New York, 2000, ISBN 3-540-64108-4 Search PubMed.
- H. M. McConnell, Structures and transitions in lipid monolayers at the air–water-interface, Annu. Rev. Phys. Chem., 1991, 42, 171–195 CrossRef CAS.
- D. P. Jackson, R. E. Goldstein and A. O. Cebers, Hydrodynamics of fingering instabilities in dipolar fluids, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 298–307 CrossRef CAS.
- A. J. Dickstein, S. Erramilli, G. E. Goldstein, D. P. Jackson and S. A. Langer, Labyrithine pattern-formation in magnetic fluids, Science, 1993, 261(5124), 1012–1015 CAS.
- W. Ostwald, Über die vermeintliche Isomerie des roten und gelben Quecksilberoxyds und die Oberflächenspannung fester Körper, Z. Phys. Chem., Stoechiom. Verwandtschaftsl., 1900, 34, 495 Search PubMed.
- I. M. Lifshitz and V. V. Slyosov, The kinetics of precipitation from supersaturated solid solutions, J. Phys. Chem. Solids, 1961, 19, 35–50 CrossRef.
- J. E. Martin, R. A. Anderson and R. L. Williamson, Generating strange magnetic and dielectric interactions: classical molecules and particle foams, J. Chem. Phys., 2003, 118, 1557 CrossRef CAS.
- N. Osterman, I. Poberaj, J. Dobnikar, D. Frenkel, P. Ziherl and D. Babic, Field-Induced Self-Assembly of Suspended Colloidal Membranes, Phys. Rev. Lett., 2009, 103, 228301 CrossRef CAS PubMed.
- P. Tierno, R. Muruganathan and T. M. Fischer, Viscoelasticity of dynamically self-assembled paramagnetic colloidal clusters, Phys. Rev. Lett., 2007, 98, 028301 CrossRef PubMed.
- P. Heinig and T. M. Fischer, Dipolar foams in Langmuir monolayers dry at low bubble fraction, J. Phys. Chem. B, 2003, 107, 11757–11762 CrossRef CAS.
- J. E. Martin and K. J. Solis, Fully alternating, triaxial electric or magnetic fields offer new routes to fluid vorticity, Soft Matter, 2015, 11, 241 RSC.
- We use the thermodynamic definition of short and long range interactions. Short range interactions cause material parameters that become independent of the shape in the thermodynamic limit. Here a shape independent line tension, with an extensive free energy, proportional to the perimeter of the object, arises from the van der Waals type of interactions. Long range interactions cause superextensive free energies and the line tension is not a material parameter but depends on the shape of the object.
- P. Tierno, P. Reimann, T. H. Johansen and F. Sagus, Giant Transversal Particle Diffusion in a Longitudinal Magnetic Ratchet, Phys. Rev. Lett., 2010, 105, 230602 CrossRef PubMed.
- K. Müller, N. Osterman, D. Babic, C. N. Likos, J. Dobnikar and A. Nikoubashman, Pattern Formation and Coarse-Graining in Two-Dimensional Colloids Driven by Multiaxial Magnetic Fields, Langmuir, 2014, 30, 5088–5096 CrossRef.
| This journal is © The Royal Society of Chemistry 2016 |