Electric field generation of Skyrmion-like structures in a nematic liquid crystal

Abstract

Skyrmions are particle-like topological objects that are increasingly drawing attention in condensed matter physics, where they are connected to inversion symmetry breaking and chirality. Here we report the generation of stable Skyrmion-like structures in a thin nematic liquid crystal film on chemically patterned patchy surfaces. Using the interplay of material elasticity and surface boundary conditions, we use a strong electric field to quench the nematic liquid crystal from a fully aligned phase to vortex-like nematic liquid crystal structures, centered on patterned patches, which carry two different sorts of topological defects. Numerical calculations reveal that these are Skyrmion-like structures, seeded from the surface boojum topological defects and swirling towards the second confining surface. These observations, supported by numerical methods, demonstrate the possibility to generate, manipulate and study Skyrmion-like objects in nematic liquid crystals on patterned surfaces.

---

1. Introduction

Skyrmions, originally introduced by Tony Skyrme to describe baryon fields,¹ are particle-like topological objects that are increasingly drawing attention in condensed matter physics. Skyrmions were observed in quantum Hall systems² and Bose–Einstein condensates.³ They appear in chiral magnets with Dzyaloshinskii–Moriya spin interaction,⁴ such as the helical ferromagnets MnSi⁵ and FeCoSi,⁷ or on symmetry breaking surfaces.⁷ Because of their nanometer size and topologically-protected stability, Skyrmions in helical ferromagnets are particularly interesting for applications in spintronics for the manipulation and storage of data.⁷ Recent spin-polarized scanning tunneling experiments in 2D ferromagnets have demonstrated the controlled generation of single Skyrmions.^6–9 Although Skyrmion-like structures have been obtained in air and room temperature,¹⁰ in most of the cases Skyrmions in solid state systems are limited to ultra-high vacuum environments and very low temperatures, which makes both their study as well as their application rather difficult.

Skyrmions and other topologically protected structures, such as hopfions, were observed recently in chiral nematic liquid crystals.^11,12 It was predicted that the blue phases of highly chiral liquid crystals could support stable Skyrmion structures.¹³ The micrometer-size and appearance of such structures in liquid crystals would allow much more direct and easy experimental investigations, but so far no experimental observation has been reported. Recently, light-controlled generation and observation of topological charges pinned on a microfiber in a nematic liquid crystal (NLC) was reported.¹⁴ Patterned patchy surfaces can be used in sensing applications,^15,16 they show impressive switching times,^17,18 or can be used in controlled generation of topological charges, as we demonstrate in this paper. The topological charge is a conserved quantity attributed to topological entities,^19,20 but has not been discussed in the context of Skyrmions yet. In this paper we demonstrate how the frustration imposed by patterned patchy surfaces leads to the controlled generation of Skyrmion-like structures in a geometrically confined non-chiral nematic liquid crystal. We show by computer simulations and experiments that the interplay between surface pattern, material constants and electric field allows for a rich variety of topological states, that are not only fascinating from a fundamental point of view but also have potential for photonic applications. We discuss the topological charge of Skyrmions on patchy surfaces and demonstrate charge conservation.

2. Experimental

2.1 Preparation of patterned SAM-on-ITO surfaces

The ITO substrates were purchased from PGO Germany (Product code: CEC100S). The ITO slides were ultrasonically cleaned with detergent (ALCONOX), base bath cleaning solution (KOH and ethanol), MilliQ-water (18.1 MΩ cm), followed by acetone (99.8%, Merck) and 2-propanol (Fluka 99.9%). At last, they were blown dry with N₂ and treated with a UV/ozone cleaner (Novascan Technologies, Inc.). 0.5 mM octadecyltrimethoxysilane (OTMS) (≥90%, Sigma Aldrich) solution was prepared by dissolving OTMS in toluene (≥99.97%, Fisher Scientific). After the OTMS solution was prepared, the cleaned ITO substrates were immediately submerged in the solution for 2 hours at 60 °C, under weak stirring. The substrates were then ultrasonically rinsed in refreshed toluene to remove any non-covalently bonded molecules. Finally, they were blown dry with N₂. Half of the prepared SAM-on-ITO plates were irradiated with an Argon Fluoride excimer laser (193 nm) through a contact-photolithography mask presenting different patterns. In details we used a squared pattern characterized by 4 × 4 μm² square size and 10 μm periodicity, which is a significant improvement in the patterning technique, compared to previous reports.¹⁷ A total dose of ∼9 J cm⁻² was applied to degrade the OTMS. To remove the photo-cleaved products, the patterned substrates were soaked in ethanol and finally blow dried with N₂.

2.2 LCs cells fabrication

LCs cells were assembled by gluing a patterned and a not patterned SAM on ITO surface with a UV-curable glue (NOA65, Norland). The cell gap of 4.0 μm was obtained by using embedded particles (Licristar, Merck) dispersed into the glue. The cells were then filled with LC materials BL087 (Merck) by capillary force above the isotropic-nematic temperature (T_IN-BL087 = 89 °C) at 100 °C for a few minutes before they were cooled down to room temperature. The cooled cells were finally sealed with epoxy glue (Epoxy Rapid, Bison). Such an approach already proved useful for functionalization of surfaces interacting with NLC for switching optimization and orientation control.^18,21

2.3 Characterization techniques

The LCs cells were first characterized by an optical microscope (Olympus BX60) viewed in filtered (Olympus IF 546) white-light transmission in cross condition between polarizer and analyser. To perform fluorescence confocal polarizing microscopy (FCPM), fluorophores molecules in μM concentration (2.5 μM Red-Nile, Sigma Aldrich) were previously mixed with the BL087 LC to fill the cells. A 530 nm laser was scanned on top of the LC cell surface and the fluorescence signal filtered through a Schott glass OG570.

3. Results and discussion

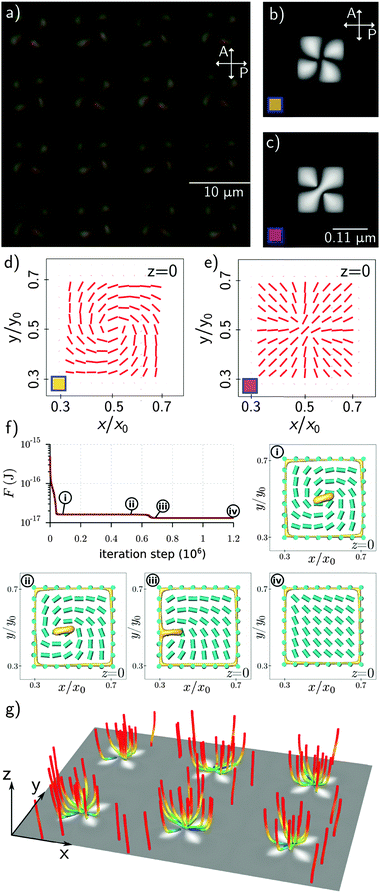
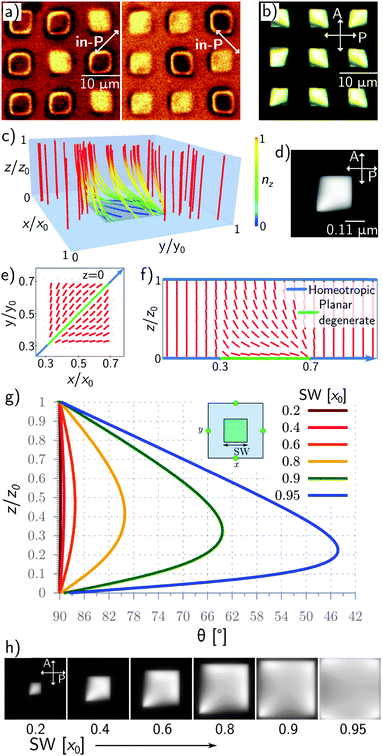
Fig. 1a shows the fluorescence confocal polarizing microscope (FCPM) images of such a surface-patterned NLC cell, with the microscope optics focused onto the patterned surface. The fluorescence is due to the dye molecules, which are dissolved in the NLC and align locally their radiative dipole moment along the NLC molecules. Bright regions of the Fig. 1a therefore correspond to the alignment of the NLC molecules along the polarization of the light that excites the fluorescence, and dark regions indicate the perpendicular local molecular alignment. One can clearly distinguish two optically different types of the NLC squares in the two panels in Fig. 1a, which alternate from bright to dark and vice versa, when the polarization is switched by 90°. Because the bright and dark squares appear when the polarization of the fluorescence-excitation light is along the diagonals of the squares, we conclude that the NLC molecules are dominantly aligned on the patterned squares along their diagonals.

Fig. 1 Surface square-patterned LC cells as advanced birefringent material layers. The squared pattern sample is characterized by 4 × 4 μm² square patches (periodicity 10 μm and cell thickness 4 μm). (a) CPM images of a squared patterned LC cell (4 × 4 μm²) changing the polarization of the incoming light (λ = 530 nm). (b) Optical Microscopy images of a similar sample viewed in white-light transmission between crossed polarizer and analyser. (c) Numerically calculated 3D-representation of the LC director in a single patterned square surrounded by homeotropically aligned LC and (d) its optical microscopy polarization micrograph. (e and f) Show two sections of the 3D picture in (a), a top view at z = 0 (e) and a side-view (f) along the diagonal highlighted in (e). (g) Director tilt angle θ across the vertical axis at the border of the cell (marked by green dots) for various relative widths of a square patch (SW). Due to periodic boundary conditions and the symmetry of the diamond-like structures, θ is the same in all of the four marked points. (h) Increase of the transmittance due to increased patch size.

Fig. 1b shows the transmission optical micrographs of the patterned NLC texture between crossed polarizers. In the regions away from the pattern, the image is dark, because the optical axis of the NLC is there directed perpendicularly to the cell's surfaces. Within the squares, the bright regions indicate an effective tilting of the optical axis of the NLC from the cell normal. One can clearly distinguish three optically distinct images with diamond-like shapes, which leads to the conclusions that – due to the symmetry of the pattern – there are actually four possible and distinctive LC structures on square-patterned surfaces. One should note that the FCPM images in Fig. 1a show the ordering of the NLC molecules within the surfaces of the squares, whereas the birefringent image in Fig. 1b reflects the volume distribution of the birefringent NLC material on the patterned surface. Details of the NLC structure on a planar degenerate square pattern in a homeotropic NLC surrounding are revealed by performing numerical modelling using the free-energy minimization of the elastically deformed nematic director field on a square-patterned surface. Specifically, we use the Landau–de Gennes free energy formulation for the bulk nematic elasticity and degree of order, and combine it with Rapini–Papoular like homeotropic and Fournier–Galatola surface free energies for homeotropic and degenerate planar surface anchoring,^22,23 respectively (for more details please refer to the ESI† algorithm). The following numerical parameters are used in the calculations: A = −0.295 × 10⁶ J m⁻², B = −2.13 × 10⁶ J m⁻², C = 1.73 × 10⁶ J m⁻² (which gives the equilibrium order parameter S_eq = 0.6). The elastic constants are K₁ = 12.1 pN, K₂ = 5.9 pN, K₃ = 23.7 pN. The surface anchoring strength was set to W^hom = 0.02 J m⁻² for homeotropic anchoring, and W^deg₂ = 0.01 J m⁻² for planar-degenerate anchoring. The equilibrium order parameter was preferred at the anchoring surfaces. The molecular dielectric anisotropy was set to ε^mol_a = 34.2. The 3-dimensional representation of the nematic structure with a minimum free-energy is shown in Fig. 1c, with two different cross-sections in Fig. 1e and f. Fig. 1e shows the top-view of the first layer of the nematic molecules on the planar degenerate square, which clearly shows a dominant molecular alignment along the diagonal of the square. This result is in perfect agreement with the FCPM images in Fig. 1a, which also shows two possible surface alignments of NLC molecules along the two diagonals of each square. The side view of the numerically calculated structure in Fig. 1f reveals a gradual increase of the local molecular tilt to match the transition from the planar alignment on the (lower) patterned square to the vertical alignment on the neighbouring (upper) glass surface. Based on the calculated NLC director distribution, we calculated the optical polarization microscopy micrograph of such a structure between crossed polarizers using the Jones matrix approach. The result is shown in Fig. 1d and is in qualitative good agreement with the experimental images, shown in Fig. 1b. Calculations has been performed to investigate also the degree of cross-talk between neighbouring cells across the cell thickness (z-axis). We explore the amount of cross-talk as a function of the width of a planar degenerate patch, where cross-talk is characterized by the director tilt angle at the cell boundary. The results in Fig. 1f show that for a patch width of 0.8 of the periodicity or larger, the director tilt angle at the boundary deviates from the vertical alignment for more than 10°, which potentially compromises the entire sample. However, large patch sizes are desirable to increase the pixel brightness, as shown in Fig. 1h. This means that to keep the homeotropic alignment intact, i.e. minimize the cross-talking among different planar compartments, we can double the square size and so double the pixel brightness.

From the perspective of topology of the director field, the experimentally and numerically obtained equilibrium structures are trivial and effectively display no topological defects. Topological defects are regions of the nematic liquid crystal, where the direction of molecular ordering is not, or is ill-defined. There is no such thing in the structures in Fig. 1a–f, except for the border region between the homeotropic and planar surface at the bottom surface. At this edge region, the nematic degree of ordering drops on account of the two counter-aligning directions, forming effective surface boojum defect structures, that are known from Janus systems.¹⁸Fig. 2a shows how the inhomogeneously aligned NLC molecules in the patterned square respond to an external electric voltage from 2 to 4 V, applied across the 4 μm-thick NLC cell. The torque imposed by the electric field tends to align the NLC molecules perpendicularly to the surface and pushes the dark edges of the polarization micrograph towards the center. The dark areas are then increased because the average tilt angle increases and the optical axis is more and more aligned perpendicularly to the glass plates. In the intermediate regime, this is accompanied by a clear change in the birefringence colors, which reflects the gradual increase of the tilt of the optical axis.

Fig. 2 Electric-field tunability of birefringence. (a) Experimental optical microscopy images viewed in white light transmission between crossed polarizers as a function of the applied voltage. (b) Simulated optical microscopy images as a function of the applied voltage and the elastic anisotropy. On the vertical axis the electric field is increased from 2 to 4 V, while on the horizontal axis the elastic constants of the simulated LC have been changed. Left column K₁ = 12.1 pN, K₂ = 5.9 pN, 2K₃ = 47.4 pN. Central column K₁ = 12.1 pN, K₂ = 5.9 pN, K₃ = 23.7 pN. Right column K₁ = K₂ = K₃ = K_av = 13.9 pN. (c) Director field at z = 0 and U = 3 V in elastically anisotropic (K₁, K₂, K₃) regime shows modulations in the lateral directions, compared to the uniform response in the elastically anisotropic (K_i = K̄) regime. (d) The director tilt angle θ across the center-point of the patterned cell (marked by a circle in (c) as a function of four applied voltages. (e) Simulated transmittance as a function of the applied field at the center point in (c) (yellow line) and as an average over all the square in (c) (brown line). Under strong electric fields the average tilt angle increases causing a significant drop of transmittance.

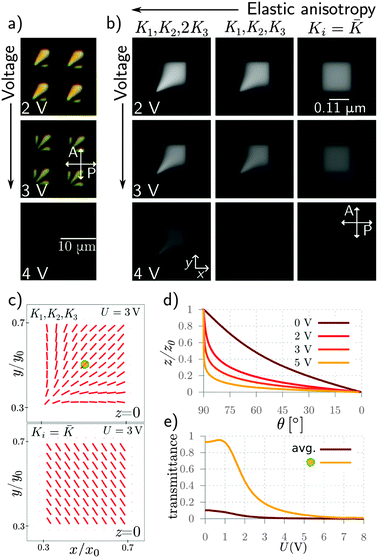
Fig. 2b shows the numerically calculated optical micrographs of such a structure between crossed polarizers, where not only the applied field was varied, but also the elastic constants of the NLC material. The experimental micrographs are fairly well reproduced by considering three different elastic constants (see middle column in Fig. 2b) using the elastic anisotropy K₃ = 2K₁ = 4K₂. If K₃ is increased even higher, the electric field effect is even more pronounced (see left column in Fig. 2b) as it pushes the dark edges of the polarization micrograph towards the center. However, when using equal elastic constants (see right column in Fig. 2), the square patched pixel, uniformly responds to the applied electric field, changing its brightness uniformly in the lateral direction without modulations. The director fields at 3 V in elastically anisotropic and isotropic regimes are shown in Fig. 2c. Detailed numerical investigation also reveals how the applied voltage suppresses the director deformation at a short length scale above the patterned surface (Fig. 2d), consequently darkening the transmission images (Fig. 2e). The transmission response shows little effect at moderate voltages (0–2 V) and a rapid fall towards zero transmission at higher voltages. Interestingly, the observed response in patterned cells shows that by choosing properly the nematic material, i.e. the elastic anisotropy, shape and intensity profile of the performing pixels can be finely tuned.

This gradual increase of the driving voltage results in fully reversible NLC structures on patterned squares, with no topological defects generated. However, it is well known that topological defects of diverse complexity can be generated in NLCs by quenching the material from the isotropic to the nematic phase via the Kibble–Zurek mechanism of charge production.^14,24–26 Similarly, defects in the NLCs can also be generated by applying a strong external electric field, which aligns the NLC molecules completely. If this is followed by a sudden decrease of the field, this could bring the NLC structure to a new equilibrium structure that could display a number of new-born topological defects. While at moderate fields one still sees a slightly colored patterned square (see Fig. 2a, third panel at 4 V), indicating that there is still a thin remnant layer of the NLC with its optical axis flat on the surface, this residual surface ordering is completely erased by applying 30 V, corresponding to an electric field of 7.5 × 10⁶ V m⁻¹. In this case a uniform homeotropic alignment is established despite the patterning and no more trace of planar aligned squares can be observed. Surprisingly, after switching-off this field, all the patterned squares attain a completely new and different structure which is shown in Fig. 3a. Instead of the diamond-like structure following the square diagonal, this novel structure clearly exhibits point topological defects, located in the center of each square. This is recognizable from the slightly spiraling dark brushes in Fig. 3a, displaying a vortex-like pattern. By rotating both the polarizer and analyzer, the dark brush and the vortex rotate, which is a clear indication of a point topological defect in the center of the square. Most likely, this point topological defect is located at the surface of the patterned square, which minimizes the total elastic distortion energy of the volume above the square. This is therefore a kind of surface “boojum” point defect, well known in liquid crystal colloids.²⁷ Note that in previous experiments on much larger patterns no boojum defects were reported.¹⁷ In order to elucidate the exact nature of these defect states, we performed numerical calculations starting from the initial director configuration of n = (y, −x, −z)/r and n = (x, y, −z)/r, respectively, and we have found many defect states. Two of these states with the lowest free energy, are presented in Fig. 3d and e. Here, the director configuration at the surface of the square is shown for each structure. The structure in Fig. 3d is a circulating director field with a point defect in the center, which is known as a circular surface boojum with a winding number +1 and the fractional topological charge of −1/2. The other most stable state is characterized by a −1 hyperbolic boojum defect in the center of the square pattern, carrying the opposite topological charge. A radial boojum can be understood as a local excitation in a uniform far-field, i.e. a Skyrmion-like object, which is initiated and stabilized by the patterned patchy surface. Such defect states are in principle thermodynamically unstable, because they usually require a higher free energy compared to the lowest, diamond-like state in Fig. 1e and f (1.23 and 1.31-times, respectively), which is leading to a spontaneous decay of these vortex-like states into the ground state (Fig. 1e and f). The no-flow approximation of the decay of a Skyrmion-like state is shown in Fig. 3f. During the decay process, a surface boojum and a disclination line at the homeotropic-planar anchoring interface reconfigure to form the equilibrium diamond-like state. Although the Skyrmion-like states spontaneously decay, we have numerically found that some of them could be stabilized in the strict elastic regime. By choosing K₁ = K₃ = 1/3 K₂₄ = 1/3 K₂ = 13.9 pN in our numerical calculations, the structure with a radial boojum becomes a state with the lowest energy. Therefore, in specific elastic regimes, new topological states with surface defects could spontaneously evolve into Skyrmion-like objects, presented in Fig. 3a. We have also tested numerically the stability of Skrymion structures under the application of an electric field in the vertical direction. Previously used initial director configurations were let to relax at the voltage of 5 V. The state characterized by a −1 hyperbolic boojum defect has quickly relaxed to the diamond-like equilibrium configuration, while a state with a circular surface boojum became metastable and did not relax to the global equilibrium structure even after the relaxational procedure was let to run for a long time. The surface confinement, or, more specifically, the frustration of the surface orientation of NLC molecules on patterned surfaces, can lead to the formation of Skyrmion-like structures. It seems that each surface square acts as a topological “seed” for the formation of a localized, particle-like structure of a Skyrmion. It is well known that the overall topological charge of the system has to be conserved at all times, and the question of conservation of the charge arises in our experiments. Namely, the boojum defect in the center of this Skyrmion-like object carries some topological charge – following the standard convention, such radial surface boojums have a fractional-charge of +1/2,²⁸ whereas there are no distinct defects and therefore no-net topological charge in the diamond-like equilibrium structures shown in Fig. 1. This difference in the topology between the Skyrmion-like structures and the no-Skyrmion profiles is compensated by the structure of the field at the border between the homeotropic and planar anchoring. Effectively, in the no-Skyrmion profile, the opposite sites of the border across the patch compensate one-another, by locally having opposite winding numbers (e.g. see Fig. 1f where the border surface defects locally have +1/4 and −1/4 winding number).

Fig. 3 Complex Skyrmion-like birefringent phases stabilized by surface patterns. (a) Experimental optical microscopy image viewed in white light transmission between crossed polarizers after the application of a potential of 30 V. (b and c) Are simulated optical microscopy images for two defect states with the lowest free energy; (d and e) are the corresponding director fields at the patterned surface (z = 0). (f) Free energy relaxation process of a Skyrmion state with insets showing the director field (cyan cylinders) and scalar order parameter (yellow isosurfaces at S = 0.5). Panels (i–iv) show: (i) formation of a boojum surface defect from the initial conditions, (ii) drift of a boojum defect towards the disclination line, (iii) annihilation of the surface defect line and the boojum defect, and (iv) the formation of a diamond-like equilibrium state. (g) An array of stabilized radial boojums effectively forming a complex birefringent layer stabilized by the anchoring patches.

However, in the Skyrmion profile, the opposite border regions have locally equal winding numbers, effectively giving surface line-defect profiles, that compensate for the topological charge carried by the centre-of-the-patch boojum defects. More generally, the results presented here show that nematic liquid crystals on patchy surfaces can allow for very versatile topological structures, as the surface defects at the border regions can compensate for very different bulk profiles, and even change their effective topological charge.

4. Conclusions

This work demonstrates that surface patterned geometries may give controlled access to novel, surface-stabilized topological structures of the nematic liquid crystals. In our experiments we used patchy surfaces with a simple geometry and it is straightforward to imagine that surface patterning with more topological complexity could give rise to much more complex nematic structures. These advanced material structures can be engineered to yield unconventional photonic responses because the material singularities are known to be transferred into the singularities of the light wave propagating in such a material.²⁶

Acknowledgements

This work was in part supported by the Slovenian Research Agency (ARRS) contracts P1-0099 and J1-6723 (I. M.), by the Netherlands Organization of Scientific Research (NWO) and by the European Research Council under the European Union's Seventh Framework Program, ERC Grant Agreement 339813 (EXCHANGE).

References

1. T. H. R. Skyrme, Nucl. Phys., 1962, 31, 556–569.
2. A. Schmeller, J. P. Eisenstein, L. N. Pfeiffer and K. W. West, Phys. Rev. Lett., 1995, 75, 4290–4293.
3. U. Al Khawaja and H. Stoof, Nature, 2001, 411, 918–920.
4. N. S. Kiselev, A. N. Bogdanov, R. Schäfer and U. K. Rößler, J. Phys. D: Appl. Phys., 2011, 44, 392001.
5. S. Mühlbauer, B. Binz, F. Jonietz, C. Pfleiderer, A. Rosch, A. Neubauer, R. Georgii and P. Böni, Science, 2009, 323, 915–919.
6. S. Heinze, K. Von Bergmann, M. Menzel, J. Brede, A. Kubetzka, R. Wiesendanger, G. Bihlmayer and S. Blügel, Nat. Phys., 2011, 7, 713–718.
7. X. Z. Yu, Y. Onose, N. Kanazawa, J. H. Park, J. H. Han, Y. Matsui, N. Nagaosa and Y. Tokura, Nature, 2010, 465, 901–904.
8. J. Sampaio, V. Cros, S. Rohart, A. Thiaville and A. Fert, Nat. Nanotechnol., 2013, 8, 839–844.
9. N. Romming, C. Hanneken, M. Menzel, J. E. Bickel, B. Wolter, K. Von Bergmann, A. Kubetzka and R. Wiesendanger, Science, 2013, 341, 636–639.
10. M. Finazzi, M. Savoini, A. R. Khorsand, A. Tsukamoto, A. Itoh, L. Duò, A. Kirilyuk, Th. Rasing and M. Ezawa, Phys. Rev. Lett., 2013, 110, 177205.
11. P. J. Ackerman, R. P. Trivedi, B. Senyuk, J. V. de Lagemaat and I. I. Smalyukh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 012505.
12. P. J. Ackerman, J. van de Lagemaat and I. I. Smalyukh, Nat. Commun., 2015, 6, 6012.
13. J.-I. Fukuda and S. Žumer, Nat. Commun., 2011, 2, 246.
14. M. Nikkhou, M. Škarabot, S. Čopar, M. Ravnik, S. Žumer and I. Muševič, Nat. Phys., 2015, 11, 183.
15. F. Zuo, Z. Liao, C. Zhao, Z. Qin, X. Li, C. Zhang and D. Liu, Chem. Commun., 2014, 50, 1857–1860.
16. E. Brasselet, N. Murazawa, H. Misawa and S. Juodkazis, Phys. Rev. Lett., 2009, 103, 103903.
17. J. Zhang, M. I. Boamfa, A. E. Rowan and T. Rasing, Adv. Mater., 2010, 22, 961–965.
18. L. Cattaneo, P. H. J. Kouwer, A. E. Rowan and Th. Rasing, J. Appl. Phys., 2013, 113, 014503.
19. N. D. Mermin, Rev. Mod. Phys., 1979, 51, 591–603.
20. H. Stark, Phys. Rep., 2001, 351, 387.
21. L. Cattaneo, J. Zhang, M. Zuiddam, M. Savoini and Th. Rasing, Nano Lett., 2014, 14, 3903–3907.
22. M. Ravnik and S. Žumer, Liq. Cryst., 2009, 36, 1201.
23. S. Čopar, M. Ravnik and S. Žumer, Materials, 2014, 7, 4272–4281.
24. T. W. B. Kibble, J. Phys. A: Math. Gen., 1976, 9, 1387–1398.
25. W. H. Zurek, Phys. Rep., 1996, 276, 177–221.
26. I. Chuang, R. Durrer, N. Turok and B. Yurke, Science, 1991, 251, 1336–1342.
27. I. I. Smalyukh, S. Chernyshuk, B. I. Lev, A. B. Nych, U. Ognysta, V. G. Nazarenko and O. D. Lavrentovich, Phys. Rev. Lett., 2004, 93, 117801.
28. G. P. Alexander, B. G. G. Chen, E. A. Matsumoto and R. D. Kamien, Rev. Mod. Phys., 2012, 84, 497.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm01726b

‡ Current address: ETH Zürich, Auguste Piccard Hof-1, 8093 Zürich, Switzerland. E-mail: E-mail: claura@phys.ethz.ch

---