Structure elucidation of a complex CO₂-based organic framework material by NMR crystallography

Abstract

A three-dimensional structural model of a complex CO₂-based organic framework made from high molecular weight, self-assembled, flexible and multi-functional oligomeric constituents has been determined de novo by solid-state NMR including DNP-enhanced experiments. The complete assignment of the ¹⁵N, ¹³C and ¹H resonances was obtained from a series of two-dimensional through space and through bond correlation experiments. MM-QM calculations were used to generate different model structures for the material which were then evaluated by comparing multiple experimental and calculated NMR parameters. Both NMR and powder X-ray diffraction were evaluated as tools to determine the packing by crystal modelling, and at the level of structural modelling used here PXRD was found not to be a useful complement. The structure determined reveals a highly optimised H-bonding network that explains the unusual selectivity of the self-assembly process which generates the material. The NMR crystallography approach used here should be applicable for the structure determination of other complex solid materials.

---

Introduction

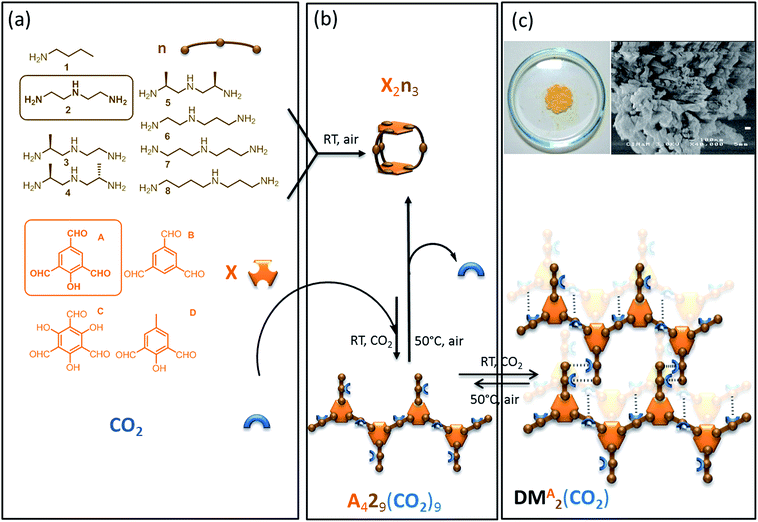
The last decades have seen an explosive growth in the production of rationally designed supramolecular materials resulting from directed self-assembly of molecular building units. Among these self-assembled molecular networks displaying promising properties, one can cite metal organic frameworks (MOFs),¹ obtained by connecting metal containing secondary units with organic linkers, and organic supramolecular solids² resulting from the connection of carbon-based building blocks. Their synthesis is based on attractive one-pot self-assembly processes which illustrate the concept of molecular tectonics.^3–5 Self-organization results from the structure of and the interactions between the rigid building blocks.⁶ Short-range, strong anisotropic interactions drive self-organization across length scales from the molecular and nano-scale level⁷ up to the micro- and milli-scale levels.^8–11 The well-defined building units, coupled with the thermodynamic control of the self-assembly process, often lead to long range structural order i.e. to highly crystalline solids.¹² X-ray diffraction can frequently be used to characterize the structural features of these self-assembled networks if they are sufficiently regular.

Such supramolecular materials can have tunable physical and chemical properties, with cavities whose size and shape are easily manipulated.¹³ However, the complete structural characterization of increasingly complex systems, that is essential to determine structure–activity relations and to then rationally improve properties, remains a considerable challenge. This notably often prevents exploration of molecular assemblies based on more flexible objects involving multiple functionalities.

In this context we have recently synthesized and described a self-assembled supramolecular solid which results from the one-pot thermodynamically controlled simultaneous reaction of two organic building blocks and CO₂ (Scheme 1).¹⁴ Notably, this reversible CO₂-based organic framework is produced by aggregation of flexible self-complementary oligomeric objects. As illustrated in Scheme 1 these oligomeric building blocks are themselves assembled in situ from the basic components, including CO₂. The covalent assembly process of the oligomers consists in the simultaneous and reversible formation of 20 carbon–nitrogen bonds of three different chemical types (imine, aminal and carbamate). Since the final material results from the packing of oligomers that were themselves spontaneously assembled from elementary units through the reversible formation of covalent bonds, this supramolecular solid is in the class of what have been dubbed “dynamic materials” by Lehn.^15–17 This particular dynamic material possesses original properties: both the material and its constitutive oligomers dissociate upon CO₂ departure in a cooperative manner, and the assembly process is found to be extremely selective in terms of building block incorporation.^18,19 Both features (reversibility and selectivity) are desirable in the context of CO₂ capture and use, as well as for selective extraction of valuable molecules from waste.²⁰ However, the material precipitates from solution as an insoluble nano-crystalline powder, which is not amenable to standard molecular level characterization. To address this problem we previously used solid-state Nuclear Magnetic Resonance (NMR) to propose basic structural features for this supramolecular system.¹⁴

Scheme 1 Double self-assembly process leading to the discovery of a 3-component dynamic material based on CO₂. (a) Elementary building blocks such as polyamines n (brown connector) and polyaldehydes X (orange hexagon) self-assemble in methanol at RT under air to yield 2-component oligomers (b), mainly X₂n₃ capsules. In the case X = A and n = 2 in the same conditions, exposure to CO₂ (blue arch) as a third building block spontaneously yields the 3-component soluble “oligodynablock” A₄2₉(CO₂)₉. This self-assembled species then itself spontaneously further self-assembles into the corresponding insoluble dynamic material DM^A₂(CO₂) as a nanocrystalline powder (electron micrograph, white bar: 100 nm) (c). Heating to around 50 °C induces CO₂ release and disassembly of the dynamic material which converts back into A₂2₃.

Here we further explore the three-dimensional molecular structure of the nano-crystalline dynamic material using an NMR crystallography approach,^21,22 and we evaluate the pertinence of powder X-ray diffraction (PXRD). Solid-state NMR spectroscopy complements diffraction methods and has recently developed into a versatile tool to determine the structures of both inorganic and molecular solids.^23–34 In combination with crystal structure prediction methods and DFT chemical shift calculations, NMR chemical shifts have recently been used to determined de novo crystal structures.²³ In particular in the context of supramolecular solids, solid-state NMR and DFT calculations have been used to explore hydrogen bonding and molecular structure in organic supramolecular systems^35,36 and to characterise structural features in MOFs, including determination of conformation changes upon adsorption or to observe the dynamic events that govern host–guest interactions.^37–42 Most recently, the superstructure of a substituted zeolitic imidazolate framework (ZIF) type MOF was elucidated by combining solid-state NMR, PXRD, and DFT calculations of NMR parameters from potential model structures.⁴³

Notably very rapid progress has recently been made by combining sophisticated spectral assignment strategies with state-of-the-art Density Functional Theory (DFT) chemical shift calculation methods. Today, this provides a platform for analysis of both ¹³C and ¹⁵N spectra,^44–46 as well as of ¹H shifts.^{22–24,47–51}

Following this general approach, here MM-QM (molecular mechanics-quantum mechanics) calculations were used to generate several different model structures of the dynamic material. The model structures were then evaluated by comparing multiple experimental and calculated NMR and PXRD parameters. A detailed structural model is proposed for the individual oligomeric constituents of the material including their exact sequence, conformation, and potential packing.

Results and discussion

Synthesis of the dynamic material

Simple molecular building blocks such as polyamines and polyaldehydes are well-known to spontaneously interconnect with each other in mild conditions (room temperature, no catalyst, open air, undistilled solvents) through the formation of reversible C–N bonds (single: aminal; double: imine) to generate dynamic combinatorial libraries.

The objects assembled from these two classes of components using reversible or dynamic covalent bonds⁵² are referred to as “oligo-dynablocks”^53–55 as they can themselves be building blocks (or dynamic tectons) to generate supramolecular structures. Here, this second level of assembly can be triggered by exposure to CO₂ which can post-functionalize the two-component oligomers. CO₂ reversibly reacts with primary or secondary amines yielding ammonium carbamate ion pairs. CO₂ exposure hence converts neutral objects into zwitterionic species. The CO₂-postfunctionalization can perturb the pre-equilibrated 2-component system and induce a redistribution of the populations toward one or several stable 3-component objects. Formation of a solid network is then a potential driving force that can displace the equilibria and select a self-complementary post-functionalized species.⁵⁶

Twenty-eight libraries corresponding to the various combinations of polyamines n(2–8) and polyaldehydes X(A–D) were screened for the formation of a dynamic material induced by reversible CO₂-postfunctionalization (Scheme 1). In the absence of CO₂, the 2-component systems were dominated by low-molecular weight entropically favoured soluble oligomers (objects involving two aromatic units at most), with the capsule made from two aldehydes and three polyamine units noted X₂n₃ being the major adduct as indicated by ESI-MS analysis (Scheme 1a and b).⁵⁷ For all combinations except one, this composition remained unchanged when CO₂ was introduced. In contrast, polyamine n = 2 and polyaldehyde X = A lead to the quantitative formation of a single 3-component dynamic material which precipitated upon CO₂ exposure as a nano-crystalline solid and re-dissolved upon gentle heating (Scheme 1b and c). As reversible linkages were used to assemble the building blocks, their average stoichiometry within the material was precisely determined by titration (¹H solution NMR for A and 2; volumetric analysis for CO₂) after acid hydrolysis of the dried powder. While 1D solid-state NMR confirmed that trialdehyde A and CO₂ were both covalently connected to the diethylenetriamine building block 2, the titration revealed that the oligo-dynablocks constituting the materials were mostly linear oligomers made of four aromatic units A condensed with nine diethylenetriamine chains 2 each bearing one molecule of CO₂ (noted A₄2₉(CO₂)₉, Scheme 1b). Thermogravimetric analysis coupled to mass spectrometry measurements additionally revealed the presence of substantial amounts of water (15 percent in mass). The water is presumably adsorbed in layers rather than integrated into the framework of the zwitterionic material as it could be entirely expulsed by heating at 70 °C under atmospheric pressure for several minutes without modification of the solid-state ¹³C CP-MAS solid-state NMR spectrum. No high molecular weight 3-component objects were detected in the mother liquor, nor was the A₄2₉ precursor present in the parent 2-component library before CO₂ exposure. The oligo-dynablocks A₄2₉(CO₂)₉ are therefore clearly stabilized by their intermolecular packing within the solid network formed.

When the stoichiometry between the building blocks A and 2 was changed, their titration after cleavage of the resulting material revealed that the average measured length of the oligomers constituting the material changed correspondingly, in agreement with equilibrium displacement rules. As a consequence, we conclude that the chain length in the objects that make up the dynamic material may display some degree of dispersity around the major chain length of 4. The analysis of the structure of these objects that are intrinsically unstable in solution (noted A₄2₉(CO₂)₉) and of their packing mode into the assembled dynamic material (noted DM^A₂(CO₂)) can therefore only be performed in the solid state.⁵⁸ However, the precipitation of DM^A₂(CO₂) as a nano-crystalline solid with some disorder in chain length and water content makes it challenging to both perform basic molecular level characterization or to determine a crystal structure. It also hampers the understanding of the precise intra- and intermolecular interactions that drive the assembly of DM^A₂(CO₂). We have therefore used solid-state NMR spectroscopy, which is not necessarily hampered by this type of disorder, in combination with quantum chemical calculations to propose a three-dimensional structural model of the dynamic material DM^A₂(CO₂).

Determining constitutional isomers

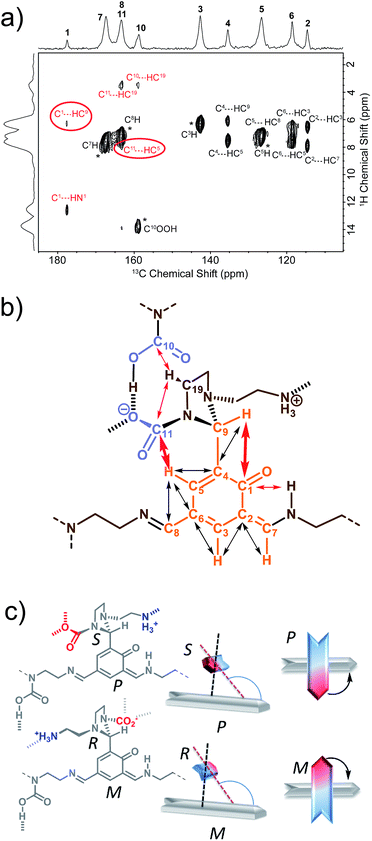
We have previously identified¹⁴ some of the functional groups borne by the oligo-dynablocks A₄2₉(CO₂)₉ from basic one-dimensional magic angle spinning ¹⁵N and ¹³C solid-state NMR spectroscopy (Fig. 1a). It is worth noting at this stage that the ¹³C CP-MAS NMR spectrum of DM^A₂(CO₂) remained unchanged when the stoichiometry of the molecular constituents was varied by tuning the initial ratio between building blocks A and 2, strongly suggesting that variations in the chain length can be accommodated by the crystal structure of the material. In order to explore the connectivity between individual heavy atoms (carbon and nitrogen), a partially ¹³C and fully ¹⁵N enriched dynamic material (referred to as DM^A₂(CO₂)*) was produced by using fully ¹³C-labeled CO₂ (to label carbamates) and ¹⁵N-labeled diethylenetriamine for the assembly process.⁵⁹ A 2D double cross-polarization (DCP) ¹⁵N–¹³C HETCOR⁶⁰ spectrum of DM^A₂(CO₂)* allowed us to assign most of the carbon nuclei directly bonded to nitrogen centers (Fig. 1c, black/nitrogen to red/carbon labels) by analogy with known shifts (N1′ and N2′ are characterized by broad peaks of low intensity and failed to provide detectable correlations with neighboring carbons except for N1′–C14). This experiment confirmed the presence of unusual chemical functionalities stabilized by the solid environment, such as the aminal carbamate moiety (carbon atom 11 and nitrogen 3′, Fig. 1b). However, the similarity of the ¹³C chemical shifts of several carbon atoms in the ethyl bridges prevented complete ¹³C assignment (Fig. 1c, purple labels). A DNP enhanced ¹³C–¹³C refocused INADEQUATE spectrum⁶¹ (Fig. 1d and e) was then recorded on the natural abundance DM^A₂(CO₂) to complete the carbon-13 assignment and to elucidate the substitution pattern of the three carbamate-diethylenetriamine side arms borne by the phenolic core of the monomeric unit.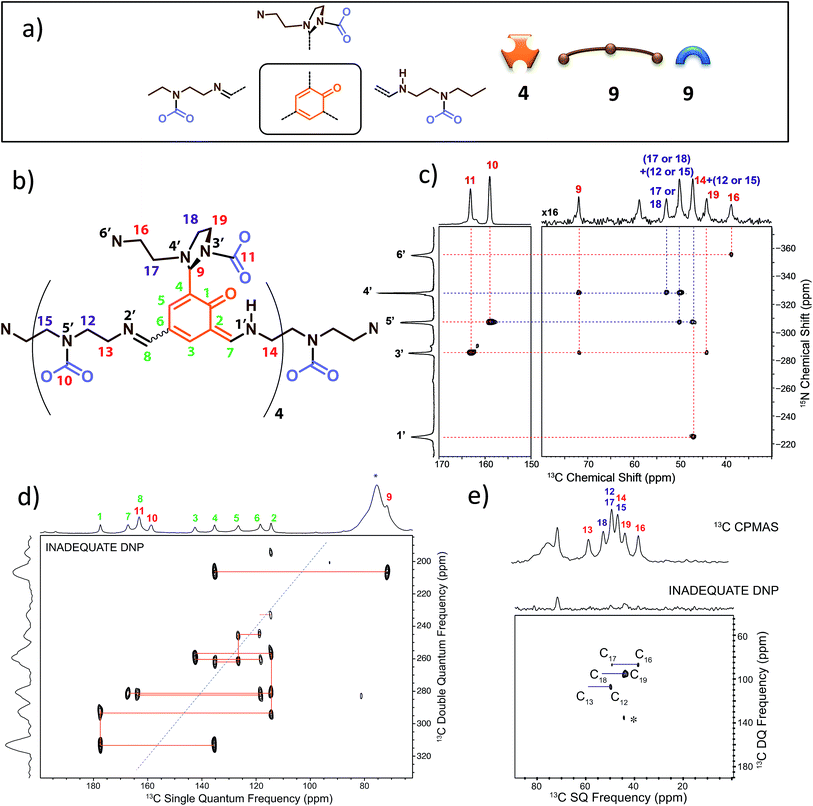

Fig. 1 (a) Building block content and molecular patterns previously identified.¹⁴ (b) Structure of the oligo-dynablock proposed here based upon solid-state NMR analysis. (c) 2D DCP ¹⁵N–¹³C HETCOR spectrum for partially ¹³C and fully ¹⁵N enriched DM^A₂(CO₂)*. Correlations between nitrogen atoms (black labels) and carbon atoms (red labels) are indicated by dashed lines. (d) 100 K DNP-enhanced 2D refocused INADEQUATE ¹³C–¹³C correlation spectrum (aromatic region only) acquired from natural isotopic abundance DM^A₂(CO₂) impregnated with a 16 mM solution of TEKPol in 1,1,2,2-tetrachloroethane. Correlations/connectivity are indicated by solid orange lines and provide iterative assignment of green labels. (e) Aliphatic region of the 2D refocused INADEQUATE ¹³C–¹³C correlation spectrum (provides unambiguous assignments of purple labels). By combining the information in the 2D DCP ¹⁵N–¹³C HETCOR spectrum and the 2D refocused INADEQUATE ¹³C–¹³C correlation spectrum it is possible to completely assign the spectra and propose the model chemical structure for the oligo-dynablock shown in (b). Carbon resonances are numbered on the spectra and assigned to the proposed structure of DM^A₂(CO₂).

The ¹³C–¹³C refocused INADEQUATE spectrum (Fig. 1d and e) indicates the direct connections between the neighboring sp² carbon atoms (C1–C10 region) of the polyaldehyde building block, including the carbonyl groups engaged in three chemically distinct types of linkages (imine, enamine and aminal). Note that we used high field dynamic nuclear polarization (DNP)^62,63 to enhance the sensitivity of the solid-state NMR experiments to enable acquisition of a refocused INADEQUATE ¹³C–¹³C correlation spectrum in a reasonable experimental time.^64,65 In order to perform DNP experiments the powdered DM^A₂(CO₂) was impregnated with a solution of the nitroxide biradical polarizing agent TEKPol⁶⁶ in 1,1,2,2-tetrachloroethane (TCE).⁶⁷ TCE was chosen since it is a non-solvent for DM^A₂(CO₂). In these experiments the protons within the DM^A₂(CO₂) crystallites are remotely polarized by proton spin diffusion.^64,68,69 DNP provides a spectacular increase in the signal-to-noise ratio as compared with analogous room temperature experiments (ESI, Fig. S6†), revealing well resolved individual scalar coupling correlations between all the carbons in the ¹³C–¹³C refocused INADEQUATE spectrum. This leads to the full assignment of the carbon nuclei (C13–C19) in the aliphatic region (Fig. 1e). In conclusion, this analysis allows us to propose the chemical structure for DM^A₂(CO₂) shown in Fig. 1b.

Determining tautomers

2D ¹H–¹³C dipolar HETCOR (Fig. 2a) and ¹H–¹⁵N solid-state refocused INEPT⁷⁰ (Fig. 2b) experiments were performed in order to identify hydrogen atoms bound to carbon and nitrogen atoms on the monomeric unit. These experiments also allowed us to explore intermolecular connections between oligo-dynablocks.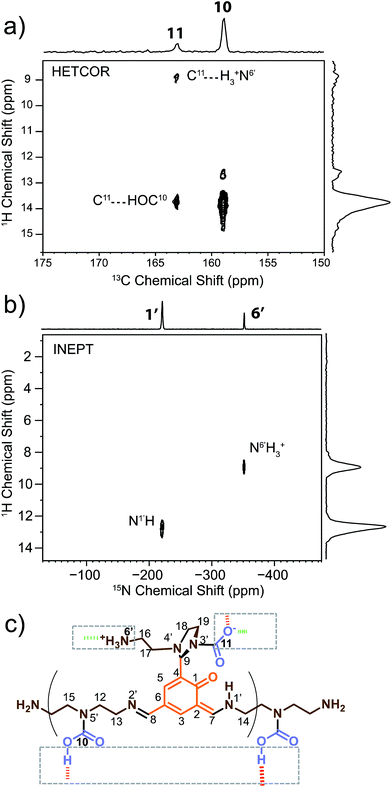

Fig. 2 Heteronuclear correlation (HETCOR) spectra for assignment of ¹H chemical shifts and determination of the protonation state and intermolecular binding modes of the oligodynablocks. (a) The carbonyl region of the ¹H–¹³C dipolar HETCOR spectrum of DM^A₂(CO₂). (b) Full ¹H–¹⁵N solid-state refocused INEPT spectrum of DM^A₂(CO₂)*; eDUMBO-1₂₂¹H homonuclear decoupling was applied during t₁ evolution to obtain high ¹H resolution.⁷¹ (c) Corresponding identified intermolecular binding modes.

By determining the protonation state of heteroatoms it was possible to identify the tautomeric forms of the various possible carbamic acid-amine and/or ammonium carbamate and imine-phenol or enamine-quinone combinations. The ¹H–¹⁵N solid-state refocused INEPT spectrum (Fig. 2b) clearly shows that of all the nitrogen atoms, only N1′ and N6′ are protonated. Comparison of the ¹H–¹³C and ¹H–¹⁵N 2D correlation spectra indicates that both N6′ (likely an ammonium nitrogen) and C11 (a carbamate carbon) show correlations to the same ¹H nuclei with a shift of 9 ppm typical of ammonium protons. This suggests that the aminoethylaminal N6′–C11 side chain exists as an ammonium – aminal carbamate ion pair (Fig. 2c).

In contrast, the diethylenetriamine central spacer is involved on its extremities in enamine and imine linkages with the aromatic units. N5′ can only be post-functionalized into a neutral carbamic acid. The ¹H–¹³C dipolar HETCOR experiment also provided some information about the intermolecular bonding between oligo-dynablocks. In this spectrum, both C10 and C11 showed correlations to ¹H nuclei with a chemical shift of ca. 13.7 ppm. This suggests that the anionic carbamate (C11) site engages in hydrogen bonds with the neutral carbamate sites (C10). Considering that C11 also engages in a hydrogen bond to the ammonium group, we can conclude that it is a pivotal anchoring group, acting as a hydrogen bond acceptor both with the ammonium center and with the carbamic acid groups of two different neighboring oligo-dynablock within the solid network (Fig. 2c).

Determining conformers

To explore the conformation of the flexible zones (namely the dihedral angles C12–C13, C14–C15, C16–C17 on the main chain and the C4–C9 dihedral angle on the bicyclic aminal-phenol system), a DNP-enhanced Lee-Goldberg (LG) CP HETCOR experiment⁷² was conducted to probe short range contacts between ¹H and ¹³C nuclei (Fig. 3a). This experiment confirmed the regioisomeric assignment and the intermolecular pairing mode through the observation of correlations between C4–H̲C5; C6–H̲C5; C6–H̲C3; C2–H̲C3; C2–H̲C7; C1–H̲N1; C11–H̲C19; C11–H̲C5 and C10–H̲C19 (Fig. 3b). Besides a C4–H̲C9 contact, two correlations (C1–H̲C9) and (C11–H̲C5) between the aminal carbamate side chain and the central aromatic core could be observed (Fig. 3a and b). A statistical analysis of the Cambridge structural database indicates that for benzylic aminal structures the planes of the six and five membered rings are systematically almost perpendicular in such molecular patterns.¹⁴ While this orientation fulfills the requirements for the inter-molecular ionic pairing between oligo-dynablocks, the aforementioned contacts between nuclei from these adjacent rings additionally tend to indicate that C9–H and C1–O bonds are almost coplanar.

Fig. 3 Coupled configurational/conformational exploration of the junction between main and side chain around the connective center C₉ through (a) a short range (τ_CP = 500 μs) DNP-enhanced ¹H–¹³C LG-CP HETCOR spectrum revealing spatial contacts. (b) Structural model with black arrows indicating correlations observed within the rigid backbone, and red arrows indicating observed correlations between flexible parts. This analysis leads to two possible enantiomeric monomeric units with opposite absolute coupled configuration/conformation on the C₉ center (c).

The perpendicular orientation of the primary and side chains, which are both non-symmetrical, results in axial chirality around the C4–C9 linkage. As C9 is itself a stereogenic center, both axial and central chirality are inter-related. In the present case, only (S,P) or (R,M) combinations of configuration and conformation are in agreement with the LG-CP HETCOR experiment (Fig. 3c).

Elucidation of tacticity and crystal structure

From the above, for a given oligomeric primary chain, two opposite absolute configurations corresponding to reversed orientations of the N3′-carbamated diethylenetriamine can be envisaged, leading to structures of varying tacticity.

To proceed further to an atomic-level model of the structure, we modelled six different trial structures of the oligo-dynablocks (shown schematically in Scheme 2 (1–6)), which differed in terms of stereochemistry. For each type of structure trial crystal structures were generated using the direct-space genetic algorithm (GA) technique incorporated in the program Genmol.^73–75 Among these six trial architectures, objects 4, 5 and 6 were true potential candidates whose sequence and structure were in full agreement with the data from the previous solid-state NMR experiments. Objects 1, 2 and 3 were reference compounds with erroneous configurations and/or conformations on part or all of the monomeric units which were deliberately included (all disagree with the analysis of the LG-CP HETCOR spectrum, in Fig. 3a). They were included to validate the ability and sensitivity of the chemical shifts to discriminate diastereoisomers on high molecular weight multi-component architectures and simultaneously elucidate their packing.

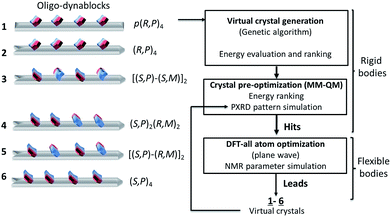Scheme 2 Crystal structure prediction process on oligo-dynablocks 1–6 with their Cahn–Ingold–Prelog configurations.

In more detail, 6 consists of isotactic (S,P)₄ oligo-dynablocks, while 5 and 4 are their syndiotactic [(S,P)-(R,M)]₂ and block (made of meso dyads) (S,P)₂-(R,M)₂ diastereoisomer respectively. 3 is also syndiotactic [(S,P)-(S,M)]₂ but displays erroneous configurations (with respect to 5) or conformations (with respect to 6) on non-adjacent monomeric units. 2 is isotactic (R,P)₄ with erroneous configurations/conformations on every unit. Finally, 1 is the regioisomer of 2 where all phenol groups are localized in para position with respect to the aminal ring (configuration referred to as: [p-(R,P)]₄) and corresponds to the structure previously suggested for DM^A₂(CO₂).¹⁴

DM^A₂(CO₂) is well beyond the scope of comprehensive crystal structure prediction today, as it has 130 heavy atoms and each of the four monomeric units of the oligo-dynablocks has at least 13 degrees of conformational freedom. In addition the models we use here neglect the presence of water in the structure, and do not consider disorder in the chain lengths. We are therefore looking for structural models that will certainly not be exact, but which will reproduce the qualitative features of the conformation and intermolecular packing in the crystal structure. The models used to generate the trial crystal structures were thus built from tetramers whose configuration and conformation agreed with most or all NMR experiments (anti conformation was chosen for the main chain and the bicyclic dihedral angle set to 90°, in agreement with NMR data). These structures were then treated as rigid bodies during the process of crystal generation and preliminary minimization. Candidate crystal structures for each of the six oligodynablock structures 1–6 were generated in the P₁ space group. For each candidate the three hundred most stable lattices were selected from a randomly generated pool and then pre-optimized by energy minimization with MM + QM calculations (see Section S1.5.1. in ESI for details†).

In the case of 2 and 6, respectively, two and three hits (labelled a–c) having a high predicted stability (lattice energy lower than −180 kcal mol⁻¹) were obtained and conserved. 1, 3, and 5 all yielded a most stable predicted structure with lattice energies lower than −105 kcal mol⁻¹. Block oligomers 4 (made of meso dyads) failed to yield stable crystal packing (lattice energies were all higher than −100 kcal mol⁻¹) and were therefore excluded.

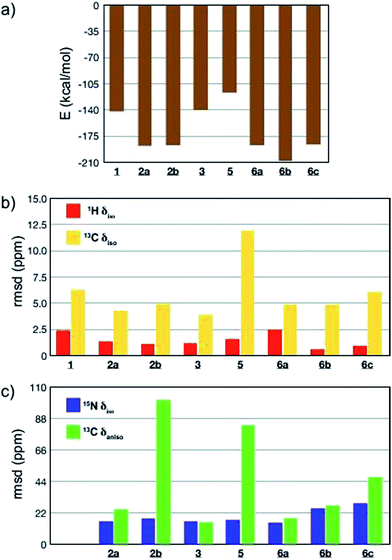
All-atom DFT geometry optimization was performed on the eight candidates obtained (1, 2a,b, 3, 5, 6a–c) and the chemical shift tensors of the resulting leads were calculated using the GIPAW (Gauge Including Projector Augmented Wave)^44,76,77 method in CASTEP.⁷⁸ To assess the quality of the proposed structures 1–3 and 5–6, they were ranked based on the combination of predicted lattice energy and four different NMR chemical shift parameters (Fig. 4; ESI, Table S18†). For the chemical shifts, root-mean-squared deviations (rmsd) between experimental and calculated values of isotropic chemical shifts (¹H, ¹⁵N and ¹³C), as well as ¹³C chemical shift anisotropy (Fig. 4; ESI, Table S18†) were computed.^24,27 Experimental ¹³C chemical shift tensor parameters were determined from a DNP-enhanced ¹³C magic angle turning (MAT) spectrum of DM^A₂(CO₂) (Fig. S9†).

Fig. 4 Comparison of agreement between calculated and experimental data for the predicted crystal structures 1–6. (a) Predicted crystal lattice energies; (b) root-mean-square deviation (rmsd) between experimental and calculated ¹H (red) and ¹³C (yellow) isotropic chemical shifts; (c) rmsd between experimental and calculated ¹⁵N isotropic chemical shifts (blue) and ¹³C chemical shift anisotropy (green).

Computed crystal energy, ¹H and ¹³C isotropic chemical shift are today reasonably well understood, and were hence chosen as quantitative indicators (Fig. 4a–c). In the particular case of ¹H chemical shifts the “cut-off value” of rmsd under which a virtual crystal is considered to be in good agreement with the experiment is usually around 0.6 ppm.^23,49 Since they have so far been less frequently used, ¹⁵N isotropic chemical shift and ¹³C chemical shift anisotropy were considered in Fig. 4c as qualitative indicators of potential discrepancy when abnormally high values of rmsd were obtained.

The results of the comparisons are summarized in Fig. 4a–c, and ESI Table S18.† Structures 1, 3 and 5 are predicted to be significantly less stable than the others, with 1 and 5 also showing significant deviations in the chemical shift parameters, and can be discounted. The case of oligo-dynablock 1 highlights the difference between the molecular and the supramolecular point of view: the C=O positioning on C₃ obviously induces a decrease in steric hindrance locally with the five-membered aminal ring but globally yields a packing of poor stability. Similarly, syndiotactic oligo-dynablocks 3 and 5 with alternate conformations and configurations on adjacent monomeric units, respectively yield structures with higher predicted energy compared to isotactic oligo-dynablocks 6. Structures 2a and 2b, which differ in the conformation of the flexible side chains of their constituents and their relative position in the structures, display contrasted scores for qualitative NMR indicators. Lattices, 2 and 6 which are formed from isotactic oligo-dynablocks are indeed predicted to be significantly more stable. Structure 2b can be discounted since it has an abnormal disagreement in the ¹³C CSA parameters. When comparing structures 2a, 6a, 6b and 6c, we see that 6c has overall only qualitative agreement. 2a, 6a and 6b all have better agreement, but we see that among them only 6b is in good agreement with the ¹H chemical shifts, with a ¹H rmsd value below 0.6 ppm. At this point we recall that structure 2 does not agree with the NMR correlation data. We therefore tentatively conclude that structure 6b, which is predicted to be the most stable, is the structure that is in best overall agreement with the ensemble of experimental data from NMR, including chemical shifts and correlation spectra. While we are certain that this is not an exact representation of the lattice (due to the disorder in chain length and solvation discussed above), we hypothesise that it is likely to contain the essential structural features of the solid.

Note that candidates 6b and 6c were the only model structures in the series whose constituents have a zwitterionic protonation state (ammonium carbamate) on the C11–N6′ chain, in agreement with experimental observations. Although the other model crystal structures were systematically generated from zwitterionic oligo-dynablocks, proton exchange during all atom DFT optimization resulted in neutral structures. The correct protonation state on the hetero-nuclei partially accounts for the lower rmsd of the ¹H chemical shift values in the structures 6b and 6c. As mentioned above, when 6b and 6c are compared on the basis of the other major structural parameters, 6b appears to be the best candidate. Note that, 6b is not in the best agreement among the set in terms of calculated and experimental isotropic ¹⁵N chemical shifts. This is particularly true for the sp² nitrogen centers N1′ and N2′ (with rmsd of 47 and 32 ppm respectively). However, these nuclei systematically yielded poor correlation for all candidate structures (the average difference along the series 5 and 6 being 35 and 33 ppm respectively). While the chemical shift of sp³ nitrogens seem to display little sensitivity to their protonation state (a 10 ppm shift on average was observed when comparing candidates 1, 2a, 2b, 5 and 6a with 6b and 6c), sp² nitrogens in salicylic systems are reported to be extremely sensitive to the proton transfer from the phenol group (from −50 to −220 ppm) and to the exact position of the proton between the oxygen and the nitrogen N1′ centers,⁷⁹ and other work has shown strong sensitivity of nitrogen shifts to the migration of protons across hydrogen bonds.⁸⁰ It is therefore expected that a very slight discrepancy in the calculated position of the N1′–H̲⋯O proton could results in large shifts in the resonance of the N1′ and to a lesser extent on N2′ which is directly conjugated to N1′ through the aromatic ring. As a result we choose the disregard these shifts in the evaluation. We note that recent reports of calculated ¹⁵N isotropic chemical shifts in the literature include both cases of excellent agreement^81,82 or systematic overestimation with respect to experimental data.⁸³

Intermolecular H-bonding drives selectivity

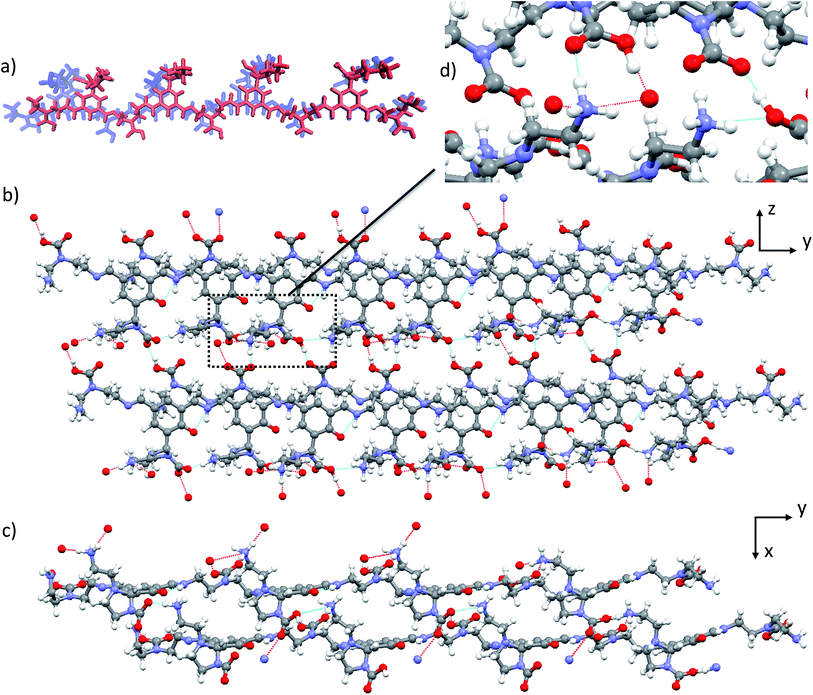
Structure 6b, which appears as the most credible model from among the idealised structures proposed here, is characterized by a significantly lower calculated energy than the other potential candidates 5, 6a and 6c. Examination of the inter-molecular binding modes in the lattice of 6b (Fig. 5b and c) reveals an optimized network of hydrogen bonds. 6b is the only structure whose ammonium and carbamate/carbamic acid moieties are engaged in three and two hydrogen bonds (Fig. 5d), respectively (vs. one and two at most in all other structures). This optimization of the hydrogen bond network not only provides subsequent stabilization to the molecular network but also presumably accounts for the significantly improved agreement between calculated and experimental data for structure 6b with respect to the remaining candidates. Importantly, this hydrogen bond network would appear to strongly depend on the nature of the constituent building blocks. In fact, polyamines of increased length or steric hindrance would compromise this optimal pairing. Therefore, the choice of the building block incorporated into the DM^A₂(CO₂) controls the packing efficiency, which in turn drives the self-assembly process. The new picture that emerges here from a simplified model appears to explain the singular selectivity previously observed for the formation of DM^A₂(CO₂).

Fig. 5 Crystal structure 6b which shows the best overall agreement with the experimental data. (a) Comparison of the structure of oligomer 6b in the crystal before (blue) and after all-atom geometry optimization with CASTEP (red). Packing between nearest neighbours along (b) z axis and (c) x axis. (d) Partial view of the intermolecular main and side chain binding.

Powder X-ray diffraction

Powder X-ray diffraction and solid-state NMR are both powerful techniques which have been used independently or in tandem for crystal structure solution.^{21,24,29,31,35,84–86} We therefore did assess the possible contribution of PXRD to the structural modelling developed here in parallel to the NMR measurements. Fig. 6 shows the PXRD pattern obtained from the nanocrystalline material, and which is found to have quite high resolution with reflections beyond 30° indicative of a structure that has long range periodicity and well defined regular structural features. At first sight, it may thus be possible to index this pattern and determine the structure. Indexing of the experimental PXRD spectrum was first attempted using the McMaille program. Despite a thorough screening of the possible Bravais lattices and cell parameters, the procedure failed, leading to several possible solutions, even when combining two polymorphic structures. The main reason for failure appeared to be the lack of well-resolved peaks at large angles.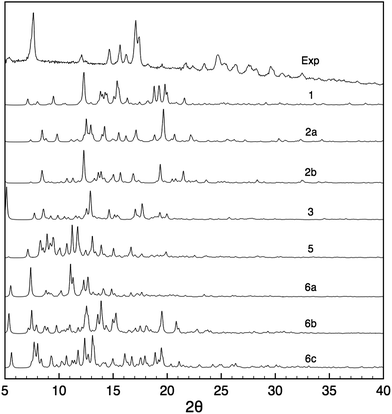

Fig. 6 Comparison between the experimental PXRD pattern and the simulated spectra for structures 1–6 after all-atom DFT optimization.

PXRD spectra were then simulated for all the candidate 1–6. It can be seen from Fig. 6 that the resulting patterns displayed very little similarity with the experimental spectrum, whether the oligomeric constituents were true candidates or not. Furthermore, the changes observed in the PXRD patterns predicted for structures before and after DFT geometry optimisation (Fig. S2†) are of the same order of magnitude as the difference between the candidate structures even though the structural changes induced by optimisation are relatively minor.

This highlights the fact that PXRD patterns are sensitive to very small structural changes, such that if the candidate structure is not within a few fractions of an angstrom in rmsd from the correct structure then poor agreement will always be obtained.⁸⁵ Notably, changes in the unit cell parameters induce large changes in the PXRD line positions and intensities, and since indexing failed here it is unlikely that the candidate structures have exactly correct cell parameters. This is especially true if we recall that that the materials here may have some dispersion in the chain lengths and the hydration states that would almost certainly induce changes with respect to the model cells predicted here. We have seen that removing some empty space (which may contain water) from the structures by changing the unit cell dimensions while keeping the atomic coordinates fixed produces large changes in the predicted PXRD patterns (Fig. S24†), while including water molecules in the same empty space in the candidate structures also changes the predicted PXRD intensities.

For well ordered crystalline materials perfect agreement with PXRD can often be obtained and would be the gold standard in validating a final structure. However, in this case of a well ordered but slightly disperse material, and where indexing fails, we see that PXRD is not a useful indicator, whereas high resolution NMR data can still be obtained and directly related to the average properties of the structures. This is an excellent example of the complimentary nature of the two methods.

Conclusions

Structural elucidation of organized nano-crystalline powdered solids made of complex molecular ingredients represents an unresolved challenge to date. Here we have applied state of the art NMR crystallography methods to obtain a proposal for the structure of a complex three-component dynamic oligomeric material by using a series of solid-state MAS NMR experiments, including DNP enhanced spectroscopy. It has allowed to obtain the complete assignment of ¹H, ¹³C and ¹⁵N resonances, and to determine a number of spatial proximities between atoms thereby providing strong constraints on possible structures. We used comparisons between experimental and calculated NMR chemical shifts to select the best model structures. This is one of the most complex systems for which solid-state NMR has been able to provide a de novo structure, starting only with the molecular formula, to date.

Since the material contains disorder both in chain length and solvation the structure proposed here is certainly not exact (for example in terms of the predicted unit cell parameters), but we suggest it does capture the essential structural features. Dispersity in terms of oligomer length, and the integration of hydration, is well beyond the current scope of the prediction tools used here. However, this did not hamper the application of NMR and the extraction of quantitative constraints on the structure, whereas they did render comparison with PXRD of no use.

These results highlight the increasing capabilities of the combination of solid-state NMR, crystal structure prediction, periodic DFT plane wave calculations (and powder X-ray diffraction) for the determination of crystal structures when single crystal X-ray diffraction is not possible. The structure determined from NMR notably suggests the presence of an optimised intermolecular hydrogen bonding network that explains why the self-assembly of the material is so selective in terms of building blocks. Small changes in the building blocks would prevent formation of the H-bond network.

Acknowledgements

We are grateful to Prof. P. Tordo, Dr O. Ouari and Dr G. Casano (Aix-Marseille Université, France) for providing the biradicals used in the DNP NMR experiments. Financial support from the Agence Nationale de la Recherche (ANR-12-JS07-0011-01), the TGIR-RMN-THC FR3050 CNRS, and Swiss National Science Foundation grant no. 160112 for conducting the research is gratefully acknowledged. This work was supported by the LABEX iMUST (ANR-10-LABX-0064) of Université de Lyon, within the program “Investissements d'Avenir” (ANR-11-IDEX-0007) operated by the French National Research Agency (ANR).

Notes and references

1. H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444.
2. S. O. Lee, D. M. Shacklady, M. J. Horner, S. Ferlay, M. W. Hosseini and M. D. Ward, Cryst. Growth Des., 2005, 5, 995–1003.
3. M. W. Hosseini, in Applications of supramolecular chemistry, ed. H.-J. Schneider, CRC Press, 2012.
4. S. Ferlay and M. W. Hosseini, in Functional supramolecular architectures for organic electronics and nanotechnology, ed. P. Samori and F. Cacialli, Wiley-VCH, 2010.
5. M. W. Hosseini, Acc. Chem. Res., 2005, 38, 313–323.
6. J.-M. Lehn, Angew. Chem., Int. Ed. Engl., 1990, 29, 1304–1319.
7. M. O'Keeffe and O. M. Yaghi, Chem. Rev., 2012, 112, 675–702.
8. E. F. Bres, S. Ferlay, P. Dechambenoit, H. Leroux, M. W. Hosseini and S. Reyntjens, J. Mater. Chem., 2007, 17, 1559–1562.
9. P. Dechambenoit, S. Ferlay and M. W. Hosseini, Cryst. Growth Des., 2005, 5, 2310–2312.
10. P. Dechambenoit, S. Ferlay, N. Kyritsakas and M. W. Hosseini, Chem. Commun., 2009, 1559–1561.
11. G. Marinescu, S. Ferlay, N. Kyritsakas and M. W. Hosseini, Chem. Commun., 2013, 49, 11209–11211.
12. M. W. Hosseini, Chem. Commun., 2005, 5825–5829.
13. H. Deng, C. J. Doonan, H. Furukawa, R. B. Ferreira, J. Towne, C. B. Knobler, B. Wang and O. M. Yaghi, Science, 2010, 327, 846–850.
14. J. Leclaire, G. Husson, N. Devaux, V. Delorme, L. Charles, F. Ziarelli, P. Desbois, A. Chaumonnot, M. Jacquin, F. Fotiadu and G. Buono, J. Am. Chem. Soc., 2010, 132, 3582–3593.
15. The term was first coined by J-M. Lehn refering to a polymeric material spontaneously obtained from monomers assembled with reversible covalent and non covalent bonds.
16. E. Kolomiets and J. M. Lehn, Chem. Commun., 2005, 1519–1521.
17. E. Moulin, G. Cormos and N. Giuseppone, Chem. Soc. Rev., 2012, 41, 1031–1049.
18. F. Fotiadu, M. Jacquin, J. Leclaire, A. Methivier, P. A. Bouillon and P. Desbois, FR Pat., 2 969 504, 2012.
19. F. Fotiadu, M. Jacquin, J. Leclaire, A. Methivier, P. Desbois and P. A. Bouillon, FR Pat., 2 969 503, 2012.
20. J. Leclaire, G. Canard, F. Fotiadu and G. Poisson, World Pat., 2014188115 A1, 2014.
21. R. K. Harris, Solid State Sci., 2004, 6, 1025–1037.
22. C. J. Pickard, E. Salager, G. Pintacuda, B. Elena and L. Emsley, J. Am. Chem. Soc., 2007, 129, 8932–8933.
23. M. Baias, J.-N. Dumez, P. H. Svensson, S. Schantz, G. M. Day and L. Emsley, J. Am. Chem. Soc., 2013, 135, 17501–17507.
24. M. Baias, C. M. Widdifield, J.-N. Dumez, H. P. G. Thompson, T. G. Cooper, E. Salager, S. Bassil, R. S. Stein, A. Lesage, G. M. Day and L. Emsley, Phys. Chem. Chem. Phys., 2013, 15, 8069–8080.
25. D. H. Brouwer, R. J. Darton, R. E. Morris and M. H. Levitt, J. Am. Chem. Soc., 2005, 127, 10365–10370.
26. B. Elena, G. Pintacuda, N. Mifsud and L. Emsley, J. Am. Chem. Soc., 2006, 128, 9555–9560.
27. K. Kalakewich, R. Iuliucci and J. K. Harper, Cryst. Growth Des., 2013, 13, 5391–5396.
28. T. Loiseau, L. Lecroq, C. Volkringer, J. Marrot, G. Ferey, M. Haouas, F. Taulelle, S. Bourrelly, P. L. Llewellyn and M. Latroche, J. Am. Chem. Soc., 2006, 128, 10223–10230.
29. L. Mafra, S. M. Santos, R. Siegel, I. Alves, F. A. Almeida Paz, D. Dudenko and H. W. Spiess, J. Am. Chem. Soc., 2012, 134, 71–74.
30. E. Salager, R. S. Stein, C. J. Pickard, B. Elena and L. Emsley, Phys. Chem. Chem. Phys., 2009, 11, 2610–2621.
31. D. V. Dudenko, P. A. Williams, C. E. Hughes, O. N. Antzutkin, S. P. Velaga, S. P. Brown and K. D. M. Harris, J. Phys. Chem. C, 2013, 117, 12258–12265.
32. X. Filip and C. Filip, Solid State Nucl. Magn. Reson., 2015, 65, 21–28.
33. D. Lüdeker and G. Brunklaus, Solid State Nucl. Magn. Reson., 2015, 65, 29–40.
34. M. Sardo, S. M. Santos, A. A. Babaryk, C. López, I. Alkorta, J. Elguero, R. M. Claramunt and L. Mafra, Solid State Nucl. Magn. Reson., 2015, 65, 49–63.
35. S. P. Brown, Solid State Nucl. Magn. Reson., 2012, 41, 1–27.
36. Z. Zujovic, A. L. Webber, J. Travas-Sejdic and S. P. Brown, Macromolecules, 2015, 48, 8838–8843.
37. Y. Jiang, J. Huang, B. Kasumaj, G. Jeschke, M. Hunger, T. Mallat and A. Baiker, J. Am. Chem. Soc., 2009, 131, 2058–2059.
38. X. Kong, H. Deng, F. Yan, J. Kim, J. A. Swisher, B. Smit, O. M. Yaghi and J. A. Reimer, Science, 2013, 341, 882–885.
39. S. Devautour-Vinot, G. Maurin, C. Serre, P. Horcajada, D. P. da Cunha, V. Guillerm, E. d. S. Costa, F. Taulelle and C. Martineau, Chem. Mater., 2012, 24, 2168–2177.
40. X. Kong, E. Scott, W. Ding, J. A. Mason, J. R. Long and J. A. Reimer, J. Am. Chem. Soc., 2012, 134, 14341–14344.
41. C. R. Murdock, N. W. McNutt, D. J. Keffer and D. M. Jenkins, J. Am. Chem. Soc., 2014, 136, 671–678.
42. J. Xu, V. V. Terskikh, Y. Chu, A. Zheng and Y. Huang, Chem. Mater., 2015, 27, 3306–3316.
43. M. Baias, A. Lesage, S. Aguado, J. Canivet, V. Moizan-Basle, N. Audebrand, D. Farrusseng and L. Emsley, Angew. Chem., Int. Ed., 2015, 54, 5971–5976.
44. C. Bonhomme, C. Gervais, F. Babonneau, C. Coelho, F. Pourpoint, T. Azais, S. E. Ashbrook, J. M. Griffin, J. R. Yates, F. Mauri and C. J. Pickard, Chem. Rev., 2012, 112, 5733–5779.
45. A. C. Dedios, J. G. Pearson and E. Oldfield, Science, 1993, 260, 1491–1496.
46. J. C. Facelli and D. M. Grant, Nature, 1993, 365, 325–327.
47. N. Mifsud, B. Elena, C. J. Pickard, A. Lesage and L. Emsley, Phys. Chem. Chem. Phys., 2006, 8, 3418–3422.
48. A. Rapp, I. Schnell, D. Sebastiani, S. P. Brown, V. Percec and H. W. Spiess, J. Am. Chem. Soc., 2003, 125, 13284–13297.
49. E. Salager, G. M. Day, R. S. Stein, C. J. Pickard, B. Elena and L. Emsley, J. Am. Chem. Soc., 2010, 132, 2564–2566.
50. J. R. Yates, S. E. Dobbins, C. J. Pickard, F. Mauri, P. Y. Ghi and R. K. Harris, Phys. Chem. Chem. Phys., 2005, 7, 1402–1407.
51. J. R. Yates, T. N. Pham, C. J. Pickard, F. Mauri, A. M. Amado, A. M. Gil and S. P. Brown, J. Am. Chem. Soc., 2005, 127, 10216–10220.
52. S. J. Rowan, S. J. Cantrill, G. R. L. Cousins, J. K. M. Sanders and J. F. Stoddart, Angew. Chem., Int. Ed., 2002, 41, 898–952.
53. N. Jouault, R. Nguyen, M. Rawiso, N. Giuseppone and E. Buhler, Soft Matter, 2011, 7, 4787–4800.
54. R. Nguyen, L. Allouche, E. Buhler and N. Giuseppone, Angew. Chem., Int. Ed., 2009, 48, 1093–1096.
55. R. Nguyen, E. Buhler and N. Giuseppone, Macromolecules, 2009, 42, 5913–5915.
56. D. M. Rudkevich and H. Xu, Chem. Commun., 2005, 2651–2659.
57. P. T. Corbett, J. K. M. Sanders and S. Otto, J. Am. Chem. Soc., 2005, 127, 9390–9392.
58. P. Jackson, K. J. Fisher and M. I. Attalla, J. Am. Soc. Mass Spectrom., 2011, 22, 1420–1431.
59. Z. J. Guo, P. J. Sadler and E. Zang, Chem. Commun., 1997, 27–28.
60. J. Schaefer, E. O. Stejskal, J. R. Garbow and R. A. McKay, J. Magn. Reson., 1984, 59, 150–156.
61. A. Lesage, M. Bardet and L. Emsley, J. Am. Chem. Soc., 1999, 121, 10987–10993.
62. T. Maly, G. T. Debelouchina, V. S. Bajaj, K.-N. Hu, C.-G. Joo, M. L. Mak-Jurkauskas, J. R. Sirigiri, P. C. A. van der Wel, J. Herzfeld, R. J. Temkin and R. G. Griffin, J. Chem. Phys., 2008, 128, 052211,  DOI:10.1063/1.2833582.
63. Q. Z. Ni, E. Daviso, T. V. Can, E. Markhasin, S. K. Jawla, T. M. Swager, R. J. Temkin, J. Herzfeld and R. G. Griffin, Acc. Chem. Res., 2013, 46, 1933–1941.
64. A. J. Rossini, A. Zagdoun, F. Hegner, M. Schwarzwalder, D. Gajan, C. Coperet, A. Lesage and L. Emsley, J. Am. Chem. Soc., 2012, 134, 16899–16908.
65. H. Takahashi, B. Viverge, D. Lee, P. Rannou and G. De Paëpe, Angew. Chem., Int. Ed., 2013, 52, 6979–6982.
66. A. Zagdoun, G. Casano, O. Ouari, M. Schwaerzwalder, A. J. Rossini, F. Aussenac, M. Yulikov, G. Jeschke, C. Coperet, A. Lesage, P. Tordo and L. Emsley, J. Am. Chem. Soc., 2013, 135, 12790–12797.
67. A. Zagdoun, A. J. Rossini, D. Gajan, A. Bourdolle, O. Ouari, M. Rosay, W. E. Maas, P. Tordo, M. Lelli, L. Emsley, A. Lesage and C. Coperet, Chem. Commun., 2012, 48, 654–656.
68. P. C. A. van der Wel, K.-N. Hu, J. Lewandowski and R. G. Griffin, J. Am. Chem. Soc., 2006, 128, 10840–10846.
69. A. C. Pinon, A. J. Rossini, C. M. Widdifield, D. Gajan and L. Emsley, Mol. Pharm., 2015, 12, 4146–4153.
70. B. Elena, A. Lesage, S. Steuernagel, A. Bockmann and L. Emsley, J. Am. Chem. Soc., 2005, 127, 17296–17302.
71. B. Elena, G. de Paepe and L. Emsley, Chem. Phys. Lett., 2004, 398, 532–538.
72. B.-J. van Rossum, C. P. de Groot, V. Ladizhansky, S. Vega and H. J. M. de Groot, J. Am. Chem. Soc., 2000, 122, 3465–3472.
73. A statistical analysis has shown that there is a strong correlation between the geometrical feature of the molecules and the space group of their crystalline phases. For more details, see ref. 74 and 75.
74. G. Pepe, S. Fery-Forgues and P. Jouanna, J. Cryst. Growth, 2011, 333, 25–35.
75. G. Pepe, R. Perbost, J. Courcambeck and P. Jouanna, J. Cryst. Growth, 2009, 311, 3498–3510.
76. C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter, 2001, 63, 245101.
77. T. Charpentier, Solid State Nucl. Magn. Reson., 2011, 40, 1–20.
78. http://www.castep.org .
79. W. Schilf, B. Kamieński, B. Kołodziej and E. Grech, J. Mol. Struct., 2004, 708, 33–38.
80. H. E. Kerr, L. K. Softley, K. Suresh, A. Nangia, P. Hodgkinson and I. R. Evans, CrystEngComm, 2015, 17, 6707–6715.
81. S. A. Joyce, J. R. Yates, C. J. Pickard and S. P. Brown, J. Am. Chem. Soc., 2008, 130, 12663–12670.
82. A. S. Tatton, T. N. Pham, F. G. Vogt, D. Iuga, A. J. Edwards and S. P. Brown, CrystEngComm, 2012, 14, 2654–2659.
83. N. Mercadal, S. P. Day, A. Jarmyn, M. B. Pitak, S. J. Coles, C. Wilson, G. J. Rees, J. V. Hanna and J. D. Wallis, CrystEngComm, 2014, 16, 8363–8374.
84. K. D. M. Harris, M. Tremayne and B. M. Kariuki, Angew. Chem., Int. Ed., 2001, 40, 1626–1651.
85. A. Meden and I. Radosavljevic Evans, Cryst. Res. Technol., 2015, 50, 747–758.
86. R. K. Harris, Analyst, 2006, 131, 351–373.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental procedures, spectra, modelled data and structures. See DOI: 10.1039/c5sc03810c

‡ Present address: Institut de Chimie des Substances Naturelles (CNRS UPR 2301), 91190 Gif-sur-Yvette, France.

---