View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/C5RP00185D (Paper) Chem. Educ. Res. Pract., 2016, 17, 731-742

Exploring a measure of science attitude for different groups of students enrolled in introductory college chemistry

Sachel M. Villafañe *a and Jennifer E. Lewis ab
aDepartment of Chemistry, University of South Florida, Tampa, Florida, 33620, USA. E-mail: svillafa@mail.usf.edu
bCenter for the Improvement of Teaching and Research in Undergraduate STEM Education, University of South Florida, Tampa, Florida 33620, USA

Received 13th October 2015 , Accepted 29th April 2016

First published on 24th May 2016

Abstract

Decisions about instruction, research, or policy often require the interpretation of student assessment scores. Increasingly, attitudinal variables are included in an assessment strategy, and it is important to ensure that interpretations of students' attitudinal status are based on instrument scores that apply similarly for diverse students. In this study, a shortened version of the Test of Science Related Attitudes (TOSRA) was used to gather validity evidence based on the internal structure of the instrument in an introductory chemistry course. Using measurement invariance analysis by sex and race/ethnicity, it was found that the internal structure holds by sex, but it did not hold by race/ethnicity in our sample. Further analysis revealed problems with the normality scales for Black students in our sample. Also, this study examined the relationship between the scales of the Shortened TOSRA, achievement in chemistry, and prior math knowledge. Using Structural Equation Modeling (SEM) it was found that two of the scales, attitude toward inquiry and career interest in science, have a small but significant influence on students' achievement in chemistry. This study highlights the importance of examining if the scores apply similarly for different groups of students in a population, since the scores of these assessments could be used to make decisions that will affect the students.

Introduction

For decades, science educators and researchers have been concerned with students' performance in introductory chemistry courses at the college level. Introductory chemistry courses are part of most STEM curricula in the U.S., but too often students struggle with these courses, creating a problem for those who want or need to continue to more advanced courses. In many instances, students feel that they cannot succeed, losing their interest and motivation to continue, which creates a bigger problem of students leaving the sciences. This problem of retention in STEM is even more concerning for students that are underrepresented in STEM fields, such as females, Hispanics and Blacks (Hurtado et al., 2010).

In chemistry education, many studies have focused on trying to understand which factors affect students' performance in chemistry and their retention in sciences in general. Some of these factors are classified as cognitive factors such as prior math achievement (Cooper and Pearson, 2012; Scott, 2012; Xu et al., 2013) and prior conceptual knowledge in science (Seery, 2009; Wagner et al., 2002; Xu et al., 2013), and some are classified as affective factors such as self-efficacy (Cook, 2013; Dalgety and Coll, 2006) and attitude (Bauer, 2008; Cukrowska et al., 1999; Xu and Lewis, 2011; Xu et al., 2013).

One factor that has been well studied in science education is attitude. Attitude has been defined as “a psychological tendency that is expressed by evaluating a particular entity with some degree of favor or disfavor” (Eagly et al., 1995). Other definitions include “attitude as a learned predisposition” to respond in a positive or negative way to situations, persons, or concepts (Aiken, 1980; Oskamp and Schultz, 2005; Triandis, 1971). Because attitude is viewed as a predisposition, it has been suggested that attitude is composed of affective, cognitive, and behavioral components that will shape one's attitude (Aiken, 1980; Wagner and Sherwood, 1969). There has been a lot of debate about how to define and measure attitude. In 1971, Klopfer provided a classification scheme to define and distinguish the affective domain aims from the nature of science aims in science education (Klopfer, 1971). According to Klopfer, there are six conceptually distinct categories for the affective domain, which are (Fraser, 1977; 1978):

(1) “Manifestation of favorable attitude toward science and scientists”

(2) “Acceptance of scientific inquiry as a way of thought”

(3) “Adoption of scientific attitudes”

(4) “Enjoyment of science learning experiences”

(5) “Development of interests in science and science-related activities”

(6) “Development of interest in pursuing a career in science”

Using these categories, Fraser developed the Test of Science-Related Attitudes (TOSRA) in 1977 (Fraser, 1977). The final version of the TOSRA consisted of seven scales representing the six categories in the Klopfer affective classification scheme (Fraser, 1978); two scales were used to represent the first category, manifestation of favorable attitude toward science and scientists, and one scale was used for each of the other five categories.

TOSRA has been widely used in the science education community since its development more than 30 years ago (Jegede and Fraser, 1989; Khalili, 1987; Schibeci and McGaw, 1981; Telli et al., 2006; Zhang and Campbell, 2011). Some researchers have stated that TOSRA is the most widely used instrument for assessing science attitudes, with high reliability and validity evidence reported in different studies (Zhang and Campbell, 2011). According to Smist et al. (1994), TOSRA is “a multidimensional instrument with a strong theoretical foundation.” These statements make TOSRA an important attitudinal instrument for science education and a good candidate to examine students' attitude in a college setting.

TOSRA previous studies

Most of the research studies performed previously with TOSRA have looked at students' science-related attitudes in middle and high school. This instrument was first used with Australian school students (Fraser, 1977, 1978; Schibeci and McGaw, 1981). Fraser (1977, 1978) administered TOSRA to different samples of Australian students as a way to gather validity and reliability evidence. He used the results from the first administration to seventh grade students in 1977 to make further modification to the scales included in TOSRA. During the next administration in 1978, he gave the instrument to students in grades 7–10, and used those results to provide validity evidence for the instrument scores. Schibeci and McGaw (1981) administered the TOSRA to high school students in Australia and provided further validity and reliability evidence for the use of TOSRA with this population. Later, TOSRA was used in cross validation studies with high school students in Australia, the U.S. (Khalili, 1987) and Indonesia (Adolphe et al., 2003). Also, it has been used with middle and high school students in Turkey (Telli et al., 2006), Nigeria (Jegede and Fraser, 1989), and the U.S. (Welch, 2010). Its multiple uses have provided a good amount of evidence for its use with middle and high school students; however, very little is known about its use with college students. In 2011, Lay and coworkers reported the use of TOSRA with pre-service science teachers in Malaysia and found that in general, they had a positive attitude toward science (Lay and Khoo, 2011). Some researchers have questioned if TOSRA is appropriate to use with college students (Dalgety et al., 2003). Some of the criticism focuses on the simplicity of its items, since students at the college level are expected to have a better understanding of science. Despite this criticism, the instrument is being used at the college level, both in the science community (Chin, 2005; Dowdy, 2005; Lay and Khoo, 2011; Robinson, 2012; Trudel and Métioui, 2011; Tulloch, 2011) and in the chemistry community (Wititsiri, 2006). Further, TOSRA has also specifically been recommended (Rahayu, 2015) as an assessment to understand students' science-related attitudes at the college level for the purpose of understanding whether the way chemistry is taught as a required course for science majors represents a barrier to majoring in STEM. We believe that TOSRA may be appropriate for this purpose, but we think it should not be used without a body of validity evidence, of which this study forms one small part. Therefore it is important to examine if TOSRA scores produce valid results for a general chemistry population, so that the chemistry and science education community has more information about the use of TOSRA at the college level.

Various research studies have provided psychometric evidence, including reliability evidence based on internal consistency and validity evidence based on internal structure, for TOSRA scores (Adolphe et al., 2003; Fraser et al., 2010; Khalili, 1987; Schibeci and McGaw, 1981). The scores on assessments, such as TOSRA, are often used to make curricular decisions (Holme et al., 2010) and sometimes students could even use these scores to make career decisions, such as whether or not to remain in STEM-related fields. Retention of students in STEM-related careers, especially for underrepresented groups, is still of concern (Hurtado et al., 2010); thus, we need to ensure that this instrument produces valid scores that apply similarly for underrepresented students as well as for the rest of the students. This process is called checking for measurement invariance (Kim and Yoon, 2011; Millsap and Everson, 1993; Xu et al., 2016). Measurement invariance is an important aspect of validity evidence based on internal structure, and previous studies have not reported this aspect of validity for TOSRA.

Once there is some evidence suggesting that the interpretations of TOSRA scores are valid for different groups of students in a college chemistry course, we can use these scores to look at the relationship of attitude with students' performance in chemistry.

Attitude and chemistry achievement relationship

In the last few decades, attitude has been proposed as one important construct in science education since students should not only learn the concepts, but they should also be interested in science. As a result, previous studies in science education have looked at the relationship between achievement and attitude (Cukrowska et al., 1999; House, 1995; Weinburgh, 1995; Xu et al., 2013). Students' science achievement in high school has been found to be significantly related to their attitudes (Gooding et al., 1990). Other studies with college chemistry students have reported positive relationships between students' attitudes toward chemistry and their achievement in first year college chemistry using correlation analysis (Cukrowska et al., 1999), logistic regression analysis (House, 1995), and structural equation modeling (Xu et al., 2013).

Prior math knowledge and chemistry achievement relationship

Another factor that has been considered important for chemistry achievement is prior math knowledge (Spencer, 1996). Since we are interested in looking at the relationship between attitude and chemistry achievement, the contribution of prior math knowledge to this relationship is important. One instrument used to measure prior math achievement is the SAT, which is the most widely used college admission test in the U.S. This test probes students' prior knowledge in different subject areas, such as reading, writing, and math. This test has been successfully used as a predictor of science performance in college (Ewing et al., 2005), and the relationship between the math area of the SAT (SATM) and students' performance in college chemistry has been well documented in previous studies (Lewis and Lewis, 2007, 2008; Spencer, 1996; Wagner et al., 2002; Xu et al., 2013). One study found that SATM scores were an important factor in determining students' grades in college-level general chemistry (Spencer, 1996). In other studies focused on college-level general chemistry, Lewis and Lewis (2007) found a medium-size correlation between SATM scores and ACS final exam scores, and Xu et al. (2013) using structural equation modeling found a strong positive effect of prior math knowledge on chemistry achievement.

TOSRA in our context

TOSRA involves, as discussed above, seven scales that represent six categories of the Klopfer classification scheme. Although all of them assess aspects of students' science-related attitudes, three scales relevant to our context were chosen for this study. The first scale is the normality of scientists. In general, this scale assesses students' beliefs about the lifestyle of a scientist. Examples of items in this scale are “Scientists can have a normal family life” and “If you met a scientist, he would probably look like anyone else you might meet”. Previous studies have indicated that students at different levels tend to have an unfavorable and sometimes a negative attitude toward the scientist image (Schibeci, 1986; Song and Kim, 1999). This negative attitude could influence students' decisions to pursue a degree in science (Kelly, 1987).

The second scale is attitude toward inquiry, which assesses students' inclination toward using inquiry as a method to perform scientific investigations in a classroom or laboratory setting. According to the National Science Education Standards framework, inquiry is an activity that involves observation, posing questions, and evaluating evidence to propose answers, explanations and predictions (Loucks-Horsley and Olson, 2000). In the context of TOSRA, we see that the items assess whether, in order to find answers to the questions or problems posed, students prefer to perform an experiment or to be told the results of an experiment. Examples of items in this scale are “I would prefer to find out why something happens by doing an experiment rather than being told” and “I would rather solve a problem by doing an experiment than be told the answer”. This scale is important and relevant to our context since scientific inquiry is used in many chemistry and science settings in which students take more responsibility for their learning by solving problems and finding their own answers, and instructors act more as facilitators by guiding their learning process. Therefore, it is important to know students' preference toward inquiry because that could influence students' decision to continue in STEM-related careers.

The third chosen scale is career interest in science, which assesses students' interest toward a career in science. This scale is important since one of our goals and the science education goal is to understand factors that could influence students' retention in STEM; therefore this scale allows us to assess students' interests at the beginning of their college career. Previous studies have reported that 35% of students switch out of STEM after their first year in college (Daempfle, 2003); thus assessing students' interest in science careers at this time could help us identify factors influencing their decisions. Examples of items in this scale are “When I leave school, I would like to work with people who make discoveries in science” and “A job as a scientist would be interesting”.

Present study

The goal of the present study is to examine students' science-related attitude scores in an introductory general chemistry course at the college level. Specifically, the aim of this study is to examine several psychometric properties of TOSRA scores in a college setting, including gathering validity evidence for the internal structure and relationships among variables. For this study, a shortened version of the TOSRA instrument is used. The research purposes guiding this study are:

(1) To examine the internal structure of the proposed model for the shortened TOSRA scores in an introductory college chemistry course.

(2) To examine the measurement invariance of the shortened TOSRA scores by sex and race/ethnicity.

(3) To examine the relationship of the shortened TOSRA scores with chemistry achievement and prior math achievement.

Method

Instruments

Attitude. Students' science-related attitudes were measured using the Test of Science-Related Attitudes (TOSRA) developed originally in 1978 by Fraser (Fraser, 1978). It consists of 70 items arranged in seven distinct scales: social implications of science, normality of scientists, attitudes toward inquiry, adoption of scientific attitudes, enjoyment of science lessons, leisure interest in science, and career interest in science. For this study, three scales were chosen. These scales were used in a previous study as an intact instrument and validity evidence for its internal structure was gathered (Fraser et al., 2010). The three scales are normality of scientists, which assesses one's belief about scientists' lifestyle (Normality hereafter), attitudes toward inquiry, which assesses one's preference toward using inquiry in science investigations (Inquiry hereafter), and career interest in science, which assesses one's future interest in a career in science (Career hereafter). The shortened instrument (Shortened TOSRA hereafter) consists of 30 items measured on a 5-point Likert scale. The 5-point Likert scale ranges from Strongly Agree (5) to Strongly Disagree (1), where the middle point (3) corresponds to Not Sure.
Prior math knowledge. Students' prior math knowledge was measured using SAT math scores, which is the quantitative part of the SAT (SATM hereafter). SAT is a standardized test used in the U.S. as a college entrance exam. The SATM scores range from 200 to 800. SATM scores have been found to have high internal consistency coefficients (Cronbach's alpha = 0.92) and are good predictors of science performance, making them widely used in academic research (Ewing et al., 2005).
Chemistry achievement. Achievement in general chemistry was measured using a secure test from the American Chemical Society (ACS). Students' scores on the First-Term General Chemistry Blended Examination from the Examinations Institute of the American Chemical Society Division of Chemical Education (ACS exam hereafter) were used. This exam consists of 40 questions divided into algorithmic and conceptual questions (Examinations Institute, 2005).

Data collection and participants

Participants were students enrolled in an introductory chemistry course during Fall 2010 at a large southeastern public research university. Students' science related attitudes were measured during the second week of classes using Shortened TOSRA. It was administered as a paper and pencil test, and 15 minutes was given to the students to complete it. Students were informed that their participation was voluntary and that the course instructor would not be provided with individualized response data but rather with an aggregate result.

Demographic information for the participants in this study (N = 1292) is shown in Table 1. As presented in Table 1, there are 670 females (51.9%) and 622 males (48.1%) in our sample. Regarding race/ethnicity, 56.2% are classified as White, 17.4% as Hispanic, 9.8% as Black, and 12.8% as Asian.

Table 1 Demographic information (N = 1292)
  No. of students Percentage
Sex
Female 670 51.9
Male 622 48.1
Race/ethnicity
White 726 56.2
Hispanic or Latino 225 17.4
Asian 166 12.8
Black 126 9.8
Unknown 18 1.4
Others 17 1.3
American Indian or Alaskan native 9 0.7

Data analysis

Descriptive statistics. Descriptive statistics were obtained using SAS 9.3 after the negatively stated items were recoded. General trends and univariate normality were assessed for each scale in Shortened TOSRA. Only complete responses were used for subsequent analyses. No imputation strategies were used for missing data. Since one of our interests is examining students' science related attitude by sex and race/ethnicity, descriptive statistics and univariate normality for each group were also examined.
General Shortened TOSRA psychometrics. Psychometric evidence was gathered for the TOSRA scores by examining their internal consistency reliability and internal structure. Internal consistency reliability as measured by Cronbach's alpha was determined for each of the three proposed scales of Shortened TOSRA using SAS 9.3. This reliability coefficient allows us to examine if the items in each scale yield consistent scores. Although Cronbach's alpha cutoffs have been reported to be dependent on the test purpose (Murphy and Davidshofer, 2005), the most common cutoff reported to determine if the scores are sufficiently reliable for research purposes is 0.7 (Cortina, 1993; Murphy and Davidshofer 2005).

The internal structure of the scores was examined using Confirmatory Factor Analysis (CFA), which has been recommended for use with instruments for chemistry education (Arjoon et al., 2013). CFA was performed using Mplus 5.2 to estimate how well the proposed model fits the data. In this case, the proposed model involves a three-factor solution, where each factor has 10 items. The proposed model was run using the Robust Maximum Likelihood (MLR) estimator, which is a preferred estimator when the data are measured on a 5-point Likert scale. To determine if the proposed model had a good fit to the data, different fit statistic guidelines were used such as Comparative Fit Index (CFI) greater than 0.90, Root Mean Square Error of Approximation (RMSEA) less than 0.06, and Standardized Root Mean Square Residual (SRMR) less than 0.08 (Cheng and Chan, 2003; Hu and Bentler, 1999).

Measurement invariance. Another aspect related to validity evidence based on the internal structure is measurement invariance (Kim and Yoon, 2011; Millsap and Everson, 1993; Xu et al., 2016). In general, measurement invariance addresses whether test scores measure the same construct similarly for different groups. Measurement invariance helps us to determine whether differences observed among groups are due to bias related to test construction or if those differences are real differences among groups on the measured construct.

Multi-group CFA was performed to examine measurement invariance of Shortened TOSRA across sex and race/ethnicity (Millsap and Everson, 1993) according to a procedure reported by Raykov et al. (2012). In this procedure, two models are compared. The first model is one where all the parameters are freely estimated for each group: configural invariance. The second model is one where both factor loadings and intercepts are set to be equal across groups: strong invariance. The two models are compared using fit statistic guidelines, similar to the CFA procedure, to determine if the models are plausible and if measurement invariance is plausible for the proposed models for each different group. This procedure is a straightforward and robust procedure, which allows us to test the strong invariance across all factor loadings and intercepts (Xu et al. 2016); which is a requirement to make a valid group mean comparison (Raykov et al., 2012; Widaman and Reise, 1997). The measurement invariance analysis was performed using Mplus 5.2 and using the MLR estimator.

Relationship with other variables. The relationship of the Shortened TOSRA scales with chemistry achievement and prior math knowledge was investigated using Structural Equation Modeling (SEM). SEM is a multivariate technique that allows the study of complex relationships among variables (Kline, 2010; Xu et al., 2013). This data analysis approach helps researchers to answer questions about how variables relate to each other and how well a proposed model of the relationships between these variables fits the data. The model was performed using Mplus 5.2 and using the MLR estimator.

Results and discussion

Descriptive statistics

Descriptive statistics were obtained for the set of variables used in this study. As shown in Table 2, the mean for each variable included in Shortened TOSRA (Normality, Attitude, Career) ranged from 3.52 to 3.83 on a 5-point Likert scale where 3 indicates Not Sure and 4 indicates Agree. In general, students in this sample have a slightly positive perception of their attitude toward science as measured by the three scales in TOSRA. The mean for the ACS exam was 26 points out of 40 possible points, and for the SATM the mean was 593. Univariate normality was assessed for the set of variables via examination of the skewness and kurtosis for each variable. As shown in Table 2, all the variables seem to follow an approximately normal distribution according to their skewness and kurtosis values of less than ±1.
Table 2 Descriptive statistics for all students participating
Scale N Mean STD Min Max Skewness Kurtosis
Normality 1292 3.83 0.51 1 5 −0.30 0.64
Inquiry 1292 3.75 0.70 1.1 5 −0.56 0.50
Career 1292 3.52 0.75 1.3 5 −0.40 −0.09
ACS exam 1130 26.04 6.75 7 40 −0.15 −0.51
SATM 1059 593 78 370 800 −0.10 −0.05

General TOSRA psychometrics

CFA. Evidence for the internal structure of the Shortened TOSRA was gathered using Confirmatory Factor Analysis (CFA). This analysis was performed on the Shortened TOSRA scores to determine if the proposed model, a 3-factor solution where each factor consists of 10 items, fits the data. The factor loadings were examined, and it was observed that for most of the items, the loadings seemed to be reasonable and all loadings were significant. To assess the model fit, different fit indices were considered, as shown in Table 3. According to Table 3, model 1 (the proposed model) fits the data in an acceptable way, but the model presents some misfit as shown by the modification indices.
Table 3 Chi-square (χ2) test of model fit and fit indices from CFA
Model χ 2 df p-Value CFI SRMR RMSEA
Note: χ2 = Chi-square, df = degrees of freedom, CFI = comparative fit index, SRMR = standardized root-mean square residual, RMSEA = root-mean square error of approximation.
1 (30 item) 1570 402 <0.001 0.920 0.040 0.047
2 (24 item) 825 249 <0.001 0.944 0.037 0.042

Modification indices revealed that some items had problems. Most high modification indices were due to item redundancy, e.g. items within a construct were worded very similarly. After evaluating the items with high modification indices, two items from each scale were deleted from the model. For example, two items that were associated with the highest modification index were item 15, “A career in science would be dull and boring”, and item 21, “A job as a scientist would be boring”. Both items were indicators of the Career factor. The high modification index obtained for these items indicated that only one of them was really needed to capture the response. The CFA was performed again for the sample with 24 items. All the items have significant loadings. The fit statistics indicate a better fit for the revised model as shown in Table 3, model 2. For the purpose of this study and subsequent data analysis, the 3-factor model with 24 items will be used.

Reliability. Internal consistency reliability was assessed using Cronbach's alpha coefficient. Cronbach's alpha for each scale in the Shortened TOSRA was obtained for both models (30 items and 24 items). As shown in Table 4, the values for Cronbach's alpha are all higher than 0.70 even with the shortened instrument, which indicates good internal consistency reliability for the three scales.
Table 4 Cronbach's alpha for both models (N = 1292)
Scale Cronbach's alpha (30 items) Cronbach's alpha (24 items)
Normality 0.778 0.772
Inquiry 0.891 0.869
Career 0.891 0.852

Measurement invariance. In general, scores from the three scales of the Shortened TOSRA suggest that students have a slightly positive attitude toward science, as defined by the instrument used. Table 5 presents the descriptive statistics for all students in the sample for the 24-item model. As very similar to Table 2, we can observe that the means range from 3.51 to 3.91, and the distributions are approximately normal according to skewness and kurtosis values.
Table 5 Descriptive statistics for the TOSRA scales (24 item model)
Scale N Mean STD Min Max Skewness Kurtosis
Normality 1292 3.91 0.54 1 5 −0.33 0.55
Inquiry 1292 3.77 0.72 1.1 5 −0.56 0.35
Career 1292 3.51 0.73 1.3 5 −0.41 −0.05

However, it is important to examine if these slightly positive results observed for our sample on each subscale hold for different groups of students. For example, we are interested to know if there are any differences between females and males regarding their science-related attitudes. Before we turn to that question, we want to examine if males and females respond in a similar manner to items on the Shortened TOSRA. We have similar questions about the different racial/ethnic groups within our population. Therefore, we examined the measurement invariance of the proposed model for different groups of students.

Descriptive statistics for group comparisons. Descriptive statistics for females and males are shown in Table 6. The means for each scale are similar for each group, with females having a slightly higher perception of the normality of scientists scale than males with a small effect size (d = 0.15), according to Cohen's guidelines to interpret the magnitude of the effect size (Cohen, 1988).
Table 6 Descriptive statistics by sex (24 item model)
Sex N Scale Mean STD Min Max Skewness Kurtosis
Females 670 Normality 3.95 0.53 1 5 −0.34 1.05
Inquiry 3.76 0.70 1.4 5 −0.51 0.25
Career 3.52 0.73 1.3 5 −0.46 0.01
Males 622 Normality 3.87 0.55 1.8 5 −0.29 0.11
Inquiry 3.78 0.74 1.1 5 −0.61 0.45
Career 3.50 0.74 1.3 5 −0.35 −0.10

Descriptive statistics for different racial/ethnic groups are shown in Table 7. Because of small sample size of some of the racial/ethnic groups, only White, Hispanic, Asian, and Black students are included for further analysis. Asian students have the lowest mean for Normality and Inquiry scales when compared to the other racial/ethnic groups; however, in general there are no large differences between groups of students in their science related-attitudes. A MANOVA was performed on the set of variables by race/ethnicity and a significant difference was found, F(9,3011) = 3.849, p < 0.0001; Wilk's Λ = 0.0973. Post hoc tests indicate that there is a significant difference between Asian and White and between Asian and Hispanic students on the Normality scale, but not between Asian and Black students. For the Inquiry scale, there is no evidence for a significant difference between the groups. It is important to check that all differences or lack of differences observed for groups of students are not an artifact of the instrument used to measure the construct of interest, in this case students' science-related attitudes.

Table 7 Descriptive statistics by race/ethnicity
Race/ethnicity N Scale Mean STD Skewness Kurtosis
White 726 Normality 3.95 0.56 −0.41 0.87
Inquiry 3.76 0.73 −0.68 0.65
Career 3.52 0.77 −0.44 −0.14
Hispanic 225 Normality 3.93 0.53 −0.31 0.15
Inquiry 3.80 0.76 −0.52 0.07
Career 3.49 0.71 −0.37 0.07
Asian 166 Normality 3.77 0.55 −0.31 0.29
Inquiry 3.67 0.66 −0.30 −0.30
Career 3.48 0.68 −0.38 0.12
Black 126 Normality 3.81 0.45 0.05 0.01
Inquiry 3.88 0.64 −0.24 −0.45
Career 3.48 0.68 −0.23 0.26

CFA for multiple groups. In order to determine if the instrument is working similarly for different groups of students, we examined measurement invariance. According to the process described by Raykov et al. (2012), the first step is to run separate CFAs for each group that is being compared. In this step, all the parameters are freely estimated (Raykov et al., 2012). The second step, called strong invariance, is to constrain both the factor loadings and the intercepts to be equal across the different groups. For both steps, the model fit is assessed using fit statistics and the proposed guidelines for fit used to assess any other CFA analysis.

Measurement invariance was examined by sex as shown in Table 8. For the first step, fit indices for both models (females and males) showed a reasonable fit as measured by the CFI, SRMR, and the RMSEA values. For the second step (strong), we can see that having the new constraints in the model does not change the interpretation of the model fit, which indicates that the measurement invariance by sex is plausible. The mean difference by sex for each factor or scale obtained from the measurement invariance procedure after controlling for measurement errors was examined. One interesting result is that, when examining the factor means for the two groups of students in the strong model, we can observe a significant difference in the factor means (0.200) for the Normality scale. This significant sex difference indicates that in our sample, females tend to have a more positive belief about scientists' lifestyle than males, and the difference seems to be real and not an artifact of the instrument used.

Table 8 Chi-square (χ2) test of model fit and fit indices: measurement invariance by sex (3-factor 24 item model)
Model χ 2 df p-Value CFI SRMR RMSEA
Note: χ2 = Chi-square, df = degrees of freedom, CFI = comparative fit index, SRMR = standardized root-mean square residual, RMSEA = root-mean square error of approximation.
Females 482 249 <0.001 0.943 0.044 0.037
Males 451 249 <0.001 0.948 0.042 0.036
Strong 1009 540 <0.001 0.942 0.050 0.037

Measurement invariance was also examined by race/ethnicity. The fit statistics for each model are shown in Table 9. For three of the groups (White, Asian, and Hispanic), the fit indices suggest an acceptable fit; however, there is a lack of model fit for the Black students. Although there is a sample size difference among our groups, the fit statistics (CFI, RMSEA, SRMS) used to evaluate the model fit and the measurement invariance are robust to sample size differences (Chen, 2007; Cheung and Rensvold, 2002; Meade and Bauer, 2007). Therefore, the small CFI value and the large RMSEA and SRMR values in comparison to the other models suggest that the model does not fit as well for this group of students. The lack of fit indicates that measurement invariance is not plausible for Black students in our sample; therefore, we cannot make claims about differences between them and other racial/ethnic group of students on this set of variables. Since the measurement invariance did not hold for Black students, the strong invariance procedure was not performed.

Table 9 Chi-square (χ2) test of model fit and fit indices: measurement invariance by race/ethnicity (3-factor 24 item model)
Model χ 2 df p-Value CFI SRMR RMSEA
Note: χ2 = Chi-square, df = degrees of freedom, CFI = comparative fit index, SRMR = standardized root-mean square residual, RMSEA = root-mean square error of approximation.
White 544 249 <0.001 0.942 0.042 0.040
Asian 310 249 0.005 0.928 0.061 0.038
Hispanic 371 249 <0.001 0.919 0.059 0.047
Black 402 249 <0.001 0.797 0.090 0.070

Individual scales. Since the measurement invariance for the 3-factor model did not hold for Black students, it is important to examine if the measurement invariance does not hold for a particular scale or for all three scales for this group of students. The next step in the analysis is to examine the measurement invariance for each scale. Before examining the measurement invariance, evidence for the internal structure was gathered for each scale. A separate one-factor solution CFA was run for the eight items representing each scale, normality of scientists, attitude toward inquiry, and career interest in science. The model fit for each CFA suggests a reasonable fit when the different fit indexes presented in Table 10 are examined.
Table 10 Chi-square (χ2) test of model fit and fit indices: CFA for each scale
Model χ 2 df p-Value CFI SRMR RMSEA
Note: χ2 = Chi-square, df = degrees of freedom, CFI = comparative fit index, SRMR = standardized root-mean square residual, RMSEA = root-mean square error of approximation.
Normality 81.45 20 <0.001 0.954 0.031 0.049
Inquiry 98.90 20 0.005 0.970 0.027 0.055
Career 110.03 20 <0.001 0.963 0.027 0.059

Since there is some validity evidence for the internal structure of each scale of the Shortened TOSRA using a one-factor solution, the measurement invariance by sex and race/ethnicity was performed for each scale as well. The measurement invariance by sex for each scale was assessed and the fit indices for male and female models as well as the strong model for each scale suggest an acceptable fit. Thus measurement invariance by sex for each of the three scales of the Shortened TOSRA is plausible and no problems were observed for these two groups of students.

The measurement invariance by race/ethnicity was also examined for each scale. The model fit indices for each scale and each racial/ethnic group is shown in Table 11. After assessing their model fit, the normality of scientist scale presents a misfit for Black students in our sample as shown by the sudden decrease in the values for the different fit indices. This misfit for Black students in the Normality scale suggests that the measurement invariance does not hold for this scale; however, it holds for the other two scales, Inquiry and Career, since the model fit is acceptable for them. These results suggest that there is a problem for the Normality scale; therefore, this scale should not be used to interpret differences based on race/ethnicity. Future analysis on this scale should include interviews to examine students' understanding and interpretation of the items in this scale including possible differences on the interpretation between different groups of students.

Table 11 Chi-square (χ2) test of model fit and fit indices: measurement invariance by race/ethnicity for each scale
Scale Model χ 2 df p-Value CFI SRMR RMSEA
Note: χ2 = Chi-square, df = degrees of freedom, CFI = comparative fit index, SRMR = standardized root-mean square residual, RMSEA = root-mean square error of approximation.
Normality White 50.01 20 <0.001 0.967 0.030 0.045
Asian 19.71 20 0.476 1.00 0.039 0.000
Hispanic 29.64 20 0.076 0.951 0.045 0.046
Black 47.67 20 0.001 0.686 0.073 0.105
Inquiry White 70.13 20 <0.001 0.962 0.029 0.059
Asian 36.99 20 0.012 0.927 0.052 0.072
Hispanic 33.45 20 0.030 0.974 0.034 0.055
Black 27.11 20 0.132 0.974 0.040 0.053
Strong 236.90 122 <0.001 0.957 0.070 0.055
Career White 91.14 20 <0.001 0.953 0.032 0.070
Asian 18.31 20 0.567 1.00 0.032 0.000
Hispanic 43.49 20 0.002 0.944 0.044 0.072
Black 23.68 20 0.257 0.978 0.044 0.038
Strong 247.37 122 <0.001 0.951 0.064 0.058

SEM. After gathering validity evidence for the internal structure, the proposed model was used to examine the relationship of students' science related attitudes with achievement in chemistry as a way to gather evidence based on their relationship with other variables. Since Shortened TOSRA has been widely used as a measure of attitude, it is interesting to look at these relationships so that it can be compared with other measures of attitude. However, since the measurement invariance did not hold for all groups of students, its relationship with achievement in chemistry was performed using the two scales for the Shortened TOSRA that have evidence for measurement invariance, Inquiry and Career. Structural Equation Modeling was used to find the relationship between achievement in chemistry and Inquiry and Career (as attitudinal scales) as shown in Fig. 1. For this model, race/ethnicity and prior math achievement were added as predictors to the model to examine their influence on this relationship. The overall fit for this model is adequate even though it has a significant χ2 (176) = 576, p = <0.001 that arises from the large sample size in the study. Other fit indices showed that the model fits the data reasonably well, such as the CFI value (0.937), the SRMR value (0.104) and the RMSEA value (0.050). 48% of the variance in chemistry achievement is explained by the set of variables in the model.
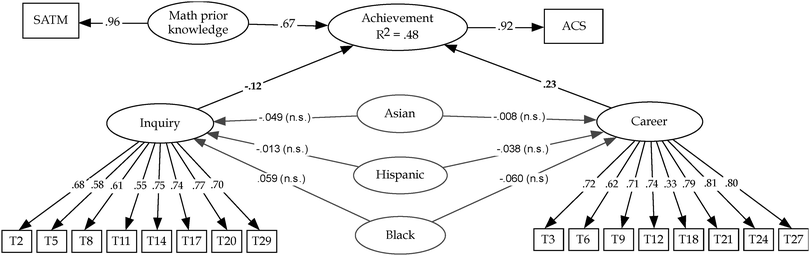
image file: c5rp00185d-f1.tif
Fig. 1 SEM model: model with standardized parameters. Note: white is the reference group; correlations of race/ethnicities with achievement and with prior math knowledge are not shown for clarity purposes.

The standardized parameter estimates from the model are shown in Fig. 1. The SEM model consists of two parts, the measurement model which includes the two scales on the Shortened TOSRA with their items and the path model which consists of the different relationships between achievement in chemistry and the predictors, TOSRA scores, prior math knowledge, and race/ethnicity. For race/ethnicity, three dummy variables representing the racial/ethnic group were added. The three variables are Asian, Hispanic, and Black. For the measurement model, each item loaded significantly in their respective factors with most of the loadings ranging from 0.55 to 0.81. A significant and moderate correlation (r = 0.42) between the two Shortened TOSRA scales, Inquiry and Career, was observed (not presented in the figure).

The relationship between achievement in chemistry with the two scales from the Shortened TOSRA and prior math achievement was also examined. All the standardized path coefficients between them achieved significance; however, the path coefficients for the two scales in the Shortened TOSRA with achievement are small. The path coefficient between inquiry and achievement is −0.12 with an effect size (f2) of 0.02, which indicates a small influence of students' attitude toward inquiry and achievement according to Cohen's rough guidelines (f2 = 0.02, 0.15, and 0.35 for small, medium and large effect sizes, respectively) (Cohen, 1988). For career, the path coefficient is 0.23 with an effect size of 0.06. The only predictor with a large effect size on achievement is prior math knowledge (f2 = 0.81), which is similar to the effect reported in another research study where achievement has been predicted using a measure of attitude and prior math knowledge (Xu et al., 2013). However this large effect size has to be taken with caution because as reported by Xu et al. (2013), the lack of other predictors such as prior chemistry knowledge in the model could lead to an overestimation of the influence of prior math knowledge on achievement.

The relationship between achievement and race/ethnicity was also examined. In this case, the standardized path coefficients between the three dummy variables, Asian, Hispanic, and Black, and the two scales are small (ranging from −0.008 to −0.060) and nonsignificant (n.s.) as shown in Fig. 1. The relationship between race/ethnicity and achievement (not presented in Fig. 1) was also nonsignificant, with values ranging from −0.011 to 0.052. These non-significant effects indicate that there are no group differences in the TOSRA scales, Inquiry and Career, or in achievement by race/ethnicity. The correlation between each racial/ethnic group and prior math knowledge was also examined in the model (not presented in Fig. 1). These correlations are small (ranging from −0.188 to 0.110) but significant differences were found in students' prior math knowledge by race/ethnicity. However, once we control the prior math knowledge in our model, the relationship between race/ethnicity and achievement becomes nonsignificant.

Conclusions and implications

The use of instruments to evaluate curriculum, courses or policies is very common (Holme et al. 2010). The instrument scores are used to make interpretations that could have an impact on different groups of students. The decisions based on those interpretations could influence students' decisions to continue or not into STEM-related fields. In this study we looked at one attitudinal measure, the Test of Science-Related Attitudes (TOSRA), to gather some validity evidence for its use at the college level, in particular, we were interested in examining if the internal structure of the instrument holds for this population and for different groups of students including underrepresented groups in STEM-related fields.

In general, three research purposes guided this study. The first research purpose examined the evidence based on the internal structure of the Shortened TOSRA with college chemistry students. It was found that the internal structure holds for the overall group of students. Two models were proposed for the Shortened TOSRA. The first proposed model has three factors where each factor has ten items each. Although the model fit for this first model was reasonable for our sample, redundancy among items was a problem; thus a second model, a three-factor model with eight items each, was proposed and tested. This second model fits the data well, and this was the model used for further analyses. The model fit obtained for the three scales is consistent with results from Fraser et al. (2010), where the structure of the scales was examined using factor analysis.

Since the internal structure of the instrument holds for our sample, the second research purpose was to explore if that internal structure still holds when focusing on different groups of students. In this case, the measurement invariance was performed by sex and race/ethnicity. For sex, the measurement invariance was plausible, which allows us to make comparisons between females and males in our sample. In this case, we found that females tend to have a more positive attitude toward the scientist lifestyle than males, which is a surprising finding since the expectation is that males would have more positive attitudes toward this lifestyle. However, even with that expectation, different research studies have mixed findings when comparing the attitudes of females and males toward science (Bui and Alfaro, 2011; Smist, 1996). In a high school setting just before starting college, Smist (1996) found that females had a more positive attitude toward scientists' lifestyles similar to our finding, but a more negative attitude toward a career in science. However, in a college setting, Bui and Alfaro (2011) found that there were no statistical differences between males and females in their attitudes toward science. For race/ethnicity, the measurement invariance was not plausible for Black students in our sample. In this case, there is no evidence that the internal structure holds for all the racial/ethnic groups in our sample. The results suggest that interpretations based on this instrument may not apply similarly to all students, especially for Black students in our sample. Further measurement invariance analysis revealed problems for the normality of scientists scale with Black students. However, the results suggest that for the other two scales, attitude toward inquiry and career interest in science, the measurement invariance is plausible by race/ethnicity in our sample.

The third research purpose used SEM to evaluate the relationship between achievement and the two scales of Shortened TOSRA taking into consideration prior math knowledge and race/ethnicity. The results indicated a small but significant influence of attitude toward inquiry and career interest on achievement when adding prior math knowledge and race/ethnicity as predictors. However, the biggest influence on achievement came from the prior math knowledge as measured by the SATM. This is consistent with previous studies that have reported that SAT math continues to be one of the major predictors of chemistry achievement (Lewis and Lewis, 2007; Spencer, 1996; Xu et al., 2013). However, it is important for the chemistry community to not only look at prior math knowledge as a factor to understand students' performance, but also to focus on other factors that have demonstrated to have some influence such as (Seery, 2009; Wagner et al., 2002; Xu et al., 2013), self-efficacy (Merchant et al., 2012; Nieswandt, 2007) and motivation (Akbas and Kan, 2007; Black and Deci, 2000). The relationship between race/ethnicity with Shortened TOSRA scales and with achievement was nonsignificant, suggesting that there are no group differences in these variables, which is comparable with results obtained from descriptive statistics and from the measurement invariance analysis.

This study has some limitations. First, the sample was drawn from a unique population of introductory chemistry in a single semester, thus the results presented in this study might not be representative of other populations. Second, the sample size is not equal across groups and it is relatively small for our underrepresented groups, Black and Hispanic students. Third, only three predictors, attitude toward inquiry, career interest in science and prior math knowledge, were included in the SEM model. Additional predictors or models were not explored as part of this study.

Despite the limitations in this study, there are several implications for chemistry education researchers. This study represents one attempt to gather validity evidence based on internal structure by sex and race/ethnicity and their relationship with the variables; however, the models in this study, including for measurement invariance and for SEM, need to be replicated in another context. The new context could include students in different chemistry courses, university types, and different countries. Furthermore, since we are interested in underrepresented groups in STEM, a replicate of the study with a bigger sample of underrepresented groups is needed to have a better understanding of the psychometric properties of the scores of the Shortened TOSRA for the different groups of students. Also, additional validity evidence such as information about responses processes should be gathered in the future to have some evidence of how students, especially underrepresented groups, are interpreting the items in each scale of the instrument. This information will help us to get some insights into the reasons the Normality scale is not working properly for Black students. For the SEM model, other factors that can influence students' achievement in chemistry could be added to the model as a way to improve the prediction and to explain the relationships better. Other possible factors that have been suggested as factors that can influence students' achievement in chemistry are prior conceptual knowledge (Seery, 2009; Wagner et al., 2002; Xu et al., 2013), self-efficacy (Merchant et al., 2012; Nieswandt, 2007), motivation (Akbas and Kan, 2007; Black and Deci, 2000), self-concept (Bauer, 2005; Lewis et al., 2009), and instructional strategies (Merchant et al., 2012; Schroeder et al., 2007). In general, more work is needed to capture and understand the different factors that can potentially influence students' achievement in chemistry.

References

  1. Adolphe F. S. G., Fraser B. J. and Aldridge J. M., (2003), A cross-national study of classroom environment and attitudes among junior secondary science students in Australia and Indonesia, in D. L. Fisher and T. Marsh (ed.) Science, mathematics and technology education for all: Proceedings of the Third International Conference on Science, Mathematics and Technology Education, Perth, Australia: Curtin University of Technology, pp. 435–446.
  2. Aiken L. R., (1980), Attitude measurement and research, New Directions for Testing and Measurement, 7, 1–24.
  3. Akbaş A. and Kan A., (2007), Affective factors that influence chemistry achievement (motivation and anxiety) and the power of these factors to predict chemistry achievement, J. Turkish Sci. Educ., 4(1), 10–20.
  4. Arjoon J. A., Xu X. and Lewis J. E., (2013), Understanding the state of the art for measurement in chemistry education research: examining the psychometric evidence, J. Chem. Educ., 90(5), 536–545.
  5. Bauer C., (2005), Beyond “student attitudes”: chemistry self-concept inventory for assessment of the affective component of student learning, J. Chem. Educ., 82(12), 1864.
  6. Bauer C., (2008), Attitude towards chemistry: a semantic differential instrument for assessing curriculum impacts, J. Chem. Educ., 85(10), 1440–1445.
  7. Black A. E. and Deci E. L., (2000), The effects of instructors' autonomy support and students' autonomous motivation on learning organic chemistry: a self-determination theory perspective, Sci. Educ.84(6), 740–756.
  8. Bui N. H. and Alfaro M. A., (2011), Statistics anxiety and science attitudes: age, gender and ethnicity factors, Coll. Student J., 45(3), 573–585.
  9. Chen F. F., (2007), Sensitivity of goodness of fit indexes to lack of measurement invariance, Struct. Equ. Modeling, 14(3), 464–504.
  10. Cheng S. and Chan A. C. M., (2003), The development of a brief measure of school attitude, Educ. Psychol. Meas., 63, 1060.
  11. Cheung G. W. and Rensvold R. B., (2002), Evaluating goodness-of-fit indexes for testing measurement invariance, Struct. Equ. Modeling, 9(2), 233–255.
  12. Chin C. C., (2005), First-year Pre-service Teachers in Taiwan—Do they enter the teacher program with satisfactory scientific literacy and attitudes toward science?”, Int. J. Sci. Educ., 27(13), 1549–1570.
  13. Cohen J., (1988), Statistical power analysis for the behavioral sciences, 2nd edn, Hillsdale, NJ: Erlbaum.
  14. Cook A. F., (2013), Exploring freshmen college students' self-efficacy, attitudes, and intentions toward chemistry, Honors College Capstone Experience/Thesis Projects, West Kentucky University, paper 399.
  15. Cooper C. I. and Pearson P. T., (2012), A genetically optimized predictive system for success in general chemistry using a diagnostic algebra test, J. Sci. Educ. Technol., 21(1), 197–205. DOI: http://10.1007/s10956-011-9318-z.
  16. Cortina J. M., (1993), What is Coefficient Alpha? An Examination of Theory and Applications, J. Appl. Psychol., 78(1), 98–104.
  17. Cukrowska E., Staskun M. G. and Schoeman H. S., (1999), Attitudes towards chemistry and their relationship to student achievement in introductory chemistry courses, South Afr. J. Chem.-Suid-Afr. Tydskr. Chem., 52(1), 8–14.
  18. Daempfle P. A., (2003), An analysis of the high attrition rates among first year college science, math, and engineering majors, J. Coll. Stud. Ret., 5(1), 37–52.
  19. Dalgety J. and Coll R. K., (2006), Exploring first-year science students' chemistry self-efficacy, Int. J. Sci. Math. Educ., 4(1), 97–116. DOI: http://10.1007/s10763-005-1080-3.
  20. Dalgety J., Coll R. K. and Jones A., (2003), Development of Chemistry Attitudes and Experiences Questionnaire (CAEQ), J. Res. Sci. Teach., 40(7), 649–668. DOI: http://10.1002/tea.10103.
  21. Dowdy J. T, (2005), Relationship between teachers' college science preparation and their attitudes toward science, Texas A&M University.
  22. Eagly A. H., Chaiken S., Petty R. E. and Krosnick J. A., (1995), Attitude strength, attitude structure, and resistance to change, Attitude strength: Antecedents and consequences, 4, 413–432.
  23. Ewing M., Huff K., Andrews M. and King K., (2005), Assessing the reliability of skills measured by the SAT® (Office of Research and Analysis, Trans.): The College Board.
  24. Examinations Institute, (2005), American Chemical Society Division of Chemical Education, First Term General Chemistry Special Examination (Form 2005): University of Wisconsin-Milwaukee (UWM).
  25. Fraser B. J., (1977), Selection and validation of attitude scales for curriculum evaluation, Sci. Educ., 61(3), 317–329. DOI: http://10.1002/sce.3730610307.
  26. Fraser B. J., (1978), Development of a test of science-related attitudes, Sci. Educ., 62(4), 509–515. DOI: http://10.1002/sce.3730620411, The whole instrument is accessible via this link: http://www.pearweb.org/atis/documents/4/identify_for.
  27. Fraser B. J., Aldridge J. M. and Adolphe F. S. G., (2010), A cross-national study of secondary science classroom environments in Australia and Indonesia, Res. Sci. Educ., 40(4), 551–571. DOI: http://10.1007/s11165-009-9133-1.
  28. Gooding C. T., Swift J. N., Schell R. E., Swift P. R. and McCroskery J. H., (1990), A causal-analysis relating previous achievement, attitudes, discourse, and intervention to achievement in biology and chemistry, J. Res. Sci. Teach., 27(8), 789–801.
  29. Holme T., Bretz S. L., Cooper M., Lewis J., Paek P., Pienta N. and Towns M., (2010), Enhancing the role of assessment in curriculum reform in chemistry, Chem. Educ. Res. Pract., 11(2), 92–97.
  30. House D. J., (1995), Noncognitive predictors of achievement in introductory college chemistry, Res. Higher Educ., 36(4), 473–490.
  31. Hu L. and Bentler P. M., (1999), Cutoff criteria for fit indexes in covariance structure analysis: conventional criteria versus new alternatives, Struct. Equ. Modeling, 6, 1–55.
  32. Hurtado S., Newman C. B., Tran M. C. and Chang M. J., (2010), Improving the rate of success for underrepresented racial minorities in STEM fields: insights from a national project, New Dir. Inst. Res., 2010(148), 5–15.
  33. Jegede O. J. and Fraser B., (1989), Influence of socio-cultural factors on secondary school students' attitude towards science, Res. Sci. Educ., 19(1), 155–163.
  34. Kelly A. (ed.), (1987), Science for girls, Open University Press.
  35. Khalili K. Y., (1987), A crosscultural validation of a test of science related attitudes, J. Res. Sci. Teach., 24(2), 127–136. DOI: http://10.1002/tea.3660240205.
  36. Kim E. S. and Yoon M., (2011), Testing measurement invariance: a comparison of multiple-group categorical CFA and IRT”, Struct. Equ. Modeling, 18(2), 212–228.
  37. Kline R. B., (2010), Principles and Practice of Structural Equation Modeling, 3rd edn, New York: Guilford Press.
  38. Klopfer L. E., (1971), Evaluation of learning in science, in Handbook of formative and summative evaluation of student learning, pp. 559–642.
  39. Lay Y. and Khoo C., (2011), The relationships between actual and preferred science learning environment and attitudes towards science among pre-service teachers in Sabah, Maaysia, Paper presented at the International Conference of Teaching and Learning, International University, Malaysia.
  40. Lewis S. E. and Lewis J. E., (2007), Predicting at-risk students in general chemistry: comparing formal thought to a general achievement measure, Chem. Educ. Res. Pract., 8(1), 32–51.
  41. Lewis S. E., Shaw J. L., Heitz J. O. and Webster G. H., (2009), Attitude counts: self-concept and success in general chemistry, J. Chem. Educ., 86(6), 744.
  42. Loucks-Horsley S. and Olson S., (2000), Inquiry and the National Science Education Standards: A Guide for Teaching and Learning, National Academies Press.
  43. Meade A. W. and Bauer D. J., (2007), Power and precision in confirmatory factor analytic tests of measurement invariance, Struct. Equ. Modeling, 14(4), 611–635.
  44. Merchant Z., Goetz E. T., Keeney-Kennicutt W., Kwok O. M., Cifuentes L. and Davis T. J., (2012), The learner characteristics, features of desktop 3D virtual reality environments, and college chemistry instruction: a structural equation modeling analysis, Comput. Educ., 59(2), 551–568.
  45. Millsap R. E. and Everson H. T., (1993), Methodology review: statistical approaches for assessing measurement bias, Appl. Psych. Meas., 17(4), 297–334.
  46. Murphy K. R. and Davidshofer C. O., (2005), Psychological Testing: Principles and Testing, 6th edn, Upper Sadler River, New Jersey.
  47. Nieswandt M., (2007), Student affect and conceptual understanding in learning chemistry, J. Res. Sci. Teach., 44(7), 908.
  48. Oskamp S. and Schultz P. W., (2005), Attitudes and opinions, Psychology Press.
  49. Rahayu S., (2015), Evaluating the affective dimension in chemistry education, in Affective Dimensions in Chemistry Education, Springer, pp. 29–49.
  50. Raykov T., Marcoulides G. A. and Li C., (2012), Measurement Invariance for Latent Constructs in Multiple Populations A Critical View and Refocus, Educ. Psychol. Meas., 72(6), 954–974.
  51. Robinson N. R., (2012), An evaluation of community college student perceptions of the science laboratory and attitudes towards science in an introductory biology course, The University of Alabama TUSCALOOSA.
  52. Schibeci R. A., (1986), Images of science and scientists and science education, Sci. Educ., 70(2), 139–149.
  53. Schibeci R. A. and McGaw B., (1981), Empirical validation of the conceptual structure of a test of science-related attitudes, Educ. Psychol. Meas., 41(4), 1195–1201.
  54. Schroeder C. M., Scott T. P., Tolson H., Huang T. Y. and Lee Y. H., (2007), A meta-analysis of national research: effects of teaching strategies on student achievement in science in the United States, J. Res. Sci. Teach., 44(10), 1436–1460. DOI: http://10.1002/tea.20212.
  55. Scott F. J., (2012), Is mathematics to blame? An investigation into high school students' difficulty in performing calculations in chemistry, Chem. Educ. Res. Pract., 13(3), 330–336.
  56. Seery M. K., (2009), The role of prior knowledge and student aptitude in undergraduate performance in chemistry: a correlation-prediction study, Chem. Educ. Res. Pract., 10(3), 227–232.
  57. Smist J. M., (1996), Science self-efficacy, attributions and attitudes toward science among high school students, Doctoral Dissertations, University of Connecticut.
  58. Smist J. M., Archambault F. X. and Owen S. V., (1994), Gender differences in attitude toward science, Paper presented at the annual meeting of the American Educational Research Association, New Orleans, LA.
  59. Song J. and Kim K. S., (1999), How Korean students see scientists: the images of the scientist, Int. J. Sci. Educ., 21(9), 957–977.
  60. Spencer H. E., (1996), Mathematical SAT test scores and college chemistry grades, J. Chem. Educ., 73(12), 1150–1153.
  61. Telli S., Cakiroglu J. and den Brok P., (2006), Turkish secondary education students' perceptions of their classroom learning environment and their attitude towards biology, in Contemporary approaches to research on learning environments, pp. 517–542.
  62. Triandis H. C., (1971), Attitude and attitude change, vol. 8, New York: Wiley.
  63. Trudel L. and Métioui A., (2011), Diagnostic of attitudes towards science held by pre-service science teachers, Int. J. Sci. Soc., 2(4), 63–83.
  64. Tulloch D., (2011), Determinants and effects of the learning environment in college classes, Curtin University, Science and Mathematics Education Centre.
  65. Wagner R. V. and Sherwood J. J., (1969), The study of attitude change, Brooks/Cole Publishing Company.
  66. Wagner E. P., Sasser H. and DiBiase W. J., (2002), Predicting students at risk in general chemistry using pre-semester assessments and demographic information, J. Chem. Educ., 79(6), 749. DOI: http://10.1021/ed079p749.
  67. Weinburgh M., (1995), Gender differences in student attitudes toward science – a metaanalysis of the literature from 1970 to 1991, J. Res. Sci. Teach., 32(4), 387–398.
  68. Welch A. G., (2010), Using the TOSRA to assess high school students' attitudes toward science after competing in the first robotics competition: an exploratory study, Eurasia J. Math. Sci. Technol. Educ., 6(3), 187–197.
  69. Widaman K. F. and Reise S. P., (1997), Exploring the measurement invariance of psychological instruments: applications in the substance use domain, in The science of prevention: methodological advances from alcohol and substance abuse research, pp. 281–324.
  70. Wititsiri S., (2006), The effect of learning environments on student attitude and cognitive achievement in physical chemistry laboratory classrooms, APERA Conference, Hong Kong.
  71. Xu X. and Lewis J. E., (2011), Refinement of a chemistry attitude measure for college students, J. Chem. Educ., 88(5), 561–568. DOI: http://10.1021/ed900071q.
  72. Xu X., Kim E. S. and Lewis J. E., (2016), Sex difference in spatial ability for college students and exploration of measurement invariance, Learn. Individ. Differ., 45, 176–184.
  73. Xu X., Villafane S. M. and Lewis J. E., (2013), College students' attitudes toward chemistry, conceptual knowledge and achievement: structural equation model analysis, Chem. Educ. Res. Pract., 14, 188–200.
  74. Zhang D. and Campbell T., (2011), The psychometric evaluation of a three-dimension elementary science attitude survey, J. Sci. Teacher Educ., 22(7), 595–612.
This journal is © The Royal Society of Chemistry 2016
Click here to see how this site uses Cookies. View our privacy policy here.