Visualization of problem solving related to the quantitative composition of solutions in the dynamic GeoGebra environment

Abstract

Problem solving in the field of quantitative composition of solutions (QCS), expressed as mass share and molar concentration, is essential for chemistry students. Since successful chemistry education is based on different mathematical contents, it is important to be proficient in both mathematical and chemistry concepts as well as interconnections between them. One of the main objectives of this study was to create dynamic worksheets, applying software GeoGebra, which makes a strong link between real life problems from the field of QCS and their visual representations. The created models offer interactive connection within triangle –numerical data, concrete and abstract visual representations of the problem. The other important issue was to investigate if application of this novel teaching approach will lead to improvement of students' achievements in QCS problem solving. Ninety students of the first, second and third year of the bachelor chemistry study program, were subjects of the research. The students were classified into experimental and control groups based on the results of the initial test. Both groups were trained in the same pool of problems from the QCS field. In the control group the traditional approach based on algebraic methods was applied. The new didactic approach to the graphical method based on the dynamic properties of GeoGebra was presented to the experimental group. After two months, the final testing of all students was conducted. The students' answers were analysed and it is shown that the results of the experimental group were significantly better than the results of students in the control group. The results of these research studies confirmed that the students' learning achievement in solving QCS problems is better when they are familiar with the GeoGebra environment.

---

Introduction

Education in chemistry, even at the basic level, is a complex human activity which demands understanding of various concepts and requires the transfer of knowledge between several scientific fields, among which mathematics and physics are the most important ones. A solid mathematical background usually represents a promising perspective toward the development of good performance in chemistry. The foundation of this relation should be searched within some similarities of these fields, which comprise not only science knowledge, but also a logical method of thinking, so much potentiated in mathematics.

Proficiency in problem solving can be considered as one of the significant indicators of chemistry knowledge and represents the most desirable outcome of a chemistry curriculum, allowing more profound and clearer understanding of the studied matter. It also provides the student with an opportunity to improve the skill to apply newly gained knowledge. The lack of mathematical literacy and especially true understanding of math concepts that are essential in chemistry education leads to mechanical application of formulaic methods that are only poorly understood by chemistry students (Leopold and Edgar, 2008).

Problem solving skills are of essential importance in all fields of chemistry, especially general (Sikirica, 2001), analytical (Pecev et al., 2002), physical chemistry (Mioč and Hercigonja, 1996), though very often they represent a serious obstacle for chemistry students, stemming more from insufficient prior mathematical knowledge and fundamental understanding of mathematical concepts (Potgieter et al., 2008). An earlier study (Pınarbasi and Canpolat, 2003) revealed that students even failed to grasp concepts of unsaturated, saturated and supersaturated solutions. Not only a better understanding of learning difficulties, but also the necessity for substantial changes in the teaching process was recognized as essential for the improvement of meaningful learning (Gil-Perez and Carrascosa, 1990). Several reasons can be identified as the most probable: chemistry professors assume that students know basic math concepts; both professors and students believe that if students have not learned the basics of math by the university course, they will not learn them ever; also, they do not want to do someone else's job teaching students the basics of mathematics because they believe it is the job of professors of mathematics in high school (Leopold and Edgar, 2008).

Previous studies have shown that deeper learning is closely linked to the better quality of learning outcomes in higher education (Prosser and Millar, 1989; Marton and Säljö, 1997). The student focused approach to the teaching which is basically aimed at changing their conceptions (Trigwell et al., 1994) helps some students to obtain a deeper approach to learning (Trigwell et al., 1999).

Contemporary trends in education put an emphasis on the interdisciplinary approach to teaching, which demands connecting different school subjects as well as different topics inside one subject into one logical entity with the aim of organizing them around one problem or topic (Roth, 1993). Superficial skills in graphic and algebraic representations in mathematics lead to even more pronounced problems in chemistry. Therefore, more attention should be dedicated to improve graphical skills and to emphasize connectivity between algebraic and graphic representations when teaching mathematics, but also to encourage the application of a graphical approach when solving chemistry problems.

Humans process information both in visual and a textual-verbal manner (Paivio, 1986). An increasing number of research studies is dedicated to the impact of external representations to a higher level of cognitive processing of information (Zimmermann and Cunningham, 1991; Tall, 2002; Arcavi, 2003; Gilbert, 2008; Rapp and Kurby, 2008). In teaching practice, depending on the mathematical or scientific content that is being studied, it is necessary to achieve an optimal relationship between symbolic and visual information, as well as between logical-analytical and visual-creative thinking.

Visual-based learning involves the application of illustrations, multimedia, visual computer interfaces and experimental work, in which students observe, form mental images, and analyse graphs and visualizations of scientific phenomena. Realization of the cognitive-visual approach means that in the teaching process is necessary to apply graphic representations, schemes, tables, conceptual maps, presentations, interactive teaching materials, simulations, applets, animations, etc. The efficiency of any kind of visual representation is to a great extent predestined by appropriate cognitive support (Kozma et al., 1997; Mayer and Moreno, 2002; Moore et al., 2013).

Various visual problem representations can be roughly divided into two groups – concrete and abstract. Concrete visual representations illustrate the real life objects corresponding to the considered problem. Since such visual representations are more interesting and evocative they are considered to enhance students' motivation, supporting them in the design of virtual reality learning environments. At the same time they have limited transfer ability, and can in some cases divert beginner students' attention from the relevant to superficial information. Abstract visual representations use conventional symbols to represent the relevant elements of the considered problem. They help students to focus on the essential characteristics of the problem, but they are more difficult to understand and may require a better foreknowledge connected with problem solving. The combination of concrete and abstract visual representations illustrates apparent real-life objects' characteristics and uses conventional symbols to represent their substantial features, benefiting in that way from the advantages of both visual representations (Moreno et al., 2011).

For effective science studies, mathematics is of essential importance and because of that it is reasonable to expect from the majority of science students to apply mathematical skills into the specific scientific topics, though Woolnough suggested that physics students experienced difficulties making links between the theories and principles of science, the mathematical tools and the studied phenomena. Although graph construction and interpretation have been identified as important outcomes of science education, numerous students have incomplete knowledge on this subject (Woolnough, 2000). Such problems could be caused by deficiencies in their mathematics knowledge or by the complex transfer process of mathematics to a new scientific domain. Transfer of learning, where some of the knowledge acquired in one domain can be used in the learning of the other domain is a quite complex process, with many cases of failure (Lobato, 2008).

The linkage between the mathematical background and understanding equations in physics was explored by Sherin who emphasized that prior to physics instruction, students should adopt at least the basic knowledge of mathematical models and learn how to explain their content (Sherin, 2001). In most cases, modern chemistry teaching at universities is dominated by a teacher-centred approach, and generally an adopted attitude that as the teacher has a greater knowledge of a given area, he will be taught better and the students will therefore learn better (Eiliks and Byers, 2009), neglecting that the only thing that can be transferred is the information, but the meaning and understanding can be formed only by the learner (Coll and Taylor, 2001; Bailey and Garrett, 2002). Very often in practice, students highly value good lectures, but this does not automatically mean that they learn better (Eiliks and Byers, 2009).

An increasing number of school-level studies have been dealing with the factors influencing technology integration (e.g.Becker, 2001; Laborde, 2001; Ruthven and Hennessy, 2002) revealing that technology integration was predominated by teachers' attitude and approach, closely linked to the social and cultural background (Artigue, 2002; Ruthven and Hennessy, 2002) as opposed to the access to technology. Educational software plays the imperative role in the integrative approach to mathematics and science education. They provide a wide range of opportunities for illustrative and appealing presentation of the contents, linking interdisciplinary information and illustrating the practical use of mathematical contents (diSessa et al., 1991; Bayraktar, 2002; Waxman et al., 2003; Li and Ma, 2010; Higgins et al., 2012; Milanovic et al., 2012; Lee et al., 2013).

There are a number of situations in the educational process when some basic mathematical concepts prove to be necessary in the study of a variety of topics from physics, chemistry, biology, etc. A typical example of a problem that is treated in mathematics as well as in chemistry classes are the problems related to the percentage of solutions. The concept of solution concentration is fundamental to solution chemistry and is featured in the Chemical Concepts Inventory designed for General Chemistry students at the College or University level (Mulford, 1996). Besides percentage of the solution, the other representations of QCS are also very important in chemistry as molar concentration (c), mass concentration (γ), molal concentration (b), molar share (x) of the solution and they are significant concepts that are learnt within various chemistry courses at the university level education in Serbia.

In this research we used GeoGebra, open-code software specially designed for educational purposes and application in the teaching and learning process from elementary school all the way to the university. Mathematical objects are represented in GeoGebra in three ways: graphically (geometrically), algebraically and numerical. All representations of one object are dynamically connected and they automatically change with the change of each representation, no matter which is the original way of creating the object. GeoGebra is a powerful visual-cognitive tool which is used in the teaching process for explaining, exploring and modeling of mathematical and other concepts and processes (Karadag and McDougall, 2009). This educational software can be used for demonstration, problem solving, problem modelling, illustration, animation and creation of an interactive applet. The application of GeoGebra dynamic models in teaching is a contemporary way of using computers in teaching. The property of simulation is also to provide the option of changing entry and exit data of models, which leads to a more profound understanding of the assumption i.e. the model that is being observed because we obtain a cognitive understanding of the way a system in question is actually functioning. The dynamic and interactive GeoGebra environment allows the user to change the given parameters and explore the consequences of those changes. These characteristics place GeoGebra into a category of computer packages for modeling and simulation. The application of models and simulations in the teaching process motivates students for further exploration and in that process they make new discoveries and acquire them personal experience and in that way increase their cognitive capacities in mathematics, but in chemistry, too (Maaß, 2010).

The general aim of the research is to examine the influence of implementation of a new teaching approach based on visualization in the GeoGebra environment on students' achievement of QCS problem solving. Bearing in mind the necessity of connecting basic graphical mathematical concepts to improve students' knowledge in the field of QCS, applying interactive software GeoGebra, the main objectives of this study were defined:

• To make an initial test the same for the 1st, 2nd and 3rd year of bachelor academic studies of chemistry at the Faculty of Science and Mathematics in Nis (Serbia), which will enable the assessment of their skills in the QCS area which is of crucial importance in chemistry education.

• To create the models using software package GeoGebra for the visualization of problem solving in the field of QCS and make them available for free download.

• To provide students with training in both algebraic (control group) and graphical ways of considering problems in the field of QCS and applying models created in GeoGebra (experimental group).

• To make a final test the same for all students, which will enable the assessment of their knowledge in solving problems in the field of QCS, after familiarization with the graphical method and models created in GeoGebra.

According to the authors' best knowledge this is the first application of interactive GeoGebra models for learning and possible enhancement of problem solving skills in the field of QCS.

Basic methods for solving problems from the field of solution mixing – a chemical approach

Problems in the field of QCS (expressed as a mass share – percentage) are typical both for chemistry and mathematics, and learning about this field in Serbia has been conducted within high school curricula of chemistry and mathematics, and continues within various chemistry curricula at the university level (general, analytical, and physical chemistry).

The main problem appears from the fact that mathematicians have the knowledge of mathematics and accordingly their approach is narrowed to strictly mathematical consideration of the problems, while chemists have the knowledge of chemistry, followed by corresponding access to problem solving. The lack of interaction in many cases leads to incomplete perception of these problems and consequently to the limited knowledge and understanding. Considering solving problems from the field of QCS as essential in chemistry education, many textbooks cover this field (Sikirica, 2001).

– Definitions of the terms which are used in solving these types of problems are:

– Mass share of the solute in solution (w),

– Mass of the solute in the solution (m_s),

– Mass of the solution (m).

We assume the following: (1) all the solutions we are taking into consideration are homogenous, (2) the mixing of the solution is instantaneous, (3) the volume of the solution mixture is equal to the sum of mixed solutions volumes and (4) volumes of the solutions cannot be negative.

The mass share of the solute in a solution is defined as the ratio of the mass of the dissolved substance to the mass of the solution.

w = m_s/m (1)

In the case of the mixing of two solutions the symbols are as follows:

w ₁ is the mass share of the solute in the first solution,

w ₂ is the mass share of the solute in the second solution,

w ₃ is the mass share of the solute in the new solution which is obtained by mixing the first and the second solution,

m _1s, m_2s, and m_3s are the masses of the solutes in the corresponding solutions and m₁, m₂, and m₃ are the masses of the corresponding solutions.

The basic ways to solve problems from the field of solution mixing are:

– Applying the formula to calculate the values

– Applying the rule of mixing

– Appling the rule of cross

– The graphical method

For the first three methods we may say that they are algebraic methods because they are based on solving linear equations or systems of equations. The methods of applying the formula or the rule of mixing and cross are dominant in the teaching and learning of chemistry in Serbia, while the graphical method is very rarely used.

The method of applying the formula in order to calculate the values. We determine the mass of the solute in the first and the second solution: m_1s = w₁m₁ and m_2s = w₂m₂. From the previous steps we derive that the mass of the solute in the new solution can be calculated as the sum of the masses of the solute in the initial solutions

m_3s = m_1s + m_2s = w₁m₁ + w₂m₂.

In this way we obtain formula (1) for calculating the mass share of the solute in the new solution, which equals

w₃ = (w₁m₁ + w₂m₂)/(m₁ + m₂) (2)

By applying formula (2) we are able to calculate any unknown variable, if the rest of them are known.

“The mixing rule”. In the process of deriving the mixing rule we begin with formula (2). By transforming this formula we come to:

w₁m₁ + w₂m₂ = w₃(m₁ + m₂)

m₁(w₁ − w₃) = m₂(w₃ − w₂)

If w₁ > w₂ then

m₁/m₂ = (w₃ − w₂)/(w₁ − w₃) (3)

If w₁ < w₂ then

m₁/m₂ = (w₂ − w₃)/(w₃ − w₁) (4)

Formulas (3) and (4) are rather convenient for solving practical problems when masses of solutions are not determined, but the solutions need to be taken in a certain ratio, to obtain a mixture with a pre-set mass share.

“The rule of cross” is the name for a diagonal scheme of the mixing rule, for a case of mixing two solutions. The initial masses and initial mass shares of the solutions are in the left corners (usually the larger share in the upper left), in the intersection the specified mass share, and in the right corner subtractions of initial mass shares and the specified mass share.

The obtained result shows in what mass ratio the first and the second solution should be mixed in order to obtain the specified mass share.

The graphical method

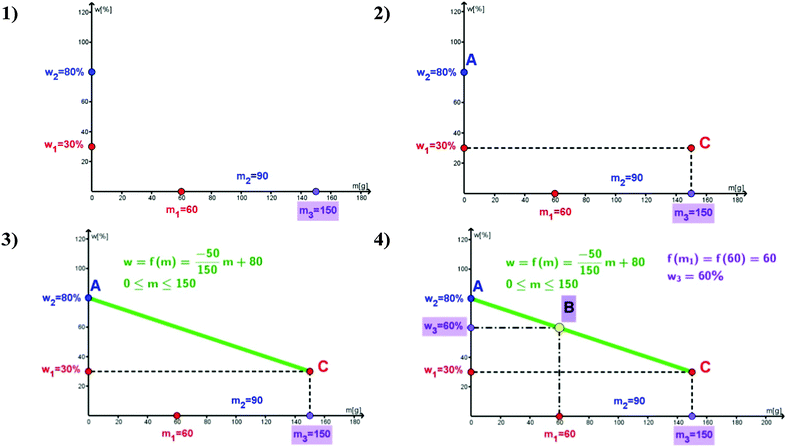
Relation (2) can be written in the form:

If the values w₁, w₂ and m₃ are constants, then w₃ is the linear function of m₁. Since 0 ≤ m₁ ≤ m₃ the mass share of the solute in the new solution is function f, defined as:

The graph of function f is segment AC shown in Fig. 1. If m = 0, then f(0) = w₂, and the point A(0,w₂) corresponds to real situation when the mass share of the new solution is equal to the mass share of the second solution (there is no first solution). If m = m₃, then f(m₃) = w₁, and the point C(m₃,w₁) corresponding to the mass share of the new solution is equal to the mass share of the first solution (there is no second solution).

Fig. 1 Graphical method – general representation for the mass share.

The graph of function f represents the graphical dependence of the mass share of newly obtained solution on the masses of the initial solutions. Mass share w₃ can be read out from the graph of function f as the ordinate of the point B(m₁,w₃) for abscissa m₁, meaning that f(m₁) = w₃ (Fig. 1).

This method, applied in its classical form, leads to an approximate result and is both time consuming and technically demanding. The use of millimeter paper can provide a more accurate result. However, these limitations are encountered only when its usage is conducted in order to calculate the exact result, but if it is applied for a better understanding of the relations between the entering data and the corresponding processes, or for verification of the result(s) obtained by using any of the computing methods it is a valuable tool for improvement of problem solving skills.

The visualization enabled by applying the graphical method in the solving mixture problems represents a powerful tool in critical assessment of the obtained results.

Presentation of the different situations in the field of QCS using graphs of linear functions is in fact an essential consideration of the substantial characteristics of the observed problem as well as quantitative relationships stemming from it, expressed with the corresponding mathematical symbols. This indicates that such visualization can be considered as an abstract visual representation.

Let us consider one common example of the problem from the field of QCS. It can be solved by using any of algebraic methods, which is common, but having in mind numerous advantages offered by the graphical method, we decided to introduce the graphical one.

Problem 1. A solution with mass of m₁ = 100 g, and solute mass percentage w₁ = 20%, was mixed with another solution with mass of m₂ = 150 g and solute mass percentage of w₂ = 50%. Calculate the solute mass percentage of the newly obtained solution w₃.

Graphically, the problem can be presented as it is shown above. In this case points A and C are given as: A(0,50) and C(250,20). Point B has abscissa equal to 100 (Vertical line m₁ = 100 intersect segment AC at point B). The ordinate of point B is in fact w₃ and it can be determined as the intersection of horizontal line containing point B and y-axes (Fig. 2).

Fig. 2 Example of the classical graphical method for mass share problem solving.

Looking at the graph (Fig. 2) the student can visually, very easy, conclude that the value of w₃ is in the range of 20% to 50%. However, obtaining such a conclusion by using the algebraic method (formula 2 and 3) is always a problem for students. Also, such visualization enables students to check out the obtained results (obtained with other methods). For example, if w₃ is over 50%, then the result is wrong and has to be corrected.

As it was mentioned before, and can be seen in this example, it is practically impossible to obtain the exact solution for w₃ (Fig. 2) by using the classical graphic method. We can say that it is close to 40%. However, the graphic presentation of the considered problem can be used together with the algebraic problem solving and for practicing some basic mathematical knowledge acquired in high school.

Let us remark that segment AC is drawn by using the coordinates of points AC, obtained from the calculations of the mass share of the solute in the new solution (relations (2), (5) and (6)). Relation (6) can be written in the form

f(m) = km + n,

where k is the slope of the line determined with f, and n is the y-intercept. Segment AC belongs to the graph of f, for 0 ≤ m ≤ m₃.

Looking at the graph, the student can conclude that function f is the decreasing linear function, and therefore the slope k is negative. It can be determined from the graph and from relation (6), wherefrom it follows that . This can be checked on the graph. Now, function f can be written as: , wherefrom it follows that w₃ = f(m₁), i.e., f(100) = 38, meaning that the solute mass percentage of newly obtained solution in our example is w₃ = 38%.

It is obvious that the visual information obtained from the graph can be connected with conceptual mathematical knowledge about linear function and enables (by applying an appropriate calculating procedure) obtaining the exact problem solution.

The presentation of QCS by the molar concentration (molarity) is very important in chemistry, because of its direct application in consideration of stoichiometric, kinetic, analytical, etc. problems, since the phenomena studied within these branches of chemistry are closely related to the concept of mole. The molar concentration (c) represents the number of moles (n) of the solute in the volume of the solution (V), usually expressed in units mol L⁻¹.

During mixing of the corresponding volumes (V₁ and V₂) of two solutions of the same substance, and of molar concentrations c₁ and c₂, the solution of volume V₃ (V₃ = V₁ + V₂) is obtained with concentration c₃, and is calculated according to the formula:

which is an analogue of formula (2).

Since there is a linear relationship between molar and percent concentrations (M – molar mass of the solute, g mol⁻¹, d – density of the solution, g mL⁻¹), as well as between the mass of solution and its volume m = Vd, graphical presentation of the mixing solution problem in the case of molar concentration is analogous to a graphical presentation for the case of mass share.

If the values c₁, c₂ and V₃ are constants, then c₃ is the linear function of V₁. Since 0 ≤ V₁ ≤ V₃ the molar concentration of the solute in the new solution is function f, defined as:

The graph of function f is segment AC shown in Fig. 3.

Fig. 3 Graphical method for molar concentration.

All other ways of QCS presentations are also linearly related to the mass share, and consequently they can be visualized by using the graph of linear function.

New didactical approach to the graphical method in the GeoGebra environment

GeoGebra software is used for algebraic and graphical presentations of mathematical contents, providing a geometry model, which, besides the visualization, allows the changing of parameters satisfying the conditions of the considered problem. The central question of discussions and analysis in the literature (Hohenwarter et al., 2008; Tatar, 2013) is addressed to the possibilities of dynamic environments, to make mathematical contents “easily seen and understood”.

The present paper deals with a new didactical approach to the graphical method of problem solving from the field of QCS, by using GeoGebra software. First the graphical method of this problem is translated from millimeter paper to the GeoGebra screen and then it is improved based on the properties of GeoGebra.

Problem 1 and its solution are visualized in Fig. 3, by using GeoGebra and its Algebra and Graphics views. There are tools for inputting the points A(0,50), C(250,20), segment AC, and finally point B. These points are presented in the Algebra and Graphics view. Point B is obtained as the intersection of the line m₁ = 100 and segment AC. Let us remark that the ordinate of point B can be seen exactly, i.e., w₃ = 38% and this is the first advantage of the GeoGebra environment.

GeoGebra has excellent graphical and dynamical facilities characterized by sliders. This means that the considered problem 1 can be extended to the problem with the parameters m₁, w₁, m₂, w₂ given in a corresponding interval. A slider can be created for each of these parameters and the corresponding solution can be constructed by using GeoGebra for any chosen values of the input parameters. In this real chemical problem the software GeoGebra enables graphically the exact determination of the mass share of the new solution w₃, which is obtained by mixing the two solutions with corresponding mass shares of the solutes, w₁, w₂, and masses, m₁, m₂ (Fig. 4).

Fig. 4 Example of the graphical method of problem solving in GeoGebra.

By using the graphical method in the GeoGebra environment the students have to determine the range of the mass shares w₁, w₂. It is obvious that 0 ≤ w₁ ≤ 100%, 0 ≤ w₂ ≤ 100%. The intervals for the masses can be taken arbitrary but these intervals must contain the prescribed masses m₁ = 100, and m₂ = 150.

Moving the sliders (i.e., changing values of input parameters) involves the corresponding changes in the Graphics view of the mixture problem. Consequently, the changes of the results of the mass share of the new solution can be followed on y-axes.

The visual dynamic and interactive GeoGebra environment enables new perception of the problems of the mixture acquiring better conceptual knowledge in this field of chemistry.

In the following part, we shall emphasize the advantages of the dynamic properties of GeoGebra software applied to the graphical method of determining the mass share, w₃ in mixing problems of solutions:

• The change of the mass shares w₁, w₂, by moving sliders

– involves the change of the result mass share, w₃;

– Always it holds w₁ ≤ w₃ ≤ w₂.

• The change of the masses m₁, m₂, by moving sliders

– involves the change of the result mass share, w₃;

– Always it holds w₁ ≤ w₃ ≤ w₂.

Previous considerations are important for chemists to assess/foster the fundamental concept that percentage of obtained solution is always between percentages of the initial solutions.

• If the mass share w₁ is increasing, and w₂ is fixed, then the solute mass share w₃ is increasing, and the difference between the values w₁ and w₃ is decreasing.

Chemical context: When the percentage of one of the initial solutions is increased, the percentage of the obtained solution is increasing too.

• If the mass m₁ is increasing, and m₂ is fixed then the solute mass share w₃ is getting closer to the mass share w₁, i.e. the difference between the values w₁ and w₃ is decreasing.

Chemical context: When increasing the mass of one of the initial solutions, percentages of this and obtained solution become closer.

The students can continue with the discussion, analysing different cases for the mass shares and masses of the solutions for specific situations – addition of water, water evaporation and addition of pure solute.

Referring to a linear dependence between the w and c, all previously discussed cases relating to w, are also valid for c, and they were the basis for creating GeoGebra worksheets for solving the problem of solution mixtures, whose concentration is given by c.

GeoGebra dynamic worksheets that correspond to each of previously mentioned cases, including QCS representation as mass share and molar concentration have been created and can be downloaded from GeoGebraTube (2015).

GeoGebra also allows the visualization and simulation of the real situation in the field of QCS, no matter how it is presented. We created GeoGebra worksheets, having in mind the results of the study by Moreno, with regard to the finding that best results were achieved when a combination of concrete and abstract visual presentations was used. All worksheets created in the GeoGebra environment include visualizations that are dynamically linked with numerical data.

The concrete visualization of the QCS problem for molar concentration in the GeoGebra environment is shown in Fig. 5, expressed by the rectangles representing quantitative relationships between the numbers of moles, volumes and concentrations in solutions. The numbers of moles correspond to the areas of rectangles (with sides – c and V). The dynamic properties of GeoGebra applied to the given rectangles enable students to notice the additivity of the volume of solution, and the number of moles of the dissolved substance. Also, the rectangles provide students with the possibility of seeing the quantitative proportions between the concentrations of the solutions. The concrete visual problem's representation has multiple roles: the connectivity with the problems from the real context, the cognitive support of algebraic methods and provides a tool for better understanding of abstract visual representations. Segment AC (Fig. 5) constructed using entering numerical data, as a function of concentration (y-axis) and volume (x-axis), represents the abstract visual representation. The changes in input data of the real QCS problem cause the corresponding changes of concrete and abstract visual representations.

Fig. 5 GeoGebra dynamic worksheet for solving the problem of mixing two solutions using molar concentration as QCS presentation.

Research methodology

The research has been conducted on a sample of 90 students (30 students of the first, second and third year of the Bachelor chemistry study program) at Faculty of Science and Mathematics in Nis. Before the research activities, we informed all students about their main scopes and goals and we asked students for participation in the research. Students applied for research on a voluntary basis. Experimental lessons and tests were conducted by special schedule and have not caused any disturbance to regular students' obligations. The lectures and tests were realised by authors of the research.

After the selection of students the initial testing was conducted in April 2015. For the purpose of research, students of each year of the study program were separated into two groups – experimental (E) and control group (C). The groups were formed after the initial testing, based on the achieved results. Precisely, the groups were formed following the students' scores, putting the pairs of students with a close point number in the different groups. The procedure was repeated for each initially tested group of students of the same year of study. In this way a rather uniform structure of both control and experimental groups was achieved, considering the year of study and level of students' knowledge of QCS, i.e. two matched, vertically stratified groups were formed.

Both groups of students were trained, by solving problems in the field of QCS for 8 hours (2 hours per week) with a different approach. In this research we applied a new didactic approach with the experimental group, using the graphical method realised in the GeoGebra environment. The traditional algebraic methods were applied with the control group. Final testing was conducted in July 2015 (approximately two months after the training).

Two tests-initial and final, from the field of QCS (considering mass share and molar concentration), were created. Both tests contained two parts. First parts of both tests consisted of the common problems from the field, with an idea to assess the extent to which the students are familiar with this area as well as to get insight into methods they usually apply in solving these types of problems. The objective of the second part of the tests was to estimate whether students have conceptual knowledge of QCS, skills to apply knowledge to new situations and ability of critical thinking. These parts of the tests were dedicated to the problems with one missing entering information (that would be necessary for obtaining unique result) and their solution was difficult by the application of purely algebraic methods. Their consideration involves substantial understanding of the chemical concept of QCS and transfer of mathematical thinking in problem solving related to QCS. The duration time of each test,initial and final, was 60 minutes. Data collection was carried out using paper-and-pencil form of test.

Initial test

First of all, the students were subjected to an initial testing. The initial test is a non-standardized test used with a purpose to examine the level of students' knowledge as well as to identify weaknesses and difficulties they encounter in the process of solving problems from the field of QCS (Table 1).

Table 1 Initial test

1.	By mixing 150 mL of NaCl solution whose molar concentration 0.2 mol L^−1, with another solution with molar concentration of 0.8 mol L^−1 and a volume of 500 mL, the new solution is obtained. Calculate the molar concentration of the new solution. Answer: molar concentration of NaCl in the new solution is _______________________.
2.	By mixing a solution of glucose whose mass share is 20% and mass of 150 g, with another solution of glucose, a new solution is obtained, the mass of which is 500 g and mass share 50%. Calculate the mass share of glucose in the second solution. Answer: mass share of glucose in second solution is ______________________.
3.	To a solution of KCl with a mass share of 45% and mass of 120 g, 60 g of water were added. Calculate the mass share of KCl in newly obtained solution. Answer: mass share of KCl in newly obtained solution is ______________________.
4.	We have 400 mL of saharose solution with a molar concentration of 0.2 mol L^−1. Certain quantity of water evaporated and a new solution with a molar concentration of 0.4 mol L^−1 was obtained. Calculate the volume of water that has evaporated. Answer: the volume of water that has evaporated is _________________________.
5.	By mixing 200 mL of NaI solution whose molar concentration is 1 mol L^−1 with another solution with a concentration of 2 mol L^−1, we get a new solution. The maximal range of NaI molar concentration in newly obtained solution is ________________________< c <________________________. Explanation:
6.	By mixing of 200 mL of KI solution molarity of 1.4 mol L^−1 with another KI solution, a new solution whose molarity is 0.2 mol L^−1 is obtained. The maximal range of the molarity of added KI solution is _____________________< c <_____________________. Explanation:
7.	To a solution of AgNO3 a certain amount of pure AgNO3 is added. Thus, a new solution is obtained, which weighs 200 g, with a mass share of 40%. The maximal range of pure AgNO3 mass which is added is __________________< m <___________________. Explanation:
8.	We have 300 g of KBr solution with a mass share of the solute of 40%. From the solution, certain quantity of water was evaporated. The maximal range of mass of water which has evaporated is _______________________< m <_____________________. Explanation:

---

The test was composed of eight problems of objective type but with different complexity. Tasks for the test were selected considering general and analytical chemistry curricula. The validity of this test is evident because it contains all the relevant notions and procedures from the field of QCS expressed as mass shares and molarity.

The first part of this test (problems from 1 to 4) contained typical problems from the area of QCS in which the unknown mass or mass share i.e. volume and molarity needed to be calculated based on the known data. The students were free to solve the problems using methods that they are familiar with. In the educational practice these problems are most often solved by using formulas or “the rule of cross”. For each correctly solved problem they obtained 10 points. The problem was considered to be correctly solved if the solving procedure and the result were correct. In the case of the incorrect result they gained 0 points.

The second part of the test (problems from 5 to 8) contained problems where the students were supposed to determine the intervals for all the possible solutions of the given problem. For each correctly determined limit of the interval, students could win 3 points. In each problem the students were supposed to give an explanation for determined limits of intervals and for each explanation got 0, 2 or 4 points, depending on the adequacy of the explanation, i.e. whether it was incorrect, partly correct or correct, correspondingly.

The training

After the initial testing, the experimental group was provided with education about the linkage between mathematical and chemical point of view in the field of solving problems of QCS. The main issue was the application of the classical graphical method for representation and solving problems in this field as well as the critical assessment of the obtained result (disregarding the way how the result was calculated). After these lectures, the GeoGebra models created earlier by authors were demonstrated. Firstly, students were introduced step-by-step to the models representing computer displays of the classic graphics methods, including the construction of graphs of linear functions illustrating the relationships between QSC and mass i.e. volume of the solution, respectively. In addition to graphics of linear functions, the corresponding simulations, as forms of concrete visual presentations of problems related to QCS, were shown as well. The numerical data, algebraic connections between them, illustrations and graphics of linear functions are linked dynamically, which are demonstrated to the students by moving the slider of the mass (volume) of the starting solution, drawing the graph of linear function (Fig. 5 and 6 in Appendix 1). At the same time changes are observed in the visual presentation by rectangles. Subsequently, models for solving specific cases from the field of QCS (mixing the two solutions, the addition of water, the evaporation of water and adding a solute in solution) were demonstrated. The teacher has shown the application of the GeoGebra environment for problem solving. All created GeoGebra models were copied by students and they were additionally encouraged to independently explore options that are enabled by created models, according to the instructions provided in the training and which are also included within each model (option Tutorial). They were also offered the possibility of consulting the teacher in the process of independent manipulation and exploitation of the models presented during the training.

Fig. 6 Geogebra dynamic worksheet for solving the problem of mixing two solutions using mass share as QCS presentation.

The control group was also provided with an education in the same duration about solving problems from the field of QCS, using worksheets with problems considering both percentage and molar concentration. Firstly, fundamental chemistry concepts from the area of QSC were explained in details as well as the necessity of application formulaic representations of mass share and molarity. Worksheets, containing the text of the problem, fields for entering data, calculations, final results and result check were used in work with students (Appendix 3). During education, attention was paid to following the general algorithm for problem solving – starting with careful reading of the problem, writing down input data, deciding on the method for problem solving, calculation and finally writing the solution on the appropriate place in the work sheet. They also were motivated by the teacher to apply various methods for the same problem solving. The control group was also encouraged to adopt a critical approach to the obtained problem solutions and they were instructed to check the validity of the result, fulfilling the field in the worksheets –result check.

Final test

The final test (Table 2) was also divided into two parts. The first part (problems from 1 to 4) contained problems of the similar type as in the initial test, but with a changed set of entry data and with a higher level of problem complexity. The answers were scored by 0 for incorrect and 10 points for the correct answer. The purpose of this part of the test was to assess if the introduction of the new teaching approach (graphical method visualized in the GeoGebra environment) led to the improvement of students' general skills in QCS problem solving. Furthermore, to perceive if the experimental group has recognized any advantages of graphical method application or still finds algebraic methods more appropriate. The second part of the test (problems from 5 to 8) also contained similar types of problems as in the initial test. The answers were scored in the same manner as corresponding problems in the initial test.

Table 2 Final test

1.	By mixing two solutions of NaOH, whose percentages by weight of the solute are equal to 50% and 10% respectively, a new solution with a mass share of 20% and a mass of 240 g is obtained. Calculate the mass of the initial two solutions. Answer: mass of the first solution is _________________________.
2.	The solution of nitric acid with a molarity of 0.3 mol L^−1 and a volume of 250 mL is mixed with a solution of nitric acid with a molar concentration of 1.5 mol L^−1. Molarity of newly obtained solution is 1 mol L^−1. Calculate the volume of the newly obtained solution. Answer: volume of the newly obtained solution is __________________________.
3.	To NaCl solution, 80 mL of water was added, obtaining in that way solution with a molar concentration of 0.6 mol L^−1 and a volume of 320 mL. Calculate the molar concentration of starting NaCl solution. Answer: molar concentration of NaCl is __________________________.
4.	To a solution of KI, 150 g of solid KI is added thereby obtaining new solution with a mass share of 55% and the mass of 400 g. Calculate the mass share of the starting solution. Answer: mass share of KI is __________________________.
5.	By mixing of 150 g of glycerol solution whose mass share is 25% with another glycerol solution with a mass share of 50% the new solution was obtained. The maximal range of the mass share of newly obtained solution is _____________________<w<___________________. Explanation:
6.	By mixing 200 mL of HCl solution whose concentration is 0.1 mol L^−1 with the other HCl solution, the new solution, with a molarity of 0.5 mol L^−1 was obtained. The molar concentration maximal range of added HCl solution is _______________<c<____________________. (Molar concentration of concentrated HCl is 12 mol L^−1) Explanation:
7.	By mixing 100 mL of H2SO4 solution whose concentration is 0.5 mol L^−1 with the other H2SO4 solution, the new solution, with a volume of 200 mL was obtained. The molar concentration maximal range of H2SO4 in the newly obtained solution is ________________<c<____________________. (Molar concentration of concentrated H2SO4 is 18.4 mol L^−1) Explanation:
8.	From the solution of K2SO4, with a mass share of 30% and mass of 500 g, certain amount of water is evaporated. The maximal range of mass of water which has evaporated is ______________________<m<________________________. Explanation:

---

Processing of data obtained from tests was done by applying Student's t-test with the significance level of p = 0.01, using Microsoft Excel 2010 software.

Results and discussion

Based on the questions imposed by the research, we established the general hypothesis that introduction of the new didactical approach to solving QCS problems (graphical methods in the GeoGebra environment) will cause better achievements of students who were subjected to it, as opposed to those who worked in a traditional way.

The results of the initial test

In part I of the initial test the students were most successful in solving problem 1. In this problem the known parameters are the solution volume and molarity of the initial solution, and most students calculated the molarity of the solute in the new solution by using formula. The students achieved the lowest scores in solving problem 4 (evaporation of water from the initial solution). In part II of the test the most successfully solved problem was problem 7 (estimation of the amount of water that evaporated from the solution) and less successfully problem 6 (estimation of molarity of the added solution).

Statistical results of the initial test are shown in Table 3. The arithmetic mean of percentages of the student's achievements in the first part of the test was 52.22%, in the second 34.81%, and on the entire test 43.51%. The calculated standard deviations for the both parts of the test, as well as for the entire test, indicates that students are nonhomogeneous with respect to the tested knowledge. There are larger standard deviations in part II of the test, in comparison to part I.

Table 3 Statistical results of the initial test

	N	M (%)	SD (%)	t	p
Part I	90	52.22	32.38	6.98	0.000
Part II	90	34.81	29.58
Test	90	43.51	28.66

---

Results of the initial test have shown that the students have achieved lower scores in the second part of the test than in the first one. In order to determine whether the difference between the achieved results in parts I and II is statistically significant, we applied the Student's t-test for difference of paired means. Based on the obtained data (t = 6.98, p = 0.000) we concluded that there exists a statistically significant difference between results achieved in parts I and II of the initial test.

Such a result was expected because students were able to solve problems in part I by applying the methods which are often used in chemistry classes in schools (use of formulas, the mixing rule, and the cross rule). However, these methods are not quite suitable for solving problems in part II of the test because it contains open-type problems. After careful observation we noticed that students used only algebraic methods for solving problems in part II of the test. It should be emphasized that none of the students had used the graphical method for solving problems in the initial test. In order to estimate which of the offered answers could be solutions of the problem, students needed to have a fundamental comprehension of the concept of QCS, as well as mathematical skills needed in the process of problem solving.

The experimental and control group formation

Based on the results the students achieved in the initial test they were divided into two groups, experimental (E) and control group (C). The formed groups consisted of 15 students from every year of study, all the levels of knowledge and similar results of the initial test (with the difference of ±2 points), both for parts of the test and the entire test, as shown in Table 4.

Table 4 Arithmetic mean and standard deviation of initial test results (%) for experimental and control groups

	N	Part I		Part II		Test
		M (%)	SD (%)	M (%)	SD (%)	M (%)	SD (%)
E	45	52.22	32.34	34.72	28.90	43.47	28.25
C	45	52.22	32.78	34.89	30.57	43.56	29.39

---

The results of the final test

The final test was done by all students. In part I of the final test the students from the E group were more successful than students from the C group. Both the groups had the highest score in solving problem 4 (addition of pure solute to the initial solution) and the lowest in solving problem 1 (problem of determining the mass of initial solution). The students from the E group were more successful in solving all the problems from part II of the test. The students from both the groups achieved the lowest score in solving problem 7 (estimation of the molar concentration range of the newly obtained solution). In problem 5 solving (estimation of the mass share range of the newly obtained solution) the best score was registered for the E group, while for the C group the highest score was for problem 8 (estimation of the mass range of evaporated water).

Statistical results of the final test are shown in Table 5. The experimental group demonstrated better results both in parts I and II of the test. The calculated standard deviations indicate that the distribution in the C group is non-homogeneous for parts I and II and the whole test, while in the E group non-homogenous distribution was registered only in part II.

Table 5 Statistical results of the final test

	N	Part I					Part II					Test
		M (%)	SD (%)	t	p	η ^2	M (%)	SD (%)	t	p	η ^2	M (%)	SD (%)	t	p	η ^2
Based on the t-test effect size η^2 represented by Cohen's η^2 – small (0.01), medium (0.06), large (0.14) (Cohen, 1988).
E	45	73.89	18.42	3.70	0.000	0.13	67.50	29.92	4.43	0.000	0.18	70.69	20.13	4.82	0.000	0.21
C	45	58.33	21.32				38.94	31.16				48.64	23.14

---

Student's t-test for the final test results showed following findings– t = 3.70, p = 0.000, for part I, t = 4.43, p = 0.000, for part II, and t = 4.82, p = 0.000, for the entire test, so we concluded that there was a significant statistical difference between groups E and C, in favor of the experimental group in parts I and II and the whole test.

The effect size of the experimental factors is medium for part I (η² = 0.13) to large, for part II (η² = 0.18) and for the whole test (η² = 0.21), meaning that the obtained difference enables a practical advantage of the experimental group compared to the control group.

Student's t-test for difference of paired means (Table 6) was applied for testing if there is a statistically significant difference between results of both groups (E and C) on parts I and II of the final test. For the E group, t = 1.47, p = 0.15, so there is not a statistically significant difference between the arithmetic means of the results for parts I and II of the test. For the C group t = 4.89, p = 0.000, so there is a statistically significant difference between arithmetical means of the results for parts I and II of the test. The application of the new approach in solving problems, for the E group has resulted in the equal success in both parts of the test, while students of the C group, as well as in the initial testing, significantly worse solved problems from part II of the test.

Table 6 Statistical results of the Student's t-test for parts I and II of the final test

	E				C
	M (%)	SD (%)	t	p	M (%)	SD (%)	t	p
Part I	73.89	18.42	1.47	0.15	58.33	21.32	4.89	0.000
Part II	67.50	29.92			38.94	31.16

---

A registered improvement in the E group results could be explained by newly gained knowledge in the field of visualization of problem solving, using dynamic software GeoGebra, since all other parameters for both groups were the same, i.e. the experimental factor caused better achievements.

Methods for solving problems

In order to acquire a deeper insight in the ways students applied for solving problems in the initial and final test, without consideration of achieved results (because their achievements were discussed in detail in the previous section) we analyzed in what extent they used each of the known methods for problem solving (algebraic, that includes application of formula, mixing rule or rule of cross and visual, which comprises concrete and abstract visualization) per each problem.

The initial test. All students were applying algebraic methods for solving problems, wherein the dominant method was formulaic. It was observed that some students in solving problems used the proportion both to define percentage and molarity and for subsequent calculations, which represents the level in chemistry problem solving, typical for the initial learning of QCS. Therefore, special attention in the training of students was dedicated to the formulaic presentations of percentage and molarity, which is the basis for the implementation of some of the algebraic methods as well as visual representations based on these algebraic methods. It was also noted that some students didn't write down the input data of the tasks, but they immediately started with solving them, which in some cases led to the incorrect inclusion in the formula, and consequently to an incorrect result.

Additional observation was that none of the students consistently verified the obtained solution. This is why in the later training, teacher insisted on the following methodological algorithm for problem solving, following specially created worksheets, either in paper (C group) or created in GeoGebra software (E group).

The final test. In comparison to the initial test, more students wrote down the input data, prior to starting any calculus, which may be considered as a consequence of the application of paper worksheets (C group) and GeoGebra worksheets (E group), which by default contain input data in the top left corner. Students have adopted this form to the highest extent. Likewise, a larger number of students have done check of the validity of the obtained solution. None of students did use proportions to define the basic chemical concepts or for later computations.

The control group. All students of the control group were applying algebraic methods for solving problems (formulaic, mixing rule and rule of the cross). When the problems about mass share from part I of the test are solved, continues to dominate the application of the formulas, but there were students who have applied the mixing rule and rule of the cross. With regard to molarity, corresponding formulas were applied too. In part II of the test, for the determination of the interval limits, they applied considerations associated with conceptual knowledge of chemistry concerning QCS and for the further calculus formulaic method.

The experimental group. The analysis of the problem solving methods for the experimental group is shown in Table 7 – concrete visual representation, abstract visual representation, visual representation (sum of concrete and abstract representations) and the algebraic method (formulaic, mixing rule or rule of the cross), per each problem, for Part I, Part II and the whole test presented as the percentage of a general number of the students, without immersion if the final result is correct or not.

Table 7 Analysis of the problem solving methods for the E group (%) in the final test

Problem	1	2	3	4	Part I	5	6	7	8	Part II	Test
a Sum of the solved problems where concrete or abstract visual representation is used. b Any of the algebraic methods was applied. c Category “Attempt to solve problem” represents sum of the categories Visual and Algebraic. d Category “No attempt to solve problem” represent samples where wasn't written anything, just written down entry data or scratched written solution.
Concrete visual representation	17.77	35.56	33.33	22.22	27.22	8.89	6.67	11.11	22.22	12.22	19.72
Abstract visual representation	35.56	20.00	24.45	40.00	30.00	77.78	68.89	53.33	44.45	61.11	45.56
Visual representation^a	53.33	55.56	57.78	62.22	57.22	86.67	75.56	64.44	66.67	73.33	65.28
Algebraic^b	28.89	31.11	31.11	28.89	30.00	6.67	8.89	8.89	15.56	10.00	20.00
Attempt to solve problem^c	82.22	86.67	88.89	91.11	87.22	93.33	84.44	73.33	82.22	83.33	85.28
No attempt to solve problem^d	17.78	13.33	11.11	8.89	12.78	6.67	15.56	26.67	17.78	16.67	14.72

---

In part I of the test (with all known inputs) students have applied both algebraic (30%) and visual representations (57.22%). For problems with molarity in most cases they used concrete visual presentations (problems 2 and 3, see Appendix 2) while in problems with mass share they mainly applied abstract presentations i.e. the graph of linear function (problems 1 and 4, see Appendix 2). In part II of the test, the much greater number of students used visual presentations: concrete (12.22%) or abstract (61.11%) with respect to the algebraic (10%) method. The fifth and sixth task, in which the conceptual knowledge of QCS is most obviously associated with graphics of linear functions, students mostly solved using abstract visual representations. In solving tasks 7 and 8, which were more complex, students are slightly less decisive to the application of the abstract method in comparison to tasks 5 and 6.

Scanned samples of student's work in the final test with correct application of the visual representations for each problem solving are presented in Appendix 2.

Limitations, implications and future research

Related to the limitations of the study, we can point out that it was conducted on a purely voluntary basis. Possibly, motivation of the students would have been higher (and correspondingly their achievements better) if the education had been incorporated in any of official study curricula (general, analytical, physical chemistry or even mathematics). This could be overcome by introducing the educators to our novel approach to teaching, recognizing its benefits and their incorporation in formal curricula. In light of the role of visualization in the formation of long-term knowledge, a possible weakness is the relatively short time between the training and final test (about two months). To some extent, unavailability of computer for each student during the training under teacher's supervision could be the possible weakness. All students received detailed instructions about installation of the software and usage of created GeoGebra models, yet it was impossible to control if all students followed them in an appropriate way, though none of them reported any problem.

In the contrast to the study limitations, some advantages cannot be disregarded. The created GeoGebra models are free and available online for both educators and students at GeoGebraTube (2015).

The proposed graphical dynamic models can be used at college, high school, and even middle school levels because they represent fundamental chemistry concepts. In addition, the models can be used by teachers for creating teaching materials, such as worksheets that might motivate students to engage in a more active way. Recently, the GeoGebra applet for mobile phones has been developed, facilitating and making models created in GeoGebra software even more available.

Further investigation in this field would comprise the incorporation of the proposed teaching approach into formal curricula at all levels of chemistry education and a complete study of its impact on chemistry knowledge of the students, as well as comparison of the application of the solely classical graphical method versus GeoGebra worksheets, in order to discern specific impact of the software intervention. Also, the other concepts used in expression of QCS (molality, mol share, and mass concentration) might be visualized and represented in the dynamic way enabled by GeoGebra software. Since the present study is one of the novel ones from the field, its impacts should be expanded and verified with students from the other Serbian high school institutions and high schools. Also it would be of essential importance to explore transfer of knowledge from the field of QCS, gained within present research, to other fields of chemistry directly corresponding to QCS, for example stoichiometry.

Conclusion

Visualization of problem solving in the field of QCS, expressed as mass share and molar concentration by applying GeoGebra dynamic software, demonstrates great potential for application in educational purposes through improvement of conceptual knowledge and ability of algorithmic solving of problems by the students. Majority of the students from the experimental group decided to apply the visual approach (using both concrete and abstract representations) to the problem solving after the training. As the software are interactive and enable visualization solving QCS related problems become simple and easy, helping students to establish functional links between corresponding structural elements of different representations (Seufert, 2003). Since students manipulate with algebraic and visual representations of the real problems, they are more likely to adopt to a greater extent mathematical and chemical concepts related to the subject, forming long-term knowledge (Kozma and Russell, 1997; Arcavi, 2003; Kozma and Russell, 2005; Gilbert, 2008). The critical point that should not be disregarded are well founded mathematical skills and knowledge about linear function and its graph implementation in chemistry, as necessary conditions for the ability to transfer (Woolnough, 2000; Britton et al., 2005; Potgieter et al., 2008) into QCS problem solving.

The created models also improved the students' ability to estimate quantitative relationships appearing in QCS problems in a well thought-out manner, as well as to have critical anticipation about the obtained results. The use of the GeoGebra models in teaching and learning of QCS problem solving had as an outcome statistically significant better results, substantiating the effectiveness of this innovative didactical approach which is in accordance with the findings of Chiu and Wu, who registered students' benefit from the multiple representations via construction of accurate mental pathways through application of simulations (Chiu and Wu, 2009).

Due to the fact that the models created in dynamic software GeoGebra deal with basic mathematical concepts and procedures which are familiar to high school students as well, the introduction of the proposed method makes sense even at a younger age. Though application of a combination of different visual representations (concrete and abstract) leads to the best cognitive achievements (Moreno et al., 2011), it would be more appropriate to use created GeoGebra models for younger students using only concrete visual representation.

The educators from high-school to the university level, who are interested in implementing innovative teaching methods that include a student centred learning approach, can benefit from the study. Also, students as participants in the learning process perceive this approach as valuable, adopting introduction of the novel approach to a great extent.

Appendix 1

GeoGebra dynamic worksheets for problem solving of QCS expressed as a mass share

In the area of QCS the following problems are most frequent: mixing of two solutions with different mass shares, addition of the solute, addition of water, and water evaporation. For each of these problems the authors of this paper have conducted a mathematical modeling process using GeoGebra software. The GeoGebra worksheet that will be described below, can be downloaded from http://https://tube.geogebra.org/material/show/id/1472101

Mixing of the two solutions with different mass shares. Based on the entry data, we distinguish the following cases

(1) w₁, w₂, m₁, m₂

(2) w₁, w₂, w₃, m₃

(3) w₁, w₂, w₃, m₁

(4) w₁, w₃, m₁, m₃

All four cases are modeled in one GeoGebra file. Fig. 6 shows the layout of the dynamic worksheet. The problem we wish to solve is chosen by checking one of the boxes shown in the upper left window corner. The text of the problem will appear, as well as the input box in which we can change the values of the entry data or by moving the corresponding sliders. By changing the values in the input box or by moving sliders we also change the corresponding values in the text of the problem. In this manner it is possible to generate new problems and their solutions. By moving sliders the values of entry parameter are changing, which leads to changes in depending variables. The sliders of the entry data defined in this manner do not allow for the wrong choice of data. If a value smaller than the minimum is entered GeoGebra shows the minimal allowed value in that input box. If a value bigger than the maximum is entered GeoGebra shows the maximum allowed value in that input box.

Observing the graphical part of the window, students can explore the consequences of these changes and draw conclusions about the dependence between the variables. Because of its dynamic nature and interactivity with the user, the created GeoGebra worksheets can be used by students for independently exploring and solving the problems of QCS.

When the worksheet user selects one of four types of problems, then in the graphical part of the window is shown only the coordinate system. Graphical solution of the problem is showing step by step, by checking boxes displayed in the bottom left corner of the window:

– Show the input data in the coordinate plane

– Show points that are required for drawing graphics

– Show graph

– Reading solutions by using graphics

The stages in the graphic solution of the problem represent the appropriate procedures which students need to conduct when solving the problem individually by using the linear function and its graph (Fig. 7). Stages are designed to follow visual cognitive processes which occur among the students when problems of QCS are solved by applying the graph of the linear function. Another option for displaying the graphics and the results is by checking the box “Results” whereby the entire graphical solution is shown (not step by step) as well as the text box with the answers to the questions set by the presented problem (Fig. 6).

Fig. 7 Stages of graphical representations of problem solution.

Tutorial

When clicked on the button “Tutorial” detail instructions will appear:

• Check one case

Clicking on one of the check-boxes you will choose the type of the problem.

• Enter data, or move the sliders

– You can change input data by typing into the corresponding fields numerical data from the problem or to move sliders for input data.

– These changes of the entering data lead to changes in the text of the problem as well as in the visual representations

– GeoGebra worksheets doesn't allow entering the data for which there is no solution.

• Below the text of the problem is placed its visual representation, presented in the form of rectangles as well as formulas that were used during algebraic solving

• Graphical solution-step by step

– Check box beside number 1. In the coordinative system entering data will appear

– Continue with checking boxes beside the numbers 2, 3 and 4, by this order and follow the steps in solving the problem of mixing solutions applying the graph of linear function

• Results

By checking this box, the results for the given problem will appear.

• When closing the GeoGebra worksheet, don't save changes.

• This tutorial is closed by clicking the button Tutorial.

Appendix 2

Examples of students' work where the graphical method was applied

Some of the students of the E group used the graphical method in the final test, after education about graphical method application for problem solving. In all presented samples input data were correctly written down, validity of the result was checked and result was written in the appropriate place.

Problem 1. A sample of solving the problem by the application of a graph of linear function (abstract representation).

Problem 2. A sample of solving the problem by applying concrete visual representation.

Problem 3. A sample of solving the problem by applying concrete visual representation.

Problem 4. A sample of solving the problem by the application of a graph of linear function (abstract representation).

Problem 5. A sample of solving the problem by the application of a graph of linear function (abstract representation).

Problem 6. A sample of solving the problem by the application of a graph of linear function (abstract representation).

Problem 7. A sample of solving the problem by the application of a graph of linear function (abstract representation).

Problem 8. A sample of solving the problem by applying concrete visual representation.

Appendix 3

Example of worksheet for control group training

Acknowledgements

The authors are deeply thankful to all students enrolled in the study. Ministry of Education, Science and Technical Development of the Republic of Serbia supported the research through the project from the frame of basic research OI 172051.

References

1. Arcavi A., (2003), The role of visual representations in the learning of mathematics, Educational Studies in Mathematics, 52, 215–241.
2. Artigue M., (2002), Learning mathematics in a CAS environment: the genesis of a reflection about instrumentation and the dialectics between technical and conceptual work, Int. J. Comput. Math. Learn., 7(3), 245–274.
3. Bailey P. D. and Garrett J., (2002), Chemical education: theory and practice, U. Chem. Educ., 6, 39–57.
4. Bayraktar S., (2002), A meta-analysis of the effectiveness of computer-assisted instruction in science education, J. Res. Technol. Educ., 34, 173–188.
5. Becker H. J., (2001), How are teachers using computers in instructions? paper presented at the meeting of the American Educational Research Association, National Survey Report, Irvine, CA: Center for Research on Information Technology and Organizations, University of California Irvine.
6. Britton S., New P. B., Sharma M. D. and Yardley D., (2005), A case study of the transfer of mathematics skills by university students, Int. J. Math. Educ. Sci. Technol., 36(1), 1–13.
7. Chiu M. H. and Wu H. K., (2009), The roles of multimedia in the teaching and learning of the triplet relationship in chemistry, in Gilbert J. K. and Treagust D. (ed.) Multiple representations in chemical education, Netherlands: Springer, pp. 251–283.
8. Cohen J. (1988), Statistical power analysis for the behavioral sciences, 2nd edn, Hillsdale, NJ: Erlbaum.
9. Coll R. K. and Taylor T. G. N., (2001), Using constructivism to inform tertiary chemistry pedagogy, Chem. Educ. Res. Prac., 2, 215–226.
10. diSessa A. A., Abelson H. and Ploger D., (1991), An overview of boxer, Journal of Mathematical Behavior, 10 (1), 3–15.
11. Eiliks I. and Byers B., (2009), Innovative Methods in Teaching and Chemistry learning in Higher Education, RSC Publishing, pp. 5–22.
12. GeoGebraTube, http://https://tube.geogebra.org/material/show/id/1472101, accessed August 2015.
13. Gilbert J. K., (2008), Visualization: an emergent field of practice and enquiry in Science Education, in Gilbert J. K., Reiner M., Nakhleh M. (ed.), Visualization: Theory and Practice in Science Education, Springer, pp. 3–24.
14. Gil-Perez D. and Carrascosa J., (1990), What Do About Science Misconceptions, Sci. Educ., 70(1), 77–93.
15. Higgins S., Xiao Z. M. and Katsipataki M., (2012), The impact of digital technology on learning: a summary for the Education Endowment Foundation Full Report, Durham University.
16. Hohenwarter J., Hohenwarter M. and Lavicza Z., (2008), Introducing dynamic mathematics software to secondary school teachers: the case of GeoGebra, Journal of Computers in Mathematics and Science Teaching, 28(2), 135–146.
17. Karadag Z. and McDougall D., (2009), Dynamic worksheets: visual learning with the guidance of Polya, MSOR Connections9(2), 13–16.
18. Kozma R. and Russell J., (2005), Students becoming chemists: developing representational competence, In Gilbert J. K. (ed.) Visualization in science education, Netherlands: Springer 121–145.
19. Kozma R. B., Russell J. W., Jones T., Wykoff J., Marx N. and Davis J., (1997), Use of simultaneous-synchronized macroscopic, microscopic, and symbolic representations to enhance the teaching and learning of chemical concepts, J. Chem. Educ., 74, 330–334.
20. Laborde C., (2001), Integration of technology in the design of geometry tasks with Cabrigeometry, Int. J. Comput. Math. Learn, 6, 283–317.
21. Lee Y. H., Waxman H., Wu J. Y., Michko G. and Lin G., (2013), Revisit the Effect of Teaching and Learning with Technology, Educ. Technol. Soc., 16(1), 133–146.
22. Leopold D. G. and Edgar B., (2008), Degree of Mathematics Fluency and Success in Second-Semester Introductory Chemistry, J. Chem. Educ., 85(5), 724–731.
23. Li Q. and Ma X., (2010), A meta-analysis of the effects of computer technology on school students' mathematics learning, Educ. Psychol. Rev., 22, 215–243.
24. Lobato J., (2008), When students don't apply the knowledge you think they have, rethink your assumptions about transfer, in Carlson M. and Rasmussen C. (ed.), Making the connection: research and teaching in undergraduate mathematics, Washington, DC: Mathematical Association of America, pp. 289–304.
25. Maaß K., (2010), Modeling in Class and the Development of Beliefs about the Usefulness of Mathematics, in Lesh R., Galbraith P., Haines C. and Hurford A. (ed.), Modelling students' modelling competencies, ICTMA 13, New York: Springer, pp. 409–420.
26. Marton F. and Säljö R., (1997), Approaches to learning, in Marton F., Hounsell D. and Entwistle N.J. (ed.), The Experience of learning, Edinburgh: Scottish Academic Press, pp. 39–58.
27. Mayer R. E. and Moreno R., (2002), Aids to computer-based multimedia learning, Learn. Instr., 12, 107–119.
28. Milanovic I., Vukobratovic R. and Raicevic V., (2012), Mathematical modelling of the effect of temperature on the rate of a chemical reaction, Croat. J. Educ., 14 (3), 681–709.
29. Mioč U. and Hercigonja R., (1996) Problems in the general course of physical chemistry, 3rd edn, Belgrade, Serbian: University of Belgrade, Faculty of physical chemistry.
30. Moore E. B., Herzog T. A. and Perkins K. K., (2013), Interactive simulations as implicit support for guided-inquiry, Chem. Educ. Res. Prac., 14(3), 257–268.
31. Moreno R., Ozogul G. and Reisslein M., (2011), Teaching with concrete and abstract visual representations: effects on students' problem solving, problem representations, and learning perceptions, J. Educ. Psychol., 103(1), 32–47.
32. Mulford D. R., (1996), An Inventory for Measuring College Students' Level Of Misconceptions in First Semester Chemistry, Unpublished M.S. thesis, Purdue University.
33. Paivio A., (1986), Mental representations: a dual coding approach, Oxford, UK: Oxford University Press.
34. Pecev T., Perović J., Miljković M., Simonović R., Stankov Jovanović, V. and Mitić V., (2002), Quantitative analytical chemistry-workbook, Niš, Serbian: PMF.
35. Pinarbaşi T. and Canpolat N., (2003), Students' understanding of solution chemistry concepts, J. Chem. Educ., 80(11), 1328–1332.
36. Potgieter M., Harding A. and Engelbrecht J., (2008), Transfer of Algebraic and Graphical Thinking between Mathematics and Chemistry, J. Res. Sci. Teaching, 45, 197–218.
37. Prosser M. and Millar R., (1989), The how and what of learning physics, Eur. J. Psychol. Educ., 4, 513–528.
38. Rapp D. and Kurby C., (2008), The ‘Ins’ and ‘Outs’ of Learning: Internal Representations and External Visualizations, in Gilbert J. K. et al. (ed.), Visualization: Theory and Practice in Science Education, Springer, pp. 29–52.
39. Roth W. M., (1993), Problem-Centered Learning for the Integration of Mathematics and Science in a Constructivist Laboratory: A Case Study, Sch. Sci. Math., 93(3), 113–122.
40. Ruthven K. and Hennessy S., (2002), A practitioner model of the use of computer-based tools and resources to support mathematics teaching and learning, Educ. Stud. Math., 49, 47–88.
41. Seufert T., (2003), Supporting coherence formation in learning from multiple representations, Learn. Instr., 13(2), 227–237.
42. Sherin B.L., (2001), How students understand physics equations, Cognition and Instruct., 19, 479–541.
43. Sikirica M., (2001), Stoichiometry, Zagreb, Croatian: Školska knjiga.
44. Tall D., (2002), Advanced Mathematical Thinking, New York, Boston, Dordrecht, London, Moscow: Kluwer Academic Publishers.
45. Tatar E. (2013), The Effect of Dynamic Software on Prospective Mathematics Teachers' Perceptions Regarding Information and Communication Technology, Australian Journal of Teacher Education, 38, 1–17.
46. Trigwell K., Prosser M. and Taylor P., (1994), Qualitative differences in approaches to teaching first year university science', High. Educ., 27, 75–84.
47. Trigwell K., Prosser M. and Waterhouse F., (1999), Relations between teachers' approaches to teaching and students' approaches to learning, High. Educ., 37, 57–70.
48. Waxman H. C., Lin M. and Michko G.M., (2003), A Meta-Analysis of the Effectiveness of Teaching and Learning With Technology on Student Outcomes, Naperville, IL: Learning Point, accessed at http:// treeves.coe.uga.edu/ edit6900/metaanalysisNCREL.pdf on June 4, 2013.
49. Woolnough J., (2000), How do students learn to apply their mathematical knowledge to interpret graphs in physics? Res. Sci. Educ., 30(3), 259–267.
50. Zimmermann W. and Cunningham S., (1991), Editor's introduction: What is mathematical visualization, in Zimmermann W. and Cunningham S. (ed.), Visualization in Teaching and Learning Mathematics, Washington, DC: Mathematical Association of America, pp. 1–8.

---