Rotation induced by uniform and non-uniform magnetic fields in a conducting fluid carrying an electric current
Abstract
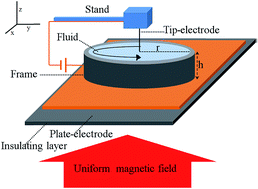
We study the dynamics of a conducting fluid carrying (i) a uniform current in the presence of a non-uniform magnetic field or (ii) carrying a non-uniform current in the presence of a uniform magnetic field, using particle image velocimetry (PIV). Our results show that the average angular velocity of the induced rotation has a power-law dependence on the electric current passing through the fluid with an exponent ≈2/3, in excellent agreement with our simulation results, for the same system. To explain the experimental observations we explore all possibilities for inducing rotation in a fluid carrying an electric current. Our theoretical discussion indicates two scenarios wherein applying electric/magnetic field on a current-carrying fluid produces rotational vortices: (i) applying a non-uniform magnetic field in the presence of an electric current and, (ii) applying a magnetic field in the presence of a non-uniform electric current. These two theoretical scenarios for inducing rotation by applying external fields agree well with our experimental observations and simulation results.


 Please wait while we load your content...
Please wait while we load your content...