The effects of Ge doping on the thermoelectric performance of p-type polycrystalline SnSe

Abstract

Recently single crystal SnSe has attracted much attention due to its unprecedented high zT (∼2.6) value, which has stimulated curiosity to study its polycrystalline counterparts by effective doping. Polycrystalline (Sn_1−xGe_x)Se specimens were prepared by melting and spark plasma sintering (SPS) to improve the thermoelectric performance and mechanical properties of pristine SnSe. This study systematically investigated the Ge doping effects and discussed the anisotropic behavior on the thermoelectric (TE) properties of SPS sintered (Sn_1−xGe_x)Se samples. We found that Ge doping not only results in a remarkable enhancement of Seebeck coefficient but also reduces the thermal conductivity of the (Sn_1−xGe_x)Se series. All Ge-doped compounds show a low thermal conductivity, which is mainly attributed to phonon scattering from disordered dopant atoms and the high anharmonic bonding nature of SnSe. This led to a maximum zT of 0.77, which was obtained at 800 K for (Sn_0.99Ge_0.01)Se, which shows an approximately 40% enhancement over the pristine polycrystalline SnSe (zT = 0.56). Consequently, (Sn_1−xGe_x)Se is a promising candidate for highly efficient thermoelectric materials.

---

Introduction

Thermoelectric (TE) technology, which enables harvesting electric power directly from waste heat, has been extensively investigated over the past decades for its potential in applications concerning power generation and electronic cooling.^1–4 Due to the efficiency constraint of the thermoelectric conversion process, there is an intense search for highly efficient thermoelectric materials. A more widespread use of thermoelectric technologies would be possible if their efficiency can be further improved. The thermoelectric conversion efficiency is characterized by the temperature dependent physical quantity, zT = S²σT/κ, where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the total thermal conductivity and T is the absolute temperature.^5,6 Based on the above relationship, ideal thermoelectric materials require a perfect combination of high power factor (S²σ) and low thermal conductivity (κ) to achieve a high zT.

Several new strategies and materials have been proposed to improve the zT over the past decades such as, through the band structure modification^7,8 and carrier concentration tuning^9,10 to optimize electrical properties; using alloying effect,⁹ nano-structuring¹¹ and solid solution¹² to reduce the lattice thermal conductivity. Some of these approaches aim to achieve high thermoelectric performance by reducing thermal conductivity. For instance, in solid solutions, defects of atomic disorders act as scattering centers of phonons, leading to the lattice thermal conductivity reduction.¹² Recent finding revealed that extreme thermoelectric properties of the earth-abundant and non-toxic single crystalline SnSe compound has provided experimental evidence of an outstanding record zT of 2.6 at 923 K.¹³ This favourable thermoelectric property is mainly attributed to its intrinsically ultralow thermal conductivity for peculiar anharmonic structure of the chemical bonds of SnSe.^13,14 Furthermore, a considerable attention has been given to the thermoelectric properties of polycrystalline SnSe^15–20 because using single crystal SnSe in TE device application is impeded by poor mechanical properties and difficult to industrial scale up. For instance, Sassi et al.¹⁵ reported zT = 0.5 of polycrystalline SnSe at around 820 K, which is much lower than those measured in single crystal SnSe¹³ due to lower electrical conductivity and higher thermal conductivity. In addition, various chemical substitutions were attempted to improve the poor electrical transport property by increasing the carrier concentration.^17,21–24 Na and Ag doping in polycrystalline SnSe can effectively tune the carrier concentration and thermal conductivity. Very recently, Ge doping is reported to have high solubility in the SnSe lattice,²⁵ however, the thermoelectric transport properties at high temperature region for this doping system has not been studied.

Herein, we explore how to engineer the thermoelectric properties of polycrystalline (Sn_1−xGe_x)Se using chemical substitution of germanium atoms on the Sn sites, and show that Ge doping enables to suppress the lattice thermal conductivity and simultaneously enhance the Seebeck coefficient, leading to a maximum zT of 0.77 at 800 K for (Sn_0.99Ge_0.01)Se along the plane perpendicular to the SPS pressing direction.

Results and discussions

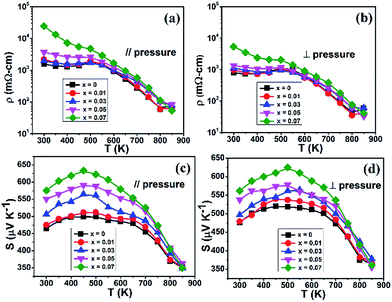
X-ray diffraction patterns of (Sn_1−xGe_x)Se, x = 0, 0.01, 0.03, 0.05 and 0.07 for powders and SPS pressed specimens are shown in Fig. 1(a)–(c) respectively. The diffraction peaks were indexed to the SnSe phase (PDF #48-1224) with an orthorhombic structure (Pnma space group). The XRD analysis confirms that all the (Sn_1−xGe_x)Se specimens are single phase without any impurity. The calculated lattice parameters of pristine SnSe (a = 11.507 Å, b = 4.154 Å and c = 4.436 Å) are consistent with the reported data.^26,27 As can be seen in Fig. S1,† the lattice parameters (a, b and c) decreased with increasing the Ge content (x) compared to the parent compound SnSe. This reduction is due to the substitution of Sn by Ge which has a smaller atomic size than Sn. According to Gharsallah M. et al. the maximum solid solution limit of Ge content in SnSe crystal is up to x = 0.3.²⁵ The structural anisotropy is observed in all SPS sintered specimens. The relative intensity of the (400) and (111) reflection peaks is especially different in the patterns of (b) and (c), and suggests that the grains tend to grow along these planes, which is similar to the conclusion for the single crystalline SnSe.¹³ The SEM image of Fig. 1(d) shows the sample morphologies of the freshly fractured surfaces parallel to sintering direction for (Sn_0.99Ge_0.01)Se. The obvious layered structures are observed arranging along the parallel direction, which indicates that the grains are preferentially reoriented to the disk plane during the sintering procedure. Since the structural anisotropy is also reflected on the thermoelectric transport properties, all samples in the following discussions were measured along parallel and perpendicular to the pressing directions, respectively.

Fig. 1 X-ray diffraction patterns of (Sn_1−xGe_x)Se for x = 0, 0.01, 0.03, 0.05 and 0.07: (a) the powders, (b) the planes perpendicular and (c) the planes parallel to the SPS pressing direction. (d) The SEM images of the fractured surfaces of SPS sintered (Sn_0.99Ge_0.01)Se bulk sample in the direction parallel to the press direction. The inset shows a magnified portion.

Fig. 2 presents the electrical transport properties of polycrystalline (Sn_1−xGe_x)Se samples which are measured along parallel and perpendicular to sintering pressure in the temperature range of 300 to 850 K. The temperature dependence of the electrical resistivity data are indicated in Fig. 2(a) and (b). The electrical resistivity of all the samples decreased with increasing temperature for T < 800 K in both directions, which shows a typical semiconducting property. Above 800 K, the resistivity slightly increased clearly for x = 0, 0.01, and 0.03. This behaviour is most likely related to the distortion of the unit cell due to the phase transition.¹⁸ According to Gharsallah M. et al., Ge inclusion induces an increased band gap energy²⁵ that leads to an increasing in electrical resistivity. Similarly, the Hall effect measurements reveal that the hole carrier concentration decreases with increasing Ge contents in the samples [Table 1]. In addition, the off-plane electrical resistivity shows a higher value than that of the in-plane direction (perpendicular to the SPS pressing direction). This anisotropy agrees well with the conclusion that reported in the single crystal SnSe.¹³

Fig. 2 Electrical resistivity and Seebeck coefficient as a function of temperature of (Sn_1−xGe_x)Se for x = 0, 0.01, 0.03, 0.05 and 0.07 in the two directions. The electrical resistivity parallel (a) and perpendicular (b) to the pressing direction. The Seebeck coefficient parallel and perpendicular to the pressing direction in (c) and (d) respectively.

Table 1 The Hall carrier concentrations (n_H), carrier motilities (μ_H), Seebeck coefficients (S) and electrical resistivity (ρ) of (Sn_x−1Ge_x)Se for x = 0, 0.01, 0.03, 0.05 and 0.07 samples at 300 K

Sample compositions	nH (10^17 cm^−3)	μH (cm^2 V^−1 s^−1)		S (μV K^−1)		ρ (mΩ m)
		∥	⊥	∥	⊥	∥	⊥
SnSe	2.56	15.56	31.06	464	476	15.67	7.85
Sn0.99Ge0.01Se	2.49	11.34	26.03	475	479	22.09	9.63
Sn0.97Ge0.03Se	2.07	15.28	27.11	506	496	19.73	11.12
Sn0.95Ge0.05Se	1.86	9.08	25.21	550	537	36.92	13.31
Sn0.93Ge0.07Se	1.28	2.09	9.02	575	561	244.61	52.98

---

The values of temperature dependent Seebeck coefficient are positive as shown in Fig. 2(c) and (d). All the samples exhibit the p-type character in both directions. The Seebeck coefficient of all specimens shows an increasing trend with increasing Ge contents in both directions, which is consistent with that of the electrical resistivity. Meanwhile, the Seebeck coefficient achieves a peak value of 630 μV K⁻¹ at around 500 K and then rapidly decreases with increasing temperature due to the thermal excitation of minority carriers. Although the Seebeck coefficient decreases drastically at high temperature compared to the low temperature region, Ge substituted samples have higher Seebeck coefficient than the pristine specimen up to 800 K. For instance, the Seebeck coefficient of pristine SnSe is 374 μV K⁻¹ at 800 K, which is lower than that of Ge (x = 0.07) substituted sample having Seebeck coefficient value of 416 μV K⁻¹ at the same temperature. This shows that Ge doping has a contribution for the enhancement of Seebeck coefficient in SnSe up to transition temperature. Additionally, the Seebeck coefficients present nearly isotropic character, and are almost independent of the crystallographic directions.¹⁸ The power factors of polycrystalline (Sn_1−xGe_x)Se sample are shown in Fig. S2.† The maximum power factor value is 4.16 μW cm⁻¹ K⁻¹ at 800 K for 1% Ge doping sample along the plane perpendicular to sintering direction, which enables to achieve a higher figure of merit. In addition, we performed thermal cycling tests to check the thermal stability of the samples. Fig. S3† shows the TE properties of (Sn_0.99Ge_0.01)Se measured after being subject to thermal cycling two times. Basically, no obvious change has been observed below 800 K from the plots.

Fig. 3 presents the temperature dependence of total thermal conductivity (κ) and lattice thermal conductivity (κ_L) for solid solution (Sn_1−xGe_x)Se measured along parallel and perpendicular to the sintering direction. Similar to that observed in the electrical resistivity, the measured thermal conductivity along different directions also shows an obvious anisotropic property. The total thermal conductivity along the plane parallel to the SPS pressing direction is lower than that along the plane perpendicular to the SPS pressing direction as shown in Fig. 3(a) and (c), which is probably due to the weak atomic connections and vibrations¹⁸ as well as the preferred orientation of (400) plane compared to the other directions. The lattice thermal conductivity κ_L of each series was calculated by subtracting electronic thermal conductivity κ_e from total thermal conductivity κ. The κ_e was evaluated from the Wiedemann Franz relation: κ_e = LTσ, where L is 1.5 × 10⁻⁸ V² K⁻²,¹³ σ is the electrical conductivity, T is the absolute temperature. The L value is obtained by fitting the Seebeck coefficient data to the reduced chemical potential, which is approaching the lower limit expected when carriers are scattered by acoustic phonons in non-degenerate semiconductors. The lowest lattice thermal conductivities measured in (Sn_1−xGe_x)Se compounds are 0.27 W m⁻¹ K⁻¹ (∥) and 0.38 W m⁻¹ K⁻¹ (⊥) at 850 K, as shown in Fig. 3(b) and (d). This calculation shows that the heat is predominantly transferred by lattice phonons, and the electronic contribution is negligible due to the high electrical resistivity. With Ge doping in SnSe solid solution system, the random distribution of isoelectric atoms results in atomic disorders, and these disorders act as scattering centers for phonons, leading to the reduction of lattice thermal conductivity.^12,25 So the lattice thermal conductivity reduction is mostly from the point defects due to the mass fluctuation scattering and strain field fluctuation scattering for phonons caused by the size and mass difference between Ge and Sn (the atomic weight of Ge and Sn are 72.63 and 118.71 g mol⁻¹) respectively.^28–32 In other expression, Ge doping in SnSe system creates enhanced phonon scatterings by the highly disordered Ge/Sn and grain boundaries.²⁵ These results show that isoelectronic substitution of Ge for Sn is an effective way to reduce the lattice thermal conductivity.

Fig. 3 Temperature dependence of total thermal conductivities of (Sn_1−xGe_x)Se for x = 0, 0.01, 0.03, 0.05 and 0.07, along the plane parallel (a) and perpendicular (c) to sintering direction. The lattice thermal conductivities along the plane parallel (b) and perpendicular (d) to SPS pressing direction.

zT as a function of temperature for all (Sn_1−xGe_x)Se samples with x = 0 to 0.07 are shown in Fig. 4. The zT values of the pristine SnSe are 0.56 and 0.54 at 800 K in the plane perpendicular and parallel to the SPS pressing direction, respectively. The result is consistent with the conclusion reported by Sassi et al.¹⁵ and Li et al.¹⁸ along the same pressing direction for pristine sample. Among several Ge doping samples, (Sn_0.99Ge_0.01)Se reaches a maximum zT of 0.77 at 800 K in the direction perpendicular to the SPS pressing direction, showing an approximately 40% enhancement over the parent compound. A little bit higher zT in the direction perpendicular to the SPS pressing direction can be understood as a higher electrical conductivity in this direction. It is also noted that except 7% Ge doping all samples show an obvious downtrend in zT values as the measured temperature is higher than 800 K. This may be due to the increasing in electrical resistivity, which is attributed from the distortion of the unit cell at the transition temperature.^13,15 These phenomena indicate that proper optimization of the transport properties of SnSe might lead to a marked improvement in the zT for the Ge doped SnSe system.

Fig. 4 The temperature dependence zT values of (Sn_1−xGe_x)Se for x = 0, 0.01, 0.03, 0.05 and 0.07 in two directions. (a) The zT values along the plane perpendicular and (b) parallel to the SPS pressing direction.

Conclusions

In summary, we investigated the TE properties of Ge-doped SnSe compounds which have been prepared by melting and spark plasma sintering. It is found that Ge doping at Sn site remarkably increases the Seebeck coefficient and reduces the electrical and thermal conductivities. The transport properties, especially electrical resistivity and thermal conductivity show an obvious anisotropic behavior. The electrical conductivity measured along the direction perpendicular to sintering pressure is higher than that of the other direction. The lower thermal conductivity compensates the larger electrical resistivity in the same direction. However, the Seebeck coefficient is almost invariant in both directions. Moreover, the significantly different mass and size of Ge atoms compared to Sn atoms give rise to a strong phonon scattering, which reduces the lattice thermal conductivity quite markedly. Consequently, this good combination of transport property leads to have a decent zT of 0.77 for (Sn_0.99Ge_0.01)Se at about 800 K in the perpendicular SPS pressing direction, showing a 40% enhancement over the parent compound. Coupled with their non-toxic nature and the fact that they never introduce major environmental concerns so that Ge doped SnSe compound offer good thermoelectric performance.

Experimental

High quality ingots with nominal compositions of polycrystalline (Sn_1−xGe_x)Se for x = 0, 0.01, 0.03, 0.05 and 0.07 were synthesized by mixing appropriate ratios of high purity elements of Sn (99.999%), Se (99.999%) and Ge (99.999%) in quartz tubes. The tubes were evacuated to a residual pressure of 5.7 × 10⁻⁵ torr and flame sealed in double tubes. The sealed quartz tubes were put into furnace and heated slowly up to 1223 K in 10 hours, and then dwelt at this temperature for 72 hours to ensure the homogeneity of composition and subsequently quenched in water. The obtained ingots were ground to fine powders with an agate mortar, and then sieved with 106 μ mesh. The powders were loaded into graphite die and densified by spark plasma sintering (SPS) at 873 K for 7 min under a uniaxial pressure of 50 MPa. The densities of the measured sample were above 95% of the theoretical value. The obtained SPS ingots were cut into slice shape for thermal conductivity measurements. Then the same samples were cut into rectangular shape for electrical property measurements. The X-ray diffraction (XRD) was performed for phase identification on polished slices and powders by using (PANalytical X'Pert PRO, CuKα radiation) diffractometer operated at 45 kV and 40 mA. The lattice parameters of samples were calculated by Rietveld refinement program using the HighScore Plus software. Fracture surface morphology was characterized using field emission scanning electron microscopy (FESEM, Hitachi, S-4800). The temperature dependent electrical conductivity and Seebeck coefficient were simultaneously measured using commercial equipment (ZEM-3, ULVAC-RIKO, Japan). The thermal conductivity (κ) was calculated from the measured thermal diffusivity (D), specific heat (C_p) and density (d) using the relationship κ = DC_pd. The thermal diffusivity was measured by a laser flash apparatus (Netzsch, LFA 457), and the data were plotted in Fig. S4.† The specific heat capacity values C_p were determined by using a differential scanning calorimeter (NETZSH, STA 449) which is consistent with experimental values reported for higher temperatures from Sassi et al.¹⁵ and Chere et al.²⁴ (plot of C_p is shown in Fig. S5†). The density was obtained using the Archimedes method shown in Table S1.† The Hall effect measurements were measured using van der Pauw method (ECOPIA HMS-5000) at 300 K under magnetic field of ±0.55 T. Uncertainties in the measurements of resistivity, Seebeck coefficient and thermal conductivity were estimated to be approximately ±3%, ±3% and ±9% respectively, which is leading to a combined experimental uncertainty of about ∼18% in zT calculations. Error bars were not used in drawing figures to increase the readability of the curves.

Acknowledgements

This work is financially supported by Academia Sinica and Ministry of Science and Technology (MOST), Taiwan, Grant No. MOST 103-2112-M-001-021-MY3.

Notes and references

1. H. J. Goldsmid, Thermoelectric Refrigeration, Temple Press Books, Ltd., London, 1964.
2. F. J. Di Salvo, Thermoelectric cooling and power generation, Science, 1999, 285, 703–706.
3. D. M. Rowe, CRC Handbook of thermoelectrics, CRC Press, Boca Raton, FL, USA; London, UK; New York, NY, USA; Washington, DC, USA, 1995.
4. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
5. D. M. Rowe, CRC Handbook of thermoelectrics: Macro to Nano, CRC Press, Taylor & Francis, Boca Raton, 2006.
6. J. P. Heremans, M. S. Dresselhaus, L. E. Bell and D. T. Morelli, When thermoelectrics reached the nano scale, Nat. Nanotechnol., 2013, 8, 471–473.
7. J. P. Heremans, V. Jovovic, E. S. Toberer, A. Saramat, K. Kurosaki, A. Charoenphakdee, S. Yamanaka and G. J. Snyder, Science, 2008, 321, 554–557.
8. Y. Pei, X. Shi, A. LaLonde, H. Wang, L. Chen and G. Snyder, Nature, 2011, 473, 66.
9. Y. Han, Z. Chen, C. Xin, Y. Pei, M. Zhou, R. Huang and L. Li, J. Alloys Compd., 2014, 600, 91–95.
10. Q. Tan, L. Zhao, J. Li, C. Wu, T. Wei, Z. Xing and M. Kanatzidis, J. Mater. Chem. A, 2014, 2, 17302.
11. J. Li, M. Zhou and T. Kita, J. Am. Chem. Soc., 2008, 130, 990.
12. H. Wang, A. LaLonde, Y. Pei and G. Snyder, Adv. Funct. Mater., 2013, 23, 1586.
13. L. D. Zhao, S. H. Lo, Y. S. Zhang, H. Sun, G. J. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373.
14. L.-D. Zhao, G. Tan, S. Hao, J. He, Y. Pei, H. Chi, H. W. S. Gong, H. Xu, V. P. Dravid, C. Uher, G. Jeffrey Snyder, C. Wolverton and M. G. Kanatzidis, Science, 2016, 351, 141–144.
15. S. Sassi, C. Candolfi, J.-B. Vaney, V. Ohorodniichuk, P. Masschelein, A. Dauscher and B. Lenoir, Appl. Phys. Lett., 2014, 104, 212105.
16. S. Sassi, C. Candolfi, J. B. Vaney, V. Ohorodniichuk, P. Masschelein, A. Dauscher and B. Lenoir, Mater. Today, 2015, 2, 690–698.
17. C. L. Chen, H. Wang, Y. Y. Chen, T. Day and G. J. Snyder, J. Mater. Chem. A, 2014, 2, 11171–11176.
18. Y. Li, X. Shi, D. Ren, J. Chen and L. Chen, Energies, 2015, 8, 6275–6285.
19. J. Carrete, N. Mingo and S. Curtarolo, Appl. Phys. Lett., 2014, 105, 101907.
20. A. Hong, L. Li, H. Zhu, Z. Yan, J. Liu and Z. Ren, J. Mater. Chem. A, 2015, 3, 13365.
21. H.-Q. Leng, M. Zhou, J. Zhao, Y.-M. Han and L.-F. Li, RSC Adv., 2016, 6, 9112.
22. K. Peng, X. Lu, H. Zhan, S. Hui, X. Tang, G. Wnag, J. Dai, C. Uher, G. Wang and X. Zhou, Energy Environ. Sci., 2016, 9, 454.
23. Q. Zhang, E. Kebede Chere, J. Sun, F. Cao, K. Dahal, S. Chen, G. Chen and Z. Ren, Adv. Energy Mater., 2015, 1500360.
24. E. K. Chere, Q. Zhang, F. Cao, K. Dahal, J. Mao and Z. Ren, J. Mater. Chem. A, 2016, 4, 1848.
25. M. Gharsallah, F. Serrano-Sanchez, N. M. Nemes, F. J. Mompean, J. L. Martinez, M. T. Fernandez-Diaz, F. Elhalouani and J. A. Alonso, Sci. Rep., 2016, 6, 26774.
26. H. Wiedemeier and H. G. Schnering, Z. Kristallogr., 1978, 148, 295–303.
27. T. Chattopadhyay, J. Pannetier and H. G. Schnering, J. Phys. Chem. Solids, 1986, 47, 879–885.
28. B. Abeles, Phys. Rev., 1960, 131, 1906.
29. S. R. Boona and D. T. Morelli, Appl. Phys. Lett., 2012, 101, 101909.
30. P. G. Klemens, Phys. Rev., 1960, 119, 507–509.
31. J. Callaway and H. C. von Baeyer, Phys. Rev., 1960, 120, 1149–1154.
32. T. A. Wubieneh, P. C. Wei, C. Yeh, S. Y. Chen and Y. Y. Chen, J. Electron. Mater., 2016, 45, 1942.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra23904h

---