Nanostructuring perovskite oxides: the impact of SrTiO₃ nanocube 3D self-assembly on thermal conductivity

Abstract

Nanostructuring the perovskite oxide SrTiO₃via 3D assemblage of nanocubes is shown to lower the thermal conductivity over a broad range of temperatures. This is particularly valuable in thermoelectric material applications. The assemblages are composed of pristine perovskite grain interiors confined by SrO or TiO₂-rich interfaces resembling Ruddlesden Popper and Magneli phases. The optimum performance in terms of the thermoelectric device applications are predicted to come from SrTiO₃ nanocubes synthesised in a Sr-rich environment, although TiO₂-rich nanocubes would have an increased strength. The vibrational fingerprint of the assemblages, characterized by a combination of lattice and molecular dynamics, display the characteristic modes of the perovskite structure and significant interface vibrational modes, some at very low frequency. TiO₂-rich assemblages display splitting of the active modes similar to anatase providing a way to distinguish them from SrO-rich assemblages. Finally, we show that the IR active low vibrational frequencies are sensitive to the structure and stacking of the nanocubes indicating that it could be an efficient experimental route for identifying and characterizing the material with very low thermal conductivity.

---

Introduction

New opportunities for power generation arise from the optimization of thermoelectric (TE) materials implemented in TE generators, where alternating series of p-type and n-type conducting materials are coupled to convert heat into electricity. Amongst the candidate materials, oxides are increasingly attracting interest, due to their stability at high temperatures and oxidizing conditions, their relatively low toxicity and the high abundance of their constituent elements, unlike conventional TE materials.^1,2 TE energy conversion efficiency is elegantly defined by the dimensionless figure of merit ZT = (TσS²)/(κ_e + κ_l), which arises from an intricate balance between the Seebeck coefficient, S, the electrical conductivity, σ, the electronic (κ_e) and lattice (κ_l) contributions to the thermal conductivity and the absolute temperature, T. Oxide materials are promising but they lag behind conventional TE materials because of their generally low electrical conductivity and high thermal conductivity. Whereas progress has been made on p-type materials,^3,4 a highly efficient n-type counterpart has yet to emerge.^5,6 SrTiO₃ is one of the most promising materials for an n-type thermoelectric oxide. SrTiO₃ systems are generally doped to improve the electrical properties; further improvement of ZT therefore comes from lowering the thermal conductivity, which is most likely to be gained via nanostructuring.⁷

Nanotechnology has changed our perspective on the manipulation of matter, but the exploitation of oxide nanostructured materials has to take into account different aspects of their production, from the synthesis to the final product. The synthetic protocol generally requires a complex procedure,^8,9 which may give rise to heterogeneous products and unwanted geometries. This ambiguity arises because the properties of the resulting nanostructured oxide are generally unknown, which suggests that a better knowledge of the properties of the nanostructure may give rise to a more refined and sustainable production approach. Computational methodologies can probe these properties and thus aid the prediction of desirable nanostructures with enhanced material properties. Successful applications relate to structural features of oxide materials, including dislocations,¹⁰ grain boundaries,^11–13 nanoparticles,^14–16 and mesostructures.^17,18 It is also worth mentioning that the generation of large repositories of material properties^19–21 is currently restricted to bulk structures, however there is no conceptual limitation to extending these repositories to more complex structures.

Nanostructuring may take many forms and can impact on both the electrical and thermal properties.^22,23 To this end, assembled SrTiO₃ nanocubes were proposed^7,24,25 due to the high density of interfaces, which inhibit thermal transport via phonons by increased scattering and confinement in sufficiently small systems. Benefits also arise from the presence of grain boundaries which may improve the electrical properties on formation of 2DEG systems²⁶ or energy filtering.²⁷ Here, we provide a strategy to generate reliable atomistic models of assemblages of SrTiO₃ nanocubes with different packing and to predict their relative stability and the contribution of extended defects in the form of TiO₂ and SrO-rich interfaces to thermal conductivity. This general procedure using nanostructured assemblages may be extended to other oxide materials with their abundant choice of structural features, and could open the route to generating a repository of nanostructures and their corresponding properties.^28,29

Methodology

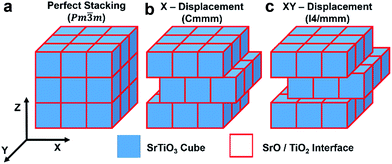
A nanocube is terminated by the six low Miller index {001} surfaces of perovskite SrTiO₃ and is charge neutral with defined stoichiometry (Table SI1†). We investigated the effect of the surface termination by generating nanocubes where all faces were either SrO or TiO₂ terminated {001} surfaces. The nanocubes were ∼7 nm, chosen as there are defined experimental routes for their synthesis and characterization.^7,24,25 This gives rise to a defined stoichiometry of Sr_1.18TiO_3.18 for the SrO-rich cube and SrTi_1.18O_3.36 for the TiO₂-rich cube, and thus provides the means to study the effect of interface composition on the lattice thermal conductivity. The nanocubes were assembled with three packing arrangements as shown in Fig. 1 using the METADISE code³⁰ to allow us to access the relative stability and sensitivity of the results to the packing.

Fig. 1 Representation of self-assembly of SrTiO₃ nanocubes in (a) a perfect cubic stacking (Pm3̄m), and displaced assemblages of (b) an X-displacement configuration in the X direction of half a cube width relative to the neighbouring cube (Cmmm) and (c) an XY-displacement configuration in the XY plane of a quarter of a cube width relative to the neighbouring cube (I4/mmm). X, Y and Z are the directions of the unit cell.

The assemblages of nanocubes were annealed at high temperature, typically 1500 K, using molecular dynamics calculations and the potential model developed by Teter³¹ (Table SI2†) to obtain thermally equilibrated {100}||{100} interfaces between the cubes. The lattice thermal conductivity was calculated using the Green–Kubo method^32,33 as implemented in the LAMMPS code.³⁴ All the nanocubes were simulated at five different temperatures. Each system was equilibrated for 50 ps with a timestep of 1 fs using an NPT triclinic ensemble with the exception of the Pm3̄m systems which were equilibrated isotropically. The ensemble employed a Nosé–Hoover thermostat and barostat. The lattice vectors were averaged every 10 fs. The simulation was deemed to converge if the energy fluctuations were consistently less than 0.1% of the average energy value and the volume fluctuations were less than 0.5% of the average volume. The averaged vectors were then imposed on the structure for the data collection phase. Heat-flux data was collected for 20 ns and the heat flux sampled every 10 fs. The heat-flux data collection was sequential for the non-displaced systems and parallel for the displaced systems (as four runs of 5 ns). The difference in data collection approaches has no significant effect as the correlation times for these systems are expected to be many orders of magnitude smaller than the individual runs. The heat-flux was numerically integrated to give the autocorrelation function, which is then averaged over a portion of the integral to reduce the noise in the thermal conductivity.³⁵

To aid in the interpretation of the spectrum of the resulting heat-flux autocorrelation function also known as the spectrum of the heat–current autocorrelation function (HCACF spectrum), we performed lattice dynamics calculations on a simple model system using the PHONOPY code^36,37 based on the force calculations from the same force field. This provides information on the phonon partial density of states (PDOS) at the Γ point and hence which species within the lattice are involved in the scattering process contributing to lowering the thermal conductivity. We present PDOS that contains only the optical phonon frequencies at the Γ point and can be compared to the HFACF spectra directly. The peaks in both PDOS and HFACF are also IR active modes as there will usually be an accompanying change in dipole with the vibration (details in ESI†).

Results and discussion

We generated assemblages of nanocubes composed of perovskite SrTiO₃ and predicted their lattice thermal conductivity as a function of the packing of cubes and the composition at the resulting interfaces. We then discuss their vibrational fingerprint as a way of providing a predictive approach for distinguishing their structure and to assessing their thermoelectric performance in lowering the thermal conductivity.

Structural characterization of nanocube assemblages

Each nanocube has six identical low Miller index {001} surfaces of 7 nm width (accessible to experiments and proposed to display lower thermal conductivity⁷). The consequence of having identical surfaces is that the nanocubes do not have ideal stoichiometry, but are Sr_1.18TiO_3.18 for the SrO-rich cube and SrTi_1.18O_3.36 for the TiO₂-rich cube. The packing assemblage is shown in Fig. 1. The perfect packing has side to side facing cubes whereas in the X-displacement configuration the adjacent cube is displaced by 3.5 nm in the X direction and in the XY-displacement configuration the adjacent cube is displaced by 3.5 nm in the X and Y directions; the configurations are referred to as Pm3̄m, Cmmm and I4/mmm respectively, reflecting the space group symmetry of the assemblages.

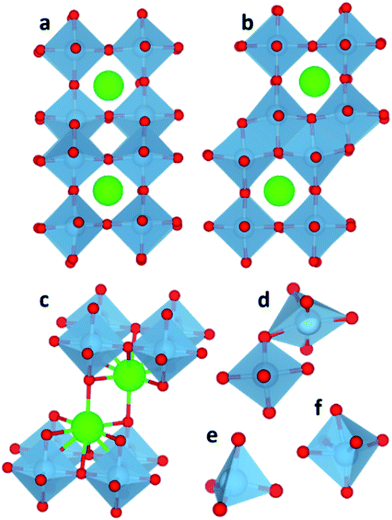
The interfaces between the nanocubes remained crystalline after annealing and show similar features regardless of the packing. Ti and Sr sites at edges and corners of the cubes have lower oxygen coordination compare to bulk species. This type of reconstruction, where SrTiO₃ nanocube shaped particles show rounded edges and corners as well as faceting has been observed experimentally³⁸ and implies that under-coordinated environments reconstruct to regain oxygen coordination. The TiO₂-rich interface has edge and corner sharing TiO₆ octahedra in different directions of the interface plane as shown in Fig. 2a and b. The interfaces, similar to bulk TiO₂ structures anatase and rutile, show 3-fold coordinated oxygen species. The SrO-rich interface has interface Sr species in a 9-fold coordination environment, as shown in Fig. 2c, where Sr retains 8 oxygen atoms from the regular cuboctahedral coordination (12 oxygen) in the perovskite structure and an apical oxygen from the Ti octahedron of the adjacent cube. On average the Sr–O distances are between 2.6 and 2.9 Å. Both SrO and TiO₂-rich interfaces display low or distorted coordination of Ti sites, generally at the edges and corners of the cubes. Some Ti cations are in a 4 fold tetrahedral coordination (Fig. 2e), which is not unusual and seen in garnets,³⁹ orthotitanates,⁴⁰ zeolites,⁴¹ and glasses.⁴²Fig. 2f shows an example of a distorted octahedron typically found at the interface, which resembles the VO₆ octahedral environment where vanadium does not reside in the oxygen equatorial plane but it is slightly displaced towards the apical oxygen. Finally, visual inspection showed that some Ti environments swap between edge sharing and corner sharing resulting in a 5-fold coordinated environment (Fig. 2d) similar to that found at the most stable {110} surface of rutile.⁴³ Distorted TiO_6−x units have been seen on {001} surfaces of SrTiO₃.^44–48

Fig. 2 The 12-fold coordination environment of Sr species at (a and b) TiO₂-rich interface and 9-fold at (c) SrO-rich interface. Coordination environments of Ti species at SrO and TiO₂-rich interfaces (d) dynamic octahedral coordination, (e) tetrahedral and (f) distorted octahedral.

Energetics of nanocube assemblages

We evaluated the relative stability of self-assembled cube configurations to determine their likely packing and the variation in packing that may be expected experimentally. To evaluate the order of stability, we calculated the excess surface energy due to the presence of TiO₂ or SrO-rich interfaces in the nanostructures, following the scheme oSrTiO₃ + mSrO + nTiO₂ → cube_assembled. The energy of the nano-assemblages and the parent bulk materials (SrTiO₃, SrO and TiO₂ anatase and rutile) were calculated using 20 ns molecular dynamics simulations at 500 K.

The SrO-rich configurations are predicted to be lower in energy than the TiO₂-rich configurations although their formation would depend on the relative chemical potential of Sr and Ti. The order of stability of the SrO-rich configurations follows the order Pm3̄m < Cmmm < I4/mmm (0.19 < 0.30 < 0.39 J m⁻²) while for the TiO₂-rich follows the order Pm3̄m < I4/mmm < Cmmm (0.51 < 0.66 < 0.76 J m⁻²). The perfect packing (Pm3̄m) of nanocubes is always more stable than any displaced assemblage of the nanocubes. These trends are also seen in the cleavage energy following the scheme cube_assembled → cube_isolated. In this case, molecular dynamics calculations were performed on isolated SrO and TiO₂-rich nanocubes at 500 K. The SrO-rich assemblages always resulted in a lower cleavage energy compared to the TiO₂-rich assemblages and for both the perfect stacking arrangement had the highest cleavage energy. The cleavage energies of SrO-rich assemblages follow the order Pm3̄m > Cmmm > I4/mmm (0.81 > 0.70 > 0.61 J m⁻²) while for the TiO₂-rich, they follow the order Pm3̄m > I4/mmm > Cmmm (1.13 < 0.97 < 0.88 J m⁻²). The higher cleavage energy of TiO₂-rich nanocubes arises from the covalent nature of the TiO₂ sublattice at the interface made of face and edge sharing cross-linked octahedral TiO₆ interfacial units (Fig. 2a and b). This suggests that when grown in excess titania, the adhesion of the cubes would be stronger and if synthesized at significantly low temperature, the cubes are predicted to self-assemble in an ordered way.

Thermal conductivity of nanocube assemblages

Before discussing the thermal conductivity of the nanocube assemblages, we consider stoichiometric bulk perovskite SrTiO₃. The cubic structure is retained during simulation with a = 3.91 Å at 500 K and a calculated thermal expansion of 1.13 × 10⁻⁵ K⁻¹ compared to the experimental value of 1.10 × 10⁻⁵ K⁻¹ (Fig. SI1†).⁴⁹ This indicates that the potential model³¹ reproduces the anharmonic interactions, which are fundamental for the evaluation of phonon–phonon scattering. The lattice thermal conductivity of bulk SrTiO₃ calculated in the temperature range between 500 K and 1300 K (Fig. 3) compares well with the experimental values for crystalline^50,51 and polycrystalline (corrected to 100% density) SrTiO₃ samples.⁵² The thermal conductivity displays a power law decay which indicates that the primary scattering mechanism arises from phonon–phonon interactions.^53,54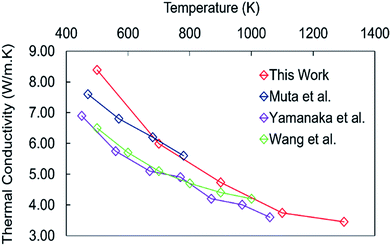

Fig. 3 Thermal conductivity of bulk SrTiO₃ calculated using the Green–Kubo method compared to experimental data.^50–52

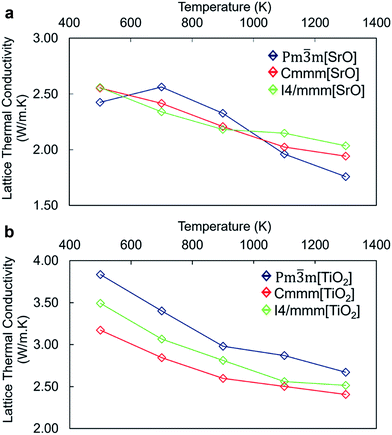
The calculated total lattice thermal conductivity of nanocube assemblages as a function of temperature (Fig. 4) is consistently lower than that of bulk SrTiO₃ and shows a small dependence on temperature in the range between 500 K and 1300 K. Unlike in bulk SrTiO₃, this behaviour is attributed to interface-acoustic phonon scattering processes which becomes the primary mechanism over the whole temperature range and dominates over acoustic–acoustic phonon scattering. A homogeneous thermal conductivity over a broad temperature range is particularly valuable in developing engineered TE material to avoid thermal shocks.

Fig. 4 Thermal conductivity of the (a) SrO-rich and (b) TiO₂-rich nanocube systems, comparing the perfect stacking (Pm3̄m) with the displaced Cmmm and I4/mmm assemblages. Analysis of the three directional components of the thermal conductivity (i.e. X, Y and Z) does not show any relevant difference and therefore is not shown.

The thermal conductivity of TiO₂-rich nanocubes is consistently higher than that of SrO-rich nanocubes by ∼1 W m⁻¹ K⁻¹ and displays a larger reduction with temperature. One could argue that as the mass ratio between cations (Ti and Sr) and oxygen, which is higher in Sr/O compared to Ti/O, would lead to a more effective scattering of heat carrying phonons in SrO-rich nanocubes. The higher thermal conductivity of TiO₂-rich nanocubes arises also from the more covalent nature of the TiO₂ sublattice at the interface made of face and edge sharing cross-linked octahedral TiO₆ interfacial units (Fig. 2a and b). There is a threshold of ∼2.5 W m⁻¹ K⁻¹, which defines the upper boundary for the thermal conductivity of SrO-rich nanocubes systems and the lower boundary of TiO₂-rich nanocubes. This indicates that the composition at the interface influences drastically phonon scattering, which is consistent with the lower excess surface and cleavage energies for SrO-rich compared to TiO₂-rich nanocubes.

Although the surface excess energies of different packing arrangements are different, this appears to be more evident in TiO₂-rich than SrO-rich nanocubes. The packing of nanocubes has indeed little impact on the lattice thermal conductivity of SrO-rich nanocubes whereas it has a larger effect on TiO₂-rich nanocubes. The difference in the thermal conductivity follows the order of stability of the different nanocube assemblages with the most stable configuration, the perfect stacking displaying the highest value and vice versa. The similar thermal conductivity of SrO-rich nanocubes indicates that the self-assemblage of nanocubes is less significant and it may not be a critical part of the synthesis. Thus, our results indicate that controlled synthetic protocols to favor high chemical potential of Sr, should be implemented to tune the composition of the resulting nanocubes, as the difference in interfacial composition has a greater impact on thermal conductivity than the packing arrangement.

Vibrational fingerprint of nanocube assemblages

For the development of approaches for characterizing and ultimately controlling thermal conductivity it is essential to begin mapping the key phonon modes involved in the scattering process. We can achieve this by computing the Fourier transform of the heat-flux autocorrelation functions (HFACF) calculated using molecular dynamics. The characteristic peaks provide a means of identifying the optic modes interacting with heat-flux. We will show that this coupled with the phonon density of states (PDOS) calculated using lattice dynamics provides a powerful combination for interpreting the vibrational properties.

The HFACF spectra of SrO-rich and TiO₂-rich nanocubes (Fig. 6) show common features, peaks at ∼6 THz, ∼14 THz and 21 THz. This is the fingerprint of the SrTiO₃ perovskite structure. To demonstrate this, one can use a simple model: bulk SrTiO₃. The PDOS of SrTiO₃ (Fig. 5) displays three vibrational modes at 5.7 THz, 14.1 THz and 22.4 THz, which are shifted to lower frequencies in the HFACF spectrum at 500 K due to finite temperature effects,⁵⁵ and correspond to motions associated with heavier Sr, Ti and lighter O species at low, middle and high frequencies, respectively. Each peak is therefore associated with the vibration of local environments of Sr atoms (12-fold cuboctahedral coordination), Ti atoms (6-fold octahedral coordination) and O atoms, which is in agreement with experimental reports of (LO) IR active modes appearing at approximately 5 THz, 14 THz and 23.5 THz in SrTiO₃.⁵⁶ Therefore the advantage of calculating HFACF spectra of polar materials is to directly reproduce the IR spectra and unlike the PDOS readily gives the peak width of each mode. This allows direct evidence of the optical scattering modes interacting with the heat-flux of the system.

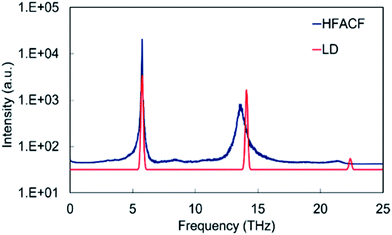Fig. 5 Displacement weighted lattice dynamics phonon DOS calculated neglecting the effect of temperature, and HFACF spectrum at 500 K of bulk SrTiO₃. The intensities (in arbitrary units) are assigned from the magnitude of the eigenvector sum and serve as a guide to the eye. The variation of HFACF spectra with temperature displays well-resolved peaks that broaden and shift to lower frequencies with increasing temperature demonstrating that large fluctuations in the autocorrelation functions are consistent with long-lived optical modes, rather than random noise (Fig. SI2†).

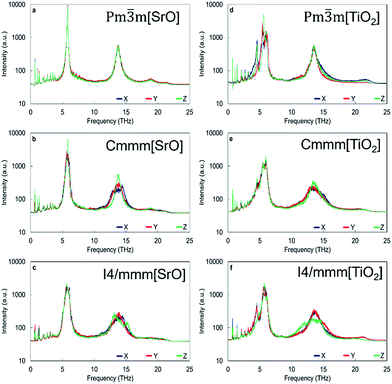
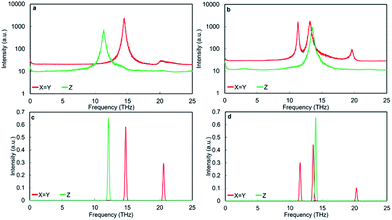
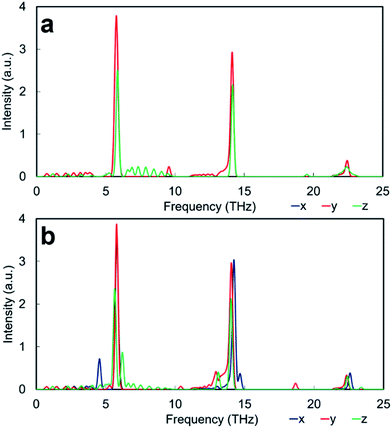
Apart from the three major peaks of the perovskite structure, all HFACF spectra for the nanocube assemblages (with the exception of Pm3̄m[SrO] assemblage) show splitting or coupling of optical modes in the region above and below ∼14 THz, which correspond to the vibration of the Ti environment. The HFACF spectra of TiO₂-rich nanocubes, unlike the SrO-rich, display also splitting of the Sr peak ∼5 THz, with a strong peak appearing at ∼4.5 THz. Furthermore, all nanocubes show many new peaks at very low frequencies below 5 THz (Fig. 6).

Fig. 6 HFACF spectra at 500 K of SrO-rich (a) Pm3̄m, (b) Cmmm and (c) I4/mmm assemblages and TiO₂-rich (d) Pm3̄m, (e) Cmmm and (f) I4/mmm assemblages. The X, Y, Z components of the HFACF spectrum are shown in blue, red and green respectively. Intensity in arbitrary units on logarithmic scale. The temperature dependence of HFACF spectra displays the same features as for bulk SrTiO₃.

Low frequency modes are more efficient in quenching the thermal conductivity and this is generally achieved in TE materials via doping to maximize the scattering of low frequency acoustic phonons through rattling modes.^57–59 However, we wanted to demonstrate that the introduction of low frequency vibrational modes can also be achieved via nanostructuring, i.e. introducing extended defects such as interfaces. Thus, the formation of assemblages of SrTiO₃ nanocubes is a way to form engineered nanostructures with structural features and interfaces parallel and perpendicular to each other that limit the phonon wavelengths, thus giving rise to new vibrational modes capable of scattering bulk acoustic modes, and ultimately lowering the lattice thermal conductivity.^60,61

Despite the HFACF spectra revealing the phonon optical frequencies interacting with the heat-flux, direct information on the species involved in specific modes is difficult to ascertain. As the vibrational fingerprint of complex nanostructures display a certain level of complexity (Fig. 6), the challenge thus becomes the interpretation of the HFACF spectra in a relatively simple way to help rationalize material synthesis. As shown for bulk SrTiO₃, the combination of lattice and molecular dynamics enables us to characterize the vibrational modes displayed in HFACF spectra. However to identify the microstructure and composition of more complex structures with suitable vibrations computationally, one has to devise simple model to mimic the interface structure and composition of the nanocube assemblages. We have therefore considered model structures to help in “fingerprinting” the complex HFACF spectra and identify the vibrational motions. First we present the SrO-rich and then the TiO₂-rich nanocubes for clarity.

Interpretation SrO-rich nanocube assemblages

The interface of SrO-rich assemblages have excess SrO with a composition of 1 : 2 Sr : O ratio compared to the 1 : 3 ratio in bulk SrTiO₃. However, the local coordination environment of Sr atoms at the interface determines the vibrational fingerprint. To demonstrate it, we used two model structures: the binary oxide SrO with Sr cations in a 6 fold coordination environment and a Ruddlesden–Popper structure, hereafter referred to as RP interface,⁶² which is characterized by 9-fold coordinated Sr environments. The RP interface is a thin films of bulk SrTiO₃ with SrO-rich interfaces equally spaced at ∼7 nm with the same composition and structure of the interface between the SrO-rich nanocubes simulated in molecular dynamics (Fig. 2c). The vibrational fingerprint of these two models determines whether they are reasonable approximants of the SrO-rich nanocube assemblage.

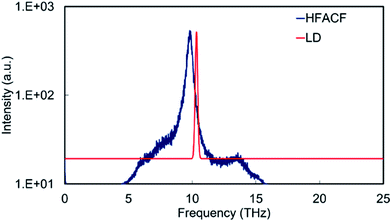
The PDOS of bulk SrO display an intense peak at ∼10 THz, which involves the vibration of the cation and anion sublattice with respect to the other (Fig. 8). The HFACF spectrum from an MD simulation of bulk SrO shows an intense peak in the same region surrounded by weak peaks at higher and lower frequencies due to the breaking of the symmetry (Fig. 8). There is a clear resemblance of the PDOS and the HFACF, although the HFACF spectrum captures the TO–LO splitting due to symmetry breaking during the simulation, the PDOS does not. This is further evidence that the HFACF spectrum can be used to approximate the IR spectrum. It is indeed noted in the literature that the phonon frequency distribution of SrO displays the transverse modes at lower frequency and the longitudinal modes at higher frequency compared to the main peak at ∼9 THz ⁶³ and that SrO IR spectrum displays a large peak between 6 THz and 14 THz.^64,65

Fig. 7 Phonon DOS calculated neglecting the effect of temperature of thin film structures of (a) SrO-rich (Ruddlesden–Popper) and (b) TiO₂-rich (Magneli) interface. Intensity in arbitrary units.

Fig. 8 HFACF spectrum at 500 K in log₁₀ scale and phonon DOS calculated neglecting the effect of temperature of stoichiometric SrO. Intensity in arbitrary units.

The PDOS of RP interface is presented in Fig. 7a. The direction across the interface is Z, whereas X and Y are parallel to the interface plane and as the interface is identically structured in the X and Y directions, they gives rise to the same PDOS. The thin film structure can be conceptually divided in to two regions. The interface region extends for ∼6 Å both sides of the interface plane, whereas the bulk region represents the grain interior. The vibrational fingerprint of RP interface displays three intense peaks at ∼6 THz, ∼14 THz and ∼22 THz characteristic of bulk Sr, Ti and O environments (Fig. 5), which correspond to the pristine perovskite grain interior. Visual inspection of the vibrations indicate that new low intensity peaks arise from modes caused by the presence of the interface but do not necessarily involve the species at the interface. This indicates that the interfaces affect the motions of atoms well away from the interface by limiting the allowed phonon mean free path. These vibrational modes appear in different directions both at lower and higher frequencies of the main bulk SrTiO₃ peaks.

A last comment is on the presence of interface modes that appear below 5 THz. These appear in the same region of rigid unit modes (RUMs) proposed in (covalently bonded) SiO₂ systems.^66,67 Visual inspection of the vibrations however did not show any correspondence to RUMs, although very low frequency modes contribute to lowering the lattice thermal conductivity via interactions with low frequency acoustic modes.

The HFACF spectrum of SrO-rich nanocubes perfectly stacked (Pm3̄m[SrO], Fig. 6a) is SrTiO₃ bulk-like (Fig. 5) with features that compare well with the PDOS of the RP interface (Fig. 7a). The splitting of Sr (∼6 THz) peaks are less pronounced, and Ti (∼14 THz) are more pronounced in Cmmm[SrO] (Fig. 6b) and I4/mmm[SrO] (Fig. 6c) structures. This split affects the vibration in different directions differently, inducing shifting of the peaks at lower or higher frequencies (red and green lines Fig. 7a). As Ti is lighter than Sr, the splitting is more pronounced.

We can therefore conclude that the vibrational fingerprint of the SrO-rich interface in the nanocube assemblages cannot be approximated by using the simple rock salt structure. Although the interface is SrO rich, the structural arrangement of the SrO units and the local coordination environment of Sr atoms at the interface are the factors which primarily influence the vibrational fingerprint.

Interpretation TiO₂-rich nanocube assemblages

For the TiO₂-rich nanocubes, we used TiO₂ rutile and anatase and a TiO₂-rich interface with the same structural characteristic (structure and composition) of the thin film made to interpret the SrO-rich interface, which resembles a Magneli structure, hereafter referred to as M interface (Fig. 2a and b).

The PDOS M TiO₂-rich interface (Fig. 7b) is more structured compared to the PDOS of RP SrO-rich interface (Fig. 7a). In the Z direction (across the interface) there is an intense interface mode at 6.2 THz (higher frequency compare to bulk Sr at ∼6 THz) due only to Sr and TiO₆ environments at the interface. There is also a satellite peak of the bulk Ti peak (∼14 THz) at a lower frequency (13.2 THz) due to interface TiO₆ vibrations. Unlike the RP interface, the PDOS in the X and Y directions are different as the structural arrangement of TiO₆ units is different in the two directions. In the Y direction, there is a characteristic O mode at 18.7 THz due to the 3 fold coordinated oxygen atoms due to interface edge sharing TiO₆ octahedra. In the X direction, the bulk Sr and Ti peaks have satellites at lower (4.5 THz) and higher (14.6 THz) frequencies respectively due only to vibration of Sr and TiO₆ environments at the interface.

The PDOS of rutile and anatase TiO₂ (Fig. 9) display resolved peaks in the region between 10 THz and 15 THz. However, it is difficult to say whether the two binary oxides are suitable for comparison with the interface of TiO₂-rich nanocube assemblages as all structures contain TiO₆ units. Visual inspection shows that several of the modes seen in the PDOS of the M TiO₂-rich interface (Fig. 7b) can be identified in the PDOS of bulk anatase (and not rutile) (Fig. 9a and c). The active mode seen in the Z direction of the PDOS of the M interface at 13.2 THz corresponds to a Ti–O bending and stretching mode at the interface and resembles the motion associated with the peak in the anatase PDOS at 12.1 THz. The peak at 12.9 THz in the PDOS Y direction of the M interface is a Ti rattling-like motion that involves the whole system but is more significant at the boundary. This is similar to the anatase mode in both PDOS X and Y directions with frequency 14.7 THz. Finally, the peak in the PDOS Y direction of the M interface at 18.7 THz is a rattling-like mode primarily involving the oxygen atoms at the interface, and resembles the mode at 20.6 THz in anatase (X and Y directions). It is interesting to note that the modes involving motion parallel to the interface plane are shifted ∼2 THz lower than their equivalents in bulk anatase (14.7 THz to 12.9 THz and 20.6 THz to 18.7 THz), whereas the mode involving motion perpendicular to the interface plane is shifted up from the anatase bulk value by ∼1 THz (12.1 THz to 13.1 THz). The shift is due to a contiguous TiO₆ network similar to bulk anatase in in-plane motions, whereas the network is disrupted by bulk SrTiO₃ in the out-of-plane motions.

Fig. 9 HFACF spectra at 500 K of stoichiometric TiO₂ (a) anatase and (b) rutile. Phonon DOS calculated neglecting the effect of temperature of stoichiometric TiO₂ (c) anatase and (d) rutile. Intensity in arbitrary units for HFACF in log₁₀ scale. X, Y and Z are the directions of the unit cell and align with the crystallographic a, b, and c directions.

Again to highlight that the HFACF spectra can approximate the IR spectra, peaks of anatase and rutile HFACF spectra can be noted in the experimental IR spectra of the materials, although the peak positions are heavily dependent on material synthesis and particle size.^68–70 This is further evidence that the PDOS and HFACF spectra of self-assembly of SrTiO₃ nanocubes can be compared with experimental IR spectra to evaluate the interface composition of the 3D assemblages.

The HFACF spectrum of TiO₂-rich nanocubes (Fig. 6) display well resolved splitting of the Sr peak at ∼6 THz characteristic of SrTiO₃ bulk (Fig. 5), independently of the stacking arrangement of nanocubes. The Sr peak always present (more or less visible in different directions) two satellite peaks at lower and higher frequencies compared to the bulk peak, due to the Sr environment adjacent to the anatase structured TiO₂-rich interface. This characteristic vibrational fingerprint of the TiO₂-rich interfaces is absent in SrO-rich interfaces, and can therefore be used to discriminate between experimental samples.

Conclusions

We demonstrated that nanostructuring perovskite oxide SrTiO₃via 3D assemblages of nanocubes lowers the lattice thermal conductivity over a broad range of temperatures. In these assemblages the pristine perovskite structure (grain interior) is confined by SrO or TiO₂-rich interfaces (superlattice systems⁷¹). Different packing arrangements of nanocubes do not affect the thermal conductivity as much as the composition of the interface itself. We found that the lowest thermal conductivity was achieved by SrTiO₃ nanocubes produced in a Sr-rich environment, although the TiO₂-rich nanocubes displayed increased strength.

To devise a strategy to identify and characterize the vibrational fingerprint of the assemblages, we proposed a combination of computational techniques, which can be used to aid experiments towards material with enhanced properties. The thermal conductivity of all assemblages is affected by interface vibrational modes, which do not necessarily require a species at the interface to participate to the vibration. Low frequency modes are of particular interest. This vibrational fingerprint can also be compared with experimental IR active modes. Thus IR vibrational spectroscopy can be used to identify the structure of the interface and discriminate material performance by the appearance of these low frequency optical modes in experimental IR spectra which indicates a material with very low thermal conductivity.

Future work on SrTiO₃ should concentrate on nanoinclusions or core–shell structures. In the latter case substitution of the A site cation (strontium) with higher valence cations (La) in the core of the nanocubes could introduce ordering of A site vacancies,^6,72 whereas further doping of the interface with higher valence transition metal on the B site (Nb or Mo) could contribute to increase the electrical conductivity.⁷³ The computational effort of predicting and identifying materials properties should concentrate on developing a dataset of engineered nanostructures in the fashion of database of bulk materials currently under development.^19–21

Acknowledgements

This work has made use of ARCHER, the UK's national HPC, via the Materials Chemistry Consortium funded by the EPSRC (EP/L000202) in resource, addition to the HPC Balena at the University of Bath. The authors acknowledge the University of Bath and the EPSRC (EP/I03601X/1 and EP/K016288/1) for funding. All data supporting this study are openly available from the University of Bath data archive at DOI: 10.15125/BATH-00321.

References

1. J. W. Fergus, J. Eur. Ceram. Soc., 2012, 32, 525–540.
2. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
3. I. Terasaki, Y. Sasago and K. Uchinokura, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 12685–12687.
4. J. D. Baran, M. Molinari, N. Kulwongwit, F. Azough, R. Freer, D. Kepaptsoglou, Q. M. Ramasse and S. C. Parker, J. Phys. Chem. C, 2015, 119, 21818–21827.
5. M. Molinari, D. A. Tompsett, S. C. Parker, F. Azough and R. Freer, J. Mater. Chem. A, 2014, 2, 14109–14117.
6. S. S. Jackson, F. Azough and R. Freer, J. Electron. Mater., 2014, 43, 2331–2336.
7. K. Koumoto, Y. F. Wang, R. Z. Zhang, A. Kosuga and R. Funahashi, Annu. Rev. Mater. Res., 2010, 40, 363–394.
8. F. Dang, K.-i. Mimura, K. Kato, H. Imai, S. Wada, H. Haneda and M. Kuwabara, CrystEngComm, 2011, 13, 3878–3883.
9. Y. Hao, X. Wang and L. Li, Nanoscale, 2014, 6, 7940–7946.
10. L. Sun, D. Marrocchelli and B. Yildiz, Nat. Commun., 2015, 6, 6294.
11. N. R. Williams, M. Molinari, S. C. Parker and M. T. Storr, J. Nucl. Mater., 2015, 458, 45–55.
12. D. J. Harris, G. W. Watson and S. C. Parker, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 134101.
13. G. Schusteritsch and C. J. Pickard, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 035424.
14. T. X. T. Sayle, M. Cantoni, U. M. Bhatta, S. C. Parker, S. R. Hall, G. Möbus, M. Molinari, D. Reid, S. Seal and D. C. Sayle, Chem. Mater., 2012, 24, 1811–1821.
15. T. X. T. Sayle, B. J. Inkson, A. Karakoti, A. Kumar, M. Molinari, G. Moebus, S. C. Parker, S. Seal and D. C. Sayle, Nanoscale, 2011, 3, 1823–1837.
16. T. X. T. Sayle, M. Molinari, S. Das, U. M. Bhatta, G. Mobus, S. C. Parker, S. Seal and D. C. Sayle, Nanoscale, 2013, 5, 6063–6073.
17. T. X. T. Sayle, S. C. Parker and D. C. Sayle, J. Mater. Chem., 2006, 16, 1067–1081.
18. P. Martin, S. C. Parker, D. C. Sayle and G. W. Watson, Nano Lett., 2007, 7, 543–546.
19. W. Setyawan, R. M. Gaume, S. Lam, R. S. Feigelson and S. Curtarolo, ACS Comb. Sci., 2011, 13, 382–390.
20. S. Wang, Z. Wang, W. Setyawan, N. Mingo and S. Curtarolo, Phys. Rev. X, 2011, 1, 021012.
21. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
22. Y. Wang, K. H. Lee, H. Hyuga, H. Kita, H. Ohta and K. Koumoto, J. Electroceram., 2010, 24, 76–82.
23. F. Dang, C. Wan, N.-H. Park, K. Tsuruta, W.-S. Seo and K. Koumoto, ACS Appl. Mater. Interfaces, 2013, 5, 10933–10937.
24. Q. Kuang and S. Yang, ACS Appl. Mater. Interfaces, 2013, 5, 3683–3690.
25. Y. Kinemuchi, K.-I. Mimura, A. Towata and K. Kato, J. Electron. Mater., 2014, 43, 2011–2016.
26. R. Z. Zhang, C. L. Wang, J. C. Li and K. Koumoto, J. Am. Ceram. Soc., 2010, 93, 1677–1681.
27. M. S. Dresselhaus, G. Chen, M. Y. Tang, R. Yang, H. Lee, D. Wang, Z. Ren, J.-P. Fleurial and P. Gogna, Adv. Mater., 2007, 19, 1043–1053.
28. D. C. Sayle, S. Seal, Z. Wang, B. C. Mangili, D. W. Price, A. S. Karakoti, S. V. Kuchibhatla, Q. Hao, G. Mobus and X. Xu, ACS Nano, 2008, 2, 1237–1251.
29. K. Huang, L. Yuan and S. Feng, Inorg. Chem. Front., 2015, 2, 965–981.
30. G. W. Watson, E. T. Kelsey, N. H. deLeeuw, D. J. Harris and S. C. Parker, J. Chem. Soc., Faraday Trans., 1996, 92, 433–438.
31. P. Canepa, PhD thesis, University of Kent, 2012.
32. M. S. Green, J. Chem. Phys., 1954, 22, 398–413.
33. R. Kubo, J. Phys. Soc. Jpn., 1957, 12, 570–586.
34. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
35. A. J. H. McGaughey, M. J. Kaviany, 8th AIAA/ASME Joint Thermophysics and Heat Transfer Conference, AIAA-2002-3343, St. Louis, Missouri, 2002.
36. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
37. A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094306.
38. F. A. Rabuffetti, H.-S. Kim, J. A. Enterkin, Y. Wang, C. H. Lanier, L. D. Marks, K. R. Poeppelmeier and P. C. Stair, Chem. Mater., 2008, 20, 5628–5635.
39. P. Tarte, Nature, 1960, 186, 234.
40. P. Tarte, Nature, 1961, 191, 1002–1003.
41. T. Blasco, M. A. Camblor, A. Corma and J. Perez-Pariente, J. Am. Chem. Soc., 1993, 115, 11806–11813.
42. G. S. Henderson and M. E. Fleet, Can. Mineral., 1995, 33, 399–408.
43. P. M. Oliver, G. W. Watson, E. Toby Kelsey and S. C. Parker, J. Mater. Chem., 1997, 7, 563–568.
44. N. Erdman, K. R. Poeppelmeier, M. Asta, O. Warschkow, D. E. Ellis and L. D. Marks, Nature, 2002, 419, 55–58.
45. N. Erdman, O. Warschkow, M. Asta, K. R. Poeppelmeier, D. E. Ellis and L. D. Marks, J. Am. Chem. Soc., 2003, 125, 10050–10056.
46. K. Johnston, M. R. Castell, A. T. Paxton and M. W. Finnis, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 085415.
47. D. S. Deak, F. Silly, D. T. Newell and M. R. Castell, J. Phys. Chem. B, 2006, 110, 9246–9251.
48. G.-Z. Zhu, G. Radtke and G. A. Botton, Nature, 2012, 490, 384–387.
49. D. de Ligny and P. Richet, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 3013–3022.
50. H. Muta, K. Kurosaki and S. Yamanaka, J. Alloys Compd., 2005, 392, 306–309.
51. Y. Wang, K. Fujinami, R. Zhang, C. Wan, N. Wang, Y. Ba and K. Koumoto, Appl. Phys. Express, 2010, 3, 031101.
52. S. Yamanaka, K. Kurosaki, T. Maekawa, T. Matsuda, S.-i. Kobayashi and M. Uno, J. Nucl. Mater., 2005, 344, 61–66.
53. M. T. Dove, Introduction to Lattice Dynamics, Cambridge University Press, Cambridge, 1993.
54. M. T. Dove, Structure and Dynamics: An Atomic View of Materials, Oxford University Press, Oxford, 2003.
55. E. S. Landry, M. I. Hussein and A. J. H. McGaughey, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 184302.
56. W. Zhong, R. D. Kingsmith and D. Vanderbilt, Phys. Rev. Lett., 1994, 72, 3618–3621.
57. M. Christensen, A. B. Abrahamsen, N. B. Christensen, F. Juranyi, N. H. Andersen, K. Lefmann, J. Andreasson, C. R. H. Bahl and B. B. Iversen, Nat. Mater., 2008, 7, 811–815.
58. M. Christensen, F. Juranyi and B. B. Iversen, Phys. B, 2006, 385, 505–507.
59. G. Nolas, J. Cohn and G. Slack, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 164.
60. Y. J. Lee, Y. H. Park and T. Hinoki, IOP Conf. Ser.: Mater. Sci. Eng., 2011, 18, 162014.
61. S. Fayette, D. S. Smith, A. Smith and C. Martin, J. Eur. Ceram. Soc., 2000, 20, 297–302.
62. M. A. McCoy, R. W. Grimes and W. E. Lee, Philos. Mag. A, 1997, 75, 833–846.
63. K. H. Rieder, R. Migoni and B. Renker, Phys. Rev. B: Solid State, 1975, 12, 3374–3379.
64. M. Galtier, G. Vidal and A. Montaner, J. Phys. Chem. Solids, 1972, 33, 2295–2302.
65. J. L. Jacobson and E. R. Nixon, J. Phys. Chem. Solids, 1968, 29, 967–976.
66. M. T. Dove, V. Heine and K. D. Hammonds, Mineral. Mag., 1995, 59, 629–639.
67. K. D. Hammonds, M. T. Dove, A. P. Giddy, V. Heine and B. Winkler, Am. Mineral., 1996, 81, 1057–1079.
68. X. Chen and S. S. Mao, Chem. Rev., 2007, 107, 2891–2959.
69. M. Grujic-Brojcin, M. J. Scepanovic, Z. D. Dohcevic-Mitrovic, I. Hinic, B. Matovic, G. Stanisic and Z. V. Popovic, J. Phys. D: Appl. Phys., 2005, 38, 1415–1420.
70. M. Ocana, V. Fornes, J. V. G. Ramos and C. J. Serna, J. Solid State Chem., 1988, 75, 364–372.
71. H. Böttner, G. Chen and R. Venkatasubramanian, MRS Bull., 2006, 31, 211–217.
72. S. R. Popuri, A. J. M. Scott, R. A. Downie, M. A. Hall, E. Suard, R. Decourt, M. Pollet and J. W. G. Bos, RSC Adv., 2014, 4, 33720–33723.
73. D. Srivastava, F. Azough, R. Freer, E. Combe, R. Funahashi, D. M. Kepaptsoglou, Q. M. Ramasse, M. Molinari, S. R. Yeandel, J. D. Baran and S. C. Parker, J. Mater. Chem. C, 2015, 3, 12245–12259.

---

Footnotes

† Electronic supplementary information (ESI) available: Details of configurations and potential model. See DOI: 10.1039/c6ra23887d

‡ Present address: Department of Chemistry, Loughborough University, Loughborough LE11 3TU, UK.

---