Tuning the conformation of floppy molecules by charge transfer

Abstract

Recent advances in electrochemistry and nano- and molecular electronics made it possible to prepare and study molecular species having fractional charges (q ≠ 0, ±1, …) that can be continuously tuned by biases. The main focus of this communication is on the impact of continuously tuning the fractional molecular charge on the molecular conformation, an effect expected to be pronounced especially in molecules possessing floppy degrees of freedom. The (4,4′)-bipyridine molecule is considered here as a benchmark case, since the torsional angle between the two pyridyl rings is known to be related to a floppy degree of freedom. Among the specific findings of this investigation one can mention the fact that, to achieve planar conformation (hence maximum electron transmittance), complete reduction (q = −1) is not necessary; the molecular conformation becomes planar already at q ⋍ −0.8. Implications of the specific results reported here for molecular electronics (e.g., molecular switches) are briefly discussed.

---

1 Introduction and background

Understanding the interplay between charge transfer across a molecule and its conformation is an issue of broad interest, encompassing fields ranging from surface science through molecular electronics and electrochemistry to molecular biology. However important the insight that could and can still be gained by investigating native molecules or straightforwardly prepared via ionization or electron attachment, these traditional studies are inherently limited: they only sample molecular species possessing an integral charge.

Recent advances in nano-/molecular electronics^1–6 and electrochemistry^7,8 made it possible to overcome this limitation. When an electron travels across a molecule linked to two electrodes under applied bias V to form a single-molecule junction, a fractional (non-integral) V-dependent charge q (0 < |q| < 1) can arise. This was demonstrated in a recent molecular electronics study,⁹ wherein concurrent transport-SERS (surface enhanced Raman spectroscopy¹⁰) data for electromigrated nanojunctions based on fullerene were acquired. Prior to this work, the effect of the potential of an electrode on the molecules adsorbed on it in terms of an effective fractional molecular charge was elaborated theoretically^11,12 in conjunction with earlier SERS studies on pyrazine molecules adsorbed on macroscopic silver electrodes under bias.¹³

Maximum changes in the fractional molecular charges achieved in the one¹³- or two-⁹electrode setups employed in these less¹³ or more⁹ recent experiments amount to δq ∼ 0.1. Recent model studies¹⁴ drew attention on the fact that the efficiency of the redox process can be substantially improved for EC-STM molecular junctions (EC: electrochemical, STM: scanning tunneling microscope).^{1,2,5–8,15,16} A much broader interval of charge values, ranging from a neutral molecular species (q = 0) to an almost complete reduced molecular species (|q| ≲ 1), can be sampled under this experimental platform. To demonstrate theoretically this possibility,¹⁴ available experimental data² for EC-STM single-molecule junctions based on viologen were employed. The active core of the viologen unit is 4,4′-bipyridine (44BPY), a benchmark molecule used to fabricate single-molecule junctions since the early days of molecular electronics.¹⁷ As emphasized in ref. 14, this is possible because under EC-STM platforms, variations of the overpotential, which plays the role of the gate potential in traditional electronics, are much more efficient in tuning the molecular charge than variations of the source-drain voltage in two-terminal setups. The extra fractional charge transferred to (q < 0) or from (q > 0) the neutral molecule interacts both with the distributions of the electrons of the isolated molecule and with the atomic nuclei. A significant effect brought about by this possibly almost complete charge transfer (0 < |q| < 1) has been recently studied within microscopical calculations:^18,19 the possibility to continuously tune the vibrational molecular properties.

Because the transferred charge interacts with the atomic nuclei of the molecule on which it resides, it can also have a significant impact on the molecular conformation. In a feedback reaction, changes in molecular conformation can have a significant impact on the charge transfer efficiency. One can expect that these effects are particularly important in molecules possessing floppy degrees of freedom²⁰ because the latter are very sensitive even to slight perturbations.

As noted above, continuous potential variations may yield continuous variations of the fractional molecular charges. This opens the exciting avenue of continuously tuning molecular conformations within bias-driven techniques.

It is the main aim of this communication to quantitatively investigate the possibility of continuously tuning the molecular conformation with the aid of bias-driven changes of the fractional molecular charge. To the best of our knowledge, this work represents the first quantitative analysis of the problem delineated above. As a specific example of floppy molecule, the already mentioned 4,4′-bipyridine molecule will be considered below. A series of interesting effects related to the floppy mode on molecular transport through this molecule were reported recently.^20–23 Because molecular electronics is one important field for which the present study may be relevant, and because electron transport through molecular junctions based on 44BPY^17,24,25 and 44BPY-related² species proceeds via the lowest unoccupied molecular orbital, we will mostly restrict ourselves below to the case of charge addition/reduction (−1 < q < 0). Brief remarks on the opposite case of charge removal/oxidation will only be made at the end of this work.

2 Results and discussion

2.1 Computational details

Most numerical results reported below were obtained via calculations done performed by running the SIESTA²⁶ trunk-462 package²⁷ in parallel.²⁸ Unlike most quantum chemical packages available or at least at our disposal, SIESTA allows computations for non-integer charge states. For such calculations, SIESTA employs a DFT (density functional theory) implementation developed in ref. 29. Similar to ref. 18 and 19, in our SIESTA calculations, we used the GGA-PBE functional and split-valence TZP (triple zeta polarized) basis sets for all atoms. As is well known, the PBE (Perdew–Burke–Ernzerhof) functional³⁰ is a parameter free functional that belongs to the broader class of GGA (conjugated gradient approximation) functionals (sometimes also called non-local functionals) for the exchange-correlation energy. Further technical details on these calculations will not be given; they can be found in ref. 18 and 19.

2.2 Impact of electron charge addition on the torsional angle of 4,4′-bipyridine

The most salient feature of the 44BPY molecule (Fig. 1) is its twisting (or torsional) angle θ. It is the very low energy needed to change this angle that makes 44BPY a floppy molecule.^20,21,23 The impact of electron charge addition on the twisting angle is depicted by the curve θ = θ(q) shown in Fig. 2, which represents the main numerical result reported in the present communication.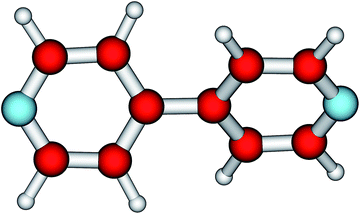

Fig. 1 The most salient feature of the 4,4′-bipyridine molecule (C₅H₄N)₂ is the twisting angle between the two pyridyl rings.

Fig. 2 The twisting angle θ between the two rings of the 4,4′-bipyridine molecule as a function of the fractional molecular charge q.

At equilibrium, the neutral molecule (q = 0, 44BPY⁰) is twisted. The two pyridyl rings are rotated relative to each other (Fig. 1).

From experimental side, the first value reported, θ = 37.3°, was measured in electron diffraction experiments.³¹ Later, values in the range 29.58° < θ < 36° were estimated based on the same experimental measurements depending on the manner of averaging the NMR dipolar coupling constants around all internal motions.^32,33

The value of the twisting angle θ(q)|_q=0 for the neutral species made the object of extensive theoretical studies at various theoretical levels: Hartree–Fock, semi-empirical, and DFT using various exchange-correlations functionals and basis sets.^21,33–39 The differences between the various aforementioned approaches amount to a few degrees; values in the range 35° < θ < 48.6° were reported.^21,33–39 The value obtained within the present SIESTA calculations is θ(q)|_q=0 = 35.0° (Fig. 2). With the same GGA-PBE exchange correlation functional, the value obtained by using the GAUSSIAN 09 suite pf programs⁴⁰ and polarized triple zeta basis sets for all atoms (g09 keywords PBEPBE and TZVP) is 36.9°. The small difference between these two values reflects the peculiar SIESTA's manner to construct strictly localized orbitals, which exactly vanishes beyond a certain radius allowing thereby a linear scaling.²⁶

To summarize, by and large, the present SIESTA estimate for θ(q)|_q=0 reasonably agrees both with the experimental values^31,32 and with other previous theoretical estimates.^21,33–39 This indicates that SIESTA's results can reasonably be trusted.

As amply discussed in the literature,^20,21,36,37 the most important structural differences between the neutral molecule 44BPY⁰ and its reduced form, the radical anion 44BPY˙⁻ (q = −1), is the fact that the latter is planar: θ(q)|_q=−1 = 0. This feature is also obtained within the present SIESTA calculations (cf. Fig. 2).

It is generally accepted that the twisting angle between the two pyridyl rings results from the interplay between two opposite tendencies. On one side, the π-electronic interaction of the pyridyl fragments, which favors a planar conformation (θ = 0) with π-electrons delocalized between the pyridyl rings. On the other side, there is the steric repulsion of the ortho hydrogen atoms, which prefers a nonplanar conformation (θ ≠ 0) wherein the steric hindrance is diminished. The trade-off between these two antagonistic effects is an optimum nonvanishing twisting angle θ(q)|_q=0 ≠ 0 in the neutral species. By adding an entire electron (complete reduction), the π-electronic interaction is enhanced, with a concomitant delocalization over the whole radical anion, which becomes planar: θ(q)|_q=−1 ≠ 0.

Unlike other (usual) quantum chemical packages, SIESTA also allows to compute not only the aforementioned values θ(q)|_q=0 and θ(q)|_q=−1 corresponding to states with integral charges, but also values θ(q) for arbitrary fractional charges of interest (−1 < q < 0). In agreement with what one can intuitively expect from the reasons delineated above, the curve θ = θ(q) calculated in this way (Fig. 2) indicates that the twisting angle decreases by progressively adding electron charge. The curve depicted in Fig. 2 reveals an aspect that cannot be guessed by straightforward intuition nor merely based on the calculated values θ(q)|_q=0 and θ(q)|_q=−1 is that, in order to reach the planar molecular conformation, transferring an entire electron (q = −1) to the neutral 44BPY molecule is not needed. A complete redox process is not necessary. A redox efficiency amounting to |q| ≈ 80% suffices to achieve a planar conformation (reasons why the planar conformation is important will be presented below).

Because the finding that a planar conformation can be reached without need to add an entire electron is one of the most important result reported in this communication, it is worth emphasizing that possible slight inaccuracies in the determination of the θ-values (like those mentioned above) do by no means affect this conclusion: changes of a few degrees in θ around the θ-values found by geometry optimization yield changes in the total energy smaller than 1 meV; changes δq ⋍ |−1 − (0.8)| = 0.2 in the molecular charge are accompanied by variations in the total energy of the order of 0.1 eV.

The above results demonstrate that the charge transfer affect the molecular conformation; the torsional angle is q-dependent. The converse is also true. Within a simplified model, the electron transmission [scr T, script letter T] through molecules consisting of n = 2 rings forming a relative angle θ—and 44BPY belongs to this category, cf. Fig. 1—scales as follows^41–43

t ∝ cos θ (1)

here, is the hopping integral t between the two rings. Eqn (1) is the consequence of the fact that, for electron hopping between π-orbitals, t is proportional to cos θ.^41–43

Fig. 3 depicts the curve of cos² θ—which is the RHS of eqn (2) for n = 2—as a function of q. It shows that, by adding |q| = 60% of an electron to the molecule, one can already reach 99% of the maximum charge transfer efficiency.

Fig. 3 The square cosine of the angle θ between the two rings of the 4,4′-bipyridine molecule—a measure of the transparency of the charge transfer process, cf. Eqn (2)—as a function of the fractional molecular charge q.

The above discussion focused on effects related to the torsional angle, as the most salient feature of this floppy molecule. One can still note that this is not the only interesting impact of the charge transfer in the 44BPY molecule. Another nontrivial impact of charge addition is the change in the total molecule length L = L(q). This effect is visualized in Fig. 4. The increase of the total molecular length upon reduction is related to the quinoidal distortion, which characterizes the radical anion 44BPY˙⁻.^21,36,37,44 According to Fig. 4, addition of an entire electron yields an increase of the molecular length amounting to

ΔL ≡ L(q)|_q=−1 − L_q|_q=0 = 0.13 Å (3)

Fig. 4 The dependence of the molecular length, expressed as the distance d_NN between the nitrogen atoms, of the 4,4′-bipyridine molecule on the fractional molecular charge q. Notice the complete reduction yields a length increase amounting to 0.13 Å.

Parenthetically, the value obtained within calculations using GAUSSIAN 09 PBEPBE/TZVP⁴⁰ is equal to the above SIESTA-based estimate. One can easily imagine that a change in the molecular length as expressed by eqn (3) is quite significant for a molecule stretched between two electrodes to form a molecular junction.

In the same vein, let us still note that, although not so spectacular as changes in conformation related to floppy modes, even changes in the total molecular length upon charge transfer may be of interest. For the 44BPY molecule, eqn (3) predicts an increased length. A length increase may not be so dramatic for a molecular junction already formed in the absence of biases; the molecule can become slightly distorted to withstand elongations given by eqn (3) in the presence of applied (gate) voltages responsible for complete charge transfer.

The increase in length upon reduction is due to the fact that the added electron that populates the LUMO is delocalized over the bipyridine molecule. This is known to yield an overall weakening of the chemical bonds, which become elongated. An opposite effect occurs in the opposite process, e.g. after electron removal. The ΔL-effect may be more dramatic for a molecular species whose length decreases.

To give a single example of this kind, let us refer to biphenyl, a molecule having a two-ring structure similar to 44BPY. One should still note that unlike, 44BPY-based junctions,^2,25 in molecular junctions based on biphenyl conduction is mediated by the highest molecular orbital; so, electron removal is of interest in the present context biphenyl dithiol junctions. Both SIESTA and GAUSSIAN 09 calculations as described above predict a decrease in the molecular length ΔL = −0.11 Å when an entire electron is removed; it is unlikely that a molecular junction would survive such a process.

3 Summary and outlook

In this communication, we have studied theoretically the impact of adding an amount 0 < |q| < 1 of electronic charge on the torsional angle θ of the (4,4′)-bipyridine molecule. An interesting result reported is that a complete reduction (q = −1) is not needed to reach the planar conformation (θ = 0) known to characterize the anionic species.

As a possible application, one can conceive to employ the dependence of the torsional angle on the fractional charge to obtain molecular switches. This route to design molecular switches based on tuning the molecular conformation by controlling the fractional molecular charge would be an alternative to the photoswitched conductivity of covalently bounded single molecule junctions⁴⁵ and photoswitchable CP-AFM (conducting probe atomic force microscopy) molecular wires⁴⁶ reported recently. In view of the n-dependence given in eqn (2), considering the impact of the charge transfer on the conformation of molecular species consisting of chains of n = 2, 3, 4, … aromatic rings would be interesting. To this, one can invoke a naive argument: the higher the exponent [2(n − 1) in the RHS of eqn (2)], the smaller is the value of a sub-unitary number (cos θ in the RHS of eqn (2)) at that power. Oligophenylene series extensively studied (e.g., ref. 47 and citations therein) may be possible candidates for further investigation, given the fact that they possess more torsional modes, that is, more floppy degrees of freedom.

Acknowledgements

Financial support for this research provided by the Deutsche Forschungsgemeinschaft (grant BA 1799/3-1) is gratefully acknowledged. This work was partially performed on the computational resources bwUniCluster and bwForCluster/JUSTUS-HPC facility funded by the Ministry of Science, Research and Arts Baden-Württemberg and the Universities of the State of Baden-Württemberg, Germany, within the framework program bwHPC.²⁸

Notes and references

1. A. Alessandrini, S. Corni and P. Facci, Phys. Chem. Chem. Phys., 2006, 8, 4383–4397.
2. I. V. Pobelov, Z. Li and T. Wandlowski, J. Am. Chem. Soc., 2008, 130, 16045–16054.
3. S. Wang, M. Ha, M. Manno, C. D. Frisbie and C. Leighton, Nat Commun., 2012, 3, 1210.
4. W. Xie, S. Wang, X. Zhang, C. Leighton and C. D. Frisbie, Phys. Rev. Lett., 2014, 113, 246602.
5. A. Alessandrini and P. Facci, in Molecular Electronics: An Experimental and Theoretical Approach, ed. I. Bâldea, Pan Stanford, 2015, ch. 9, pp. 325–352.
6. J. M. Artés-Vivancos, J. Hihath and I. Díez-Pérez, in Molecular Electronics: An Experimental and Theoretical Approach, ed. I. Bâldea, Pan Stanford, 2015, ch. 8, pp. 281–324.
7. A. Alessandrini and P. Facci, Eur. Polym. J., 2016, 83, 450–466.
8. J. Izquierdo and C. Kranz, Eur. Polym. J., 2016, 83, 428–449.
9. Y. Li, P. Doak, L. Kronik, J. B. Neaton and D. Natelson, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1282–1287.
10. M. Takase, S. Yasuda and K. Murakoshi, Front. Phys., 2016, 11, 1–12.
11. F. Avila, D. J. Fernandez, J. F. Arenas, J. C. Otero and J. Soto, Chem. Commun., 2011, 47, 4210–4212.
12. F. Avila, C. Ruano, I. López-Tocón, J. F. Arenas, J. Soto and J. C. Otero, Chem. Commun., 2011, 47, 4213–4215.
13. J. Soto, D. J. Fernández, S. P. Centeno, I. L. Tocón and J. C. Otero, Langmuir, 2002, 18, 3100–3104.
14. I. Bâldea, Phys. Chem. Chem. Phys., 2014, 16, 25942–25949.
15. N. J. Tao, Phys. Rev. Lett., 1996, 76, 4066–4069.
16. J. M. Artés, M. López-Martínez, A. Giraudet, I. Díez-Pérez, F. Sanz and P. Gorostiza, J. Am. Chem. Soc., 2012, 134, 20218–20221.
17. B. Xu and N. J. Tao, Science, 2003, 301, 1221–1223.
18. I. Bâldea, Chem. Phys., 2016 DOI:10.1016/j.chemphys.2016.08.024.
19. I. Bâldea, RSC Adv., 2016, 6, 93715–93721.
20. I. Bâldea, Europhys. Lett., 2012, 99, 47002.
21. I. Bâldea, H. Köppel and W. Wenzel, Phys. Chem. Chem. Phys., 2013, 15, 1918–1928.
22. I. Bâldea, Nanoscale, 2013, 5, 9222–9230.
23. I. Bâldea, J. Phys. Chem. C, 2014, 118, 8676–8684.
24. F. Chen, X. Li, J. Hihath, Z. Huang and N. Tao, J. Am. Chem. Soc., 2006, 128, 15874–15881.
25. J. R. Widawsky, P. Darancet, J. B. Neaton and L. Venkataraman, Nano Lett., 2012, 12, 354–358.
26. J. M. Soler, E. Artacho, J. D. Gale, A. Garcia, J. Junquera, P. Ordejon and D. Sanchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779.
27. Available at http://www.icmab.es/dmmis/leem/siesta/.
28. bwHPC and bwHPC-C5 (http://www.bwhpc-c5.de/) Computational resources funded by the Ministry of Science, Research and Arts Baden-Württemberg and the Universities of the State of Baden-Württemberg, Germany, and the German Research Foundation (DFG).
29. J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Phys. Rev. Lett., 1982, 49, 1691–1694.
30. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
31. A. Almenningen and O. Bastiansen, Skr. - K. Nor. Vidensk. Selsk., 1958, 4, 1 . We refer to the experimental results of this work as cited, e.g., in ref. 36.
32. J. W. Emsley, D. S. Stephenson, J. C. Lindon, L. Lunazzi and S. Pulga, J. Chem. Soc., Perkin Trans. 2, 1975, 1541–1544.
33. Á. J. Pérez-Jiménez, J. C. Sancho-García and J. M. Pérez-Jordá, J. Chem. Phys., 2005, 123, 134309.
34. V. Barone, F. Lelj, C. Cauletti, M. N. Piancastelli and N. Russo, Mol. Phys., 1983, 49, 599–619.
35. V. Barone, F. Lelj, L. Commisso, N. Russo, C. Cauletti and M. Piancastelli, Chem. Phys., 1985, 96, 435–445.
36. L. Ould-Moussa, O. Poizat, M. Castellà-Ventura, G. Buntinx and E. Kassab, J. Phys. Chem., 1996, 100, 2072–2082.
37. M. Castellà-Ventura and E. Kassab, J. Raman Spectrosc., 1998, 29, 511–536.
38. Z. Zhuang, J. Cheng, X. Wang, B. Zhao, X. Han and Y. Luo, Spectrochim. Acta, Part A, 2007, 67, 509–516.
39. E. Kassab and M. Castellà-Ventura, J. Phys. Chem. B, 2005, 109, 13716–13728.
40. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT, 2010.
41. F. Pauly, J. K. Viljas, J. C. Cuevas and G. Schön, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 155312.
42. H. Kondo, J. Nara, H. Kino and T. Ohno, J. Chem. Phys., 2008, 128, 064701.
43. J. C. Cuevas and E. Scheer, Molecular Electronics: An Introduction to Theory and Experiment, World Scientific Publishers, 2010.
44. H. Kihara and Y. Gondo, J. Raman Spectrosc., 1986, 17, 263–267.
45. C. Jia, A. Migliore, N. Xin, S. Huang, J. Wang, Q. Yang, S. Wang, H. Chen, D. Wang, B. Feng, Z. Liu, G. Zhang, D.-H. Qu, H. Tian, M. A. Ratner, H. Q. Xu, A. Nitzan and X. Guo, Science, 2016, 352, 1443–1445.
46. D. Taherinia, C. E. Smith, S. Ghosh, S. O. Odoh, L. Balhorn, L. Gagliardi, C. J. Cramer and C. D. Frisbie, ACS Nano, 2016, 10, 4372–4383.
47. Z. Xie, I. Bâldea, C. Smith, Y. Wu and C. D. Frisbie, ACS Nano, 2015, 9, 8022–8036.

---

Footnote

† Also at National Institute for Lasers, Plasmas, and Radiation Physics, Institute of Space Sciences, RO 077125, Bucharest-Măgurele, Romania.

---