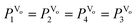Mechanism of aging effect in hybrid-doped BaTiO₃ ceramics: electronegativity and ionic radius

Abstract

Physical properties of ferroelectric materials are usually tailored (for high operation temperature, temperature stability, etc.) through introduction of acceptor and donor dopants that usually induce different aging phenomena. Hence it is of great interest to understand the aging behavior in the presence of both acceptors and donors. In this work, we report the aging effect in hybrid-doped BaTiO₃ ceramics, reflected by the time-dependent change of polarization (P)–electric field (E) hysteresis loops in these cases with different dopant combinations of acceptors (Mn³⁺, Fe³⁺, Co³⁺) and donors (Nb⁵⁺, La³⁺). The results indicate that the electronegativity and the ionic radius of acceptors, rather than the substitution site of the donors, play the key role in the formation of defect pairs which dominates the aging effect in hybrid-doped ferroelectrics. Finally, we propose a unified microscopic mechanism for the aging phenomena in hybrid-doped ferroelectrics, and it provides direct instructions for manipulating the aging effect in hybrid-doped ferroelectric materials.

---

Introduction

Ferroelectric materials have found extensive applications in actuators and sensors due to their ferroelectric and electromechanical properties.¹ In order to realize property tailoring, acceptor and donor ions (classified by their relevant valence to substituted ions) are usually doped in the matrix materials.^2–12 It has been well observed that acceptor doped ferroelectric materials exhibit exotic aging phenomena, i.e. double polarization (P)–electric field (E) hysteresis loops^13,14 and recoverable electrostriction,^15,16 which are not observed in donor doped ferroelectrics.¹

According to former studies, the aging effect in ferroelectrics mainly stems from the symmetry conforming property of point defects, i.e. the oxygen vacancies which form defect dipoles with substituted acceptor ions.¹⁰ Rather than boundary effects (grain boundary effect and domain wall effect), ferroelectric aging is verified to be mainly a volume effect¹⁶ which could be observed not only in ceramics¹¹ but also in single crystals.¹⁶ On the one hand, ferroelectrics doped with both acceptors and donors are common in application, and achieve high electrostrain because of the presence of aging effect.^17,18 On the other hand, in some cases, extra donors could eliminate aging effect which has great impact on the stability and reliability of ferroelectric devices, making the potentially high electrostrain invalid.^19,20 Considering a systematical and unified explanation of aging phenomena in hybrid-doped cases remains unclear, it is of great interest to investigate the aging phenomena in presence of both acceptors and donors, and to study how to manipulate it in hybrid-doped cases.

Thus in this letter, we take the substituted dopants' site, the acceptor/donor ratio and the choice of different acceptors are inescapably considered as the factors to influence aging effect in hybrid-doped BaTiO₃, prepared three groups of ceramic samples corresponding to different combinations of acceptors and donors. Group 1 is BaTiO₃ ceramics doped with acceptor Mn³⁺ (Ti⁴⁺ site acceptor) while La³⁺ (Ba²⁺ site donor) or Nb⁵⁺ (Ti⁴⁺ site donor) is chosen as donor. For Group 2 and Group 3, we chose Fe³⁺ and Co³⁺ as Ti⁴⁺ site acceptor respectively, with Nb⁵⁺ or La³⁺ as donor to fabricate hybrid-doped BaTiO₃ samples Fe³⁺ & donor (Nb⁵⁺ or La³⁺) and Co³⁺ & donor (Nb⁵⁺ & La³⁺). As will be seen in the following, the experimental results indicate that the electronegativity and ionic radius of acceptors rather than the substitution sites of donors dominant the aging process, manifested by the appearance of double P–E hysteresis loops or not. The acceptors with higher electronegativity and smaller ionic radius tend to attract donors to form acceptor–donor pairs (defect pairs) rather than to introduce locally diffusible defects (oxygen vacancies) that attribute mainly to the aging phenomena. With the unified mechanism we propose here to interpret the observed aging phenomena in hybrid-doped BaTiO₃, manipulation of aging effect and the associated high electrostrain can be realized effectively.

Experimental

All three different groups of hybrid-doped BaTiO₃ ceramics were fabricated by a conventional solid-state reaction method of BaCO₃, TiO₂, MnO₂, Fe₂O₃, Co₃O₄, Nb₂O₅ and La₂O₃ (≥99.9%, all from Alfa Aesar), abbreviated as BT–1A (acceptor)–xD (donor) (x is the atomic percentage number of donor concentration), where A (acceptor) could be Mn, Fe or Co fixed at 1 at% while D (donor) is La³⁺ or Nb⁵⁺ varies from 0.5 at% (acceptor-dominant), 1.0 at% (equal-doped) and 1.5 at% (donor-dominant). The valence of dopants Mn, Fe, Co, and La is mainly 3+; Nb is 5+ when sintered at proper temperate (1300–1400 °C for 4 h) in air.^21–26 The formula of the compositions (Ba_y/100La_x/100)(Ti_0.99A_0.01)O₃ is abbreviated as BT–1A–xLa (x is the atomic percentage number of La concentration. e.g. BT–1Mn–0.5La stands for 1.0 at% Mn and 0.5 at% La doped BaTiO₃). Likewise, the composition Ba(Ti_[99−x]/100A_0.01Nb_x/100)O₃ is abbreviated as BT–1A–xNb (x varies from 0.5 to 1.5 denoting the percentage number of Nb concentration). Aging treatment was carried out at 50 °C (<T_C) for 10 days to establish an equilibrium defect state. Before aging, all the samples undergo “deaging treatment”, a procedure of being held at 180 °C (>T_C) for half an hour in order to eliminate the restoring aging effect, and quenched to room temperature, thus we get unaged samples. The in situ XRD data were recorded by Shimadzu XRD-7000 using Cu K_α X-ray radiation (λ = 0.154 nm) with θ–2θ diffraction geometry. In order to avoid the local stress due to intergranular interaction of the bulk sample, the ceramic specimen for XRD measurement was ground into fine-sized powder.²⁷ SEM micrographs of the fractured surface of specimens were taken by scanning electron microscope JSM-7000F. The P–E hysteresis loops and the electrostrain were measured with Radiant Workstation and MTI 2000 photonic sensor at room temperature. The frequency of the measurement was fixed at 10 Hz.

Results and discussion

We performed XRD test to check the structure of the samples. In Fig. 1, the X-ray diffraction patterns of acceptor-dopant hybrid-doped samples show a single tetragonal phase. Equal-doped and donor-dominant cases' XRD results are similar with acceptor-dopant case, showing in the ESI.† All XRD data suggest good quality of the samples (no secondary phase).

Fig. 1 XRD diffraction patterns of BT–1A–0.5D hybrid-doped cases (A = Mn³⁺, Fe³⁺ or Co³⁺, D = Nb⁵⁺ or La³⁺).

The SEM images are shown in Fig. 2 for acceptor-dominant hybrid-doped BaTiO₃ samples. All samples' SEM images could be checked in the ESI.† The homogeneous and completely fine-grained microstructure with grain size ranged from 1.0–4.0 μm, without any indication of abnormal grains.

Fig. 2 SEM images of the fractured surface of (a) BT–1Mn–0.5Nb, (b) BT–1Fe–0.5Nb, (c) BT–1Co–0.5Nb, (d) BT–1Mn–0.5La, (e) BT–1Fe–0.5La, (f) BT–1Co–0.5La specimens.

P–E hysteresis loops and electrostrain of BT–1Mn–xNb and BT–1Mn–xLa (x = 0.5, 1.0, 1.5) before and after aging are shown in Fig. 3. All the unaged samples (black dotted line) show a normal hysteresis loop and non-recoverable butterfly-like electrostrain while all aged samples exhibit typical double hysteresis loops and recoverable butterfly-like electrostrain. As can be seen in this figure, increasing doping amount of La³⁺ or Nb⁵⁺ does not weaken the aging effect resulted from Ti⁴⁺ site acceptors.

Fig. 3 P–E hysteresis loops and electrostrain before and after aging for BT–1Mn–xNb and BT–1Mn–xLa sample. (a1) (b1) (a2) (b2) x = 0.5, (c1) (d1) (c2) (d2) x = 1.0, (e1) (f1) (e2) (f2) x = 1.5. All the aged samples show double hysteresis loops and recoverable butterfly-like electrostrain, contrasting normal single hysteresis loop and non-recoverable butterfly-like electrostrain (black dotted line) before aging.

The hysteresis loops and electrostrain of BT–1Fe–xNb and BT–1Fe–xLa (x = 0.5, 1.0, 1.5) before and after aging are shown in Fig. 4. All unaged BT–1Fe–xNb and BT–1Fe–xLa samples (black dotted line) show a normal hysteresis loop and non-recoverable butterfly-like electrostrain. As for aged BT–1Fe–1.0Nb exhibit double hysteresis loops and recoverable butterfly-like electrostrain after aging. For aged BT–1Fe–xLa samples, aging effect only appears in BT–1Fe–0.5La (red line).

Fig. 4 P–E hysteresis loops before and after aging for BT–1Fe–xNb and BT–1Fe–xLa samples, (a1) (b1) (a2) (b2) x = 0.5, (c) (d) x = 1.0, (e) (f) x = 1.5. Aged BT–1Fe–1.5Nb, BT–1Fe–1.0La and BT–1Fe–1.5La samples remain single hysteresis loop and non-recoverable butterfly-like electrostrain (blue line), while BT–1Fe–0.5Nb, BT–1Fe–1.0Nb and BT–1Fe–0.5La show double hysteresis loops and recoverable butterfly-like electrostrain after aging (red line). The electrostrain values decrease as the donor increase.

The hysteresis loops and electrostrain of BT–1Co–xNb and BT–1Co–xLa (x = 0.5, 1.0, 1.5) before and after aging are shown in Fig. 5. Similar with the aging results of BT–1Fe–xD, all unaged BT–1Co–xNb and BT–1Co–xLa samples (black dotted line) show normal hysteresis loops and non-recoverable butterfly-like electrostrain. As for aged BT–1Co–xNb samples, aging effect is only absent in aged BT–1Co–1.5La sample (blue line) while the other two display double hysteresis loop and recoverable butterfly-like electrostrain. For aged BT–1Co–xLa samples, aging effect only appears in acceptor-dominant case BT–1Co–0.5La (red line).

Fig. 5 P–E hysteresis loops before and after aging for BT–1Co–xNb and BT–1Co–xLa samples, (a1) (b1) (a2) (b2) x = 0.5, (c1) (d1) (c2) (d2) x = 1.0, (e1) (f1) (e2) (f2) x = 1.5. Aged BT–1Co–1.5Nb, BT–1Co–1.0La and BT–1Co–1.5La samples remain single hysteresis loop and non-recoverable butterfly-like electrostrain (blue line), while BT–1Co–0.5Nb, BT–1Co–1.0Nb and BT–1Co–0.5La show double hysteresis loops and recoverable butterfly-like electrostrain after aging (red line). And the electrostrain value decrease as the amount of donor increase.

Up to now, there are three hybrid-doped BaTiO₃ ceramics distinguished by different acceptors: BT–1Mn–xD (D is Nb⁵⁺ or La³⁺); BT–1Fe–xD; BT–1Co–xD, shown in Table 1. Based on their P–E hysteresis loops, these three hybrid-doped cases are classified two groups: Group I including BT–1Mn–xD, exhibit obvious aging effect no matter the amount of acceptor or donor is dominant. It suggests that the existence of donors would not eliminate the aging effect caused by acceptors; Group II including BT–1Fe–xD and BT–1Co–xD characterize the typical performance of donor-doped ferroelectrics that they could reduce the aging effect as the amount of donors increases.

Table 1 Aging results of hybrid-doped BaTiO₃ BT–1A–xD (A = Mn³⁺, Fe³⁺, Co³⁺; D = Nb⁵⁺, La³⁺ and x = 0.5, 1, 1.5)

	Mn^3+			Fe^3+			Co^3+
a O represents occurrence of double hysteresis loops.b X represents no occurrence of double hysteresis loops.
Electronegativity	1.55			1.83			1.88
Ionic radius in pm^34	72			69			68.5
x (amount of donor)	0.5	1	1.5	0.5	1	1.5	0.5	1	1.5
Nb^5+ (Ti^4+ donor)	O^a	O	O	O	O	X	O	O	X^b
La^3+ (Ti^4+ donor)	O	O	O	O	X	X	O	X	X

---

The results indicate that the choice of acceptor is the main factor to influence the aging phenomenon, not the occupancy sites of donor ions. In two former hybrid-doped BaTiO₃ cases, they provided self-consistent explanations for the microscopic mechanism of their ad hoc systems: BT–1Mn–xNb hybrid-doped case¹⁷ and BT–1Fe–xLa case²⁰ which are also performed in our experiment and displayed same aging results. These two hybrid-doped BaTiO₃ cases indicate that the appearance of ferroelectric aging phenomenon depends on the distribution of dopants in BaTiO₃. However, only in accordance these two hybrid-doped cases, influence generated from dopants' sites cannot be ruled out. A unified mechanism for aging effect in hybrid-doped BaTiO₃ caused by arrangement and interaction of dopants remains unclear.

To understand our results, it is natural to analyze the configuration of dopants distribution. As mentioned in the introduction, aging phenomenon is induced by the migration of oxygen vacancies. Thus, if acceptor and donor form defect pairs when the amount of acceptors is less than that of donors, there will be no oxygen vacancies due to the charge neutrality caused by defect pairs, the aging phenomenon would not exist.^10,17

Considering the distribution of dopants in BT–1Mn–xLa cases (x = 0.5, 1.0, 1.5) as shown in Part I, acceptor occupies Ti⁴⁺ site and La³⁺ occupies Ba²⁺ site randomly in different crystal lattices. During sintering process, as what have been discussed in the former work about BT–1Mn–xNb,¹⁷ to maintain the local charge neutrality, oxygen vacancies generate. Upon aging process [in ferroelectric tetragonal phase], the distribution symmetry of defects i.e. oxygen vacancies around a defect ion changes from cubic to tetragonal, and a defect dipole moment forms related to the non-centric distribution of charged point defects. For well-aged samples, under an external electric field, domains switch along the direction of electric field while the defect symmetry remains unchanged, still in cubic symmetry. P_D which denotes the defect dipole keeps the original orientation and behaves as the restoring force. This model well explains the observed double-hysteresis-loop of Group I cases and acceptor-dominant case in BT–1Fe–xD and BT–1Co–xD where the Ti⁴⁺ site is substituted with Fe³⁺ or Co³⁺. By comparison, in BT–1Fe–1.5D and BT–1Co–1.5D cases, when the donor is dominant as shown in Fig. 6 Part II, defect ion Fe³⁺ or Co³⁺ and donors would form defect pairs to keep local charge neutral that means no oxygen vacancies and no aging phenomenon. However, in equally doped cases with Fe³⁺ or Co³⁺ as acceptors, aging effect exists in BT–1Fe–1Nb and BT–1Co–1Nb cases that acceptor and donor are substituted in the same site (Ti⁴⁺ site), while in La³⁺ (Ba²⁺ site donor) doped cases BT–1Fe–1La and BT–1Co–1La, aging effects is absent. Due to more space limitation of two dopants substituted in the same site of one crystal lattice, in that hybrid-doped case dopants are more likely to distribute separately. Therefore, the experiment results of Group II suggest that compared with the choice of acceptors the site donors occupy plays an inferior role in aging process.

Fig. 6 Microscopic illustration of BT–1A–xD (x = 0.5, 1.0, 1.5). Part I is for Mn³⁺ doped and BT–1A–0.5Nb, BT–1A–1Nb, BT–1A–0.5La samples (A is Fe³⁺ or Co³⁺), they both show double hysteresis loops after aging. (a) In Fresh state, the defect symmetry around acceptor and donor both keep cubic. (b) After aging, the defect symmetry around acceptor changes to a tetragonal symmetry and defect dipole P_D generates, while defect symmetry around donor remains cubic. denotes the conditional probability of finding an oxygen vacancy (V_o) around at i (i = 1, 2, 3, 4) around an acceptor. For Ti⁴⁺ site donor (represented by D⁵⁺) shown in (b1), is the conditional probability of finding a Ba²⁺ vacancy at site i (i = 1, 2, 3, 4) around a donor. Ba²⁺ site donor (represented by D³⁺) cases are shown in (b2). After aging and in equilibrium state, the change of oxygen vacancies makes . Because the immobility of cation vacancies V_Ba and Ba²⁺ site dopants, . The outer larger rectangle represents crystal symmetry; the inner smaller black rectangle represents defect symmetry around acceptor, while the blue cubic represents the defect symmetry caused by a substituted donor. (c) When electric field is applied, P_s turns to the direction of electric field while the defect dipole remains the original direction, and P_D acts as a restoring force to reverse domain switching to (b). Part II illustrates aging results in BT–1A–1.5Nb, BT–1A–1La, BT–1A–1.5La (A is Fe³⁺ or Co³⁺), aging effect is absent in these cases. (e3) The formation of defect pairs causes the local charge to keep neutral, thus no oxygen vacancies generate, . (g) When electric field is removed, the direction of P_s will be changed by the electric field and cannot return to the original direction, which displays a non-recoverable P–E loop pattern, also, no aging phenomenon is observed in these two cases.

The observed aging phenomena suggest that the key factor to influence the generation of oxygen vacancies in hybrid-doped BaTiO₃ ceramics is whether the acceptors and donors form defect pairs. The experiment results exhibit that the hybrid-doped ferroelectrics which bear the same acceptors, no matter donor occupies Ti⁴⁺ site or Ba²⁺ site, would show similar hysteresis-loop patterns. In order to understand the experiment results, we would analyze the microscopic mechanism of defect pairs. Due to the attractive interaction among point defects, if the total energy of defect-pair state is lower than the isolated point defect state, the acceptor–donor pairs would be formed.^28,29

Now, we analyze the different defects distribution in Group I and Group II hybrid-doped BaTiO₃ according to the attractive interaction among point defects. One of the most important chemical properties of an atom is electronegativity (EP) which quantifies the tendency of an atom or a functional group to attract electrons (or electron density) towards itself.^30–32 The EP of an atom is affected by both its atomic number and the distance between its valence electrons and the charge nucleus.³¹ According to the periodic table of electronegativity with the Pauling scale, the EP values of Mn, Fe, Co are 1.55, 1.83, 1.88,³³ respectively as shown in Table 1. Therefore, it is possible for Mn³⁺ and donors to form defect pairs due to its EP is less than those of Fe and Co, suggesting weaker ability of attracting electron from donor. As a result, Mn³⁺ and donor tend to distribute separately. Also from the viewpoint of ionic radius of acceptors, defect pairs containing acceptor of larger ionic radius would cause the lattice distortion. That leads to higher total energy of this defect-pair state than that of the acceptors Fe³⁺ and Co³⁺ tend to be more likely to form pairs with donors in order to lower the energy of the whole hybrid-doped BaTiO₃ system. As for Mn³⁺ as acceptor, it is less isolate defect state.^35,36 Compared with Fe³⁺ and Co³⁺, Mn³⁺ bears larger ionic radius, thus being less likely to form defect pairs with donors (as shown in Table 1). However, in former works, doping effect analyzed by impedance is common^37–39 while the relationship between aging effect and impedance or conductivity is rare mentioned. It is worth further and systematically research.

Conclusions

In conclusion, all Mn³⁺ doped hybrid-doped BaTiO₃ ceramics show double hysteresis loops after aging, while in Fe³⁺ or Co³⁺ doped cases when the amount of donors is no less than acceptors, there are no occurrences of double hysteresis loops after aging. The experimental results indicate that the electronegativity and ionic radius of the acceptor rather than the sites which the donors occupy play the decisive role in the aging phenomena of hybrid-doped BaTiO₃ ceramics (BT–1Mn–xNb, BT–1Mn–xLa, BT–1Fe–xNb, BT–1Fe–xLa, BT–1Co–xNb and BT–1Co–xLa). As for the aging phenomena in hybrid-doped ferroelectrics, the present study provides not only a unified microscopic explanation but also an effective approach for the manipulation, probably benefiting practical applications of ferroelectric devices.

Acknowledgements

This work was supported by the National Basic Research Program of China (Grant No. 2012CB619401); the National Natural Science Foundation of China (Grants No. 51431007, No. 51471125, No. 51222104, No. 51371134, 51422704 and No. 51601140).

References

1. K. Uchino, Ferroelectric Devices, CRC Press, Inc., 2nd edn, 2009.
2. X. Sun, J. Chen, R. Yu, X. Xing, L. Qiao and G. Liu, Sci. Technol. Adv. Mater., 2008, 9, 025004.
3. G. H. Haertling, J. Am. Ceram. Soc., 1999, 82, 797–818.
4. G. I. Distler, V. P. Konstantinova, Y. M. Gerasimov and G. A. Tolmacheva, Nature, 1968, 218, 762–765.
5. C. H. Yang, J. Seidel, S. Y. Kim, P. B. Rossen, P. Yu, M. Gajek, Y. H. Chu, L. W. Martin, M. B. Holcomb, Q. He, P. Maksymovych, N. Balke, S. V. Kalinin, A. P. Baddorf, S. R. Basu, M. L. Scullin and R. Ramesh, Nat. Mater., 2009, 8, 485–493.
6. W. Ke and J. F. Li, Adv. Funct. Mater., 2010, 20, 1924–1929.
7. Z. Cheng, X. Wang, S. Dou, H. Kimura and K. Ozawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 2101.
8. N. H. Chan and D. M. Smyth, J. Am. Ceram. Soc., 2006, 67, 285–288.
9. Q. Tan, J.-F. Li and D. Viehland, Philos. Mag. B, 1997, 76, 59–74.
10. X. Ren, Nat. Mater., 2004, 3, 91–94.
11. L. X. Zhang, W. Chen and X. Ren, Appl. Phys. Lett., 2004, 85, 5658–5660.
12. Z. Yao, R. Chu, Z. Xu, J. Hao and G. Li, RSC Adv., 2016, 6, 33387–33392.
13. Y. Y. Guo, J.-M. Liu, Y. F. Guo, T. Wei, Y. J. Guo and N. Zhang, AIP Adv., 2015, 5, 097107.
14. Y. Pu, D. Liu and X. Shi, Vacuum, 2014, 99, 38–41.
15. M. I. Morozov and D. Damjanovic, J. Appl. Phys., 2010, 107, 034106.
16. L. X. Zhang and X. Ren, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 4108.
17. W. Liu, W. Chen, L. Yang, L. Zhang, Y. Wang, C. Zhou, S. Li and X. Ren, Appl. Phys. Lett., 2006, 89, 172908.
18. J. H. Kim, D. H. Kim, T. H. Lee, T. G. Lee, B. Y. Kim, S. Nahm, C. Y. Kang and J. Ryu, J. Am. Ceram. Soc., 2016 DOI:10.1111/jace.14469.
19. D. Xue, J. Gao, L. Zhang, H. Bao, W. Liu, C. Zhou and X. Ren, Appl. Phys. Lett., 2009, 94, 082902.
20. C. Zhou, W. Liu, H. Bao, J. Gao, D. Xue and X. Ren, Ferroelectrics, 2010, 404, 141–146.
21. L. Srisombat, S. Ananta, B. Singhana, T. R. Lee and R. Yimnirun, Ceram. Int., 2013, 39, S591–S594.
22. G. V. Lewis, C. R. A. Catlow and R. E. W. Casselton, J. Am. Ceram. Soc., 1985, 68, 555–558.
23. K. S. Katti, M. Qian, F. Dogan and M. Sarikaya, J. Am. Ceram. Soc., 2002, 85, 2236–2243.
24. T. L. Phan, P. D. Thang, T. A. Ho, T. V. Manh, T. D. Thanh, V. D. Lam, N. T. Dang and S. C. Yu, J. Appl. Phys., 2015, 117, 2845.
25. M. Prades, N. Masó, H. Beltrán, E. Cordoncillo and A. R. West, J. Am. Ceram. Soc., 2008, 91, 2364–2366.
26. A. Kirianov, N. Ozaki, H. Ohsato, N. Kohzu and H. Kishi, Jpn. J. Appl. Phys., 2001, 40, 5619–5623.
27. J. Gao, S. Ren, L. Zhang, Y. Hao, M. Fang, M. Zhang, Y. Dai, X. Hu, D. Wang and L. Zhong, Appl. Phys. Lett., 2015, 107, 113.
28. G. A. Baraff and M. Schlüter, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 7346–7348.
29. S. B. Zhang, S.-H. Wei and A. Zunger, Phys. Rev. Lett., 1997, 78, 4059–4062.
30. R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, J. Chem. Phys., 1978, 68, 3801–3807.
31. R. P. Iczkowski and J. L. Margrave, J. Am. Chem. Soc., 1961, 83, 72A–79A.
32. A. L. Allred and E. G. Rochow, J. Inorg. Nucl. Chem., 1958, 5, 264–268.
33. L. Pauling, Nature, 1960, 145, 644–645.
34. R. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
35. E. Patino and A. Stashans, Ferroelectrics, 2001, 256, 189–200.
36. E. Patiño, F. Erazo and A. Stashans, Mater. Lett., 2001, 50, 337–340.
37. F. D. Morrison, A. M. Coats, D. C. Sinclair and A. R. West, J. Electroceram., 2001, 6, 219–232.
38. S.-H. Yoon, C. A. Randall and K.-H. Hur, J. Am. Ceram. Soc., 2009, 92, 2944–2952.
39. Y. Seok Hyun and K. Hwan, Jpn. J. Appl. Phys., 1999, 38, 4824.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra23546h

---