Microfluidic fabrication of composite hydrogel microparticles in the size range of blood cells

Abstract

The fabrication of alginate hydrogel microparticles with embedded liposomes and magnetic nanoparticles for radiofrequency controlled release of encapsulated chemical cargo was considered. An extractive gelation process was implemented in a microfluidic device, which enabled the production of uniform composite microparticles of dimensions comparable to those of blood cells (between 5 and 10 μm). The critical parameters that control the extractive gelation process were systematically explored and feasible values that provide microgel particles of a defined size and morphology were identified. First, the initial water-in-oil droplet is formed in a flow-focusing junction whose size is controlled by the flow-rate of the oil phase. Then, the train of droplets is sandwiched between two streams of oil containing calcium ions. In that way, a flux of water molecules from the droplets towards the continuous phase as well as a transport of calcium ions towards the disperse phase are initiated. The final microparticle properties were thus found to be sensitive to three elementary sub-processes: (i) the initial droplet size; (ii) the extraction of water into the oil phase, which was controlled by the volume of the oil phase and its initial moisture content; and (iii) the kinetics of ionic cross-linking of the alginate matrix, which was controlled by the varying calcium concentration. The size and morphology of the final composite microgels were fully characterized.

---

1 Introduction

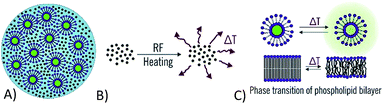
Recent research in the field of drug delivery systems has resulted in the first prototypes of chemical robots – hydrogel composite microparticles, which are able to store, release and chemically process active components encapsulated in the particles as a result of external radiofrequency signals.¹ The functional components (liposomes, magnetic nanoparticles, enzymes) are encapsulated in the alginate gel (Fig. 1A). Alginate is a biopolymer soluble in water, which gels in the presence of multivalent ions like calcium.² The purpose of the alginate matrix is to hold all the functional components together in a single composite particle, and at the same time allow rapid diffusion of low molecular weight payloads out of the particle once they are released from the liposomes. In addition, alginate is biodegradable and can be relatively easily functionalized e.g. by the attachment of targeting antibodies. The functional components encapsulated into the alginate matrix were iron oxide nanoparticles (Fig. 1B) for radiofrequency heating³ and MRI visualization,⁴ liposomes (Fig. 1C) for storage and release of active molecules or their precursors,⁵ and optionally also immobilized enzymes that facilitate the conversion of pro-drugs to active substances.¹ Liposomes are spherical structures formed by a phospholipid bilayer, which are able to release the active matter in response to a temperature stimulus (Fig. 1C).⁶ The permeability of liposomes can be significantly increased once they are heated above their phase transition temperature. In the case of chemical robots, the needed temperature change is achieved by iron oxide nanoparticles upon exposure to external radio-frequency magnetic field.³

Fig. 1 (A) Composite alginate microparticle; (B) iron oxide nanoparticles that locally dissipate energy in the radio-frequency alternating magnetic field; (C) liposomes that locally release encapsulated chemical payload in response to a temperature change.

Early prototypes of chemical robots were fabricated by the drop-on-demand inkjet printing method,^3,7 and have characteristic dimensions around 50 μm. However, for in vivo applications in drug delivery, it is necessary to further reduce their size to that of the blood cells⁸ or lower, i.e. approximately by a factor of 10 in diameter (a factor of 1000 in volume), which is a challenging task. For instance, human erythrocytes (red blood cells) have a characteristic diameter of 6–8 μm and various types of leukocytes (white blood cells) can have characteristic diameters ranging from 10–12 μm for neutrophils up to 12–15 μm for large lymphocytes.⁹

Several techniques exist to fabricate alginate microparticles such as inkjet printing,¹⁰ spray drying,¹¹ membrane emulsification¹² or synthesis by a microfluidic chip.^13–22 Overall, synthesis of the alginate microparticles on a custom design microfluidic chip appears like the most feasible technique to synthesize monodisperse alginate microparticles. By appropriate design of the microfluidic chip, it is possible to prepare a wide range of different alginate microparticles, although it turns out that the size of the microparticles is a limiting factor if blood cell-sized particles are desired. For example, Liu et al. produced monodisperse alginate microparticles with diverse shapes (such as plugs, disks, microspheres, rods or threads) in a microfluidic chip with two individual flow-focusing channels and a synthesizing channel where the gelation of the microparticles was obtained. The smallest particles had a diameter of 30 μm.¹⁵ Yeh et al. used a T-junction channel to produce a w/o emulsion, which was gelled in the bulk by CaCl₂. They encapsulated nanoparticles into alginate microparticles with diameters ranging from 70 to 220 μm.²⁰ Pectin-alginate Janus hydrogel microparticles with average diameter of 90 μm were synthesized by Marquis et al.¹⁶ by a flow focusing channel and gelled by internal gelation.²² Finally, Zhang et al. prepared 40 μm alginate microparticles in a microfluidic chip, where on-chip gelation was achieved by providing sufficient residence time in the microchannel.²¹

It has been shown that a further reduction of the particle size on the microfluidic chip is possible by using an organic solvent with a non-negligible water solubility as the continuous phase. In that way, it enables partial extraction of water from the droplets, consequently reducing their size. Rondeau and Cooper-White¹⁸ have demonstrated the principle of extractive gelation using dimethyl carbonate (DMS) as a continuous phase. By extractive gelation, Seki's group^19,23 has produced collagen and alginate microparticles in the size range lower than 10 μm. By varying the initial alginate concentration and using methyl acetate as the continuous phase they achieved pure alginate microparticles with a diameter of 6 μm. In addition to pure alginate microparticles, it was also shown that DNA molecules can be immobilized in the gel; however, the particle size with immobilized DNA increased up to 20 μm.¹⁹ The principle of extraction coupled with both internal and external gelation was also applied to pectin microparticles and the possibility to control not only size but also morphology was demonstrated.¹⁷

The objective of the present work was to achieve a reduction in particle size by the principle of extractive gelation, while exploring the possibility to incorporate functional components (magnetic nanoparticles and liposomes) into the hydrogel matrix. Previously, such functional components have never been incorporated into hydrogel microparticles produced by microfluidics. We are introducing a method to produce monodisperse composite alginate microparticles with a sub 10 μm characteristic size using a custom-designed microfluidic chip that implements extractive gelation (Fig. 2). First, droplets of aqueous solution of alginate in the continuous oil phase are formed in a flow-focusing channel. Second, gelation of the droplets is established in a long wavy channel by diffusion of calcium ions from the continuous phase. At the same time, the volume of the droplets is reduced by partial extraction of water into the continuous phase. Depending on the volumetric flow-rates of the aqueous and the oil phase, different conditions of the production were mapped and the effect of extraction on the achievable size of the microparticles was evaluated. The influence of the calcium concentration on the buckling of the alginate microparticles and their final morphology was also part of our investigation. The ideal conditions to produce monodisperse microparticles and to incorporate functional components (iron oxide nanoparticles, liposomes) were found.

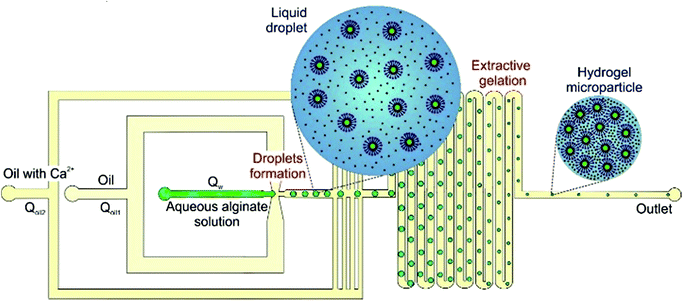Fig. 2 Workflow principle of the production of composite alginate microparticles in the 5–10 micrometers size range.

2 Materials and methods

2.1 Chemicals

The following chemicals were used: polydimethylsiloxane (PDMS, Sylgard 184, Aldrich), 1-undecanol (99%, Aldrich), calcium iodide (98%, Aldrich), tris(2-amino-2-hydroxymethylpropane-1,3-diol) (Sigma), Abil (Abil EM 90, Prospector), Alginate Protanal LF 10/60FT (FMC Biopolymer), Triton X-100 (Sigma). Deionized water was filtered by Aqual 25 (Aqual, Czech Republic).

2.2 Fabrication of microfluidic chip

The chip was made by a standard soft lithography technique. The master was fabricated from a photoresist on a silicon wafer according to a previously published protocol.²⁴ The PDMS-based microfluidic device was fabricated by pouring PDMS prepolymer in a 1 : 5 cross-linking ratio onto the master. After curing at 70 °C for 22 minutes the polymer was lifted off with the pattern on its surface. Separately, a cover glass was coated with PDMS in a 1 : 14 cross-linking ratio and cured at 70 °C for 26 minutes.²⁵ The thin layer of PDMS on the cover glass was achieved by spin-coating (Spin 150, 2000 rpm for 40 s). The final microfluidic chip was assembled by fusing the PDMS piece together with the PDMS-coated glass and left in an oven at 70 °C overnight. The bonding was achieved due to diffusion of excess cross-linker from the PDMS piece to the thin layer of PDMS on the glass. The bonding achieved in this way was sufficient for the pressures used in subsequent fluidic experiments. Being made from PDMS, the channel walls were hydrophobic. The width of the microchannel at the flow focusing orifice was 50 μm, whereas the width of the rest microchannels was 85 μm. The height of the microchannels was 22 μm. A schematic of the microfluidic chip layout and a capture of microparticle production can be found in ESI-1.†

2.3 Principle of alginate microparticle formation

Droplets of alginate aqueous solution were formed in the flow focusing section of the microfluidic device, as shown in ESI-1.† The disperse phase was aqueous alginate solution (1% w/w) with a viscosity of 32 mPa s and the continuous phase was 1-undecanol with 5% w/w of surfactant Abil Em 90. The chosen surfactant concentration was the result of a separate optimization study, detailed in ESI-2.† The flow focusing geometry offers a convenient method to produce monodisperse droplets (typical coefficient of variation 1.3%). Once droplets were formed, a second stream of immiscible liquid was introduced (1-undecanol with 5% w/w Abil Em 90 and 2% CaI₂) in the next section (Fig. 2) to initiate the gelation of the alginate droplets due to diffusion of calcium ions. The gelation then continued in the long wavy channel (130 mm) in the third section of the microfluidic device (Fig. 2). Calcium ions have to be introduced after the formation of the droplets to avoid pre-mature gelation of alginate in the flow-focusing orifice, which would cause instabilities during the droplet formation. Following the introduction of the continuous phase, the alginate droplets decrease their volume not only due to cross-linking by Ca²⁺, but primarily due to the extraction of water from the disperse to the continuous phase (the solubility of water in 1-undecanol without surfactant at room temperature was found to be 2.7% v/v by FTIR spectroscopic measurements, which is consistent with values reported in the literature²⁶). At the same time, the solubility of 1-undecanol in water is negligible, therefore no mass transfer of the oil phase into the droplets takes place.

2.4 Parametric investigation of extractive gelation

The extraction of water from the droplets is affected by the volume ratio between the continuous and the disperse phase; this dependency was systematically investigated to control the size of the produced microparticles. The flow rate ratio, and thus the volume ratio, of the oil to the aqueous phase was investigated in a range lying from 10 to 100. The lower limit is given by the need to separate individual water droplets in the flow-focusing section, and the upper limit is given by the pressure conditions in the microfluidic chip (to avoid back flow). However, not only the ratio but also the absolute values of the flow-rates of all phases influence the morphology of the alginate microparticles. Different flow rates of the disperse phase (Q_w = 2–12 μl h⁻¹) and the continuous phase (Q_oil1 = 50–190 μl h⁻¹ and Q_oil2 = 10–150 μl h⁻¹) were studied, where Q_w denotes the flow rate of the alginate solution, Q_oil1 refers to the oil flow rate into the flow focusing section, Q_oil2 refers to the oil flow rate into the gelation section, and Q_oil = Q_oil1 + Q_oil2 will be used to denote the overall flow rate of the oil phase. For all the studied combinations of flow rates, the stable dripping regime was present but vastly different final particle morphology was observed, as will be discussed in Section 3.2. The aqueous solution of alginate and both oils were supplied to the microchannels by means of digitally controlled syringe pumps (neMESYS, low pressure module, Cetoni) attached to PTFE poly(tetrafluoroethylen) tubes (Adtech). The process of microparticles formation was observed and recorded by a high-speed camera (Redlake Motion Pro) attached to an inverted optical microscope (Olympus CKX 41). Video images taken during the microparticle formation process were analyzed by image analysis software ImageJ.

2.5 Preparation of composite alginate–magnetic–liposome microparticles

To prepare alginate microparticles that also contain functional components (magnetic nanoparticles and liposomes), the disperse phase was prepared as follows: 1 ml of 2% w/w aqueous solution of alginate was filtered to remove any impurities (0.2 μm pore filter, Sartorius Biotech) and mixed with 500 μl of magnetic nanoparticle suspension in deionized water (10 g l⁻¹) and 500 μl suspension of liposomes purified by gel chromatography and stirred for 10 minutes. The details of the preparation of the magnetic nanoparticles and the liposomes are provided in ESI-3, ESI-4 and 5.† After mixing of the alginate solution with the magnetic nanoparticle and the liposome suspensions, the final alginate concentration was 1% w/w, i.e. the same as in the pure alginate experiments described above. The continuous phase was also identical as in the case of pure alginate experiments, i.e. 1-undecanol with 5% w/w Abil Em 90 for the flow-focusing section and 1-undecanol with 5% w/w Abil Em 90 and 2% CaI₂ in the gelation section. Both phases were introduced into the microfluidic chip by PTFE tubes and the system was controlled as described above (Section 2.4). The microparticles were collected outside of the chip in a beaker connected with the outlet of the chip via PTFE tubes (0.33 mm ID × 0.75 mm OD), separated from the oil phase by magnetic decantation and finally washed by deionized water three times. The internal structure of the microparticles was visualized by laser scanning confocal microscopy (Olympus Fluoview FV-1000).

2.6 Release kinetics measurement

In order to confirm the ability of the composite alginate–magnetic–liposome microparticles to store and release encapsulated chemical payload, the liposomes were loaded by a fluorescent dye carboxyfluorescein (CF) as described in ESI-5,† which has excitation/emission wavelength at 490/516 nm. Two types of release measurements were of interest: spontaneous leakage of liposomes during storage (which is undesirable), and controlled release of CF from liposomes by external stimuli (which is desirable). In both cases, the fluorescence of the bulk solution containing the alginate–magnetic–liposome microparticles was measured by a fluorescence spectrometer Cary Eclipse (Agilent Technologies). Typically, 5 μl of concentrated microparticle suspension was dispersed in 500 μl of isotonic 10 mM Tris–HCl buffer. The fluorescence was always normalized to that corresponding to complete release of all encapsulated CF.¹ To determine the amount of encapsulated CF the liposomes were destroyed by surfactant Triton X-100 (50 μl of 1% solution). To confirm the destruction of all liposomes after adding the Triton, the sample was heated to 65 °C for one hour, no increase of fluorescence was then observed, therefore the destruction was sufficient. The fluorescence intensity was measured at 25 °C for all samples.

2.7 Radiofrequency heating set-up

The radiofrequency heating of the composite microparticles was characterized by monitoring the temperature rise of a microparticle suspension exposed to alternating magnetic field. 10 μl of closely packed microparticles in an insulated plastic vial were placed into a double-turn (20 mm ID), water-cooled copper coil induction head connected to 900 kHz RF generator (PowerCube 64/900, CEIA, Italy). The sample temperature was measured by a fiber-optic temperature sensor (Neoptix).

3 Results and discussion

3.1 Effect of flow rates on droplet shrinking

Droplets of water in oil (w/o) were produced in the flow focusing device under the stable dripping regime (Fig. 3A) corresponding to the shear induced droplet formation. In the shear driven droplet break-up the diameter of the produced droplets depends only on the capillary number: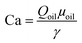 , where Q_oil is the flow rate of the continuous phase, μ_oil is the dynamic viscosity of the continuous phase and γ is the interfacial tension between the two phases.²⁷ The droplet diameter decreases continuously with increasing capillary number, therefore with increasing Q_oil (Table 1). The flow rate of the disperse phase has a negligible effect on the droplet size, however it has an effect on the frequency of the break-up.

As described above, particle size reduction was achieved by partially extracting water from the droplets formed in the flow focusing section of the chip into the surrounding oil phase. For extraction experiments described in this section, none of the oil phase contained calcium ions, so the size decrease of the microparticles was purely due to extraction (no gelation took place). We evaluated the volume change of the droplets by image analysis. Images of the droplets were taken in two locations (130 mm distant from each other), i.e. just behind the flow focusing section of the chip and just before the outlet from the chip (Fig. 3B). The droplet volume was calculated by considering the disk shape of the droplet as follows: 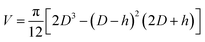, where the D is measured diameter of the droplet and h is the height of the channel, for D > h. For cases when D < h the droplet volume was evaluated simply as the volume of a sphere. The extent of shrinkage will be described by a ratio R_V = V_final/V_orig, were V_final and V_orig denote the final and the original droplet volume, respectively.

Fig. 3 (A) Droplet formation in the flow focusing device. (B) An example of droplet shrinkage; the scale bar is 50 μm.

Table 1 Conditions of alginate microparticles preparation and their circularity

	C Ca^2+ [% w/w]	D in [μm]	Q w [μl h^−1]	Q oil1 [μl h^−1]	Q oil2 [μl h^−1]	Circ
A	0.9	41	5	110	90	0.59
B	0.5	33	5	150	50	0.93
C	0.5	41	5	110	90	0.78
D	0.5	47	5	50	150	0.51
E	0.1	33	5	150	50	0.83
F	0.1	41	5	110	90	0.85

---

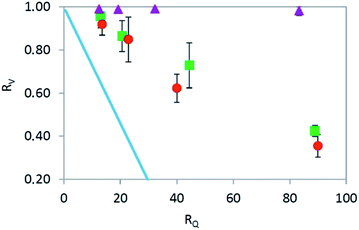
The volume change of the droplet by extraction depends on two factors: the ratio R_Q between the continuous and the disperse phase, i.e. R_Q = Q_oil/Q_w and the contact time between the two phases. The ratio R_Q determines the extraction capacity of the oil phase in the limiting case of sufficiently long residence time in the microfluidic chip for extraction equilibrium to be established. Indeed, considering the solubility K of water in oil (on a volume basis) and the planar geometry of the system where capillary pressure is negligible, the theoretical volume ratio R^eq_V at equilibrium is R^eq_V = 1 − KR_Q. The evolution of the droplet shrinking ratio R_V as a function of the ratio R_Q is reported in Fig. 4. It can be seen that the droplets are systematically decreasing their volume with increasing amount of the continuous phase, with a possibility to decrease the volume of the droplets by as much as 60%. However, the observed volume reduction is also limited by kinetics (i.e., the residence time in the chip might not be sufficiently long for extraction equilibrium to be established). The trend of volume change was found to be almost identical regardless of whether the disperse phase was water or 1% w/w aqueous solution of alginate (Fig. 4). As a reference, experiments where the continuous phase was 1-undecanol previously saturated by water were also performed. As expected, no extraction and therefore no shrinking was observed.

Fig. 4 Droplet shrinking ratio R_V as a function of dilution R_Q in dry 1-undecanol (water () and 1% alginate solution () as the disperse phase), and in 1-undecanol pre-saturated by water (). The continuous line corresponds to the theoretical limit of equilibrium shrinkage ().

3.2 Effect of extractive gelation on microparticle size and morphology

The above section dealt with a non-gelling case, i.e. extraction-only without alginate cross-linking by Ca²⁺. In the present section, the second oil stream (Q_oil2) already contained dissolved calcium ions and therefore the extraction and gelation processes took place simultaneously. In that case, the morphology and monodispersity of the final alginate microparticles are influenced by several variables, i.e. flow rates of both continuous phases (Q_oil1 and Q_oil2), flow rate of the disperse phase (Q_w), ratio between the phases, concentration of calcium ions, concentration of surfactant, and concentration of alginate. To simplify the system, the concentration of surfactant (5% w/w) and aqueous alginate solution (1% w/w) were always kept the same, as well as the ratio R_Q. The different concentration of calcium ions in the system can be established by changing the flow rates of the oil without (Q_oil1) and with (Q_oil2) calcium ions and by the initial concentration of CaI₂, while maintaining the overall oil flow rate (Q_oil = Q_oil1 + Q_oil2) constant, as shown in Table 1.

Particles were produced under the stable dripping regime corresponding to the shear induced droplet formation, hence the initial droplet size is exclusively function of Q_oil1 as discussed above. At the outlet from the chip all microparticles had a round shape, yet the final microparticles collected in the reservoir had different morphologies. The morphology change is happening in the tube connecting the outlet of the chip with the reservoir. Three main morphologies were observed: round shaped microparticles, slightly deformed microparticles and microparticles with a collapsed structure. As the microparticles (emulsion) are pushed through the tube, they are exposed to shear stress. Compressed emulsion has an elastic behavior therefore it deforms its shape under the shear stress.²⁸

The morphological changes of the microparticles in the tube are influenced by the character of the partially gelled microparticles that are leaving the chip (diameter, shell thickness). Depending on the initial drop size (D_in) and calcium content (C_Ca²⁺) the morphology of the microparticles varies from the spherical to the folded object with a variable degree of deformation (Table 1 and Fig. 5). The morphology is quantified by the circularity defined as: 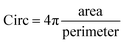, with a value of 1 indicating a perfect circle.

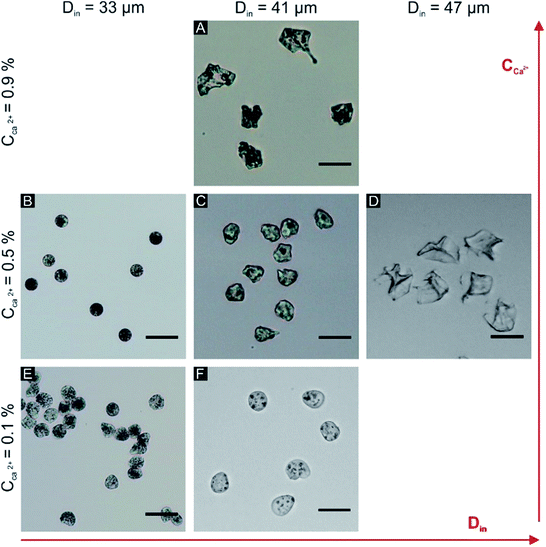Fig. 5 Different morphologies of alginate microparticles; the scale bar is 20 μm, the conditions (A–F) correspond to parameter values given in Table 1.

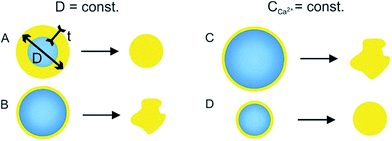
The influence of calcium ions concentration and the initial droplet size on the final morphology of the alginate microparticles was evaluated in order to explain the microparticle deformation. The rates of gelation and water extraction jointly determine the buckling (collapse of a spherical shell under external pressure) of the microparticles. The critical stress applied to a hollow sphere that leads to buckling is proportional to the ratio between the thickness of the shell and the diameter of the core (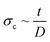, where σ_c​ is critical external stress for buckling, t is thickness of the shell and D is diameter).²⁹ In this case the shell is the cross-linked alginate gel and the core is the still un-crosslinked aqueous phase. If rapid surface gelation takes place before water extraction, such as in the case of high Ca²⁺ concentration and/or large initial droplet size, the particle will buckle upon the final extraction of water from the core (particles in Fig. 5A and D, mechanism in Fig. 6B and C). On the other hand, the combination of low initial droplet size and/or low calcium ion concentration (therefore low rate of cross-linking) leads to particles that have a sufficiently thick shell relative to the diameter of the core (or in the limit, are cross-linked throughout their volume), so that they can withstand the external pressure during water extraction and not buckle, retaining their spherical shape (particles in Fig. 5B, E and F, mechanism in Fig. 6A and D).

Fig. 6 Scheme of buckling mechanism during droplet gelation.

Even if the microparticles do not buckle under the external pressure in the tube they can still slightly deform their shape under the flow. When the concentration of calcium ions is very low, the formed shell is weak, therefore the particles behave more like a viscous liquid and they gell in this drop-shape deformation (Fig. 5E and F). The ideal conditions to obtain monodisperse microparticles with a high circularity were: flow rate of the disperse phase Q_w = 5 μl h⁻¹, flow rates of the continuous phases Q_oil1 = 150 μl h⁻¹ and Q_oil2 = 50 μl h⁻¹, and concentration of calcium ions in the oil 0.5% w/w (Fig. 5B). Based on a sample of 500 particles, the mean diameter d = 10.5 ± 0.5 μm and circularity Circ = 0.93 ± 0.04 were evaluated, and the coefficient of variation in diameter (defined as the standard deviation divided by the mean diameter) was as low as 4.7%.

For the particles with the highest circularity (Fig. 5B, Q_oil1 = 150 μl h⁻¹, Q_oil2 = 50 μl h⁻¹), their mean diameter was evaluated for changing R_Q ratio, which was achieved by changing the flow of the disperse phase. The mean particle diameter as function of the R_Q ratio is plotted in Fig. 7. The observed asymptotic behavior of the size reduction is due to a rise of osmotic pressure induced by increased alginate concentration. For instance, for microparticle with a final diameter 10 μm and initial diameter 33 μm the alginate concentration increased from 1% to roughly 36% after extraction. Therefore, it is possible to achieve further reduction of the particle size by decreasing the initial alginate concentration below 1%. The final microparticle diameter significantly decreased with a lower initial alginate concentration as can be seen in Table 2.

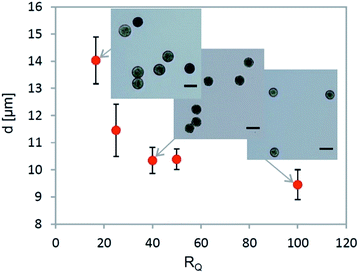Fig. 7 The mean particle diameter of the final alginate microparticles as a function of the ratio R_Q; for all the cases D_in = 33 μm.

Table 2 Final microparticles diameter for different initial concentration of alginate and constant R_Q = 50 and D_in = 33 μm.

C alg [%]	d [μm]
1	10.5 ± 0.5
0.025	7.1 ± 0.6
0.01	5.7 ± 0.4

---

3.3 Microstructure of alginate–magnetic–liposome microparticles

Once the parameters necessary for the formation of spherical and monodisperse alginate microgels in the desired size range have been found, the next step was the encapsulation of both functional components, i.e. magnetic nanoparticles and liposomes. Since the particles are prepared by extractive gelation, not just alginate but also liposomes and magnetic nanoparticles increase their concentration in the particle. This increase of concentration was found to lead to premature leakage of CF from the liposomes, caused by steric interactions inside of the microparticle (the liposomes are “squeezed” during the extraction phase). To minimaze the steric interaction, we decreased the concentration of the magnetite nanoparticle solution until no leakage of CF from the liposomes was observed and at the same time the composite microparticles still retained their magneto-responsive properties (i.e. they align and migrate when exposed to an external magnetic field Fig. 8B) the final composition of the microparticles was the following: 2.5% v/v of magnetite nanoparticle solution (10 g l⁻¹), 25% v/v of liposome solution and 72.5% v/v of aqueous solution of alginate (0.025% w/w). The presence of intact fluorescein-loaded liposomes in the composite alginate microparticles was visualized by confocal microscopy (Fig. 8C and D). The concentration of the encapsulated magnetite nanoparticles also has an effect on the extractive gelation; with a lower concentration of magnetite nanoparticles it is possible to further decrease the final microparticle diameter to d = 5.1 ± 0.3 μm.

Fig. 8 Composite microparticles (A) and their orientation in the magnetic field (B); (C) an overlay of optical and confocal fluorescent image of microparticles; (D) confocal image of microparticle.

3.4 Stimuli-responsive release from alginate–magnetic–liposome microparticles

To confirm the ability of the composite particles to store and release a chemical payload, the release kinetics of an encapsulated fluorescence dye from the composite microparticles was evaluated. The phase transition of the phospholipid bilayer in the liposomes (made from DPPC and cholesterol in a molar ratio DPPC : cholesterol = 2 : 1) is above 45 °C. Therefore, the composite microparticles were exposed repeatedly to a temperature pulse of 45 °C for 10 minutes and then cooled down and maintained at room temperature (25 °C) for 15 min, while measuring the fluorescence of the surrounding solution. As shown in Fig. 9, a step increase of the released fluorescein concentration was observed after each temperature pulse in the sequence, while no fluorescein was released during the periods at 25 °C. This proves that by controlling temperature of the composite microparticles, a repeated on-demand release can be achieved and the diffusion process can be stopped and restarted several times.

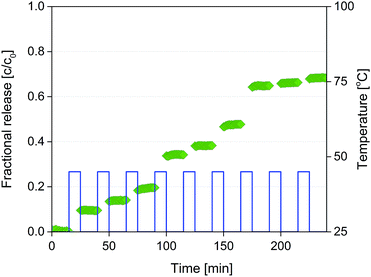Fig. 9 Diffusion of CF from composite microparticles during the temperature burst release experiments.

To evaluate the ability of composite alginate microparticles with encapsulated iron oxide to heat up in the radiofrequency field and to reach temperatures necessary for the phase transition of the liposomes, composite alginate microparticles were prepared from sodium alginate (0.025% w/w) dissolved in a concentrated (10 g l⁻¹) solution of iron oxide nanoparticles. The temperature rise of the resulting microparticles was measured as described in Section 2.7 and the results are summarized in Fig. 10, which shows that the microparticles can indeed reach the desired temperature 45 °C in less than 20 s at 100% power of RF generator. In addition, by modulating the power of the RF generator, the time at which the phase transition temperature is reached can be controlled.

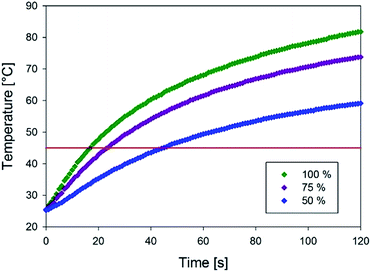Fig. 10 Temperature rise of microparticles in the alternating magnetic field for different powers (100%, 75% and 50%) of the RF generator.

4 Conclusion

The present work demonstrates the feasibility of microfluidic fabrication of composite alginate microparticles with incorporated functional components (magnetic nanoparticles and liposomes that contain a chemical payload) in the size range comparable to that of blood cells. The extractive gelation process was used for down-scaling the droplet volume produced in a flow-focusing junction, and on-chip gelation with subsequent magnetic separation of the produced gel microparticles was employed as a separation and purification method. The ability to separate and purify the produced microparticles from the oil/surfactant mixture is often neglected in the microfluidic literature, but this is a crucial step for any further application of the microparticles (for example in biological applications). In the present work, the parametric sensitivity of the extractive gelation process was systematically explored and a feasible parameter range that ensured both sufficient quality of the particles (spherical, monodisperse) and acceptable production rate, was found. It was shown that by optimizing the initial concentration of all components (alginate, liposomes, magnetic nanoparticles), the final composite microparticles can be both stable (i.e. no undesired leakage from the liposomes), magneto-responsive, and provide on-demand release functionality when exposed to temperature cycles.

Acknowledgements

A. P. would like to acknowledge support by the City of Ostrava Fellowship and the French Government Scholarship. A. Z and F. S would like to acknowledge support by the Grant Agency of the Czech Republic (project no. 13-37055S). We are grateful to Sotio a. s., for supporting this work.

References

1. M. Ullrich, J. Hanus and F. Stepanek, Chem. Eng. Sci., 2015, 125, 191–199.
2. W. R. Gombotz and S. F. Wee, Adv. Drug Delivery Rev., 2012, 64, 194–205.
3. J. Hanus, M. Ullrich, J. Dohnal, M. Singh and F. Stepanek, Langmuir, 2013, 29, 4381–4387.
4. N. Sarvasova, P. Ulbrich, V. Tokarova, A. Zadrazil and F. Stepanek, Powder Technol., 2015, 278, 17–25.
5. M. Ullrich, J. Hanus, J. Dohnal and F. Stepanek, J. Colloid Interface Sci., 2013, 394, 380–385.
6. W. W. Sulkowski, D. Pentak, K. Nowak and A. Sulkowska, J. Mol. Struct., 2005, 744, 737–747.
7. P. Haufova, J. Dohnal, J. Hanus and F. Stepanek, Colloids Surf., A, 2012, 410, 52–58.
8. G. Alici, Expert Rev. Med. Devices, 2015, 12, 703–715.
9. W. S. Beck, Hematology, MIT Press, Cambridge, Mass., 1991.
10. J. Dohnal and F. Stepanek, Chem. Eng. Sci., 2011, 66, 3829–3835.
11. K. Moebus, J. Siepmann and R. Bodmeier, Eur. J. Pharm. Sci., 2012, 45, 358–366.
12. J. K. Oh, R. Drumright, D. J. Siegwart and K. Matyjaszewski, Prog. Polym. Sci., 2008, 33, 448–477.
13. Y. D. Hu, G. Azadi and A. M. Ardekani, Carbohydr. Polym., 2015, 120, 38–45.
14. K. S. Huang, T. H. Lai and Y. C. Lin, Lab Chip, 2006, 6, 954–957.
15. K. Liu, H. J. Ding, J. Liu, Y. Chen and X. Z. Zhao, Langmuir, 2006, 22, 9453–9457.
16. M. Marquis, J. Davy, B. Cathala, A. Fang and D. Renard, Carbohydr. Polym., 2015, 116, 189–199.
17. M. Marquis, J. Davy, A. P. Fang and D. Renard, Biomacromolecules, 2014, 15, 1568–1578.
18. E. Rondeau and J. J. Cooper-White, Langmuir, 2008, 24, 6937–6945.
19. S. Sugaya, M. Yamada, A. Hori and M. Seki, Biomicrofluidics, 2013, 7, 054120.
20. C.-H. Yeh, Q. Zhao, S.-J. Lee and Y.-C. Lin, Sens. Actuators, A, 2009, 151, 231–236.
21. H. Zhang, E. Tumarkin, R. Peerani, Z. Nie, R. M. A. Sullan, G. C. Walker and E. Kumacheva, J. Am. Chem. Soc., 2006, 128, 12205–12210.
22. H. Zhang, E. Tumarkin, R. M. A. Sullan, G. C. Walker and E. Kumacheva, Macromol. Rapid Commun., 2007, 28, 527–538.
23. M. Yamada, A. Hori, S. Sugaya, Y. Yajima, R. Utoh, M. Yamato and M. Seki, Lab Chip, 2015, 15, 3941–3951.
24. J. R. Anderson, D. T. Chiu, H. Wu, O. Schueller and G. M. Whitesides, Electrophoresis, 2000, 21, 27–40.
25. S. R. Quake and A. Scherer, Science, 2000, 290, 1536–1540.
26. M. Góral, B. Wiśniewska-Gocłowska and A. Mączyński, J. Phys. Chem. Ref. Data, 2006, 35, 1391–1414.
27. G. F. Christopher and S. L. Anna, J. Phys. D: Appl. Phys., 2007, 40, R319–R336.
28. T. G. Mason, J. Bibette and D. A. Weitz, Phys. Rev. Lett., 1995, 75, 2051–2054.
29. B. B. Pan and W. C. Cui, Mar. Struct., 2010, 23, 227–240.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra23003b

---