Enhanced dielectric and energy storage performance of surface treated gallium ferrite/polyvinylidene fluoride nanocomposites†
Biplab Adakab,
Ipsita Chinyaac and
Shrabanee Sen*a
aSensor and Actuator Division, CSIR-Central Glass and Ceramic Research Institute, India. E-mail: shrabanee@cgcri.res.in
bSchool of Material Science and Nanotechnology, Jadavpur University, India
cAcademy of Scientific and Innovative Research, CSIR-CGCRI, India
First published on 24th October 2016
Abstract
The ceramic–polymer nanocomposites composed of gallium ferrite (GFO) nanoparticles and employing sodium dodecylsulphate (SDS) as surfactant and polyvinylidene fluoride (PVDF) as matrix have been fabricated by solvent casting followed by hot-press technique. It was found that modified GFO nanoparticles favours nucleation and stabilization up to ∼84% electroactive phase (β- and γ-phase) in PVDF. Fourier transform infrared spectroscopy (FTIR) results revealed that the interfacial electrostatic interaction between nanoparticle surface charge and CH2/CF2 – molecular dipole of PVDF favoured nucleation of electroactive phase. Compared to the pristine PVDF, much higher dielectric constant (εr ∼ 25 at 10 kHz frequency) with low loss factor (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ ∼ 0.02 at 10 kHz) was achieved in the composite film. In addition, the nanocomposite showed higher electrical energy density (Ud ∼ 3.88 mJ cm−3 at an electric field 6 kV mm−1) compared to pristine PVDF which determined their applicability as flexible energy density capacitor.
δ ∼ 0.02 at 10 kHz) was achieved in the composite film. In addition, the nanocomposite showed higher electrical energy density (Ud ∼ 3.88 mJ cm−3 at an electric field 6 kV mm−1) compared to pristine PVDF which determined their applicability as flexible energy density capacitor.
1. Introduction
Nowadays polymer–ceramic nanocomposites have gained immense attention due to their increased performance, easy processing and flexibility. Poly(vinylidene fluoride) (PVDF) and its composites with wide ranges of nanoparticles of various materials are widely studied because of their piezo-, pyro- and ferroelectric properties.1–9 These multifunctional properties along with high elasticity and easy processability make this material interesting for numerous technological applications such as energy harvesting, storage, sensors and actuators, and biomaterials in the biomedical field.4PVDF is a semi crystalline polymer material with around 50% crystallinity having five crystalline phases. Depending on their chain conformations as trans (T) or gauche (G) linkages crystalline phases are classified as non-polar α-phase and ε-phase, as well as polar β-phase, γ-phase, and δ-phase. Among the phases α-phase has most common crystal structure (TG+TG−), β-phase has all trans (TTTT) zigzag structure and γ-phase has (T3G+T3G−) structure.4–8 The electro active phases i.e. β-phase and γ-phase are more attractive as they have high ferroelectric properties due to spontaneous polarization resulting in high piezoelectric and pyroelectric8,9 properties. γ-Phase has high energy storage properties than β-phase due to the non-early saturation of polarization under a high electric field.10 High energy storage capacitors have great importance due to their potential in electronic devices and power system field. Energy density which define the storage capacity, is defined as
 | (1) |
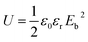 | (2) |
Gallium ferrite (GFO) has magnetic and piezoelectric properties which has been already investigated for application as magnetoelectric ferrimagnet.33,34 In this work, we report the crystal phase transformation; surface morphology; dielectric response of a new; flexible and light weight GFO/PVDF composite with and without surface modification using anionic surfactant sodium dodecylsulfate (SDS).
2. Experimental section
2.1 Materials
Gallium nitrate [Ga(NO3)3·6H2O, Sigma-Aldrich, USA], ferric nitrate [Fe(NO3)3·9H2O, Sigma-Aldrich, USA], PVDF pellets [![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) w ≈ 275
w ≈ 275![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, Sigma-Aldrich, USA], N,N-dimethyl formamide (DMF, Merck, India), sodium dodecyl sulphate (SDS,
000, Sigma-Aldrich, USA], N,N-dimethyl formamide (DMF, Merck, India), sodium dodecyl sulphate (SDS, ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) w ≈ 288.37 g mol−1, Merck, India) were used for this work.
w ≈ 288.37 g mol−1, Merck, India) were used for this work.
2.2 Synthesis of nanoparticles
Gallium ferrite (GFO) nanoparticles were prepared by citrate nitrate process which has been reported earlier.35 For synthesis of surface modified GFO nanoparticles it was treated in 1 litre of 0.1 milli mole concentration of SDS aqueous solution. The SDS concentration was kept below its critical micelles concentration with respect to nanoparticles so that all SDS molecules were available for surface modification. The solution was heated at 120 °C and continuously stirred for 1 h. To remove the extra SDS from the SGFO (SDS modified GFO) nanoparticles, it was washed in distilled water and the nanoparticles were collected by centrifugation (8000 rpm). Then it was dried in oven at 110 °C for 12 h to dry out the moisture and obtain the final product.2.3 Preparation of PVDF nanocomposite films
The nanocomposites were prepared in solution casting method in two steps. First 8 wt% PVDF was dissolved in DMF and then different wt% (with respect to PVDF only) of nanoparticles (GFO and SDS modified GFO) were mixed in the PVDF–DMF solution and stirred vigorously for 2 days and drop casted on glass slide to prepare films after sonication in an ultrasonic bath (power of 250 W) for 20 minutes. The drop casted films were dried in oven at 120 °C for 6 h to evaporate DMF. In this work we have used 0.25 wt%, 0.5 wt%, 1 wt% of GFO and SDS modified GFO as filler. Films without nanoparticle was named as PVDF and nanocomposites with 0.25 wt%, 0.5 wt%, 1 wt% GFO nanoparticle were named as GFO-0.25, GFO-0.5, GFO-1 respectively and for SDS modified GFO nanoparticle were named as SGFO-0.25, SGFO-0.5, SGFO-1 respectively. Further 3–4 films of each composite were taken and hot pressed by Carver Press at 150 °C applying 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 lb pressure for 20 min. In this way a simple, light weight hybrid composite using SDS modified GFO doped PVDF was fabricated.
000 lb pressure for 20 min. In this way a simple, light weight hybrid composite using SDS modified GFO doped PVDF was fabricated.
2.4 Characterization
Zeta potential measurements of the nanoparticles were performed at 25 °C temperature to determine the surface charge on the particles using Zetasizer (Malvern Instrument Limited, UK). X-ray diffraction (XRD) measurements were carried out using X'pert Pro MPD diffractometer (PANalytical system Netherlands) with nickel-filtered CuKα (λ = 0.15404 nm). The characteristics vibrational modes were analysed using Fourier transform infrared spectroscopy (FT-IR) (Shimadzu; FTIR-8400S). The surface morphology of the samples was examined by scanning electron microscopy (SEM Supra 35VP). Both sides of the thick films were painted with conductive silver paste and dried at 120 °C. The ferroelectricity measurement were done by a FE test system (aixact TF Analyzer 2000). All the ferroelectric hysteresis loops were measured at room temperature at different frequencies. The dielectric study was performed with a precision impedance analyser (6500 B Wayne Kerr) in the frequency range of 100 Hz to 1 MHz.3. Results and discussion
The zeta potential distribution of the GFO nanoparticles and SDS modified GFO nanoparticles are shown in the Fig. 1. The obtained value of zeta potential of GFO nanoparticle is −21.1 mV. The negative value of zeta potential indicates negative surface charge on the GFO nanoparticles.20,36 The mechanism of SDS adsorption on GFO depends on electrostatic and hydrophobic interactions37,38 [Fig. 2]. As GFO surface was negatively charged, SO42− (head group) anion of SDS will be repulsed by surface charge of GFO and hydrophobic tail will be repulsed by water in solution, so there may be a tendency of the tail side to get adsorb on the GFO particle surface. Thus both electrostatic and hydrophobic interactions in the solution promote the tail side to adsorb on GFO surface and leaving SO42− anion to the outer-sphere. The negatively charged head of SDS thus makes the surface of SDS modified GFO nanoparticle to be negatively charged which was also confirmed from the negative zeta potential distribution plot. The value of zeta potential after modification was found to be −23.5 mV i.e. more negative than unmodified GFO which indicates that surface modified GFO nanoparticle are more negatively charged.36The diffraction patterns of GFO calcined powders are shown in Fig. 3(a). The formation of single phase compound was observed. The peak positions of the XRD pattern fitted well with reported values of GaFeO3 phase (JCPDS PDF#761005). The crystallite size was calculated using Scherrer equation and was found to be ∼12 nm. Further X-ray Diffraction (XRD) pattern of the pure PVDF polymer and PVDF nanocomposites were done and analysed to explain the influence of the ceramic nanoparticles on the crystal structure of the polymer matrix [Fig. 3(b)]. The XRD patterns confirmed that the addition of ceramic particles influenced the formation of polar γ-phase in PVDF matrix. For pristine PVDF several characteristic diffraction peaks are observed at 2θ ≈ 17.6, ≈18.3°, ≈19.9° and ≈26.5° which are corresponding to the diffraction from planes (100), (020), (110) and (021) respectively and represent the nonpolar α-phase polymorph.4,39 As the nanofiller concentration in the composite increased the more intense peaks appeared at 2θ ≈ 20.1° and ≈18.5° corresponding to (002) and (020) planes which represent polar γ-phase polymorph. Beside this; the peaks of 2θ ≈ 17.6° and ≈26.5° which represent the α-phase gradually decreased and disappeared for higher filler concentration in PVDF matrix.39 From the figure it was clear that SDS modified GFO nanoparticle is more effective than unmodified GFO nanoparticle for γ-phase formation in PVDF as the intense peak totally shifted to 2θ ≈ 20.1° and peak at 26.5° disappeared for 1 wt% GFO nanoparticle loading. The same effect can be produced by 0.5 wt% SDS modified GFO particle. The result indicates that there was a good interaction between SDS modified GFO particles and PVDF matrix which was more effective in phase transformation from nonpolar α-phase to polar γ-phase.
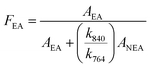
Further analysis of the formation of the different phases in pristine PVDF and composites were done by FTIR [Fig. 4(a)]. The characteristic absorption bands for pristine PVDF are observed at 408, 531, 614, 764, 796, 854, 976, 1146, 1213, 1383 cm−1 for α-phases; 510, 840, 1274 cm−1 for β-phases and 431, 840, 1233 cm−1 for γ-phases.4,39,40 Due to the common TTT configuration absorption bands of the α-phase and γ-phase of PVDF are sometimes superimposed each other creating difficulty in phase separation.39 From the FTIR plot it was clear that pristine PVDF film has dominating nonpolar α-phase along with small fraction of polar β- and γ-phase. But as the filler concentration was gradually increased the intensity of the absorption bands for α-phase gradually decreased and bands for mainly polar γ-phase along with β-phase gradually increased. This means that nanoparticles have played an important role in crystalline phase transformation (nonpolar α-phase to polar β and γ-phases) in PVDF. The content of the electroactive phase fraction (FEA) in the nanocomposites film can be calculated from the equation4,13,41
 | (3) |
Fig. 5(a–c) shows the SEM micrographs of PVDF; GFO-1 and SGFO-1 composites. In case of PVDF micrographs, it was observed that the region contained brush like morphology which may be associated with the presence of consolidation defects in the PVDF matrix. In Fig. 5(b) the black square marked the presence of GFO particles which indicated that agglomeration has taken place in the PVDF matrix and this may be due to the high surface energy of the GFO particles. The homogeneous dispersion of the nanoparticles was visible from Fig. 5(c) resulting from surface modification by SDS.31
Fig. 6(a) and (b) shows the variation of dielectric constant (εr) of the composites over the wide range of frequency from 100 Hz to 1 MHz at room temperature. It was observed that the value of dielectric constant decreases with increasing frequency and increases with increasing nanoparticle addition. The increase in the value of the dielectric constant is due to Maxwell–Wagner interfacial space charge polarization. According to these models, composite of nanoparticles embedded in a PVDF matrix can be imagined as consisting of conducting grains (nanoparticles) separated by highly resistive grain boundaries (PVDF matrix). The accumulation of space charge polarization at the grain boundaries may result in the increase in the value of dielectric constant. The enhancement in the dielectric constant after surface modification was observed [Fig. 5]. Surface modification benefits the homogeneous distribution of GFO nanoparticles in the polymer matrix as seen in SEM and thus introduces more amount of space charge and interfacial polarization.6,42,43
 | ||
| Fig. 6 The frequency dependent dielectric constant of (a) GFO–PVDF composites (b) SGFO–PVDF composites. | ||
There are various theoretical models in order to predict the effective dielectric constant of the composite. The most simple and commonly used dielectric theoretical model is Lichtenecker's44 which is also known as the logarithmic mixture rule.
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) εeff = φ1 εeff = φ1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε1 + φ2 ε1 + φ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε2 ε2
| (4) |
Another theoretical model is Maxwell's model44 where the effective dielectric constant is described by the following equation.
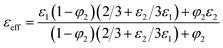 | (5) |
Furukawa45 predicted a model for 0–3 composite assuming no interfacial effect in the composite, low loading of second phase (φ2 ≪ 1) and ε2 ≫ ε1, where the effective dielectric constant is described as
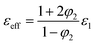 | (6) |
The effective medium theory (EMT) model46 has been established considering morphology of the particles. According to this model the effective dielectric constant is given by
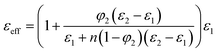 | (7) |
But the predicted theoretical value of effective dielectric constant by the above mentioned models do not follow the experimental value, as the models do not consider particle–particle dipole interactions or the influence of the nanoparticles on the surrounding medium (i.e. phase transformation of PVDF due to interaction with nanoparticles). So there exist an “interphase” regions at polymer–filler interfaces.47–49 The interphase region has different dielectric properties from that of the polymer and ceramics. Vo and Shi47 developed a theoretical model to describe the effect of this interphase region on the effective dielectric constant of polymer nanocomposite. Surfactants are commonly employed to enhance the compatibility between the polymer phase and filler phase (nanoparticle) of composite systems. They effectively change the characteristics of the interphase region of polymer–ceramic composite and thus change the effective dielectric constant of the composite.48 Thus PVDF-modified GFO composite have higher value of dielectric constant as compared to the same fraction of addition of ceramic particles. The variation of dielectric constant with nanoparticle loading was observed and it was concluded that up to 3.5 wt% maximum dielectric constant was observed for SGFO composites [Fig. S1†].
Fig. 7(a and b) shows the variation of dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) of the samples with frequency ranging from 100 Hz to 1 MHz at room temperature for PVDF/GFO composites and PVDF/SDS modified GFO composites with increase in filler loading. It was observed that the dielectric loss of the composite increases as the ceramic nanofiller concentration increase. The dispersion and amount of nanoparticles are the key factors responsible for the change in dielectric loss. The ceramic filler (GFO) has higher dielectric loss (due to higher leakage current) than that of polymer matrix. The increase in nanoparticle dispersion creates more interfacial area and PVDF polymer chains are separated into smaller domains by the increasing conductive network. Thus dielectric loss increases with the increase in ceramic filler loading.6,42 For SDS modified GFO nanoparticles loading in PVDF, the dielectric loss increase more than that of pure PVDF, and was much more as compared to the same wt% unmodified GFO nanoparticles. This may be due to the good dispersion of modified GFO nanoparticle; which creates more interfacial area and smaller or thinner domains of PVDF polymer chain. Thus, movement of PVDF molecules may increase or more dipoles can rotate resulting increase of dielectric loss.6 This effect is further confirmed from the ac conductivity plot of the composites before and after surface modification [Fig. 8(a and b)]. For a dielectric material, a.c. conductivity can be obtained as
δ) of the samples with frequency ranging from 100 Hz to 1 MHz at room temperature for PVDF/GFO composites and PVDF/SDS modified GFO composites with increase in filler loading. It was observed that the dielectric loss of the composite increases as the ceramic nanofiller concentration increase. The dispersion and amount of nanoparticles are the key factors responsible for the change in dielectric loss. The ceramic filler (GFO) has higher dielectric loss (due to higher leakage current) than that of polymer matrix. The increase in nanoparticle dispersion creates more interfacial area and PVDF polymer chains are separated into smaller domains by the increasing conductive network. Thus dielectric loss increases with the increase in ceramic filler loading.6,42 For SDS modified GFO nanoparticles loading in PVDF, the dielectric loss increase more than that of pure PVDF, and was much more as compared to the same wt% unmodified GFO nanoparticles. This may be due to the good dispersion of modified GFO nanoparticle; which creates more interfacial area and smaller or thinner domains of PVDF polymer chain. Thus, movement of PVDF molecules may increase or more dipoles can rotate resulting increase of dielectric loss.6 This effect is further confirmed from the ac conductivity plot of the composites before and after surface modification [Fig. 8(a and b)]. For a dielectric material, a.c. conductivity can be obtained as
| σ′ = 2πfε0ε′′r | (8) |
 | ||
| Fig. 8 The frequency dependent a.c. conductivity of (a) GFO–PVDF composites (b) SGFO–PVDF composites. | ||
The results show that an increase in the a.c. conductivity of the composites with respect to the pure polymer film, was due to the of the large leakage current due to the formation of a conducting filler network as mentioned earlier.
The room temperature ferroelectric (D–E) hysteresis loop of pure PVDF and composites by applying sinusoidal signal of 0.1 Hz frequency for low applied potentials are shown in Fig. 9(a and b). The remnant electric displacement (Dr) and saturation electrical displacement (Ds) value increases with the increase of GFO nanoparticle concentration and reach to Dr ∼ 0.1 μC cm−2 and Ds ∼ 0.23 μC cm−2 for 1 wt% loading of GFO which are respectively 42% and 46% greater than that of pristine PVDF. This result indicates that GFO nanoparticle has some effects on PVDF in increasing polarization. The incorporation of GFO into PVDF matrix accelerates the internal charge of the nanocomposites which is required to compensate and stabilize the polarization domain. Further nanoparticles can act as heterogeneous nucleation centres for the ferroelectric domains. Fillers also promote higher polarization (D = ε0E + P) levels through interfacial interaction with polymer dipoles.39,50 For SGFO-1 composite, the values obtained are Dr ∼ 0.16 μC cm−2 and Ds ∼ 0.38 μC cm−2 which are respectively ∼128% and 277% greater than that of pristine PVDF, indicating the effect of addition of surfactant.
Stored energy density can be calculated from the hysteresis graph as
 | (9) |
 | ||
| Fig. 10 Variation of energy storage density of GFO–PVDF composites and SGFO–PVDF composites at 5.7 kV mm−1 applied electric field. | ||
The electric breakdown strength of both the composites with unmodified and modified GFO particles are shown in Fig. S2.† The enhancement in the modified GFO composites indicates that the presence of SDS on surface of GFO particles leads to the homogeneous distribution of the nanoparticles within the polymer matrix.
4. Conclusions
PVDF nanocomposite consisting of different percentage of GFO nanoparticle was fabricated. Further surface modification of the composites were done by addition of SDS. High percentage (i.e. ∼84%) of electroactive phase (β and γ) was obtained in a simple way which shows the high compatibility between the ceramic and polymer matrix after addition of surfactant. There was an enhancement of dielectric constant after addition of surfactant for all the composition of the films. Similarly the value of the energy density and breakdown strength also increased for the surfactant added composites. Thus it may be concluded that these GFO added PVDF films with high electroactive phase can be explored as flexible film capacitor for green energy technology.Acknowledgements
Mr Biplab Adak would like to acknowledge Director CSIR-CGCRI for providing him the opportunity to do his M. Tech thesis work in Sensor and Actuator Division, CSIR-CGCRI. The authors would also like to thank Mr Sk. Md Mursalin for his support for synthesis of GFO nanoparticles.References
- E. Fukada and T. Furukawa, Ultrasonics, 1981, 19, 31–39 CrossRef CAS.
- E. Fukada and T. Sakurai, Polym. J., 1971, 2, 656–662 CrossRef CAS.
- N. Murayama, K. Nakamura, H. Obara and M. Segawa, Ultrasonics, 1976, 14, 15–24 CrossRef CAS.
- P. Martins, A. C. Lopes and S. L. Mendez, Prog. Polym. Sci., 2014, 29, 683–706 CrossRef.
- A. Salimi and A. A. Yousefi, Polym. Test., 2003, 22, 699–704 CrossRef CAS.
- C. W. Tang, B. Li, L. Sun, B. Lively and W. H. Zhong, Eur. Polym. J., 2012, 48, 1062–1072 CrossRef CAS.
- J. Zheng, A. He, J. Li and C. C. Han, Macromol. Rapid Commun., 2007, 28, 2159–2162 CrossRef CAS.
- J. Gome, J. S. Nunes, V. Sencadas and S. L. Mendez, Smart Mater. Struct., 2010, 19, 065010 CrossRef.
- D. H. Chang and Y. S. Yoon, Jpn. J. Appl. Phys., 2002, 41, 7234–7238 CrossRef CAS.
- W. Li, Q. Meng, Y. Zheng, Z. Zhang, W. Xia and Z. Xu, Appl. Phys. Lett., 2010, 96, 192905 CrossRef.
- H. Tang and H. A. Sodano, Nano Lett., 2013, 13, 1373–1379 CAS.
- Y. Wang, X. Zhou, Q. Chen, B. Chu and Q. Zhang, IEEE Trans. Dielectr. Electr. Insul., 2010, 17, 1036–1042 CrossRef CAS.
- V. Sencadas, R. Gregorio Jr and S. L. Méndez, J. Macromol. Sci., Part B: Phys., 2009, 48, 514–525 CrossRef CAS.
- G. H. Kim, S. M. Hong and Y. Seo, Phys. Chem. Chem. Phys., 2009, 11, 10506–10512 RSC.
- S. Yu, W. Zheng, W. Yu, Y. Zhang, Q. Jiang and Z. Zhao, Macromolecules, 2009, 42, 8870–8874 CrossRef CAS.
- S. Manna and A. K. Nandi, J. Phys. Chem. C, 2007, 111, 14670–14680 CAS.
- P. Costa, J. Silva, V. Sencadas, C. M. Costa, F. W. J. van Hattum, J. G. Rocha and S. L. Méndez, Carbon, 2009, 47, 2590–2599 CrossRef CAS.
- V. Sencadas, P. Martins, A. Pitães, M. Benelmekki, J. L. G. Ribelles and S. L. Méndez, Langmuir, 2011, 27, 7241–7249 CrossRef CAS PubMed.
- J. N. Pereira, V. Sencadas, V. Correia, V. F. Cardoso, W. Han, J. G. Rocha and S. L. Méndez, Composites, Part B, 2015, 72, 130–136 CrossRef.
- P. Martins, C. M. Costa, M. Benelmekki, G. Botelho and S. L. Méndez, CrystEngComm, 2012, 14, 2807–2811 RSC.
- B. Jaleh, P. Fakhri, M. Noroozi and N. Muensit, J. Inorg. Organomet. Polym. Mater., 2012, 22, 878–885 CrossRef CAS.
- S. Manna, S. K. Batabyal and A. K. Nandi, J. Phys. Chem. B, 2006, 110, 12318–12326 CrossRef CAS PubMed.
- L. Priya and J. P. Jog, J. Polym. Sci., Part B: Polym. Phys., 2002, 40, 1682–1689 CrossRef CAS.
- T. U. Patro, M. V. Mhalgi, D. V. Khakhar and A. Misra, Polymer, 2008, 49, 3486–3499 CrossRef CAS.
- C. T. Huang, J. Song, W. F. Lee, Y. Ding, Z. Gao, Y. Hao, L. J. Chen and Z. L. Wang, J. Am. Chem. Soc., 2010, 132, 4766–4771 CrossRef CAS PubMed.
- M. M. Alam, S. K. Ghosh, A. Sultana and D. Mandal, Nanotechnology, 2015, 26, 165403 CrossRef PubMed.
- K. Park, C. K. Jeong, J. Ryu, G. T. Hwang and K. J. Lee, Adv. Energy Mater., 2013, 3, 1539–1544 CrossRef CAS.
- B. Saravanakumar, R. Mohan, K. Thiyagarajan and S. J. Kim, RSC Adv., 2013, 3, 16646–16656 RSC.
- Z. H. Lin, Y. Yang, J. M. Wu, Y. Liu, F. Zhang and Z. L. Wang, J. Phys. Chem. Lett., 2012, 3, 3599–3604 CrossRef CAS PubMed.
- R. C. Smith, C. Liang, M. Landry, J. K. Nelson and L. S. Schadler, IEEE Trans. Dielectr. Electr. Insul., 2008, 15, 187–196 CrossRef CAS.
- S. Siddabattuni, T. P. Schuman and F. Dogan, ACS Appl. Mater. Interfaces, 2013, 5, 1917–1927 CAS.
- S. Siddabattuni, T. P. Schuman and F. Dogan, Mater. Sci. Eng., B, 2011, 176, 1422–1429 CrossRef CAS.
- M. B. Mohamed, A. Senyshyn, H. Ehrenberg and H. Fuessa, J. Alloys Compd., 2010, 492, L20–L27 CrossRef CAS.
- K. Sawada and N. Nagaosa, Phys. Rev. Lett., 2005, 95, 237402 CrossRef PubMed.
- S. Sen, N. Chakraborty, P. Rana, M. Narjinary, S. D. Mursalin, S. Tripathy, D. K. Pradhan and A. Sen, Ceram. Int., 2015, 41, 10110–10115 CrossRef CAS.
- P. Martins, C. Caparros, R. Gonçalves, P. M. Martins, M. Benelmekki, G. Botelho and S. L. Mendez, J. Phys. Chem. C, 2012, 116, 15790–15794 CAS.
- M. J. Rosen, Surfactants and interfacial phenomena, Wiley, New Jersey, 3rd edn, 2004, ch. 2, pp. 34–104 Search PubMed.
- X. Gao and J. Chorover, J. Colloid Interface Sci., 2010, 348, 167–176 CrossRef CAS PubMed.
- S. K. Karan, D. Mandal and B. B. Khatua, Nanoscale, 2015, 7, 10655–10666 RSC.
- R. Gregorio Jr and R. C. Capitão, J. Mater. Sci., 2000, 35, 299–306 CrossRef.
- S. Sarkar, S. Garain, D. Mandal and K. K. Chattopadhyay, RSC Adv., 2014, 4, 48220–48227 RSC.
- X. Wang, W. Li, L. Luo, Z. Fang, J. Zhang and Y. Zhu, J. Appl. Polym. Sci., 2012, 125, 2711–2715 CrossRef CAS.
- J. Gutiérrez, P. Martins, R. Gonçalves, V. Sencadas, A. Lasheras, S. L. Mendez and J. M. Barandiarán, Eur. Polym. J., 2015, 69, 224–231 CrossRef.
- P. Thomas, K. T. Varughese, K. Dwarakanath and K. B. R. Varma, Compos. Sci. Technol., 2010, 70, 539–545 CrossRef CAS.
- T. Furukawa, K. Fujino and E. Fukada, Jpn. J. Appl. Phys., 1976, 15, 2119–2129 CrossRef CAS.
- Y. Rao, J. Qu, T. Marinis and C. P. Wong, IEEE Trans. Compon. Packag. Technol., 2000, 23, 680–683 CrossRef CAS.
- H. T. Vo and F. G. Shi, Microelectron. J., 2002, 33, 409–415 CrossRef CAS.
- M. G. Todda and F. G. Shi, J. Appl. Phys., 2003, 94, 4551–4557 CrossRef.
- M. S. Ozmusul and R. C. Picu, Polym. Compos., 2002, 23, 110–119 CrossRef CAS.
- T. Prabhakaran and J. Hemalatha, Mater. Chem. Phys., 2013, 137, 781–787 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra22939e |
| This journal is © The Royal Society of Chemistry 2016 |







