Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A multiple length scale description of the mechanism of elastomer stretching†
J. Neuefeinda,
A. L. Skov*b,
J. E. Danielscd,
V. Honkimäkid,
B. Jakobsen e,
J. Oddershedef and
H. F. Poulsenf
e,
J. Oddershedef and
H. F. Poulsenf
aChemical and Engineering Materials Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA
bDanish Polymer Centre, DTU Chemical Engineering, Søltofts Plads, 2800 Kongens Lyngby, Denmark. E-mail: al@kt.dtu.dk
cSchool of Materials Science and Engineering, UNSW Australia, Kensington 2052, NSW, Australia
dEuropean Synchrotron Radiation Facility, BP 220, 38043 Grenoble, France
eGlass and Time, Department of Sciences, Roskilde University, P.O. Box 260, 4000 Roskilde, Denmark
fNeutrons and X-rays for Materials Physics, DTU Physics, Fysikvej, 2800 Kongens Lyngby, Denmark
First published on 3rd October 2016
Abstract
Conventionally, the stretching of rubber is modeled exclusively by rotations of segments of the embedded polymer chains; i.e. changes in entropy. However models have not been tested on all relevant length scales due to a lack of appropriate probes. Here we present a universal X-ray based method for providing data on the structure of rubbers in the 2–50 Å range. First results relate to the elongation of a silicone rubber. We identify several non-entropic contributions to the free energy and describe the associated structural changes. By far the largest contribution comes from structural changes within the individual monomers, but among the contributions is also an elastic strain, acting between chains, which is 3–4 orders of magnitude smaller than the macroscopic strain, and of the opposite sign, i.e. extension of polymer chains in the direction perpendicular to the stretch. This may be due to trapped entanglements relaxing to positions close to the covalent crosslinks.
Introduction
Polymer chains (with diene polymers as exemption) can take many different shapes as any two neighboring segments in the polymer chain can rotate with respect to each other. Polydimethylsiloxane (PDMS) constitutes one of the most flexible polymers due to the almost free rotation of the Si–O bonds in the polymer backbone. This general freedom of polymers implies that by adjusting the chemical structure and by mixing constituents it is possible to make materials with a large variety of structural organizations and associated physical and mechanical properties, ranging from liquid over gel-like towards hard and brittle materials. Rubbers arise from crosslinked polymer chains and are characterized by the ability to be stretched elastically to a much larger extent than crystalline materials such as metal and ceramics.The theory of rubber elasticity is a cornerstone in our understanding of the structure–property relationship of polymers. The classical models1,2 are based on the hypothesis that chains on average become longer in the tensile direction by chain-segments rotating with respect to each other. All interactions between chains are neglected and the response is purely entropic. A number of revised models of rubber elasticity3–12 have been proposed dealing with the constraint of the chains on each other (entanglements), but they are still entropy based, and the generalizations tend to be phenomenological in nature.
However, experimental data have confirmed that rubber elasticity is not solely entropic of nature. As an example, microcrystalline domains in the polymer introduce enthalpic contributions to the free energy of the rubber. Crystalline domains appear very commonly in rubbers and provide the entire elasticity for thermoplastic elastomers, which behave mechanically as rubbers when stretched in the temperature range between their glass transition temperature and melting temperature. Enthalpic contributions are also encountered when the polymer chains are stretched beyond the so-called maximum chain extensibility region where the rubber becomes strongly strain-hardened. In this regime the polymers no longer elongate by chain-segment rotation, but encounter chain-stretching, i.e. bond angles are changed. Usually the enthalpic contributions are determined from calorimetric experiments, but this technique does not reveal any details on the origin of the enthalpy change.
Crosslinked PDMS, also known as silicone rubbers or elastomers, are commonly used as model rubbers since the chemical structure of PDMS can be carefully adjusted to provide variable and controlled network structures for model verification, and the silylation chemistry crosslinking reaction proceeds more or less ideally without any significant side reactions. Furthermore, PDMS possesses a very low glass transition temperature and no melting temperature, which indicates that the number of microcrystalline domains is vanishing. The polymer chains are in addition extremely flexible and thus very high stretches are allowed before the polymer chains enter the maximum stretchability region, for instance strains up to 1400% for a very lightly crosslinked silicone elastomer.13 Therefore, unfilled silicone rubbers should in principle possess entropic contributions to the free energy only.
A main difficulty for validating structural models of polymer networks is the lack of experimental techniques to visualize the individual polymer chains without altering the chemical structures such as via labeling. This has implied that the models are typically tested on a macroscopic scale, e.g. by comparing predicted stress–strain curves to results of mechanical testing.3,14 In terms of structural techniques, small angle X-ray and neutron scattering (SAXS/SANS) have provided information on the average size and asymmetry of the end-to-end distribution of the chains.15,16 Likewise spectroscopy has been used to probe the atomic configurations17 and deuterium magnetic resonance to probe segment orientation in rubbers.18 However, none of these probes provide information on the intermediate scale of the interaction between neighboring chains.
To enable studies on the entire 2–50 Å length scale we introduce the use of diffraction by hard X-rays, emerging from a synchrotron source. X-ray diffraction from laboratory sources has been used in the past to determine the average atom positions in the un-deformed state19 and coarse structural changes taking place during deformation.20 In comparison the high energy synchrotron data we present below are associated with much smaller correction terms leading to more accurate data21 and hence allowing for a more ambitious data analysis approach.
Experimental
Sample preparation
Three synthesized networks were prepared from three different di-functional vinyl-terminated PDMS polymers (V31, V35, and V41) and two low-molecular weight hydride-containing crosslinkers with different functionalities, namely phenyltris(dimethylsiloxy)silane (functionality f of 3) and tetrakis(dimethylsiloxy)silane (f = 4) (trade names SIP6826.0 and SIT7278.0, respectively) via a simple addition reaction. All polymers were purchased from Gelest Inc. The telechelic vinyl-functional PDMS and the 3-functional crosslinker are both illustrated in ESI Fig. S1.† The addition reaction between the hydride and the vinyl groups was catalyzed by a platinum cyclovinylmethyl-siloxane complex (511) provided by Hansechemie AG used in a concentration of approximately 10 ppm. No solvents were utilized. Sample details are given in Table 1.| Polymer | Mn (g mol−1) | PDI | Average number of monomers in chain | Average number of entanglements per chain | Cross-linker functionality | Young's modulus (MPa) |
|---|---|---|---|---|---|---|
| V31 | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.3 | 391 | 2.4 | 3 | 0.2 |
| V35 | 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
1.5 | 668 | 4.1 | 4 | 0.4 |
| V41 | 62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
1.6 | 841 | 5.2 | 4 | 0.4 |
| Elastosil | — | — | — | >1 | — | 1.0 |
As a fourth sample we tested Elastosil RT625 (abbreviated as Elastosil in the following) – a commercial composite PDMS elastomer, which includes amongst other a reinforcing silica filler. Elastosil is supplied as a two-component silicone rubber by Wacker Chemie AG. It is a rather strong silicone elastomer due to the presence of filler particles, which makes the apparent crosslink density higher due to a reduced mobility of the silicone chains. Based on density information, the commercial composite elastomer comprises significant amounts of silica.
Great care was taken to eliminate mixing problems, such as introduction of air bubbles and crosslinking inhomogeneity. Two premixes were prepared, namely PDMS/catalyst and PDMS/crosslinker. For Elastosil the premixes were supplied. In this way both low and high viscosity components could be mixed sufficiently long without any reaction taking place. More details on the mixing procedure can be found in Larsen et al.14 Next, the two premixes were mixed for 10 minutes at ambient temperature before the partly cured reaction mixture was poured into the mold, kept at 10 °C. The mold was then transferred to an oven at 50 °C where it was kept for 2 hours to ensure complete reaction before slowly being cooled to room temperature.
All samples were molded as cylindrical dog-bone shaped specimens. The two end plates contained holes in order to let excess material and air out and to further increase the area on the plate to which the elastomer should adhere. The samples had a diameter of 4.0 mm at the midpoint and a length of 16 mm (measured from end plate to end plate). More details on the utilized testing settings can be found in Bejenariu et al.22
Mechanical properties
The mechanical properties of the four types of samples were probed on a vertical filament stretch rheometer, where the elastic moduli were determined from ideal elongational flow data in the linear regime. The experiments were performed at constant Hencky strain rates of ν = 0.02 s−1 and ν = 0.002 s−1, respectively. More details on the sample preparation can be found in Jensen et al.23 Reversing large amplitude oscillatory elongational measurements24 were performed on the strongest (Elastosil) and softest (V31) networks at a strain rate ν = 0.02 s−1 in order to clarify the dynamic behaviour at a slow frequency comparable to the effective strain rate applied in the experiments at the synchrotron. Elastosil has an elastic modulus of ∼1 MPa and the softest elastomer (V31) has an approximately five times lower elastic modulus. The corresponding stress–strain curves are shown in ESI Fig. S2.† The Elastosil sample shows a slight degree of strain softening and it can also be observed that there is a relatively high hysteresis. Both observations are due to filler materials rearranging with slow dynamics (Mullins effect) in the commercial rubber. The softest (V31) rubber shows a very small degree of hysteresis and behaves approximately linearly in the investigated strain region. The other two soft rubbers show no hysteresis due to the more ideal crosslinking resulting from the four-functional crosslinker. The shortest polymer was crosslinked with the 3-functional crosslinker as it otherwise became too brittle to be stretchable.Synchrotron setup
The in situ experiment took place at beamline ID15B at the European Synchrotron Radiation Facility. The various rubber specimens were repeatedly stretched and un-stretched in steps from the un-deformed state (λ = 1) to elongations of up to 200% (λ = 3). Samples were loaded using a Linkam TST350 thermo-mechanical tensile testing cell. The load stage was equipped with a 20 N load cell and self-centring grips which assured that the applied load was uniaxial. The load resolution of the cell was 1 mN and loading rates were <1 mm s−1.The X-ray beam was monochromatized and focused in the horizontal plane by means of a bent Si-511 crystal.25 The samples were illuminated with a 0.3 × 0.3 mm2 pencil beam in transmission geometry. The energy of the incident radiation was 89.07 keV. The acquisition time of the diffraction patterns was 50 s. The area detector used was a flat panel Pixium 4700 detector by Thales,26 with 1920 × 2640 pixels and an active area of 295.68 × 406.56 mm2. With the detector positioned 312 mm from the sample, the transmission set-up allowed the acquisition of data within a Q-range of 0.5 to 18.5 Å−1, see Fig. 1 for a schematic of the setup.
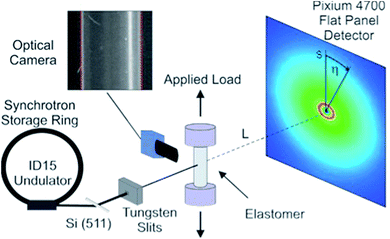 | ||
| Fig. 1 Schematic diagram showing the high-energy X-ray diffraction setup used during the experiment. | ||
After every measurement, an exposure was made with a high-resolution video camera, positioned next to the sample at an angle of 90° with respect to the beam. This was used to calibrate for drifts of the sample position in the direction of the beam. The incident radiation was monitored with a Si-pin diode, and all diffraction patterns were normalized by this reading. The X-ray background was measured without the sample and subtracted from the diffraction patterns. Diffraction images were corrected using a known flat field gain correction and dead pixels were excluded from the analysis.
Theory
Scattering formalism
The following summary of relevant equations builds on Warren.27 Bragg's law implies the following correlation between the momentum transfer, Q, the X-ray wavelength λx and the scattering angle 2θ:
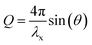 | (1) |
Assuming the face normal of the 2D detector to be parallel to the direction of the incoming beam we have s/L = tan(2θ), where s is the radial detector coordinate and L is the sample-detector distance, cf. Fig. 1. It follows that the intensity distribution on the detector can be characterized in terms of coordinates Q and η, with the azimuthal detector coordinate η defined in Fig. 1.
The cylindrical symmetry imposed by the tensile deformation implies that we can express the η-variation of the intensity distribution by a Legendre expansion.28,29 In the following we assume that expanding in two terms is sufficient. The real space pair distribution g(r) is then composed of an isotropic term g0(r) and an anisotropic term g2(r). These are related to corresponding Q-space terms, the structure functions s0(Q) and s2(Q) respectively, by means of two Fourier–Bessel transformations:
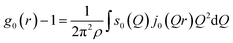 | (2) |
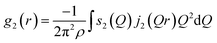 | (3) |
Details of data analysis
After integration into 10° segments in η all data Iraw(Q,η) are corrected for (i) a geometric factor Cg(Q) relating to a varying sample to detector pixel distance, (ii) a polarization dependent part of the Thomson cross-section Cp(Q,η) for horizontally polarized incident radiation and (iii) a varying instrumental background Ibackg(Q,η):| Icorr(Q,η) = Cg(Q)Cp(Q,η)[Iraw(Q,η) − Ibackg(Q,η)] | (4) |
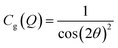 | (5) |
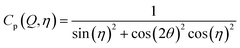 | (6) |
The corrected intensity for the un-deformed samples is averaged azimuthally, i.e. over η, and the averaged intensity is multiplied with the intensity ratio between the deformed and un-deformed samples. This is done to remove the effect of remaining spatial inhomogeneities in the detector response.
The intensity ratios are then analysed as Legendre components. Using again only two terms we have:
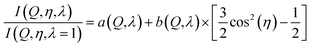 | (7) |
Because the diameter of the sample decreases with the elongation λ, the illuminated volume becomes smaller. Furthermore the Legendre coefficients, a(Q,λ) and b(Q,λ), are affected by small (<1%) absorption effects caused by the varying amount of material in the path of the scattered X-rays. Both effects are conveniently accounted for by a low pass Fourier-filter technique. We thus determine a common normalization factor CNV(Q,λ). The Q-dependence is small and only contains components varying so slowly with Q that they cannot be confounded with interatomic structures. The isotropic intensity of the un-deformed sample is normalized to an absolute cross section by comparison with the sum of the atomic self plus Compton scattering by a second normalization factor CN(Q), which increases slightly with Q. Thus we have:
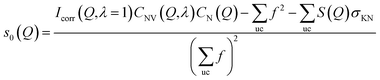 | (8) |
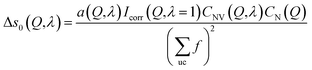 | (9) |
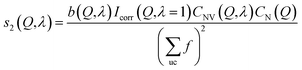 | (10) |
Analysis of isotropic bond distance and bond angle distributions
In the following we setup a model for comparison with the intra-chain isotropic data. Initially we note that the structure at the monomer level is characterized by the distance distribution of Si–O and Si–C bonds as well as the Si–O–Si, O–Si–O, C–Si–C and C–Si–O bond angles. All distances involving the H atoms are neglected as they contribute very little to X-ray scattering. The distance distributions are assumed to be Gaussians, each characterized by an equilibrium distance r and a width σ. This leads in momentum transfer space to a sum of Debye type terms, one for each atomic pair AB considered:
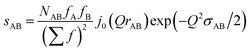 | (11) |
Likewise, the change in the intra-chain structure upon deformation (Δs0 of eqn (9)) can be characterized by two additional parameters per atomic pair, one characterizing the change in equilibrium distance Δr, and another characterizing the change in width Δσ. For atom pair AB the fit function is consequently:
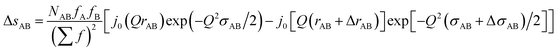 | (12) |
If the intramolecular potentials VAB(r) are known, it is in principle easy to calculate the energy change associated with the change in the intramolecular distance distribution P:
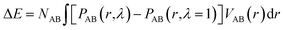 | (13) |
Results and discussion
Separating entropic and non-entropic contributions from diffraction data
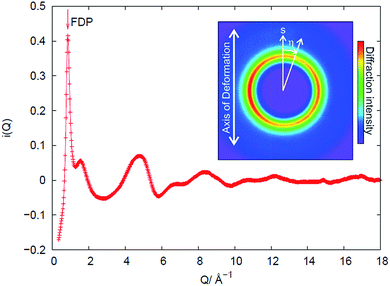
An example of the X-ray diffraction patterns acquired is shown in Fig. 2. As mentioned above, the patterns can be described in terms of radial (s) and azimuthal (η) co-ordinates, with s being related to radial distance in reciprocal space, Q, as given by eqn (1). The most prominent feature is the first diffraction peak (FDP). The position of the FDP is well known to become anisotropic in η during deformation, an effect attributed to the alignment of chains.30As anticipated in the theory section above, we find that for all samples and all elongations only the first two terms in the Legendre expansion of I(Q,η) are significant, even with the high signal-to-noise levels provided by the synchrotron approach. Having determined a(Q) and b(Q) according to eqn (7), the isotropic s0(Q) and anisotropic s2(Q) structure factors can be derived as outlined in the theory section. Fig. 2 shows an example of s0(Q) for sample V31. The structure factors s0(Q) and s2(Q) are related by Fourier transform to two corresponding radial pair distribution functions (PDFs) in real space, cf. eqn (2) and (3). From models of the rubber structure one can generate these PDFs and following the reverse Fourier-transform it is therefore possible to compare predicted and experimental sets of s0 and s2. Displayed in Fig. 3 is the difference between the stretched and the un-stretched state: Δs0(λ = 2) = s0(λ = 2) − s0(λ = 1) and Δs2(λ = 2) = s2(λ = 2). Noticeable, high accuracy data is available in the entire Q-range from 0.5 Å−1 to 18.5 Å−1. Provided the experimental data is of sufficient quality as in the present experiment the reverse Fourier-transform approach outlined above can be used for optimization of model parameters. The Fourier relationship also implies that we can separate the inter-chain and intra-chain contributions to the structure factors, as the former dominates at small Q and the latter at Q ≥ 6 Å−1.19 A description of rubber elasticity based solely on entropy implies that Δs0 is identical to zero. It is evident from Fig. 3(a) that this is not the case, and the following sections are devoted to analyzing these non-entropic contributions in greater detail.
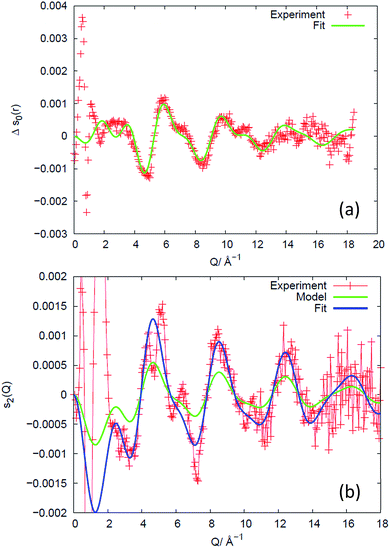 | ||
| Fig. 3 Experimental results for sample V31 (+) expressed as the difference in structure factors between the stretched (λ = 2) and the un-stretched state, and comparison to structural models of the intra-chain behaviour, valid for Q ≥ 6 Å−1. (a) Isotropic part, revealing changes in bond-lengths and bond-angles. The data are compared to a fit of a structural model of the monomer. The fitted parameter values are listed in Table S2.† (b) Anisotropic part, revealing the preferred direction of chain segments of various lengths. A state-of-the-art model based on non-interacting chains (green) predicts the correct shape of the intensity variation with Q but underestimates the degree of preferential direction. With the degree of preferred direction as the sole fitting parameter a satisfying fit is reached (blue). | ||
Non-entropic intra-chain behaviour
The PDF (Fig. 4(a)) counterpart to Δs0 (Fig. 3(a)) reveals that there is little evidence for change in the average structure beyond 4 Å, hence the structural changes mainly relate to changes within the monomer (the unit segment in the chain). To describe these changes, we fit the high-Q part of Δs0, as exemplified for sample V31 in Fig. 3(a), to the simple model of the monomer comprising average bond lengths, bond angles and widths of distributions (eqn (12)). The results of the fit are listed in Table 2. The relative changes in bond angles and bond lengths are small – of order 10−4 – but as a general observation the width parameter of all atomic pairs increases on deformation. The best fits of Δs0 and the corresponding real space PDF are shown in Fig. 3(a) and 4(a), respectively. A quite satisfactory fit to the experimental data is also obtained when average distances are constant (Δr = 0). The results for the isotropic melt are in close agreement with the results of Sides et al.19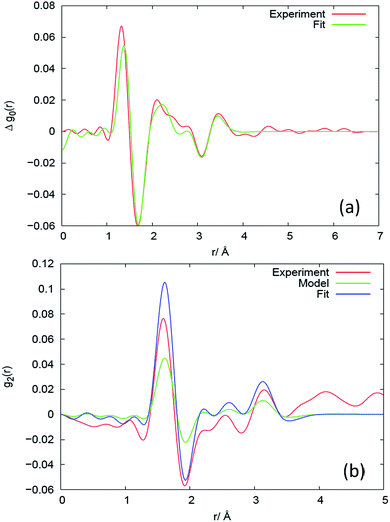 | ||
| Fig. 4 Results in real space for the (a) isotropic and (b) anisotropic response at different length scales for sample V31, expressed as the difference between the deformed (λ = 2) and the un-deformed state. The corresponding plots for Q-space are shown in Fig. 3. The experimental results are compared to models, as explained in the caption to Fig. 3. | ||
| r, σ (λ = 1) | Δr, Δσ (λ = 2 − λ = 1) | Relative change Δr/r, Δσ/σ | |
|---|---|---|---|
| rSiO/Å | 1.642 | −6.0 × 10−4 | −3.7 × 10−4 |
| σSiO/Å | 0.111 | 4.5 × 10−3 | 4.0 × 10−2 |
| rSiC/Å | 1.869 | −2.8 × 10−4 | −1.5 × 10−4 |
| σSiC/Å | 0.143 | 4.4 × 10−3 | 3.1 × 10−2 |
| rSiSi/Å | 3.160 | −4.2 × 10−4 | −1.3 × 10−4 |
| σSiSi/Å | 0.139 | 3.5 × 10−3 | 2.5 × 10−2 |
| rOO/Å | 2.736 | 1.2 × 10−3 | 4.6 × 10−4 |
| σOO/Å | *0.080 | −5.4 × 10−3 | −6.8 × 10−2 |
| rCC/Å | 3.055 | −10.4 × 10−3 | −3.4 × 10−3 |
| σCC/Å | *0.080 | 7.8 × 10−3 | 9.7 × 10−2 |
| rOC/Å | 2.858 | 1.0 × 10−4 | 3.6 × 10−5 |
| σOC/Å | 0.200 | 1.2 × 10−2 | 6.0 × 10−2 |
![[double bond splayed right]](https://www.rsc.org/images/entities/char_e00a.gif) OSiO/° OSiO/° |
112.8 | 7.9 × 10−2 | 7.0 × 10−4 |
![[double bond splayed right]](https://www.rsc.org/images/entities/char_e00a.gif) CSiC/° CSiC/° |
109.6 | −5.5 × 10−1 | −5.0 × 10−3 |
![[double bond splayed right]](https://www.rsc.org/images/entities/char_e00a.gif) SiOSi/° SiOSi/° |
148.4 | −5.3 × 10−2 | −3.6 × 10−4 |
Non-entropic inter-chain behaviour – mesoscopic strain
In Fig. 3(a) there is also evidence for a structural change around Q = 0.86 Å−1. This change corresponds to a shift ΔQ in the Q-position of the FDP between the stretched and un-stretched state. The peak position of the first diffraction peak (FDP) and its shift in Q as a function of η for different elongations λ, as exemplified in Fig. 5(a) for sample V31 at λ = 2.08, is determined by two methods that were found to give very similar results. In the first a parabola was fitted to the near peak region and the peak position was assigned to the maximum of the parabola. The second is a correlation method.31 The peak positions shown in Fig. 5(b) are obtained by the parabola method. As shown in Fig. 5(b) we find evidence for a sinusoidal type variation of ΔQ with η. This is the signature of a strain ε = −ΔQ/Q, acting between chains on a mesoscopic length scale of 10–50 Å.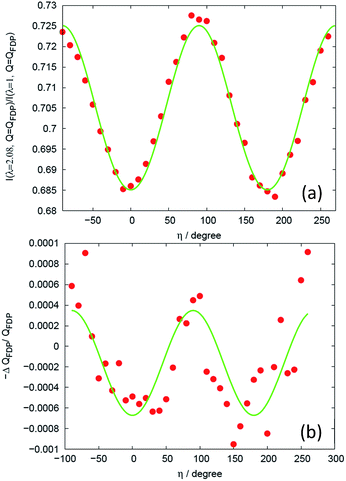 | ||
| Fig. 5 Analysis of mesoscopic strain. (a) Intensity ratio between the deformed and the un-deformed state at the position of the intensity maximum of the FDP for sample V31 and λ = 2.08. The solid line is the fit of eqn (14). (b) Relative shift in peak position of the intensity maximum. The solid line is a fit to a sinusoidal function. | ||
The results of a similar analysis applied to all data sets are shown in Fig. 6(a). Evidently, within experimental uncertainty, all four samples display a linear relationship between the elongation and the strain components ε∥ and ε⊥, representing the strains in the directions parallel and perpendicular to the elongation, respectively. The response with λ varies strongly from sample to sample, but falls on a universal straight line when plotted against the degree of chain alignment, cf. Fig. 6(b). The hypothesis of a strong correlation between strain and chain alignment is corroborated by the fact that upon un-stretching both strain and chain order vanished. On a note it is observed that for some samples (including the V41 sample used in Fig. 6) the peak positions averaged over all orientations drifted systematically by about 2 × 10−4. This presumably artificial drift (caused for example by an unstable sample position) has been corrected for in Fig. 3(a). It does not affect Fig. 6(b), since Fig. 6(b) only involves the difference in peak position between parallel and perpendicular orientation.
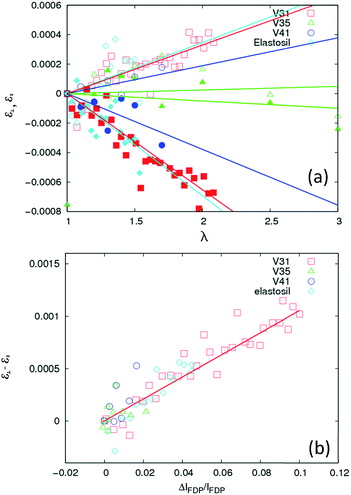 | ||
| Fig. 6 Characterization of the strain ε, acting between chains. (a) Variation as a function of elongation parameter λ for the four types of rubber: V31, V35, V41 and Elastosil. Open and filled symbols refer to the strain components ε⊥, and ε∥, perpendicular (η = 90°) and parallel (η = 0°) to the direction of the elongation respectively (η is defined in Fig. 2). Solid lines are fits of straight lines through (0, 0). (b) Linear correlation between the difference between strain components, ε⊥ − ε∥, and the inter-chain ordering – measured by the relative intensity difference of the FDP at η = 0° and η = 90°. | ||
The elastic inter-chain strain ε is of the order 6 × 10−4 (Fig. 6) at λ = 2. Notably, this strain response at the 10–50 Å scale is associated with two unusual properties. Firstly, it is 3–4 orders of magnitude smaller than the macroscopic strain. In contrast, for crystalline and amorphous materials with solid-like elasticity the relation is close to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Secondly, the sign is remarkable: the compressive direction of the strain is along the macroscopic tensile direction. This may be explained by entanglements introducing restraints on the polymer chain. All investigated rubbers include entanglements as the molecular entanglement weight of PDMS is 12 kg mol−1.32 When the rubber is stretched the locked entanglements relax and one possible way to do so is for the entanglement to slide along the chain and approach the line/plane of the restricting crosslinks. Thereby the polymer chain will experience a stretch in the compressive direction (short part of polymer chain) and the longer part of the polymer chain will be released and allowed to possess ideal behaviour with respect to random walk behaviour as for traditional polymer deformation descriptions.
1. Secondly, the sign is remarkable: the compressive direction of the strain is along the macroscopic tensile direction. This may be explained by entanglements introducing restraints on the polymer chain. All investigated rubbers include entanglements as the molecular entanglement weight of PDMS is 12 kg mol−1.32 When the rubber is stretched the locked entanglements relax and one possible way to do so is for the entanglement to slide along the chain and approach the line/plane of the restricting crosslinks. Thereby the polymer chain will experience a stretch in the compressive direction (short part of polymer chain) and the longer part of the polymer chain will be released and allowed to possess ideal behaviour with respect to random walk behaviour as for traditional polymer deformation descriptions.
Non-entropic energy contributions
For calculation of the energy change associated with the change in the intra-molecular distance distribution P derived from the results in Table 2 we utilize eqn (13). Unfortunately, the potentials VAB(r) as defined in eqn (13) are not known to a high accuracy and additional uncertainty is introduced from the fact that experimental data are convoluted by an instrumental resolution function. However, based on the intra-molecular potentials of Frischknecht et al.33 we calculate values in the order of ΔE = 1 kJ mol−1 (of monomer). It is possible that the increased width of the distance distribution in part is the result of an inhomogeneous strain distribution such as sometimes found in computer models of entangled networks.34Assuming that on the molecular level the energy required for generating the inter-chain strain (of the order 6 × 10−4 at λ = 2 according to Fig. 6) is given by the larger bulk modulus rather than Young's modulus,35 and is ultimately related to the energy required for the methyl side groups to move from their equilibrium positions, we estimate for the inter-chain contribution ΔE = 0.5Kε2M/ρ ≈ 0.01 J mol−1, orders of magnitudes smaller than what we just estimated for the intra-chain contributions.
In conclusion these results indicate that intra-chain energy is the dominating energetic contribution to the elasticity in PDMS based rubbers. The effect is noticeable even at the smallest steps of elongation: ∼10%, and approximately linear in the strain regime investigated.
Anisotropic contribution
For completeness, we comment also on the anisotropic structure factor. As shown in Fig. 3(b), the largest effect is seen below Q = 2 Å−1 (out of scale on the figure). This is the previously mentioned well-known effect of ordering of the chains. It is informative to compare the results in Fig. 3(b) to predictions from a state-of-the-art model,34 which does not take chain interaction into account. In this model an ensemble of isolated self-avoiding molecular chains is generated and the macroscopic strain condition is imposed. The potentials of Frischknecht et al.33 are utilized as basis for the model. Let the chains have end-to-end vectors (x0, y0, z0) and let the averages of the absolute projections be 〈|x0|〉 = 〈|y0|〉 = 〈|z0|〉. To represent the stretched rubber, by simulated annealing we eliminate chains from and re-include chains into this ensemble such that the end-to-end distance distribution at the end fulfills the macroscopic strain condition (with z being the tensile axis):| 〈|z|〉 = λ〈|z0|〉, 〈|x|〉 = 〈|x0|〉/√λ, 〈|y|〉 = 〈|y0|〉/√λ | (14) |
The predicted response is shown in Fig. 3(b) as a green curve. The predicted shape is in good agreement with the experiment, but the amplitude is not. Using the amplitude as the only fit parameter a satisfying fit is obtained (blue curve). The four samples all exhibit a similar behavior and quality of fit to data. However, the fitted amplitude – listed in Table 3 – varies substantially. We attribute these variations in amplitude to different levels of preferred directionality of chain segments caused by different degrees of chain entanglement. We find that the individual SiO bonds point preferentially in the tensile direction. The degree of preferred orientation depends on the number of monomer units in the model. For a 391 monomer chain – that equals the average chain length in V31 – we find a 1.9% increased likelihood of parallel orientation at λ = 2. We tested another deformation model, the affine model,36 which enforces eqn (14) to be valid for each chain instead of only for the ensemble averages, leading to similar results.
| V31 | V35 | V41 | Elastosil | |
|---|---|---|---|---|
| Preferred orientation parameter (%) | 1.9 | 0.2 | 0.6* | 1.4* |
Based on the above results we argue that the analysis of the anisotropic structure factor provides a unique possibility to test models of chain interaction. The results in Fig. 3(b) for higher Q's are novel, and represent an opportunity for testing models on different length-scales.
Physical interpretation of the preferred orientation parameter
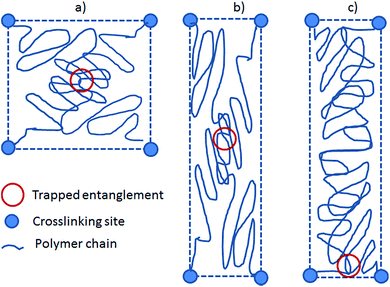
The preferred orientation parameter may seem random from the above results, but from the network characteristics in Table 1 it is obviously related to the chain mobility with high chain mobility leading to increased preferred orientation. Firstly, for the unfilled networks the preferred orientation parameter of V31 is significantly larger than that of V35 and V41. To understand this recall that a crosslinker with functionality of f = 3 causes a very soft network since partial crosslinking reaction (due to steric hindrance etc.) will contribute to chain extension rather than result in crosslinking sites. Furthermore, looking on one particular PDMS chain from a 3-functional crosslinker, this chain will only have two anchoring points and thus be much more mobile compared to that from a 4-functional crosslinker. Hence, the chain mobility of V31 (f = 3) will be increased relative to that of V35 and V41 (both f = 4). Secondly, the preferred orientation parameter for the filled elastomer is high, and this may simply be due to the low crosslinking density since the commercial elastomer contains significant amounts of fillers leading to physical interactions only and thereby also a reduction of the chemical crosslinking density; i.e. increased chain mobility.These results are counterintuitive from the point of view that increased chain mobility should lead to easier relaxation and thus less preferred orientation. However, they can be explained by the following hypothesis. Here we simplify the system to two “1-time” entangled polymer chains confined by four crosslinking sites placed at the four corners of a square. This is illustrated in Fig. 7. When the system is stretched, the chains and entanglement will relax. When the entanglement relaxes, it finds an energy minimum by moving to a position close to the nearest pair of crosslinking sites, either above or below the entanglement depending on its original position.
Each polymer chain can then be considered as a short part (with the main orientation perpendicular to the stretch) and a long part (with the main orientation along the stretch). The entropy of the entire chain is described as the sum of entropies of the two parts, which will give an overall energy minimum when the long part is as long as possible. In other words, the short parts of the chains will align in the plane perpendicular to the stretch to allow the long parts of the chains as much entropy as possible. More chain mobility will then allow the entanglement to come closer to the pair of confining crosslinks and thus result in increased preferred orientation of the polymer chains. The simplified derivations have been shown in ESI† where it is shown that entropy is gained by allowing the entanglement to slide and that bond stretching can be facilitated energetically.
Additionally, this hypothesis can describe why a microscopic stretch occurs perpendicular to the macroscopic stretch direction. This will be possible if dH < TdS, i.e. if the gain in entropic energy is larger than the enthalpic increase from the stretching of Si–O bonds.
Finally this can lead towards a better understanding of the behavior of silicone-based dielectric elastomers for which constitutive equations have been proposed.37–40 Despite the proposed constitutive equations being excellent in describing the mechanical properties of the elastomers, the explanation of why the electrical breakdown strength is increased with strength for non-hardening elastomers remain unanswered.41
Conclusions
This work demonstrates the limitations of the current type of models for describing rubber elasticity, in particular the need to include non-entropic terms. This is done by means of a novel X-ray based method enabling the determination of the structural changes of rubbers on the 2–50 Å length scale during in situ stretching. By using high-energy X-rays from a synchrotron the data acquisition is sufficiently fast avoiding any noticeable plastic flow.The investigated silicone rubbers range from very soft with no reinforcing agents to a commercial silicone elastomer with reinforcing agents. Universally we find that:
• Within experimental noise, the data can be modelled using only the first two terms in the Legendre expansion in eqn (7); an isotropic and an anisotropic term.
• An elastic inter-chain strain response appears at the scale of 10–50 Å with the compression direction along the macroscopic tensile direction. The strain is of the order 6 × 10−4 at an elongation of λ = 2, corresponding to an energy contribution of the order of 0.01 J mol−1. The response with λ varies with entanglement, but falls on a universal straight line when plotted against the degree of chain alignment. This strain is hypothesized to arise from trapped entanglements relaxing to positions near the confining pair of crosslinking sites, thereby allowing a strong alignment of the short part of the chain in order to maximize the entropy of the long part of the chain.
• The intra-chain contribution to the free energy is substantially larger, in the order of ΔE = 1 kJ mol−1. While the relative change of bond lengths and bond angles is of the order 10−4, the bond length and bond angle distributions are 5–10% wider at λ = 2. These features appear in the anisotropic part of the scattering signal and can be described qualitatively by a simple model of the response of an isolated self-avoiding molecular chain. However, the amplitudes vary substantially with sample, but can in all cases be well accounted for by a one-variable fit. We attribute these variations in amplitude to different levels of preferred directionality of chain segments caused by different degrees of chain entanglement.
The experimental approach presented is generic and may find use also for in situ studies of polymers in the glass, liquid and semi-crystalline states. Likewise, it may be extended to use with isotope substituted samples and neutron diffraction for studies of chain interaction. Furthermore, from the application standpoint, we point out that mapping of strain is made possible by this study in products made of rubber such as tires and seals as well as in other polymeric products such as paints and thermoplastics.
Acknowledgements
Part of this work was performed at Oak Ridge National Laboratory, supported by the Scientific User Facilities Division of the Office of Basic Energy Sciences, US Department of Energy Office of Science. Other parts were supported by the Danish National Research Foundation and the Danish Natural Science Research Council. We acknowledge experimental help by A. G. Bejenariu and R. Godiksen and discussions with P. Sommer-Larsen, K. Mortensen, N. Hansen, D. Juul Jensen and V. Urban. ESRF is acknowledged for provision of beamtime. For loan and assistance using the load cell we thank G. Portale. The Danish Agency for Science, Technology and Innovation is acknowledged for travel support via DANSCATT. This manuscript has been authored by UT-Battelle, LLC under Contract No. DE-AC05-00OR22725 with the U.S. Department of Energy. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes. The Department of Energy will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).Notes and references
- P. J. Flory, The Principles of Polymer Chemistry, Cornell University Press, Ithaca, New York, 1953 Search PubMed.
- P. J. Flory, Science, 1975, 188, 1268 CAS.
- K. Urayama, T. Kawamura and S. Kohjiya, Polymer, 2009, 50, 347 CrossRef CAS.
- X. J. Xing, P. M. Goldbart and L. Radzihovsky, Phys. Rev. Lett., 2007, 98, 075502 CrossRef PubMed.
- B. Mergell and R. Everaers, Macromolecules, 2001, 34, 5675 CrossRef CAS.
- S. F. Edwards, H. Takano and E. M. Terentjev, J. Chem. Phys., 2000, 113, 5531 CrossRef CAS.
- M. Rubinstein and S. Panyukov, Macromolecules, 1997, 30, 8036 CrossRef CAS.
- R. Everaers and K. Kremer, Macromolecules, 1995, 28, 7291 CrossRef CAS.
- M. Rubinstein, L. Leibler and J. Bastide, Phys. Rev. Lett., 1992, 68, 405 CrossRef CAS PubMed.
- P. G. De Gennes, Faraday Discuss. Chem. Soc., 1979, 68, 96 RSC.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Clarendon Press, Oxford, 1986 Search PubMed.
- S. F. Edwards, Proc. Phys. Soc., 1967, 92, 9 CrossRef CAS.
- J. Goff, S. Sulaiman, B. Arkles and J. P. Lewicki, Adv. Mater., 2016, 28, 2393 CrossRef CAS PubMed.
- A. L. Larsen, K. Hansen, P. Sommer-Larsen, O. Hassager, A. Bach, S. Ndoni and M. Jørgensen, Macromolecules, 2003, 36, 10063 CrossRef CAS.
- E. Straube, V. Urban, W. Pyckhout-Hintzen, D. Richter and C. J. Glinka, Phys. Rev. Lett., 1995, 74, 4464 CrossRef CAS PubMed.
- C. Svaneborg, G. S. Grest and R. Everaers, Phys. Rev. Lett., 2004, 93, 257801 CrossRef PubMed.
- V. M. Litvinov and P. P. De, Spectroscopy of rubber and rubbery materials, ChemTec Publishing, Toronto, 2002 Search PubMed.
- P. Sotta, Macromolecules, 1998, 31, 3872 CrossRef CAS.
- S. W. Sides, J. Curro, G. S. Grest, M. J. Stevens, T. Soddemann, A. Habenschuss and J. D. Londono, Macromolecules, 2002, 35, 6455 CrossRef CAS.
- G. R. Mitchell in Order in the amorphous state of polymers, ed. S. E. Keinath, R. L. Miller and J. K. Rieke, Plenum Press, New York, 1987 Search PubMed.
- H. F. Poulsen, J. Neuefeind, H.-B. Neumann, J. R. Schneider and M. D. Zeidler, J. Non-Cryst. Solids, 1995, 188, 63 CrossRef CAS.
- A. G. Bejenariu, H. K. Rasmussen, A. L. Skov, O. Hassager and S. M. Frankaer, Rheol. Acta, 2010, 49, 807 CrossRef CAS.
- M. K. Jensen, H. K. Rasmussen, A. L. Skov and O. Hassager, Rheol. Acta, 2011, 50, 729 CrossRef CAS.
- M. K. Jensen, O. Hassager, H. K. Rasmussen, A. L. Skov, A. Bach and H. Koldbech, Rheol. Acta, 2010, 49, 1 CrossRef.
- P. Suortti, T. Buslaps, V. Honkimäki, M. Kretzschmer, M. Renier and A. Shukla, Z. Phys. Chem., 2001, 215, 1419 CrossRef CAS.
- J. E. Daniels and M. Drakopoulos, J. Synchrotron Radiat., 2009, 16, 463 CrossRef CAS PubMed.
- B. E. Warren, X-ray diffraction, Dover, New York, 1990 Search PubMed.
- H. D. Deas, Acta Crystallogr., 1952, 5, 542 CrossRef.
- G. R. Mitchell and R. Lovell, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1981, 37, 189 CrossRef.
- S. M. Ohlberg, L. E. Alexander and E. L. Warrick, J. Polym. Sci., 1958, 27, 1 CrossRef CAS.
- H. F. Poulsen, J. A. Wert, J. Neuefeind, V. Honkimäki and M. Daymond, Nat. Mater., 2005, 4, 33 CrossRef CAS.
- L. J. Fetters, D. J. Lohse, D. Richter, T. A. Witten and A. Zirkel, Macromolecules, 1994, 27, 4639 CrossRef CAS.
- A. L. Frischknecht and J. G. Curro, Macromolecules, 2003, 36, 2122 CrossRef CAS.
- R. Everaers and K. Kremer, J. Mol. Model., 1996, 2, 293 CrossRef CAS.
- D. Tabor, Polymer, 1994, 35, 2759 CrossRef CAS.
- W. Kuhn and F. Grün, Kolloid-Z., 1942, 101, 248 CrossRef CAS.
- L. Liu, Y. Liu, J. Leng and K. Lau, Smart Mater. Struct., 2011, 20, 115015 CrossRef.
- L. Liu, Y. Liu, B. Li, K. Yang, T. Li and J. Leng, Smart Mater. Struct., 2011, 20, 075004 CrossRef.
- Z. Suo, Acta Mech. Solida Sin., 2010, 23, 549–578 CrossRef.
- X. Zhao and Z. Suo, Phys. Rev. Lett., 2010, 104, 178302 CrossRef PubMed.
- F. B. Madsen, A. E. Daugaard, S. Hvilsted and A. L. Skov, Macromol. Rapid Commun., 2016, 37, 378–413 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra22802j |
| This journal is © The Royal Society of Chemistry 2016 |