Modeling and experimental study on the solubility and mass transfer of CO2 into aqueous DEA solution using a stirrer bubble column

Abstract

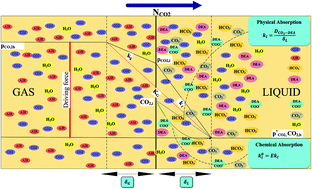
In this research, the chemical absorption rate and solubility of carbon dioxide into DEA aqueous solutions were investigated in a stirrer bubble column. Experiments envelopment the molarity of DEA, CO₂ partial pressures and stirrer speed are 0.2–2.0 M, 300–450 kPa and 0–600 rpm, respectively. The DEA and CO₂ concentration and gas–liquid flow rate effects on the mass transfer performance were measured in terms of CO₂ capture efficiency, loading, mass transfer flux and mass transfer coefficient. A thermodynamic model, according to the Pitzer's G^E model is provided for the equilibrium solubility of CO₂ in DEA aqueous solutions. The results have shown that the CO₂ loading in range of 0.16–0.40 and mass transfer rate in range of 0.36 × 10⁻⁵ to 0.97 × 10⁻⁵ kmol m⁻² s⁻¹ increases with DEA concentration and CO₂ partial pressure. Also the results indicate that the quantity of k_l increases with addition of DEA concentration, liquid and gas flow rate. Film parameter increases with increasing of DEA concentration and decreases with increasing of CO₂ partial pressure. Absorption percent of CO₂ was varied in range of 30–57%. The maximum absorption rate of CO₂ at partial pressure of 45 kPa has been obtaining 1.8 g min⁻¹ when the DEA concentration is 2.0 M.