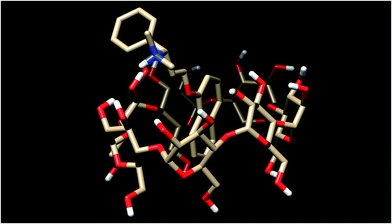
NMR, CD and UV spectroscopic studies reveal uncommon binding modes of dapoxetine to native cyclodextrins

Abstract

Complex formation between the selective serotonin reuptake inhibitor drug (S)-dapoxetine (Dpx) and β-, γ-, and methylated γ-cyclodextrins (CyDs) was studied by complementary experimental techniques. Phase solubility studies indicated 1 : 1 stoichiometry for all CyDs, with β-CyD being the most effective to enhance the solubility of and form the most stable complex with Dpx. ¹H NMR titrations and Job's method of continuous variation were also employed to corroborate the stoichiometry and association constants with γ- and β-CyDs. The simultaneous evaluation of titration datasets of several Dpx and CyD protons revealed for both CyDs that the best fit was achieved when the coexistence of Dpx·CyD and 2Dpx·CyD complexes were assumed. This finding was rather unanticipated considering the smaller cavity size of β-CyD, which inspired further investigations. The UV hypochromism and circular dichroism spectroscopic data suggested the inclusion of two Dpx molecules into the CyD cavity (albeit to a less extent with β-CyD). This conclusion was fully supported by 2D ROESY and 1D NOESY NMR spectra, observing NOEs between the inner methine protons of CyDs and both the phenyl and naphthyl ring protons of Dpx. Additional molecular dynamics calculations identified the energetically most favoured species for both the Dpx·CyD and 2Dpx·CyD complexes.

---

Introduction

Dapoxetine, (S)-N,N-dimethyl[3-(naphthalen-1-yloxy)-1-phenylpropyl]amine hydrochloride, (Priligy®) is a novel, short acting selective serotonin reuptake inhibitor that has been developed specifically as an on-demand oral treatment of premature ejaculation.¹ Dapoxetine is a rather lipophilic tertiary amine (Fig. 1), therefore its water solubility is highly pH-dependent. The solubility of the free base falls to the low μg mL⁻¹ range, so this uncharged form is practically insoluble. With decreasing pH, the proportion of the cationic form rises, according to the log K = 8.6 protonation constant of dapoxetine.¹ In order to improve the aqueous solubility and chemical stability of a drug compound, generally co-solvents, polymers, and macrocycles (or cavitands) such as cyclodextrins (CyDs) are applied.²

Fig. 1 Chemical structure of the free base form of (S)-dapoxetine (left, with numbering of its carbon skeleton) and schematic representation of the native CyDs, with the location of its carbon-bonded protons (right).

The principal advantages of native CyDs in the pharmaceutical industry are their low toxicity and low pharmacological activity as well as their well-defined chemical structure.³ These are water-soluble cyclic oligosaccharides composed of α-1,4-linked D-glucopyranose units. The most commonly used ones are the α-, β- and γ-CyDs composed of six, seven and eight glucose units, respectively.⁴ CyDs are toroidal molecules with a truncated cone structure. Secondary hydroxyl groups are located on the wider side of the ring, while the primary hydroxyls are positioned on the opposite, narrower end of the torus. The hydroxyl groups on the exterior surface of the molecule render CyDs more hydrophilic. The interior of the torus is hallmarked by two ‘rings’ of CH groups (H3 and H5), a ring of glycosidic ether oxygen atoms and H6 located near the narrower ‘primary’ rim of the cavity (Fig. 1). This low polarity central void is able to encapsulate either partially or entirely a wide variety of guest molecules of suitable size and shape, resulting in a supramolecular, non-covalent association, being the resultant entity known as a host–guest inclusion complex.^4,5 The most common pharmaceutical application of CyDs is the improvement of solubility, stability and bioavailability of the encapsulated species.³ Among the above mentioned CyDs, β- and γ-CyDs with an inner cavity diameter of 6.0–6.5 Å and 7.5–8.3 Å, respectively, and a depth of 7.9 Å are the most widely used, because of theirs excellent ability to incorporate hydrophobic aromatic rings of organic guest molecules in aqueous solution.

Our previous studies have revealed that both β- and γ-CyD derivatives form inclusion complexes with (S)-dapoxetine (Dpx).⁶ Especially γ-CyD derivatives were found to be suitable hosts for the enantioseparation of Dpx: the randomly methylated γ-CyD enabled a spectacular resolution value of R_s = 7 in chiral capillary electrophoresis (CCE). Another recent study⁷ has showed that the enantiomers of dapoxetine and its metabolites could successfully be separated with a single-isomer carboxymethyl γ-CyD as chiral resolving agent in CCE. However, no in-depth studies have yet been devoted to the complexation of dapoxetine by CyDs, although these cavitands, besides enantioseparation, can also enhance the aqueous solubility of the drug.

The current study is aimed at a more profound understanding of the inclusion complex formation between Dpx and native β- and γ-CyDs, as well as the randomly methylated γ-CyD (RAMEG). Besides the practically important aspect of improving its solubility (assessed by phase solubility studies), extensive ¹H NMR, UV and circular dichroism spectroscopic investigations were also performed in order to investigate the stoichiometry of association, to determine stability constants and to gain insight into the structure of the complexes formed. The spectroscopic studies were complemented by molecular modeling to explore the structure of energetically favourable inclusion complexes.

Materials and methods

Materials

The free base of Dpx was synthesized according to a modified literature procedure,⁸ while CyDs were received from Cyclolab Ltd. (Budapest, Hungary). D₂O (99.9 atom% D) was purchased from VWR Chemicals, while acetic acid-d₄ was obtained from Cambridge Isotope Laboratories Inc. Other base chemicals of analytical grade were from commercial suppliers and used without further purification. All solutions were prepared from doubly distilled Millipore water (specific conductivity: 1.1 μS cm⁻¹).

Phase solubility studies

Phase solubility studies were carried out in a pH 7.40 phosphate buffer according to the method described by Higuchi and Connors.⁹ Excess amounts of Dpx (1.5 mg) were added to 1 mL solutions with CyD concentrations ranging from 1 to 50 mM (for β-CyD: 1 to 10 mM). The obtained suspensions were shaken at 25.0 ± 0.5 °C for 24 h. After attaining equilibrium, the samples were centrifuged and the concentration of Dpx was determined spectrophotometrically on a Jasco V-550 instrument at 291 nm. The intrinsic solubility (S₀) of Dpx was determined by following the same sample preparation protocol in the absence of CyD. Phase solubility profiles were constructed by plotting the measured solubility of Dpx as a function of total (analytical) CyD concentration, c_CyD. The stability constant of the presumed 1 : 1 complex formed in the following equilibrium,can be calculated from the slope of the linear segment of the phase solubility profile using the following equation:

The solubilizing capacity of CyD was estimated by the complexation efficiency parameter (CE), determined also from the phase solubility profile and yielding the concentration ratio of the complexed and free CyD:

By combining eqn (3) with mass balance equations and assuming that all Dpx is complexed by CyD, CE allows the estimation of the optimal host/guest concentration ratio for maximizing the solubilization efficiency:

The correlation between CE and the molecular weights (MW) of the constituents leads to the evaluation of the increase in formulation bulk as follows:

Nuclear magnetic resonance spectroscopy measurements

The majority of NMR experiments were carried out in D₂O at 25 °C on a 600 MHz Varian DDR NMR spectrometer (Agilent Technologies, Palo Alto, CA, USA) of the Semmelweis University, equipped with a 5 mm inverse-detection gradient (IDPFG) probehead. Standard pulse sequences and processing routines available in VnmrJ 3.2C/Chempack 5.1 were used. The complete resonance assignments of the Dpx or the CyDs were achieved direct ¹H–¹³C, long-range ¹H–¹³C, and scalar spin–spin connectivities, derived from 1D ¹H, ¹³C, 2D gCOSY, zTOCSY or ROESY, ¹H,¹³C-gHSQCAD or gHMBCAD (ⁿJ_CH = 8 Hz) experiments, respectively. ¹H chemical shifts in all experiments were referenced to the methyl peak (δ = 3.32 ppm) of internal CH₃OH added in 20 μM concentration and known not to interact with CyDs.

Job's method of continuous variation. The ¹H NMR titration of Dpx according to Job's method^10,11 was conducted in unbuffered acidic (40 mM CD₃COOD) D₂O solutions at 25 °C. The total molar concentration of the two components was kept constant at 3 mM, but the mole fraction of Dpx, x_Dpx = c_Dpx/(c_Dpx + c_CyD) was varied gradually in 0.1 unit steps from 0.0 to 1.0. ¹H chemical shifts δ^Dpx,i were recorded for several (ith) Dpx protons and for those exhibiting a monotonic displacement Δδ^Dpx,i = δ^Dpx,i − δⁱ_Dpx with respect to the δⁱ_Dpx chemical shift of the free component, the absolute values of displacement values |Δδ^Dpx,i| were used to construct the Job's plots. Analogous plots were generated for selected protons of the CyD.

¹H NMR titrations. Since the method of continuous variation does not necessarily provide the best experimental design for stability constant determination,¹¹ a separate titration was performed under similar circumstances (at 25 °C and in 10 mM CD₃COOD solution adjusted to pH* 5.2 with NaOD), but holding c_Dpx constant and increasing the CyD concentration. The 1.0 mM stock solution of Dpx was added to vials containing weighed amounts of CyDs (β-CyD: 0.1 to 12.0 mM; γ-CyD: 0.1 to 25.0 mM) and the mixtures were sonicated and transferred to NMR tubes. The samples were equilibrated for 24 h before acquiring the ¹H NMR spectra.

The chemical shift titration is one of the most widely used procedures to determine stability constants of inclusion complexes.^11,12 Its principles are available in the literature, also for higher stoichiometries than the simplest 1 : 1 case.^13,14 Our calculation procedure is briefly outlined below for a more complex system, assuming the concurrent formation of Dpx·CyD and 2Dpx·CyD species, which will be denoted hereafter as the {Dpx·CyD, 2Dpx·CyD} equilibrium model. Formation of the 2Dpx·CyD species is described by a second stepwise association constant, K₂₁:

To evaluate speciation, the equilibrium concentrations [CyD] and [Dpx] are calculated for each titration point from the total concentrations c_CyD and c_Dpx by solving numerically the nonlinear mass balance equations:

c_CyD = [CyD] + [Dpx·CyD] + [2Dpx·CyD] = [CyD](1 + K₁₁[Dpx] + K₁₁K₂₁[Dpx]²) (7)

c_Dpx = [Dpx] + [Dpx·CyD] + 2[2Dpx·CyD] = [Dpx](1 + K₁₁[CyD] + 2K₁₁K₂₁[CyD][Dpx]) (8)

The kinetics of complexation was found to occur in the fast-exchange regime¹¹ on the chemical shift ‘timescale’ at both 600 and 800 MHz. Under these circumstances, the chemical shift (δ^Dpx,i) of the ith carbon-bound measured in each titration point is the weighted average of those in the free Dpx δⁱ_Dpx and in the complexes δⁱ_Dpx·CyD and δⁱ_2Dpx·CyD,

where χ denotes molar fraction with respect to the total Dpx concentration. If CyD protons are also monitored during complex formation, similar relationships hold for the observed chemical shift of the jth CyD proton,where the χ molar fractions are normalized to the total CyD concentration.

Chemical shifts of the free components, δⁱ_Dpx and δ^j_CyD can easily be determined from the spectra of Dpx or CyD stock solutions. On the other hand, the chemical shifts specific for the complexes should be iteratively calculated together with the equilibrium constants via computer fitting of functions in eqn (9) and/or (10) to the experimental titration datasets.^13–16 While this curve-fitting is usually straightforward for the simplest 1 : 1 case, for higher stoichiometries it may be difficult or even impossible (no convergence), unless started from initial parameters sufficiently close to the true solution.^13,15 Strong mathematical correlation of spectral and equilibrium parameters was identified as the source of these difficulties,¹³ which can be circumvented by (i) measuring a large number of titration points and (ii) simultaneous fitting on the titration datasets of the maximum possible number of guest (and host) protons.^13,16 In the spirit of such a global analysis, input data of our multivariate data evaluation included the total concentrations c_Dpx and c_CyD for each titration point, known chemical shifts of the free components and the observed chemical shifts of the Dpx and CyD protons most responsive to complexation-induced chemical shift changes (CICS or Δδ). The OPIUM computer program (M. Kyvala, Ivan Lukes, 1995; available from: http://www.natur.cuni.cz/%7Ekyvala/opium.html) was used to perform the least-squares fitting of the model equations like eqn (9) and (10) to the datasets in order to determine equilibrium constants as common parameters as well as the complex-specific chemical shifts for each nucleus involved in the calculation. Several stoichiometric models (1 : 1, 2 : 1, 1 : 2 etc.) were tested and besides the chemometric criteria also chemical considerations were used the select the most appropriate equilibrium model (see below). From the resulting complex stability constants, the Hyss program¹⁷ was employed to generate the species distribution plots and the fitted NMR titration curves were generated in Microsoft Excel.

NOE type experiments. The average extent of penetration and the direction of inclusion were investigated by nuclear Overhauser effect (NOE) type experiments on two samples: 1.5 mM β-CyD/1.5 mM Dpx and 2.1 mM γ-CyD/0.9 mM Dpx, both in acidic (40 mM CD₃COOD) D₂O solution. NOE is a manifestation of cross relaxation between two nonequivalent nuclear spins that are close enough (<5 Å) through space, its intensities being scaled with r⁻⁶, where r represents the mean distance between the protons.^12,18 Since the tumbling rate of CyD complexes (characterized by the τ_c correlation time) at 600 MHz measurement frequency (ω₀) render NOEs very small or zero (ω₀ × τ ≈ 1), hence difficult to detect, NOE cross peaks were observed in the rotating frame, where ω₀ × τ < 1 always holds true. 2D ROESY spectra with 512 increments were recorded using a mixing time of 300 ms during a spin-lock of 2.2 kHz.

To discern the overlapping NOE signals recorded at 600 MHz, selective 1D NOESY measurements were run on the same samples using the 800 MHz Varian NMR System spectrometer of Gedeon Richter Plc., equipped with a salt-tolerant ¹H{¹³C/¹⁵N} cryoprobe. At this higher frequency, NOEs were observed in the negative regime (ω₀ × τ > 1) and gave cleaner spectra than the corresponding 1D ROESYs. Selective inversion of each CyD proton signal was accomplished employing 50 Hz wide q3 pulses of ca. 72 ms duration. Since T₁ relaxation times became longer at 800 MHz, 1D NOESY spectra were recorded employing mixing times ranging from 400 to 900 ms. Similarly to previous observations,¹⁸ a consistent pattern of NOE enhancements could be observed within this range of mixing times, so the spectra with t_mix = 0.6 s (for β-CyD) and 0.9 s (for γ-CyD) yielding intense NOE peaks are presented and discussed below.

Circular dichroism (CD) and UV absorption spectroscopic measurements

CD and UV absorption spectra were acquired at 25 ± 0.2 °C on a JASCO J-715 spectropolarimeter equipped with a Peltier thermostat. All spectra were monitored in continuous scanning mode between 190 and 350 nm at a rate of 100 nm min⁻¹, with a step size of 0.2 nm, response time of 1 s, four accumulations, 1 nm bandwidth, using a 1 cm path-length quartz cuvette (Hellma, USA). UV absorption spectra were obtained by conversion of the high tension (HT) voltage applied to the photomultiplier tube into absorbance units. CD/UV curves of drug and drug–CyD samples were corrected by spectral contribution of blank aqueous solution.

CD/UV spectroscopic titrations of Dpx with β- and γ-CyD were performed by successive addition of CyD stock solutions (15 and 70 mM) to 1.8 mL aqueous sample of the drug (23 and 30 μM).

JASCO CD spectropolarimeters record CD data as ellipticity (‘Θ’) in units of millidegrees (mdeg). The quantity of ‘Θ’ was converted to molar circular dichroic absorption coefficient (Δε in M⁻¹ cm⁻¹) using the equation Δε = Θ/(33 982cl), where, ‘c’ is the molar concentration of the drug (mol L⁻¹), and ‘l’ is the optical pathlength expressed in cm.

Molecular modeling

All calculations were performed by the SYBYL 7.2 program (Tripos Inc., St. Louis, MO). The initial geometries of the CyDs were based on structures 3CGT and 1P2G in the Brookhaven Protein Database¹⁹ derived from the literature.^20,21 Initial optimization applied on the structures by MMFF94 force field²² with 8.0 Å cut-off distance for the non-bonded interactions, 0.7 hydrogen-bond scaling factor and distance dependent dielectric function (ε = 78.3), until 0.01 RMS gradient was reached with the BFGS algorithm. Molecular dynamic calculations were performed in NVT ensemble, T = 298 K (1.0 fs step increment and 5.0 fs snapshot interval, with 1000 fs total run length for the complexes and the CyDs, and 5000 fs for Dpx).

The resulting 201 structures within each guest orientation for each CyD, and the uncomplexed CyDs were re-optimized, as well as the 1001 generated conformers of the Dpx. According to the energy values of the optimized structures, the lowest energy ones were taken into account for the interaction energies. Structures are visualized by the UCSF Chimera²³ software, developed by the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco (supported by NIGMS P41-GM103311).

Results and discussion

Phase solubility studies

Phase solubility studies are widely used to evaluate the ability of CyDs to enhance the aqueous solubility of organic guest molecules. They also give access to the physicochemical parameters involved in complex formation,²⁴ listed in Table 1. The solubility of Dpx at pH 7.4 increases with the concentration of CyDs (see Fig. S1 in ESI†). For the comparison of solubility profiles with native and semisynthetic CyDs, the study was extended to RAMEG, which has a suitable cavity size and forms water soluble inclusion complexes in the studied concentration range. A_L-Type profile was obtained with RAMEG, while B_S-type profiles were observed in the case of native CyDs with Dpx. This could be attributed to the limited aqueous solubility of inclusion complexes of native CyDs with poorly soluble guests leading to their precipitation.²⁴ The slopes of the A_L-type graphs and the linear segment of B_S-type profiles were less than one, indicating the formation of 1 : 1 inclusion complexes and K₁₁ values were calculated (Table 2). β-CyD yielded the highest stability constant, followed by RAMEG and γ-CyD. Nevertheless, the K₁₁ values obtained from phase solubility profiles are generally apparent ones, combining several effects on the guest solubility like inclusion complexation, the possible self-association of poorly soluble guests, self-aggregation of CyD/guest complexes, as well as non-inclusion interaction or micelle formation.²⁴ For RAMEG, K₁₁ is averaged over the manifold of differently methylated CyD species.

Table 1 Summary of the phase solubility results of Dpx/CyD complexes (the estimated stability constants are listed separately in Table 2)

S0 (mg L^−1)	1.74
a The maximum concentration of Dpx in the presence of highest concentration of CyDs studied herein.
CyD	β-CyD	γ-CyD	RAMEG
St^a/S0	6.32	5.13	30.48
CE	0.0050	0.0024	0.0034
Molar ratio	1 : 199	1 : 419	1 : 296
Increase in form. bulk	740	1778	1422

---

Table 2 Equilibrium association constants [in M⁻¹, defined by eqn (1) and (6)] of Dpx/CyD complexes, obtained in aqueous solution at 25 °C by different methods

Complex		Equilibrium constant, measured by
		Phase solubility	^1H NMR	UV	CD
Dpx·β-CyD	K11	886	915	—	—
2Dpx·β-CyD	K21	—	276	—	—
Dpx·γ-CyD	K11	420	661	515	595
2Dpx·γ-CyD	K21	—	447	—	—
Dpx·RAMEG	K11	594	—	—	—

---

NMR spectroscopy

The ¹H NMR spectrum and the chemical shift assignment of free Dpx in a slightly acidic solution are given in Fig. S2.†

Complex formation with γ-CyD. The ¹H NMR study of the Dpx/γ-CyD interaction was commenced by determining the stoichiometry of association. In Fig. 2, maxima of the Job's plot curves for Dpx are located either near x_Dpx = 0.5 (for H3′ and H15) pointing to 1 : 1 stoichiometry or near x_Dpx = 0.67 (for H1) suggesting the formation of a 2Dpx·CyD complex, or in between these limiting values (H12 and H13). These intriguing profiles of chemical shift displacements may be rationalized by assuming a model with two coexistent complex species: {Dpx·CyD, 2Dpx·CyD}. This hypothesis is corroborated by the complementary Job's plots of the CyD protons, showing extrema in the interval 0.33 < x_CyD < 0.50.

Fig. 2 Job's plots for selected protons of Dpx (A) and γ-CyD (B).

The behaviour of aromatic Dpx signals upon the titration with γ-CyD is depicted in Fig. S3.† In order to obtain reliable and unbiased association constants, the chemical shifts of H3, H2, H2′, H6, H7, H12, H13, H14, H15 of Dpx and H3′ of γ-CyD were recorded and involved in the multivariate evaluation. The remaining protons of both molecules gave either overlapping signals or non-monotonic titration curves (vide infra) or proved to be almost insensitive to complexation.

The experimental titration curve of the most sensitive Dpx nucleus, H12 is shown in Fig. 3 as a representative example. Obviously, this dataset could poorly be fitted by assuming either the formation of a single Dpx·CyD or a single 2Dpx·CyD complex. On the other hand, employing the two-species {Dpx·CyD, 2Dpx·CyD} model suggested by Job's plots leads to almost perfect fitting of the experimental dataset (for results including goodness-of-fit indicators, see Table S2†).

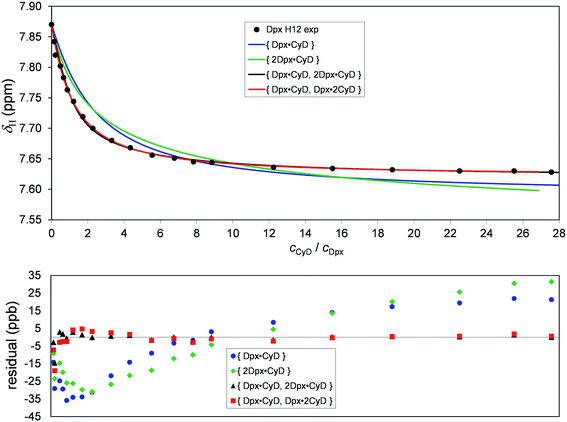Fig. 3 Chemical shift profile of Dpx H12 upon titration with γ-CyD. Four equilibrium models fitted with the OPIUM program are shown in solid curves and the corresponding residuals are shown below.

There are literature examples of guest·2CyD complexes, where sterically distant hydrophobic moieties of guest are encapsulated by two separate hosts.²⁵ Since Dpx has two aromatic rings separated by a ‘spacer’, it seemed interesting to try fitting the {Dpx·2CyD} or the {Dpx·CyD, Dpx·2CyD} models, although they are unsupported by the Job's plots. While the former one gave an unsatisfactory representation of the experimental data, the hypothetic {Dpx·CyD, Dpx·2CyD} model yielded a surprisingly good fitting, with only slightly worsened chemometric indicators (see Table S1†). The same ranking of equilibrium models can be concluded visually from the titration curves of the simultaneously fitted Dpx H1, H3, H3′, H13, H15 and CyD H3′ protons (see Fig. S4–S15†). On the other hand, the aforementioned four equilibrium models provided almost equally good fits for the titration datasets of H2, H2′, H6, H7, H8 and H14 of Dpx, so the model selection would have been much less reliable by observing only these protons during titration. These findings are in line with the notion of previous publications^13,15 that equilibrium evaluation programs cannot be used as ‘black box’, since (almost) equally good fitting of titration data may also be achieved by a chemically unrealistic model.

It is unique (but not unprecedented^14,26–29) that a single γ-CyD host associates with two guest molecules, so the following arguments are presented in support of this unusual stoichiometry.

(i) Although the single-species {Dpx·CyD} or {2Dpx·CyD} models failed to describe most of the experimental titration profiles, the resulting K₁₁ and K₂₁ equilibrium constants are in good agreement with those emerging from the best two-species model (see Table S1†). In contrast, K₁₁ increases “mathematically” 6.5-fold upon ‘addition’ of a coexisting Dpx·2CyD complex, which seems to be structurally unrealistic (cf. propranolol³⁰).

(ii) The hitherto not discussed H9 exhibits a non-monotonic (“biphasic”) titration curve, which obviously cannot be fitted with a model assuming a single 1 : 1 complex (Fig. 4). The species distribution diagram calculated for the best equilibrium model shows that the 2Dpx·CyD complex reaches its peak concentration of 16% at c_CyD ≈ 2 mM, where the minimum of the H9 titration dataset is also located. Since this titration curve was omitted from the global analysis, its separate fitting session was performed with the K₁₁, K₂₁ values fixed and the adjustable parameters being only δ^H19_Dpx·CyD and δ^H19_2Dpx·CyD. A perfect fit was achieved, while the hypothetic {Dpx·CyD, Dpx·2CyD} model reproduces the minimum with a poorer goodness-of-fit.

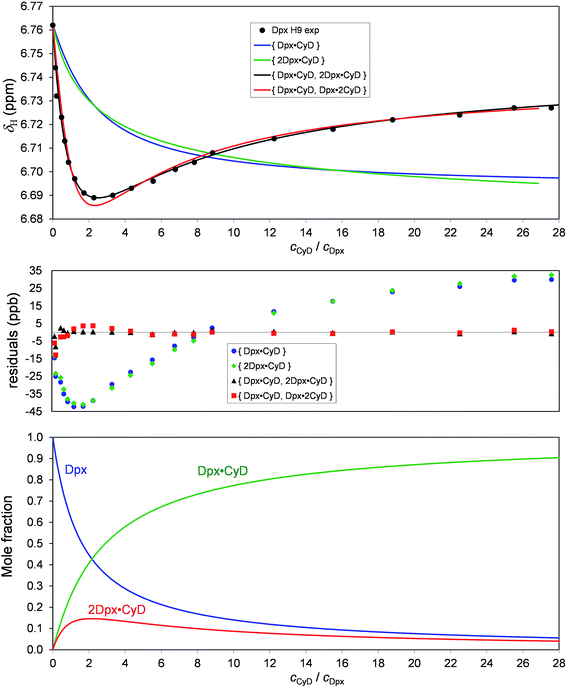Fig. 4 Chemical shift profile of Dpx H9 upon titration with γ-CyD, with fitting curves of four equilibrium models and the residuals. The corresponding species distribution is shown below.

Since the {Dpx·CyD, 2Dpx·CyD} model was substantiated as the most probable one, the corresponding equilibrium constants are listed in Table 2, while the chemical shift displacements of individual protons characteristic to the Dpx·CyD and 2Dpx·CyD complexes are summarized in Fig. S16.† These Δδⁱ values reflect changes in electron density during complex formation and the negative sign observed for the aromatic Dpx protons is consistent with the hypothesis that both aromatic rings are included in the cavity of γ-CyD. The H3, H5 and, to a lesser extent, H6 protons of CyD exhibit upfield complexation-induced shifts of twice to 20-fold magnitude as compared to Δδ of its remaining protons. This is attributed to the ring current effect and/or the hydrophobic effect of the included guest molecule.¹⁴ Nevertheless, Δδⁱ values merely report the change in electron density at the corresponding proton positions and thus not always represent a straightforward means to assess the geometry of the complexes formed, dipolar cross-relaxation (NOE) data provide a more reliable handle for that purpose.

In the 2D ROESY spectrum (Fig. S17†), the H3 and H5 protons residing in the cavity of γ-CyD show NOE cross-peaks with both the naphthyl and phenyl protons. The spectral region near 7.3 ppm was rather crowded at 600 MHz, so in order to observe the aromatic NOEs at a better resolution, selective 1D NOESY spectra were run at 800 MHz. Upon inversion of the H2, H4 or H6 protons of γ-CyD, no significant NOEs were observed on the Dpx protons (spectra not shown), rendering an outer-sphere, non-inclusion-type interaction²⁶ of at least one Dpx molecule improbable. On the other hand, protons from both aromatic rings of Dpx ‘responded’ to the inversion of H3 and H5 of γ-CyD (Fig. 5). A deeper insertion of the naphthyl ring from the secondary side of the CyD can be inferred from the NOEs in relation to that derived for the phenyl ring. One possible rationalization of the results is the simultaneous inclusion of both aromatic rings in the CyD cavity. But according to speciation calculations, 44% of all Dpx molecules were present as Dpx·CyD and 15% as 2Dpx·CyD complex in the sample used for the 1D NOESY measurements. The observed NOEs may thus well include a contribution from two isomeric 1 : 1 complexes, encapsulating either the naphthyl or the phenyl ring of Dpx.

Fig. 5 Aromatic region of the 800 MHz selective 1D NOESY spectra of 0.9 mM Dpx and 2.1 mM γ-CyD with 0.9 s mixing time. (A) H3 proton of CyD inverted; (B) H5 proton of CyD inverted; (C) the proposed topology of inclusion: in the complex Dpx·CyD, the macrocycle encapsulates either the naphthyl or the phenyl ring, whereas in 2Dpx·CyD two Dpx molecules reside in the cavity of the same host.

Complex formation with β-CyD. The Job's plots for most Dpx and β-CyD protons in Fig. 6 indicate that this system is closer to the simple 1 : 1 binding stoichiometry than the Dpx/γ-CyD system. Nonetheless, Job's plot profiles of H3, H9, H10 and H13 of Dpx do have their maxima shifted towards x_Dpx ≈ 0.6, suggesting a small contribution of a 2Dpx·CyD complex.

Fig. 6 Job's plots for selected protons of Dpx (A) and β-CyD (B).

From the separate ¹H NMR titration conducted for stability constant determination (Fig. S18†), chemical shifts of seven Dpx and five β-CyD protons measured at 19 host/guest ratios were subjected to multivariate analysis. Table S2† shows that the globally best fit was achieved by the {Dpx·CyD, 2Dpx·CyD} model, being again only marginally superior to the hypothetical {Dpx·CyD, Dpx·2CyD} one. Employing the single-species models {Dpx·CyD} and {2Dpx·CyD} yielded gradually worse fits, whereas the hypothetical {Dpx·2CyD} model was qualified to be inappropriate. Concerning the fitted datasets individually, the Dpx H1, H2′, H12 and H15 protons as well as H1 and H5 of CyD failed to differentiate between the equilibrium models, while titration profiles of the remaining protons were significantly better fitted by the two-species models (Fig. S19–S30†). The chemometric indicators revealed again merely a slight preference of the {Dpx·CyD, 2Dpx·CyD} model over {Dpx·CyD, Dpx·2CyD}. However, considering the Job's plot results the former stoichiometry was chosen as the most appropriate one. The resulting equilibrium constants are listed in Table 2, while the calculated species distribution is depicted in Fig. S31.†

There are literature examples on the cavity size-dependent stoichiometry of cyclodextrin complexes. Metoprolol formed a 2 : 1 complex with γ-CyD and a single 1 : 1 complex with β-CyD,¹⁴ while pheniramines were shown to produce a mixture of 2 : 1 and 1 : 1 complexes with carboxymethylated β-CyDs.²⁷

Since β-CyD has a smaller cavity size than γ-CyD, formation of a 2Dpx·β-CyD complex was a highly unpredictable outcome of our study. To explore its possible structure, the chemical shift displacement values concomitant with the formation of Dpx·CyD and 2Dpx·CyD complexes were inspected first (Fig. S32†). The greatest changes could be observed for the propyl protons, similarly to the γ-CyD case, while Δδ of the naphthyl protons were roughly the half of that found for the γ-CyD complexes. Unfortunately, the phenyl protons gave highly overlapped signals at 600 MHz near 7.4 ppm, so no information could be gained on their titration behaviour. From the ‘viewpoint’ of β-CyD, the complexation-induced upfield shifts were three times higher for the inner H3, H5 and for H6 located near the primary rim than that recorded for H4, indicating the inclusion of hydrophobic part(s) of Dpx into the cavity.

To obtain further, atomic-level information on the inclusion geometry, NOE experiments were also carried out. The 2D ROESY spectrum in Fig. S33† reveals that only the inner H3, H5 (and slightly H6) protons of β-CyD give intermolecular contacts with the aromatic protons of Dpx, confirming the inclusion of its naphthyl ring. The crowded spectrum region between 7.3 and 7.5 ppm does not enable to draw a firm conclusion about inclusion of the phenyl ring. With the better resolution of the selective 1D NOESY spectra at 800 MHz (Fig. 7), a weak NOE between H6 of Dpx and H3 of CyD could be detected. Deep immersion of the naphthyl ring into CyD cavity is nicely reflected by stronger NOEs of CyD H5 with Dpx H12, H13, H14 and H15, while CyD H3 gives stronger NOEs with H11 or H10 of the O-substituted part of the naphthyl ring. According to our speciation calculations, 37% of all Dpx molecules was present as Dpx·CyD and only 15% as 2Dpx·CyD complex in the NMR sample used in the NOE measurement. Thus, the same cautionary comments hold true regarding the possible encapsulation of both aromatic rings as discussed for γ-CyD. Finally, none of our NOE experiments revealed dipolar correlations between β-CyD and the aliphatic protons of Dpx.

Fig. 7 Aromatic region of the 800 MHz selective 1D NOESY spectra of 1.5 mM Dpx and 1.5 mM β-CyD with 0.6 s mixing time. (A) H3 proton of CyD inverted; (B) H5 proton of CyD inverted; (C) the proposed topology of inclusion: in the complex Dpx·CyD, the macrocycle encapsulates either the naphthyl or the phenyl ring, whereas in 2Dpx·CyD two Dpx molecules reside in the cavity of the same CyD molecule.

Circular dichroism and UV absorption spectroscopy

UV and CD spectroscopic properties of Dpx. The UV absorption curve of Dpx is dominated by the π–π* transitions of the naphthalene moiety (Fig. 8). The two overlapping long-wavelength bands above 250 nm can be assigned to the symmetry-forbidden ¹L_b and ¹L_a transitions, respectively. The lowest-energy peak around 320 nm is allied to the ¹L_b while the broader band centered at 291 nm to the ¹L_a transition. In analogy with the results obtained for α-naphthol, the respective transition dipole moments are polarized along the short (¹L_a) and the long axis (¹L_b) of the naphthalene ring.^31,32

Fig. 8 CD and UV absorption spectrum of Dpx measured at 25 °C in aqueous solution (pH ∼ 4). Corresponding symmetry designations of the π–π* excitations are shown. Inset: Δε_max values of α- and β-substituted chiral naphthalene derivatives reported in the literature. From top to bottom: (S)-naproxen,³⁹ (R)-2,2-dimethyl-3α-naphthylbutane,⁴⁰ (S)-4-dimethylamino-2-(naphthalen-2-yl)-butan-2-ol,⁴¹ (S)-4-dimethylamino-2-(6-methoxynaph-thalen-2-yl)-butan-2-ol.⁴¹

In contrast to these weak bands, a much more intense absorption peak can be observed on the short-wavelength side of the spectrum (λ_max at 211 nm) flanked by a shoulder around 230 nm (Fig. 8). Such a shoulder or a resolved absorption maximum is characteristic to naphthalene derivatives bearing an electron-donating group at the α-position,^33,34 and it is not the vibronic sub-band of the ¹B_b peak but belongs to a separate π–π* excitation (¹A_g) as it was clearly demonstrated by its distinct solvent dependent shift.³⁵ Both transitions are electronic dipole allowed and polarized along the long axis of the naphthalene nucleus.^31,33 It is to be noted that the contribution of the phenyl ring to the UV spectrum of Dpx is negligible due to its dipole forbidden, low-intensity ¹L_b and ¹L_a transitions.³⁶

The shape as well as spectral position of the CD bands of free Dpx resemble to that of the UV curve (Fig. 8). Asymmetric perturbation of the ¹L_b and ¹L_a transitions can be accounted for by the weak, positive signal displayed between 250 and 330 nm. In the spectral region of the higher-energy transitions, a positive peak (¹B_b, λ_max at 216 nm) and a partially resolved band of the same sign can be seen (λ_max ≈ 233 nm). Noticeably, the molar circular dichroic absorption coefficient (Δε_max) of the 216 nm signal is comparable or even higher than that was reported for naproxen³⁷ and other naphthalene derivatives possessing a chiral center attached directly to the ring at α- or β-position^38,39 (Fig. 8). In stark contrast to these compounds, the asymmetric carbon atom in Dpx is separated by four single bonds from the naphthyl unit. At the first sight, it seems that this side-chain can adopt various conformations, the different chiroptical contributions of which should largely cancel each other giving rise to a much smaller Δε_max value. Contrary to this, the relatively intense ¹B_b CD signal suggests the prevalence of some conformational species having decisive contribution to the net rotatory strength.

UV and CD spectroscopic studies of the interaction of Dpx with β- and γ-CyD. In order to elucidate the Dpx/CyD interactions, CD/UV spectroscopic titrations were conducted by adding concentrated stock solution of γ- or β-CyD into the aqueous solution of Dpx. Upon consecutive increase of the γ-CyD concentration, the ε_max value at 211 nm exhibited a gradual reduction (Fig. 9). In parallel with the developing hypochromism, the lower-energy shoulder was gradually red shifted and finally displayed as a resolved peak with a λ_max around 232 nm. The spectral position of the most intense UV band at 211 nm remained invariant during the titration procedure. The absorbance spectra exhibited an isosbestic point at 233 nm indicating an equilibrium between free and CyD-bound drug species (Fig. 9). β-CyD provoked similar, but less pronounced absorption spectroscopic changes (Fig. S34†). In relation to γ-CyD, substantially weaker hypochromism was obtained with β-CyD (the decrease of ε_max is 2500 vs. 4200 M⁻¹ cm⁻¹).

Fig. 9 Changes of the CD and UV absorption spectrum of 30 μM Dpx measured upon sequential addition of γ-CyD into the sample solution (pH ∼ 4).

As UV spectroscopic data reported for naphthols and naphthylamines had shown,^34,40 introduction of an electron-donating group at α-position results in the splitting of the ¹B_b band of the parent naphthalene molecule into two components, assigned to a lower energy ¹A_g and a higher-energy ¹B_b state, respectively.^31,41 This can be ascribed to the interaction of non-bonding electrons of the substituent with the π-system of the aromatic nucleus by mixing intramolecular charge-transfer character to the locally excited states. Hydrogen-bonding, however, considerably decreases the electron donating ability of the substituent shifting the ¹A_g band to lower wavelengths.³⁵ Due to intermolecular H-bonds between the alkoxy group and water molecules, this band can only be observed as a shoulder in the spectrum of free Dpx measured in aqueous solution (Fig. 8). In aprotic solvents, however, such as dioxane or acetonitrile it exhibits a large bathochromic shift and appears as a well resolved peak (Fig. S35†). Analogously, the red shift obtained in the presence of CyDs is the diagnostic sign for the incorporation of the alkoxy substituted naphthyl moiety of Dpx into the aprotic environment of the CyD cavity.

Taken collectively, all of the above spectroscopic changes attest the formation of Dpx–CyD inclusion complexes. The UV hypochromism, however, suggests one host-two guests interaction, corroborating our NMR titration results. The spatial proximity of the naphthyl–naphthyl or naphthyl–phenyl rings of drug molecules associated to the same macrocycle favours dipole–dipole coupling between the π–π* transition moments which may result in hypo- or hyperchromic effect in the respective absorption band depending on the relative intermolecular disposition of the chromophores.^42,43 Reversal and cancellation of the hyperchromism obtained at very high molar excess of γ-CyD lends further credence to the 1 : 2 host : guest stoichiometry. As shown in Fig. 10, above the CyD concentration of 5 mM the ε_max value begins to rise and at the end of the titration it approximately reaches its starting level. This can be explained by the dissociation of the 1 : 2 complexes with the concomitant increase of the 1 : 1 species showing a UV profile similar to the free drug molecules. It is worth to mention that ¹³C NMR spectroscopic results also demonstrated the 1 : 2 binding of (±)-naproxen to γ-CyD.⁴⁴ Interestingly, absorption spectrum of the β-blocker (±)-propranolol having a Dpx related α-substituted naphthyl moiety did not show any appreciable changes either in the presence of β- or γ-CyD (data not shown). This finding refers to the role of the phenyl ring of Dpx in the stabilization of the 1 : 2 inclusion form.

Fig. 10 CD and UV absorption changes plotted against the γ-CyD concentration of the sample of 30 μM Dpx. Δε: molar circular dichroic absorption coefficient of the drug. ε₀: molar absorption coefficient of Dpx in CyD-free solution. ε_i: ε values calculated at increasing concentrations of γ-CyD. Solid lines were obtained by non-linear curve fitting analysis for “one site – total and nonspecific binding” using the Prism 6 software. Estimated values of dissociation constants (K_d) are shown.

Owing to their asymmetric cavity, CyDs may induce CD signals in the absorption region of entrapped achiral guest molecules^45–47 or modify the intrinsic CD profile of chiral analytes.^48,49 Dpx represents the latter case showing the gradual development of a resolved positive CD band at 239 nm allied to the red shifted ¹A_g transition (Fig. 9). Besides the absorption spectroscopic changes, it is the additional sign of drug-CyD binding and as such, it can be used to estimate the stability constant (Fig. 10). The K_d values calculated from the CD and UV spectroscopic data are in a good correlation with each other and also with that obtained from phase solubility and NMR experiments (Table 2). Importantly, in contrast to the UV data points Δε values of the new CD feature showed no decline during the titration (Fig. 10). This renders the drug–drug intermolecular chiral exciton coupling mechanism^47,50,51 for the 239 nm CD peak unlikely since in that case, the CD amplitudes should decrease with dissociation of the 1 : 2 complexes. For instance, an intermolecular sandwich type dimer of naphthyl–naphthyl or naphthyl–phenyl rings of two Dpx molecules included in the same CyD pore but lacking internal twisting gives rise to no exciton CD signals.⁴⁷ The conventional saturation binding profile of the CD data implies that a particular chiral species persists through the whole titration which is responsible for the induced CD band. It is reasonable to consider the asymmetric perturbation of a naphthyl moiety engulfed within the CyD cavity both in the 1 : 2 and 1 : 1 complexes. Taking into account the positive sign of the resolved ¹A_g dichroic peak (Fig. 9), the sector rule of Kajtár⁴⁶ proposes the axial penetration of the naphthyl moiety into the hydrophobic CyD cavity, so its long-axis polarized π–π* transition moments are parallel to the symmetry axis of the host. Noticeably, transferring of Dpx from the bulk aqueous solution into aprotic solvents simulates the UV but not the CD spectroscopic changes (Fig. S35†). The red shift as well as the intensification of the ¹A_g CD band occur only upon interaction with the chiral layer of γ-CyD. It is worth to mention that the conformation of Dpx embedded within the cavity may allow intramolecular chiral exciton coupling between high-energy transitions of the naphthyl and phenyl ring which can also contribute the observed CD spectroscopic changes.

It seems that the smaller pocket of β-CyD alters profoundly the binding mode of Dpx molecules. Albeit the weak hypochromism also suggests the presence of 1 : 2 complexes, the λ_max value of the ¹B_b CD peak exhibits a blue shift and the Δε_max of the red shifted ¹A_g CD band lags behind that was found with γ-CyD (Fig. S34†). The vibrational fine structure displayed between 220 and 240 nm on the CD curves may be the consequence of the tight, sterically restricted fit of the naphthalene ring in the pore of β-CyD. It may happen that the larger portion of the second Dpx molecule in the 1 : 2 complexes may lie around the entrance of the cavity exposed to the bulk water phase.

Molecular modeling

Energies. The interaction energies (Table 3) are the differences between the energies of the complexes and the sum of the energy of the host and the guest (the latter one is multiplied with the number of the guest molecules involved):

E(interaction) = E(complex) − [E(CyD) + E(Dpx)] (1 : 1 complexes)

E(interaction) = E(complex) − [E(CyD) + 2E(Dpx)] (1 : 2 complexes)

Table 3 Calculated interaction energies in various Dpx/CyD complexes

CyD : Dpx included moiety^a	1 : 2 (nap, nap)	1 : 2 (phe, nap)	1 : 2 (phe, phe)	1 : 1 (nap)	1 : 1 (phe)
a nap: naphthalene, phe: phenyl ring of Dpx included into the cavity.
β-CyD	−18.6441	−22.8121	−16.6543	−17.4424	−16.4024
γ-CyD	−24.6823	−20.9274	−18.6062	−17.0864	−12.5464

---

The results show the preference of the embedding of the naphthyl moiety into the apolar cavity of the host molecules in the 1 : 1 complexes, as well as the tendencies for the 1 : 2 complexes involving at least one naphthalene ring in the host–guest interactions. In the case of the γ-CyD, there is more space within the cavity, therefore the entrapment of both naphthyl groups is favourable. It is obvious however, that the energy gain of the complex formation is larger in the first step than in the second one, witnessed by the pair-wise comparison of the complex interaction energies of the 1 : 1 complexes and the differences between the 1 : 1 and 1 : 2 complex interaction energies.

Structures. In the 1 : 1 complex with the β-CyD (Fig. 11), the naphthyl ring is preferentially embedded in the cavity, and the same occurs with the γ-CyD.

Fig. 11 Molecular model of the lowest-energy structure of the Dpx β-CyD complex.

In the 2Dpx·γ-CyD complex with the naphthyl moieties of both Dpx guests in the cavity (Fig. 12), the two aromatic rings are arranged nearly parallel, the average distance between them being ca. 4 Å. The same tendency is present in the corresponding β-CyD complex, but only one of the naphthyl moieties fits firmly in the cavity, the other one resides partly outside.

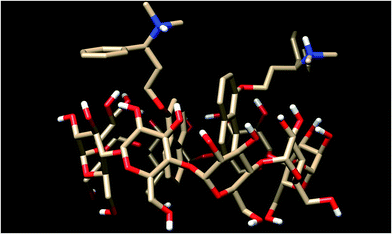Fig. 12 Optimized structure for the 2Dpx·γ-CyD complex obtained by molecular modeling, with two naphthyl rings within the cavity.

If one Dpx molecule has its naphthalene ring embedded in the cavity of the γ-CyD (Fig. 13), while a second one has the benzene ring embedded, a less tight fit is obtained. The same applies to the corresponding complex of the β-CyD, but the phenyl moiety resides here mainly outside from the cavity.

Fig. 13 Optimized structure for the 2Dpx·γ-CyD complex by molecular modeling, with different aromatic rings in the cavity.

Conclusions

An important finding of the current study is that the large inner void of γ-CyD can accommodate the aromatic rings of two protonated Dpx molecules. Intermolecular NOEs were detected with ring protons of both the phenyl and naphthyl rings. In-depth analysis of the UV titration profile also emphasized the importance of inclusion of the naphthyl unit and this ‘mixed’ binding mode was identified as the energetically most favoured one by molecular dynamics calculations. Besides this major mode of interaction, however, an ensemble of complexes with less populated geometries may be present in dynamic equilibrium. Moreover, our speciation calculations show that the most abundant species in all investigated solutions is the Dpx·CyD complex, with mainly the naphthyl group engulfed in the CyD cavity, as witnessed by the NOEs and complexation-induced shifts of its protons, the usual saturation profile of the CD titration curve and corroborated by molecular modeling. β-Cyclodextrin forms a more stable 1 : 1 complex with Dpx. The naphthyl ring is preferentially inserted, its sterically restricted fitting in the smaller cavity is supported by NOEs and the CD/UV titration results and confirmed by molecular modeling. Surprisingly, ¹H NMR-based Job's plots and titrations curves undoubtedly prove the simultaneous formation of a 2Dpx·CyD complex, albeit its impact on NOEs and CD/UV data is less significant than in the γ-CyD case. Here again, the superposition of several geometries can be suspected, with the dominant inclusion of the naphthyl ring of Dpx.

The third principal finding of our study is related to the evaluation of NMR titration curves. In accordance with previous notions,^13,16 the reliable and unbiased calculation of equilibrium constants for stoichiometric models beyond the simple 1 : 1 case is feasible only by considering the titration datasets of the maximum possible number of ‘reporter’ nuclei of both the guest and host molecules. Even performing the multivariate regression in this spirit, we were surprised to experience that the hypothetic {Dpx·CyD, Dpx·2CyD} model yielded almost the same perfect quality of fit as the best {Dpx·CyD, 2Dpx·CyD} model, with only marginal preference of the latter in terms of goodness-of-fit criteria and the distribution of the residuals. Thus, using evaluation programs as ‘black box’ and relying only on chemometric criteria is discouraged, independent experimental proofs should be considered by selecting the true equilibrium model. In our case, Job's method of continuous variation and the careful analysis of CD/UV titrations proved unequivocally that the co-existing complex has the formula 2Dpx·CyD instead of Dpx·2CyD.

Acknowledgements

The financial support from OTKA PD 109373 is highly appreciated and the authors are grateful to Cyclolab Ltd. for the generous support of cyclodextrins. The authors are indebted to Prof. Csaba Szántay, Head of Spectroscopic Research Department and Dr István Greiner, the Research Director of Gedeon Richter Plc. for supporting this study.

References

1. A. M. Feige, M. R. Pinsky and W. J. G. Hellstrom, Clin. Pharmacol. Ther., 2011, 89, 125–128.
2. T. Lofttson and M. E. Brewster, J. Pharm. Sci., 1996, 85, 1017–1025.
3. K. Uekama, Chem. Pharm. Bull., 2004, 52, 900–915.
4. J. Szejtli, Chem. Rev., 1998, 98, 1743–1754.
5. K. A. Connors, Chem. Rev., 1997, 97, 1325–1358.
6. G. Neumajer, T. Sohajda, A. Darcsi, G. Tóth, L. Szente, B. Noszál and S. Béni, J. Pharm. Biomed. Anal., 2012, 62, 42–47.
7. G. Benkovics, I. Fejős, A. Darcsi, E. Varga, M. Malanga, É. Fenyvesi, T. Sohajda, L. Szente, S. Béni and J. Szemán, J. Chromatogr. A, 2016, 1467, 445–453.
8. A. Darcsi, G. Tóth, J. Kökösi and S. Béni, J. Pharm. Biomed. Anal., 2014, 96, 272–277.
9. T. Higuchi and K. A. Connors, Adv. Anal. Chem. Instrum., 1965, 4, 117–212.
10. P. Job, Ann. Chim., 1928, 9, 113–203.
11. L. Fielding, Tetrahedron, 2000, 56, 6151–6170.
12. H. J. Schneider, F. Hacket, V. Rudiger and H. Ikeda, Chem. Rev., 1998, 98, 1755–1786.
13. W. Al-Soufi, P. R. Cabrer, A. Jover, R. M. Budal and J. V. Tato, Steroids, 2003, 68, 43–53.
14. Y. Ikeda, F. Hirayama, H. Arima, K. Uekama, Y. Yoshitake and K. Harano, J. Pharm. Sci., 2004, 93, 1659–1671.
15. H. Dodziuk, K. S. Nowinski, W. Kozminski and G. Dolgonos, Org. Biomol. Chem., 2003, 1, 581–584.
16. G. Székely, B. Csordás, V. Farkas, J. Kupai, P. Pogány, Z. Sánta, Z. Szakács, T. Tóth, M. Hollósi, J. Nyitrai and P. Huszthy, Eur. J. Org. Chem., 2012, 3396–3407.
17. L. Alderighi, P. Gans, A. Ienco, D. Peters, A. Sabatini and A. Vacca, Coord. Chem. Rev., 1999, 184, 311–318.
18. C. R. Jones, C. P. Butts and J. N. Harvey, Beilstein J. Org. Chem., 2011, 7, 145–150.
19. H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242.
20. A. K. Schmidt, S. Cottaz, H. Driguez and G. E. Schulz, Biochemistry, 1998, 37, 5909–5915.
21. N. Pinotsis, D. D. Leonidas, E. D. Chrysina, N. G. Oikonomakos and I. M. Mavridis, Protein Sci., 2003, 12, 1914–1924.
22. T. A. Halgren, J. Comput. Chem., 1999, 20, 730–748.
23. E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612.
24. T. Loftsson, D. Hreinsdóttir and M. Másson, J. Inclusion Phenom. Macrocyclic Chem., 2007, 57, 545–552.
25. A. Jover, R. M. Budal, W. Al-Soufi, F. Meijide, J. Vázquez Tato and R. A. Yunes, Steroids, 2003, 68, 55–64.
26. A. Hazekamp and R. Verpoorte, Eur. J. Pharm. Sci., 2006, 29, 340–347.
27. C. F. Dignam, L. A. Randall, R. D. Blacken, P. R. Cunningham, S.-K. G. Lester, M. J. Brown, S. C. French, S. E. Aniagyei and T. J. Wenzel, Tetrahedron: Asymmetry, 2006, 17, 1199–1208.
28. T. Uyar, A. El-Shafei, X. Wang, J. Hacaloglu and A. E. Tonelli, J. Inclusion Phenom. Macrocyclic Chem., 2006, 55, 109–121.
29. K. Higashi, Y. Tozuka, K. Moribe and K. Yamamoto, J. Pharm. Sci., 2010, 99, 4192–4200.
30. G. Castronuovo and M. Niccoli, Bioorg. Med. Chem., 2006, 14, 3883–3887.
31. S. Suzuki, T. Fujii and H. Baba, J. Mol. Spectrosc., 1973, 47, 243–251.
32. Y. Tanizaki and S. Kubodera, J. Mol. Spectrosc., 1967, 24, 1–18.
33. M. R. Whipple, M. Vasak and J. Michl, J. Am. Chem. Soc., 1978, 100, 6844–6852.
34. H. G. de Laszlo, Proc. R. Soc. London, Ser. A, 1926, 111, 355–379.
35. H. Baba and S. Suzuki, J. Chem. Phys., 1961, 35, 1118–1127.
36. W. C. Johnson, L. P. Fontana and H. E. Smith, J. Am. Chem. Soc., 1987, 109, 3361–3366.
37. S. Wenzel and V. Buss, J. Phys. Org. Chem., 1992, 5, 748–754.
38. P. Salvadori, O. Piccolo, C. Bertucci, R. Menicagli and L. Lardicci, J. Am. Chem. Soc., 1980, 102, 6859–6860.
39. O. Azzolina, S. Collina, G. Brusotti, D. Rossi, A. Callegari, L. Linati, A. Barbieri and V. Ghislandi, Tetrahedron: Asymmetry, 2002, 13, 1073–1081.
40. H. Baba and S. Suzuki, Bull. Chem. Soc. Jpn., 1961, 34, 82–88.
41. S. Suzuki and T. Fujii, J. Mol. Spectrosc., 1976, 61, 350–359.
42. M. Weissbluth, Q. Rev. Biophys., 1971, 4, 1–34.
43. I. Leray, J.-P. Lefevre, J.-F. Delouis, J. Delaire and B. Valeur, Chem.–Eur. J., 2001, 7, 4590–4598.
44. G. Bettinetti, F. Melani, P. Mura, R. Monnanni and F. Giordano, J. Pharm. Sci., 1991, 80, 1162–1170.
45. K. Kano, M. Tatsumi and S. Hashimoto, J. Org. Chem., 1991, 56, 6579–6585.
46. M. Kajtár, C. Horváth-Toró, É. Kuthi and J. Szejtli, Acta Chim. Acad. Sci. Hung., 1982, 110, 327–355.
47. S. Wenzel, T. Brinschwitz, F. Lenzmann and V. Buss, J. Inclusion Phenom. Mol. Recognit. Chem., 1995, 22, 277–284.
48. Á. Stadler-Szöke, M. Vikmon, J. Szejtli and M. Kajtár, J. Inclusion Phenom., 1985, 3, 71–84.
49. J. H. Shi and Y. F. Zhou, Spectrochim. Acta, Part A, 2011, 83, 570–574.
50. V. Buss, Angew. Chem., Int. Ed. Engl., 1991, 30, 869–870.
51. N. Yoshida, H. Yamaguchi, T. Iwao and M. Higashi, J. Chem. Soc., Perkin Trans. 2, 1999, 379–386.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra22431h

---