Effect of 7S/11S ratio on the network structure of heat-induced soy protein gels: a study of probe release

Abstract

The release behavior of poly(ethylene glycol) (PEG) with different molecular weights (M_w): 6000, 20 000, 100 000 and 400 000 g mol⁻¹ from heat-induced soy protein gels as a function of the 7S/11S protein ratio was investigated. Results showed that time-related release of PEG from gel network fit the Fick's second law. PEG diffusion coefficients depended on the PEG size and gel network structure, which increased with increasing 11S ratio in gel or decreasing probe molecular weight. Moreover, the diffusion of PEG with higher molecular weight was more sensitive to the variations of gel internal network. The changes of PEG diffusion coefficients in soy protein gel were consistent with the variations of gel structure characterized by scanning electron microscopy (SEM). Gels formed at lower 11S ratio were composed of homogeneous spherical aggregates structure, while gels formed at higher 11S ratio showed higher extent of macro-phase separation and coarser network with larger pores.

---

1. Introduction

Soy proteins have been widely applied in food products, due to their highly nutritive value and ability to improve texture. The gelation ability is the basis for traditional Asian soy products, such as tofu.^1–6 Soy protein consists of two major components β-conglycinin (7S), and glycinin (11S), both of which are responsible for gelling property. The 7S fraction contains three subunits namely: α′, α and β with molecular weights of 71 kDa, 67 kDa and 50 kDa, which are associated in various combinations through non-covalent interaction, particularly hydrophobic interaction. The 11S fraction is a hexamer of six subunits of acidic A polypeptides (37–42 kDa) and basic B polypeptides (17–20 kDa) dimers linked by disulfide bond. Heating treatment would cause irreversible disruption of the quaternary of β-conglycinin and glycinin globulins, and subsequent dissociation into subunits (a few nm). These subunits interact each other by hydrophobic bond or disulfide linkage to form short strands (a dozen nm), and the strands associate with itself to form longer straight or branched strands (tens of nm).⁷ Finally, a gel network can be formed form these strands units above a critical protein concentration.

The effect of 7S/11S ratio on textural properties of soy protein gels has been extensively studied. Ji et al.⁸ found that higher 11S ratio resulted in lower yield but higher firmness and cohesiveness of tofu. Heat-set soy protein gels prepared above 93 °C for 30 min with a high 11S ratio (2.41) were firmer than those of a low 11S ratio (0.88).⁹ Renkema et al.¹⁰ reported that at the same pH and protein concentration, glycinin gels were stiffer and fractured at higher strain than β-conglycinin gels. Nakamura et al.¹¹ also observed that 11S formed a harder gel than 7S when heated at 100 °C, pH 7.6, and ionic strength of 0.5 M. It was concluded that 11S fraction mainly determined the mechanical property of soy protein gels.¹² In present study, the structural differences among the heat-induced soy gels with varying 7S/11S ratios were investigated from the point of view of probe release.

Gels can be used as vehicles for delivering nutrients or drugs, and understanding the solutes release behavior from gels has received increased attention in recent years.^13–16 In gels and in other porous media, the pore diameter, interfiber space and other microstructure dimensions influence the diffusion of probe. On the other way round, diffusion data can aid interpretation of the structural change in gel. The probe adopted for studying release behavior out of gel is PEG. PEG had been used to detect the structural change of heat-induced protein gels by pulsed field gradient nuclear magnetic resonance (PFG-NMR). Several researchers^17–22 found that PEG diffusion coefficients in casein gel decreased with increasing protein concentration and probe size, moreover, the diffusion coefficients of larger PEG increased after coagulation of casein gel. Colsenet et al.^23,24 studied PEG self-diffusion as a function of NaCl concentration, denaturation time and protein concentration in whey protein gel, and reported that PEG diffusion coefficients decreased with increasing NaCl or protein concentration but increased along with denaturation time. One of the main conclusion of these works was that the structure of gels could be researched by determining the self-diffusion of PEG by PEG-NMR. In already equilibrated system such as protein solution and gel, there is no volume variation and mass transfer. Nevertheless, the molecules are in motion and diffusion occurs without the presence of a concentration gradient. In such circumstance, the diffusion is defined as self-diffusion.²⁵ In the present study, the diffusion of PEG is induced by the space gradient concentration between the gel and buffer, and little is currently known on the correlation between the microstructural change of gel and the probe release kinetic.

This study was a continuation of the precious research, while in this work PEG were used as probes instead of non-network proteins. A key advantage was obtained: a wide range of molecular weight. The correlation between release behavior of PEG and structural change in heat-induced soy gel, particularly the influence of probe size and 11S ratio was investigated. The diffusion coefficients of PEG with different molecular weights were determined according to the Fick's second law. SEM was applied to confirm the results in diffusion procedure.

2. Materials and methods

2.1. Materials

Preparation of soy 7S-rich and 11S-rich proteins. Low-temperature defatted soy flakes were supplied by Shandong Wonderful Industrial and Commercial Co. Ltd. 7S-Rich and 11S-rich fractions were separated from flakes as described by Nagano et al.²⁶ The protein contents, determined by the micro-Kjeldahl method, are 92.48 ± 0.19 and 98.11 ± 0.31 for 7S-rich and 11S-rich proteins, respectively. The protein compositions of the proteins were analyzed by reducing SDS-PAGE and the results were shown in Table 2 in the form of 11S ratio (%).

The PEG polymers with four different molecular weights (6000, 20 000, 100 000 and 400 000 g mol⁻¹) and low polydispersity indices (M_w/M_n = 1.06, 1.06, 1.10 and 1.08, respectively) were obtained from Sigma-Aldrich (Shanghai, China) Trading Co., Ltd. The diffusion coefficient and hydrodynamic radius (R_h) of PEG was determined by Dynamic Light Scattering (DLS) followed the methods of Choi et al.²⁷ and Linegar et al.²⁸ The PEG dispersion was prepared the day prior to use by dispersing 0.1% (w/w) PEG powders in deionized water (pH 7.0). After filtration (0.22 μm) the samples were measured using a Zetasizer Nano ZS instrument (Malvern Instruments). The intensity correlation function, g⁽²⁾(τ) is related to the electric field correlation function, g⁽¹⁾(τ), by the following equation, g⁽²⁾(τ) = B(1 + f|g⁽¹⁾(τ)|²). Here, τ is the lag time, B is the baseline, and f is an instrumental parameter determined by deviation from an ideal correlation. The relaxation time distributions were obtained by analyzing g⁽¹⁾(τ) by the CONTIN algorithm. Diffusion coefficients (D₀) were obtained with a nonlinear algorithm. The hydrodynamic radius (R_h) of PEG in water was calculated by Stokes–Einstein equation:

where k is the Boltzmann constant (1.38 × 10⁻²³ J K⁻¹), T is the Kelvin constant (293.5 K), and η is the water viscosity (1.0 × 10⁻³ Pa s at 25 °C).

All polymers and other reagents were used without further purification.

2.2. Preparation of protein gels

Rehydration of protein powder at desired 7S/11S ratios was performed by stirring at 25 °C in deionized water at 18% (w/v) protein concentration (soy gels with lower protein concentration are too weak to handle). 0.1% (w/w) PEG was added to protein suspension. After being centrifuged at 40 000g for 20 min for air removal, the suspension was transferred into a sealed Teflon vessel with 6.5 cm high and 3.0 cm internal diameter (Ruinike Co., Ltd., Nanjing, China). After the heating procedure from 25 to 100 °C (approximately 300 s), the vessels were heated for 30 min and then immediately cooled by tap water and stored at 4 °C in a refrigerator overnight.

2.3. PEG release measurements

The gel was cut into slices with 1.5 mm thick by a razor and transferred into a 500 mL glass bottle (Biocolor Co., Ltd., Shanghai, China) with tenfold (w/v) 0.01 M sodium phosphate buffer (pH 7.0). 0.02% (w/v) NaN₃ was used as an anti-bacteria agent. The bottle was gently shaken in shaker incubator at 25 °C for 108 h for reaching an equilibrium state. During the diffusion process, 0.8 mL samples were periodically taken out and the equal quantity of fresh buffer was added in. Determination of PEG was following the method of Russell et al.²⁹ The collected samples were mixed with 5% BaCl₂ (10 : 1, v/v), then centrifuged at 10 000 rpm for 10 min. An appropriate amount of the supernatant was mixed with 0.24 mL 5% (w/w) BaCl₂, then diluted to 9.8 mL with deionized water, and finally 0.2 mL 0.05 M iodine solution was added. OD₅₀₀ was determined using a spectrophotometer to calculate the PEG concentration according to the calibration curve.

2.4. Determination of the PEG diffusion coefficient (D)

PEG diffusion coefficient was calculated by the Fick's second law,³⁰ as follow:where M_t and M₀ represent the amount of PEG released at time t and the amount of PEG in gel slices at time 0, respectively; δ is the gel thickness. Eqn (2) can be simplified towhere k is the slope of the fitted curve.

2.5. Power law dependence of diffusion coefficients and PEG molecular weights

For the solutes with different molecular weights (M_w), there is a correlation between hydrodynamic radius (R_h) and the cubic root of molecular weight and solute density:
where N_a is the Avogadro constant. Based on Stokes–Einstein equation:

A simple power law giving a description of the relationships between PEG diffusion coefficients and its molecular weight can be gained:

D = AM_w^−α (4)

where A and α are a preexponential factor and a characteristic exponent, respectively.

2.6. Scanning electron microscopy (SEM)

SEM images were obtained using a Hitachi S4800 field emission scanning electron microscope (Hitachi High-Technologies Co., Japan), and the acceleration voltage was 10 kV. The detailed preparation protocol was followed the method of Colsenet et al.²³ The JPEG color images at ×80 000 were binary segmented using the threshold function of the open source image analysis package ImageJ (v1.50) at default settings. The pore number and area were estimated by particle analyze process.

2.7. Statistical analysis

All determinations were carried out for at least three times. Experiment data were analyzed by analysis of standard deviations and variance (ANOVA) using SAS 9.1.

3. Results and discussion

3.1. PEG diffusion coefficients in water

The hydrodynamic radius (R_h) of the PEG with different molecular weights in water (0.1%, w/v) determined by DLS and diffusion coefficients (D₀) calculated with Stokes–Einstein equation (eqn (1)) were shown in Table 1. Apparently, the D₀ value decreased with increasing probe R_h or molecular weight.

Table 1 Hydrodynamic radius and diffusion coefficients in water of PEG calculated with the Stokes–Einstein equation

Mw (g mol^−1)	D0 (m^2 s^−1)	Rh (nm)
6000	8.92 ± 0.49 × 10^−11	3.41 ± 0.14
20 000	4.76 ± 0.31 × 10^−11	6.22 ± 0.32
100 000	2.46 ± 0.12 × 10^−11	17.12 ± 0.45
400 000	1.40 ± 0.09 × 10^−11	29.41 ± 1.84

---

3.2. Release of PEG from soy protein gels

3.2.1 Effect on the release of PEG. In gel system, the release behavior of solute encapsulated can be controlled by characteristic dimensions, interactions and degradation rate of gels. In addition, the control of variations of gel mesh size is of great importance to design solute delivery devices. In the present study, the release kinetic of probe out of gel was investigated to find the correlation between the release of solute and the structural change in gel. The mass release of PEG (M_w from 6000 to 400 000 g mol⁻¹) from soy protein gels generated at different 11S ratios was measured at different diffusion time. Fig. 1a gave a representative PEG release profile with a molecular weight of 20 000 g mol⁻¹. As shown in Fig. 1a, at initial diffusion time (12 h), higher PEG release rate was obtained in 11S-rich gel than 7S-rich gel. Similarly, higher release rates of PEG with molecular weights of 100 000 and 400 000 g mol⁻¹ were also observed in gels with higher 11S ratio (data not shown), which implied that mass transport was easier in gels with higher 11S ratio. However, no effect of gel structure change on the release rate of PEG 6000 g mol⁻¹ was found (date not shown). For PEG 6000 g mol⁻¹, the time needed to release 100% from gel slice to the buffer was about 9 h, while this value increased to 15 h, 36 h and 72 h (data not shown) for PEG 20 000, 100 000 and 400 000 g mol⁻¹, respectively.

Fig. 1 Examples of release kinetics of PEG-20 000 from 7S-rich and 11S-rich gels. (a) The relative PEG mass released in the buffer (M_t/M₀) versus time (h). (b) Relative PEG mass release as a function of the square root of the diffusion time.

3.2.2 Effect on PEG diffusion coefficients. As shown in Fig. 1b, it was observed that there was a linear relationship between M_t/M₀ and the square root of diffusion time t during initial stage (particularly for first 12 hours). This result indicated that the release behavior of PEG out of gels was controlled by Fickian diffusion process. Thus, the diffusion coefficients of PEG can be calculated according to eqn (3). The results were summarized in Table 2, which shows that diffusion coefficients decreased from 2.68 ± 0.25 × 10⁻¹¹ to 1.25 ± 0.12 × 10⁻¹² m² s⁻¹ as the molecular weights of PEG increased from 6000 to 400 000 g mol⁻¹. The diffusion coefficients of PEG determined by PFG-NMR in whey protein gels decreased from 6.0 × 10⁻¹¹ to 3.0 × 10⁻¹¹ m² s⁻¹ with the molecular weights of PEG increased from 1080 to 82 250 g mol⁻¹,²³ which were in the same range as in this study. In comparison, the D values of PEG with a series of molecular weights of 4000, 12 000, 20 000, and 36 000 g mol⁻¹ in calcium alginate hydrogels³¹ were 8.9 × 10⁻¹¹, 3.8 × 10⁻¹¹, 2.0 × 10⁻¹¹, and 1.3 × 10⁻¹¹ m² s⁻¹, respectively, which were higher than the D values of the PEG with the same molecular weight in soy protein gels. This might be due to higher density network structure in soy gel than calcium alginate hydrogel.

Table 2 Diffusion coefficients of PEG with different molecular weights in soy protein gels prepared at different 11S ratios^a

Gels	11S ratio (%)	DPEG (m^2 s^−1)
		6000	20 000	100 000	400 000
a Means with different letters are significantly different at 5% level.
7S-Rich	32.7 ± 0.3	2.54 ± 0.17 × 10^−11a	1.03 ± 0.06 × 10^−11b	3.21 ± 0.08 × 10^−12d	1.25 ± 0.12 × 10^−12i
A	44.3 ± 0.4	2.53 ± 0.14 × 10^−11a	1.06 ± 0.08 × 10^−11b	3.41 ± 0.07 × 10^−12e	1.48 ± 0.11 × 10^−12j
B	55.9 ± 0.4	2.59 ± 0.17 × 10^−11a	1.14 ± 0.02 × 10^−11b	3.68 ± 0.18 × 10^−12f	1.71 ± 0.04 × 10^−12k
C	74.3 ± 0.5	2.66 ± 0.21 × 10^−11a	1.28 ± 0.06 × 10^−11c	4.36 ± 0.13 × 10^−12g	2.35 ± 0.17 × 10^−12l
11S-Rich	92.6 ± 0.5	2.68 ± 0.25 × 10^−11a	1.42 ± 0.16 × 10^−11c	5.21 ± 0.21 × 10^−12h	2.98 ± 0.07 × 10^−12m

---

As expected, the D values of PEG decreased with increasing molecular weights from 6000 to 400 000 g mol⁻¹, which was in accordance with previous studies in hydrogels that the protein diffusion coefficients decreased with increasing protein size.^32–34 However, no significant changes in diffusion coefficients were found for PEG-6000 g mol⁻¹ among gels. Salami et al.³⁵ came to the same results that for small probes (R_h ≈ 3 nm), the changes in diffusion coefficients measured by PFG-NMR were not significant, and hence the rennet coagulation had no effect on the diffusion of small probes. Diffusion coefficients of 20 000, 100 000 and 400 000 g mol⁻¹ PEG decreased with increasing in 11S ratio in gels. The increase in PEG diffusion coefficients with increasing 11S ratio in gels indicated that a more porous gel network was formed at higher 11S ratio, which would resulted in a decrease of the obstruction effect when PEG molecule was diffusing through the pores.

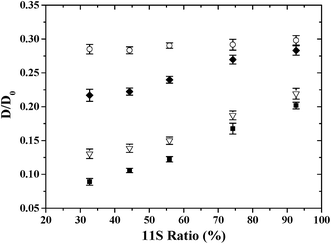
The effect of 11S ratio on the D/D₀ values of PEG was shown in Fig. 2. D/D₀ decreased with 11S ratio in gel system studied, except for the smallest PEG (6000 g mol⁻¹) where no significant changes in D/D₀ were found. Moreover, the decrease was more pronounced for 400 000 g mol⁻¹ PEG (−58.3% as the 11S ratio decreased from 92.6% to 32.7% in gels) than 100 000 g mol⁻¹ PEG (−38.4%) and 20 000 g mol⁻¹ PEG (−27.2%). Thus as expected, diffusional hindrances were the most severe for large macromolecules.^17–21 Colsenet et al.²³ reported that the diffusion of PEG with larger size was more sensitive to the whey protein gel microstructural change as a function of denaturation time.

Fig. 2 Plot of the normalized PEG diffusion coefficients (D/D₀) in heat-induced soy protein gels (represented by 11S ratio in the proteins) for different PEG molecular mass: ○: 6000 g mol⁻¹, ◆: 20 000 g mol⁻¹, ▽: 100 000 g mol⁻¹ and ■: 400 000 g mol⁻¹.

3.2.3 Power law dependence of diffusion coefficients and PEG molecular weights. Good fits to eqn (4) were obtained (Fig. 3) for the diffusion coefficients of PEG with four different molecular weights in gels. The eqn (4) was constantly suggested to describe the diffusion of polymer, in which α increased from 0.55 in diluted system³⁶ to 2.0 in concentrated system.³⁷ The characteristic exponent α would tend to 1 for non-entangled polymer chain when the gel network mesh size decreased and approached the solute radius, which was described by Rouse model.³⁸ And when the mesh size was much smaller than the radius of solute, the structure of the flexible solute, such as PEG, would be forced to diffuse in gel matrix in a wormlike behavior; and in this case, the reptation theory worked.³⁹ In the present study, the α value increased from 0.54 to 0.74 with decreasing 11S ratio in gels form 92.6% to 32.7%. The gel networks described here were not dense enough to trigger the reptation mechanism, because the α value was smaller than 1. But they were dense enough to induce Rouse mechanism. The gradual shift of power law exponent α value with decreasing 11S ratio indicated that more density of gel network was formed at lower 11S ratio.

Fig. 3 Power law representation of PEG diffusion coefficients in soy protein gels as a function of the PEG molecular weights.

3.2.4 Effect on microstructure of gel. Microstructures of soy protein gels with different 11S ratios were investigated by using scanning electron microscopy (SEM). SEM images of gels at ×80 000 and ×30 000 magnifications are presented in Fig. 4. The gels were composed of almost spherical linked aggregates which formed the three-dimensional network of compact clusters. Fig. 4 shows a clear difference in gel network structure for different 11S ratios. A more compacter and homogenous gel network with small pores could be found in 7S-rich gel. A heterogenous structure with highly porous network could be observed in 11S-rich gel. Similarly, Hermansson⁴⁰ reported that the β-conglycinin gel was more homogenous and the network was more strongly crosslinked than that of glycinin investigated by TEM. Furthermore, in SEM pictures at ×80 000 (Fig. 4a–e), the protein aggregate particle which was the basic composition unit of gel network was larger in gel prepared at lower 11S ratio. This result directly and visibly confirmed that, in the same protein concentration, protein aggregates formed by 11S fractions were compacter than by 7S proteins. The reasons might lie in: a much denser aggregate structure could be formed through hydrophobic bond by 11S protein basic polypeptides which contained more hydrophobic amino acids than 7S subunits.^41–43 Therefore, higher extent of micro-phase separation in the forming of gel network would be induced by the formation of denser protein aggregates. And it is understandable that more space was left empty in the gel network with higher 11S ratio, which was attributed to a more heterogeneous gel structure formed by heat-induced compacter 11S protein aggregates.

Fig. 4 SEM images of soy protein gels formed at different 11S ratios at ×80 000 (a–e) and ×30 000 (f–j) magnifications.

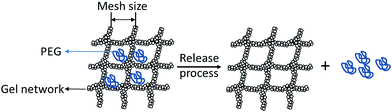
The size distribution of pores and the ratio of pores' area in a certain size range to total pores' area in each SEM picture at ×80 000 (Fig. 4a–e) were shown in Fig. 5. It is obvious that larger pores with higher area ratio can be observed in soy gel with higher 11S ratio. Even pores of radius higher than 200 nm were found in gels with 74.3% and 92.6% 11S ratio. Furthermore, the ratio of pores with sizes in a range of 0–100 nm decreased as increasing 11S ratio. SEM images were in good accordance with PEG diffusion coefficients. The more porous structure of gels showed good correlation with the higher PEG (M_w > 6000 g mol⁻¹) diffusion coefficients (Table 2), which was in agreement with previous findings of PEG or dextran self-diffusion coefficients fluctuation as an effect of microstructural changes in different protein gels. Balakrishnan et al.^44,45 traced the mobility of dextran in heat-induced β-lactoglobulin gels, and found dextran diffusion coefficients decreased with increasing the density of gel network. Feunteun et al.²⁰ studied the influence of renneting time on casein gel microstructure by measuring the diffusion of PEG using PEG-NMR, and found that changes in PEG diffusion coefficients in gels could be explained by the progressive compaction of casein gel network caused by the occurrence of structural rearrangements. Fig. 6 gives a pictorial view of PEG diffusing in gel network. Obviously, the diffusion of tracers in such gels appeared to be almost fully controlled by the volume that was accessible to particles. For PEG with different molecular weight or hydrodynamic radius, the increase in the probe size would result in a greater resistance of diffusing in gel matrix. When the tracer's size was much smaller than the network pore, then the diffusing obstacle effect could be neglected. Thus, no effect of gel structural change on the diffusion of PEG 6000 was found in Fig. 2. For PEG with the same molecular weight but higher than 6000 g mol⁻¹, the increase of diffusion coefficient in gels with higher 11S ratios could be explained by the increase in volume fraction and pore sizes induced by denser aggregates formed at higher 11S ratios, and more space was thus accessible to PEG to diffuse freely, leading to the increase of PEG diffusion coefficient.

Fig. 5 Gel pore size distribution as obtained from image analysis of SEM pictures at ×80 000. The column stands for the ratio between the pores' area in a certain size range and the total pores' area in a single SEM picture. The scatter point stands for the ratio between the pores' number in a certain size range and the total pores' number in a single SEM picture. (a–e) Correspond to Fig. 4a–e respectively.

Fig. 6 Pictorial view of PEG mass transfer in gel network.

4. Conclusion

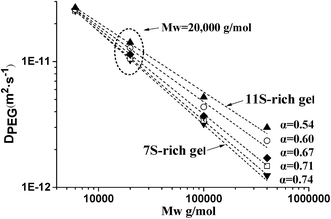
In summary, the results of this study showed that different network structures of heat-induced soy protein gels could be characterized by determining the release kinetics of PEG with various molecular weights. Compared to small probes, the diffusion of PEG with higher molecular weight was more sensitive to the microstructural change of soy protein gel prepared at different 11S ratios. The diffusion of probe was closely related to the change of gel network. A power law relationship gave a description of the solute diffusion coefficient versus molecular weight relationship, for which the exponent (α) shifted to higher values with the decrease of 11S ratio in gels, indicating that a denser and homogenous gel network was formed at lower 11S ratio in the mixture. These results were confirmed by SEM experiment. More homogenous gel networks with small pores was corresponding to gels with lower 11S ratio, while heterogenous structures with highly porous network containing compacter protein aggregates was observed in gels with higher 11S ratio.

Acknowledgements

We are grateful to Mr Wu and Mr Wang (Electron Microscopy Core Laboratory, School of Biological Engineering in Jiangnan University) for helpful discussion and assistance with the SEM experiments.

References

1. K. Kohyama, Y. Sano and E. Doi, J. Agric. Food Chem., 1995, 43, 1808–1812.
2. T. Li, X. Rui, W. Li, X. Chen, M. Jiang and M. Dong, J. Agric. Food Chem., 2014, 62, 8594–8601.
3. V. Poysa, L. Woodrow and K. Yu, Food Res. Int., 2006, 39, 309–317.
4. S. P. Stanojevic, M. B. Barac, M. B. Pesic and B. V. Vucelic-Radovic, J. Agric. Food Chem., 2011, 59, 7368–7376.
5. K. Toda, K. Chiba, K. Yagasaki, K. Takahashi, M. Hajika and T. Ono, ACS Symp. Ser., 2010, 1059, 255–276.
6. A. Yang, H. Smyth, M. Chaliha and A. James, Food Sci. Nutr., 2015, 4, 207–215.
7. K. Nishinari, Y. Fang, S. Guo and G. Phillips, Food Hydrocolloids, 2014, 39, 301–318.
8. M. Ji, T. Cai and K. Chang, J. Food Sci., 1999, 64, 763–767.
9. J. Kang II, Y. Matsumura and T. Mori, J. Am. Oil Chem. Soc., 1991, 68, 339–345.
10. J. Renkema, J. Knabben and T. Van Vliet, Food Hydrocolloids, 2001, 15, 407–414.
11. T. Nakamura, S. Utsumi and T. Mori, Agric. Biol. Chem., 1986, 50, 2429–2435.
12. F. Van Kleef, Biopolymers, 1986, 25, 31–59.
13. K. H. Bae and M. Kurisawa, Biomater. Sci., 2016, 4, 1184–1192.
14. J. Norton, Y. G. Espinosa, R. Watson, F. Spyropoulos and I. Norton, Food Funct., 2015, 6, 663–678.
15. X. Yang, H. M. Trinh, V. Agrahari, Y. Sheng, D. Pal and A. K. Mitra, AAPS PharmSciTech, 2016, 17, 294–306.
16. K. H. Bae, F. Lee, K. Xu, C. T. Keng, S. Y. Tan, Y. J. Tan, Q. Chen and M. Kurisawa, Biomaterials, 2015, 63, 146–157.
17. R. Colsenet, O. Soderman and F. Mariette, Macromolecules, 2005, 38, 9171–9179.
18. R. Colsenet, O. Soderman and F. Mariette, Magn. Reson. Imaging, 2005, 23, 347–348.
19. S. Le Feunteun and F. Mariette, J. Agric. Food Chem., 2007, 55, 10764–10772.
20. S. Le Feunteun and F. Mariette, Macromolecules, 2008, 41, 2079–2086.
21. S. Le Feunteun and F. Mariette, Macromolecules, 2008, 41, 2071–2078.
22. S. Salami, C. Rondeau-Mouro, J. van Duynhoven and F. Mariette, Food Hydrocolloids, 2013, 31, 248–255.
23. R. Colsenet, O. Söderman and F. Mariette, J. Agric. Food Chem., 2006, 54, 5105–5112.
24. R. Colsenet, O. Söderman and F. Mariette, Macromolecules, 2006, 39, 1053–1059.
25. L. Masaro and X. Zhu, Prog. Polym. Sci., 1999, 24, 731–775.
26. T. Nagano, M. Hirotsuka, H. Mori, K. Kohyama and K. Nishinari, J. Agric. Food Chem., 1992, 40, 941–944.
27. Y.-W. Choi, S. Lee, K. Kim, P. S. Russo and D. Sohn, J. Colloid Interface Sci., 2007, 313, 469–475.
28. K. L. Linegar, A. E. Adeniran, A. F. Kostko and M. A. Anisimov, Colloid J., 2010, 72, 279–281.
29. R. Russell, A. Mc Gilliard, P. Berger and J. Young, J. Dairy Sci., 1982, 65, 1798–1803.
30. P. L. Ritger and N. A. Peppas, J. Controlled Release, 1987, 5, 37–42.
31. E. Favre, M. Leonard, A. Laurent and E. Dellacherie, Colloids Surf., A, 2001, 194, 197–206.
32. E. Carvajal-Millan, S. Guilbert, M.-H. Morel and V. Micard, Carbohydr. Polym., 2005, 60, 431–438.
33. W. Hennink, H. Talsma, J. Borchert, S. De Smedt and J. Demeester, J. Controlled Release, 1996, 39, 47–55.
34. E. W. Merrill, K. A. Dennison and C. Sung, Biomaterials, 1993, 14, 1117–1126.
35. S. Salami, C. Rondeau-Mouro, J. van Duynhoven and F. O. Mariette, J. Agric. Food Chem., 2013, 61, 5870–5879.
36. P. De Gennes, Nature, 1979, 282, 367–370.
37. H. Tao, T. P. Lodge and E. D. von Meerwall, Macromolecules, 2000, 33, 1747–1758.
38. P. E. Rouse Jr, J. Chem. Phys., 1998, 108, 4628–4633.
39. P.-G. de Gennes, J. Chem. Phys., 1971, 55, 572–579.
40. A. M. Hermansson, J. Sci. Food Agric., 1985, 36, 822–832.
41. D.-B. Yuan, X.-Q. Yang, C.-H. Tang, Z.-X. Zheng, I. Ahmad and S.-W. Yin, Food Res. Int., 2009, 42, 700–706.
42. J. Guo, X.-Q. Yang, X.-T. He, N.-N. Wu, J.-M. Wang, W. Gu and Y.-Y. Zhang, J. Agric. Food Chem., 2012, 60, 3782–3791.
43. S.-R. Dong, H.-H. Xu, B.-Y. Li, W. Cheng and L.-G. Zhang, J. Cereal Sci., 2016, 70, 263–269.
44. S. Babu, J.-C. Gimel and T. Nicolai, Eur. Phys. J. E: Soft Matter Biol. Phys., 2008, 27, 297–308.
45. G. Balakrishnan, D. Durand and T. Nicolai, Biomacromolecules, 2010, 12, 450–456.

---