The role of exchange–correlation functional on the description of multiferroic properties using density functional theory: the ATiO3 (A = Mn, Fe, Ni) case study†
Abstract
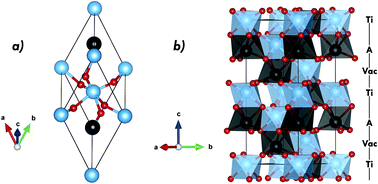
In this study, ab initio density functional theory calculations were performed on ATiO3 (A = Mn, Fe, Ni) materials for multiferroic applications. Structural, magnetic, electronic and topological analysis were investigated as regard the A-site cation effect. Concerning the prediction of new multiferroic candidates in silico, the role of different exchange-correlation functionals was reviewed. From such properties was verified that PBE0 functional performs the best for ATiO3 compounds overcoming the deficiency of standard LDA and PBESol functionals and get the better of B3LYP, PBE0+D and B3LYP+D. Regarding the A-site cation effect, calculated structural parameters follow the ionic radii trend moving from Mn to Ni, resulting in more ordered AO6 clusters; while, the TiO6 distortion increases. Using magneto-structural and magneto-electronic parameters, the antiferromagnetic exchange coupling constant was rationalized from GKA rules. The increase of the antiferromagnetic order along the transition metal series was explained from the 3d orbital occupancy and A–O bond interactions. DOS and band structure profiles clarify the semiconductor behavior as regard the 3d crystal field splitting for both A-site and Ti cations. Further, electronic results suggest the existence of intermetallic connection (A–O–Ti–O–A); whereas, topological analysis in the framework of quantum theory of atom in molecules was carried out to evaluate the A–O and Ti–O bond interaction through the analyses of ∇2ρ sign at bond critical point and of the charge-transfer parameter obtained from net charges.

 Please wait while we load your content...
Please wait while we load your content...