Enhanced thermoelectric performance in a percolated bismuth sulfide composite†
Deniz P. Wong‡
 a,
Wei-Lun Chien‡ac,
Chien-Yu Huangab,
Cheng-en Changac,
Abhijit Gangulyb,
Lian-Ming Lyua,
Jih-Shang Hwangc,
Li-Chyong Chen*b and
Kuei-Hsien Chen
a,
Wei-Lun Chien‡ac,
Chien-Yu Huangab,
Cheng-en Changac,
Abhijit Gangulyb,
Lian-Ming Lyua,
Jih-Shang Hwangc,
Li-Chyong Chen*b and
Kuei-Hsien Chen *a
*a
aInstitute of Atomic and Molecular Sciences, Academia Sinica, Taipei, Taiwan. E-mail: chenkh@pub.iams.sinica.edu.tw
bCenter for Condensed Matter Sciences, National Taiwan University, Taipei, Taiwan. E-mail: chenlc@ntu.edu.tw
cInstitute of Optoelectronic Sciences, National Taiwan Ocean University, Keelung, Taiwan
First published on 3rd October 2016
Abstract
We synthesized a bismuth-rich bismuth sulfide (Bi2+xS3) to improve the electrical conductivity. A percolated composite was obtained by mixing Bi2+xS3 with commercial Bi2S3 so that the other thermoelectric parameters were not compromised. The Bi2+xS3 acted as a conductive percolating channel within the Bi2S3 matrix. This percolation approach retained the high Seebeck coefficient of the Bi2S3 matrix while improving the electrical conductivity. A dimensionless figure of merit (zT) up to five times that of the pure Bi2S3 sample was achieved.
Introduction
Rapid economic development has resulted in higher energy demands, which have, in turn, led to climate change. The search for alternative, cheap and sustainable energy sources is now a major research goal.1 One technology that has attracted attention for over 100 years takes advantage of the thermoelectric effect, a phenomenon that produces electricity through temperature gradients. Thermoelectric technology can be used to convert waste heat to electricity.2Solid-state thermoelectric technology has been successfully implemented in radioisotope thermoelectric generators to provide power to satellites when solar power is insufficient.3 Thermoelectric coolers without moving parts are used in low-noise, high-sensitivity detectors.4 Apart from these niche applications, technological developments have been limited by the low efficiency and high cost of thermoelectric devices.5 The effectiveness of thermoelectric materials can be gauged based on the dimensionless figure of merit or the zT value as defined in eqn (1). As shown in eqn (2), a higher zT value directly translates to a higher energy conversion efficiency (η). The zT values of state-of-the-art thermoelectric materials are, on average, between 1 and 2. This translates to a power conversion efficiency of 15–20% at 800 K.6 However, these materials cannot easily be implemented in real applications because of their high cost and environmental and health concerns. By contrast, materials that have been identified to be both safe and low cost often have lower efficiencies, which limits their commercial viability. The zT value is dependent on the Seebeck coefficient (S), the electrical conductivity (σ), the thermal conductivity (κ) and the temperature (T) (eqn (1)). These parameters are closely intertwined, making it difficult to attain the maximum possible zT value of a material.
 | (1) |
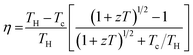 | (2) |
Tellurides have been the benchmark materials for thermoelectric technologies. However, due to their scarcity and the use of toxic elements such as lead (Pb) in their production, an alternative sustainable material is now required. Bismuth sulfide (Bi2S3) is promising in this respect because of its abundance, high Seebeck coefficient and low thermal conductivity. The major obstacle to this material reaching a respectable zT value is its low electrical conductivity.7–9
Most of the previously reported strategies for improving the thermoelectric properties of materials focused on reducing the thermal conductivity through phonon scattering. The incorporation of various scale structures into the matrix to disrupt the phonon pathways has been relatively successful.10–13 Another important, yet difficult, route is to improve the power factor component (S2σ) of the material. We used a percolating composite approach that combined one material with a high Seebeck coefficient and a low electrical conductivity and one material with a high electrical conductivity but low Seebeck coefficient. Similar to percolation – that is, the movement and filtering of fluids through porous materials – we refer to the movement of carriers (electrons for n-type semiconductors or holes for p-type semiconductors) in channels (conducting paths) surrounded by an insulating matrix. According to percolation theory, percolation paths can be created above a certain (volume) ratio of the conducting material which allow the conducting behaviour of the composite sample to follow that of a pure conducting material.14–17 The percolation approach is typically used in organic-based thermoelectric materials to improve performance.18–20 We extended this approach to inorganic crystals. Our goal was to use this concept to improve the overall electrical conductivity of our material without undermining the Seebeck coefficient, which usually occurs in highly conducting samples.
Experimental details
We selected bismuth sulfide as a model system for this study. Bismuth sulfide has a low thermal conductivity and a low electrical conductivity, resulting in a low power factor. We also synthesized a sample with good electrical conductivity, but at the cost of a lower Seebeck coefficient, which can be achieved by creating vacancies. By combining these two samples with different characteristics, a percolated composite system was formed. Because these two samples have the same phase, but different vacancy levels, a single-phase heterojunction composite system is formed with a high power factor (S2σ), resulting in an improvement in the zT value via percolation.Synthesis of pristine bismuth sulfide (Bi2S3)
To obtain a near-stoichiometric Bi2S3 sample, commercially obtained Bi2S3 (99.9%, Alfa Aesar) and sulfur powder (99.5%, Sigma-Aldrich) were mixed together by hand-milling and were then sintered under an N2 atmosphere at 570 °C for 1 h.Synthesis of bismuth-rich bismuth sulfide (Bi2+xS3)
Bismuth chloride (7.8 mmol BiCl3, 98+%, ACROS) and 11.7 mmol of sodium sulfide nonahydride (Na2S·9H2O, extra pure, ACROS) were added to 60 and 40 ml of deionized water, respectively. The solutions were stirred for 5 min before mixing together with continuous stirring for another 30 min. The mixed solution was then transferred into a Teflon-lined stainless-steel autoclave (100 ml capacity), sealed and maintained at 150 °C for 20 h. The products were washed several times with deionized water and acetone and then dried under ambient air.Mixed samples
Mixed samples were obtained by combining pristine (Bi2S3) and bismuth-rich bismuth sulfide (Bi2+xS3) powders at weight ratios of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, 8
0, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 6
2, 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, 4
4, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 and 0
6 and 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 to produce composite materials. The mixed powders were dispersed in 10 ml of acetone and were then stirred continuously in air until most of the acetone had evaporated. The mixed powders were compressed using a cold press at a pressure of 125 MPa. The samples were then sintered under N2 at 500 °C for 15 min.
10 to produce composite materials. The mixed powders were dispersed in 10 ml of acetone and were then stirred continuously in air until most of the acetone had evaporated. The mixed powders were compressed using a cold press at a pressure of 125 MPa. The samples were then sintered under N2 at 500 °C for 15 min.
Structural analysis
The morphology of the bulk samples was observed using field-emission scanning electron microscopy (FESEM, JEOL6700) with an energy-dispersive spectrometry attachment (Oxford Instruments) to determine the atomic ratio of bismuth and sulfur. X-ray powder diffraction (Bruker D8) was used to analyse the phases present.Thermoelectric properties
The Seebeck coefficient and electrical conductivity were measured at 323–523 K in an He atmosphere using a Seebeck coefficient/electrical resistance measuring system (ZEM-3 Ulvac-Riko, Japan). We used Hall measurements to analyse the mobility and carrier concentration (ECOPIA, HMS-3000) at different temperatures. The thermal conductivity (κ) was calculated based on the relationship κ = DCpd. The thermal diffusivity (D) was measured using an LFA457 instrument (Netzsch), the specific heat capacity (Cp) was measured using a TG-DSC111 (SETARAM) instrument and the density (d) was measured using the Archimedes method.Results and discussion
Percolated Bi2S3 samples were obtained after combining the commercially obtained Bi2S3 and the hydrothermally synthesized Bi2S3 samples. Fig. 1a shows a representative SEM image from the Bi2S3 composite with the 40 wt% bismuth-rich Bi2S3. From the free fracture surface, the sample shows a large crystal size with a relative density >95% based on the Archimedes method. Similar observations were made for the pure samples (Fig. S1†). The TEM image (Fig. 1b) showed a good crystal quality and a diffraction pattern consistent with the previously reported orthorhombic crystal structure.21 | ||
| Fig. 1 (a) Scanning electron micrograph and (b) high-resolution transmission electron micrograph (with corresponding SAED pattern) of Bi2S3 composite with 40 wt% bismuth-rich Bi2S3 sample. | ||
From the XRD pattern (Fig. 2), we observed the presence of peaks associated with bismuth metal in the sample prepared using the hydrothermal method. On mixing this sample with commercially obtained Bi2S3, the peak intensity decreased as the amount of Bi2S3 prepared hydrothermally decreased. The presence of a peak for bismuth metal can be attributed to the loss of sulfur during the annealing step after synthesis. Table 1 shows the Bi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S ratios of the prepared samples determined by EDS. The bismuth content increased relative to commercially obtained Bi2S3 as the hydrothermally synthesized sample was added into the composite system.
S ratios of the prepared samples determined by EDS. The bismuth content increased relative to commercially obtained Bi2S3 as the hydrothermally synthesized sample was added into the composite system.
 | ||
| Fig. 2 X-ray diffraction pattern of Bi2S3 composites based on various weight ratios of the bismuth-rich Bi2S3 material (* indicates peak of bismuth metal). | ||
| Sample | Composition (at%) | Mobility (cm2 V−1 S−1) | Carrier concentration (1017 cm−3) |
|---|---|---|---|
Bi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S S |
|||
| Bi2S3 | 2.04![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
15.92 | 4.59 |
| 20% | 2.10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
73.56 | 78.85 |
| 40% | 2.15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
99.14 | 159.73 |
| Bi2+xS3 | 2.35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
201.1 | 200.21 |
| Bi2S3 (ref. 8) | 2.00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
5.1 | 5 |
To evaluate the thermoelectric properties of the composite, the temperature-dependent Seebeck coefficient and the electrical conductivity were measured for each sample. Fig. 3 shows that the overall Seebeck coefficient of the commercially obtained Bi2S3 was higher than that of hydrothermally synthesized Bi2S3. By contrast, their electrical conductivities showed an inverse relationship. As the hydrothermally synthesized Bi2S3 component was added to the commercially obtained Bi2S3 matrix, the Seebeck coefficient decreased, while there was a significant improvement in the electrical conductivity. The decrease in the Seebeck coefficient can be explained by the increase in the carrier concentration in the composite (Table 1). The addition of the bismuth-rich Bi2S3 sample to commercially obtained Bi2S3 created a conducting composite that behaved like a percolation system. Fig. S2† shows that the addition of bismuth-rich Bi2S3 increased the electrical conductivity and reached saturation at around 40 wt%. This behaviour is similar to that of a composite system which follows percolation theory, in which there is a threshold amount of conducting material that can be added before the effect is saturated.22,23 The Seebeck coefficient did not reduce as much as the electrical conductivity increased and therefore an optimized power factor could be obtained.
 | ||
| Fig. 3 (a) Temperature-dependent Seebeck coefficient and (b) electrical conductivity of Bi2S3 composites based on various weight ratios of the bismuth-rich Bi2S3 samples. | ||
To confirm the percolation-like pathway, a sample of the 40 wt% bismuth-rich Bi2S3 sample was probed on a polished surface using conducting atomic force microscopy. Fig. 4 shows the height and current images of the sample surface. Despite adding only 40 wt% Bi2S3, the sample showed conducting behaviour across the whole surface area. We also synthesized a sample using a longer annealing time. This created a sample with a higher sulfur loss similar to the composition of the 40 wt% bismuth-rich Bi2S3 sample. Fig. S3† shows that the electrical conductivity of this sample was lower than that of the composite. This indicates that a percolated system has advantages over traditional defect engineering in enhancing electrical conductivity.
 | ||
| Fig. 4 Atomic force microscopy images of the 40 wt% bismuth-rich Bi2S3 sample in (a) height mode and (b) current mode. | ||
With the improvement in electrical conductivity, a slight increase in thermal conductivity was also observed (Fig. 5a), which was partly a result of the electronic contribution. By combining all the thermoelectric parameters, an optimized zT value of 0.26 was achieved for the sample with 40 wt% bismuth-rich Bi2S3 (Fig. 5b). This is higher than the zT values of 0.03 and 0.12 for the 0 and 100% bismuth-rich Bi2S3 samples, respectively. Through the percolation approach, we were able to improve the thermoelectric performance of the material by seven times that of the commercially available sample and by twice that of the pristine bismuth-rich Bi2S3 sample. The improvement was mainly due to the improvement in electrical conduction via percolation and the lower reduction in the Seebeck coefficient. We thus demonstrated an effective technique of improving the thermoelectric properties via a percolation approach.
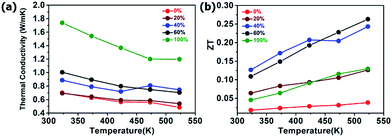 | ||
| Fig. 5 Temperature-dependent (a) thermal conductivity and (b) dimensionless figure of merit of Bi2S3 composites based on various weight ratio of the Bismuth-rich Bi2S3 material. | ||
Conclusions
We used a percolation approach to improve the thermoelectric performance of a material by improving its power factor instead of the commonly adopted approach of reducing the thermal conductivity. The percolation approach demonstrated in this study allowed us to maintain the electrical conductivity of the conducting component at a threshold amount while mitigating the reduction in the Seebeck coefficient. As a result, an optimized power factor and a significant increase in the zT value (0.26) for Bi2S3 were achieved even without doping or control of the nanoscale morphology reported by other groups. A combination of this approach with existing methods of reducing the thermal conductivity could improve the viability of low-cost thermoelectric materials with poor electrical conductivity.Acknowledgements
The authors thank the NanoCore, the Core Facilities for Nanoscience and Nanotechnology of Academia Sinica for technical support and the Center for Sustainability Science of Academia Sinica, Taiwan for financial support.Notes and references
- L. E. Bell, Science, 2008, 321, 1457 CrossRef CAS PubMed.
- Thermoelectrics Handbook Macro to Nano, ed. D. M. Rowe, CRC Press, Boca Raton, FL, 2006 Search PubMed.
- T. M. Tritt and M. A. Subramanian, MRS Bull., 2006, 31, 188 CrossRef.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105 CrossRef CAS PubMed.
- L. E. Bell, J. Electron. Mater., 2009, 38, 1344 CrossRef CAS.
- C. B. Vining, Nat. Mater., 2009, 8, 83 CrossRef CAS PubMed.
- W. Liu, K. C. Lukas, K. McEnaney, S. Lee, Q. Zhang, C. P. Opeil, G. Chen and Z. Ren, Energy Environ. Sci., 2013, 6, 552 CAS.
- Z. H. Ge, B. P. Zhang and J. F. Li, J. Mater. Chem., 2012, 22, 17589 RSC.
- Z. H. Ge, B. P. Zhang, P. P. Shang, Y. Q. Yu, C. Chen and J. F. Li, J. Electron. Mater., 2011, 40, 1087 CrossRef CAS.
- B. Poudel, Q. Hao, Y. Ma, Y. Lan, A. Minnich, B. Yu, X. Yan, D. Wang, A. Muto, D. Vashaee, X. Chen, J. Liu, M. S. Dresselhaus, G. Chen and Z. Ren, Science, 2008, 320, 634 CrossRef CAS PubMed.
- A. J. Minnich, M. S. Dresselhaus, Z. F. Ren and G. Chen, Energy Environ. Sci., 2009, 2, 466 CAS.
- L. D. Zhao, V. P. Dravid and M. G. Kanatzidis, Energy Environ. Sci., 2014, 7, 251 CAS.
- L. D. Zhao, B. P. Zhang, W. S. Liu and J. F. Li, J. Appl. Phys., 2009, 105, 023704 CrossRef.
- N. Lu, L. Li and M. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 195205 CrossRef.
- S. Stankovich, D. A. Dikin, G. H. B. Dommett, K. M. Kohlhaas, E. J. Zimney, E. A. Stach, R. D. Piner, S. T. Nguyen and R. S. Ruoff, Nature, 2006, 442, 282 CrossRef CAS PubMed.
- W. Bauhofer and J. Z. Kovacs, Compos. Sci. Technol., 2009, 69, 1486 CrossRef CAS.
- J. K. W. Sandler, J. E. Kirk, I. A. Kinloch, M. S. P. Shaffer and A. H. Windle, Polymer, 2003, 44, 5893–5899 CrossRef CAS.
- V. Andrei, K. Bethke and K. Rademann, Phys. Chem. Chem. Phys., 2016, 18, 10700 RSC.
- D. Kim, Y. Kim, K. Choi, J. C. Grunlan and C. Yu, ACS Nano, 2010, 4, 513 CrossRef CAS PubMed.
- C. Yu, Y. S. Kim, D. Kim and J. C. Grunlan, Nano Lett., 2008, 8, 4428 CrossRef CAS PubMed.
- J. C. Lin, R. C. Sharma and Y. A. Chang, J. Phase Equilib., 1996, 17, 132 CrossRef CAS.
- A. L. Efros and B. I. Shklovskii, Phys. Status Solidi B, 1976, 76, 475 CrossRef CAS.
- J. P. Clerc, G. Giraud, J. M. Laugier and J. M. Luck, Adv. Phys., 1990, 39, 191 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra21418e |
| ‡ Contributed equally. |
| This journal is © The Royal Society of Chemistry 2016 |
