Emergence of low dimensional ferroelectricity in Pr_0.67Ca_0.33MnO₃ nanocrystal arrays

Abstract

We discuss the emergence of low dimensional ferroelectricity in self-organized Pr_0.67Ca_0.33MnO₃ nanocrystalline arrays deposited on a Si substrate. We observe sharp switching of the electric polarization under an external electric field with nearly rectangular hysteresis loops which persist up to 150 K. We discuss the polarization switching kinetics within the framework of the Kolmogorov–Avrami–Ishibashi model which gives a maximum domain wall speed of ∼1 m s⁻¹. Polarized Raman spectroscopy shows evidence of isolated ferroelectric domains even at room temperature.

---

Introduction

The emergence of multiferroicity in general and ferroelectricity in particular at reduced dimensions has been at the forefront of research towards nanoelectronic applications in recent years.^1–6 Besides the technological aspect, such studies have called into question our present understanding regarding the plausibility of emerging functional properties at the nanoscale. For example, Lee et al. recently proposed, generalizing on theoretical calculations and experimental measurements on nanometer thick films of the cubic perovskite SrTiO₃, that size reduction could in fact lead to the emergence of ferroelectric properties in otherwise non-ferroelectric bulk systems.⁷ Stengel et al. demonstrated a novel mechanism of ferroelectricity at a metal–oxide interface that led to an overall enhancement of the ferroelectric instability of the film, rather than its suppression.⁸ On the other hand, there are several studies which claim that below a certain critical size, ferroelectricity disappears (for a review on this see ref. 9). One of our own studies¹⁰ regarding the direct experimental evidence of multiferroicity in the charge ordered nanocrystalline manganite Pr_0.67Ca_0.33MnO₃ (PCMO), which discusses the particle size driven tunability of ferroelectric polarization, belongs to the former category. The origin of ferroelectricity in PCMO in that case being linked with Zener polaron (ZP) ordering¹¹ eventually leads to the suppression of ferroelectricity with the reduction of particle size. However, the ferroelectric response is enhanced in nanocrystalline samples so long as ZP ordering is not destroyed.¹⁰ In any case, the finite conductivity and the associated problem of leakage current makes it difficult to get saturated P–E loops with sharp reproducible switching for such nanocrystalline PCMO systems which exhibit ZP ordering. In this article, we discuss the origin of sharp ferroelectric switching in self-organized arrays of PCMO nanoislands deposited on a Si substrate.

Depending on the interface energies and the lattice mismatch, the hetero-epitaxial growth modes responsible for the self organization of arrays of three dimensional islands are generally divided into two distinct categories: first, Volmer–Weber (VW) which is characterized by island growth and second, Stranski–Krastanov (SK), which is characterized by layer by layer growth followed by island growth.¹⁴ There are several reports which utilize these growth modes to fabricate self-organized arrays of ferroelectric capacitors. For example, the formation of self organized ferroelectric triangular shaped nano-islands at the initial stage of growth in PbTiO₃ and PZT films grown on Pt(111)/SiO₂/Si(100) has been reported.^12,13 M. Alexe et al.¹⁵ studied the switching properties of self assembled Bi₄Ti₃O₁₂ ferroelectric memory cells by scanning force microscopy working in the piezoresponse mode. On the other hand, so far as manganites are concerned, the focus has been more on growing self-assembled epitaxial films on a Si substrate with a SrTiO₃ buffer layer.^16,17

Experimental details

Thin films of PCMO were grown on Si(100) and SrTiO₃(100) (STO) substrates by Pulsed Laser Deposition (PLD). The target PCMO was prepared in two steps – firstly, we have synthesized a nanocrystalline sample by a standard sol–gel method. Powders of Pr₆O₁₁, CaCO₃ and MnO₂ having 99.99% purity (Sigma Aldrich), used as starting materials, were preheated to remove any absorbed moisture. The corresponding oxides were converted into nitrates using 45–50% concentrated nitric acid. Suitable amounts of citric acid and water were added to the mixed solution. This solution was stirred for 1 hour and then slowly evaporated in a water bath at a temperature of 55–60 °C until a gel was formed. The obtained gel turns into a black porous powder at higher temperatures. The nanocrystalline sample was prepared by annealing the pelletized powder at 1000 °C for 6 hours. Secondly, the nanocrystalline sample was further sintered at 1400 °C for 36 hours to obtain the PCMO target with a diameter of around 20 mm. Before the deposition of the thin films, silicon substrates (un-doped) were cleaned with piranha solution to remove any organic residues. The substrates were further ultrasonicated for 15 minutes each in three different solutions – acetone, iso-propyl alcohol and distilled water. Finally the substrates were dried with a nitrogen air gun and heated at 100 °C for 15 minutes. An excimer laser of wavelength λ = 248 nm having an energy density of 2.5 J cm⁻² was used during the deposition. The target to substrate distance, pulse repetition rate and substrate temperature were 4.5 cm, 10 Hz and 500 °C respectively. The films were deposited at two different oxygen pressures of 250 mTorr and 15 mTorr followed by in situ annealing at 500 °C for 15 minutes with an oxygen flow of 1 bar. Finally the films were subjected to post annealing in air at 800 °C for 2 hours. The deposition time was kept at 40 minutes for all the samples.

The characterization of the thin films and target was done by XRD θ–2θ scans at room temperature by using a PANalytical X’pert diffractometer having wavelength of 1.54 Å (Cu-K_α) with a scan rate of 1° per minute. The surface topography of all the films was studied by atomic force microscopy (AFM). The magnetic properties were measured using a Quantum Design Physical Property Measurement System (PPMS) while the ferroelectric properties were studied using a Radiant ferroelectric tester (Precision Premier II) which uses virtual ground circuitry. The dielectric constant and ferroelectric polarization measurements were carried out using the “Positive-Up–Negative-Down” (PUND) method. A number of parallel electrodes of dimensions 3 mm × 0.5 mm with a separation of ∼1 mm were made using silver paint (Alfa Aesar) in a lateral (in-plane) contact geometry. The dimensions of all the samples were 10 mm × 5 mm. The polarized Raman spectroscopy was carried out using an STR Raman spectrometer (Airix Corporation, Japan) which had a half wave plate as a polarizer and analyzers of 0° and 90° polarization.

Results and discussion

Surface topography and magnetic characterization

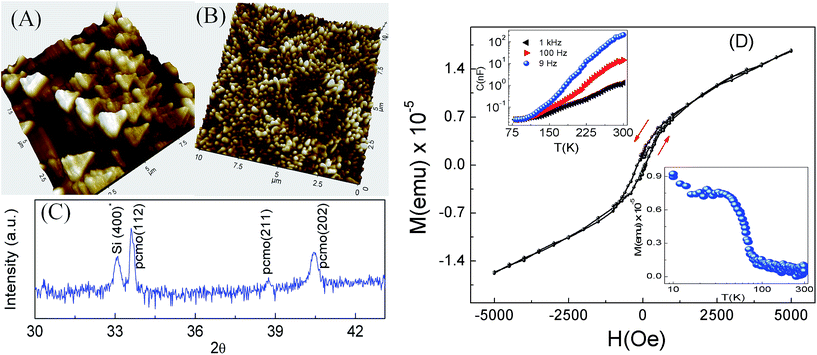
We label the PCMO films grown on the Si(100) substrate at an oxygen pressure of 15 mTorr as PCMO|Si 1 and the one grown at 250 mTorr as PCMO|Si 2. Similarly, PCMO films grown on STO at an oxygen pressure of 15 mTorr and 250 mTorr are labeled as PCMO|STO 1 and PCMO|STO 2, respectively. The surface topography of the PCMO thin films was examined by atomic force microscopy (AFM). The estimated maximum thickness of the films is around 100 nm. Fig. 1A shows an AFM image of the PCMO|Si 1 thin film indicating the formation of self assembled nano-islands with a triangular shape anisotropy. The pseudo-cubic lattice parameter of polycrystalline PCMO is 3.83 Å whereas the lattice constant of silicon is 5.43 Å leading to a huge lattice mismatch of ∼29.4%. As a result, the X-ray diffraction pattern of PCMO|Si 1 (Fig. 1C) shows (202) and (211) peaks apart from the (112) peak with a corresponding pseudocubic lattice constant of 3.41 Å rather than any epitaxial growth. The island formation in PCMO|Si 1 is facilitated by the low substrate temperature of 500 °C and the low oxygen pressure during the deposition. The shape of the islands depends on the lattice structure at the surface of the underlying substrate. The crystal structure of Si(100) has a 3-fold rotational symmetry¹⁸ on the surface resulting in triangle shaped island growth of the PCMO film. Similar types of self assembled Si/Ge nano structures have been observed at the Si(111) surface.^19,20 In general, with increasing oxygen pressure, the size of the plume increases, which in turn affects the thickness and surface morphology of the films.²¹ Consequently, for PCMO|Si 2 (not shown), the density of the islands is increased and the shape anisotropy is reduced with enhanced oxygen pressure. Conversely, in lattice matched PCMO|STO 1 (Fig. 1B) and PCMO|STO 2, epitaxial film growth is observed. The estimated RMS roughness for PCMO|Si 1 is 40 nm whereas the same for PCMO|STO 1 is a few nm, clearly indicating different growth modes in the two cases. In lattice mismatched systems, the atoms of the films are more strongly coupled to each other than to the substrate, leading to the formation of islands as described within the framework of the Volmer–Weber (VW) growth mechanism (for a review see ref. 14).

Fig. 1 Atomic force microscopy (AFM) images of PCMO|Si 1 (A) and PCMO|STO 1 (B). (C) The X-ray diffraction pattern of PCMO|Si 1 indicates the polycrystalline nature of the film. Si(400)* represents a (400) Bragg reflection at half the wavelength of the Cu-K_α radiation. (D) Magnetization versus magnetic field hysteresis loop at 10 K for PCMO|Si 1. Inset (top left): the temperature dependence of the capacitance measured by the “PUND” method with a maximum applied field of 50 V cm⁻¹ for different pulse widths. Inset (bottom right): temperature dependence of the field cooled (FC) dc magnetization at H = 1 kOe.

Fig. 1D shows the magnetization versus magnetic field hysteresis loop for PCMO|Si 1 at 10 K. Ferromagnetic hysteresis is observed in the low magnetic field range below 2500 Oe with the absence of saturation until 5000 Oe. The temperature dependence of the field cooled dc magnetization (bottom right inset of Fig. 1D) taken at H = 1 kOe clearly indicates the onset of ferromagnetic ordering near 50 K. The Curie–Weiss (CW) temperature obtained from the inverse susceptibility has a value of 40 K which is lower than that of nanocrystalline PCMO.¹⁰ However, the magnetic anomaly associated with ZP ordering is not observed in this case. Previous experiments on epitaxial films also report the absence of the ZP anomaly in the magnetic and transport measurements.²² The dielectric measurements were carried out by the “PUND” method^23,24 in which the sample is subjected to rectangular voltage pulses with a maximum field of 50 V cm⁻¹ and different pulse widths ranging from 1 Hz to 1 kHz. In the top left inset of Fig. 1D, the monotonic increase of the capacitance with the temperature is shown for PCMO|Si 1 with the absence of any dielectric anomaly. Similar observations were recorded for other samples too. This is in agreement with previous reports on nanocrystalline PCMO.¹⁰ Overall, the dielectric and magnetic measurements fail to detect any structural phase transition but the presence of ferromagnetic correlation in the self assembled nanocrystalline array of PCMO with a corresponding Curie–Weiss temperature of 40 K is established.

Ferroelectric hysteresis and switching kinetics

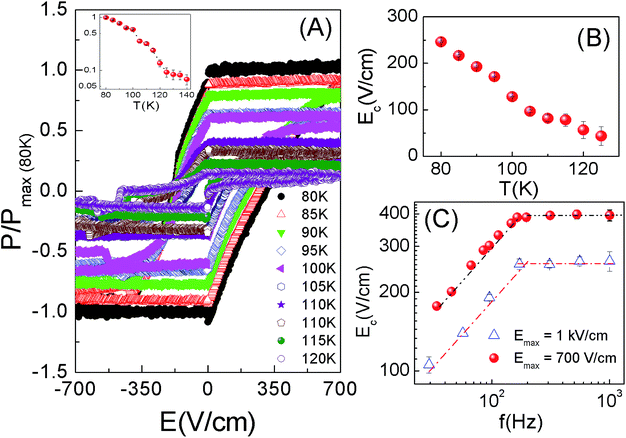
We have explored the ferroelectric properties by measuring the remanent electric polarization based on the PUND method. Traditional P–E loops are generally composed of ferroelectric, parasitic, or stray capacitance and conductive contributions. Therefore, the PUND method or double wave method^23,24 is a better tool to measure the switching polarization vs. electric field loops. Here, we have measured the remanent electric polarization using a set of 5 ‘monopolar’ triangular voltage pulses based on the PUND method. First, a preset pulse sets the polarization of the sample in a certain direction and during this no measurement is made. Second, a switched triangular pulse of amplitude V₀ and pulse width t₀ is applied in the opposite direction to the preset pulse, which reverses the sign of the polarization, and gives a half hysteresis loop associated with the electric polarization which includes remanent and non-remanent components. In the third step, a ‘non-switched’ pulse of the same amplitude and pulse duration is applied in same direction as that of the preceding pulse, which captures a half hysteresis loop containing only the non-remanent contribution to the polarization. The difference between the half hysteresis loops measured in step 2 and 3 gives the switching polarization only. Similarly, for step 4 and 5 this is repeated but in the opposite direction. The combination of the half hysteresis loops obtained from the differences between steps 2 and 3, and between steps 4 and 5, gives the complete set of four quadrant hysteresis P_SW–E loops. Instead of the rectangular pulses applied in the capacitive measurements, here we have applied triangular pulses so that the rate of change of the electric field over time should be fairly constant except for the reversal points. The switching electric polarization versus electric field (P_SW–E) loops were studied for all four samples at different temperatures from 80 K–300 K. The maximum applied field was 1 kV cm⁻¹ with different pulse widths ranging from 1 Hz to 1 kHz. Fig. 2A shows the P_SW–E loops for PCMO|Si 1 at different temperatures from 80 K–120 K for a pulse width of 1 Hz. The saturation polarization decreases with increasing temperature (inset of Fig. 2A), which is typical of conventional ferroelectric materials. The observed P_SW–E loops show sharp reproducible switching up to 150 K (Fig. 2A). On the other hand, PCMO|Si 2, in which the coverage density of the islands is enhanced and the shape anisotropy is reduced, does not show ferroelectric hysteresis (figure not shown) within the same field range and temperature range of interest. This indicates that the ferroelectricity strongly depends on the film morphology.

Fig. 2 (A) Remanent electric polarization of PCMO|Si 1 at different temperatures from 80 K–120 K taken by the “PUND” method with a pulse width of 1 kHz with a maximum applied field of 1 kV cm⁻¹. Inset: the corresponding saturation polarization versus temperature. (B) Corresponding temperature dependence of the coercive field for a pulse width of 1 kHz, (C) frequency dependence of the coercive field at 80 K for two different maximum applied electric fields of 700 V cm⁻¹ (solid red) and 1 kV cm⁻¹ (open blue).

Fig. 2B shows the temperature dependence of the coercive electric field (E_c) for PCMO|Si 1 for a pulse width of 1 kHz. The maximum applied field (E_max) is sufficiently higher than the coercive field thus ruling out artifacts associated with P–E loops. The increase in coercivity with decreasing temperature is consistent with thermally activated ferroelectric switching. On the other hand, the frequency dependence of the coercive field (E_c) at a constant temperature (Fig. 2C) follows a power law behaviour²⁵E_c ∼ f^α with exponent α = 0.5. It is evident from Fig. 2C that the value of α is nearly the same for two different E_max values of 700 V cm⁻¹ and 1 kV cm⁻¹ indicating that the E_c values are fairly genuine. Moreover, if we compare PCMO|Si 1 and PCMO|STO 1 which have different growth modes, the coercivity in PCMO|STO 1 is almost 6 times than that of PCMO|Si 1 (inset, Fig. 3).

Fig. 3 Time dependence of the normalized remanent electric polarization for PCMO|Si 1 for E_max = 600 V cm⁻¹ at 80 K. Solid red and dotted green lines represent fitting the experimental data by the KAI and the NLS model respectively. Inset (bottom right): the Lorentzian distribution for the NLS fitted curve. Inset (top left): comparison between the normalized P–E loops at 80 K for PCMO|Si 1 and PCMO|STO 1 for a pulse width of 315 Hz with E_max values of 1 kV cm⁻¹ and 3 kV cm⁻¹ respectively.

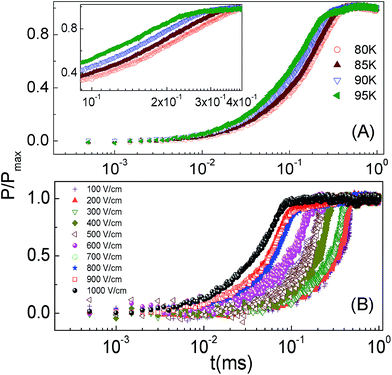
The switching time t_s, defined as the time in which the value of the polarization decreases to 90% of its saturation value, ranges from 300–700 μs depending on the applied electric field. The decrease of the switching time with increasing E_max indicates that the energy required for domain nucleation is mainly supplied by the applied electric field. Moreover, since PCMO|Si 1 comprises isolated self assembled nanostructures, the process of domain nucleation is most likely to occur separately in these islands and the switching time captures the collective behaviour of the fraction of the volume which has switched. Although the Kolmogorov–Avrami–Ishibashi (KAI) model^26,27 (which is based on the nucleation of domains expanding unrestricted under an external electric field until they encounter another expanding domain) is extensively used to describe ferroelectric switching dynamics, it seems, ex ante, that the nucleation-limited-switching (NLS) model^28,29 which assumes the existence of multiple nucleation centers having independent switching kinetics would be the most suitable one to describe the system under study. The switching kinetics in the latter case are described in terms of the distribution function of the local nucleation probabilities. In order to clarify the nature of the exponentially fast polarization switching, we have fitted the experimental data by the KAI model as well as the NLS model assuming a Lorentzian distribution of the average logarithmic switching times (Fig. 3). We find that even with the narrowest possible distribution (other than a delta function where the NLS model reduces to the KAI model) the KAI model gives a better fit to the experimental data. If P(t) is the switched remanent polarization at any instant t, its time evolution as given by the KAI model is,

P(t) = P_max[1 − exp{−(t/τ)ⁿ}] (1)

where P_max is the saturation polarization, τ is the characteristic time of polarization reversal and n is the dimensionality over which the domain nucleation takes place.

We performed switching time measurements by varying the maximum electric field E_max. At a given temperature, the electric field was increased to a set value E_max, at which we measured the elapsed time until the electric polarization is switched (Fig. 4B). We fitted the results using the exponential function in the KAI model²⁶ to extract the characteristic timescale τ. The characteristic time clearly increases with decreasing temperature (Fig. 4A) following the Arrhenius behaviour τ = τ₀ exp(ε_a/kT) (not shown) which implies thermally activated switching with corresponding time scale τ₀ = 10 μs and energy scale ε_a = 20.4 meV. Moreover, the characteristic time τ versus electric field obeys Merz’s Law which describes domain wall motion,³⁰

τ = τ_∞ exp(E_a/E_max) (2)

where τ_∞ is the long time relaxation factor and E_a is the corresponding activation electric field. Interestingly, the classic theoretical treatment of Merz’s law developed by Miller and Weinreich³¹ involves the nucleation of an atomically thin triangular plate which expands in the same plane.

Fig. 4 Time dependence of the normalized remanent electric polarization for PCMO|Si 1 (A) at different temperatures from 80 K–100 K at an applied electric field of 1 kV cm⁻¹; inset: a blow-up of the same figure. (B) The same at 80 K for different applied electric fields from 100 V cm⁻¹ to 1 kV cm⁻¹.

Fig. 5B shows the characteristic time τ plotted against the inverse of the applied electric field at different temperatures. The fitting parameters obtained from Merz’s law are E_a = 965 V cm⁻¹ and τ_∞ = 10 μs. Apart from this, the electric field and temperature dependence of the dimensionality is shown in Fig. 5C. Finally, the characteristic time being a function of the applied electric field E_max as well as temperature T, we present our data for τ (E_max, T) in the form of a linear scaling plot of T ln(τ/τ*) as a function of T/E_max, where τ* is a scaling parameter. This makes an interesting comparison with the ubiquitous scaling behaviour observed in case of nucleation and propagation mediated switching in nanomagnets.^32,33 The slope of the power law scaling plot gives the effective activation field E_a ∼ 805 V cm⁻¹ while the effective energy barrier calculated from the intercept turns out to be 24.2 meV. In order to calculate the activation volume, we follow the method prescribed by Chong et al.³⁴ The activation volume is computed at zero polarization i.e. near the coercive field in the P–E loop that corresponds to the fastest switching rate.

Fig. 5 (A) Scaling plot of the switching time τ (E_max, T) for several electric fields E_max and temperatures where T ln(τ/τ*) is plotted against T/E_max. Top inset: coercive field plotted as a function of the logarithm of the current density. Bottom inset: logarithm of the current density plotted against the inverse of the temperature. (B) Characteristic time τ is plotted against the inverse of the electric field at different temperatures. (C) The dimensionality n is plotted against the electric field at different temperatures.

Assuming that the direction of the electric polarization is parallel to the applied electric field, the activation volume (V*) can be calculated from the following relation³⁴

where j is the switched current density and E is the electric field in the neighborhood of the coercive field E_C. One can also calculate the energy barrier from the slope of the vs. 1/T plot. The energy barrier thus calculated is 25 meV, close to the value obtained from the scaling plot, while the thermally activated volume (see insets, Fig. 5A) turns out to be in the range 4.4 nm³ to 7.3 nm³ which is much smaller than the size of the individual islands. The activation volume is over-estimated since the nucleation field could be well below the coercive field. In any case, the activation volume being much smaller than the size of the nanoislands reinforces our justification of the applicability of the KAI model to the present case rather than the NLS model. Taking the time scale associated with switching in the separate islands to be ∼10–20 μs and the average size of the islands as ∼2–3 μm, one can estimate the maximum domain wall speed which is of the order of 1 m s⁻¹.

The value of n (dimensionality) obtained from fitting the normalized polarization versus time by the KAI model²⁶ varies between 1 and 2 depending on the applied electric field and temperature. The general observation is that n is close to 2 for lower electric field values and it decreases to 1 for higher electric fields. Moreover, the value of n decreases on increasing the temperature, too, suggesting a transition from predominantly isotropic domain growth to predominantly anisotropic growth with the increase of the electric field and temperature. The decrease of n with the increasing electric field is somewhat unusual given the previous reports on other more conventional ferroelectrics. One of the possible reasons is that here the nucleation occurs simultaneously in various nano-islands. When the electric field is low, the domain nucleation occurs homogeneously in all the islands resulting in isotropic domain growth but as the electric field increases, the probability of nucleation among favorably oriented nano-islands increases compared to the others leading to anisotropic domain growth. Similar phenomena are expected with increasing temperature as well.

Polarized Raman spectroscopy

In order to explore the local inhomogeneity of the switching behavior, we have carried out polarized Raman spectroscopy³⁵ over different regions of the sample PCMO|Si 1. Fig. 6A shows an optical microscope image of the sample at room temperature, which shows a clear contrast between the blue and yellow regions. Let us label the blue regions as R1 and yellow regions as R2. The polarized Raman spectroscopy images are taken separately at the regions R1 and R2 (Fig. 6B) of the sample with parallel and crossed configurations of the polarizer and analyzer. In region R1, the peak intensity at 1446 cm⁻¹ in the crossed position is 28% of that in the parallel configuration, whereas in region R2, the intensity in the crossed position only decreases to 90% of that in the parallel position. Polarized Raman spectroscopy conclusively identifies isolated regions like R2 showing ferroelectric Raman modes surrounded by regions like R1 having only non-polar modes. The AFM images of PCMO|Si 1 taken at intermediate length scales between an optical micrograph on one hand and Fig. 1A on the other show that the whole sample can be divided into two spatial regions with different densities of nanocrystals as well as completely different configuration symmetries (Fig. 6C and D). This might explain why we do not observe any net macroscopic polarization at room temperature. At room temperature there are isolated polar domains surrounded by non-polar regions which might undergo a ferroelectric phase transition at a lower temperature. The minimum switching time scale observed in our case is 10 μs at an E_max of 1 kV cm⁻¹, similar to BiFeO₃ thin films under a much higher electric field of 250 kV cm⁻¹.³⁶ On the other hand, the observed low coercive field (∼200–400 V cm⁻¹), which is already underestimated considering the local inhomogeneity of the system, is similar to that reported for soft BaTiO₃ ceramics³⁷ and some organic ferroelectrics.³⁸

Fig. 6 (A) Optical microscopy image of PCMO|Si 1 shows the colour contrast of the blue (R1) and yellow (R2) regions. The scale bar represents 200 μm. (B) The room temperature polarized Raman spectra with parallel and crossed configurations of the polarizer and analyzer are shown for the R1 and R2 regions. (C) AFM image corresponding to the region R2 and (D) AFM image corresponding to the region R1 at an intermediate length scale showing regions with different configurational symmetries of the arrays of nanocrystals.

Conclusion

In conclusion, we have presented evidence of emerging ferroelectricity in self organized PCMO nanostructured arrays grown on Si substrates. The polarization measurements reveal sharp ferroelectric switching up to 150 K in self assembled nanostructures with shape anisotropy, while ferromagnetic ordering is observed below 40 K. This is in sharp contrast with epitaxially grown films which show ferroelectric reversal at a significantly higher electric field value. The polarization switching dynamics are attributed to the nucleation and growth of domains as described by the KAI model occurring separately in different islands. Polarized Raman spectroscopy along with optical and AFM imaging consistently provide evidence of local inhomogeneity and isolated ferroelectric domains even at room temperature. The observed fast switching of the electric polarization combined with the low coercive field holds exciting prospects for future nano-electronic applications.

Acknowledgements

VKS acknowledges CSIR, New Delhi for providing financial support. The authors wish to acknowledge the Department of Science and Technology, Govt. of India (FIST DST Project No. 20060268) for the Pulsed Laser Deposition facility.

References

1. R. Ramesh and N. A. Spaldin, Nat. Mater., 2007, 6, 21.
2. P. Yu, Y. H. Chu and R. Ramesh, Philos. Trans. R. Soc., A, 2012, 370, 4856.
3. D. Sando, A. Barthelemy and M. Bibes, J. Phys.: Condens. Matter, 2014, 26, 473201.
4. B. Zhao, Z. Chen, J. Meng, H. Lu, D. Wei Zhang and A. Jiang, J. Appl. Phys., 2015, 117, 204103.
5. L. Zhang, Z. Xu, L. H. Cao and X. Yao, Mater. Lett., 2007, 61, 1130.
6. I. Bretos, R. Jimenez, C. Gutierrez-Lazaro, I. Montero and M. L. Calzada, Appl. Phys. Lett., 2014, 104, 092905.
7. D. Lee, H. Lu, Y. Gu, S.-Y. Choi, S.-D. Li, S. Ryu, T. R. Paudel, K. Song, E. Mikheev, S. Lee, S. Stemmer, D. A. Tenne, S. H. Oh, E. Y. Tsymbal, X. Wu, L.-Q. Chen, A. Gruverman and C. B. Eom, Science, 2015, 349, 1314.
8. M. Stengel, D. Vanderbilt and N. A. Spaldin, Nat. Mater., 2009, 8, 392.
9. T. M. Shaw, S. Trolier-McKinstry and P. C. Mcintyre, Annu. Rev. Mater. Sci., 2000, 30, 263.
10. V. K. Shukla, S. Mukhopadhyay, K. Das, A. Sarma and I. Das, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 245126.
11. A. Daoud-Aladine, J. Rodriguez-Carvajal, L. Pinsard-Gaudart, M. T. Fernandez-Diaz and A. Revcolevschi, Phys. Rev. Lett., 2002, 89, 097205.
12. M. Shimizu, H. Fujisaw, H. Niu and K. Honda, J. Cryst. Growth, 2002, 237, 448.
13. H. Nonomura, H. Fujisawa, M. Shimizu, H. Niu and K. Honda, Jpn. J. Appl. Phys., 2003, 42, 5918.
14. V. A. Shchukin and D. Bimberg, Rev. Mod. Phys., 1999, 71, 1125.
15. M. Alexe, A. Gruverman, C. Harnagea, N. D. Zakharov, A. Pignolet, D. Hesse, H. Niu and J. F. Scott, Appl. Phys. Lett., 1999, 75, 1158.
16. D. Hunter, J. B. Dadson, K. Zhang, B. Lasley, K. Lord, T. M. Williams, R. R. Rakhimov, J. Zhang and D. J. Sellmyer, J. Appl. Phys., 2006, 99, 08Q307.
17. A. K. Pradhan, J. B. Dadson, D. Hunter, K. Zhang, S. Mohanty, E. M. Jackson, B. Lasley-Hunter, K. Lord, T. M. Williams and R. R. Rakhimov, J. Appl. Phys., 2006, 100, 033903.
18. P. E. Blochl, C. Joachim and A. J. Fisher, Computations for the Nanoscale, Springer Science, France, 1993.
19. B. Voigtlander, M. Kawamura, N. Paul and V. Cherepanov, J. Phys.: Condens. Matter, 2004, 16, S-1535.
20. U. Kohler, J. E. Demuth and R. J. Hamers, J. Vac. Sci. Technol., A, 1989, 7, 2860.
21. A. Tselev, R. K. Vasudevan, A. G. Gianfrancesco, L. Qiao, P. Ganesh, T. L. Meyer, H. N. Lee, M. D. Biegalski, A. P. Baddrof and S. V. Kalinin, ACS Nano, 2015, 9, 4316.
22. S. K. Singh, S. B. Palmer, D. McK Paul and M. R. Lees, Appl. Phys. Lett., 1996, 69, 263.
23. H. Naganuma, Y. Inoue and S. Okamura, Appl. Phys. Express, 2008, 1, 061601.
24. M. Fukunaga and Y. Noda, J. Phys. Soc. Jpn., 2008, 77, 064706.
25. J. F. Scott, Integr. Ferroelectr., 1996, 12, 71.
26. Y. Ishibashi and Y. Takagi, J. Phys. Soc. Jpn., 1971, 31, 506.
27. S. Mo Yang, J.-G. Yoon and T. W. Noh, Curr. Appl. Phys., 2011, 11, 1111.
28. A. K. Tagantsev, I. Stolichnov, N. Setter, J. S. Cross and M. Tsukada, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 214109.
29. J. Y. Jo, H. S. Han, J.-G. Yoon, T. K. Song, S.-H. Kim and T. W. Noh, Phys. Rev. Lett., 2007, 99, 267602.
30. W. Merz, Phys. Rev., 1954, 95, 690.
31. R. C. Miller and G. Weinreich, Phys. Rev., 1960, 117, 1460.
32. W. Wernsdorfer, B. Doudin, D. Mailly, K. Hasselbach, A. Benoit, J. Meier, J.-P. Ansermet and B. Barbara, Phys. Rev. Lett., 1996, 77, 1873.
33. R. H. Victora, Phys. Rev., 1989, 63, 457.
34. K. B. Chong, F. Guiu and M. J. Reece, J. Appl. Phys., 2008, 103, 014101.
35. C. D. Allemand, Appl. Spectrosc., 1970, 24, 348.
36. D. Pantel, Y.-H. Chu, L. W. Martin, R. Ramesh, D. Hesse and M. Alexe, J. Appl. Phys., 2010, 107, 084111.
37. K. Nagata and I. Iida, Ferroelectrics, 1989, 94, 249.
38. S. Horiuchi and Y. Tokura, Nat. Mater., 2008, 7, 357.

---