Magnetic manipulation of electric orders in Co₄NbTaO₉

Abstract

Magnetic, dielectric and magnetoelectric properties of the polycrystalline Co₄NbTaO₉ have been investigated in this paper. The antiferromagnetic phase transition of this compound is identified at the temperature of 23.6 K. Anomalies in the temperature-dependent dielectric constants and pyroelectric currents emerge around its magnetic transition point under magnetic field, and increase with the increasing external magnetic field. Antiferromagnetic fluctuation and domain effect are considered to be response for the phenomenon observed in this compound.

---

1. Introduction

Materials with A₄B₂O₉ structure have received a great deal of attention for their rich interplay among charge, spin, and orbital degrees of freedom.^1–9 Many fascinating physical and chemical properties, such as linear coupling between magnetic and electric orders, multiferroic behaviors, microwave dielectric properties, and photocatalytic activities, have been observed in this type of functional materials.^1–12 As members of this family, large variations in chemical composition are allowed, for example, A = Mg²⁺, Ca²⁺, Sr²⁺, Ba²⁺, Mn²⁺, Fe²⁺, Co²⁺, Ni²⁺, Cu²⁺, Zn²⁺, Cd²⁺, Pb²⁺; and B = Nb⁵⁺, Ta⁵⁺, V⁵⁺, etc.^1–22 So many different combinations make the resultant products show various interesting performances. As reported, when A and B sites are substituted by Mg and Nb atoms respectively, a corundum-type compound with the chemical formula Mg₄Nb₂O₉ is generated, which exhibits pronounced microwave dielectric properties.^10,11 Another example, Sr₄Ta₂O₉ can be served as a prototype material to split water into H₂ and O₂ due to its photocatalytic activities.¹² Recently, it is found that with the cooperative substitutions of bivalent magnetic cations (Mn, Co, and Ni) and alkali-earth cations (Sr, Ba) for A sites, series of antiferromagnets develop in the form of two-dimensional triangular lattices, which show celebrated magnetic properties like spin frustration and strong quantum spin fluctuation at low temperature.^23–26 Among them, several trigonal antiferromagnets like Ba₃NiNb₂O₉, Sr₃NiTa₂O₉, Ba₃MnNb₂O₉, and Ba₃CoNb₂O₉ with effective spin-1 or spin-1/2 present successive striking magnetic transitions accompanying magnetic multiferroicity.^23–26

When A = Co, an interesting family of materials is formed, which crystallizes in α-Al₂O₃ type structure and contains two different crystallographic positions occupied with magnetic ions.^{1–4,6,7,20,21} Two representative members in this family, of which the B sites are replaced by Nb or Ta, were discovered in the 1960s by Bertaut et al.¹⁶ As reported, both of the two materials are stacked in a hexagonal crystal structure corresponding to the space group P3̄C1, which can be derived from the corundum structure. In these materials, the oxide-anion layers closely pack with two-third of the octahedral sites filled by Co and Nb (Ta) ions in an ordered 2 : 1 ratio. Thereinto, one sheet is built up of alternating edge-sharing Co_IO₆ and NbO₆ octahedras, while the neighboring sheet is constituted with Co_IIO₆ octahedras by sharing edges. The two sheets, which are in forms of hexagonal rings centered on the threefold axis, are alternatively stacked. The crystal symmetries have been established ever since they were firstly synthesized, while their spin configures are still under debate. As assumed by Schwarz et al., the magnetic moments of Co or Mn form chains parallel to the c-axis with chain–chain antiferromagnetic coupling.²⁰ While, different opinions are proposed recently by Cao and Khanh et al. that the magnetic moments arrange in the basal plane with disparate magnetic symmetries rather than along the trigonal axis.^1,21 Nevertheless, the magnetoelectric effects of these materials have been confirmed in poly- and single crystals, respectively.^1,3 Not only magnetically tunable electric polarization, but also electric control of magnetism has been detected in Co₄Nb₂O₉, which demonstrates that antiferromagnetic phase can be modified by electric field, showing a cross-control of magnetism and polarization in this compound.³ Moreover, several other investigations on magnetic or electric properties of these compounds have also been conducted. For instances, through substitution of Co by Mn, Schwarz et al. found that in a wide doping range the magnetic structure of these materials are consistent with the parent phase Co₄Nb₂O₉, which indicates that linear coupling between magnetic and electric properties can be expected in (Co_1−xMn_x)₄Nb₂O₉.²⁰ Besides, Dhanasekhar et al. recently found that Fe-substituted Co₄Nb₂O₉ show low-field magnetoelectric effect with no variation of the spin-flop fields.⁷ Those results manifest that the materials with Mn- or slight Fe-substitution reserve the linear magnetoelectric effect of Co₄Nb₂O₉, which indicates the spin configures could keep unchanged. In this manuscript, polycrystalline Co₄NbTaO₉ is prepared to study its magnetic and electric properties. It is found that linear magnetoelectric effect still work when partial Nb ions are replaced by Ta ions, from which indirect information of magnetic structure can be obtained by characterizing the magnetoelectric performances.

2. Experimental details

Polycrystalline Co₄NbTaO₉ samples were prepared by conventional solid sintering method. The highly purified powder of Co₃O₄, Nb₂O₅ and Ta₂O₅ were chosen as raw materials and thoroughly ground together in stoichiometric ratio, followed by annealing at 1173 K for 10 h in muffle furnace. The resultant products were pelletized and then sintered at 1373 K for 5 h in air with intermediate grindings. The phase purity and crystallinity of these samples were checked by the X-ray diffraction (XRD) with Cu kα radiation and normal θ–2θ scanning method at room temperature. Refinement of the XRD data was performed using Rietveld method in the general structure analysis system (GSAS) program. The morphology and elemental mappings were examined by scanning electron microscope (Zeiss, Germany) with energy-dispersive-spectroscopy (EDS). The temperature dependent magnetization was obtained using the superconducting quantum interference device magnetometer (SQUID, Quantum Design). With golden pastes depositing on the sample surfaces as electrodes, the dielectric property and electric polarization were measured by the physical properties measurement system (PPMS, Quantum Design). Dielectric properties of the resulting pellets were carried out by using a Precision Impedance Analyser (Agilent 4294 A). The polarization was obtained by integrating the pyroelectric current performed using a Keithley 6514 electrometer in the warming process at a rate of 3 K min⁻¹ without any electric bias. While, electric and magnetic field cooling (ME poling procedure) from a temperature above the Néel temperature (T_N) are indispensable to obtain single antiferromagnetic domains. In the process of pyrocurrent measurement, magnetic field was kept applying on the sample all along.

3. Results and discussion

Fig. 1(a) shows the room-temperature θ–2θ XRD spectra of Co₄NbTaO₉ along with Rietveld refinement. These patterns, in which no impurities are observed, are consistent with the standard hexagonal corundum phase with space group P3̄c1, revealing that these samples crystallize well. Energy dispersive spectroscopy (EDS) analysis (inset of Fig. 1(a)) shows that this compound mainly contains four kinds of chemical elements (Co, Nb, Ta and O) in a 4 : 1 : 1 : 9 atomic ratios within the instrumental accuracy. To further confirm the homogeneity, SEM measurements of the sample are performed. Fig. 1(b) shows the pore morphology of this compound, in which micrometer-scaled grains can be roughly evaluated. Moreover, the elemental mappings of Co₄NbTaO₉ have been characterized. As presented in Fig. 1(c)–(e), homogeneous distributions of Co, Nb, Ta and O are observed.

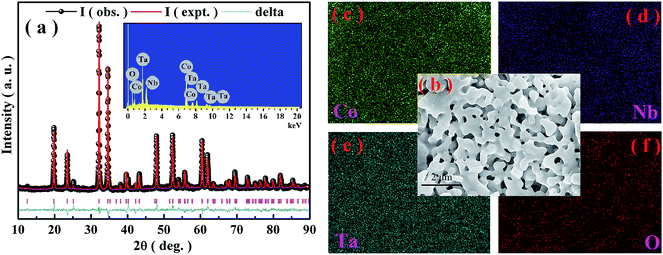Fig. 1 (a) Room temperature XRD patterns with Rietveld refinement and EDS (inset); (b) morphology; (c) Co-mapping; (d) Nb-mapping; (e) Ta-mapping; (f) O-mapping of Co₄NbTaO₉.

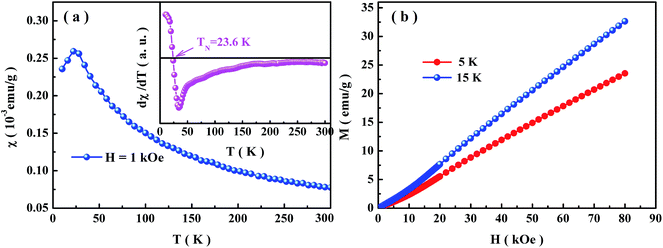
Fig. 2 shows the magnetic characterization of Co₄NbTaO₉. As plotted in Fig. 2(a), temperature dependence of the dc magnetic susceptibilities χ_dc(T) = M/H, which is determined from the measured magnetization (M) in the presence of an external magnetic field H_dc = 1 kOe, has been carried out for this compound. These data are presented for the traditional ZFC cooled cases. The significant features of these data are χ_dc(T) peaking at a temperature near 23 K, suggesting that antiferromagnetic exchange interaction plays a dominant role in determining the magnetic properties of Co₄NbTaO₉. In the inset of Fig. 2(a), the Néel temperature corresponding to the temperature where dχ_dc(T)/dT = 0 is obtained around 23.6 K. Below the ordered temperature, it can be observed that the magnetization increases upon increasing field and doesn't saturate even when the external field reaches 80 kOe (Fig. 2(b)), indicating that Co₄NbTaO₉ is antiferromagnet. Since only the Co²⁺ ions in this compound are magnetic, the effective magnetic moments μ_eff, which can be obtained by fitting linear part of the inverse magnetic susceptibility 1/χ_dc(T) between 200 and 300 K to the Curie–Weiss law χ_dc(T) = C/(T + T_θ) (C is the Curie–Weiss constant with a value of N_Aμ_eff²/3K_BT and T_θ is the Curie–Weiss temperature),²⁷ is found approximately to be 4.8 μ_B. The effective magnetic moment derived from the inverse magnetic susceptibility of Co₄NbTaO₉ has exceeded the spin-only value of Co²⁺ in the high spin configuration ,¹ which indicates that orbital angular moments make contributions via the spin–orbit coupling.

Fig. 2 (a) Temperature evolution of magnetization at 1 kOe after zero-field cooling from room temperature to 2 K; the inset shows the temperature-dependent dχ/dT, from which the absolute antiferromagnetic transition temperature can been obtained. (b) The field dependence of magnetization at 5 and 15 K, respectively.

The temperature-dependent dielectric constant under various magnetic fields is shown in Fig. 3. At zero magnetic field, the dielectric constant doesn't show any anomaly or peak in the measured temperature interval. On application of a magnetic field of 20 kOe, a feeble peak feature appears. And, the intensity of the peak becomes more and more pronounced with increasing the magnitude of magnetic field, demonstrating strong coupling between magnetism and dielectric properties. Interestingly, the dielectric peaks observed in magnetic field take place around the magnetic transition temperature, indicating the anomalies are from spin origin. As reported, the dielectric anomalies in the linear magnetoelectric material Co₄Nb₂O₉ are ascribed to antiferromagnetic fluctuation,⁴ which could be suitable for Co₄NbTaO₉ as well, since the crystal structure and magnetic properties of these two compounds are analogous.

Fig. 3 Temperature-dependent dielectric constants measured in the presence of different magnetic fields.

As mentioned above, Co₄NbTaO₉ would be a potential material to display magnetoelectric coupling effect, which stimulates us to verify this performance. Here, pyroelectric method are adopted to characterize the electric polarization of this compound, since the polarization originated from spin order is rather weak respected to those of the conventional ferroelectrics.²⁸ In Fig. 4, pyroelectric measurements have been conducted in zero electric field upon warming from low temperature (5 K) under a constant magnetic field. As illustrated, the pyroelectric current keeps in constant with the increasing temperature under zero magnetic field, which indicates that the ground state of this sample isn't polarized. However, after cooling the sample under the coaction of magnetic and electric field (20 kOe, 667 kV m⁻¹), the displacement current is released gradually with the increasing temperature, and reaches an apparent peak at about 23.6 K, following an abrupt drop down to zero, implying the electric polarization emerges in this compound. Noteworthily, the temperature, where the pyroelectric current peak arises, keeps consistent with the characteristic magnetic transition temperature of Co₄NbTaO₉, which indicates that the existence of possible relationship between electric polarization and magnetism. And then, when the sample are annealed in other three enhanced magnetic and electric field (40, 60 and 80 kOe, 667 kV m⁻¹), the current peaks, of which the intensities increase with the increasing magnetic field, still show up at the magnetic transition temperature. Those results suggest that the electric polarization of Co₄NbTaO₉ can be enhanced by the external magnetic field. To check the reliability of electric polarization in this compound, the temperature-dependent pyroelectric current with different warming rates (1, 3, and 5 K min⁻¹) are detected after the sample is cooled under magnetic and electric field simultaneously (80 kOe, 667 kV m⁻¹).²⁹ As presented in the inset of Fig. 4, the onset temperature of current peaks keep consistent, and the integrations of three I–T curves are almost identical (not shown), which demonstrates that the pyroelectric current is intrinsic.²⁹

Fig. 4 Pyroelectric current as a function of temperature under different magnetic fields. The inset shows the measured pyroelectric current under 80 kOe in warming procedure at 1, 3, and 5 K min⁻¹.

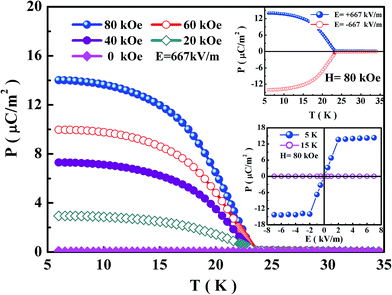
To intuitively reveal the relationship between magnetic and electric properties of Co₄NbTaO₉, temperature-dependent pyroelectric current under various magnetic fields have been integrated. Results for the electric polarization are illustrated in Fig. 5. As shown, no electric polarization can be observed under zero magnetic field, which is consistent with the pyrocurrent measurement. However, when this compound experiences annealing in the magnetic field of 20 kOe, a remarkable electric polarization emerges below the magnetic ordered temperature. Moreover, upon increasing the external magnetic field, the electric polarization increases monotonously. Up to 80 kOe, the value of electric polarization reaches 14 μC m⁻², which can be compared to those of NdCrTiO₅, MnTiO₃, Cr₂O₃, FeSb₂O₄ and MnGa₂O₄, manifesting that the magnetoelectric effect in this compound is considerable.^30–34 Through plotting the magnetic-field dependent electric polarization under 5 and 15 K, it can be found that polarization increases proportional to the magnetic field (not shown), which demonstrates that this compound behaves as a linear magnetoelectric material. To verify the reliability of the spin-related polarization in Co₄NbTaO₉, electric polarization as a function of the temperature has been characterized under positive and negative poling electric fields respectively. As shown in the upper inset of Fig. 5, a rather symmetric temperature-dependent polarization curve is observed, indicating that the electric polarization can be reversed by electric field. Finally, the effect of poling electric field on polarization under 80 kOe is summarized in the lower inset of Fig. 5. As presented, no variation of the polarization with applied electric field is observed at 30 K which slightly exceeds the magnetic transition temperature, suggesting that this sample isn't polarized at this temperature. While, the polarization at 5 K can be reversed by electric field, showing a typical ferroelectric-like behavior in magnetic ordered state. This phenomenon of electric-field dependent polarization, in which polarization can be overturned by the applied electric field, could be ascribed to switching of the antiferromagnetic domains.^1,32 Besides, the electric polarization of this compound initially increase with increasing electric field, and then become saturated and independent to the electric field up to 7 kV cm⁻¹, demonstrating that the magnetoelectric domains kept stabilities during the poling process as well.

Fig. 5 Temperature-dependent electric polarization under various magnetic fields. The upper inset plots the symmetric temperature-dependent polarization curve under different cooling condition. The lower inset shows the poling electric field dependence of polarization at 80 kOe.

The linear magnetoelectric effect has been extensively investigated in many other antiferromagnetic materials like Cr₂O₃, MnTiO₃, NdCrTiO₅, FeSb₂O₄, MnGa₂O₄, and so on, in which magnetic-field induced electric polarization arises in their long-rang magnetic phase.^30–34 According to the earlier studies, domain effect can be responsible for this special magnetoelectric behavior of these materials. The experiments performed by Brown et al. using spherical neutron polarimetry show that these linear magnetoelectric compounds are antiferromagnets, in which two different antiferromagnetic domains with equal volume fractions and opposite magnetoelectric coefficients exist.³⁵ Generally, to obtain a magnetoelectric effect in those antiferromagnetic materials, magnetoelectric annealing, which means cooling the samples in applied magnetic and electric field, is necessary.^{1–4,30–34} Under zero magnetic field, no magnetoelectric response has been detected, indicating that the ground state isn't polarized, which is ascribed to the cancellation of the magnetoelectric effect of those domains. While, after annealing the sample in magnetic and electric field simultaneously, one type of the antiferromagnetic domains would dominate over the other ones, which leads to appearance of the net magnetoelectric effect. As for Co₄NbTaO₉, it exhibits typical antiferromagnetic behavior and linear response between magnetic and electric ordering below the Néel temperature, which suggests that domain effect could take responsibilities for the coupling performances as well. To further understand the magnetoelectric effect in this compound, microscopic mechanism for this performance should be discussed. From the view of spin-driven electric polarization, three main mechanisms are proposed to understand the magnetoelectric effects in those single-phase materials.^36–38 One of them called spin-current model (inverse Dzyaloshinskii–Moriya (DM) interaction), which successfully explains the relationships between electric and magnetic orders in those magnetic multiferroics like Tb(Dy)MnO₃, hexaferrite, MnWO₄ and so on, involves spin–orbit coupling.^28,39–41 This relativistic term plays an important role in determining the spin-related ferroelectric polarization of those materials with spiral or cyclical magnetic structure, which also acts as a key factor for the occurrence of linear magnetoelectric effect in single-phase materials. According to the earlier report, Scaramucci et al. found that orbital contributions can take effect in some linear magnetoelectric compounds with large spin–orbit coupling and low symmetry polar oxygen coordination, which is verified in Cr₂O₃, LiCoPO₄, and TbPO₄.⁴² With regard to Co₄NbTaO₉, linear responses between magnetic and electric order are observed, which is similar to those in the pure and Mn- (Fe-) doped Co₄Nb₂O₉, suggesting that the magnetic configures of these materials could be identical. Besides, the spin structures of Co₄Nb₂O₉ imitates that of Cr₂O₃, which indicates that the magnetoelectric effect of these two materials have the same approach. Based on this, the spin-induced electric polarization in Co₄NbTaO₉ could partially originate from the contributions of orbital degrees of freedom, since it shows strong spin–orbit couplings and crystallizes in a hexagonal structure, both of which are same with those of Co₄Nb₂O₉ and Cr₂O₃.

4. Conclusion

In summary, we have synthesized polycrystalline Co₄NbTaO₉ to investigate its crystal structure, magnetic, electric properties and the coupling effect between electric and magnetic degrees of freedoms. This compound crystallized in group space P3̄C1, and each constituted element distributes homogeneously. The dielectric anomaly and electric polarization develop below the Néel temperature only when an external magnetic field is applied, and increase with the increasing magnetic field. From traditional views, the observed magnetoelectric effect in Co₄NbTaO₉ can be ascribed to domain effect, while orbital contributions has also been taken into consideration for understanding this special magnetoelectric performances in an alternative way. These phenomenon emerged in this compound implies fascinating physics behind and potential application prospect for information storage.

Acknowledgements

This work is supported by the Natural Science Foundation of Jiangsu Province (BK20150392), Zhejiang Provincial Natural Science Foundation of China (Grant No. LQ15A040006), National Natural Science Foundation of China (Grant No. 11604027, 11374043, 11174043 and 51371004), Natural science fund for colleges and universities in Jiangsu Province (Grant No. 14KJB480001) and Public Projects of Zhejiang Province (Grant No. 2013C31073).

References

1. N. D. Khanh, N. Abe, H. Sagayama, A. Nakao, T. Hanashima, R. Kiyanagi, Y. Tokunaga and T. Arima, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 075117.
2. T. Kolodiazhnyi, H. Sakurai and N. Vittayakorn, Appl. Phys. Lett., 2011, 99, 132906.
3. Y. Fang, Y. Q. Song, W. P. Zhou, R. Zhao, R. J. Tang, H. Yang, L. Y. Lv, S. G. Yang, D. H. Wang and Y. W. Du, Sci. Rep., 2014, 4, 3860.
4. Y. P. Lu, C. X. Ji, Y. L. Sun, Y. Fang, L. Zhang, Z. D. Han, B. Qian, X. F. Jiang and W. P. Zhou, J. Alloys Compd., 2016, 679, 213–217.
5. Y. Fang, W. P. Zhou, S. M. Yan, R. Bai, Z. H. Qian, Q. Y. Xu, D. H. Wang and Y. W. Du, J. Appl. Phys., 2015, 117, 17B712.
6. I. V. Solovyev, and T. V. Kolodiazhnyi, arXiv:1606.06394, 2016.
7. C. Dhanasekhar, S. K. Mishra, R. Rawat, A. K. Das, and A. Venimadhav, arXiv:1606.04689, 2016.
8. Y. Fang, S. Yan, L. Zhang, Z. Han, B. Qian, D. Wang and Y. Du, J. Am. Ceram. Soc., 2015, 98, 2005–2007.
9. B. B. Liu, Y. Fang, Z. D. Han, S. M. Yan, W. P. Zhou, B. Qian, D. H. Wang and Y. W. Du, Mater. Lett., 2016, 164, 425–427.
10. A. Kan and H. Ogawa, J. Alloys Compd., 2004, 364, 247–249.
11. A. Kan, H. Ogawa, A. Yokoi and Y. Nakamura, J. Eur. Ceram. Soc., 2007, 27, 2977–2981.
12. K. Yoshioka, V. Petrykin, M. Kakihana, H. Kato and A. Kudo, J. Catal., 2005, 232, 102–107.
13. A. B. Gaikwadd, S. C. Navalea, V. Samuelc, A. V. Muruganb and V. Ravi, Mater. Res. Bull., 2006, 41, 347–353.
14. H. Ehrenberg, G. Wltschek, H. Weitzel, F. Trouw, J. H. Buettner, T. Kroener and H. Fuess, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 9595.
15. O. Khamman, J. Jainumpone, A. Watcharapasorn, and S. Ananta, arXiv:1605.06952, 2016.
16. E. F. Bertaut, L. Corliss, F. Forrat, R. Aleonard and R. Pauthenet, J. Phys. Chem. Solids, 1961, 21, 234–251.
17. M. Waburg and H. Müller-Buschbaum, Monatsh. Chem., 1986, 117, 131–138.
18. N. V. Tarakina, A. P. Tyutyunnik, V. G. Zubkov, T. V. D'yachkova, Y. G. Zainulin, H. Hannerz and G. Svensson, Solid State Sci., 2003, 5, 459–463.
19. A. Blonska-Tabero, J. Therm. Anal. Calorim., 2008, 93, 707.
20. B. Schwarz, D. Kraft, R. Theissmann and H. Ehrenberg, J. Magn. Magn. Mater., 2010, 322, L1–L3.
21. Y. Cao, Y. Yang, M. Xiang, Z. Feng, B. Kang, J. Zhang, W. Ren and S. Cao, J. Cryst. Growth, 2015, 420, 90–93.
22. C. D. Ling, M. Avdeev, R. Kutteh, V. V. Kharton, A. A. Yaremchenko, S. Fialkova, N. Sharma, R. B. Macquart, M. Hoelzel and M. Gutmann, Chem. Mater., 2009, 21(16), 3853–3864.
23. J. Hwang, E. S. Choi, F. Ye, C. R. Dela Cruz, Y. Xin, H. D. Zhou and P. Schlottmann, Phys. Rev. Lett., 2012, 109, 257205.
24. M. Liu, H. Zhang, X. Huang, C. Ma, S. Dong and J. Liu, Inorg. Chem., 2016, 55(6), 2709–2716.
25. M. Lee, E. S. Choi, X. Huang, J. Ma, C. R. Dela Cruz, M. Matsuda, W. Tian, Z. L. Dun, S. Dong and H. D. Zhou, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224402.
26. M. Lee, J. Hwang, E. S. Choi, J. Ma, C. R. Dela Cruz, M. Zhu, X. Ke, Z. L. Dun and H. D. Zhou, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 104420.
27. K. Matsuhira, Y. Hinatsu, K. Tenya and T. Sakakibara, J. Phys.: Condens. Matter, 2000, 12, L649.
28. T. Kimura, T. Goto, H. Shintani, K. Ishizaka, T. Arima and Y. Tokura, Nature, 2003, 426, 55–58.
29. L. Zhao, T.-L. Hung, C.-C. Li, Y.-Y. Chen, M.-K. Wu, R. K. Kremer, M. G. Banks, A. Simon, M.-H. Whangbo, C. Lee, J. S. Kim, I. Kim and K. H. Kim, Adv. Mater., 2012, 24, 2469–2473.
30. J. Hwang, E. S. Choi, H. D. Zhou, J. Lu and P. Schlottmann, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 024415.
31. N. Mufti, G. R. Blake, M. Mostovoy, S. Riyadi, A. A. Nugroho and T. T. M. Palstra, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 104416.
32. A. Iyama and T. Kimura, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 180408.
33. A. Iyama, Y. Wakabayashi, N. Hanasaki and T. Kimura, Jpn. J. Appl. Phys., 2014, 53, 05FB02.
34. R. Saha, S. Ghara, E. Suard, D. H. Jang, K. H. Kim, N. V. Ter-Oganessian and A. Sundaresan, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 014428.
35. P. J. Brown, J. B. Forsyth and F. Tasset, J. Phys.: Condens. Matter, 1998, 10, 663–672.
36. H. Katsura, N. Nagaosa and A. V. Balatsky, Phys. Rev. Lett., 2005, 95, 057205.
37. S. Ishiwata, Y. Kaneko, Y. Tokunaga, Y. Taguchi, T.-H. Arima and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 100411.
38. T. H. Arima, J. Phys. Soc. Jpn., 2011, 80, 052001.
39. N. Abe, K. Taniguchi, H. Umetsu, S. Ohtani and T. Arima, J. Phys.: Conf. Ser., 2010, 200, 012001.
40. T. Kimura, Annu. Rev. Condens. Matter Phys., 2012, 3, 93–110.
41. O. Heyer, N. Hollmann, I. Klassen, S. Jodlauk, L. Bohatý, P. Becker, J. A. Mydosh, T. Lorenz and D. Khomskii, J. Phys.: Condens. Matter, 2006, 18, L471.
42. A. Scaramucci, E. Bousquet, M. Fechner, M. Mostovoy and N. A. Spaldin, Phys. Rev. Lett., 2012, 109, 197203.

---