Insight into the defect–molecule interaction through the molecular-like photoluminescence of SiO₂ nanoparticles

Abstract

Luminescence properties due to surface defects in SiO₂ are the main keystone with particles that have nanoscale dimensions, thus motivating their investigation for many emission related applications in the last few decades. A critical issue is the role played by the atmosphere that, by quenching mechanisms, weakens both the efficiency and stability of the defects. A deep knowledge of these factors is mandatory in order to properly limit any detrimental effects and, ultimately, to offer new advantageous possibilities for their exploitation. Up to now, quenching effects have been interpreted as general defect conversion processes due to the difficulty in disentangling the emission kinetics by the action of the specific quenchers. To overcome this limit, we report a time-resolved investigation of the effects induced in specific controlled molecular environments (N₂, O₂, CO₂ and H₂O) on the exceptional molecular-like luminescence that is observed around 3.0–3.4 eV in SiO₂ nanoparticles. A comparison with the effects under vacuum indicates changes of the luminescence intensity and lifetime that agree with two quenching mechanisms, static and dynamic. The peculiarity of the spectral features, together with a powerful investigation approach, makes this the system of choice to probe inside the dynamics of the molecule–defect interactions and to reveal promising characteristics for molecular-sensing purposes.

---

1 Introduction

In the last few decades, nanomaterials have received great interest due to the pivotal role played by the high specific surface area that arises when nanoscale sizes are reached (S ≥ 100 m² g⁻¹). The reduced size imposes constraints on the surface, thereby introducing defects which lead to the development of localized electronic states, so that optical activity may arise. In such a manner, the nanostructures become nanoemitters that can accomplish appealing and smart solutions in modern technological fields, from lighting to photovoltaics and photonics, biomedical applications, sensing and analytical measurements.^1–7 However, it is difficult to look at the emission properties of the surface states excluding the interplay between the defects and the surroundings. If, on the one hand, the interaction with the environment can adversely affect the stability of the emitting defects, then alternatively, its controlled modulation can play an advantageous role, which allows us to make nanoparticles into real nanoprobes.^5,6,8–10

In this respect, silica nanoparticles (SiO₂ NPs) stand out as a paradigmatic system. The characteristic and wide photon emissivity (from IR to UV) of SiO₂ NPs, due to peculiar defects on the surface,^11–16 strongly depends on their interactions with external factors. In our previous work,¹⁷ the irradiation-induced conversion toward stable and metastable configurations of the luminescent defects was already pointed out. More recently,⁷ this issue has been placed at the forefront through a study, at the single particle level, of the photostability of luminescent defects. Likewise, the role of these molecules in the environment is critical when determining both the stability and efficiency of the luminescent centers. Many examples are reported in the literature in which quenching and/or a shift of the emission properties are observed under controlled atmosphere conditions.^14,18–23 General conversion processes are supposed to explain the phenomenological observations, all of them involving transformations of the defects in non-emitting complexes through reactions with the specific atomic or molecular species. However, a deep understanding of the dynamics of the interactions is lacking, the role of the quenchers being unclarified in the process. In fact, the mechanisms underlying the quenching effect dramatically depend on the defect–quencher interaction, which can affect the concentration of the luminescent defects through physico-chemical reactions (static quenching), or by changing the quantum yield of the emission process due to collisions (dynamic quenching).²⁴

The knowledge of such emission-related mechanisms is mandatory in order to limit the detrimental effects of the quenching, especially if a high luminescence efficiency is required. On the other hand, modulation of such effects definitely reveals great opportunities for using SiO₂ NPs as luminescent probes in sensing. In order to have an attractive sensor, in addition to high sensitivity, an ideal requirement is an antenna-like response which makes it possible to appreciate point by point variations. Therefore, it is more convenient to deal with very sharp spectral lines that are characteristic of an isolated chromophore, rather than with the broad emission bands generally observed from SiO₂ NPs. Notwithstanding, after vacuum treatment, an unusually sharp vibronic emission at room temperature is found in the UV spectrum of SiO₂ NPs, between 3.0 eV and 3.5 eV.^20,23 In it, two vibrational progressions of frequency ∼1370 cm⁻¹ and ∼360 cm⁻¹ are singled out, with outstanding homogeneous characteristics resembling those of a molecular-like system.^23,25 The observation of two vibration modes is consistent with a defect structure containing more than two atoms and, even though these vibrational frequencies are in agreement with the stretching and bending calculated for O₂ related defects,²⁶ the clear attribution of the structured PL is still debated. As it only appears in a vacuum, one hypothesis is that it originates from a surface defect. Its disappearance in air implies sensitivity to the molecules of the atmosphere. Therefore, whatever the structure of the emitting center, all of the features pioneer new perspectives on the sensing applications of luminescent SiO₂ NPs.

In this work, after demonstrating that the defects are located at the surface of SiO₂ NPs, a detailed investigation of both the structured emission spectrum and its lifetime under controlled atmospheres will highlight that this peculiar emission is selectively sensitive to the effects induced by the specific molecular species that compose the ambient atmosphere, both non-polar (N₂, O₂, CO₂) and polar (H₂O). By means of this study, the chance to go deep into the dynamics of the quenching mechanism will be presented, discerning their origin as due to a reduction of the luminescent species or a decreasing of the quantum yield.

2 Experimental method

We have studied different types of Aerosil® fumed SiO₂ NPs provided in powder form by Evonik-Industries. Their structural and morphological properties, given by XRD, IR, SEM and TEM characterizations, are reported in the on-line catalog.²⁷ The values of specific surface area (S) and diameter (d) of the NPs, used for the present investigation, are reported in Table 1. In order to obtain self-supporting samples, the powder was pressed at 300 MPa into tablets of thickness ∼1 mm.

Table 1 Characteristics of the fumed SiO₂ NPs investigated in the present work²⁷

Fumed silica type (nickname)	S (m^2 g^−1)	d (nm)
Aerosil 300 (AE300)	300 ± 30	7 ± 1
Aerosil 200 (AE200)	200 ± 25	12 ± 2
Aerosil 150 (AE150)	150 ± 15	14 ± 2
Aerosil 90 (AE90)	90 ± 15	20 ± 2
Aerosil OX 50 (AE50)	50 ± 15	40 ± 2

---

The emission properties were studied using a time-resolved photoluminescence (PL) technique. Pulsed light at excitation energy E_exc = 3.69 eV (pulse width ∼5 ns, repetition rate 10 Hz) was provided by a VIBRANT OPOTEK optical parametric oscillator laser system, pumped by the third harmonic (3.50 eV) of a Nd:YAG laser. The fluence/pulse, monitored with a pyroelectric detector, was maintained at Φ = 0.2 mJ cm⁻². The emitted light was spectrally resolved by a monochromator (SpectraPro 2300i, PI/Acton) equipped with a grating with 300 grooves per mm and blazed at 500 nm. The spectra were acquired by an intensified charge coupled device (CCD) camera, driven by a delay generator (PI-MAX Princeton Instruments), that allows the time acquisition parameters (integration time ΔT and time delay T_D) to be set. All the spectra hereafter reported were detected with an emission bandwidth of 0.2 nm (∼2 meV in the 3.0–3.5 eV region of interest) and are corrected for the monochromator dispersion. The reliability of the intensity measurements was guaranteed both by repeatability tests and by acquisitions averaged over 60 spectra. In this way the fluctuations due to the laser radiation were minimized and the signal to noise ratio was enhanced; the uncertainty of 1% is associated with the intensity values. PL measurements were performed by placing the sample in a cryostat in a standard front scattering geometry. A vacuum pump was used to stabilize the pressure down to 10⁻⁷ kPa. Once vacuum was achieved, by connecting the cryostat to different gas tanks, PL spectra were also acquired under N₂, O₂ and CO₂ atmosphere. Moreover, by putting highly pure water in a vessel, pre-evacuating and connecting it to the sample chamber, measurements under H₂O atmosphere were performed. In all cases, a fixed gas pressure of about 0.1 kPa was maintained in the cryostat.

3 Results and discussion

The systematic study of PL dependency on the sizes of SiO₂ NPs is shown in Fig. 1. The graph was obtained by acquiring the spectrum for each sample that was emitted under vacuum, and reporting the peak intensity at E_em = 3.34 eV as a function of the specific surface. In the inset, two representative spectra are shown. All the intensities are normalized with respect to the value recorded in the AE300 sample (I_AE300). No difference is noticeable in either the shape of the spectra or in the peak positions, thus indicating that these features do not depend on the particle size. On the other hand, the monotonic increasing of the PL signal upon increasing the specific surface area clearly proves that the defects responsible for this PL activity are located at the surface of the SiO₂ NPs. The observed trend can be accounted for by a power law of the type I ∝ S^m. Through a best fit analysis, carried out using the function log(I/I_AE300) = m log(S), m = 2.17 ± 0.10. The PL intensity is proportional to the number of emitting centers in the excited state (N). Indicating with σ the surface defect density (N/S), the non-linear trend can be interpreted as an almost linear increasing of σ with increasing S. In turn, the higher the value of S, the higher the probability of finding the defects on the surface. This finding relates the origin of the defects to the bond strains on the surface, which are stronger when the curvature radius of the NPs is decreased.²⁸ On this basis, the results obtained for the highest specific surface area sample will be presented from here on, it being understood that they are general for all types of material under investigation.

Fig. 1 Logarithmic plot of the PL intensity monitored at E_em = 3.34 eV in a vacuum as a function of the specific surface area of the samples under investigation. The intensity values are normalized to those detected in the AE300 sample. The red line is the best fit curve of the data. The inset shows the spectra emitted by the AE300 (black line) and AE150 (blue line) samples.

Since the structured PL is specific only to the vacuum condition and is strongly reduced in ambient atmosphere (by a factor of 100), the surface defects are sensitive to the molecules of the air. By interacting with them, these species lead to PL quenching. To go inside this mechanism, the defect–molecule interaction was investigated by selecting some of the most abundant molecules of the atmosphere. The effect induced on the features of the PL, due to the interaction of the defects with N₂, O₂, CO₂ and H₂O, is reported in the four panels of Fig. 2. All spectra are normalized to the intensity monitored in a vacuum at E_em = 3.34 eV. This comparison points out that the PL is reduced by 20% under N₂ (a), 50% in O₂ (b), 30% under CO₂ (c) and 60% if H₂O molecules are in the environment (d). It is worthwhile to note that, consistent with the spectrum acquisition time (90 s), the emission features reported in Fig. 2 are those observed immediately after connecting the sample chamber to the specific molecules’ reservoir. However, as evidenced by the kinetics shown in the four panels of Fig. 3, not only these effects are stable over the time but they are also reversible. The graphs were obtained by progressively acquiring the spectra emitted by the sample as a function of time, during which cyclic exposures to the different molecules were performed. Since, during the kinetics, variations were not observed in the PL shape or in the peak positions, the PL intensity at E_em = 3.34 eV is reported in the various plots as a function of time. In all cases the PL intensity is normalized to the value in a vacuum at the beginning of the experiments. Systematically, the intensity maintains its quenching value during exposure to the specific environment and comes back to the initial value once the vacuum conditions are restored.

Fig. 2 Comparison between the PL emitted in a vacuum and in N₂ (a), O₂ (b), CO₂ (c) and H₂O (d). All the spectra are acquired with ΔT = 250 ns and T_D = 115 ns and are normalized to the intensity monitored in a vacuum at E_em = 3.34 eV.

Fig. 3 PL intensity monitored at E_em = 3.34 eV under cyclic exposure to N₂ (a), O₂ (b), CO₂ (c) and H₂O (d). The values are normalized to the intensity in a vacuum at the beginning of the kinetics. The rectangles highlight the time intervals during which the system is under the specific atmosphere.

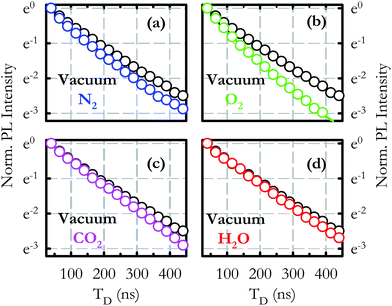
Investigation of the lifetime τ under the different atmospheres was also carried out and comparison with the decay in a vacuum is presented in the four panels of Fig. 4. All the curves are obtained by monitoring the PL intensity at E_em = 3.34 eV as a function of T_D. With respect to the vacuum condition, τ (graphically intended as the time necessary to reduce the PL intensity by a factor e) decreases in N₂ and O₂, whereas it remains almost the same under CO₂ and H₂O. In all cases non-pure exponential trends are observed. This effect was already known in a vacuum and it was attributed to the inhomogeneous distribution of decay rates of the luminescent defects.²³ It looks likely that such an inhomogeneity is also reflected in the lifetime in controlled atmospheres. In order to obtain an accurate quantitative estimation, each τ is derived by best fitting the curves with the stretched exponential function I(t) = I₀e^−(t/τ)γ, γ being the stretching parameter.²⁹ In a vacuum τ_v = (142 ± 1) ns, whereas τ = (111 ± 1) ns in N₂, τ = (95 ± 1) ns in O₂, τ = (139 ± 2) ns in CO₂ and τ = (142 ± 2) ns in H₂O.

Fig. 4 Comparison between the PL decay monitored in a vacuum and in N₂ (a), O₂ (b), CO₂ (c) and H₂O (d). For viewing purposes, the graphs are presented in a semilogarithmic scale and are obtained by detecting the peak intensity at E_em = 3.34 eV from T_D = 40 ns to T_D = 450 ns with ΔT = 25 ns. All the curves are normalized to the intensity at T_D = 40 ns.

For the sake of completeness, the same experiment was carried out under He atmosphere and no difference with respect to the vacuum condition was observed, both in the PL intensity and lifetime. The lack of any variation when an inert gas was in the environment reveals that the quenching observed under the other atmospheres is the real effect of the defect–molecule interaction. On the other hand, at the pressure value under which the experiments were performed (0.1 kPa), phenomena like light attenuation due to the presence of gas in the sample chamber are ruled out.

The overview of the results listed in Table 2 allows discussion of these findings by using different levels of detail. At first sight, the PL intensity under controlled atmosphere is weaker than that monitored in a vacuum, with the quenching extent being dependant on the species in the environment. Therefore, regardless of the origin of the process, it is possible to exactly identify each molecule only by looking at the effect induced on the PL spectrum due to the defect–molecule interaction. From this point of view, this finding reveals the potential of this system as a luminescent sensor for molecules, at least for the species that have been taken into account. In this regard, however, this is just the first insight towards all the investigations which are necessary to make this potential into a reality. In fact, a systematic analysis on varying the molecules concentration (Stern–Volmer study) is needed in order to fix the detection limits.²⁴

Table 2 Quantitative results derived from Fig. 2 and 4 by monitoring the intensity (I) and lifetime (τ) of the peak at E_em = 3.34 eV under the different atmospheric conditions. The values are normalized to the corresponding conditions under vacuum (I_v and τ_v)

Environments	I/Iv	τ/τv
N2	0.80 ± 0.01	0.78 ± 0.01
O2	0.49 ± 0.01	0.67 ± 0.01
CO2	0.67 ± 0.01	0.98 ± 0.01
H2O	0.41 ± 0.01	1.00 ± 0.01

---

The causes of quenching in the controlled atmosphere can also be investigated. Can the observed quenching effects be interpreted according to a unique process? In order to address this issue, comparison between the emission efficiency under controlled atmosphere and in a vacuum is required. In the latter case, as schematically sketched in Fig. 5(a), the quantum efficiency, η_v, is determined by radiative and non-radiative decay rates (k_r and k_nr, respectively) through the relation: η_v = k_r/(k_r + k_nr) = k_rτ_v.

Fig. 5 Schematic representation of the excitation/emission kinetics of the defect in a vacuum (a) and in N₂ (b), causing a dynamic PL quenching process, and in H₂O (c), where the PL decrease is due to a static quenching mechanism.

Under a N₂ atmosphere, τ/τ_v < 1. Since I/I_v = τ/τ_v, a dynamic mechanism is at the origin of the quenching, with collisions between the N₂ molecules and the defects being responsible.²⁴ As depicted in Fig. 5(b), such collisions provide the defects with an additional non-radiative channel to dissipate the energy from the excited state, with a decay rate k_col. The quantum efficiency observed in N₂ can be written as η_N2 = k_r/(k_r + k_nr + k_col) = k_rτ_N2, with η_N2 < η_v. Ultimately this means that, with respect to the vacuum, the quenching observed in N₂ is due to a decrease in the efficiency of the emission process.

Both in CO₂ and H₂O, the lifetime does not follow the reduction of the PL intensity, remaining unchanged with respect to the vacuum (τ = τ_v and I/I_v < 1). In these cases the quenching is static, meaning that it is limited by recombination processes which change the number of defects via the formation of non-luminescent complexes.²⁴ Therefore, for the defects reacting with CO₂ or H₂O, the excitation is hindered, as schematically represented in Fig. 5(c) for the specific case of the H₂O molecule. However, for the unreacted centers the emission efficiency remains the same as in a vacuum. The PL quenching observed in these cases is due to a decrease in the number of emitting defects, the effect remaining distinguishable throughout its extent. It is worth noting that, although H₂O and CO₂ are diametrically opposite in their features, being polar and apolar molecules, respectively, they influence the emitting centers in a similar way. The reversibility of the quenching and the immediate recovery of the vacuum conditions (Fig. 3) rule out a transformation of the defect through a chemical reaction with these species and indicates a weak interaction, likely due to the physisorption of such molecules at the defect sites. Due to these considerations, a polar defect is expected to be responsible for the structured PL. The deepening of this issue is out of the scope of the present work and needs specific investigations. In this respect, the systematic Stern–Volmer study should give useful information about the bi-molecular quenching constant and, in turn, the dipole moment of the emitting center. At this stage, this is just an insight that may allow the chance to gain more knowledge on the defect structure.

Since I/I_v ≠ τ/τ_v and τ/τ_v ≠ 1, in O₂ the quenching is neither purely dynamic nor purely static, but it is due to a combined collisional- and reaction-limited process. In this case the percentage of the defects reacting with the O₂ molecules can be also estimated. In fact, I/I_v gives the overall number of luminescent centers which are not quenched by O₂ molecules. It takes into account both the unreacted defects (D) and those centers which are not quenched by collisions (τ/τ_v), that is (I/I_v) = D(τ_O2/τ_v). By using the results reported in Table 2, it follows that D ∼ 0.34. This means that ∼66% of defects form non-luminescent complexes by reacting with the O₂ molecules. Also in this case, the reversibility of the quenching indicates a physisorption of such molecules at the defect sites.

Taking into account the distinction between the different defect–molecule interactions, quenching and recovery kinetics would be expected to exhibit different trends. However, as seen in Fig. 3, the same abrupt transitions are observed between vacuum–atmosphere and atmosphere–vacuum conditions and also between environments. This is due to the difference between the interactions and measurement timescales, the latter setting the lower limit for the kinetics investigations (tens of seconds). Therefore, the observations reported in the present study reflect a macroscopic overview of the phenomena. In this respect, reducing the spectra acquisition down to timescales that are comparable with the PL lifetime could give interesting insights into the microscopic dynamics of the processes.

Once the influence of each species is known, the study of the effects induced by species that give static or dynamic quenching is relevant to understand their influence on the phenomenology in complex atmospheres, such as air. In particular, it may be an additive process or, alternatively, one species could be more effective than another.

In summary, all the species under investigation give rise to the stable and reversible quenching of the structured PL, ranging from 20% to 60%. The process is dynamic in N₂, static in CO₂ and H₂O, and it is a combination of both in O₂. These findings highlight that, if the phenomenology is the same, the role of the quencher is crucial. In fact, the relative weight between the different processes, ultimately determined by the specific defect–molecule interaction, together with the distinguishable extent of the quenching effects, sets the PL selectivity with respect to the species. In a general sense, the knowledge of the kinetics underlying the quenching mechanisms is fundamental for the right interpretation of the observations and, ultimately, for the control and exploitation of such effects.

4 Conclusions

The exceptional structured emission arising in a vacuum from the surface defects of SiO₂ NPs is a system of choice to investigate the dynamics of molecule–defect interactions. In fact, both the homogeneous and sharp features, due to the disentanglement of the defects from the matrix, and the sensitivity to the ambient surroundings, make this emission like an antenna in an environment. The results have shown that the investigation of both the PL and lifetime in a controlled atmosphere is a powerful method to distinguish molecules, thus indicating a promising tool for sensing purposes. Moreover, this approach of investigation is remarkable in that it goes deep into the understanding of the causes of the quenching. In fact, these findings have pointed out that the mechanisms are not all the same; their origins are governed by the quantum efficiency of the emission processes in the specific atmospheres, in turn determining a static or dynamic quenching.

Acknowledgements

L. Spallino acknowledges the financial support provided by the Russian Foundation for Basic Research 2016/2018 (project No. 16-32-60063). A. F. Zatsepin is thankful for the partial financial support obtained from the Ministry of Education and Science of the Russian Federation (project No. 3.2016.2014/K). A special gratitude goes to the group of the Laboratory of Advanced Materials Physics (Palermo University) for their valuable and stimulating discussions. G. Napoli and G. Tricomi are acknowledged for their technical assistance.

References

1. C. Liu, Z. Zhao, R. Zhang, L. Yang, Z. Wang, J. Yang, H. Jiang, M. Han, B. Liu and Z. Zhang, J. Phys. Chem. C, 2015, 119, 8266.
2. F. Priolo, T. Gregorkiewicz, M. Galli and T. F. Krauss, Nat. Nanotechnol., 2014, 9, 19.
3. B. Zhou, B. Shi, D. Jin and X. Liu, Nat. Nanotechnol., 2015, 10, 924.
4. E. Rampazzo, L. Prodi, L. Petrizza and N. Zaccheroni, in Luminescent Silica Nanoparticles Featuring Collective Processes for Optical Imaging, ed. S. Sortino, Springer International Publishing, Cham, 2016, pp. 1–28.
5. M. Schäferling, Angew. Chem., Int. Ed., 2012, 51, 3532.
6. F. P. Zamborini, L. Bao and R. Dasari, Anal. Chem., 2011, 541.
7. L. Tarpani, D. Ruhlandt, L. Latterini, D. Haehnel, I. Gregor, J. Enderlein and A. I. Chizhik, Nano Lett., 2016, 16, 4312.
8. S. Bonacchi, D. Genovese, R. Juris, M. Montalti, L. Prodi, E. Rampazzo and N. Zaccheroni, Angew. Chem., Int. Ed., 2011, 50, 4056.
9. D. Genovese, S. Bonacchi, R. Juris, M. Montalti, L. Prodi, E. Rampazzo and N. Zaccheroni, Angew. Chem., Int. Ed., 2013, 52, 5965.
10. Y. F. Wang, J. Che, Y. Zheng, Y. Y. Zhao, F. Chen, S. B. Jin, N. Q. Gong, J. Xu, Z. B. Hu and X. J. Liang, J. Mater. Chem. B, 2015, 3, 8775.
11. Y. D. Glinka, S. H. Lin and Y. T. Chen, Appl. Phys. Lett., 1999, 75, 778.
12. Y. D. Glinka, S. H. Lin and Y. T. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 035404.
13. T. Uchino, N. Kurumoto and N. Sagawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 233203.
14. L. Vaccaro, A. Morana, V. Radzig and M. Cannas, J. Phys. Chem. C, 2011, 115, 19476.
15. C. Zhang and J. Lin, Chem. Soc. Rev., 2012, 41, 7938.
16. A. Rimola, D. Costa, M. Sodupe, J. Lambert and P. Ugliengo, Chem. Rev., 2013, 113, 4216.
17. L. Spallino, L. Vaccaro, S. Agnello and M. Cannas, J. Lumin., 2013, 138, 39.
18. S. Banerjee, S. Honkote and A. Datta, J. Phys. Chem. C, 2011, 115, 1576.
19. S. Banerjee, S. Maity and A. Datta, J. Phys. Chem. C, 2011, 115, 22804.
20. A. Anjiki and T. Uchino, J. Phys. Chem. C, 2012, 116, 15747.
21. C. M. Carbonaro, R. Corpino, P. C. Ricci, M. Salis and A. Anedda, J. Mater. Sci., 2013, 48, 4452.
22. C. M. Carbonaro, R. Corpino, P. C. Ricci, D. Chiriu and M. Salis, J. Phys. Chem. C, 2014, 118, 26219.
23. L. Spallino, L. Vaccaro, L. Sciortino, S. Agnello, G. Buscarino, M. Cannas and F. Gelardi, Phys. Chem. Chem. Phys., 2014, 16, 22028.
24. J. Lakowicz, Principles of Fluorescence Spectroscopy, Springer, New York, 2007.
25. L. Spallino, L. Vaccaro, M. Cannas and F. Gelardi, J. Phys.: Condens. Matter, 2015, 27, 365301.
26. A. Mebel, A. Zyubin, M. Hayashi and S. Lin, Thin Films Nanostruct., 2007, 34, 67.
27. Evonik Industries online catalog, http://corporate.evonik.com, 2010.
28. G. Vaccaro, S. Agnello, G. Buscarino and F. M. Gelardi, J. Phys. Chem. C, 2010, 114, 13991.
29. D. C. Johnston, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 184430.

---