Insight into the acidic group-induced nitration mechanism of 2-methyl-4,6-dihydroxypyrimidine (MDP) with nitronium†
Abstract
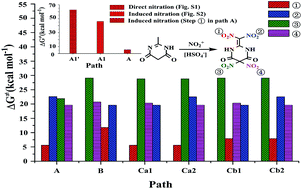
The strong desire for developing promising candidates of insensitive nitro energetic materials has spurred numerous attempts to discern the nitration details. The nitration mechanism of 2-methyl-4,6-dihydroxypyrimidine (MDP) with nitronium (NO2+) to form 2-dinitromethylene-5,5-dinitropyrimidine-4,6-dione is studied via DFT-B3LYP/6-311G(d,p) method. The possible nitration pathways are excavated and illustrated. Herein, a unique/incredible induction/enhancement of the co-existing acidic group of HSO4− to the targeted nitration is definitively proposed. The impact of the introduction order of four nitro groups (–NO2) on the title nitration is systematically demonstrated. It is suggested that the proposed induction of HSO4− may effectively promote/catalyze not only the NO2+ attack, but the H-transfer and H-abstraction as well, and thus dramatically decreases the activation free energy of the nitration system. Moreover, the NO2+ attack may be dynamically affected by the pre-introduced –NO2 and the resulted fluctuation of charge distribution in the pre-intermediates, which has been primarily supported via the calculated atomic charge, Coulomb attraction and Fukui function. It is indicated that the preferential dinitration on –CH3 with the induction of HSO4− (path A) is the most likely pathway. It is optimistically expected that the present study may provide a theoretical basis to the research and engineering tests of the title nitration, and promote the exploration of related insensitive energetic materials.

 Please wait while we load your content...
Please wait while we load your content...