A cyclometalated (C^C*) platinum(II) NHC complex decorated via different carboranes to tune the photodeactivation mechanism: a theoretical investigation

Abstract

Unveiling the photodeactivation mechanisms of transition metal complexes is crucial for designing high-efficiency phosphorescent materials. Herein, the photodeactivation mechanisms of cyclometalated (C^C*) platinum(II) N-heterocyclic carbene (NHC) complexes modified by carboranes were systematic study with the help of the density functional theory (DFT) and time-dependent density functional theory (TD-DFT). In order to illustrate the photodeactivation mechanisms, three vital photodeactivation processes, namely radiative decay process, temperature-independent nonradiative decay process and thermally activated nonradiative photodeactivation process, were taken into account. On the basis of calculated results, the emission wavelengths of the cyclometalated (C^C*) platinum(II) N-heterocyclic carbene (NHC) complex can be effectively tuned via the carborane-functionalized ligand structures. Meanwhile, compared with the original (NHC)Pt(II)(acac) complex, the radiative decay processes can be facilitated and the nonradiative decay processes can be managed via attaching distinct carboranes to the main ligand of the (NHC)Pt(II)(acac) complex, indicating that this is a feasible strategy for obtaining high-performance phosphorescence emitters.

---

Introduction

Transition metal complexes, as high-efficiency phosphorescence emitters doped into organic light-emitting diodes (OLEDs), have aroused extensive attention in both experiment and theory.^1–10 Therein, over the past decades, phosphorescent Pt(II) and Ir(III) complexes have been widely synthesized and designed. The internal quantum efficiency of Pt(II) and Ir(III) complexes can theoretically reach up to 100% via harvesting both the singlet and triplet excitons for emission due to the strong spin–orbital coupling (SOC) effect introduced by the heavy atom.^11–14 In addition, the photophysical properties and luminescence quantum yields of phosphorescent Pt(II) and Ir(III) complexes can be effectively tuned and improved via reasonably designing or modifying ligands, which were reported in many experimental and theoretical investigations.^4,15–19 The corresponding methods include the introduction of electron-withdrawing or electron-donating substituents, the change of the conjugated structures. Therefore, unquestionably, how to design and modify the ligand structures of Pt(II) and Ir(III) complexes to achieve excellent phosphorescent emitters become an extremely crucial problem in this area.

In general, compared with other coordinated ligands, the N-heterocyclic carbene (NHC) ligands can show some distinctive properties, including exceptionally strong σ-bonding and easily tunable electronic properties. Additionally, the strong ligand field of carbene can lift the energy of the metal-centered d–d excited state, leading to the increase the energy gap between the metal-centered d–d excited state and emissive excited state, which is beneficial for avoiding the nonradiative decay process and improving the phosphorescent quantum yield. Furthermore, the corresponding NHC-based phosphorescent materials are believed to have long operational lifetime, owing to the good stability of the metal–carbene bond. Accordingly, adopting the NHC as a cyclometalated ligand to coordinate with Pt is a sagacious strategy for obtaining the promising phosphorescent material with high emission quantum yield.^20–23 The emissive properties and phosphorescent quantum yields of NHC-based metal Pt complexes can be regulated and controlled via wisely modifying the ligand. Very recently, Thomas Strassner and coworkers reported a series of high-efficiency bidentate (NHC)Pt(acac) complexes with enlarging the π system.²⁴ On the basis of their investigation, they found the nonradiative processes of the bidentate (NHC)Pt(acac) complexes can be effectively suppressed via enlarging the phenyl ring at the backbone of the main ligand. In other words, the rigidity of bidentate (NHC)Pt(acac) complexes can be enhance by means of this method, which is desirable in designing the phosphorescent materials.^25–28 Hence, these (NHC)Pt(acac) complexes with enlarging the π-conjugation combine with the modification of substituent may be an efficient strategy to achieve high-efficiency phosphorescent emitters.

Due to the three-dimensional bulky geometric cage structures, the icosahedral carboranes, which include 1,2-, 1,7- and 1,12-C₂B₁₀H₁₂, that is, o-, m-, p-carborane, can exhibit unique electronic effects and thermal stability. For the three isomers, the carbon atoms show distinct electron-withdrawing properties, which obey the order o > m > p. Therein, the 1,2-C₂B₁₀H₁₂ (o-carborane) not only has the strongest electron-withdrawing property on the carbon atom, but also possesses an extraordinary C–C bond. As the variability and rotational mobility of the C–C bond in solution, the o-carborane can result in intensively change of the emission properties of the transition metal complexes.^25,29–35 In addition, the carboranes cage, as bulky groups, will strongly hinder the intermolecular interaction in solution and condensed phase, facilitating minimum of emission quenching introduced by aggregation.^36–41 Owing to these special virtues of carboranes, they have aroused popular interest as a reliable method to tune the phosphorescence of transition metal complexes in recent years. As the previous reports shown, the carboranes, which are added into the ligand structures of complexes, can cause the alteration of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) energy levels, leading to tuning the emissive wavelengths and phosphorescent quantum yields.^42–44 To sum up, the carboranes used to tune the emissive property and phosphorescent quantum yield offer a useful strategy to design and obtain high-performance phosphorescent emitters, which are summarized in the review reported by Zhao and coworkers.⁴⁵ Compared with the Ir(III) complexes, the carboranes-functionalized ligands are still in its infancy for the Pt(II) complexes and only o-carborane has been applied as the chelating unit of the cyclometalated ligand. Accordingly, undoubtedly, the carboranes-functionalized ligand structures should be designed to investigate the influence on the emissive properties and phosphorescent quantum yields of Pt(II) complexes.

In this paper, the structure–property relationship was unveiled by means of density functional theory (DFT) and time-dependent density functional theory (TD-DFT) to illustrate influence of carboranes on the emissive wavelengths and photodeactivation mechanisms of (NHC)Pt(acac) complexes. We hope this detailed exploration can provide some useful and valuable information for facilitating and improving the progress of high-performance transition metal complexes doped into OLED as phosphorescent emitters.

Computational details

In this system, the non-spin-polarized and spin-polarized DFT methods were performed to optimize the geometries of ground states and triplet excited states (spin multiplicity is 3) without consideration of the symmetry constraints. The ‘spin-unrestricted’ or ‘spin-polarized’ indicates that the calculation will be performed using different orbitals for different spins. The ‘spin-restricted’ or ‘non-spin-polarized’ uses the same orbitals for alpha and beta spins. Herein, the complex 1 is chosen to confirm the computed method because it is an experiment complex with the available experimental values. Therefore, the computed results can better compare to the experimental measurements, demonstrating the reliability of calculated method. On the basis of previous study,⁴⁶ the PBE0 functional⁴⁷ was the suitable functional for the geometric optimization of experimental molecule. Therefore, the PBE0 functional was also employed to obtain the optimized geometries of ground states and triplet excited states for all the studied complexes in this system. Additionally, in order to explore the temperature-dependent nonradiative decay processes, the geometries of states involved in the potential energy surface curves, including the metal centered d–d excited states (MC), transition states (TS) between T₁ and MC states, and minimal energy crossing points (MECP), were calculated by PBE0 method. Therein, according to the methodology proposed by Persson's work,^48,49 the electron configurations of ³MC d–d states were optimized. The MECPs were obtained via using the sobMECP program, which was a modified version of Harvey's MECP program.^50,51 Based on the optimized geometries, the frequency computations were carried out to ensure the reliability of these obtained states. In addition, intrinsic reaction coordinates (IRC) were also calculated to illustrate the reasonability of transition states. Stability calculations were carried out to verify that the all wave functions are stable. Besides, the Huang–Rhys factors (S_j) for all normal modes were obtained by means of Franck–Condon calculation via “freq = fc, prtmat = 12”. According these parameters, the Duschinsky matrix and shift vector (K_j) can be printed, which are used to calculate the Huang–Rhys factors based on the equation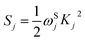 . Where the K_j is the shift vector of the jth normal mode and ω^S_j refers to the frequency of ground state of the jth normal mode. A detailed theoretical background is shown in the document titled “Vibrationally-resolved electronic spectra in GAUSSIAN 09”.

The all above mentioned computations were achieved via using the Gaussian 09 quantum chemical program package.⁵² The LANL2DZ basis set⁵³ was employed for heavy atom Pt, and the light atoms (C, H, O, N, B, F) were described by 6-31G(d) basis set.⁵⁴

With the purpose of exploring the radiative decay processes, the TD-DFT/PBE0 including SOC calculations with the zero-order regular approximation (ZORA) Hamiltonian^55,56 were performed on the T₁ optimized geometries to obtain the radiative decay rate constants and zero-point splitting (ZFS) parameters, which were implemented in the ADF2014.04 program package.^57–59 The all electron TZP and DZP basis sets were used for transition metal atom and non-metal atoms, respectively.

Results and discussion

Optimized ground state and the lowest-lying triplet excited state structures

In this paper, in order to explore the role of carboranes, three complexes, namely, 1a, 1b and 1c, respectively, are designed via combining the rigidity of (NHC)Pt(acac) complex and the unique electronic and steric properties of carboranes. The corresponding chemical structures are plotted in Fig. 1 (group 1). Moreover, the electron-donating (tert-butyl) and electron-withdrawing (trifluoromethyl) groups are applied to replace the H atoms on carbon atoms of carboranes, which are utilized to tune the phosphorescence of (NHC)Pt(acac) complexes. Therefore, the group 2 and group 3 include molecule 2a, 2b, 2c, 3a, 3b and 3c are designed to systemically explore the role of substituted carboranes, which are shown in Fig. 1. The optimized geometry of complex 1 is shown in Fig. 2, along with labelled key atoms. The main structural parameters of all studied complexes are collected in Table S1.†

Fig. 1 Chemical structures of investigated platinum(II) complexes with carborane substitution.

Fig. 2 Optimized geometric structure of investigated 1 complex in the ground state at the PBE0/LANL2DZ level.

As shown in Table S1,† the metal related bond lengths of all investigated complexes are nearly identical at S₀ states, which are not more than 0.014 angstrom. Therein, the metal related bonds include Pt1–C1, Pt1–C3, Pt1–O1 and Pt1–O2. Additionally, the bond angles, namely, O1–Pt1–O2 and C1–Pt1–C3, only change 0.4 and 0.1 degree, respectively. Furthermore, the dihedral angles C2–N1–C1–Pt1 and N1–C1–Pt1–O1 present the almost the same trend, respectively. According to the calculated results, it is indicated that the carborane substituents can cause slight effects on the geometry structures for all investigated platinum(II) complexes at S₀ states.

The T₁ excited state, as an important role in photodeactivation process, determines the emissive property and phosphorescent quantum yield. Moreover, the structure distortion between T₁ excited state and S₀ state not only influences the temperature-independent nonradiative decay process, but also affects the spectrum bandwidth and colour purity. Therefore, it is necessary to explore and optimize the geometries of T₁ states of these studied complexes. The computed main parameters, i.e. metal-related bond lengths, bond angles, and dihedral angles of all investigated complexes at T₁ states are summarized in Table S1.† However, based on these calculated values, the structure distortions cannot be well illustrated. In order to solve this problem, the RMSD (root mean square displacement/deviation) valves are computed by means of VMD software⁶⁰ and the results are shown in Fig. S1.† Fig. S1† can clearly reflect the structural distortion during the transition of S₀ to T₁ excited states. On the basis of the values shown in Fig. S1,† the complexes 2a and 3a experience distinct structure distortion and corresponding RMSD values are 0.203 and 0.102, respectively. For the 2a and 3a, rotation of tert-butyl and trifluoromethyl in the T₁ excited states leads to the geometric distortion. According to the energy-gap,⁶¹ the distinct structural distortion can enhance the electron-vibrational coupling constant (Huang–Rhys factor) of the T₁ and S₀ states, strongly facilitating the nonradiative decay process. Thus, the complexes 2a and 3a may possess the largest nonradiative decay constants among the all studied complexes. Naively, in films/solution, it can be hypothesized that the carborane will have various conformations, which will eliminate such rotation, leading to decrease the electron-vibrational coupling constant (Huang–Rhys factor).

Phosphorescent properties and Huang–Rhys factors

In order to explore the emission properties of all studied complexes in detail, the emission wavelengths were calculated, together with the maximal Huang–Rhys factors (S_max), and corresponding values are summarized in Table 1. The Huang–Rhys factor, as an important parameter, can reflect the structural change between excited state and the ground state, which depends on the degree of overlap between two vibrational wave functions of initial and final states. When the Huang–Rhys factor equal 0, it is indicated that the geometries between the excited state and ground state are same equilibrium, resulting in only a sharp peak, which corresponds to the 0–0 transition. Actually, with an increase the S-value, the vibronic progression is observed. Because the intensity of all the vibronic progressions can affect the overall emission bandwidth, the small Huang–Rhys factor implies that the spectrum has narrow bandwidth and higher colour purity. In addition, if the maximum Huang–Rhys factor is smaller than 1, the 0–0 transition possesses the highest intensity. Therefore, when the maximum Huang–Rhys factor is smaller than 1, the maximum absorption or emission peaks are corresponding to 0–0 transition due to the significant vibrational overlaps between the two states. While, when the maximum Huang–Rhys factor is larger than 1, the maximum absorption or emission peaks are corresponding to vertical transition because vibrational overlap between the ground vibrational state of the T₁ would be with a higher vibrational state of the ground state. In a nutshell, the Huang–Rhys factor can be regarded as an indicator, illustrating the relationship between the geometric change and spectrum.

Table 1 Calculated lowest-lying triplet energy values for all the investigated complexes together with the maximal Huang–Rhys factors (S_max)

	λ (nm)	Smax	Exp.^a (nm)
a Available experimental values from ref. 24.
1	488	0.58	476
1a	498	0.56
1b	498	0.57
1c	497	0.58
2a	554	—
2b	498	0.57
2c	496	0.61
3a	550	—
3b	500	0.56
3c	498	0.57

---

According to the Table 1, the maximum Huang–Rhys factors of complexes 1, 1a, 1b, 1c, 2b, 2c, 3b and 3c are 0.58, 0.56, 0.57, 0.58, 0.57, 0.61, 0.56 and 0.57, respectively. Meanwhile, for complexes 2a and 3a, they possess the large geometric distortion from S₀ to T₁ states owing to the rotation of tert-butyl and trifluoromethyl (2a and 3a). Therefore, in this case, the Franck–Condon calculations used to obtain the Huang–Rhys factors should be unreliable and the corresponding Duschinsky matrixes are rather diffuse. Additionally, a large structural distortion reflects a large displacement between the two potential minima, and clearly, the vibrational overlap between the ground vibrational state of the T₁ state would be with a higher vibrational state of the ground state. Therefore, in such a case, the peak maximum would not be 0–0 transition. Hence, the related maximum Huang–Rhys factors of 2a and 3a are not collected in Table 1. These computed results can clearly illustrate the complexes 2a and 3a exhibit larger geometric distortion between T₁ and S₀ states than other studied complexes, which are consistent with the RMSD values. Additionally, on the basis of the values of maximum Huang–Rhys factors, the emission wavelengths of complexes 1, 1a, 1b, 1c, 2b, 2c, 3b, 3c and 2a, 3a are corresponding to 0–0 transition and vertical transition of T₁ → S₀, respectively. As shown in Table 1, the calculated emission wavelengths of all studied complexes are 488, 498, 498, 497, 554, 498, 496, 550, 500 and 498 nm, respectively. Therein, the computed emission wavelength of complex 1 is in close proximity to the experimental value, demonstrating that the calculated method applied to predict emission wavelength is reasonable and reliable. Interestingly, compared with the complex 1, the emission wavelengths of complexes 1a, 1b, 1c, 2b, 2c, 3b and 3c with strong rigidity are almost invariable, which only red-shift around 12 nm. In addition, for complexes 2a and 3a, the emission wavelengths exhibit obvious red-shift and the corresponding values are 66 and 62. On the basis of these computed emission wavelengths, we can propose a conclusion, that is, the variety of emission wavelength depends on the structural distortion between T₁ and S₀ state. In another word, the emission wavelengths of (NHC)Pt(II)(acac) can be effectively tuned via attaching the carboranes with different electronic properties to the cyclometalated (C^C*) ligand at least in gas. Surely, in films/solution, the variety of emission wavelength maybe slight owing to eliminate the rotation of carboranes.

With the purpose of exploring the transition character, the computation of the natural transition orbitals (NTOs) was preformed based on the optimized geometries of T₁ excited states for all complexes. The NTOs plots with the highest eigenvalues (λ_i) close to 1 are depicted in Fig. S3.† The unoccupied NTOs are represented as “electron” transition orbitals, while the occupied NTOs are denoted as “hole” transition orbitals. As shown in Fig. S3,† for the investigated complexes, NTO hole and NTO electron are mainly distributed on the main ligands which have two phenyl cycles, thus, the transition natures of these complexes can be assigned to intraligand charge transfer (ILCT). Here, in order to quantitatively evaluate the ³MLCT contribution, the molecular orbital (MO) compositions of 5d (Pt) in the hole–electron pairs of NTOs involved in emitting excited states are computed and listed in Table S2.† For all complexes with carboranes, their ³MLCT compositions in the electron transition of the T₁ state only increased slightly as compared to 1. This is beneficial for facilitating the radiative decay process and implying the complexes with carboranes may have slightly strong SOC and phosphorescence quantum efficiency.

Phosphorescent quantum efficiency

In general, for the transition metal complexes, the phosphorescent quantum yields dependent on the radiative decay rate constants and nonradiative decay rate constants. Therefore, the phosphorescent quantum yields can be calculated as formula (1).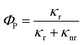where the κ_r is the radiative decay rate constant and the κ_nr refers to the nonradiative decay rate constant. According to eqn (1), in order to achieve large phosphorescent quantum yield, the radiative decay process must fast and the nonradiative decay process must slow.

Radiative decay rate constants

According to previous report,^{6,9,10,46,62,63} TD-DFT including the spin–orbital coupling calculations with ZORA Hamiltonian can reproduce the phosphorescent lifetimes and radiative decay rate constants of the transition metal complexes. The computed the ZFS parameters, radiative decay rate constants and the available experimental value are collected in Table 2. The difference between the experimental and theoretical value is acceptable, which is closely related with the circumstance used for obtaining the relative decay rate constant.^63–65 The ZFS parameter, as an important indicator that has closely relationship with ³MLCT contribution in the emission state, can predict the magnitude of radiative rate constants (κ_r).^66,67 As displayed in Table 2, the ZFS parameters of 1, 1a–1c, 2a–2c and 3a–3c are 1.94, 1.45, 1.53, 2.18, 1.61, 1.53, 2.18, 1.61, 1.53, 1.61 cm⁻¹, respectively. According to the calculated ZFS parameters, the complex 1c and 2c have the largest values than the corresponding ones of other complexes, suggesting that the complex 1c and 2c may possess the largest radiative rate constants among the all studied complexes. Seen from Table 2, the radiative rate constants of all investigated complexes are 2.01 × 10³, 4.37 × 10³, 3.37 × 10³, 6.29 × 10³, 3.29 × 10³, 3.53 × 10³, 3.57 × 10³, 3.03 × 10³, 3.73 × 10³, 3.55 × 10³ s⁻¹, respectively, which are almost identical with the tendency of the ZFS parameters, indicating that the ZFS parameters can well predict the radiative rate constants at least for 1c. Seen from the values of computed radiative decay rate constant, we can obtain some meaningful conclusions used for understanding the influence of carboranes on rigid (NHC)Pt(II)(acac) complex. Firstly, the carboranes-functionalized main ligand of (NHC)Pt(II)(acac) complex can cause increase of radiative decay rate constant, which is beneficial for enhancing the phosphorescent quantum yield. Secondly, compared with the complexes 1a and 1c, the radiative decay rate constants of 2a, 3a, 2c and 3c are decrease, indicating that o-carborane and p-carborane modified with trifluoromethyl or tert-butyl groups have less perfect performance. In contrary, the radiative decay rate constants of 2b and 3b are increase, indicating m-carborane modified with trifluoromethyl or tert-butyl groups can facilitate the radiative decay processes.

Table 2 ZFS parameters (cm⁻¹) and radiative rate constants κ_r (s⁻¹) for the all complexes together with the available experimental values

Complex	ZFS	κr	κr (exp)^a	Φ^a
a Available experimental values from ref. 24.
1	1.94	2.01 × 10^3	5.50 × 10^3	0.58
1a	1.45	4.37 × 10^3
1b	1.53	3.37 × 10^3
1c	2.18	6.29 × 10^3
2a	1.61	3.29 × 10^3
2b	1.53	3.53 × 10^3
2c	2.18	3.57 × 10^3
3a	1.61	3.03 × 10^3
3b	1.53	3.73 × 10^3
3c	1.61	3.55 × 10^3

---

In order to further elaborate radiative decay processes and explore the factors determined the radiative rate, the transition dipole moments, singlet–triplet splitting energies and SOC matrix elements of all complexes are calculated based on the optimized the lowest-lying geometric structures, which are listed in Table S3.† As shown in Table S3,† for all designed complex, they possess the larger SOC matrix elements than complex 1, indicating that the spin–orbital coupling is more effective in all designed complexes than complex 1. For all designed complexes, the strong spin–orbital coupling can be attributed to the more ³MLCT character in T₁ excited state, which can be seen from the spin density and NTOs plots (Fig. S2 and Table S2†). In the nutshell, the effective spin–orbital coupling between T₁ excited state and the singlet excited states leads to the largest radiative decay rate constant.

Nonradiative decay rate constants

Temperature-independent nonradiative decay processes. According to energy-gap law,⁶¹ the temperature-independent nonradiative decay rate constant can be estimated via two factors, that is, energy gap and geometric distortion between the emission state and ground state. In addition, the SOC matrix element between the emission state and ground state is also calculated to illustrate the temperature-independent nonradiative decay process. The corresponding values are collected in Table 3. On the basis of computed values shown in Table 3, the complexes 2a and 3a possess the largest maximum Huang–Rhys factors and the SOC matrix elements between the emission state and ground state. Meanwhile, 2a and 3a possess the smaller energy difference between S₀ and T₁ state compared with those of other studied complexes (shown in Table 1), based on the energy-gap law, facilitating the temperature-independent nonradiative decay processes. Therefore, depend on the calculated results, the conclusion can be drawn that complexes 2a and 3a may exhibit the largest temperature-independent nonradiative decay rate constants among all investigated complexes. However, the simple energy-gap law is insufficient to describe the global nonradiative decay processes. Hence, temperature-dependent nonradiative decay processes of all complexes are explored to completely elaborate the nonradiative decay processes.

Table 3 The SOC matrix elements 〈T₁|H_SOC|S₀〉 (in cm⁻¹), the maximum Huang–Rhys factor (S_max) of the normal modes and the nonradiative decay rate constants for all the investigated complexes

	〈T1|HSOC|S0〉	Smax	κnr (exp.)
1	5.87	0.58	3.90 × 10^3
1a	9.63	0.56
1b	9.12	0.57
1c	9.32	0.58
2a	11.14	—
2b	8.96	0.57
2c	9.20	0.61
3a	11.13	—
3b	9.27	0.56
3c	9.25	0.57

---

Temperature-dependent nonradiative decay processes. Because the simple energy-gap law is insufficient for elaborating the nonradiative decay processes, thus the temperature-dependent nonradiative decay processes of all complexes are explored in this system, including the T₁, ³MC, TS[T₁/³MC] and MECP[³MC/S₀], were calculated to completely unveil the nonradiative decay processes. Therein, the ³MC state plays a significant role during the photodeactivation process because ³MC state from emission state via thermal population can cause an effective temperature-dependent nonradiative decay pathway. Therefore, a detailed and cleared picture of ³MC state formation is curial for well understanding the emissive properties and luminescence efficiencies of the transition metal complexes. In general, the ³MC state possesses two distinctive characters. One respect, the spin density of complex is mainly distributed on the transition metal. Another aspect, the complex adopts distorted geometric structure in the ³MC state. As shown in Fig. S5,† for all investigated complexes, the computed spin densities are predominantly located on transition metal and there are distinct structural distortions caused by acac ligand, demonstrating that the obtained ³MC states are reliable. Furthermore, in order to illustrate the ³MC → T₁ conversion, the TS[T₁/³MC], which connects the emission state and ³MC state, has been investigated as well. Compared with the emission states the transition states have more spin densities distributed on metal atom, which are plotted in Fig. S4.† An endeavor is an attempt to achieve the transition state of complex 3a, unfortunately, it is not successful. However, this shortcoming can cause slight effect on the conclusion proposed in this paper (see below). Once the formation of ³MC state via thermal population, it has two different patterns of transformation, including return to the emission state and jump into the minimal energy crossing point (MECP) between the ³MC and ground state (¹GS) potential energy surfaces. When the system can provide enough energy for reaching the ³MC state and the ³MC state is close to MECP in energy, the radiative route, namely, ³MC state returns back to the ground state, will rapidly occur. For all complexes, the computed geometries and spin densities of MECP are depicted in Fig. S6.† As shown in Fig. S6,† the all complexes have distorted geometric structures and the spin densities are predominantly distributed on the Pt metal, which are similar to those of the ³MC states, indicating that the minimal energy crossing points possess evident metal-centered character.

Once the geometries and energies of these triplet excited states are obtained by means of DFT method, the schematic potential energy profiles of the deactivation pathways for the studied complexes can be completely constructed, which consist of the minimal energies of the triplet excited states and the reaction coordinates, that is, the average Pt-L (L denotes as coordination atoms) bond lengths and are displayed in Fig. 3. On the basis of above-mentioned studies in phosphorescent properties, the emission states of this investigated system are T₁ excited states, which obey the Kasha rule. Meanwhile, based on the optimized geometries of the T₁ excited states, the radiative decay processes and the temperature-independent nonradiative processes are detailed explored (see above). Accordingly, herein, only the thermally activated nonradiative photodeactivation mechanisms are amply elaborated with the help of potential energy profiles displayed in Fig. 3. As plotted in Fig. 3, for the temperature-dependent nonradiative processes in all studied complexes, there are two rate-determining steps, including the population of the ³MC via TS and the relative energy between the ³MC and ¹GS/³MC surface crossing point. In addition, the detailed structural parameters are shown in Fig. S7–S16.† For all complexes in this system, the energy differences between the ³MC and MECP are 2.6, 2.5, 2.6, 2.6, 1.7, 2.6, 2.7, 1.7, 2.5 and 2.6 kcal mol⁻¹, demonstrating that the carboranes can cause slight effect on the second rate-determining step. However, for the first rate-determining step, the carboranes and modified carboranes-functionalized main ligand of (NHC)Pt(II)(acac) complex can elevate the activation energy barriers, implying that the carboranes and modified carboranes are beneficial for averting the temperature-dependent nonradiative processes. Among these complexes, the energy barrier of 2a is 16.9 kcal mol⁻¹, which increases 4.8 kcal mol⁻¹ in energy compared to that of 1.

Fig. 3 Schematic potential energy profiles of the deactivation pathways for the studied complexes.

Conclusions

The density functional theory (DFT) and time-dependent density functional theory (TD-DFT) have been successfully employed to unveil the photodeactivation mechanism of cyclometalated (C^C*) platinum(II) NHC complexes functionalized by distinct carboranes, including the radiative decay processes and the nonradiative decay processes. According to the calculated results, we can conclude that the molecular rigidity and emission wavelength can be effectively tuned via adding the carboranes on the main ligand of (NHC)Pt(II)(acac) complex. We also show that the radiative decay process can be facilitated via attaching the distinct carboranes to main ligand of (NHC)Pt(II)(acac) complex. In addition, the o-, m-, p-carbrones and o-, m-, p-carbrones substituted via electron-donating or electron-withdrawing groups, as effective tool, can functionally tune the thermally activated nonradiative photodeactivation mechanisms.

In summary, the photodeactivation mechanism of (NHC)Pt(II)(acac) complex can be controlled via modifying the main ligand with functionalized carboranes. For all complexes, they exhibit larger radiative decay rate constants than that of (NHC)Pt(II)(acac) complex. However, for 2a and 3a, they show larger nonradiative decay rate constants, which is harmful for phosphorescent quantum yields. Consequently, this defect may inevitably hinder they become the most promising phosphorescent materials among the studied complexes.

We hope the computed results can provide some useful information for designing highly efficient Pt(II) complexes.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 21573030), the Chongqing Science & Technology Commission, China (Grant No. CSTC2013JCYJA50028), and the Scientific Research Foundation of Chongqing University of Arts and Sciences (R2013CJ03). The calculations were performed at the Supercomputing Centre of Chinese Academy of Sciences.

Notes and references

1. J. Feldman, G. D. Vo, C. D. McLaren, T. C. Gehret, K.-H. Park, J. S. Meth, W. J. Marshall, J. Buriak, L. M. Bryman and K. D. Dobbs, Organometallics, 2015, 34, 3665–3669.
2. P. Tao, W. L. Li, J. Zhang, S. Guo, Q. Zhao, H. Wang, B. Wei, S. J. Liu, X. H. Zhou and Q. Yu, Adv. Funct. Mater., 2015, 26, 881–894.
3. S. Zhang, J. C. Xia, Z. G. Wu, G. Z. Lu, Y. Zhao and Y. X. Zheng, Eur. J. Inorg. Chem., 2016, 2016, 2556–2561.
4. P. K. Chow, G. Cheng, G. S. M. Tong, W. P. To, W. L. Kwong, K. H. Low, C. C. Kwok, C. Ma and C. M. Che, Angew. Chem., 2015, 127, 2112–2117.
5. M. Bachmann, D. Suter, O. Blacque and K. Venkatesan, Inorg. Chem., 2016, 55, 4733–4745.
6. Y. Luo, Y. Xu, L. Tian, W. Zhang, M. Li and W. Shen, Inorg. Chim. Acta, 2015, 435, 109–116.
7. Y. Wu, G.-G. Shan, H.-B. Li, S.-X. Wu, X.-Y. Ren, Y. Geng and Z.-M. Su, Phys. Chem. Chem. Phys., 2015, 17, 4771–4771.
8. Y. Li, L. Y. Zou, A. M. Ren, M. S. Ma and J. X. Fan, Chem.–Eur. J., 2014, 20, 4671–4680.
9. W. Zhang, Y. Luo, Y. Xu, L. Tian, M. Li, R. He and W. Shen, Dalton Trans., 2015, 44, 18130–18137.
10. Y. Luo, Y. Xu, W. Zhang, M. Li, R. He and W. Shen, ChemPhysChem, 2016, 17, 69–77.
11. M. Baldo, S. Lamansky, P. Burrows, M. Thompson and S. Forrest, ApPhL, 1999, vol. 75, pp. 4–6.
12. C. Adachi, M. A. Baldo, M. E. Thompson and S. R. Forrest, J. Appl. Phys., 2001, 90, 5048–5051.
13. M. Baldo, D. O'brien, Y. You, A. Shoustikov, S. Sibley, M. Thompson and S. Forrest, Nature, 1998, 395, 151–154.
14. Y. Sun, N. C. Giebink, H. Kanno, B. Ma, M. E. Thompson and S. R. Forrest, Nature, 2006, 440, 908–912.
15. X. Zhang, A. M. Wright, N. J. DeYonker, T. K. Hollis, N. I. Hammer, C. E. Webster and E. J. Valente, Organometallics, 2012, 31, 1664–1672.
16. E. Baranoff, S. Fantacci, F. De Angelis, X. Zhang, R. Scopelliti, M. Grätzel and M. K. Nazeeruddin, Inorg. Chem., 2010, 50, 451–462.
17. T. Karatsu, M. Takahashi, S. Yagai and A. Kitamura, Inorg. Chem., 2013, 52, 12338–12350.
18. J. Zhao, Y. Yu, X. Yang, X. Yan, H. Zhang, X. Xu, G. Zhou, Z. Wu, Y. Ren and W.-Y. Wong, ACS Appl. Mater. Interfaces, 2015, 7, 24703–24714.
19. Y. Liu, X. Sun, Y. Wang and Z. Wu, Dalton Trans., 2014, 43, 11915–11924.
20. Z. M. Hudson, C. Sun, M. G. Helander, Y.-L. Chang, Z.-H. Lu and S. Wang, J. Am. Chem. Soc., 2012, 134, 13930–13933.
21. Y. Unger, D. Meyer, O. Molt, C. Schildknecht, I. Münster, G. Wagenblast and T. Strassner, Angew. Chem., Int. Ed., 2010, 49, 10214–10216.
22. A. Tronnier, A. Poethig, E. Herdtweck and T. Strassner, Organometallics, 2014, 33, 898–908.
23. A. I. Solomatina, D. Krupenya, V. V. Gurzhiy, I. Zlatkin, A. P. Pushkarev, M. N. Bochkarev, N. A. Besley, E. Bichoutskaia and S. P. Tunik, Dalton Trans., 2015, 44, 7152–7162.
24. A. Tronnier, A. Pöthig, S. Metz, G. Wagenblast, I. Münster and T. Strassner, Inorg. Chem., 2014, 53, 6346–6356.
25. A. M. Prokhorov, T. Hofbeck, R. Czerwieniec, A. F. Suleymanova, D. N. Kozhevnikov and H. Yersin, J. Am. Chem. Soc., 2014, 136, 9637–9642.
26. G. S. M. Tong and C. M. Che, Chem.–Eur. J., 2009, 15, 7225–7237.
27. J. A. Treadway, B. Loeb, R. Lopez, P. A. Anderson, F. R. Keene and T. J. Meyer, Inorg. Chem., 1996, 35, 2242–2246.
28. G. S. M. Tong, K. T. Chan, X. Chang and C.-M. Che, Chem. Sci., 2015, 6, 3026–3037.
29. A. Weller, Nat. Chem., 2011, 3, 577–578.
30. B. P. Dash, R. Satapathy, E. R. Gaillard, J. A. Maguire and N. S. Hosmane, J. Am. Chem. Soc., 2010, 132, 6578–6587.
31. A. Ferrer-Ugalde, A. González-Campo, C. Viñas, J. Rodríguez-Romero, R. Santillan, N. Farfán, R. Sillanpää, A. Sousa-Pedrares, R. Núñez and F. Teixidor, Chem.–Eur. J., 2014, 20, 9940–9951.
32. J. Guo, D. Liu, J. Zhang, J. Zhang, Q. Miao and Z. Xie, Chem. Commun., 2015, 51, 12004–12007.
33. C. Tang and Z. Xie, Angew. Chem., Int. Ed., 2015, 54, 7662–7665.
34. L. Zhu, W. Lv, S. Liu, H. Yan, Q. Zhao and W. Huang, Chem. Commun., 2013, 49, 10638–10640.
35. K.-R. Wee, Y.-J. Cho, S. Jeong, S. Kwon, J.-D. Lee, I.-H. Suh and S. O. Kang, J. Am. Chem. Soc., 2012, 134, 17982–17990.
36. S. J. Farley, D. L. Rochester, A. L. Thompson, J. A. Howard and J. G. Williams, Inorg. Chem., 2005, 44, 9690–9703.
37. C. Shi, H. Sun, X. Tang, W. Lv, H. Yan, Q. Zhao, J. Wang and W. Huang, Angew. Chem., 2013, 125, 13676–13680.
38. L. Zhu, X. Tang, Q. Yu, W. Lv, H. Yan, Q. Zhao and W. Huang, Chem.–Eur. J., 2015, 21, 4721–4730.
39. K. Kokado and Y. Chujo, J. Org. Chem., 2010, 76, 316–319.
40. H. Naito, Y. Morisaki and Y. Chujo, Angew. Chem., Int. Ed., 2015, 54, 5084–5087.
41. A. Ferrer-Ugalde, E. J. Juárez-Pérez, F. Teixidor, C. Viñas, R. Sillanpää, E. Pérez-Inestrosa and R. Núñez, Chem.–Eur. J., 2012, 18, 544–553.
42. C. Shi, H. Sun, Q. Jiang, Q. Zhao, J. Wang, W. Huang and H. Yan, Chem. Commun., 2013, 49, 4746–4748.
43. Y. H. Lee, J. Park, S. J. Jo, M. Kim, J. Lee, S. U. Lee and M. H. Lee, Chem.–Eur. J., 2015, 21, 2052–2061.
44. T. Kim, H. Kim, K. M. Lee, Y. S. Lee and M. H. Lee, Inorg. Chem., 2012, 52, 160–168.
45. X. Li, H. Yan and Q. Zhao, Chem.–Eur. J., 2016, 22, 1888–1898.
46. Y. Luo, Y. Xu, W. Zhang, W. Li, M. Li, R. He and W. Shen, J. Phys. Chem. C, 2016, 120, 3462–3471.
47. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
48. M. Abrahamsson, M. J. Lundqvist, H. Wolpher, O. Johansson, L. Eriksson, J. Bergquist, T. Rasmussen, H.-C. Becker, L. Hammarström and P.-O. Norrby, Inorg. Chem., 2008, 47, 3540–3548.
49. T. Bark and R. P. Thummel, Inorg. Chem., 2005, 44, 8733–8739.
50. J. N. Harvey and M. Aschi, Phys. Chem. Chem. Phys., 1999, 1, 5555–5563.
51. J. N. Harvey, M. Aschi, H. Schwarz and W. Koch, Theor. Chem. Acc., 1998, 99, 95–99.
52. M. Frisch, T. G. Wrucks, H. B. Schlegel, et al., Gaussian 09, Gaussian, Inc., Wallingford, CT, 2009.
53. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310.
54. P. Hariharan and J. A. Pople, Mol. Phys., 1974, 27, 209–214.
55. J. Snijders, E. Baerends and P. Ros, Mol. Phys., 1979, 38, 1909–1929.
56. E. Van Lenthe, J. Snijders and E. Baerends, J. Chem. Phys., 1996, 105, 6505–6516.
57. G. Te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
58. C. F. Guerra, J. Snijders, G. Te Velde and E. Baerends, Theor. Chem. Acc., 1998, 99, 391–403.
59. E. J. Baerends, T. Ziegler and J. Autschbach, et al., ADF2014, SCM, Amsterdam, year, http://www.scm.com.
60. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
61. J. S. Wilson, N. Chawdhury, M. R. Al-Mandhary, M. Younus, M. S. Khan, P. R. Raithby, A. Köhler and R. H. Friend, J. Am. Chem. Soc., 2001, 123, 9412–9417.
62. Y. Liu, X. Sun, Y. Wang and Z. Wu, Dalton Trans., 2014, 43, 11915–11924.
63. K. Mori, T. P. Goumans, L. E. Van and F. Wang, Phys. Chem. Chem. Phys., 2014, 16, 14523–14530.
64. Y. Wu, G. G. Shan, H. B. Li, S. X. Wu, X. Y. Ren, Y. Geng and Z. M. Su, Phys. Chem. Chem. Phys., 2015, 17, 2438–2446.
65. T. T. Feng, F. Q. Bai, L. M. Xie, Y. Tang and H. X. Zhang, RSC Adv., 2016, 6, 11648–11656.
66. H. Yersin, W. Humbs and J. Strasser, in Electronic and Vibronic Spectra of Transition Metal Complexes II, Springer, 1997, pp. 153–249.
67. H. Yersin, W. Humbs and J. Strasser, Coord. Chem. Rev., 1997, 159, 325–358.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra18631a

---